A Fuzzy Virtual Actuator for Automated Guided Vehicles
Abstract
:1. Introduction
How can a control and diagnosis subsystem for an AGV be developed, which realizes a fuzzy virtual actuator that uses the information of residuals created with an appropriate analytical model of the AGV and combines this information with expert knowledge or experimental data in order to increase the fault-tolerance of the AGV.
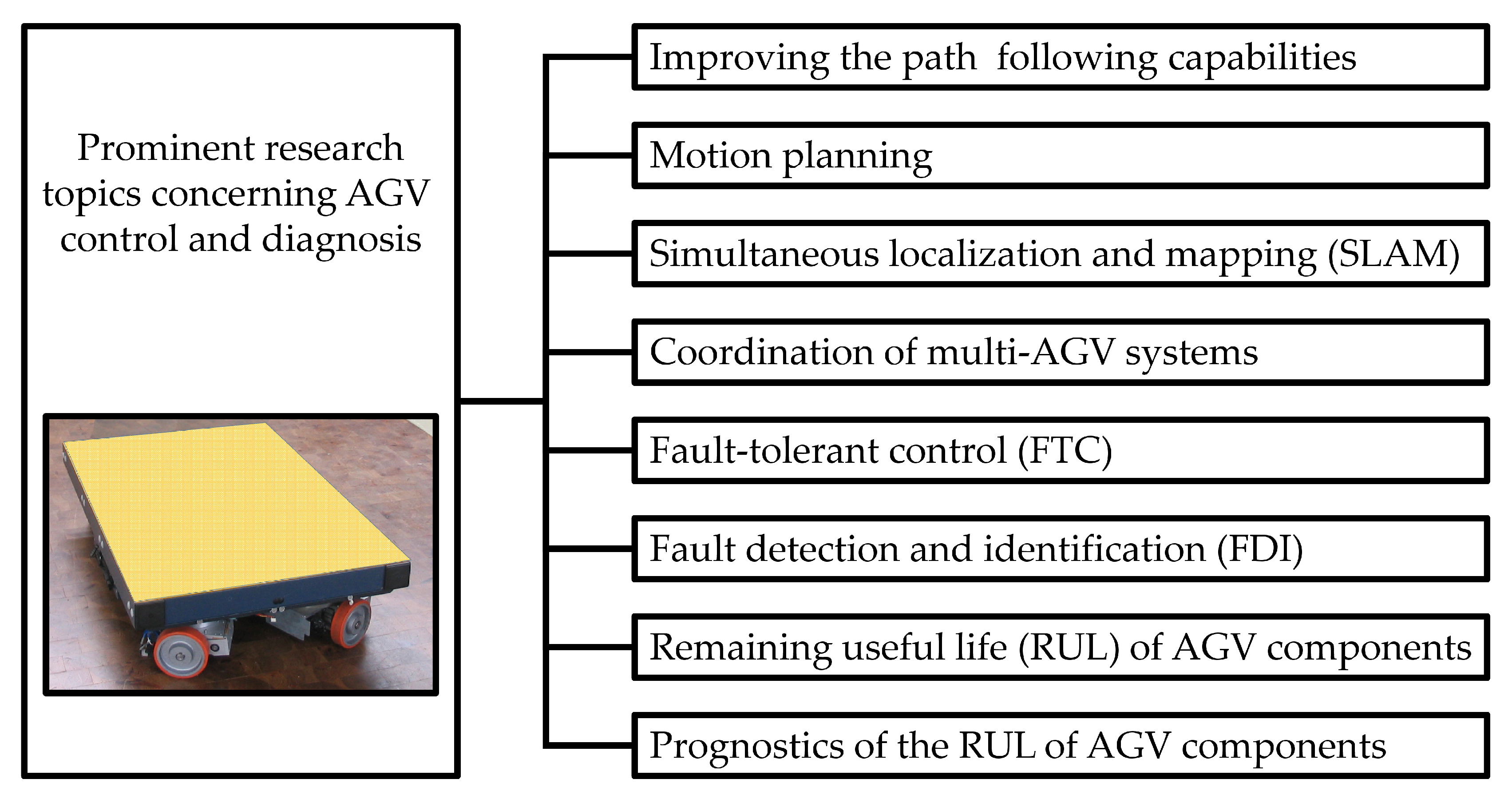
2. State of the Art
- Parameter identification-based approaches [32].
3. Application Example: A Transportation Platform
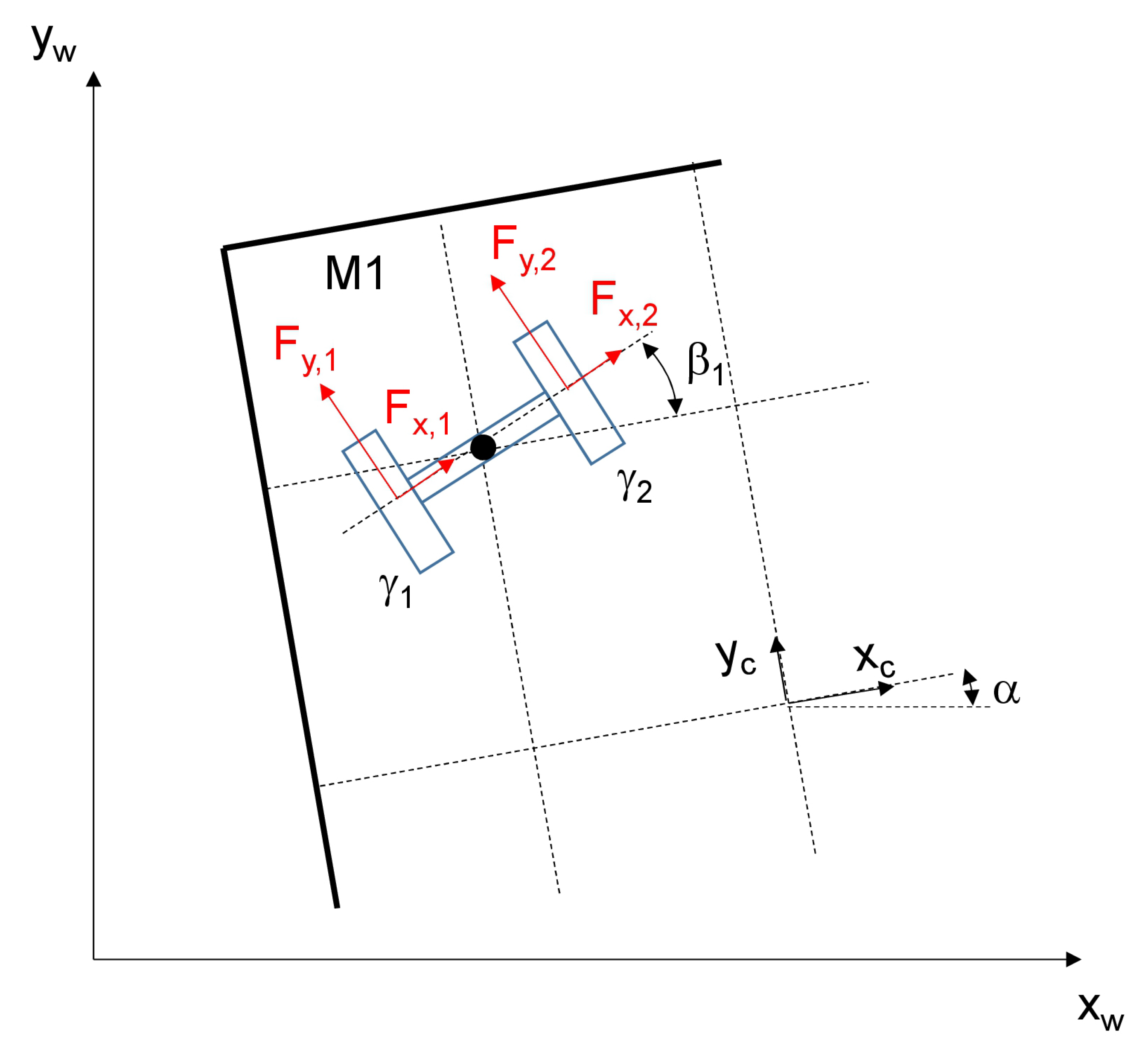
4. Mathematical Model of the Transportation Platform
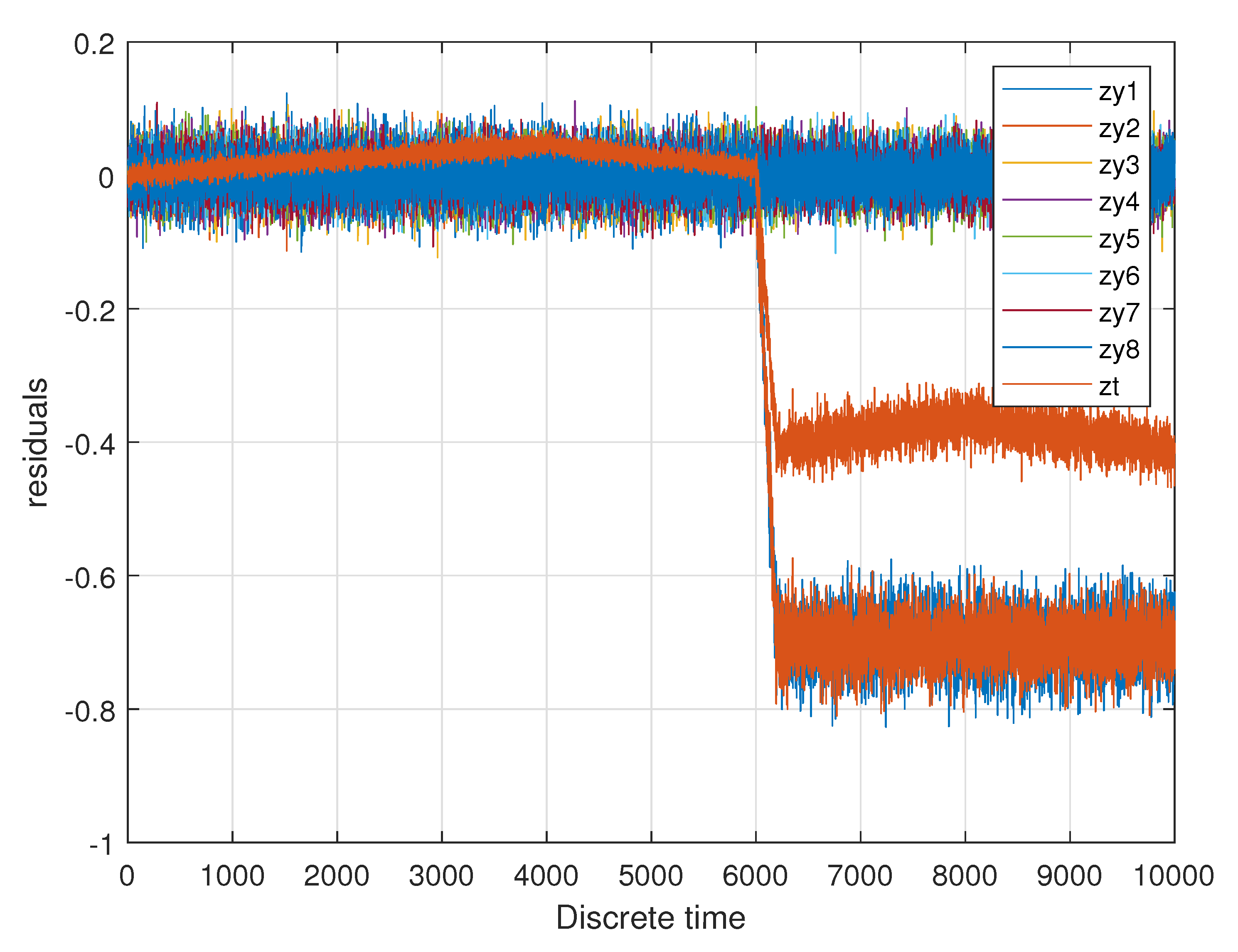
5. Fault Detection and Identification with a Virtual Sensor
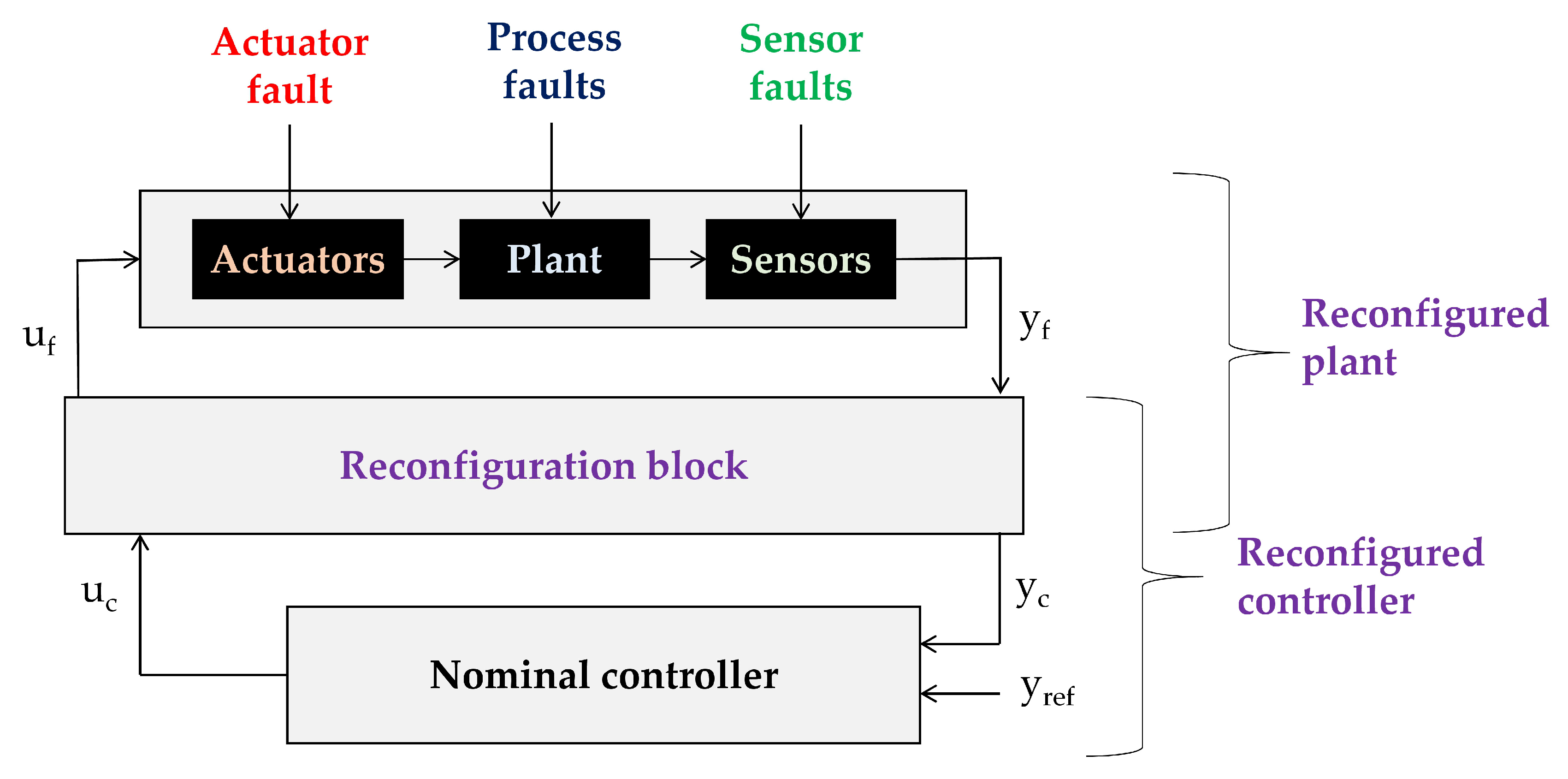
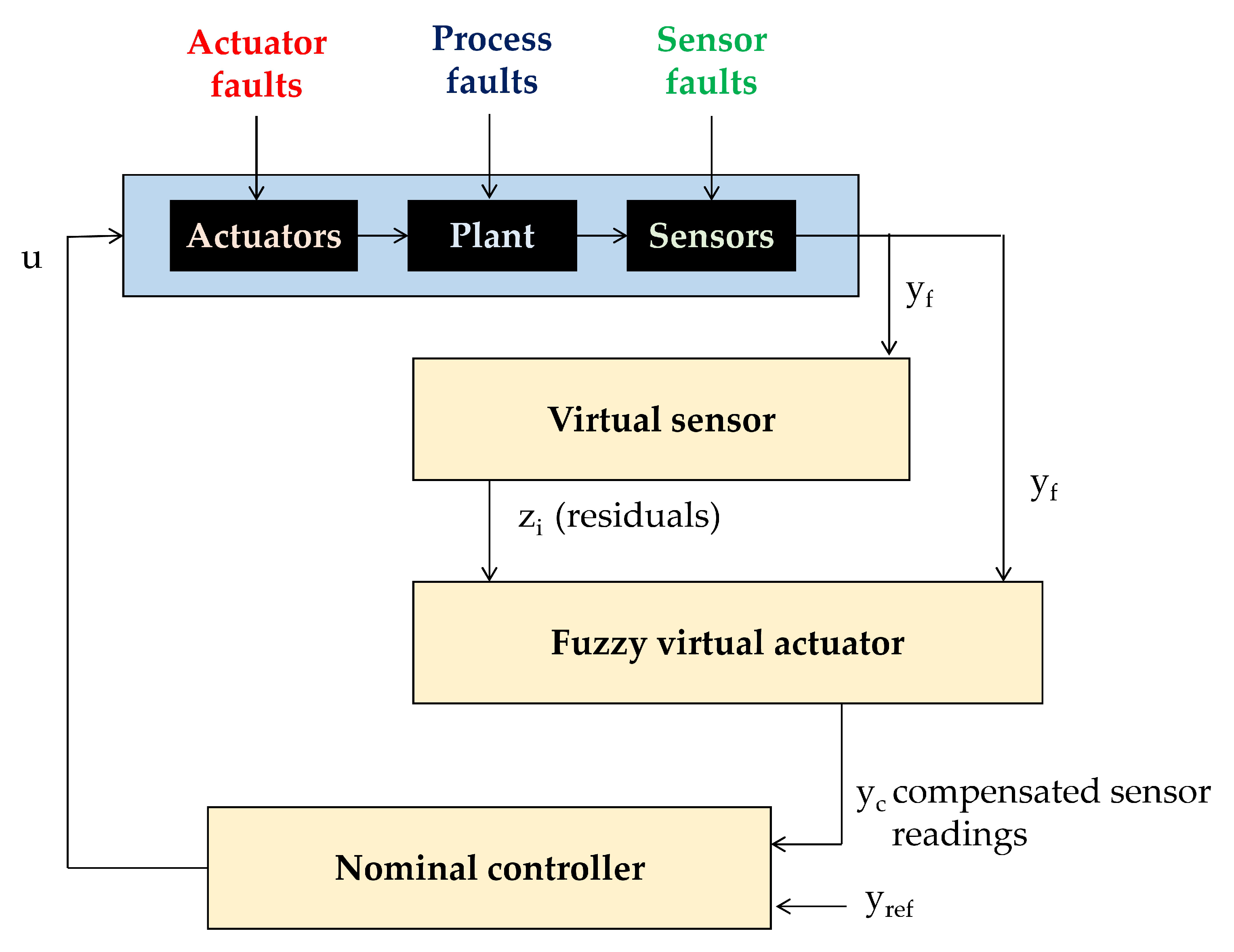
6. Design of a Fuzzy Virtual Actuator
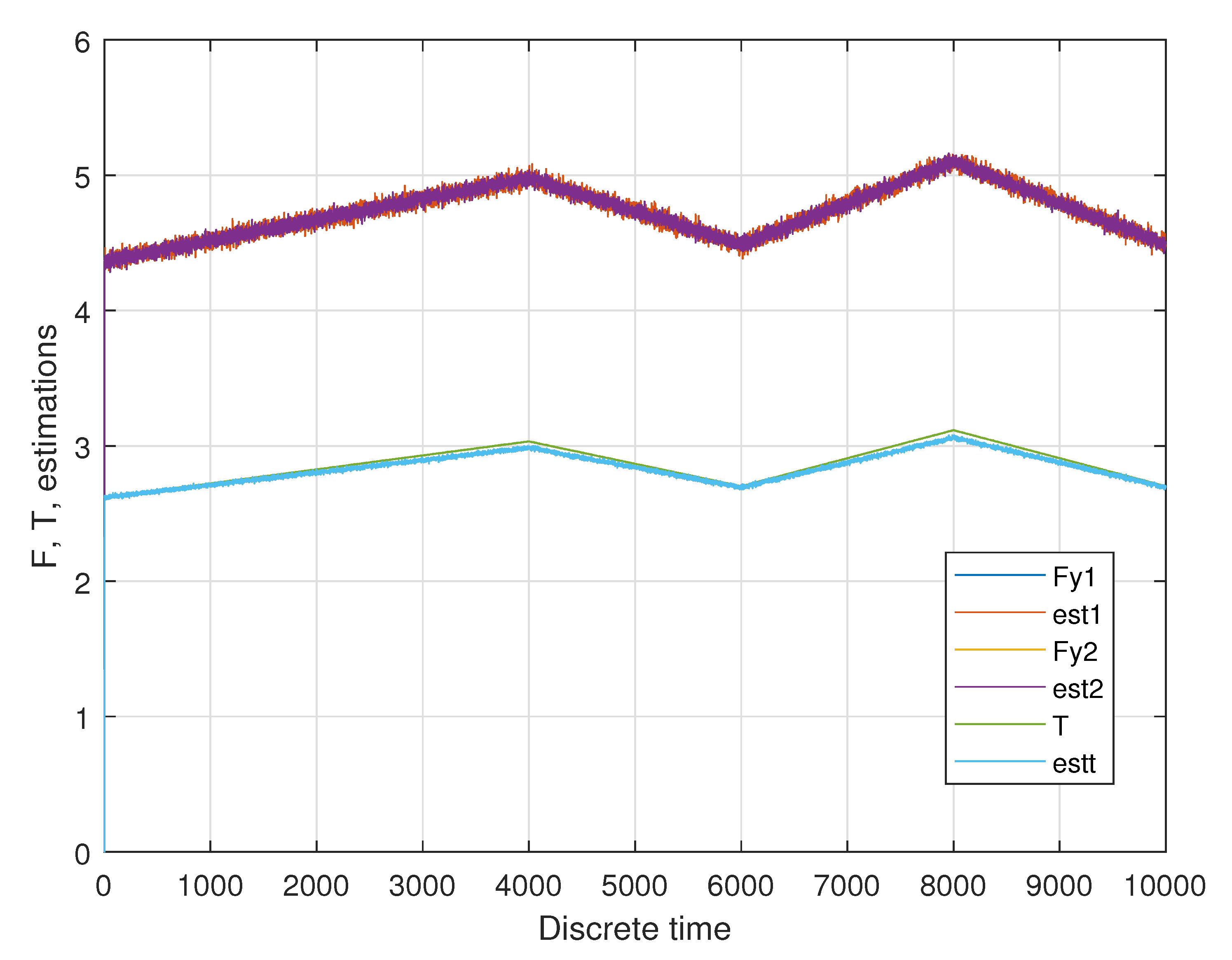
7. Evaluation
8. Conclusions and Outlook
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AFAC | Actuator failure avoidance online charging schemes |
| AGV | Automated guided vehicle |
| A-NSGA | Non-dominated sorting based genetic algorithm |
| CPN | Colored Petri nets |
| FDI | Fault detection and identification |
| FRVPN | Fuzzy reasoning and verification Petri net |
| FTC | Fault-tolerant control |
| IoT | Internet of Things |
| LPV | Linear parameter varying |
| PID | Proportional-Integral-Derivative |
| RUL | Remaining useful life |
| SLAM | Simultaneous localization and mapping |
| TS | Takagi–Sugeno |
Appendix A
References
- Simani, S.; Alvisi, S.; Venturini, M. Fault tolerant control of a simulated hydroelectric system. Control Eng. Pract. 2016, 51, 13–25. [Google Scholar] [CrossRef]
- Filasova, A.; Serbak, V. Design of Fuzzy Based Virtual Actuator for a Class of Nonlinear Systems. Control Eng. 2012, 10/2, 75–80. [Google Scholar] [CrossRef]
- Hua, C.; Jing, H.; Wang, R.; Yan, F.; Chadli, M. Robust H infinty output-feedback control for path following of autonomous ground vehicles. Mech. Syst. Signal Process. 2016, 70–71, 414–427. [Google Scholar] [CrossRef]
- Li, B.; Liu, H.; Xiao, D.; Yu, G.; Zhang, Y. Centralized and optimal motion planning for large-scale AGV systems: A generic approach. Adv. Eng. Softw. 2017, 106, 33–46. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y. Fault-Tolerant Cooperative Motion Planning of Connected and Automated Vehicles at a Signal-Free and Lane-Free Intersection. IFAC-PapersOnLine 2018, 51, 60–67. [Google Scholar] [CrossRef]
- Sprunk, C.; Lau, B.; Pfaff, P.; Burgard, W. An Accurate and Efficient Navigation System for Omnidirectional Robots in Industrial Environments. Auton. Robot. 2016, 41, 473–493. [Google Scholar] [CrossRef]
- Lau, B.; Sprunk, C.; Burgard, W. Efficient grid-based spatial representations for robot navigation in dynamic environments. Robot. Auton. Syst. 2013, 61, 1116–1130. [Google Scholar] [CrossRef]
- Beinschob, P.; Reinke, C. Graph slam based mapping for agv localization in large-scale warehouses. In Proceedings of the 2015 IEEE International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 3–5 September 2015; pp. 245–248. [Google Scholar]
- Temeltas, H. A Real-Time Localization Method For Agvs In Smart Factories. Int. Sci. J. Sci. Bus. Soc. 2018, 3, 45–50. [Google Scholar]
- Fazlollahtabar, H.; Saidi-Mehrabad, M.; Balakrishnan, J. Integrated Markov-neural reliability computation method: A case for multiple automated guided vehicle system. Reliab. Eng. Syst. Saf. 2015, 135, 34–44. [Google Scholar] [CrossRef]
- Elena Cardarelli, E.; Digani, V.; Sabattini, L.; Secchi, C.; Fantuzzi, C. Cooperative cloud robotics architecture for the coordination of multi-AGV systems in industrial warehouses. Mechatronics 2017, 45, 1–13. [Google Scholar] [CrossRef]
- Yan, R.; Dunnett, S.; Jackson, L. Novel methodology for optimising the design, operation and maintenance of a multi-AGV system. Reliab. Eng. Syst. Saf. 2018, 178, 130–139. [Google Scholar] [CrossRef]
- Antakly, D.; Loiseau, J.; Abbou, R. A Temporised Conflict-Free Routing Policy for AGVs. IFAC-PapersOnLine 2017, 50, 11169–11174. [Google Scholar] [CrossRef]
- Bocewicz, G.; Banaszak, Z.; Nielsen, I.; Muszynski, W. Re-scheduling of AGVs Steady State Flow. IFAC-PapersOnLine 2017, 50, 3493–3498. [Google Scholar] [CrossRef]
- Mendonca, M.; Charun, I.; Neves, F.; Arruda, L. A cooperative architecture for swarm robotic based on dynamic fuzzy cognitive maps. Eng. Appl. Artif. Intell. 2017, 59, 122–132. [Google Scholar] [CrossRef]
- Klosowski, G.; Gola, A.; Amila, T. Computational Intelligence in Control of AGV Multimodal Systems. IFAC-PapersOnLine 2018, 51, 1421–14274. [Google Scholar] [CrossRef]
- Mihaly, A.; Gaspar, P. Reconfigurable Fault-Tolerant Control of In-Wheel Electric Vehicles with Steering System Failure. IFAC-PapersOnLine 2015, 48, 49–54. [Google Scholar]
- Rotondo, D.; Puig, V.; Nejjari, F. A Virtual Actuator Approach for Fault Tolerant Control of Switching LPV Systems. In Proceedings of the 19th World Congress of the International Federation of Automatic Control (IFAC), Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Mrugalska, B.; Stetter, R. Health Aware Model-Predictive Control of Cooperative AGV-based Production System. Sensors 2019, 19, 532. [Google Scholar] [CrossRef] [Green Version]
- Stetter, R. Fault-Tolerant Design and Control of Automated Vehicles and Processes. Insights for the Synthesis of Intelligent Systems; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Witczak, M. Fault Diagnosis and Fault-Tolerant Control Strategies for Non-Linear Systems; Lecture Notes in Electrical Engineering; Springer International Publishing: Heidelberg, Germany, 2014; Volume 266, p. 229. [Google Scholar]
- Mahmoud, M.; Jiang, J.; Zhang, Y. Active Fault Tolerant Control Systems: Stochastic Analysis and Synthesis; Springer: Berlin, Germany, 2003. [Google Scholar]
- Ding, S. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Chen, J.; Patton, R.J. Robust Model-based Fault Diagnosis for Dynamic Systems; Kluwer Academic Publishers: London, UK, 1999. [Google Scholar]
- Aouaouda, S.; Chadli, M.; Shi, P.; Karimi, H. Discrete-time H_ / H-inf sensor fault detection observer design for nonlinear systems with parameter uncertainty. Int. J. Robust Nonlinear Control 2015, 25, 339–361. [Google Scholar] [CrossRef]
- López-Estrada, F.; Ponsart, J.; Astorga-Zaragoza, C.; Camas-Anzueto, J.; Theilliol, D. Robust sensor fault estimation for descriptor–lpv systems with unmeasurable gain scheduling functions: Application to an anaerobic bioreactor. Int. J. Appl. Math. Comput. Sci. 2015, 25, 233–244. [Google Scholar] [CrossRef] [Green Version]
- Stetter, R.; Witczak, M.; Pazera, M. Virtual Diagnostic Sensors Design for an Automated Guided Vehicle. Appl. Sci. 2018, 8, 702. [Google Scholar] [CrossRef] [Green Version]
- Mendonca, L.F.; Sousa, J.; da Costa, J.M.G. Fault Isolation using Fuzzy Model-Based Observers. IFAC Proc. Vol. 2006, 39, 735–740. [Google Scholar] [CrossRef]
- Kolesov, N.V. Fault Diagnosis in Dynamic Systems Using Fuzzy Interacting Observers. Adv. Fuzzy Syst. 2013, 2013, 874393. [Google Scholar] [CrossRef] [Green Version]
- Foo, G.; Zhang, X.; Vilathgamuwa, M. A sensor fault detection and isolation method in interior permanent-magnet synchronous motor drives based on an extended Kalman filter. IEEE Trans. Ind. Electron. 2013, 60, 3485–3495. [Google Scholar] [CrossRef]
- Pourbabaee, B.; Meskin, N.; Khorasani, K. Sensor fault detection, isolation, and identification using multiple-model-based hybrid Kalman filter for gas turbine engines. IEEE Trans. Control Syst. Technol. 2016, 24, 1184–1200. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.; Ferdowsi, H.; Sarangapani, J. Model-based fault detection, estimation, and prediction for a class of linear distributed parameter systems. Automatica 2016, 66, 122–131. [Google Scholar] [CrossRef] [Green Version]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control; Springer: New York, NY, USA, 2003. [Google Scholar]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M. Diagnosis and Fault-Tolerant Control; Springer: New York, NY, USA, 2016. [Google Scholar]
- De Oca, S.; Puig, V. Fault-Tolerant Control using a Virtual Actuator using LPV Techniques: Application to a Two-Degree of Freedom Helicopter. IFAC Proc. Vol. 2010, 43, 416–421. [Google Scholar] [CrossRef]
- Seron, M.; De Dona, J.; Richter, J. Bank of Virtual Actuators for Fault Tolerant Control. In Proceedings of the 18th World Congress of the International Federation of Automatic Control (IFAC), Milano, Italy, 28 August–2 September 2011. [Google Scholar]
- Rotondo, D.; Ponsart, J.C.; Theilliol, D.; Nejjari, F.; Puig, V. A virtual actuator approach for the fault tolerant control of unstable linear systems subject to actuator saturation and fault isolation delay. Annu. Rev. Control 2015, 39, 68–80. [Google Scholar] [CrossRef] [Green Version]
- Rotondo, D.; Ponsart, J.C.; Nejjari, F.; Theilliol, D.; Puig, V. Virtual actuator-based FTC for LPV systems with saturating actuators and FDI delays. In Proceedings of the 3rd Conference on Control and Fault-Tolerant Systems (SysTol), Barcelona, Spain, 7–9 September 2016. [Google Scholar]
- Wang, Y.; Rotondo, D.; Puig, V.; Cembrano, G.; Zhao, Y. Fault-tolerant Control of Discrete-time Descriptor Systems using Virtual Actuators. In Proceedings of the 2019 4th Conference on Control and Fault Tolerant Systems (SysTol), Casablanca, Morocco, 18–20 September 2019; pp. 147–152. [Google Scholar]
- Yadegar, M.; Meskin, N.; Afshar, A. Fault-tolerant control of linear systems using adaptive virtual actuator. Int. J. Control 2019, 92, 1729–1741. [Google Scholar] [CrossRef]
- Pizzi, N.; Kofman, E.; De Dona, J.A.; Seron, M.M. Actuator fault tolerant control based on probabilistic ultimate bounds. ISA Trans. 2019, 84, 20–30. [Google Scholar] [CrossRef]
- Ting, Y.; Lu, B.; Chen, C.; Wang, G. A fuzzy reasoning design for fault detection and diagnosis of a computer-controlled system. Eng. Appl. Artif. Intell. 2008, 21, 157–170. [Google Scholar] [CrossRef] [Green Version]
- Gentil, S.; Lesecq, S.; Barraud, A. Improving decision making in fault detection and isolation using model validity. Eng. Appl. Artif. Intell. 2009, 22, 534–545. [Google Scholar] [CrossRef]
- Escobet, A.; Nebot, A.; Mugica, F. PEM fuel cell fault diagnosis via a hybrid methodology based on fuzzy and pattern recognition techniques. Eng. Appl. Artif. Intell. 2014, 36, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Shaker, M.; Patton, R. Active sensor fault-tolerant output feedback tracking control for wind turbine systems via T-S model. Eng. Appl. Artif. Intell. 2014, 34, 1–12. [Google Scholar] [CrossRef]
- Vafamand, N.; Asemani, M.; Khayatiyan, A. A robust L1 controller design for continuous-time TS systems with persistent bounded disturbance and actuator saturation. Eng. Appl. Artif. Intell. 2016, 56, 212–221. [Google Scholar] [CrossRef]
- Krokavec, D.; Filasova, A.; Serbak, V. Virtual actuator based fault tolerant control design for Takagi-Sugeno fuzzy systems. In Proceedings of the 2016 IEEE 14th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 21–23 January 2016. [Google Scholar]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modelling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Wu, S.T.; Shao, Y.J. Adaptive vibration control using a virtual-vibration-absorber controller. J. Sound Vib. 2007, 305, 891–903. [Google Scholar] [CrossRef]
- Bian, Y.; Gao, Z. Nonlinear vibration absorption for a flexible arm via a virtual vibration absorber. J. Sound Vib. 2017, 399, 197–215. [Google Scholar] [CrossRef]
- Krenk, S.; Hogsberg, J. Equal modal damping design for a family of resonant vibration control formats. J. Vib. Control 2013, 19, 1294–1315. [Google Scholar] [CrossRef]
- Heidari, H.; Monjezi, B. Vibration control of imbalanced Jeffcott rotor by virtual passive dynamic absorber with optimal parameter values. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4278–4288. [Google Scholar] [CrossRef]
- Reddy, K.K.; Chen, J.; Behal, A.; Marzocca, P. Multi-Input/Multi-Output Adaptive Output Feedback Control Design for Aeroelastic Vibration Suppression. J. Guid. Control Dyn. 2007, 30, 1040–1048. [Google Scholar] [CrossRef]
- Beltran-Carbajal, F.; Valderrabano-Gonzalez, A.; Rosas-Caro, J.C.; Favela-Contreras, A. Output feedback control of a mechanical system using magnetic levitation. ISA Trans. 2018, 57, 352–359. [Google Scholar] [CrossRef] [PubMed]
- Liao, G.; Xu, Y.; Wei, F.; Ge, R.; Wan, Q. Investigation on the phase-based fuzzy logic controller for magnetorheological elastomer vibration absorber. J. Intell. Mater. Syst. Struct. 2017, 28, 728–739. [Google Scholar] [CrossRef]
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Lloret, J.; Kumar, S.; Sha, R.R.; Prasad, M.; Prakash, S. Virtualization in Wireless Sensor Networks: Fault Tolerant Embedding for Internet of Things. IEEE Internet Things J. 2018, 5, 571–580. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Yu, H.; Lin, Z.; Liu, N.; Sun, H.; Liu, M. Efficient Actuator Failure Avoidance Mobile Charging for Wireless Sensor and Actuator Networks. IEEE Access 2019, 7, 104197–104209. [Google Scholar] [CrossRef]
- Ullah, W.; Hussain, I.; Shehzadi, I.; Rahman, Z.; Uthansaku, P. Tracking a Decentralized Linear Trajectory in an Intermittent Observation Environment. Sensors 2020, 20, 2127. [Google Scholar] [CrossRef] [Green Version]
- Schneider, M.; van de Molengraft, M.; Steinbuch, M. Benefits of over-actuation in motion systems. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Ryll, M.; Buelthoff, H.; Giordano, P. Overactuation in UAVs for Enhanced Aerial Manipulation: A Novel Quadrotor Concept with Tilting Propellers. In Proceedings of the 6th International Workshop on Human-Friendly Robotics, Rome, Italy, 25–26 September 2013. [Google Scholar]
- Ziemniak, P.; Stania, M.; Stetter, R. Mechatronics Engineering on the Example of an Innovative Production Vehicle. In Proceedings of the 17th International Conference on Engineering Design (ICED’09); Norell Bergendahl, M., Grimheden, M., Leifer, L., Skogstad, P., Lindemann, U., Eds.; The Design Society: Glasgow, UK, 2009; Volume 1, pp. 61–72. [Google Scholar]
- Stetter, R.; Paczynski, A. Intelligent Steering System for Electrical Power Trains. In Proceedings of the Emobility—Electrical Power Train, Leipzig, Germany, 8–9 November 2010; pp. 1–6. [Google Scholar]
- Gillijns, S.; De Moor, B. Unbiased minimum-variance input and state estimation for linear discrete-time systems. Automatica 2007, 43, 111–116. [Google Scholar] [CrossRef]


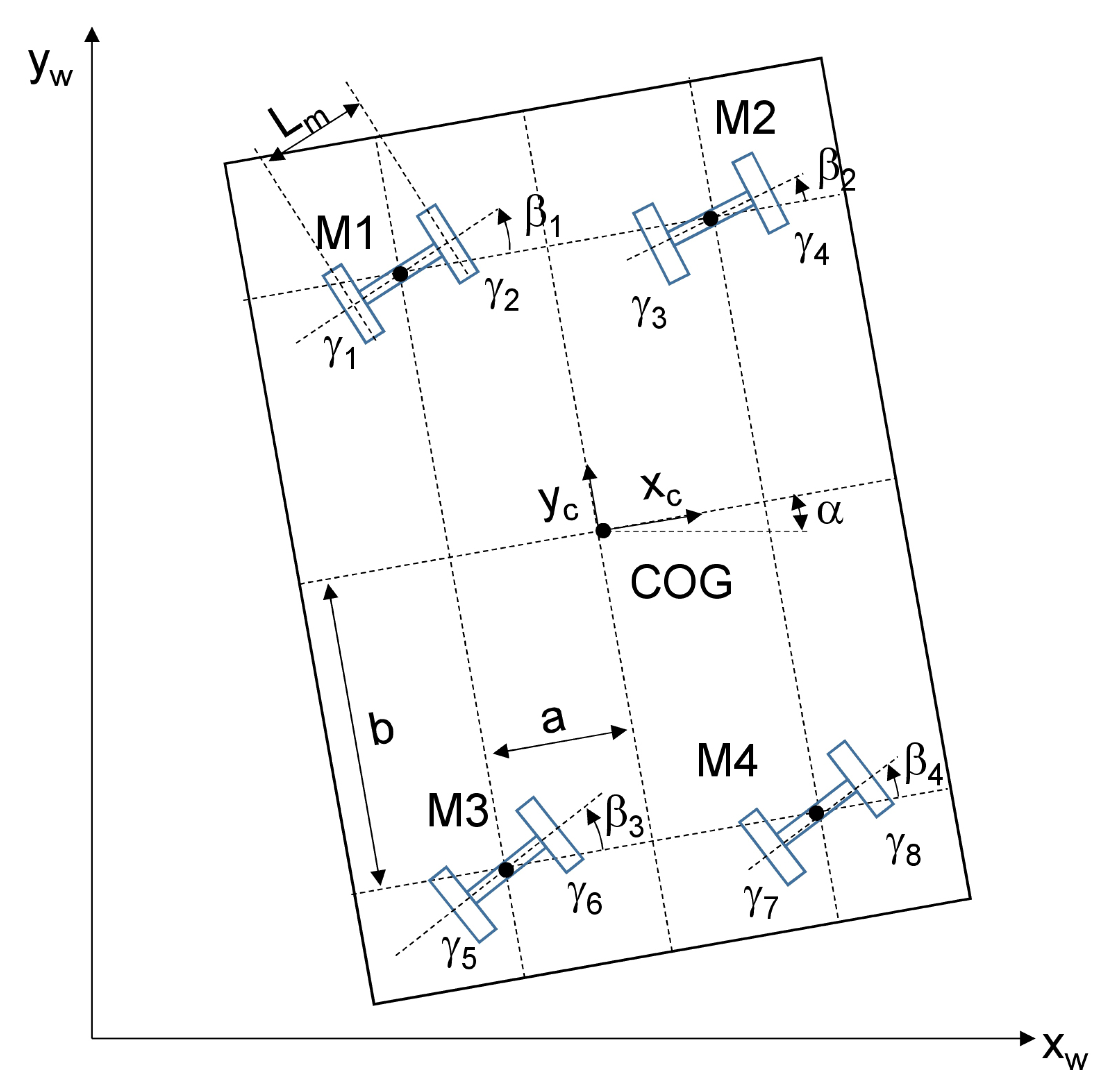




| center of gravity | |
| number of drive modules | |
| number of wheels | |
| directions | |
| b | distance between modules and COG (y-direction) |
| a | distance between modules and COG (x-direction) |
| distance between wheel contact point of the j-th wheel and the ICR | |
| drive module gauge | |
| vehicle angle | |
| vehicle angular velocity (yaw rate) | |
| vehicle angular acceleration | |
| position of the vehicle in the world coordinate system | |
| position of the vehicle in the center coordinate system | |
| lateral velocity of the vehicle | |
| longitudinal velocity of the vehicle | |
| lateral acceleration of the vehicle | |
| longitudinal acceleration of the vehicle | |
| m | mass |
| steering angle of the i-th drive module | |
| angular velocity of the i-th drive module | |
| angular acceleration of the i-th drive module | |
| angle of the j-th wheel | |
| angular velocity of the j-th wheel | |
| angular acceleration of the j-th wheel | |
| sum of forces causing lateral motion | |
| sum of forces causing longitudinal motion | |
| longitudinal force on the j-th wheel | |
| total lateral force on the j-th wheel | |
| T | total torque acting on all wheels |
| torque distribution coefficient | |
| coefficient summarizing additional inertia in the drivetrain | |
| rolling friction coefficient | |
| wheel moment of inertia | |
| drive module moment of inertia | |
| AGV moment of inertia around z-axis | |
| wheel effective radius |
| Variable | Unit | Value |
|---|---|---|
| m | kg | 89 |
| m | 0.075 | |
| a | m | 0.196 |
| b | m | 0.399 |
| 1.1 | ||
| 0.04 | ||
| 578.18 | ||
| 4.15 | ||
| 0.00871513 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stetter, R. A Fuzzy Virtual Actuator for Automated Guided Vehicles. Sensors 2020, 20, 4154. https://doi.org/10.3390/s20154154
Stetter R. A Fuzzy Virtual Actuator for Automated Guided Vehicles. Sensors. 2020; 20(15):4154. https://doi.org/10.3390/s20154154
Chicago/Turabian StyleStetter, Ralf. 2020. "A Fuzzy Virtual Actuator for Automated Guided Vehicles" Sensors 20, no. 15: 4154. https://doi.org/10.3390/s20154154
APA StyleStetter, R. (2020). A Fuzzy Virtual Actuator for Automated Guided Vehicles. Sensors, 20(15), 4154. https://doi.org/10.3390/s20154154





