Biometric Measurement of Anterior Segment: A Review
Abstract
:1. Introduction
2. Approaches in Measuring the Anterior Segment
2.1. Pattern Projection
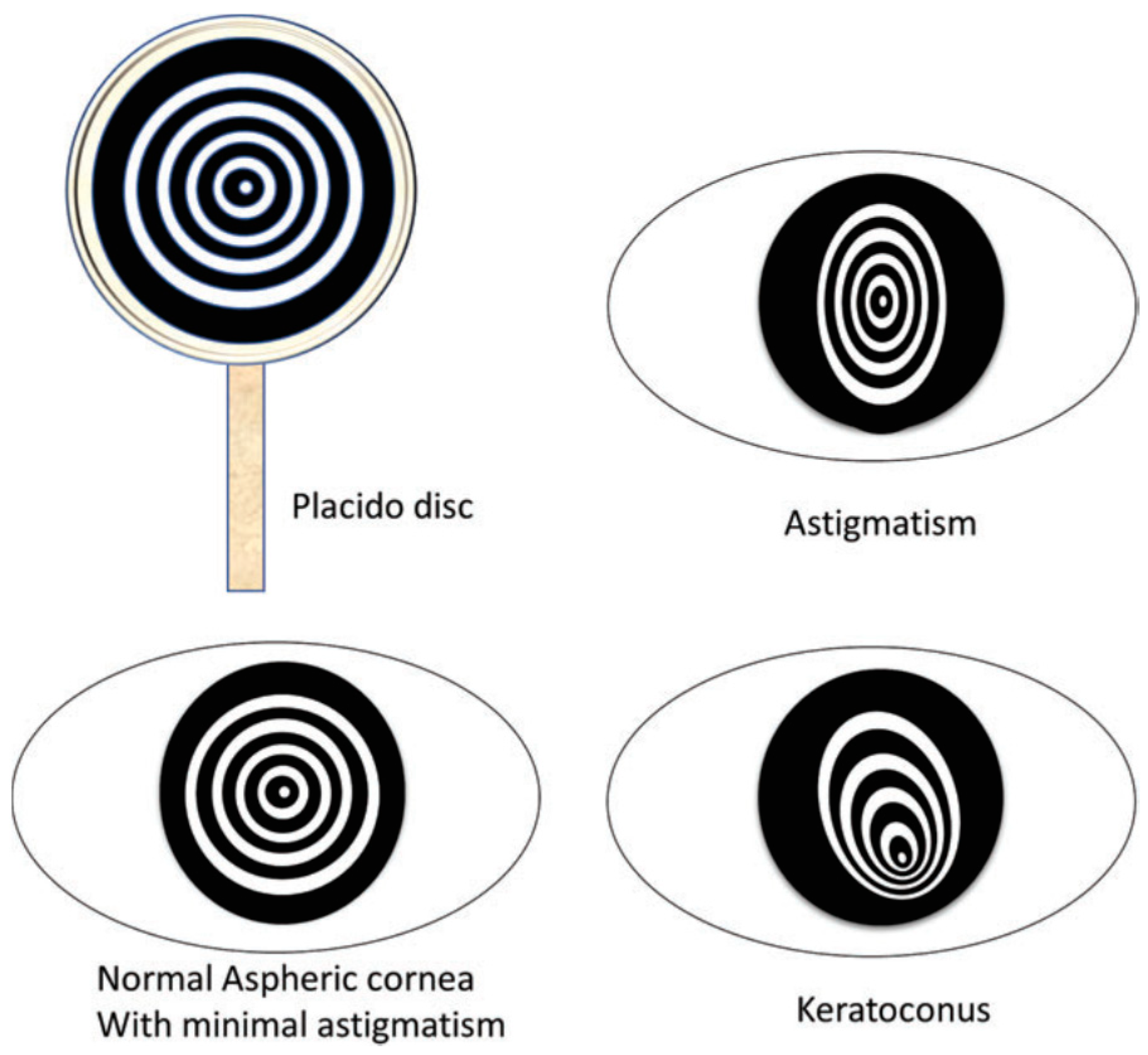
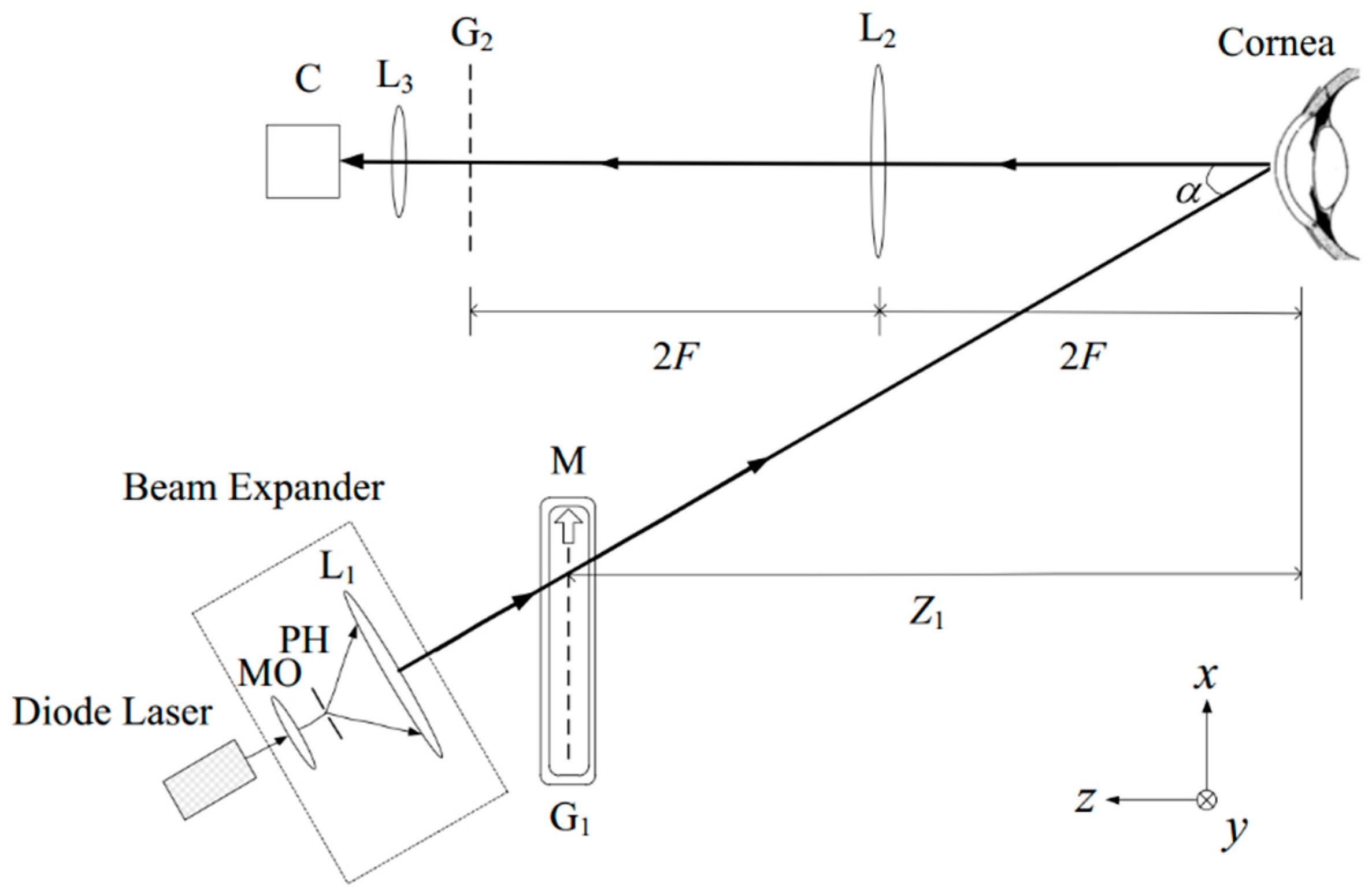
2.1.1. Placido Disk
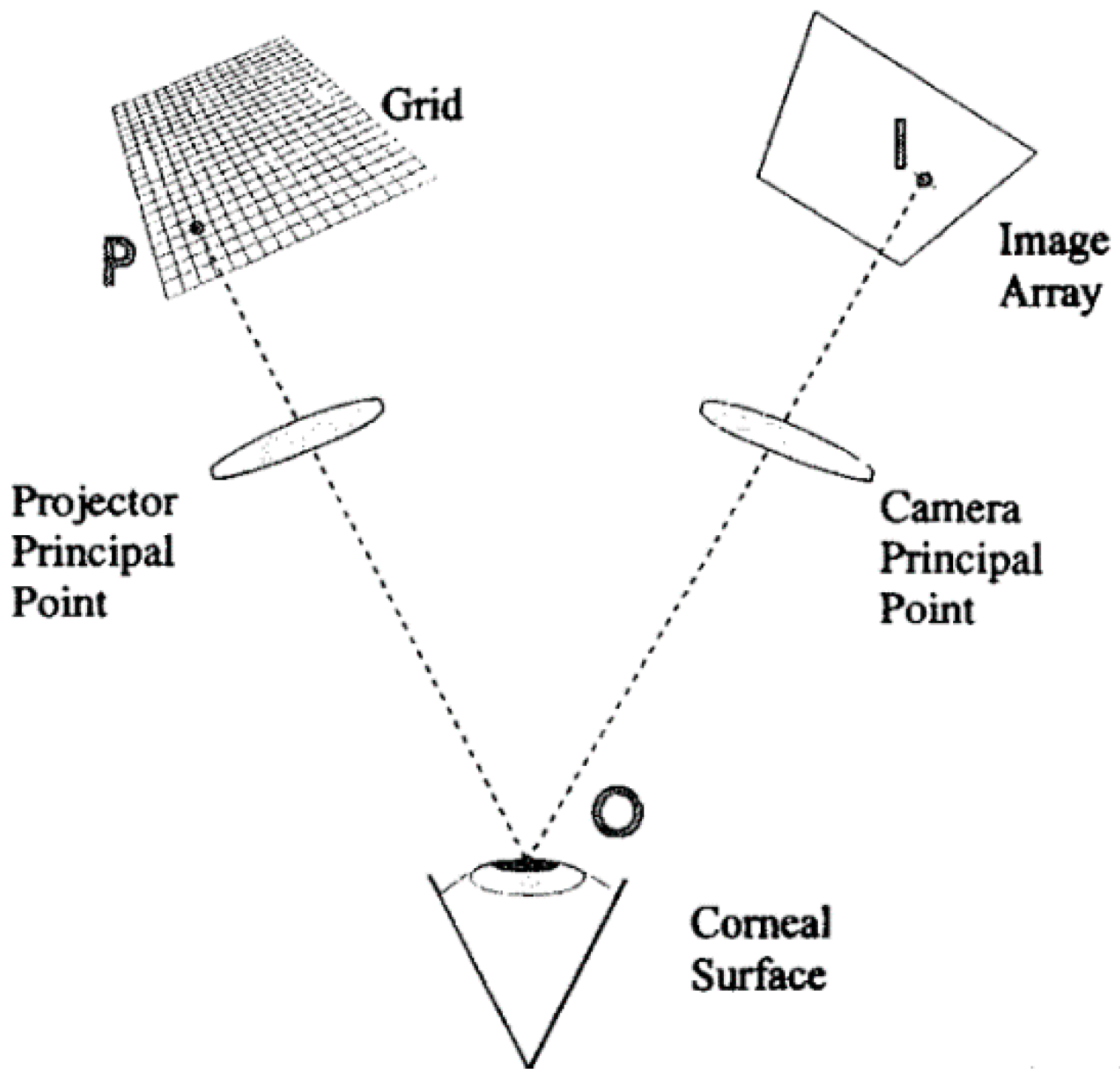
2.1.2. Rasterstereography
2.2. Interferometry
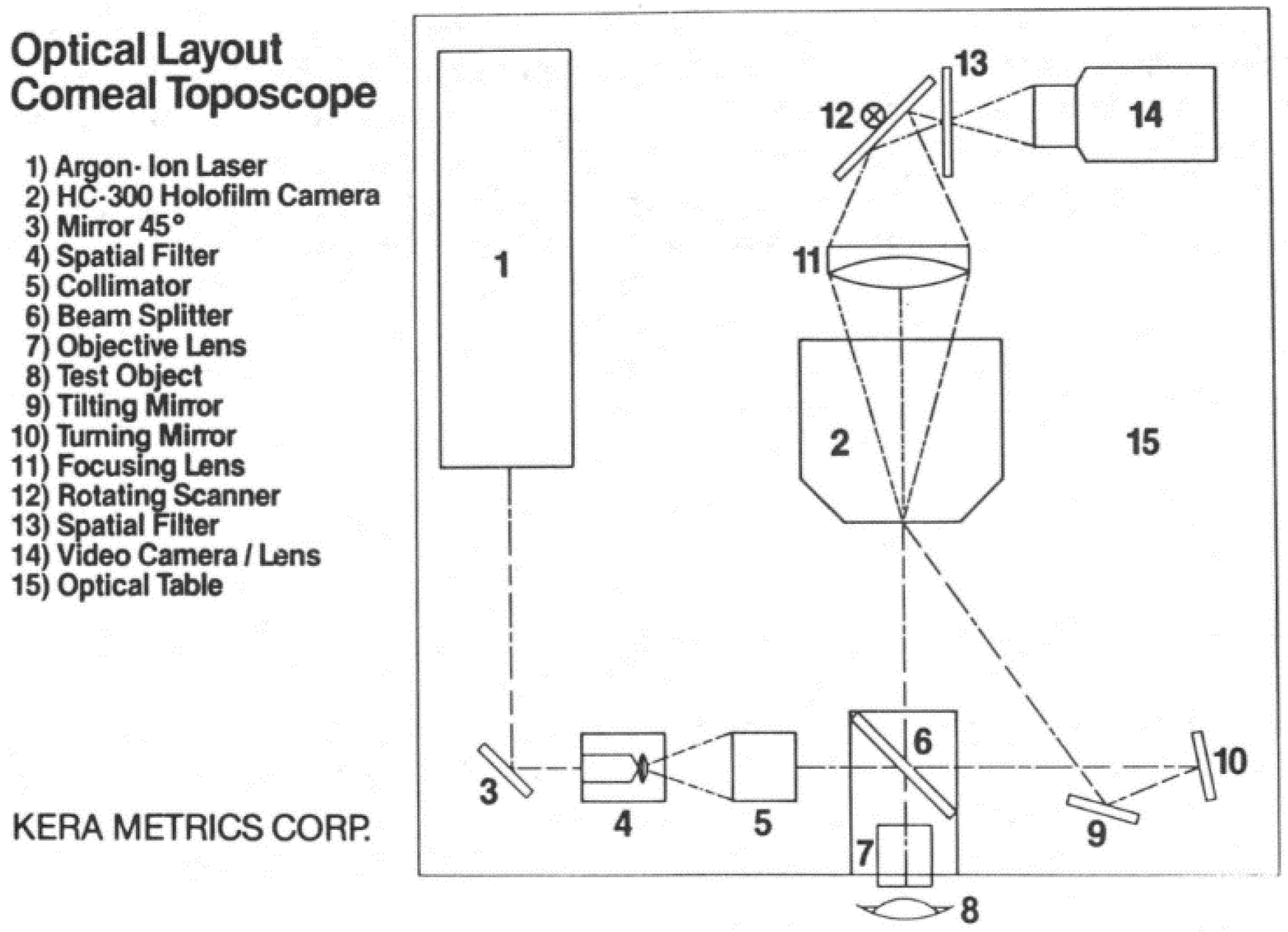
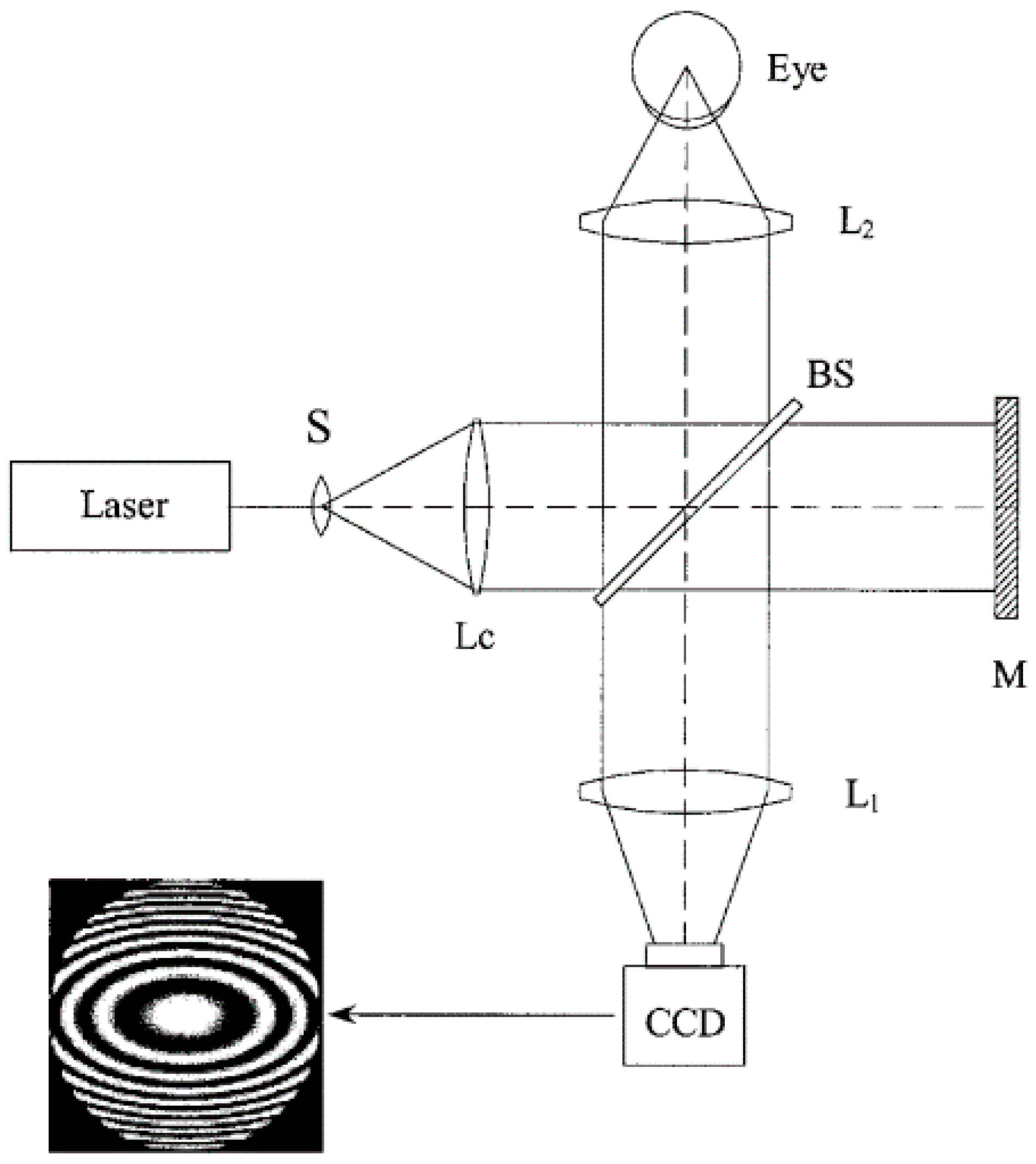
2.2.1. Holographic Technique
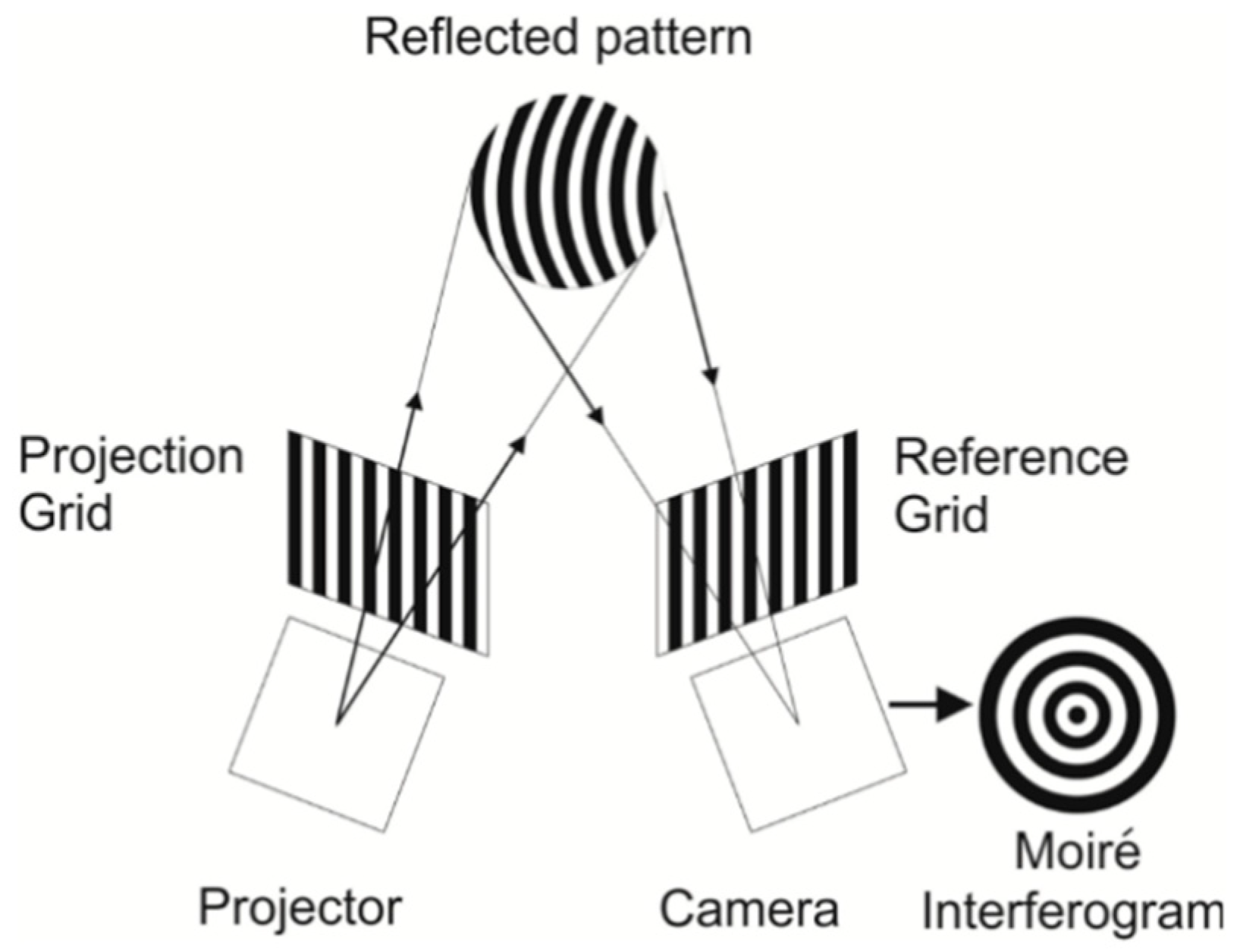
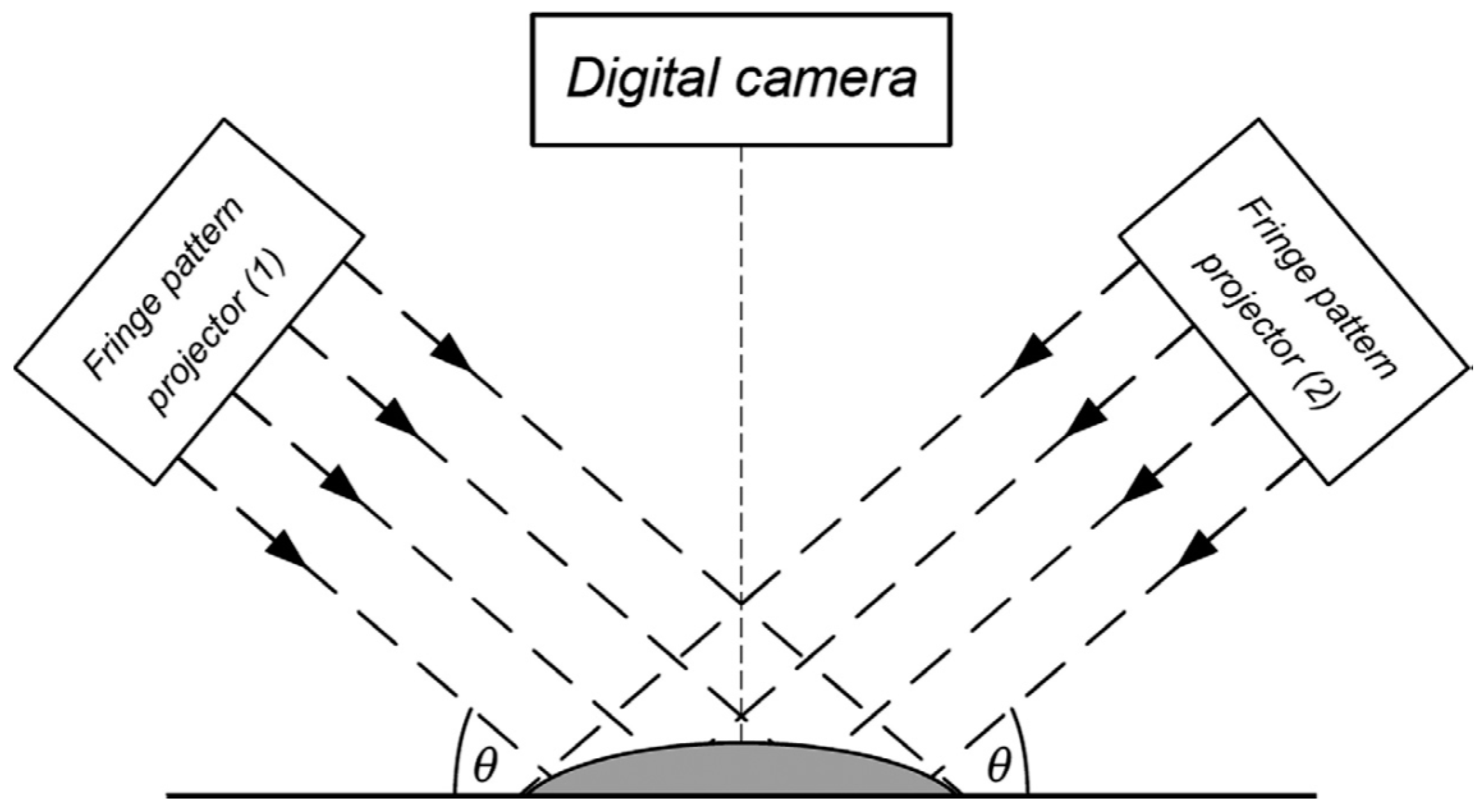
2.2.2. Moiré Technique
2.2.3. Twyman-Green Interferometer
2.2.4. Fourier Transform Profilometry
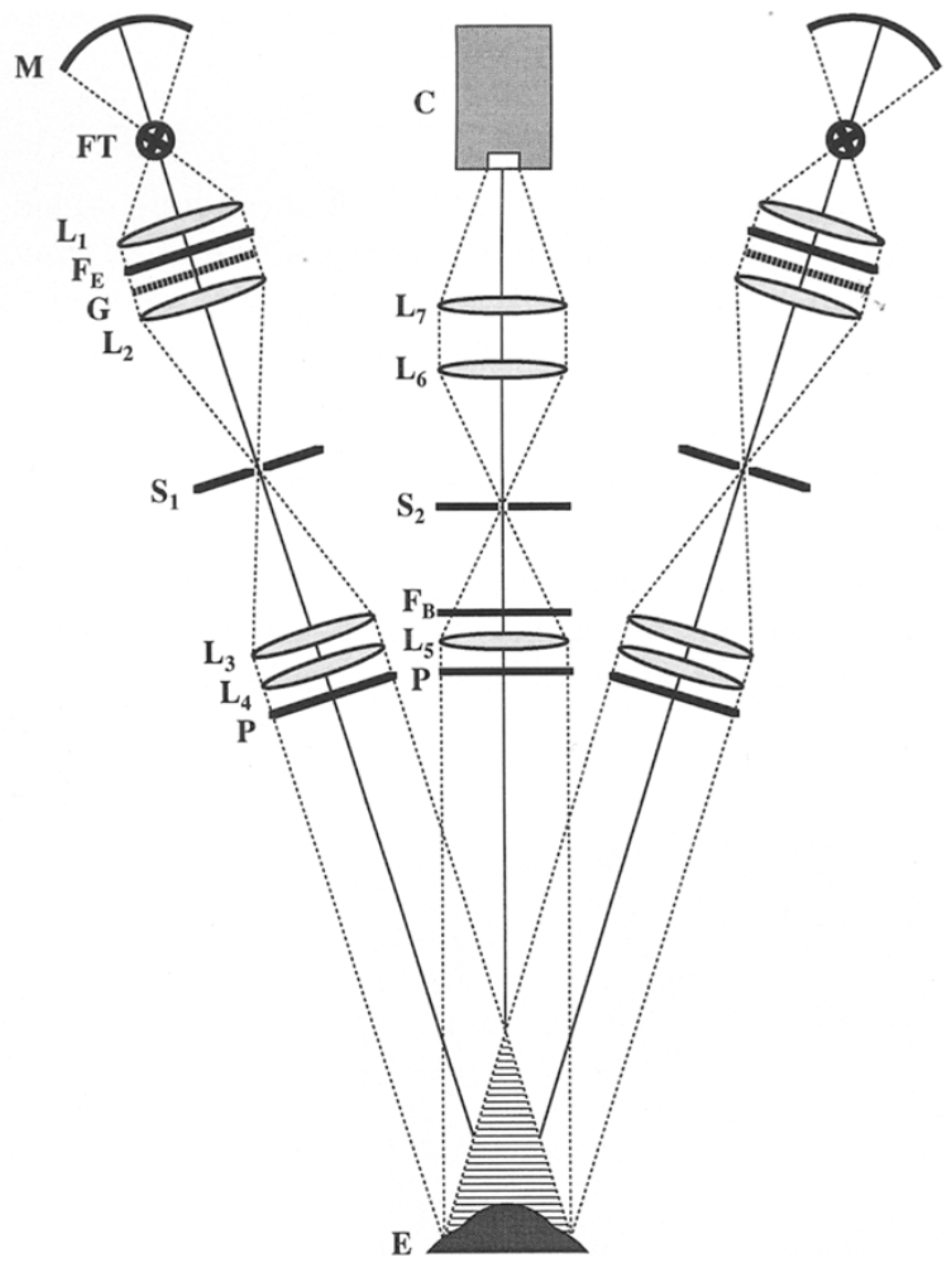
2.3. Scanning-Slit
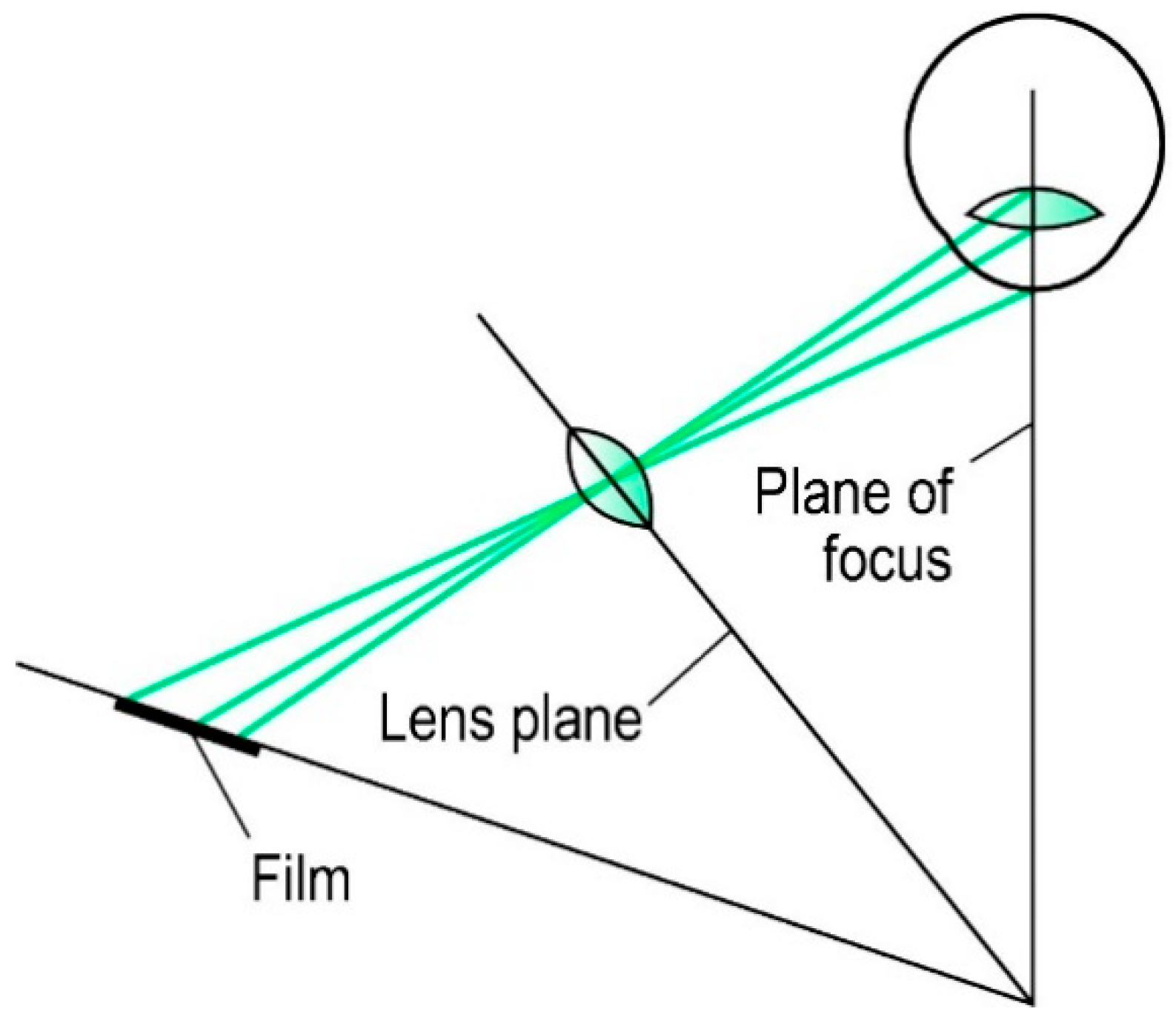
2.4. Scheimpflug Imaging
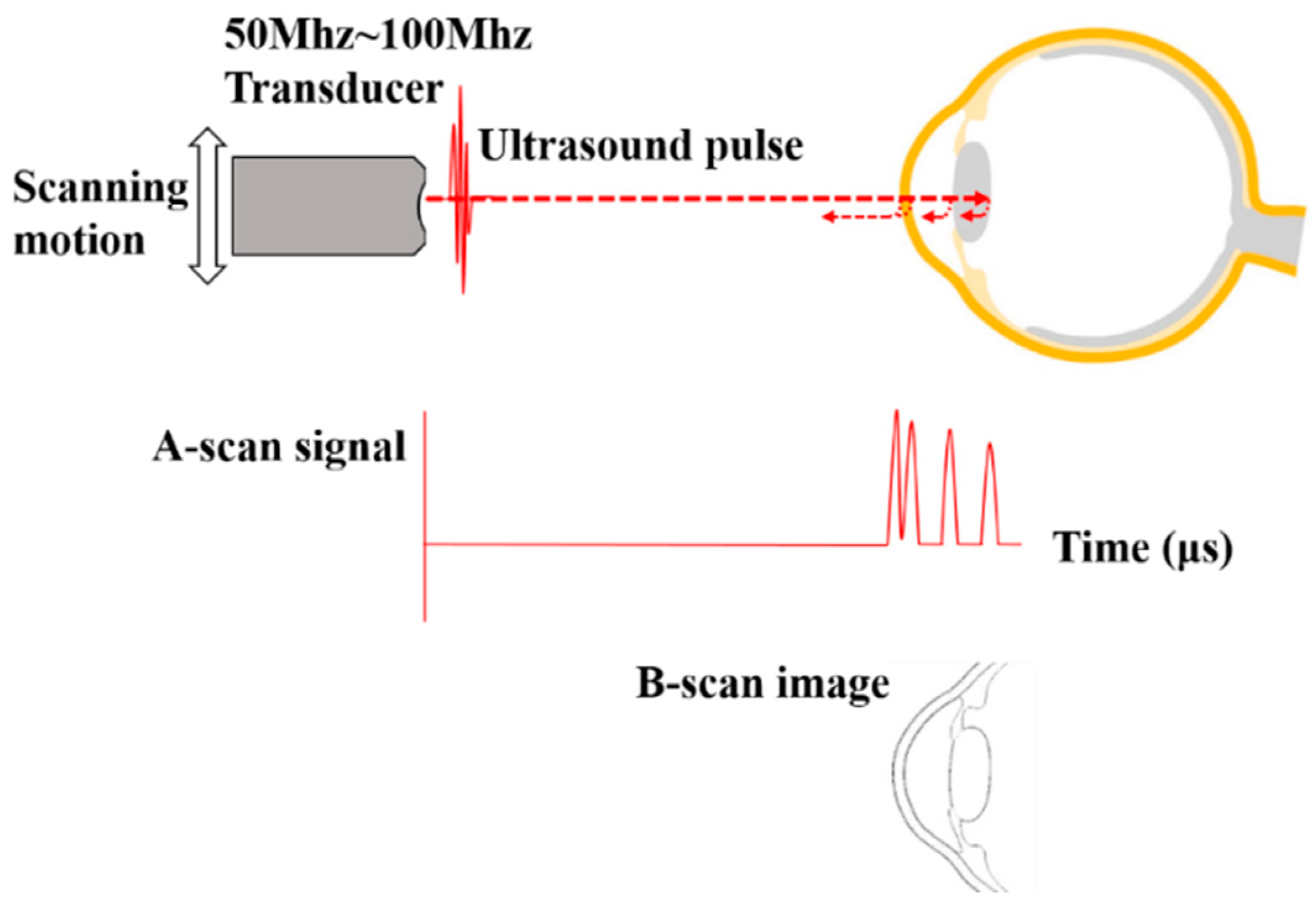
2.5. Ultrasound Biomicroscopy
2.6. Optical Coherence Tomography
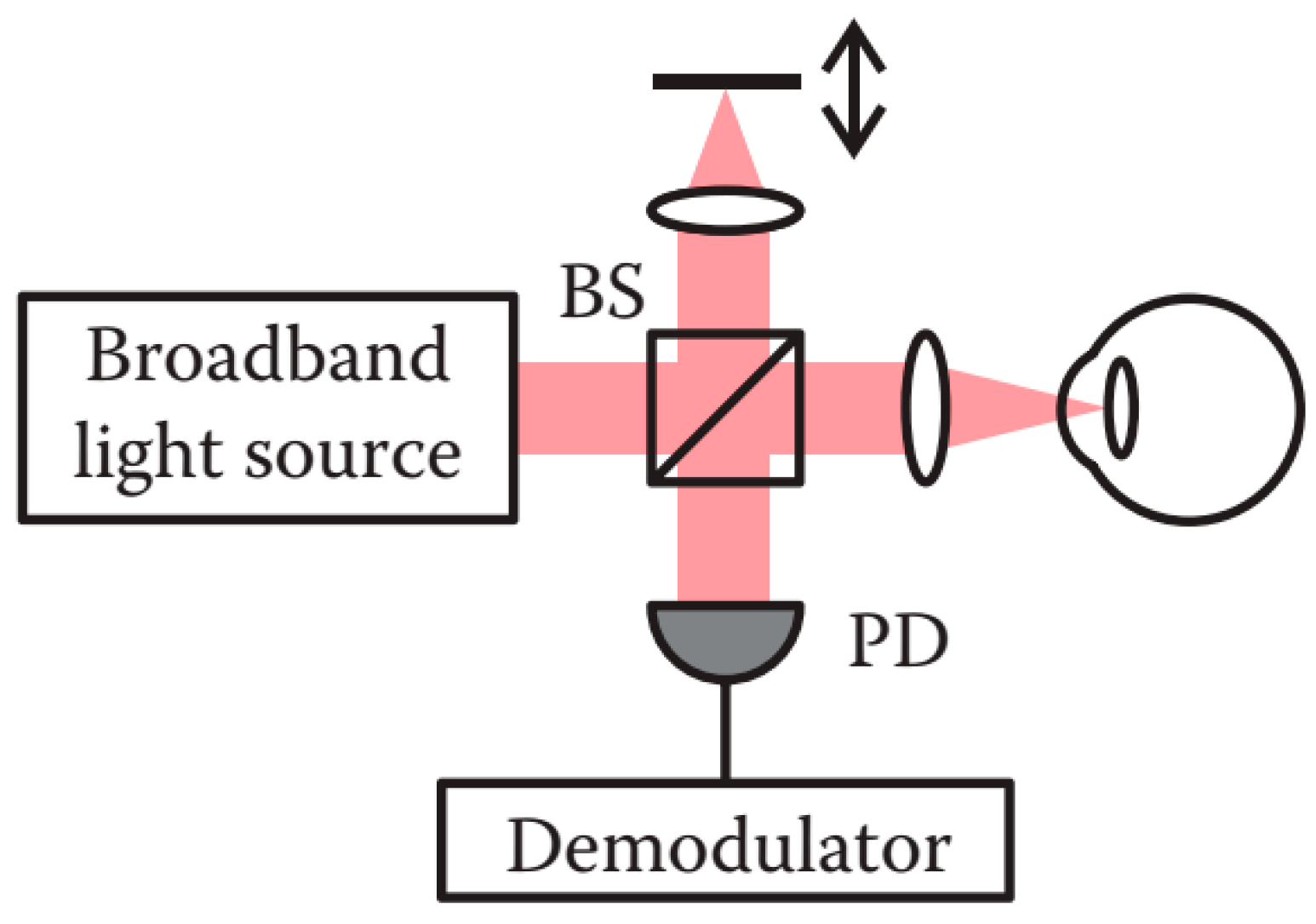
2.6.1. Time Domain OCT
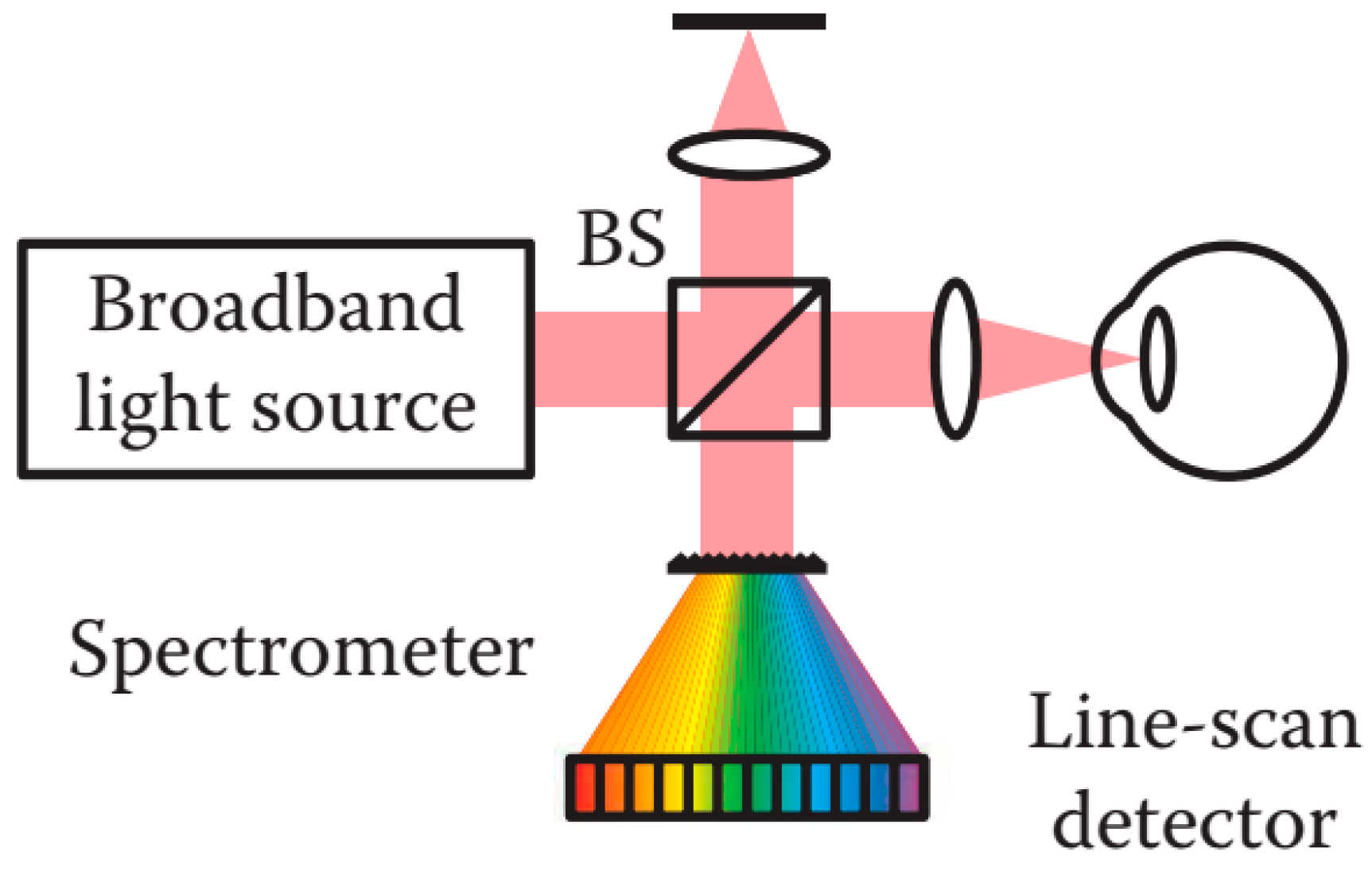
2.6.2. Fourier Domain OCT
Spectral Domain OCT
Swept Source OCT
2.6.3. Full Field OCT
3. Challenges and Perspectives
3.1. Motion Artefacts
- Minimizing the motion
- Appending additional information or increasing the acquisition speed
- Correcting motion artifacts in the image registration
3.2. Intraocular Multiple Scattering Effects
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bron, A.; Tripathi, R.; Tripathi, B. Wolff’s Anatomy of the Eye and Orbit, 8th ed.; Chapman & Hall Medical: London, UK, 1997. [Google Scholar]
- Schwiegerling, J. Field Guide to Visual and Ophthalmic Optics; SPIE: Bellingham, WA, USA, 2004. [Google Scholar]
- Cognard, T.E.; Goncharov, A.; Devaney, N.; Dainty, C.; Corcoran, P. A Review of Resolution Losses for AR/VR Foveated Imaging Applications. In Proceedings of the 2018 IEEE Games, Entertainment, Media Conference (GEM), Galway, Ireland, 15–17 August 2018; pp. 1–9. [Google Scholar]
- Davson, H. Physiology of the Eye; Macmillan International Higher Education: London, UK, 1990. [Google Scholar]
- LeGrand, Y.; ElHage, S.G. Physiological Optics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Von Helmholtz, H. Helmholtz’s Treatise on Physiological Optics; Dover Publications: Mineola, NY, USA, 1962. [Google Scholar]
- Efron, N. Contact Lens Practice E-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Smith, T.W. Corneal topography. Doc. Ophthalmol. 1977, 43, 249–276. [Google Scholar] [CrossRef] [PubMed]
- Forrester, J.V.; Dick, A.D.; McMenamin, P.G.; Roberts, F.; Pearlman, E. The Eye E-Book: Basic Sciences in Practice; Elsevier Health Sciences: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Reinstein, D.Z.; Gobbe, M.; Archer, T.J. Anterior segment biometry: A study and review of resolution and repeatability data. J. Refract. Surg. 2012, 28, 509–520. [Google Scholar] [CrossRef] [PubMed]
- Mireskandari, K.; Tehrani, N.N.; VandenHoven, C.; Ali, A. Anterior segment imaging in pediatric ophthalmology. J. Cataract Refract. Surg. 2011, 37, 2201–2210. [Google Scholar] [CrossRef] [PubMed]
- Kuo, A.N.; McNabb, R.P.; Zhao, M.; LaRocca, F.; Stinnett, S.S.; Farsiu, S.; Izatt, J.A. Corneal biometry from volumetric SDOCT and comparison with existing clinical modalities. Biomed. Opt. Express 2012, 3, 1279–1290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polans, J.; Jaeken, B.; McNabb, R.P.; Artal, P.; Izatt, J.A. Wide-field optical model of the human eye with asymmetrically tilted and decentered lens that reproduces measured ocular aberrations. Optica 2015, 2, 124–134. [Google Scholar] [CrossRef] [Green Version]
- Dai, P.; Wang, B.; Bao, C.; Ju, Y. Constructing a computer model of the human eye based on tissue slice images. J. Biomed. Imaging 2010, 2010, 15. [Google Scholar] [CrossRef] [Green Version]
- Donnelly, W. The Advanced Human Eye Model (AHEM): A personal binocular eye modeling system inclusive of refraction, diffraction, and scatter. J. Refract. Surg. 2008, 24, 976–983. [Google Scholar] [CrossRef]
- Bahrami, M.; Goncharov, A.V. Geometry-invariant GRIN lens: Finite ray tracing. Opt. Express 2014, 22, 27797–27810. [Google Scholar] [CrossRef]
- Sheil, C.J.; Bahrami, M.; Goncharov, A.V. An analytical method for predicting the geometrical and optical properties of the human lens under accommodation. Biomed. Opt. Express 2014, 5, 1649–1663. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Fang, F. Advances and challenges of soft contact lens design for myopia control. Appl. Opt. 2019, 58, 1639–1656. [Google Scholar] [CrossRef]
- Zeng, L.; Fang, F. Advances and challenges of intraocular lens design. Appl. Opt. 2018, 57, 7363–7376. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-J.; Kim, M.; Hyeon, M.G.; Choi, Y.; Kim, B.-M. Full ocular biometry through dual-depth whole-eye optical coherence tomography. Biomed. Opt. Express 2018, 9, 360–372. [Google Scholar] [CrossRef] [PubMed]
- Belin, M.W.; Khachikian, S.S. An introduction to understanding elevation-based topography: How elevation data are displayed—A review. Clin. Exp. Ophthalmol. 2008, 37, 14–29. [Google Scholar] [CrossRef] [PubMed]
- Mandell, R.B. Jesse Ramsden: Inventor of the ophthalmometer. Optom. Vis. Sci. 1960, 37, 633–638. [Google Scholar] [CrossRef] [PubMed]
- Belin, M.W.; Khachikian, S.S.; Ambrósio, R., Jr. Elevation Based Corneal Tomography; JP Medical Ltd.: New Delhi, India, 2012. [Google Scholar]
- Rubin, M.L. Optics for Clinicians; Triad Publishing Company: Gainesville, FL, USA, 1974. [Google Scholar]
- McNabb, R.P.; LaRocca, F.; Farsiu, S.; Kuo, A.N.; Izatt, J.A. Distributed scanning volumetric SDOCT for motion corrected corneal biometry. Biomed. Opt. Express 2012, 3, 2050–2065. [Google Scholar] [CrossRef]
- Kirgiz, A.; Atalay, K.; Kaldirim, H.; Cabuk, K.S.; Akdemir, M.O.; Taskapili, M. Scheimpflug camera combined with placido-disk corneal topography and optical biometry for intraocular lens power calculation. Int. Ophthalmol. 2017, 37, 781–786. [Google Scholar] [CrossRef] [PubMed]
- Brody, J.; Waller, S.; Wagoner, M. Corneal topography: History, technique, and clinical uses. Int. Ophthalmol. Clin. 1994, 34, 197–207. [Google Scholar] [CrossRef]
- Levene, J.R. The true inventors of the keratoscope and photo-keratoscope. Br. J. Hist. Sci. 1965, 2, 324–342. [Google Scholar] [CrossRef]
- Schanzlin, D.J.; Robin, J.B. Corneal Topography (Measuring and Modifying the Cornea); Springer: New York, NY, USA, 1992. [Google Scholar]
- Gullstrand, A. Procedure of the rays in the eye. Imagery-Laws of the first order. In Helmholtz’s Treatise on Physiological Optics; English translation edited by Southall JP; Optical Society of America: Rochester, NY, USA, 1924; Volume 1, pp. 350–358. [Google Scholar]
- Ambrósio, R.; Belin, M.W. Imaging of the cornea: Topography vs tomography. J. Refract. Surg. 2010, 26, 847–849. [Google Scholar] [CrossRef] [Green Version]
- Assiri, A.A. A Clinical and Ultrastructural Investigation of the Cornea in Keratoconus; Cardiff University: Cardiff, UK, 2006. [Google Scholar]
- Klyce, S.D. Computer-assisted corneal topography. High-resolution graphic presentation and analysis of keratoscopy. Investig. Ophthalmol. Vis. Sci. 1984, 25, 1426–1435. [Google Scholar]
- Ramamurthy, S.; Reddy, J.C.; Jhanji, V. Topography and tomography in the diagnosis of corneal ectasia. Expert Rev. Ophthalmol. 2015, 10, 215–228. [Google Scholar] [CrossRef]
- Drexler, W.; Baumgartner, A.; Findl, O.; Hitzenberger, C.K.; Sattmann, H.; Fercher, A.F. Submicrometer precision biometry of the anterior segment of the human eye. Investig. Ophthalmol. Vis. Sci. 1997, 38, 1304–1313. [Google Scholar]
- Fan, R.; Chan, T.C.; Prakash, G.; Jhanji, V. Applications of corneal topography and tomography: A review. Clin. Exp. Ophthalmol. 2018, 46, 133–146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, J.; Lu, W.; Savini, G.; Hu, L.; Pan, C.; Wang, J.; Tan, W.; Chen, J.; Wang, Q. Evaluation of corneal thickness using a Scheimpflug–Placido disk corneal analyzer and comparison with ultrasound pachymetry in eyes after laser in situ keratomileusis. J. Cataract Refract. Surg. 2013, 39, 1074–1080. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Savini, G.; Schiano-Lomoriello, D.; Hoffer, K.J. Repeatability of automatic measurements by a new anterior segment optical coherence tomographer combined with Placido topography and agreement with 2 Scheimpflug cameras. J. Cataract Refract. Surg. 2018, 44, 471–478. [Google Scholar] [CrossRef]
- Schultze, R.L. Accuracy of corneal elevation with four corneal topography systems. J. Refract. Surg. 1998, 14, 100–104. [Google Scholar] [CrossRef]
- Brenner, D. Modeling the cornea with the topographic modeling system videokeratoscope. Optom. Vis. Sci. 1997, 74, 895–898. [Google Scholar] [CrossRef]
- Yaron, S.R.; Anthony, B.N.; Peter, J.M. Videokeratography of the Fellow Eye in Unilateral Keratoconus. Ophthalmology 1993, 100, 181–186. [Google Scholar]
- Knoll, H.A.; Stimson, R.; Weeks, C.L. New photokeratoscope utilizing a hemispherical object surface. J. Opt. Soc. Am. 1957, 47, 221. [Google Scholar] [CrossRef]
- Mejía-Barbosa, Y.; Malacara-Hernández, D. A Review of Methods for Measuring Corneal Topography. Optom. Vis. Sci. Off. Publ. Am. Acad. Optom. 2001, 78, 240–253. [Google Scholar] [CrossRef] [Green Version]
- Rand, R.; Howland, H.C.; Applegate, R. Mathematical Model of a Placido Disk Keratometer and Its Implications for Recovery of Corneal Topography. Optom. Vis. Sci. 1997, 74, 926–930. [Google Scholar] [CrossRef] [PubMed]
- Piñero, D.P. Technologies for Anatomical and Geometric Characterization of the Corneal Structure and Anterior Segment: A Review. Semin. Ophthalmol. 2015, 30, 161–170. [Google Scholar] [CrossRef]
- Olsen, T. On the calculation of power from curvature of the cornea. Br. J. Ophthalmol. 1986, 70, 152–154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seitz, B.; Langenbucher, A.; Nguyen, N.X.; Kus, M.M.; Küchle, M. Underestimation of intraocular lens power for cataract surgery after myopic photorefractive keratectomy. Ophthalmology 1999, 106, 693–702. [Google Scholar] [CrossRef]
- Belin, M.W.; Cambier, J.L.; Nabors, J.R.; Ratliff, C.D. PAR Corneal Topography System (PAR CTS): The clinical application of close-range photogrammetry. Optom. Vis. Sci. Off. Publ. Am. Acad. Optom. 1995, 72, 828–837. [Google Scholar] [CrossRef] [PubMed]
- Belin, M.W. Intraoperative raster photogrammetry—The PAR Corneal Topography System. J. Cataract Refract. Surg. 1993, 19, 188–192. [Google Scholar] [CrossRef]
- Jongsma, F.; de Brabander, J.; Hendrikse, F. Review and classification of corneal topographers. Lasers Med. Sci. 1999, 14, 2–19. [Google Scholar] [CrossRef]
- Azar, D.T.; Koch, D. LASIK (Laser In Situ Keratomileusis): Fundamentals, Surgical Techniques, and Complications; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Smolek, M.K. Holographic interferometry of intact and radially incised human eye-bank corneas. J. Cataract Refract. Surg. 1994, 20, 277–286. [Google Scholar] [CrossRef]
- Baker, P.C. Holographic contour analysis of the cornea. In Noninvasive Diagnostic Techniques in Ophthalmology; Springer: Berlin/Heidelberg, Germany, 1990; pp. 82–98. [Google Scholar]
- Grolman, B.; Lawton, K. The hologram and its ophthalmic potential. Optom. Vis. Sci. 1966, 43, 351–363. [Google Scholar]
- Friedlander, M.H.; Mulet, M.; Buzard, K.A.; Granet, N.; Baker, P.C. Holographic interferometry of the corneal surface. In Proceedings of the Holography, Interferometry, and Optical Pattern Recognition in Biomedicine, Los Angeles, CA, USA, 21–22 January 1991. [Google Scholar]
- Kasprzak, H.T.; Kowalik, W.; Jaronski, J.W. Interferometric measurements of fine corneal topography. In Optical and Imaging Techniques in Biomedicine; International Society for Optics and Photonics: Bellingham, WA, USA, 1995; Volume 2329, pp. 32–40. [Google Scholar]
- Politch, J. Optical and long wave holography: Potential applications in ophthalmology. Doc. Ophthalmol. 1977, 43, 165–175. [Google Scholar] [CrossRef]
- Burris, T.E.; Holmes-Higgin, D.K.; Silvestrini, T.A.; Scholl, J.A.; Proudfoot, R.A.; Baker, P.C. Corneal asphericity in eye bank eyes implanted with the intrastromal corneal ring. J. Refract. Surg. 1997, 13, 556–567. [Google Scholar]
- Burris, T.E.; Baker, P.C.; Ayer, C.T.; Loomas, B.E.; Mathis, M.L.; Silvestrini, T.A. Flattening of central corneal curvature with intrastromal corneal rings of increasing thickness: An eye-bank eye study. J. Cataract Refract. Surg. 1993, 19, 182–187. [Google Scholar] [CrossRef]
- Kasprzak, H.; Foerster, W.; von Bally, G. Holographic measurement of changes of the central corneal curvature due to intraocular pressure differences. Opt. Eng. 1994, 33, 198–203. [Google Scholar] [CrossRef]
- Stavroulakis, P.; Leach, R.K. Invited review article: Review of post-process optical form metrology for industrial-grade metal additive manufactured parts. Rev. Sci. Instrum. 2016, 87, 041101. [Google Scholar] [CrossRef]
- Mandell, R.B.; Polse, K.A. Keratoconus: Spatial Variation of Corneal Thickness as a Diagnostic Test. Arch. Ophthalmol. 1969, 82, 182–188. [Google Scholar] [CrossRef]
- Kawara, T. Corneal topography using moiré contour fringes. Appl. Opt. 1979, 18, 3675–3678. [Google Scholar] [CrossRef]
- Adachi, I.P.; Adachi, Y.; Frazer, R.E. Real-Time Analysis Keratometer. U.S. Patents US4692003A, 8 September 1987. [Google Scholar]
- Corbett, M.C.; O’brart, D.P.; Bertho, A.T.; Jongsma, F.H.; Marshall, J. Corneal topography using a new moire image-based system. Eur. J. Implant Refract. Surg. 1995, 7, 353–370. [Google Scholar] [CrossRef]
- Jongsma, F.H.; Hendrikse, F.; Stultiens, B. Development of a wide field height eye topographer: Validation on models of the anterior eye surface. Optom. Vis. Sci. Off. Publ. Am. Acad. Optom. 1998, 75, 69–77. [Google Scholar] [CrossRef]
- Chang, W.-Y.; Chen, K.-H.; Chen, D.-C.; Tseng, J.-K.; Chen, S.-T.; Sun, H.-Y.; Chen, J.-H.; Hsu, K.Y. Corneal surface reconstruction by using heterodyne Moiré method. In Optical Methods for Inspection, Characterization, and Imaging of Biomaterials; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8792, p. 87920B. [Google Scholar]
- Chang, W.-Y.; Chen, K.-H.; Chen, D.-C.; Tseng, J.-K.; Chen, S.-T.; Sun, H.-Y.; Chen, J.-H.; Hsu, K.Y. Heterodyne moiré interferometry for measuring corneal surface profile. Opt. Lasers Eng. 2014, 54, 232–235. [Google Scholar] [CrossRef]
- Risaliti, R.; Ronchi, L. An interferometric non-contact method for the determination of the shape of the cornea or other smooth reflecting objects. Atti de la Fondazione Giorgio Ronchi 1990, 45, 79–87. [Google Scholar]
- Hochberg, E.B.; Baroth, E.C. Method and Apparatus for White-Light Dispersed-Fringe Interferometric Measurement of Corneal Topography. U.S. Patents US5317389A, 31 May 1994. [Google Scholar]
- Rottenkolber, M.; Podbielska, H. High precision Twyman-Green interferometer for the measurement of ophthalmic surfaces. Acta Ophthalmol. Scand. 1996, 74, 348–353. [Google Scholar] [CrossRef] [PubMed]
- Licznerski, T.J.; Kasprzak, H. Reconstruction of the corneal topography from lateral-shearing interferograms. In Proceedings of the 11th Slovak-Czech-Polish Optical Conference on Wave and Quantum Aspects of Contemporary Optics, Stará Lesná, Slovakia, 21–25 September 1998; International Society for Optics and Photonics: Bellingham, WA, USA, 1999. [Google Scholar]
- Kowalik, W.; Garncarz, B.E.; Kasprzak, H. Corneal topography measurement of the eye by means of radial shearing interferometer. In Proceedings of the 12th Czech-Slovak-Polish Optical Conference on Wave and Quantum Aspects of Contemporary Optics, Velké Losiny, Czech Republic, 12–15 September 2000; International Society for Optics and Photonics: Bellingham, WA, USA, 2001. [Google Scholar]
- Kasprzak, H.; Jaronski, J.W. Measurement of fine dynamic changes of corneal topography by use of interferometry. In Proceedings of the Interferometry XI: Applications, Seattle, WA, USA, 7–11 July 2002. [Google Scholar]
- Licznerski, T.J.; Jaronski, J.; Kosz, D. Novel double path shearing interferometer in corneal topography measurements. In Proceedings of the Medical Imaging, Warsaw, Poland, 28 August–2 September 2005. [Google Scholar]
- Micali, J.D.; Greivenkamp, J.E. Dual interferometer for dynamic measurement of corneal topography. J. Biomed. Opt. 2016, 21, 085007. [Google Scholar] [CrossRef] [Green Version]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Lasers Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Jang, Y.-S.; Kim, S.-W. Distance Measurements Using Mode-Locked Lasers: A Review. Nanomanuf. Metrol. 2018, 1, 131–147. [Google Scholar] [CrossRef]
- Klein, S.; Corzine, J.; Corbin, J.A.; Wechsler, S.; Carney, T. Wide-angle cornea-sclera (OCULAR) topography. In Proceedings of the Ophthalmic Technologies XII, San Jose, CA, USA, 19–25 January 2002. [Google Scholar]
- Iskander, D.R.; Wachel, P.; Simpson, P.N.D.; Vaquero, A.; Andrade De Jesus, D. Principles of operation, accuracy and precision of an Eye Surface Profiler. Ophthalmic Physiol. Opt. 2016, 36, 266–278. [Google Scholar] [CrossRef]
- Buytaert, J.A.; Dirckx, J.J. Moiré profilometry using liquid crystals for projection and demodulation. Opt. Express 2008, 16, 179–193. [Google Scholar] [CrossRef]
- Rao, S.N.; Raviv, T.; Majmudar, P.A.; Epstein, R. Role of Orbscan II in screening keratoconus suspects before refractive corneal surgery. Ophthalmology 2002, 109, 1642–1646. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, A.J.; Pflugfelder, S.C. Evaluation of corneal thickness and topography in normal eyes using the Orbscan corneal topography system. Br. J. Ophthalmol. 1999, 83, 774–778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nayak, B.K.; Dharwadkar, S. Corneal topography and tomography. J. Clin. Ophthalmol. Res. 2015, 3, 45. [Google Scholar] [CrossRef]
- Artal, P. Handbook of Visual Optics, Volume Two: Instrumentation and Vision Correction; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Nilforoushan, M.R.; Speaker, M.; Marmor, M.; Abramson, J.; Tullo, W.; Morschauser, D.; Latkany, R. Comparative evaluation of refractive surgery candidates with Placido topography, Orbscan II, Pentacam, and wavefront analysis. J. Cataract Refract. Surg. 2008, 34, 623–631. [Google Scholar] [CrossRef]
- Guilbert, E.; Saad, A.; Grise-Dulac, A.; Gatinel, D. Corneal thickness, curvature, and elevation readings in normal corneas: Combined Placido–Scheimpflug system versus combined Placido–scanning-slit system. J. Cataract Refract. Surg. 2012, 38, 1198–1206. [Google Scholar] [CrossRef]
- Crawford, A.Z.; Patel, D.V.; McGhee, C.N.J. Comparison and Repeatability of Keratometric and Corneal Power Measurements Obtained by Orbscan II, Pentacam, and Galilei Corneal Tomography Systems. Am. J. Ophthalmol. 2013, 156, 53–60. [Google Scholar] [CrossRef]
- Swartz, T.; Marten, L.; Wang, M. Measuring the cornea: The latest developments in corneal topography. Curr. Opin. Ophthalmol. 2007, 18, 325–333. [Google Scholar] [CrossRef]
- Millodot, M. Dictionary of Optometry and Vision Science E-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Koretz, J.F.; Strenk, S.A.; Strenk, L.M.; Semmlow, J.L. Scheimpflug and high-resolution magnetic resonance imaging of the anterior segment: A comparative study. JOSA A 2004, 21, 346–354. [Google Scholar] [CrossRef]
- Wegener, A.; Laser-Junga, H. Photography of the anterior eye segment according to Scheimpflug’s principle: Options and limitations—A review. Clin. Exp. Ophthalmol. 2009, 37, 144–154. [Google Scholar] [CrossRef]
- Montalbán, R.; Piñero, D.P.; Javaloy, J.; Alió, J.L. Intrasubject repeatability of corneal morphology measurements obtained with a new Scheimpflug photography–based system. J. Cataract Refract. Surg. 2012, 38, 971–977. [Google Scholar] [CrossRef]
- Savini, G.; Carbonelli, M.; Barboni, P.; Hoffer, K.J. Repeatability of automatic measurements performed by a dual Scheimpflug analyzer in unoperated and post-refractive surgery eyes. J. Cataract Refract. Surg. 2011, 37, 302–309. [Google Scholar] [CrossRef]
- Salouti, R.; Nowroozzadeh, M.H.; Zamani, M.; Fard, A.H.; Niknam, S. Comparison of anterior and posterior elevation map measurements between 2 Scheimpflug imaging systems. J. Cataract Refract. Surg. 2009, 35, 856–862. [Google Scholar] [CrossRef]
- Boscia, F.; la Tegola, M.G.; Alessio, G.; Sborgia, C. Accuracy of Orbscan optical pachymetry in corneas with haze. J. Cataract Refract. Surg. 2002, 28, 253–258. [Google Scholar] [CrossRef]
- Milla, M.; Piñero, D.P.; Amparo, F.; Alió, J.L. Pachymetric measurements with a new Scheimpflug photography–based system: Intraobserver repeatability and agreement with optical coherence tomography pachymetry. J. Cataract Refract. Surg. 2011, 37, 310–316. [Google Scholar] [CrossRef]
- Lackner, B.; Schmidinger, G.; Skorpik, C. Validity and Repeatability of Anterior Chamber Depth Measurements with Pentacam and Orbscan. Optom. Vis. Sci. 2005, 82, 858–861. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubbelman, M.; van der Heijde, G.; Weeber, H.A. The thickness of the aging human lens obtained from corrected Scheimpflug images. Optom. Vis. Sci. 2001, 78, 411–416. [Google Scholar] [CrossRef] [PubMed]
- Rosales, P.; Marcos, S. Pentacam Scheimpflug Quantitative Imaging of the Crystalline Lens and Intraocular Lens. J. Refract. Surg. 2009, 25, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Brown, N. An advanced slit-image camera. Br. J. Ophthalmol. 1972, 56, 624–631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dragomirescu, V.; Hockwin, O.; Koch, H.R.; Sasaki, K. Development of a New Equipment for Rotating Slit Image Photography According to Scheimpflug’s Principle; Karger Publishers: Basel, Switzerland, 1978; pp. 118–130. [Google Scholar]
- Hockwin, O.; Dragomirescu, V.; Laser, H.; Wegener, A.; Eckerskorn, U. Measuring Lens transparency by scheimpflug photography of the anterior eye segment: Principle, instrumentation, and application to clinical and experimental ophthalmology. J. Toxicol. Cutan. Ocul. Toxicol. 1987, 6, 251–271. [Google Scholar] [CrossRef]
- Sparrow, J.; Brown, N.; Shun-Shin, G.A.; Bron, A. The Oxford Modular Cataract Image Analysis System. Eye 1990, 4, 638–648. [Google Scholar] [CrossRef]
- Sasaki, K.; Sakamoto, Y.; Shibata, T.; Emori, Y. The Multi-Purpose Camera: A New Anterior Eye Segment Analysis System. Ophthalmic Res. 1990, 22 (Suppl. 1), 3–8. [Google Scholar] [CrossRef]
- Rabsilber, T.M.; Khoramnia, R.; Auffarth, G. Anterior chamber measurements using Pentacam rotating Scheimpflug camera. J. Cataract Refract. Surg. 2006, 32, 456–459. [Google Scholar] [CrossRef]
- Shankar, H.; Taranath, D.; Santhirathelagan, C.T.; Pesudovs, K. Anterior segment biometry with the Pentacam: Comprehensive assessment of repeatability of automated measurements. J. Cataract Refract. Surg. 2008, 34, 103–113. [Google Scholar] [CrossRef]
- Grewal, D.; Jain, R.; Brar, G.; Grewal, S.P.S. Pentacam Tomograms: A Novel Method for Quantification of Posterior Capsule Opacification. Investig. Ophthalmol. Vis. Sci. 2008, 49, 2004–2008. [Google Scholar] [CrossRef]
- Turner, S.J.; Lee, E.; Hu, V.; Hollick, E. Scheimpflug imaging to determine intraocular lens power in vivo. J. Cataract Refract. Surg. 2007, 33, 1041–1044. [Google Scholar] [CrossRef] [PubMed]
- Khurana, R.N.; Li, Y.; Tang, M.; Lai, M.M.; Huang, D. High-speed optical coherence tomography of corneal opacities. Ophthalmology 2007, 114, 1278–1285. [Google Scholar] [CrossRef]
- Turner, J. Wide-Field Anterior Ocular Surface Morphometrics; Cardiff University: Cardiff, UK, 2011. [Google Scholar]
- Jain, R.; Grewal, S. Pentacam: Principle and clinical applications. J. Curr. Glaucoma Pract. 2009, 3, 20–32. [Google Scholar] [CrossRef]
- Karnowski, K.; Kaluzny, B.J.; Szkulmowski, M.; Gora, M.; Wojtkowski, M. Corneal topography with high-speed swept source OCT in clinical examination. Biomed. Opt. Express 2011, 2, 2709–2720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konstantopoulos, A.; Hossain, P.; Anderson, D.F. Recent advances in ophthalmic anterior segment imaging: A new era for ophthalmic diagnosis? Br. J. Ophthalmol. 2007, 91, 551–557. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meinhardt, B.; Stachs, O.; Stave, J.; Beck, R.; Guthoff, R. Evaluation of biometric methods for measuring the anterior chamber depth in the non-contact mode. Graefe’s Arch. Clin. Exp. Ophthalmol. 2006, 244, 559. [Google Scholar] [CrossRef]
- Amano, S.; Honda, N.; Amano, Y.; Yamagami, S.; Miyai, T.; Samejima, T.; Ogata, M.; Miyata, K. Comparison of central corneal thickness measurements by rotating Scheimpflug camera, ultrasonic pachymetry, and scanning-slit corneal topography. Ophthalmology 2006, 113, 937–941. [Google Scholar] [CrossRef] [PubMed]
- Buehl, W.; Stojanac, D.; Sacu, S.; Drexler, W.; Findl, O. Comparison of three methods of measuring corneal thickness and anterior chamber depth. Am. J. Ophthalmol. 2006, 141, 7–12.e1. [Google Scholar] [CrossRef]
- Cook, C.A.; Koretz, J.F. Methods to obtain quantitative parametric descriptions of the optical surfaces of the human crystalline lens from Scheimpflug slit-lamp images. I. Image processing methods. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1998, 15, 1473–1485. [Google Scholar] [CrossRef]
- Ortiz, S. Quantitative Anterior Segment Optical Coherence Tomography. Ph.D. Thesis, Institute of Optics, University of Valladolid, Valladolid, Spain, 2012. [Google Scholar]
- Silverman, R.H. High-resolution ultrasound imaging of the eye—A review. Clin. Exp. Ophthalmol. 2009, 37, 54–67. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishnan, S.; Goldsmith, J.; Huang, D.; Westphal, V.; Dueker, D.K.; Rollins, A.M.; Izatt, J.A.; Smith, S.D. Comparison of optical coherence tomography and ultrasound biomicroscopy for detection of narrow anterior chamber angles. Arch. Ophthalmol. 2005, 123, 1053–1059. [Google Scholar] [CrossRef] [Green Version]
- Dada, T.; Sihota, R.; Gadia, R.; Aggarwal, A.; Mandal, S.; Gupta, V. Comparison of anterior segment optical coherence tomography and ultrasound biomicroscopy for assessment of the anterior segment. J. Cataract Refract. Surg. 2007, 33, 837–840. [Google Scholar] [CrossRef]
- Foster, F.S.; Pavlin, C.J.; Harasiewicz, K.A.; Christopher, D.A.; Turnbull, D.H. Advances in ultrasound biomicroscopy. Ultrasound Med. Biol. 2000, 26, 1–27. [Google Scholar] [CrossRef]
- Pavlin, C.J.; Foster, F.S. Ultrasound Biomicroscopy of the Eye; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- He, M.; Wang, D.; Jiang, Y. Overview of Ultrasound Biomicroscopy. J. Curr. Glaucoma Pract. 2012, 6, 25–53. [Google Scholar] [CrossRef]
- Nolan, W. Anterior segment imaging: Ultrasound biomicroscopy and anterior segment optical coherence tomography. Curr. Opin. Ophthalmol. 2008, 19, 115–121. [Google Scholar] [CrossRef]
- Mundt, G.H.; Hughes, W.F. Ultrasonics in Ocular Diagnosis. Am. J. Ophthalmol. 2018, 189, xxviii–xxxvi. [Google Scholar] [CrossRef]
- Baum, G.; Greenwood, I. The application of ultrasonic locating techniques to ophthalmology. II. Ultrasonic slit lamp in the ultrasonic visualization of soft tissues. AMA Arch. Ophthalmol. 1958, 60, 263–279. [Google Scholar] [CrossRef]
- Molgat, Y.M.; Pavlin, C.J.; Hurwitz, J.J. Ultrasound biomicroscopy as a diagnostic tool in space-occupying lesions of the superotemporal conjunctival fornix. Orbit 1993, 12, 121–126. [Google Scholar] [CrossRef]
- Pavlin, C.; Harasiewicz, K.; Foster, F.S. Ultrasound Biomicroscopy of Anterior Segment Structures in Normal and Glaucomatous Eyes. Am. J. Ophthalmol. 1992, 113, 381–389. [Google Scholar] [CrossRef]
- Pavlin, C.; Sherar, M.D.; Foster, F.S. Subsurface Ultrasound Microscopic Imaging of the Intact Eye. Ophthalmology 1990, 97, 244–250. [Google Scholar] [CrossRef]
- Pavlin, C.; Harasiewicz, K.; Sherar, M.D.; Foster, F.S. Clinical Use of Ultrasound Biomicroscopy. Ophthalmology 1991, 98, 287–295. [Google Scholar] [CrossRef]
- Hrynchak, P.; Simpson, T. Optical Coherence Tomography: An Introduction to the Technique and its Use. Optom. Vis. Sci. 2000, 77, 347–356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, C.; Wang, J.; Jiao, S. Dual channel dual focus optical coherence tomography for imaging accommodation of the eye. Opt. Express 2009, 17, 8947–8955. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishnan, S.; Rollins, A.M.; Roth, J.E.; Yazdanfar, S.; Westphal, V.; Bardenstein, D.S.; Izatt, J.A. Real-time optical coherence tomography of the anterior segment at 1310 nm. Arch. Ophthalmol. 2001, 119, 1179–1185. [Google Scholar] [CrossRef] [Green Version]
- Drexler, W.; Liu, M.; Kumar, A.; Kamali, T.; Unterhuber, A.; Leitgeb, R. Optical coherence tomography today: Speed, contrast, and multimodality. J. Biomed. Opt. 2014, 19, 071412. [Google Scholar] [CrossRef]
- Ang, M.; Baskaran, M.; Werkmeister, R.M.; Chua, J.; Schmidl, D.; Dos Santos, V.A.; Garhöfer, G.; Mehta, J.S.; Schmetterer, L. Anterior segment optical coherence tomography. Prog. Retin. Eye Res. 2018, 66, 132–156. [Google Scholar] [CrossRef]
- Stockman, A. Anterior Segment Optical Coherence Tomography. Cornea 2018, 37 (Suppl. 1), S9–S10. [Google Scholar] [CrossRef]
- Pawley, J. Handbook of Biological Confocal Microscopy; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Sharma, R.; Sharma, A.; Arora, T.; Sharma, S.; Sobti, A.; Jha, B.; Chaturvedi, N.; Dada, T. Application of anterior segment optical coherence tomography in glaucoma. Surv. Ophthalmol. 2014, 59, 311–327. [Google Scholar] [CrossRef]
- Bouma, B. Handbook of Optical Coherence Tomography; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Frosz, M.H.; Juhl, M.; Lang, M.H. Optical Coherence Tomography: System Design and Noise Analysis; Risø National Laboratory: Roskilde, Denmark, 2001. [Google Scholar]
- Fercher, A.; Drexler, W.; Hitzenberger, C.; Lasser, T. Optical Coherence Tomography—Principles and Applications. Rep. Prog. Phys. 2003, 66, 239–303. [Google Scholar] [CrossRef]
- Burcheri-Curatolo, A. Advances of Full-Field Optical Coherence Tomography (FFOCT) for Clinical Applications and Developmental Biology. Ph.D. Thesis, Université Pierre et Marie Curie-Paris VI, Paris, France, 2012. [Google Scholar]
- Raghunathan, R.; Singh, M.; Dickinson, M.; Larin, K.V. Optical coherence tomography for embryonic imaging: A review. J. Biomed. Opt. 2016, 21, 050902. [Google Scholar] [CrossRef] [Green Version]
- Soe, N.; Tian, J.; Marziliano, P.; Wong, H.-T. Anterior Chamber Angle Shape Analysis and Classification of Glaucoma in SS-OCT Images. J. Ophthalmol. 2014, 2014, 1–12. [Google Scholar]
- Monroy, G.L.; Won, J. Clinical translation of handheld optical coherence tomography: Practical considerations and recent advancements. J. Biomed. Opt. 2017, 22, 121715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, K.-C.; Li, R.-J.; Xu, P. Design and Verification of Micro/Nano-Probes for Coordinate Measuring Machines. Nanomanuf. Metrol. 2019, 2, 1–15. [Google Scholar] [CrossRef]
- Izatt, J.A.; Hee, M.R.; Swanson, E.A.; Lin, C.P.; Huang, D.; Schuman, J.S.; Puliafito, C.A.; Fujimoto, J.G. Micrometer-scale resolution imaging of the anterior eye in vivo with optical coherence tomography. Arch. Ophthalmol. 1994, 112, 1584–1589. [Google Scholar] [CrossRef]
- Grieve, K.; Dubois, A.; Simonutti, M.; Paques, M.; Sahel, J.; Le Gargasson, J.F.; Boccara, C. In vivo anterior segment imaging in the rat eye with high speed white light full-field optical coherence tomography. Opt. Express 2005, 13, 6286–6295. [Google Scholar] [CrossRef]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [Green Version]
- De Boer, J.F.; Leitgeb, R.; Wojtkowski, M. Twenty-five years of optical coherence tomography: The paradigm shift in sensitivity and speed provided by Fourier domain OCT [Invited]. Biomed. Opt. Express 2017, 8, 3248–3280. [Google Scholar] [CrossRef] [Green Version]
- Potsaid, B.; Baumann, B.; Huang, D.; Barry, S.; Cable, A.E.; Schuman, J.S.; Duker, J.S.; Fujimoto, J.G. Ultrahigh speed 1050nm swept source/Fourier domain OCT retinal and anterior segment imaging at 100,000 to 400,000 axial scans per second. Opt. Express 2010, 18, 20029–20048. [Google Scholar] [CrossRef] [Green Version]
- Baskaran, M.; Ho, S.W.; Tun, T.A.; How, A.C.; Perera, S.A.; Friedman, D.S.; Aung, T. Assessment of Circumferential Angle-Closure by the Iris–Trabecular Contact Index with Swept-Source Optical Coherence Tomography. Ophthalmology 2013, 120, 2226–2231. [Google Scholar] [CrossRef]
- Jancevski, M.; Foster, C.S. Anterior segment optical coherence tomography. In Seminars in Ophthalmology; Taylor & Francis: Abingdon, UK, 2010; Volume 25, pp. 317–323. [Google Scholar]
- An, L.; Li, P.; Lan, G.; Malchow, D.; Wang, R. High-resolution 1050 nm spectral domain retinal optical coherence tomography at 120 kHz A-scan rate with 6.1 mm imaging depth. Biomed. Opt. Express 2013, 4, 245–259. [Google Scholar] [CrossRef]
- Choma, M.A.; Sarunic, M.V.; Yang, C.; Izatt, J. Sensitivity advantage of swept source and Fourier domain optical coherence tomography. Opt. Express 2003, 11, 2183–2189. [Google Scholar] [CrossRef] [Green Version]
- Wieser, W.; Draxinger, W.; Klein, T.; Karpf, S.; Pfeiffer, T.; Huber, R. High definition live 3D-OCT in vivo: Design and evaluation of a 4D OCT engine with 1 GVoxel/s. Biomed. Opt. Express 2014, 5, 2963–2977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fercher, A.; Hitzenberger, C.; Kamp, G.; El-Zaiat, S.Y. Measurement of Intraocular Distances by Backscattering Spectral Interferometry. Opt. Commun. 1995, 117, 43–48. [Google Scholar] [CrossRef]
- Grulkowski, I.; Liu, J.J.; Zhang, J.Y.; Potsaid, B.; Jayaraman, V.; Cable, A.E.; Duker, J.S.; Fujimoto, J.G. Reproducibility of a Long-Range Swept-Source Optical Coherence Tomography Ocular Biometry System and Comparison with Clinical Biometers. Ophthalmology 2013, 120, 2184–2190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bajraszewski, T.; Wojtkowski, M.; Szkulmowski, M.; Szkulmowska, A.; Huber, R.; Kowalczyk, A. Improved spectral optical coherence tomography using optical frequency comb. Opt. Express 2008, 16, 4163–4176. [Google Scholar] [CrossRef]
- Grulkowski, I.; Liu, J.J.; Potsaid, B.; Jayaraman, V.; Lu, C.D.; Jiang, J.; Cable, A.E.; Duker, J.S.; Fujimoto, J.G. Retinal, anterior segment and full eye imaging using ultrahigh speed swept source OCT with vertical-cavity surface emitting lasers. Biomed. Opt. Express 2012, 3, 2733–2751. [Google Scholar] [CrossRef] [Green Version]
- Mazlin, V.; Xiao, P.; Dalimier, E.; Grieve, K.; Irsch, K.; Sahel, J.A.; Fink, M.; Boccara, A.C. In vivo high resolution human corneal imaging using full-field optical coherence tomography. Biomed. Opt. Express 2018. [Google Scholar] [CrossRef] [Green Version]
- Ghouali, W.; Grieve, K.; Bellefqih, S.; Sandali, O.; Harms, F.; Laroche, L.; Paques, M.; Borderie, V. Full-Field Optical Coherence Tomography of Human Donor and Pathological Corneas. Curr. Eye Res. 2015, 40, 526–534. [Google Scholar] [CrossRef]
- Mikulewitsch, M.; Auerswald, M.M.; von Freyberg, A.; Fischer, A. Geometry measurement of submerged metallic micro-parts using confocal fluorescence microscopy. Nanomanuf. Metrol. 2018, 1, 171–179. [Google Scholar] [CrossRef]
- Drexler, W.; Fujimoto, J.G. Optical Coherence Tomography: Technology and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Akiba, M.; Chan, K.P.; Tanno, N. Full-field optical coherence tomography by two-dimensional heterodyne detection with a pair of CCD cameras. Opt. Lett. 2003, 28, 816–818. [Google Scholar] [CrossRef]
- Grieve, K.; Moneron, G.; Dubois, A.; Gargasson, J.F.L.; Boccara, C. Ultrahigh resolution ex vivo ocular imaging using ultrashort acquisition time en face optical coherence tomography. J. Opt. A Pure Appl. Opt. 2010, 7, 368–373. [Google Scholar] [CrossRef]
- Dubois, A.; Moneron, G.; Boccara, C. Thermal-light full-field optical coherence tomography in the 1.2 μm wavelength region. Opt. Commun. 2006, 266, 738–743. [Google Scholar] [CrossRef] [Green Version]
- Apelian, C.; Harms, F.; Thouvenin, O.; Boccara, A.C. Dynamic full field optical coherence tomography: Subcellular metabolic contrast revealed in tissues by interferometric signals temporal analysis. Biomed. Opt. Express 2016, 7, 1511. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boccara, C.; Harms, F.; Latrive, A. Full-field OCT: A non-invasive tool for diagnosis and tissue selection. SPIE Newsroom 2013, 201310, 004933. [Google Scholar] [CrossRef] [Green Version]
- Mazlin, V.; Xiao, P.; Scholler, J.; Grieve, K.; Irsch, K.; Sahel, J.A.; Fink, M.; Boccara, C. Ultra-High Resolution Full-Field OCT (FFOCT) for Cornea and Retina. In Imaging and Appl. Opt. 2018 (3D, AO, AIO, COSI, DH, IS, LACSEA, LS&C, MATH, pcAOP); Optical Society of America: Orlando, FL, USA, 2018; p. IM3B.1. [Google Scholar]
- Arnaud, D.; Laurent, V.; Alber-Claude, B.; Emmanuel, B. High-resolution full-field optical coherence tomography with a Linnik microscope. Appl. Opt. 2002, 41, 805–812. [Google Scholar]
- Akiba, M.; Maeda, N.; Yumikake, K.; Soma, T.; Nishida, K.; Tano, Y.; Chan, K.P. Ultrahigh-resolution imaging of human donor cornea using full-field optical coherence tomography. J. Biomed. Opt. 2007, 12, 041202. [Google Scholar] [CrossRef]
- Fercher, A.F. Optical coherence tomography–development, principles, applications. Zeitschrift für Medizinische Physik 2010, 20, 251–276. [Google Scholar] [CrossRef]
- Fankhauser, F.; Kwasniewska, S. Lasers in Ophthalmology: Basic, Diagnostic, and Surgical Aspects: A Review; Kugler Publications: The Hague, The Netherlands, 2003. [Google Scholar]
- Xiao, S.; Beckmann, L.; Zhang, H.F. Visible-light optical coherence tomography: A review. J. Biomed. Opt. 2017, 22, 1–14. [Google Scholar]
- Chong, S.P.; Zhang, T.; Kho, A.; Bernucci, M.T.; Srinivasan, V.J. Ultrahigh resolution retinal imaging by visible light OCT with longitudinal achromatization. Biomed. Opt. Express 2018, 9, 1477. [Google Scholar] [CrossRef] [Green Version]
- Ortiz, S.; Siedlecki, D.; Pérez-Merino, P.; Chia, N.; de Castro, A.; Szkulmowski, M.; Wojtkowski, M.; Marcos, S. Corneal topography from spectral optical coherence tomography (sOCT). Biomed. Opt. Express 2011, 2, 3232–3247. [Google Scholar] [CrossRef] [Green Version]
- Westphal, V.; Rollins, A.M.; Radhakrishnan, S.; Izatt, J.A. Correction of geometric and refractive image distortions in optical coherence tomography applying Fermat’s principle. Opt. Express 2002, 10, 397–404. [Google Scholar] [CrossRef] [PubMed]
- Ortiz, S.; Siedlecki, D.; Grulkowski, I.; Remon, L.; Pascual, D.; Wojtkowski, M.; Marcos, S. Optical distortion correction in optical coherence tomography for quantitative ocular anterior segment by three-dimensional imaging. Opt. Express 2010, 18, 2782–2796. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Kuo, A.N.; Izatt, J.A. 3D refraction correction and extraction of clinical parameters from spectral domain optical coherence tomography of the cornea. Opt. Express 2010, 18, 8923–8936. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Avanaki, M.R.N.; Cernat, R.; Tadrous, P.J.; Tatla, T.; Podoleanu, A.G.; Hojjatoleslami, S.A. Spatial Compounding Algorithm for Speckle Reduction of Dynamic Focus OCT Images. IEEE Photonics Technol. Lett. 2013, 25, 1439–1442. [Google Scholar] [CrossRef]
- Eybposh, M.H.; Turani, Z.; Mehregan, D.; Nasiriavanaki, M. Cluster-based filtering framework for speckle reduction in OCT images. Biomed. Opt. Express 2018, 9, 6359–6373. [Google Scholar] [CrossRef] [PubMed]
- Adabi, S.; Rashedi, E.; Clayton, A.; Mohebbi-Kalkhoran, H.; Chen, X.W.; Conforto, S.; Avanaki, M.N. Learnable despeckling framework for optical coherence tomography images. J. Biomed. Opt. 2018, 23, 1–12. (In English) [Google Scholar] [CrossRef] [Green Version]
- Martin, R. Cornea and anterior eye assessment with placido-disc keratoscopy, slit scanning evaluation topography and scheimpflug imaging tomography. Indian J. Ophthalmol. 2018, 66, 360. [Google Scholar]
- Singh, K.D.; Logan, N.S.; Gilmartin, B. Three-dimensional modeling of the human eye based on magnetic resonance imaging. Investig. Ophthalmol. Vis. Sci. 2006, 47, 2272–2279. [Google Scholar] [CrossRef]
- De La Zerda, A.; Paulus, Y.M.; Teed, R.; Bodapati, S.; Dollberg, Y.; Khuri-Yakub, B.T.; Blumenkranz, M.S.; Moshfeghi, D.M.; Gambhir, S.S. Photoacoustic ocular imaging. Opt. Lett. 2010, 35, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Richdale, K.; Sinnott, L.T.; Bullimore, M.A.; Wassenaar, P.A.; Schmalbrock, P.; Kao, C.Y.; Patz, S.; Mutti, D.O.; Glasser, A.; Zadnik, K. Quantification of age-related and per diopter accommodative changes of the lens and ciliary muscle in the emmetropic human eye. Investig. Ophthalmol. Vis. Sci. 2013, 54, 1095–1105. (In English) [Google Scholar] [CrossRef] [Green Version]
- Hermans, E.A.; Pouwels, P.J.; Dubbelman, M.; Kuijer, J.P.; van der Heijde, R.G.; Heethaar, R.M. Constant volume of the human lens and decrease in surface area of the capsular bag during accommodation: An MRI and Scheimpflug study. Investig. Ophthalmol. Vis. Sci. 2009, 50, 281–289. (In English) [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.; Zhang, H.F. Photoacoustic imaging of the eye: A mini review. Photoacoustics 2016, 4, 112–123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, S.; Rao, B.; Maslov, K.; Wang, L.V. Label-free photoacoustic ophthalmic angiography. Opt. Lett. 2010, 35, 1–3. (In English) [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ho, L.C.; Sigal, I.A.; Jan, N.J.; Yang, X.; Van Der Merwe, Y.; Yu, Y.; Chau, Y.; Leung, C.K.; Conner, I.P.; Jin, T.; et al. Non-invasive MRI Assessments of Tissue Microstructures and Macromolecules in the Eye upon Biomechanical or Biochemical Modulation. Sci. Rep. 2016, 6, 32080. (In English) [Google Scholar] [CrossRef] [PubMed]
- Wu, N.; Ye, S.; Ren, Q.; Li, C. High-resolution dual-modality photoacoustic ocular imaging. Opt. Lett. 2014, 39, 2451–2454. [Google Scholar] [CrossRef]
- Chen, F.K.; Viljoen, R.D.; Bukowska, D.M. Classification of image artefacts in optical coherence tomography angiography of the choroid in macular diseases. Clin. Exp. Ophthalmol. 2016, 44, 388–399. [Google Scholar] [CrossRef]
- Falavarjani, K.G.; Al-Sheikh, M.; Akil, H.; Sadda, S.R. Image artefacts in swept-source optical coherence tomography angiography. Br. J. Ophthalmol. 2017, 101, 564–568. [Google Scholar] [CrossRef]
- Montuoro, A.; Wu, J.; Waldstein, S.; Gerendas, B.; Langs, G.; Simader, C.; Schmidt-Erfurth, U. Motion artefact correction in retinal optical coherence tomography using local symmetry. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2014; pp. 130–137. [Google Scholar]
- Zakharov, P.; Talary, M.; Boss, D.; Mrochen, M. Motion artefacts simulation in the imaging of the ocular media. In European Conference on Biomedical Optics; Optical Society of America: Rochester, NY, USA, 2015; p. 95411H. [Google Scholar]
- Ricco, S.; Chen, M.; Ishikawa, H.; Wollstein, G.; Schuman, J. Correcting motion artifacts in retinal spectral domain optical coherence tomography via image registration. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2009; pp. 100–107. [Google Scholar]
- Wegener, A.; Laser, H. Image analysis and Sheimpflug photography of anterior segment of the eye—A review. Klinische Monatsblatter fur Augenheilkunde 2001, 218, 67–77. [Google Scholar] [CrossRef]
- Mueller-Breitenkamp, U.; Hockwin, O. Scheimpflug photography in clinical ophthalmology. A review. Ophthalmic Res. 2009, 24 (Suppl. 1), 47–54. [Google Scholar] [CrossRef]
- Resink, S.G.; Steenbergen, W.; Boccara, A.C. State-of-the art of acoust-optic sensing and imaging of turbid media. J. Biomed. Opt. 2012, 17, 040901. [Google Scholar] [CrossRef]
- John, R.; Rezaeipoor, R.; Adie, S.G.; Chaney, E.J.; Oldenburg, A.L.; Marjanovic, M.; Haldar, J.P.; Sutton, B.P.; Boppart, S.A. In vivo magnetomotive optical molecular imaging using targeted magnetic nanoprobes. Proc. Natl. Acad. Sci. USA 2010, 107, 8085–8090. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shemonski, N.D.; South, F.A.; Liu, Y.-Z.; Adie, S.G.; Carney, P.S.; Boppart, S.A. Computational high-resolution optical imaging of the living human retina. Nat. Photonics 2015, 9, 440. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adie, S.G.; Graf, B.W.; Ahmad, A.; Carney, P.S.; Boppart, S.A. Computational adaptive optics for broadband optical interferometric tomography of biological tissue. Proc. Natl. Acad. Sci. USA 2012, 109, 7175–7180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yaroslavsky, L.; Caulfield, H.J. Computational vision in nature and technology. arXiv 2007, arXiv:physics/0703096. [Google Scholar]





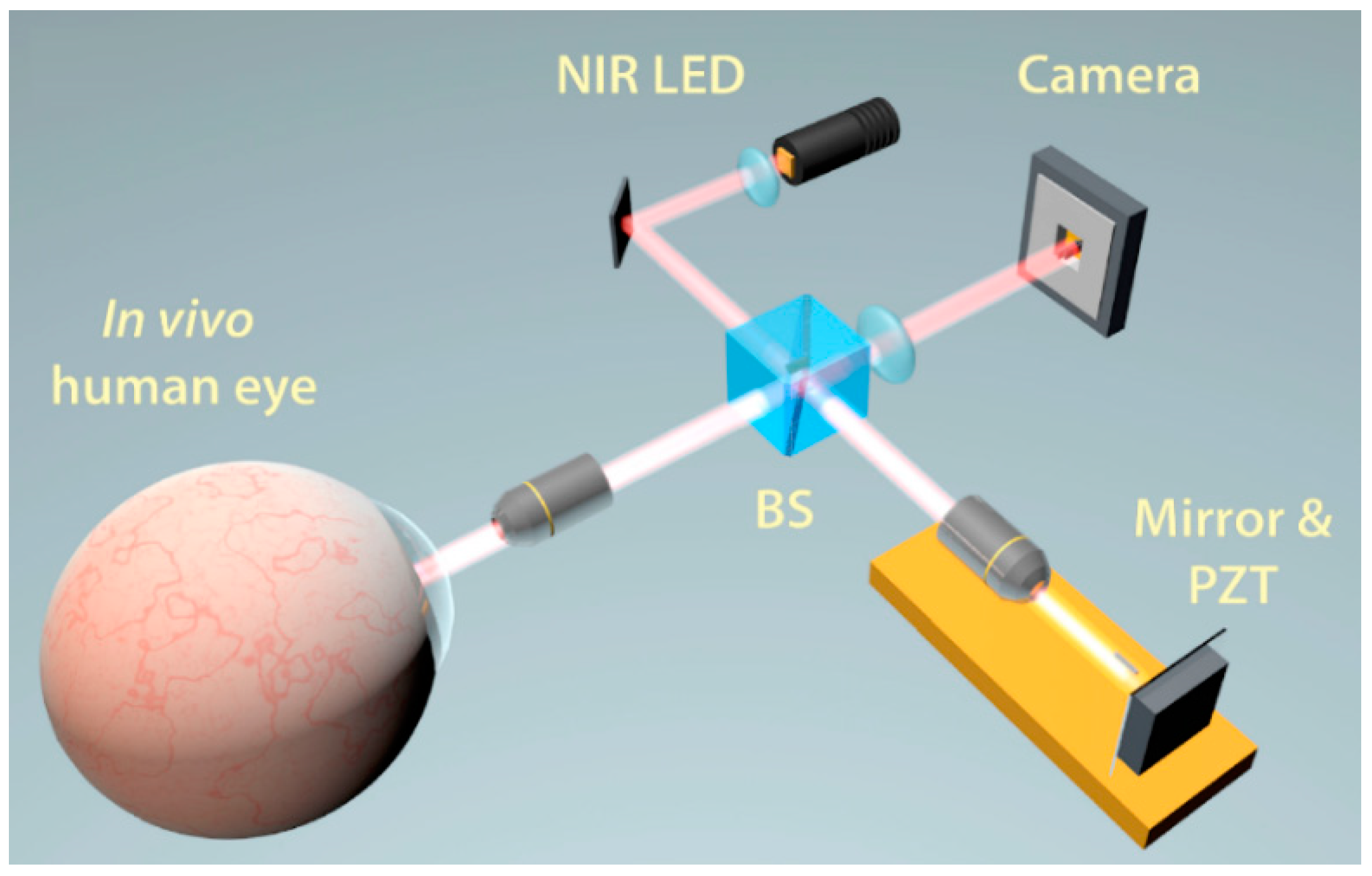
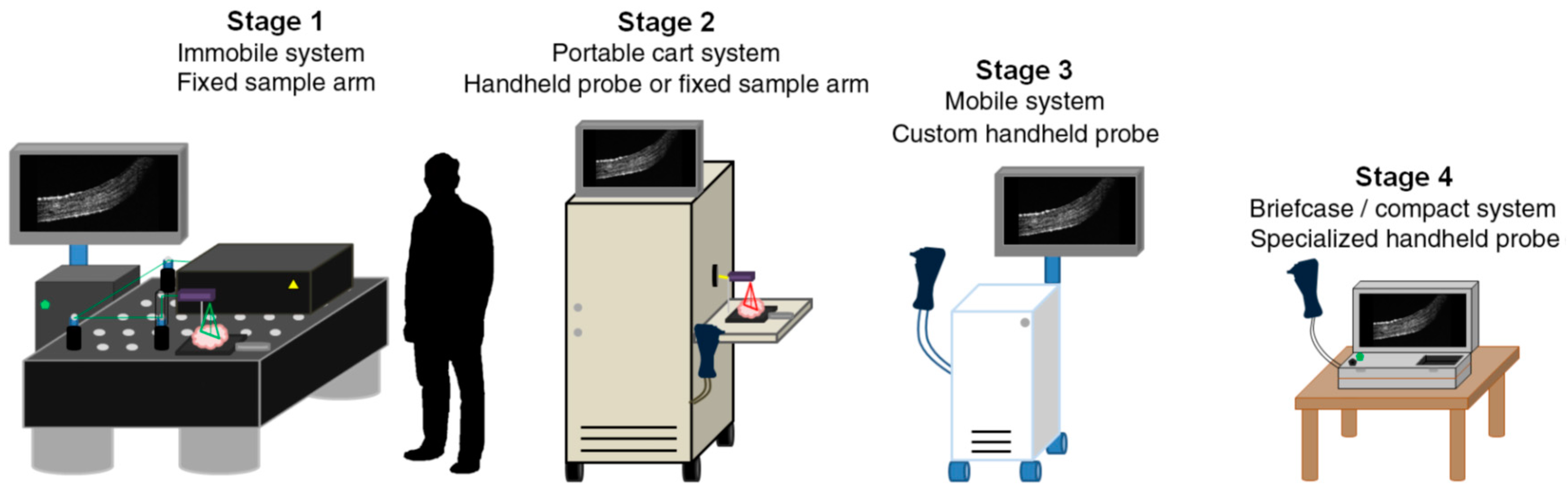
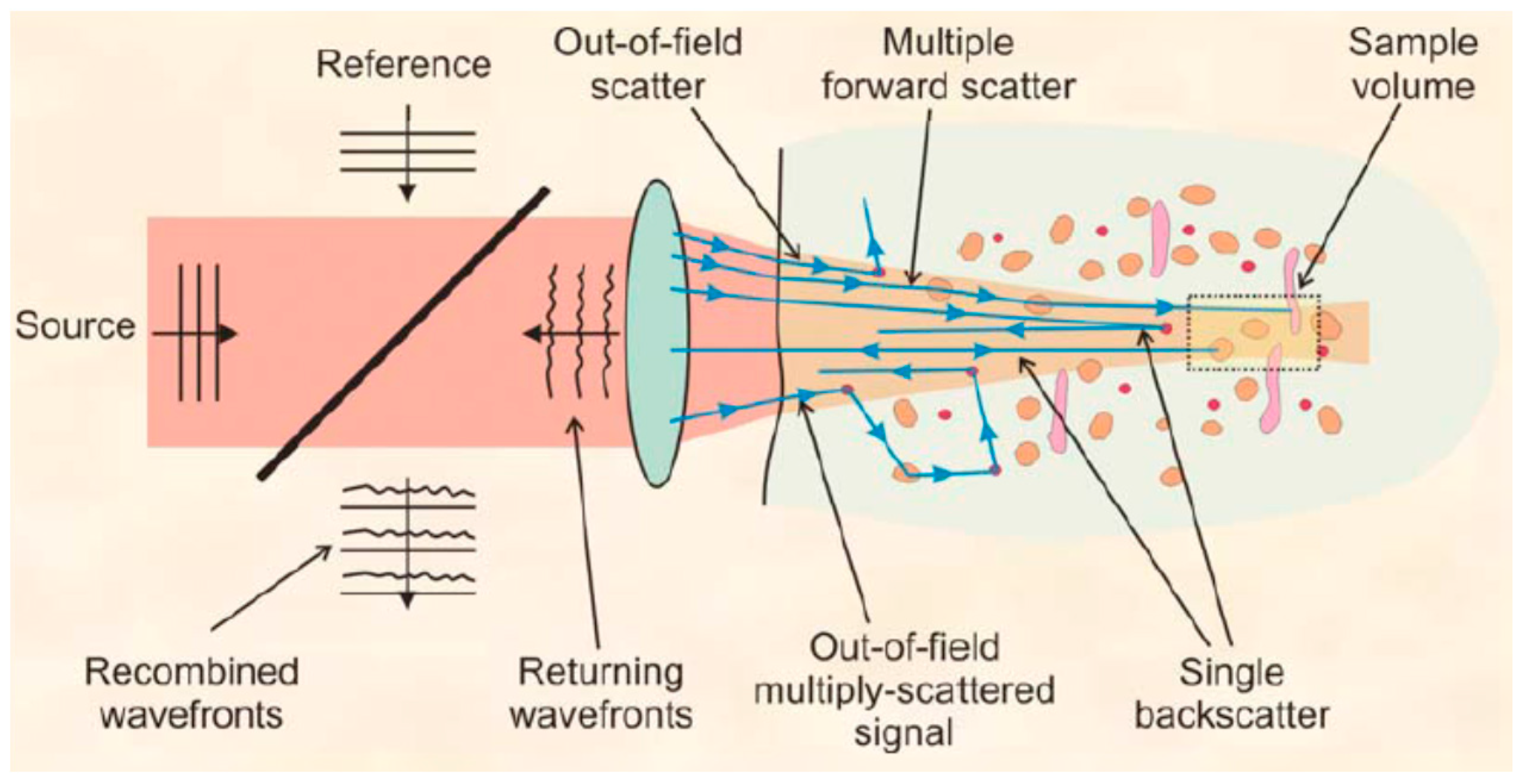
| OCT Categories | Pros. | Cons. |
|---|---|---|
| TD-OCT | simple construction and signal processing method | low scanning speed and low detection sensitivity |
| SD-OCT | significant detection efficiency | strong SNR roll-off in depth and low detection resolution of the spectral distribution |
| SS-OCT | reduced fringe wash-out effects, lower sensitivity attenuation, higher detection efficiency, improved imaging speed and higher sensitivity | the intrinsic instability of the light sources and still adopt the point scanning scheme |
| FF-OCT | en-face (transverse) tomographic images directly without point-by-point raster scanning, simplicity and a larger field of view | difficult to align the optical pathway, inherent sensitivity to motion, the crucial degradation of the contrast and image resolution with the imaging depth |
| Measuring Strategy | Technologies | Speed | Resolution | Covering Area | Penetration Depth | Major Limitations |
|---|---|---|---|---|---|---|
| Pattern projection | Placido disk a | tens of ms/image b | 10 μm | 14 mm in diameter | only the anterior corneal surface | Surface reconstruction of the irregular cornea fails as a result of that the rings or raster patterns could merge or cross in this case. |
| Rasterstereography [49,111] | tens of ms/image b | 4 μm | over 12 mm in diameter | |||
| Interferometry | Holographic technique [53,55] | 1 ms | 0.1 μm | entire corneal surface | The hologram is particularly easy to be affected by the vibrations and air turbulence. | |
| Moiré technique [67] | 1 s | 2.6 μm | 7 mm in square | The fine structures or those with a larger gradient on the cornea would be erased due to the inevitable application of the low-pass filter in the Moiré technique, TGI, and FTP. | ||
| TGI [76] | tens of ms/image b | 6 μm | 6 mm in square | |||
| FTP [80] | <1 s | <10 μm | 20 mm in diameter | |||
| Parallel line scanning | Scanning-slit [186] | 1.5 s | >10 μm | 11 mm in diameter | anterior segment | Utilizing parallel line scanning causes difficulty in the image registration due to the lack of shared points during scanning. The depth of focus is so limited that the imaging quality of the lens is poor. |
| Rotational line scanning | Scheimpflug imaging [10,186] | 1~2 s | <10 μm | 14~16 mm in diameter | anterior segment | Visualization of the entire lens and anterior chamber is inaccessible. |
| Point scanning | UBM [45,126] | 50~100 ms/B-Scan | 20~50 μm, 150 μm c | over 20 mm in diameter | from the anterior segment to the retina d | As an immersion technique, the contact and time-consuming nature limit its application. |
| TD-OCT [10,137] | 2000 A-Scans/s | 18 μm | 16 mm in width | Quantitative measurement can only be retrieved accurately upon the correction of the fan and optical distortions. OCT is unable to see through the opaque tissues. | ||
| SD-OCT [10,137] | >300,000 A-Scans/s | 5 μm | 13 mm in width | |||
| SS-OCT [10,137] | >2,000,000 A-Scans / s | 8 μm | 12 mm in width | |||
| En-face tomographic imaging | FF-OCT [150,163,172] | tens of ms/image b | 1 μm | 1~2 cm2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Kang, C.; Fang, F. Biometric Measurement of Anterior Segment: A Review. Sensors 2020, 20, 4285. https://doi.org/10.3390/s20154285
Liu B, Kang C, Fang F. Biometric Measurement of Anterior Segment: A Review. Sensors. 2020; 20(15):4285. https://doi.org/10.3390/s20154285
Chicago/Turabian StyleLiu, Bin, Chengwei Kang, and Fengzhou Fang. 2020. "Biometric Measurement of Anterior Segment: A Review" Sensors 20, no. 15: 4285. https://doi.org/10.3390/s20154285
APA StyleLiu, B., Kang, C., & Fang, F. (2020). Biometric Measurement of Anterior Segment: A Review. Sensors, 20(15), 4285. https://doi.org/10.3390/s20154285





