LdsConv: Learned Depthwise Separable Convolutions by Group Pruning
Abstract
:1. Introduction
- We integrate the weight pruning method into the depthwise separable convolutional filter and develop the two-stage training framework.
- We design an efficient convolution filter named Learned Depthwise Separable Convolution, which can be directly inserted into the existing CNNs. It can not only reduce and computational cost, but also improve the accuracy of the model.
- We validate the effectiveness of the proposed LdsConv through extensive ablation studies. To facilitate further studies, our source code, as well as experiment results, will be available at https://github.com/Eutenacity/LdsConv.
2. Related Work
2.1. High Efficiency Convolutional Filter
2.2. Model Compression
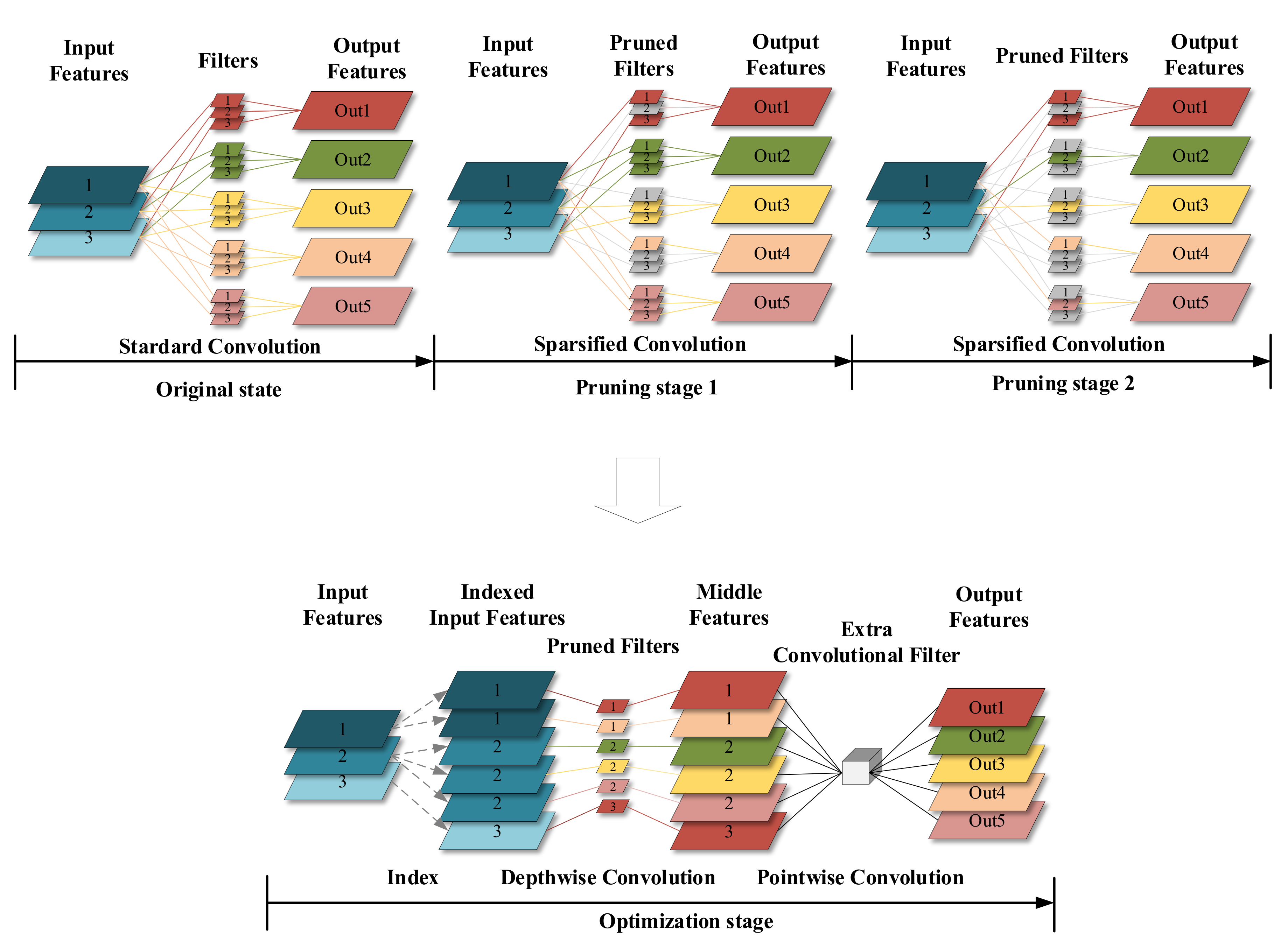
3. Method
3.1. Depthwise Separable Convolution
3.2. Learned Depthwise Separable Convolution
3.2.1. Group Pruning
3.2.2. Pruning Criterion
3.2.3. Pruning Factor
3.2.4. Stage Factor
3.2.5. Balance Loss Function
3.2.6. Additional Pointwise Convolution
3.2.7. Learning Rate
3.3. The Implementation of LdsConv
3.3.1. Standard Convolution
3.3.2. Depthwise Separable Convolution
4. Experiment
4.1. Ablation Study on Cifar
4.1.1. Training Details
4.1.2. Implement on DenseNet-BC-100
4.1.3. Effect of Stage Factor
4.1.4. Effect of Pruning Factor
4.1.5. Effect of Balance Loss Function
4.1.6. Effect of Group Cardinality
4.1.7. Effect of Two-Stage Training Framework
4.1.8. Results on Other Models
4.2. Results on ImageNet
4.2.1. Training Details
4.2.2. Model Configurations
4.2.3. Comparison on ImageNet
4.2.4. Comparison with Model Compression Methods
4.3. Comparison with Similar Works
4.4. Network Visualization with Grad-CAM
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep Convolutional Networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Du, M.; Ding, Y.; Meng, X.; Wei, H.L.; Zhao, Y. Distractor-aware deep regression for visual tracking. Sensors 2019, 19, 387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lyu, J.; Bi, X.; Ling, S.H. Multi-level cross residual network for lung nodule classification. Sensors 2020, 20, 2837. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Zhang, Y.; Yang, M.; Zhao, Y. Visual tracking via deep feature fusion and correlation filters. Sensors 2020, 20, 3370. [Google Scholar] [CrossRef] [PubMed]
- Hwang, Y.J.; Lee, J.G.; Moon, U.C.; Park, H.H. SSD-TSEFFM: New SSD using trident feature and squeeze and extraction feature fusion. Sensors 2020, 20, 3630. [Google Scholar] [CrossRef]
- Liang, S.; Gu, Y. Towards robust and accurate detection of abnormalities in musculoskeletal radiographs with a multi-network model. Sensors 2020, 20, 3153. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient Convolutional Neural Networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50× fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient Convolutional Neural Network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6848–6856. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Wei, B.; Hamad, R.A.; Yang, L.; He, X.; Wang, H.; Gao, B.; Woo, W.L. A deep-learning-driven light-weight phishing detection sensor. Sensors 2019, 19, 4258. [Google Scholar] [CrossRef] [Green Version]
- Ying, C.; Klein, A.; Christiansen, E.; Real, E.; Murphy, K.; Hutter, F. Nas-Bench-101: Towards reproducible neural architecture search. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 7105–7114. [Google Scholar]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized evolution for image classifier architecture search. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4780–4789. [Google Scholar]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning transferable architectures for scalable image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8697–8710. [Google Scholar]
- Liu, C.; Zoph, B.; Neumann, M.; Shlens, J.; Hua, W.; Li, L.J.; Li, F.-F.; Yuille, A.; Huang, J.; Murphy, K. Progressive neural architecture search. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 19–34. [Google Scholar]
- Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2016, arXiv:1611.01578. [Google Scholar]
- Pham, H.; Guan, M.Y.; Zoph, B.; Le, Q.V.; Dean, J. Efficient neural architecture search via parameter sharing. arXiv 2018, arXiv:1802.03268. [Google Scholar]
- Hutter, F.; Kotthoff, L.; Vanschoren, J. Automated Machine Learning: Methods, Systems, Challenges; Springer Nature: Berlin, Germany, 2019. [Google Scholar]
- Singh, P.; Verma, V.K.; Rai, P.; Namboodiri, V.P. Hetconv: Heterogeneous kernel-based convolutions for deep CNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 4835–4844. [Google Scholar]
- Chen, Y.; Fang, H.; Xu, B.; Yan, Z.; Kalantidis, Y.; Rohrbach, M.; Yan, S.; Feng, J. Drop an Octave: Reducing spatial redundancy in Convolutional Neural Networks with Octave Convolution. arXiv 2019, arXiv:1904.05049. [Google Scholar]
- Liao, S.; Yuan, B. CircConv: A structured Convolution with low complexity. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4287–4294. [Google Scholar]
- Vanhoucke, V. Learning visual representations at scale. ICLR Invit. Talk 2014, 1, 2. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep Neural Networks with pruning, trained quantization and Huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Zhu, L.; Deng, R.; Maire, M.; Deng, Z.; Mori, G.; Tan, P. Sparsely aggregated Convolutional Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 186–201. [Google Scholar]
- Luo, J.H.; Wu, J.; Lin, W. Thinet: A filter level pruning method for deep Neural Network compression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5058–5066. [Google Scholar]
- Singh, P.; Kadi, V.S.R.; Verma, N.; Namboodiri, V.P. Stability based filter pruning for accelerating deep CNNs. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 9–11 January 2019; pp. 1166–1174. [Google Scholar]
- He, Y.; Zhang, X.; Sun, J. Channel pruning for accelerating very deep Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1389–1397. [Google Scholar]
- Li, H.; Kadav, A.; Durdanovic, I.; Samet, H.; Graf, H.P. Pruning filters for efficient ConvNets. arXiv 2016, arXiv:1608.08710. [Google Scholar]
- He, Y.; Kang, G.; Dong, X.; Fu, Y.; Yang, Y. Soft filter pruning for accelerating deep Convolutional Neural Networks. arXiv 2018, arXiv:1808.06866. [Google Scholar]
- Singh, P.; Manikandan, R.; Matiyali, N.; Namboodiri, V. Multi-layer pruning framework for compressing single shot multibox detector. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 1318–1327. [Google Scholar]
- Singh, P.; Verma, V.K.; Rai, P.; Namboodiri, V.P. Leveraging filter correlations for deep model compression. arXiv 2018, arXiv:1811.10559. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-Net: ImageNet classification using binary Convolutional Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; pp. 525–542. [Google Scholar]
- Park, E.; Yoo, S.; Vajda, P. Value-aware quantization for training and inference of Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 580–595. [Google Scholar]
- Zhang, D.; Yang, J.; Ye, D.; Hua, G. LQ-Nets: Learned quantization for highly accurate and compact deep Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 365–382. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Cai, Z.; Vasconcelos, N. Cascade R-CNN: delving into high quality object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6154–6162. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; pp. 630–645. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; So Kweon, I. CBAM: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Hu, M.; Lin, H.; Fan, Z.; Gao, W.; Yang, L.; Liu, C.; Song, Q. Learning to recognize chest-Xray images faster and more efficiently based on multi-kernel depthwise convolution. IEEE Access 2020, 8, 37265–37274. [Google Scholar] [CrossRef]
- Wang, X.; Kan, M.; Shan, S.; Chen, X. Fully learnable group convolution for acceleration of deep Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9049–9058. [Google Scholar]
- Zhang, Z.; Li, J.; Shao, W.; Peng, Z.; Zhang, R.; Wang, X.; Luo, P. Differentiable learning-to-group channels via groupable Convolutional Neural Networks. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 3542–3551. [Google Scholar]
- Guo, J.; Li, Y.; Lin, W.; Chen, Y.; Li, J. Network decoupling: From regular to depthwise separable convolutions. arXiv 2018, arXiv:1808.05517. [Google Scholar]
- Huang, G.; Liu, S.; Van der Maaten, L.; Weinberger, K.Q. Condensenet: An efficient densenet using learned group convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2752–2761. [Google Scholar]
- Huang, G.; Li, Y.; Pleiss, G.; Liu, Z.; Hopcroft, J.E.; Weinberger, K.Q. Snapshot ensembles: Train 1, get m for free. arXiv 2017, arXiv:1704.00109. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE conference on computer vision and pattern recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; Technical Report; Citeseer: Princeton, NJ, USA, 2009. [Google Scholar]
- Yu, R.; Li, A.; Chen, C.F.; Lai, J.H.; Morariu, V.I.; Han, X.; Gao, M.; Lin, C.Y.; Davis, L.S. NISP: Pruning networks using neuron importance score propagation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9194–9203. [Google Scholar]
- He, Y.; Liu, P.; Wang, Z.; Hu, Z.; Yang, Y. Filter pruning via geometric median for deep Convolutional Neural Networks acceleration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 4340–4349. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE international conference on computer vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]






| Model | Accuracy (%) | GFLOPs | Params (M) |
|---|---|---|---|
| Lds-DenseNet-BC-100 (s = 2) | 76.9 | 0.23 | 0.64 |
| Lds-DenseNet-BC-100 (s = 4) | 77.3 | 0.23 | 0.64 |
| Lds-DenseNet-BC-100 (s = 6) | 76.3 | 0.23 | 0.64 |
| Lds-DenseNet-BC-100 (s = 8) | 76.6 | 0.23 | 0.64 |
| Lds-DenseNet-BC-100 (s = 6) | 77.4 | 0.23 | 0.64 |
| Lds-DenseNet-BC-100 (s = 8) | 77.9 | 0.23 | 0.64 |
| Lds-DenseNet-BC-100 (k = 1) | 76.3 | 0.21 | 0.6 |
| Lds-DenseNet-BC-100 (k = 2) | 77.3 | 0.23 | 0.64 |
| Lds-DenseNet-BC-100 (k = 3) | 77.3 | 0.25 | 0.71 |
| Lds-DenseNet-BC-100 (k = 4) | 76.8 | 0.28 | 0.74 |
| Lds-DenseNet-BC-100 (k = 1) | 76.8 | 0.21 | 0.6 |
| Lds-DenseNet-BC-100 (k = 2) | 77.7 | 0.23 | 0.64 |
| Lds-DenseNet-BC-100 (k = 3) | 77.6 | 0.25 | 0.71 |
| Lds-DenseNet-BC-100 (k = 4) | 77.1 | 0.28 | 0.74 |
| Lds-ResNet50 (N = 4) | 80.1 | 2.87 | 14.97 |
| Lds-ResNet50 (N = 8) | 80.9 | 2.87 | 14.97 |
| Lds-ResNet50 (N = 16) | 79.8 | 2.87 | 14.97 |
| Lds-ResNet50 (N = 32) | 79.8 | 2.87 | 14.97 |
| Dw-DenseNet-BC-100 | 74.6 | 0.21 | 0.6 |
| Lds-DenseNet-BC-100 (k = 2) w/o AC | 76.2 | 0.3 | 0.79 |
| Model | Accuracy (%) | GFLOPs | Params (M) |
|---|---|---|---|
| MobileNet [9] | 77.1 | 0.62 | 3.31 |
| Lds-MobileNet | 78.0 | 0.51 | 2.74 |
| ResNet50 [1] | 80.2 | 4.46 | 23.71 |
| Lds-ResNet50 | 80.9 | 2.86 | 14.97 |
| ResNet152 [1] | 81.7 | 14.20 | 58.34 |
| Lds-ResNet152 | 82.0 | 8.66 | 35.53 |
| SE-ResNet50 [43] | 81.2 | 4.46 | 26.22 |
| Lds-SE-ResNet50 | 81.5 | 2.87 | 16.54 |
| DenseNet-BC-100 [42] | 77.7 | 0.30 | 0.79 |
| Lds-DenseNet-BC-100 | 77.7 | 0.23 | 0.64 |
| Model | Error% (Top-1) | GFLOPs | Params (M) |
|---|---|---|---|
| MobileNet [9] | 29.0 | 0.57 | 4.2 |
| Lds-MobileNet | 26.7 | 0.49 | 3.7 |
| ResNet50 [1] | 24.7 | 3.86 | 25.6 |
| Lds-ResNet50 | 22.9 | 2.71 | 16.8 |
| ResNet152 [1] | 23.0 | 11.30 | 60.2 |
| Lds-ResNet152 | 21.2 | 7.14 | 37.4 |
| SE-ResNet50 [43] | 23.3 | 3.87 | 28.1 |
| Lds-SE-ResNet50 | 22.0 | 2.71 | 17.1 |
| SE-ResNet152 [43] | 21.6 | 11.32 | 66.8 |
| Lds-SE-ResNet152 | 20.7 | 7.15 | 38.2 |
| DenseNet121 [42] | 25.0 | 2.88 | 8.0 |
| Lds-DenseNet121 | 24.2 | 1.99 | 6.5 |
| DenseNet264 [42] | 22.2 | 5.86 | 33.3 |
| Lds-DenseNet264 | 21.7 | 4.72 | 29.9 |
| Model | Error% (Top-1) | GFLOPs | FLOPs↓ (%) |
|---|---|---|---|
| ThiNet-70 [30] | 27.9 | - | 36.8 |
| NISP [56] | 27.3 | - | 27.3 |
| FPGM-only 30% [57] | 24.4 | - | 42.2 |
| Lds-ResNet50-extreme | 23.4 | 2.28 | 40.9 |
| Model | Error% (Top-1) | GFLOPs | Params (M) |
|---|---|---|---|
| FLGC-ResNet50 [48] | 34.2 | 1.0 | 7.6 |
| ND-ResNet50 [50] | 26.7 | 3.12 | 20.6 |
| DGConv-ResNet50 [49] | 23.3 | 2.46 | 14.6 |
| Lds-ResNet50 | 22.9 | 2.71 | 16.8 |
| Lds-ResNet50-extreme | 23.4 | 2.28 | 14.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.; Ding, Y.; Wei, H.-L.; Pan, X.; Zhang, Y. LdsConv: Learned Depthwise Separable Convolutions by Group Pruning. Sensors 2020, 20, 4349. https://doi.org/10.3390/s20154349
Lin W, Ding Y, Wei H-L, Pan X, Zhang Y. LdsConv: Learned Depthwise Separable Convolutions by Group Pruning. Sensors. 2020; 20(15):4349. https://doi.org/10.3390/s20154349
Chicago/Turabian StyleLin, Wenxiang, Yan Ding, Hua-Liang Wei, Xinglin Pan, and Yutong Zhang. 2020. "LdsConv: Learned Depthwise Separable Convolutions by Group Pruning" Sensors 20, no. 15: 4349. https://doi.org/10.3390/s20154349
APA StyleLin, W., Ding, Y., Wei, H.-L., Pan, X., & Zhang, Y. (2020). LdsConv: Learned Depthwise Separable Convolutions by Group Pruning. Sensors, 20(15), 4349. https://doi.org/10.3390/s20154349







