Intelligent Controller Design by the Artificial Intelligence Methods
Abstract
:1. Introduction
1.1. Related Work
1.2. The Features of the Proposed Solution
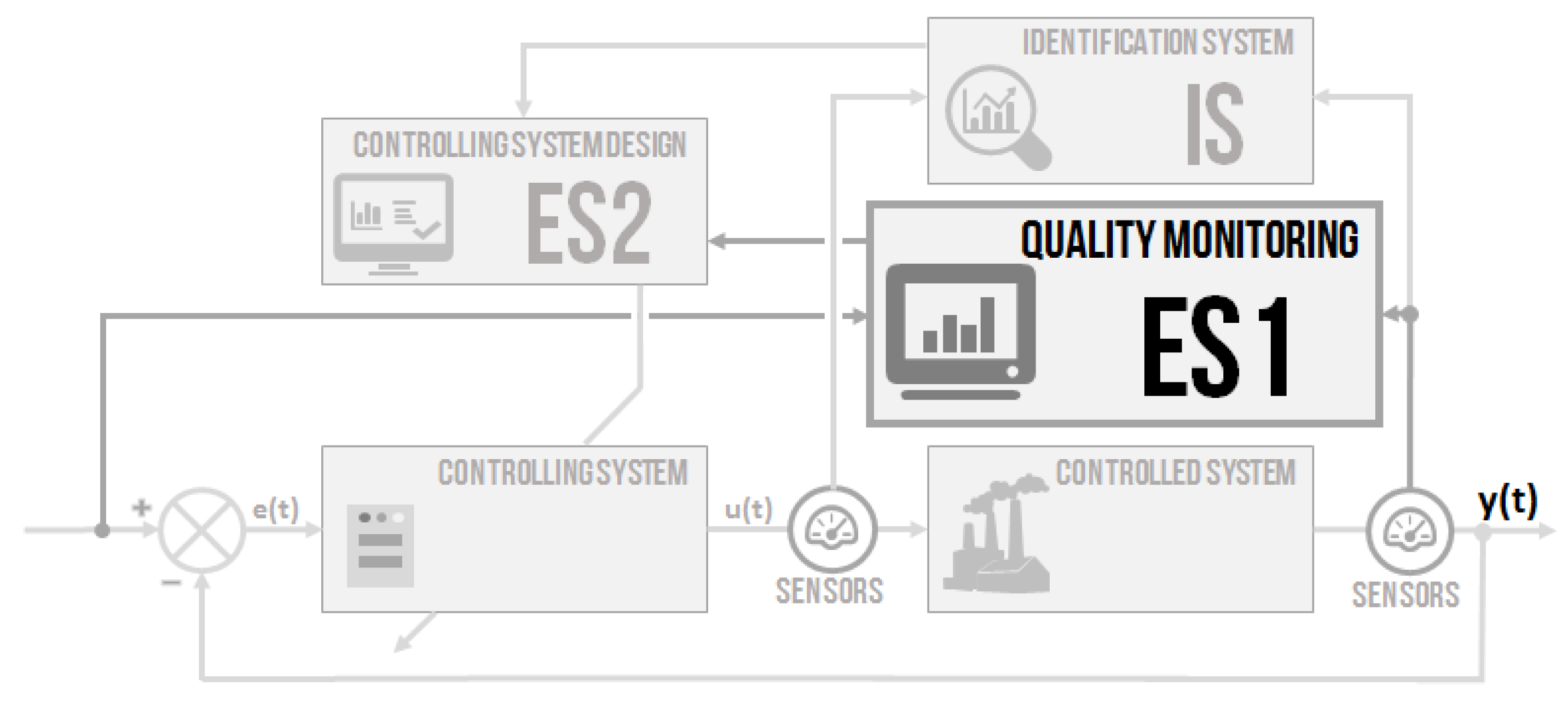
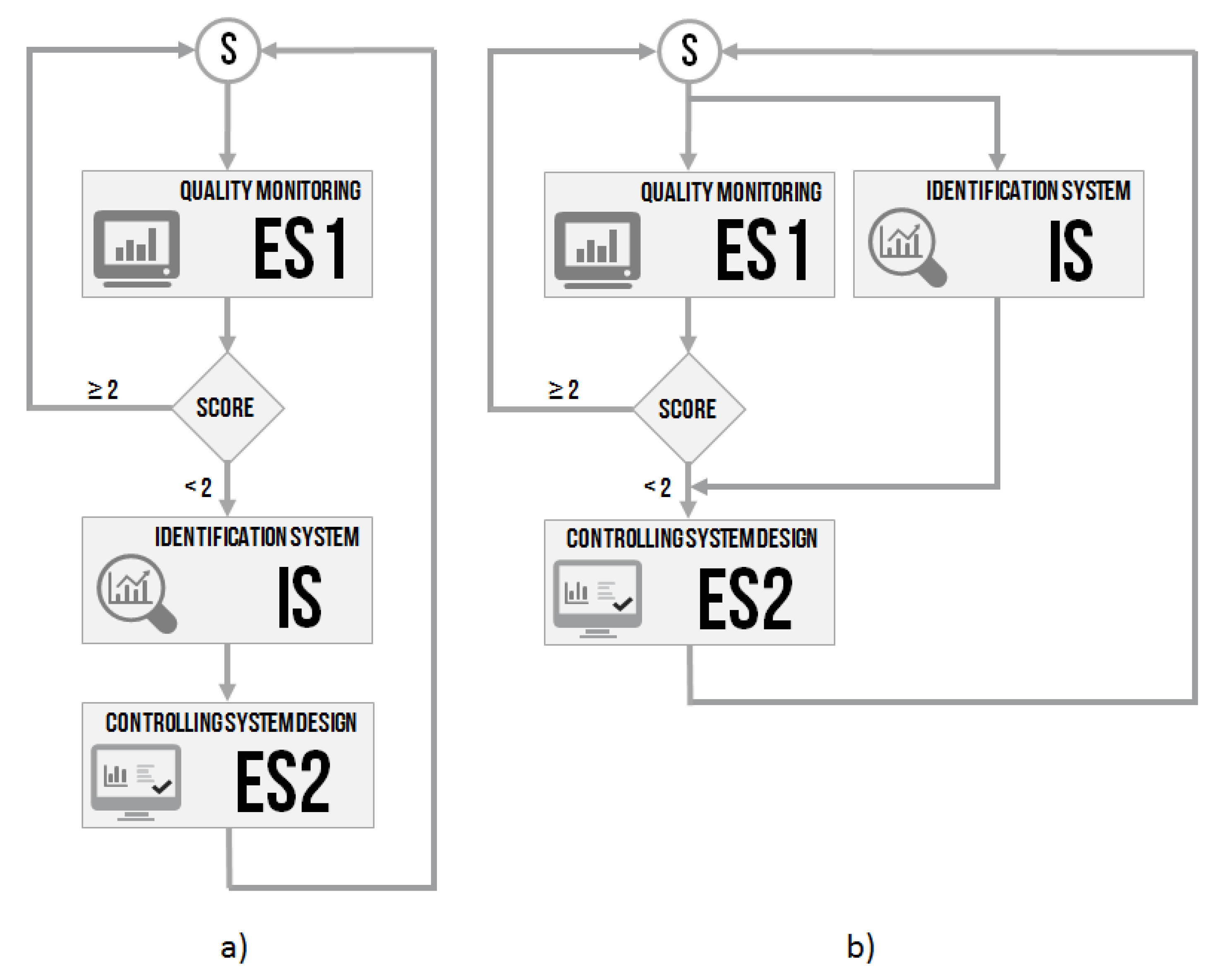
2. Materials and Methods
2.1. Quality Monitoring–ES1
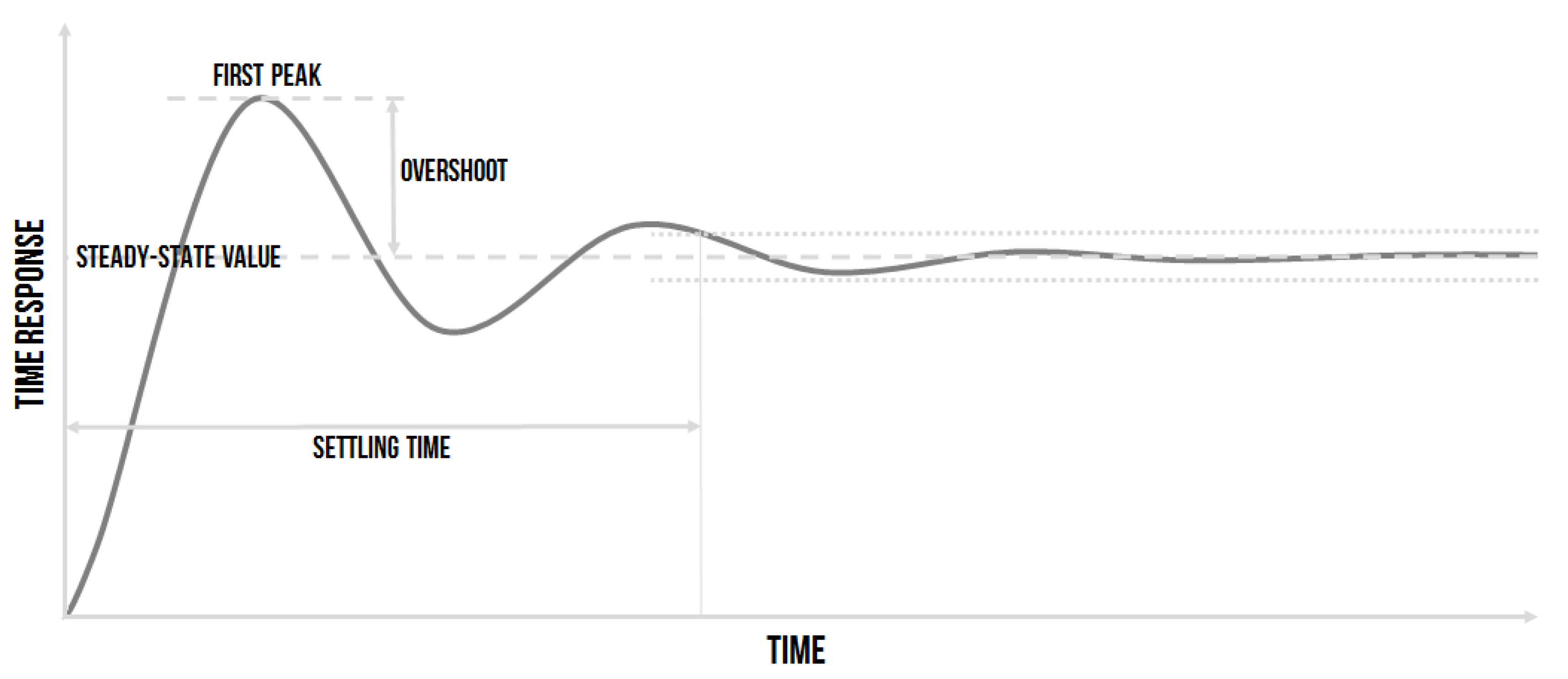
2.1.1. Quality Monitoring Inputs
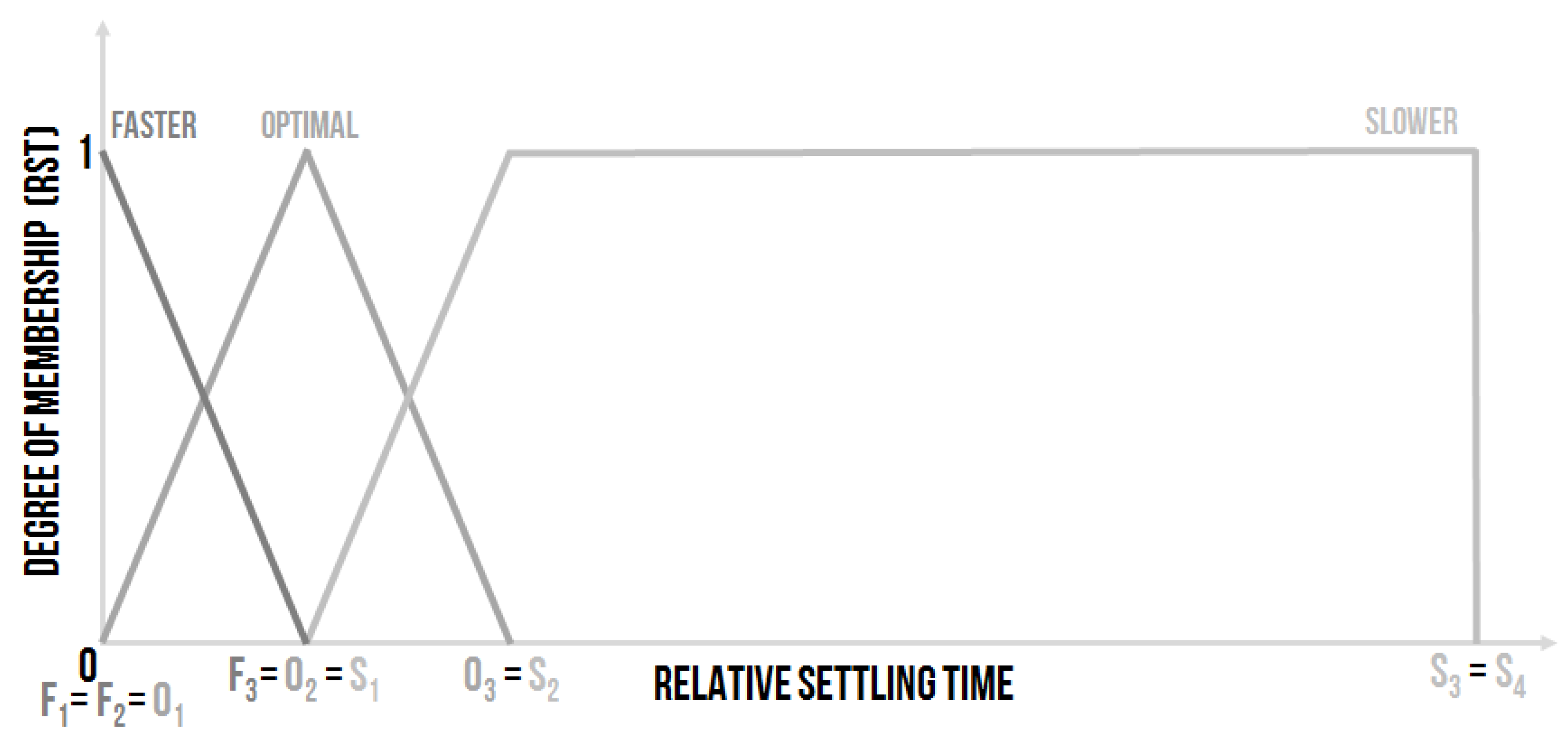
- Faster–the settling time, in comparison with the previous settling time, is shorter
- Optimal–the settling time and the previous settling time are almost the same
- Slower–the settling time, in comparison with the previous settling time, is longer
- Faster–, where e.g., , and , it means Faster—, the right border is equal to the idea that, in this point, the RST of previous and actual time course are the same and do not belong to this linguistic Faster value.
- Optimal–, where e.g., , and , it means Optimal—. The Optimal value means that the actual settling time is around the value of the previous settling time and is not greater than two times. The right border could be set as another value, in this case the monitoring system is not going to be so “strict”.
- Slower–, where e.g., , , and , it means Slower–. The value of can also be set to the other value according to the value of ; the bigger and (proposing = ) are the less strict the monitoring system is. The values exceeding the limit of are considered as equal to , as the limit of the linguistic Slower value.
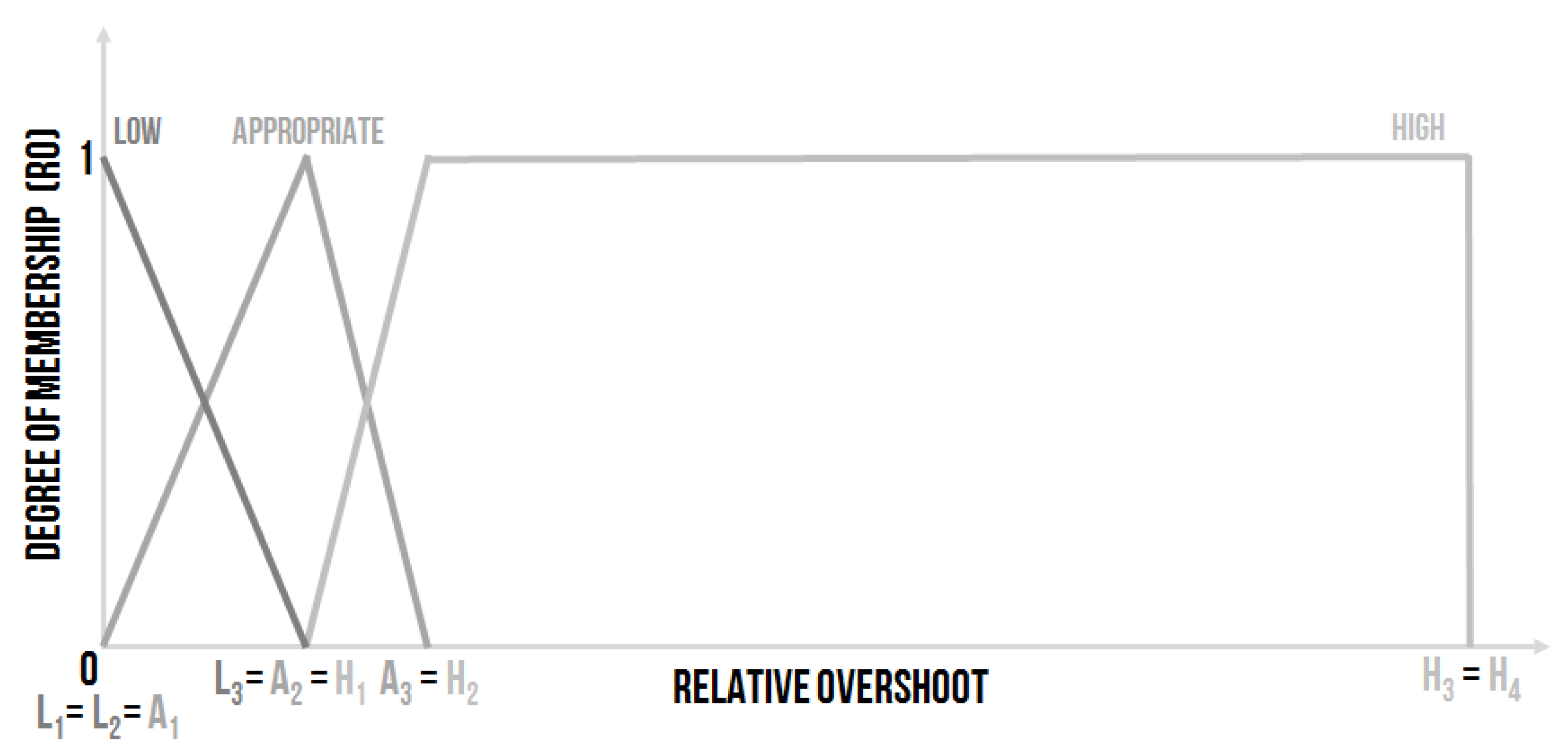
- Low–the relative overshoot is small, and, from the controlling point of view, it is a good state.
- Appropriate–the value of the relative overshoot is small enough, the border for the acceptable overshoot is often set as 20%.
- High–the relative overshoot is high, which is not good for many controlled systems and especially for the sensors (which are used for the measurement of the required value). The influence of a high overshoot on the sensors could be fatal. The sensors can be destroyed by a high overshoot, which is a better option. Or, the high overshoot can damage the sensor, but the sensor will function, although inaccurately. The poor functionality of the sensor will not be clear at first sight, and the entire system will work unpredictably.
- Low–, where e.g., , , and , it means Low–.
- Appropriate–, where e.g., , and , it means Appropriate–.
- High–, where e.g., , , and , it means High–.
- Low–, where e.g., , and , it means Low–.
- Appropriate–, where e.g., , and , it means Appropriate–.
- High–, where e.g., , , and , it means High–.
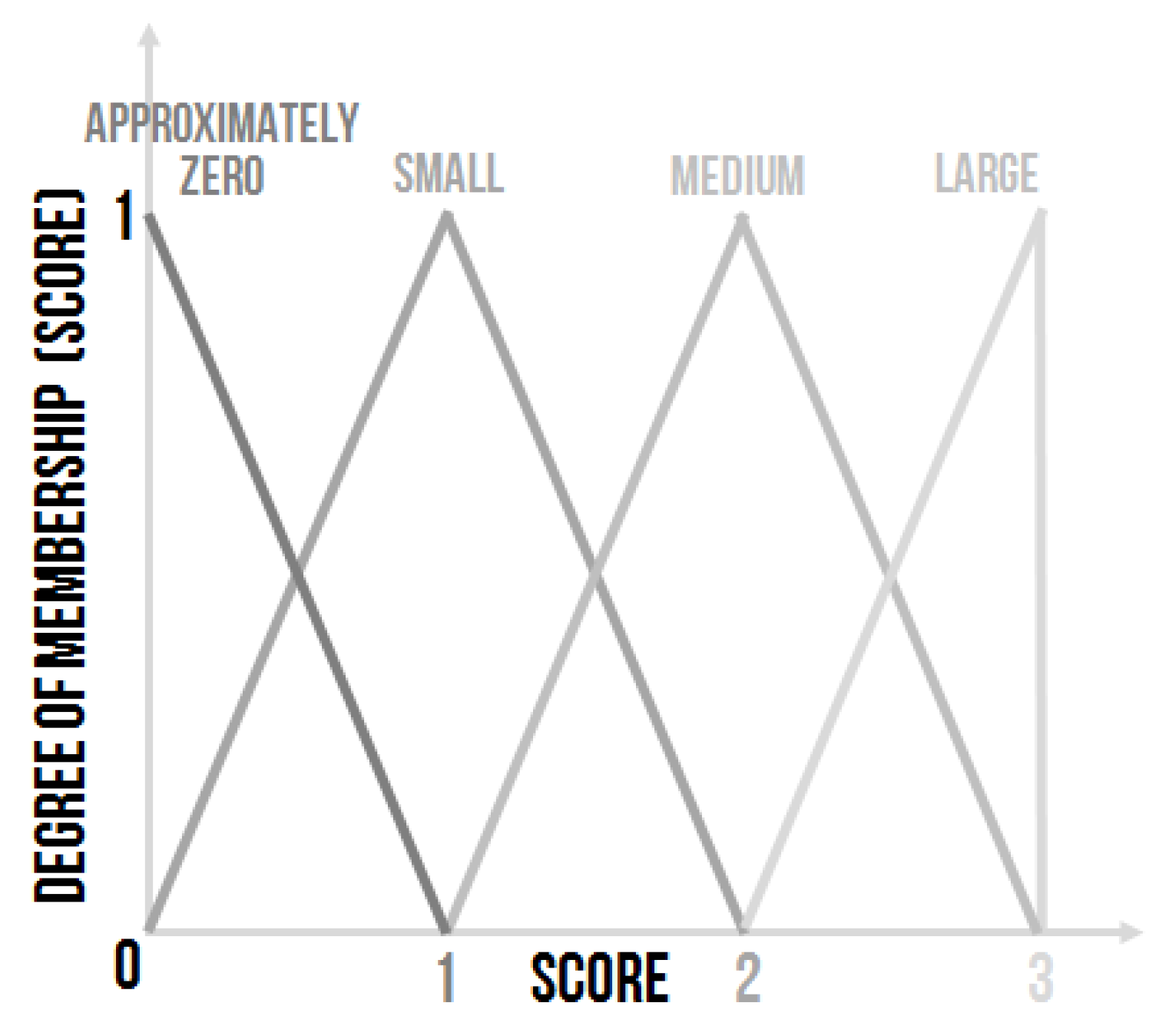
2.1.2. Quality Monitoring Output
- Approximately zero—,
- Small—,
- Medium—,
- Large—.
2.1.3. Quality Monitoring System Knowledge Base
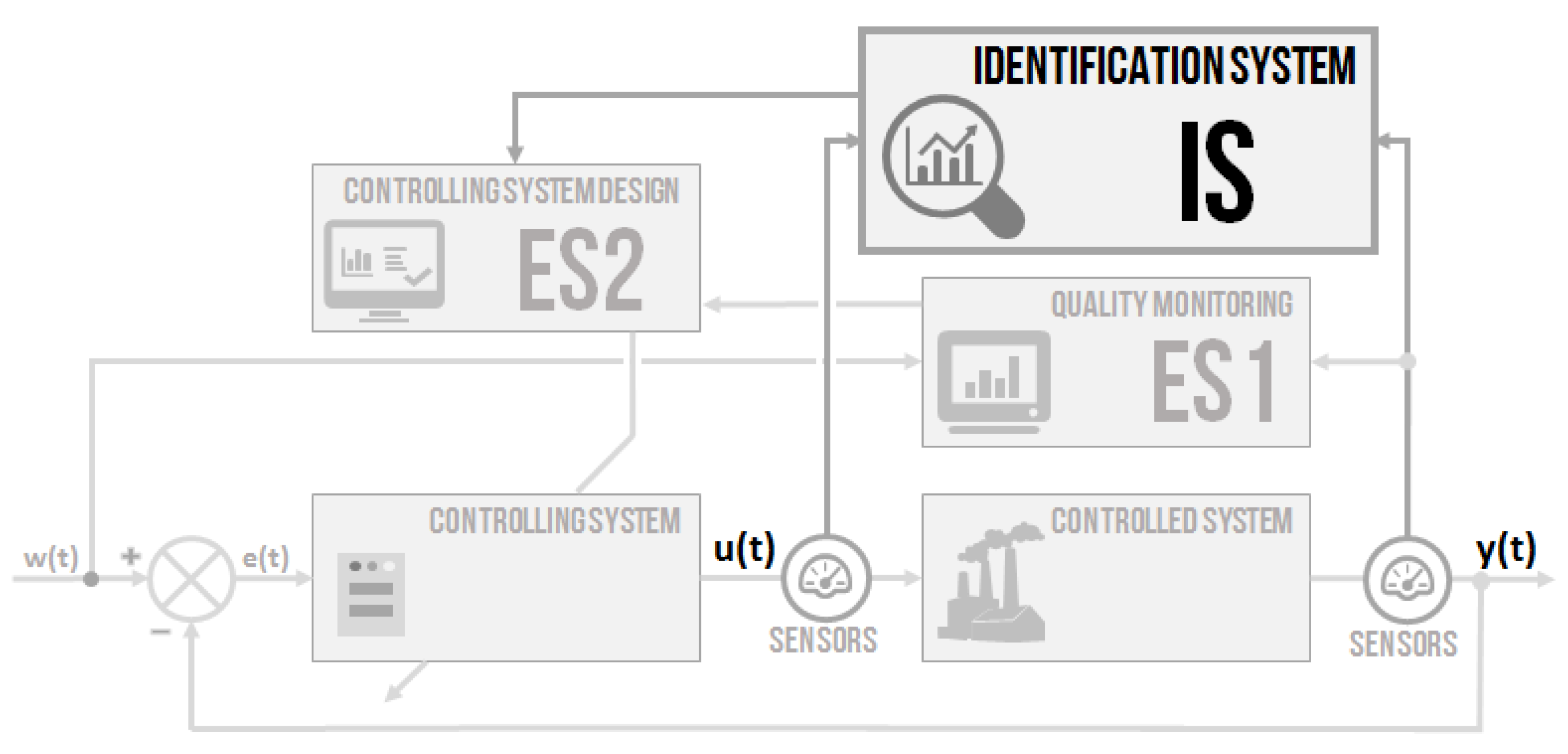
2.2. Identification System–IS
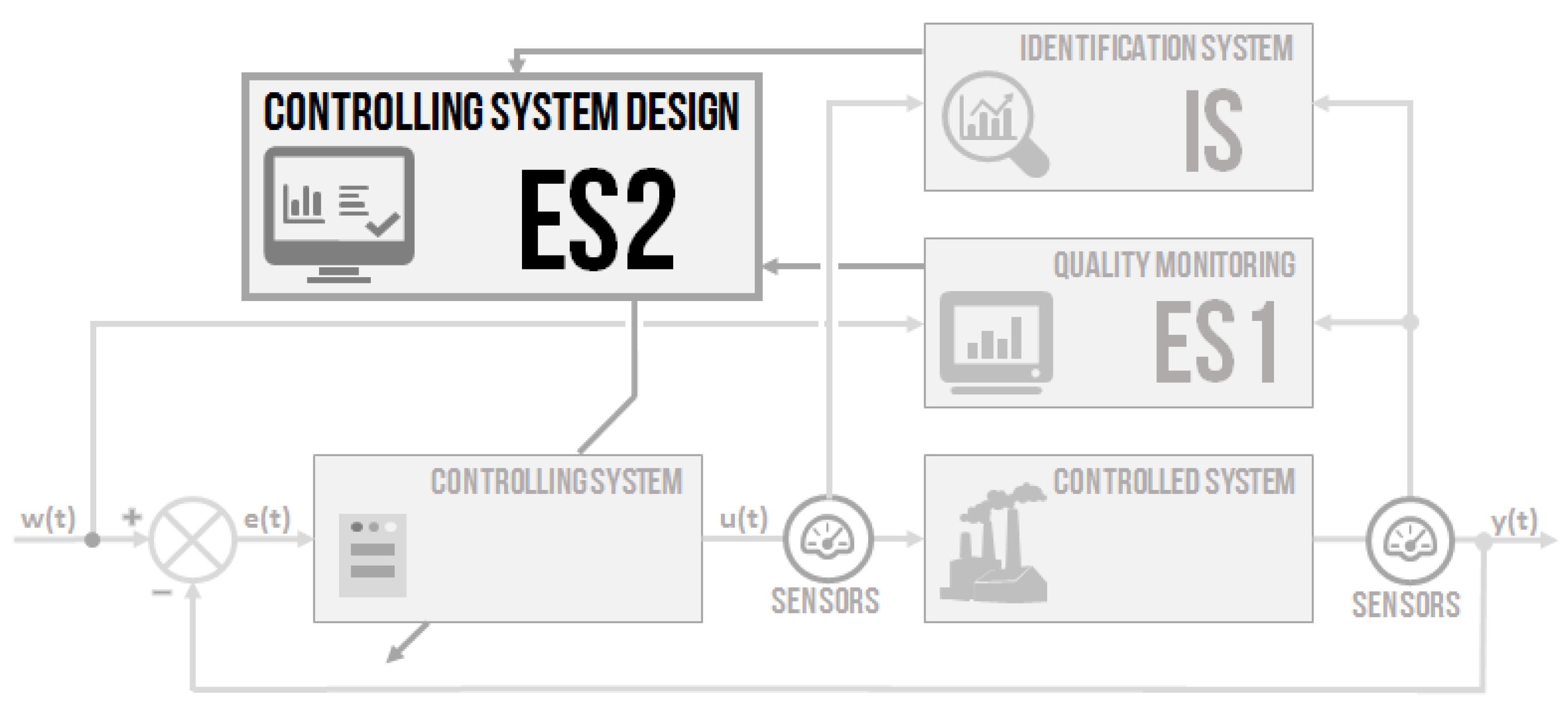
2.3. Controlling System Design–ES2
2.3.1. Controlling System Design Inputs
- ,
- ,
- ,
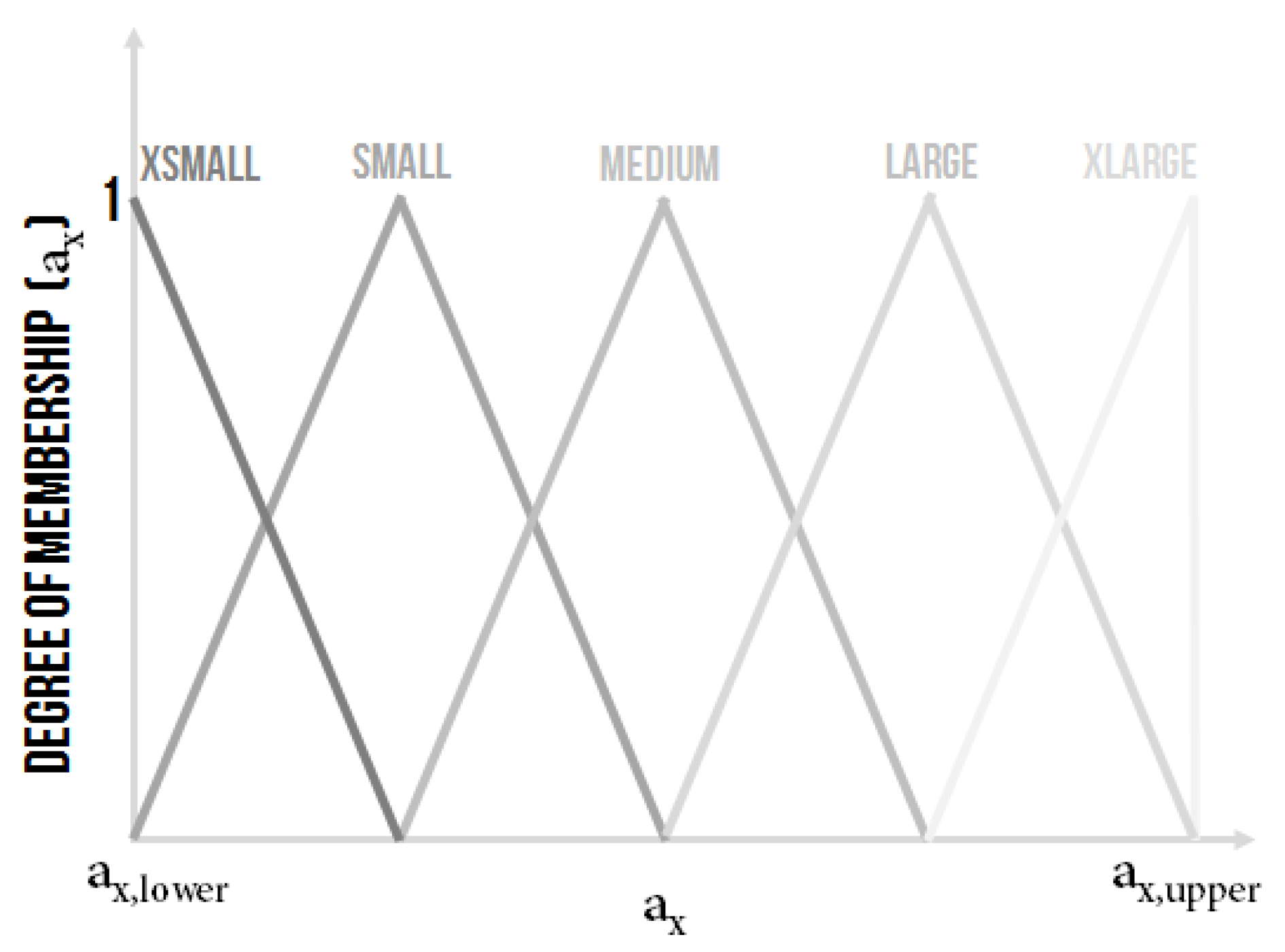
- XSmall (XS)–,
- Small (S)–,
- Medium (M)–,
- Large (L)–,
- XLarge (XL)–.
- XSmall (XS)–,
- Small (S)–,
- Medium (M)–,
- Large (L)–,
- XLarge (XL)–.
- XSmall (XS)–,
- Small (S)–,
- Medium (M)–,
- Large (L)–,
- XLarge (XL)–.
2.3.2. Controlling System Design Output
2.3.3. Controlling System Design Knowledge Base
- 10.
- 11.
- 12.
- 13.
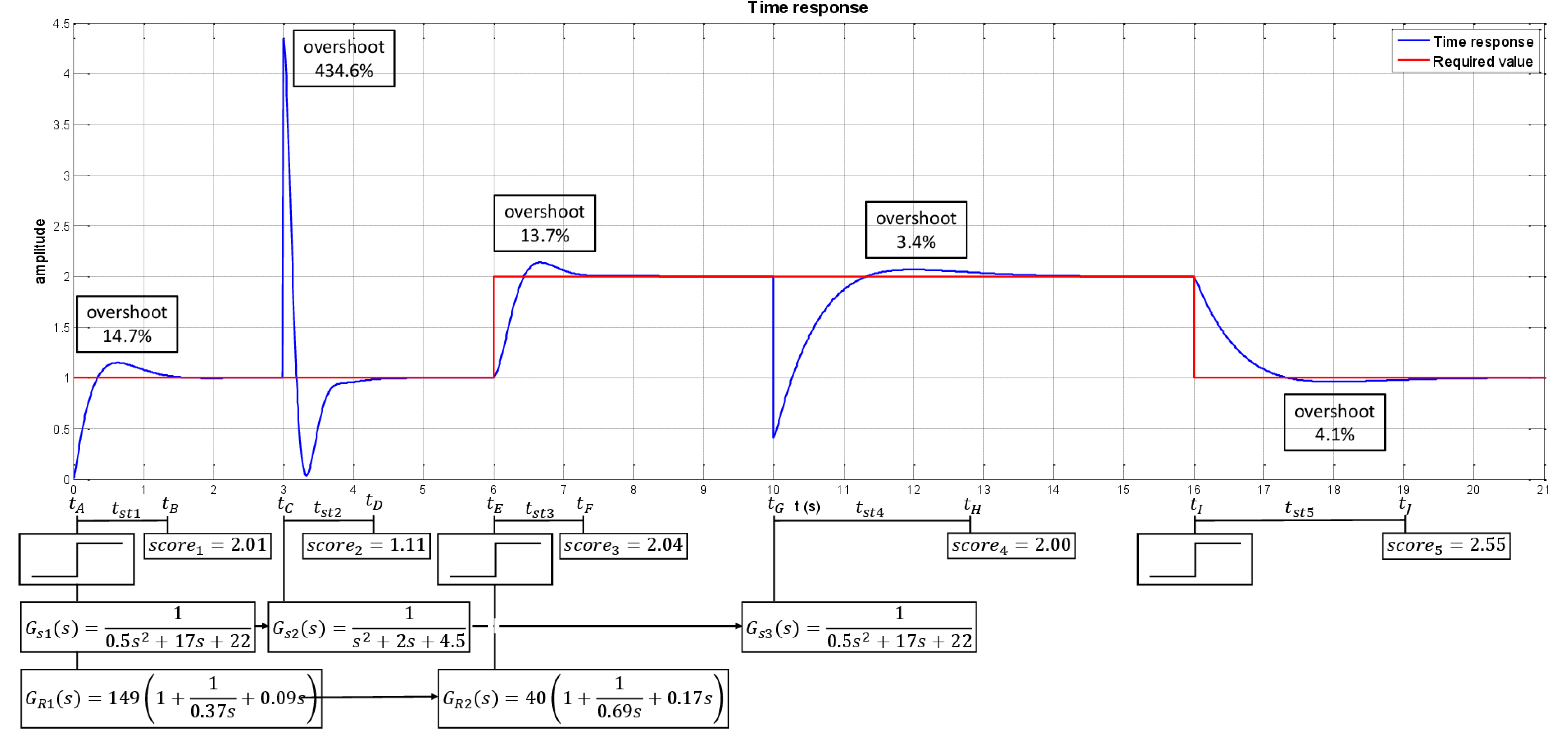
3. Results
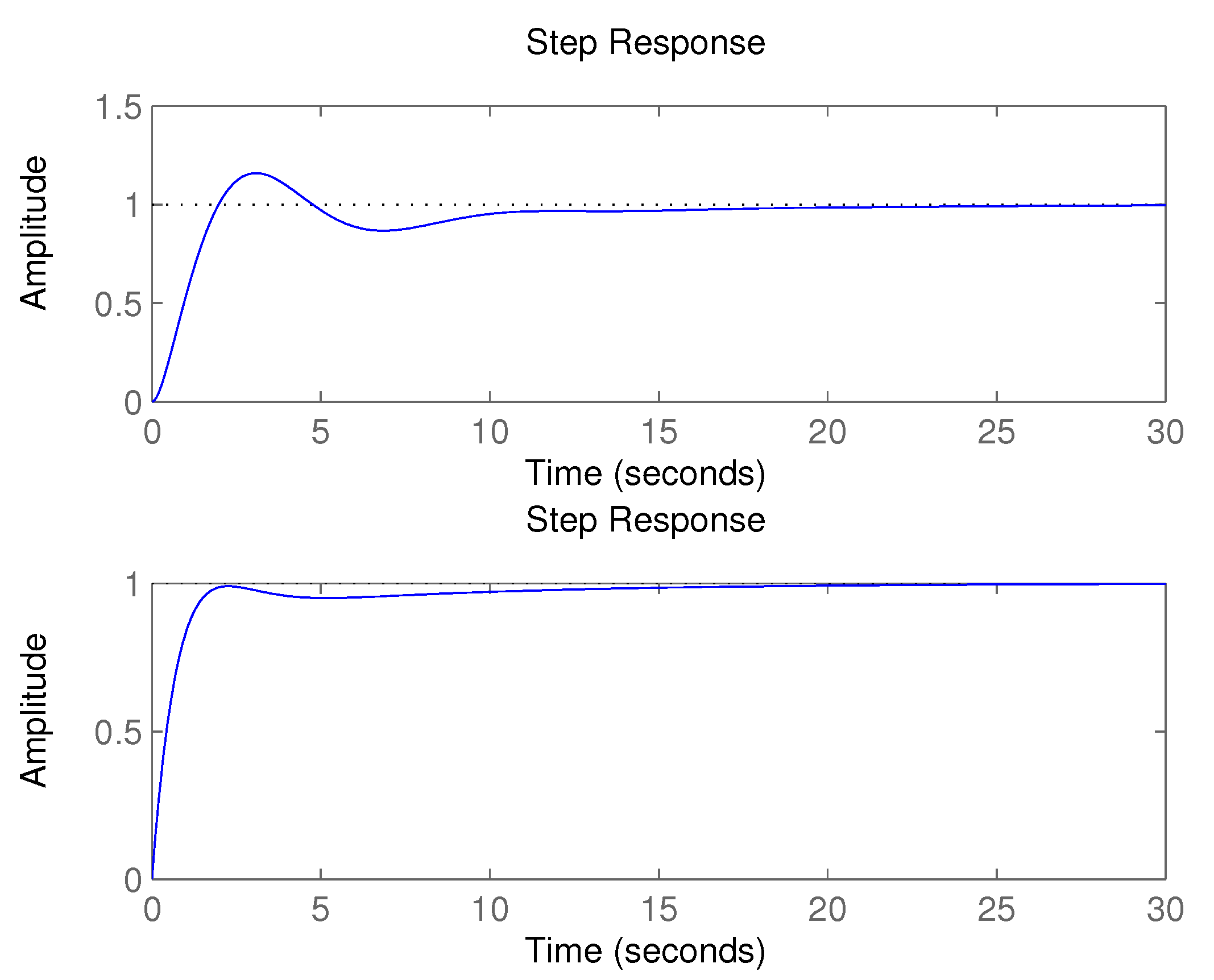
3.1. Monitoring of Control Process Quality–ES1
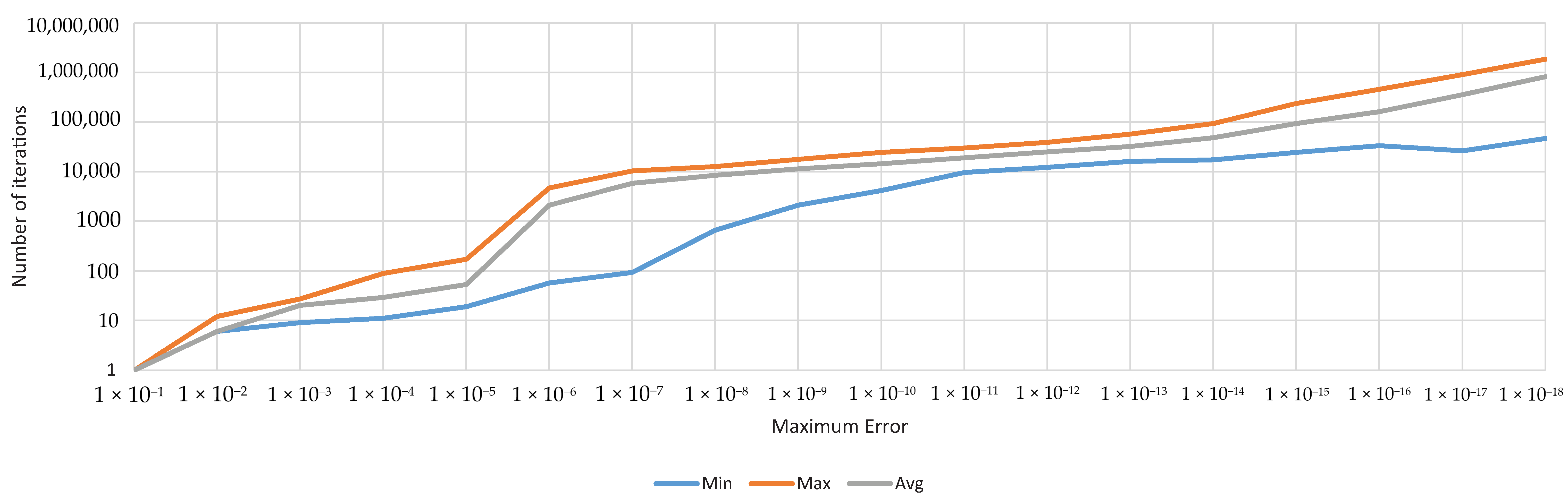
3.2. Identification of Transfer Function Parameters–IS
Genetic Algorithms Parameters
- Crossover probability—0.9,
- Mutation probability—0.2,
- Population size—31,
- Offspring size—30,
- Selection—rank weighting,
- Crossover—interpolation between two individuals [50],
- Mutation—movement on each dimension by ±0.1× random number.
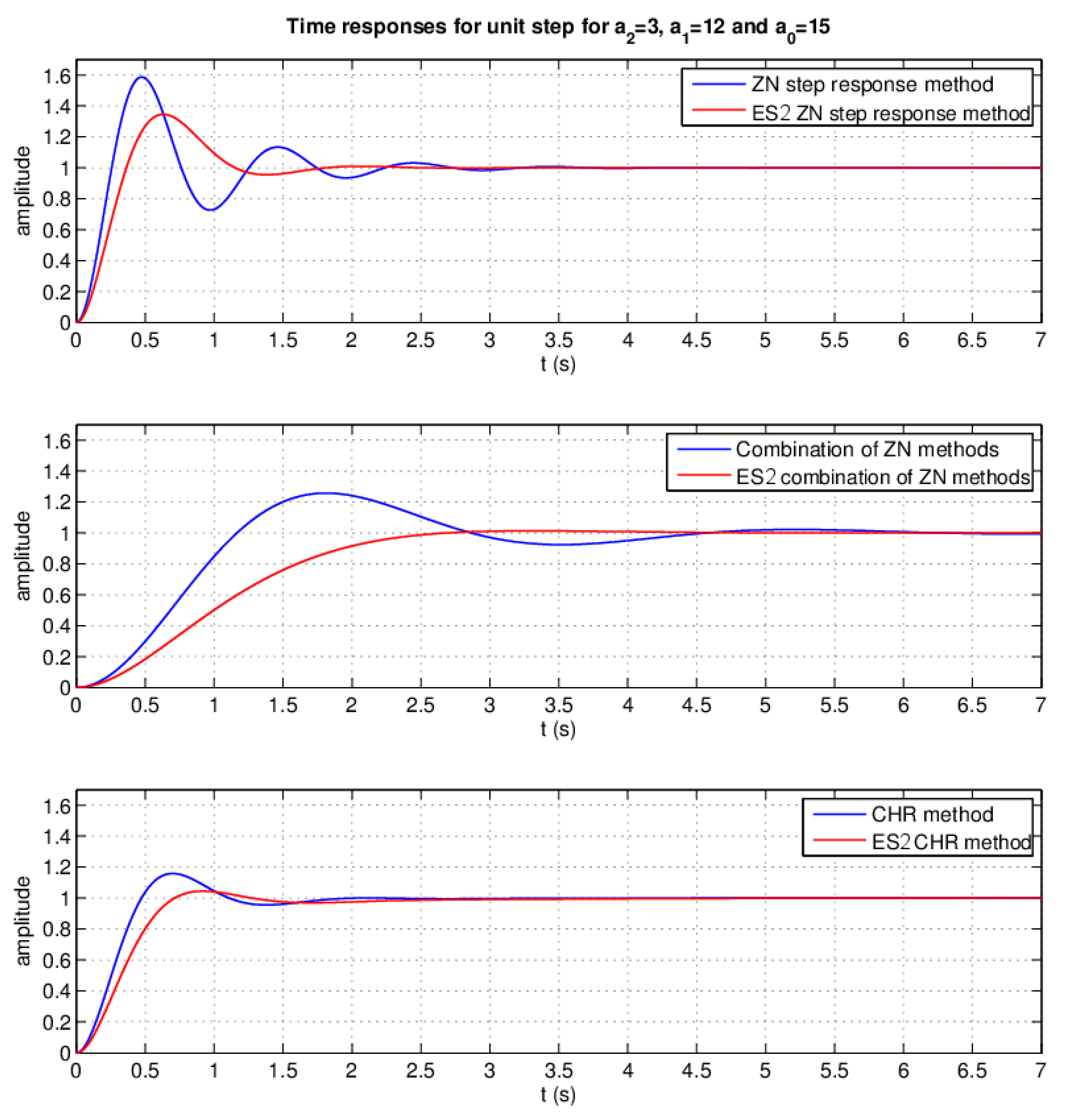
3.3. Controlling System Design–ES2
3.4. Intelligent Controller
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| A | Identificator for value Appropriate |
| CHR | Chein, Hrones and Reswick |
| COA | Center of Area |
| e(t) | Control error |
| ES | Expert System |
| ES1 | Monitoring Expert System |
| ES2 | Controlling System Design |
| F | Identificator for value Faster |
| G | Transfer Function |
| GA | Genetic Algorithms |
| H | Identificator for value High |
| IS | Identification System |
| J | Fitness Function |
| K | Gain of Proporcional Component |
| L | Identificator for value Low and Large |
| M | Identificator for value Medium |
| MO | Maximal Overshoot |
| O | Identificator for value Optimal |
| PID | Proportional–Integral–Derivative |
| RO | Relative Overshoot |
| RST | Relative Settling Time |
| s | Laplace Operator |
| S | Identificator for value Slower and Small |
| sec | Time unit second—for clear usage it is not used s, which is used for Laplace Operator |
| ST | Settling Time |
| T | Sampling Period |
| Time Constant of Derivator | |
| TDKNOW | Time Constant of Derivator obtained by Expert System |
| Time Constant of Integrator | |
| TIKNOW | Time Constant of Integrator obtained by Expert System |
| u(t) | Control variable |
| U | Laplace Image of Control Variable (System Input) |
| w(t) | Setpoint—required variable |
| XL | Identificator for value XLarge |
| XS | Identificator for value XSmall |
| y(t) | Controlled variable |
| Y | Laplace Image of Process Variable (System Output) |
| ZN | Ziegler–Nichols |
References
- Äström Karl, J.; Hägglund, T. PID Controllers: Theory, Design and Tuning, 2nd ed.; Instrument Society of America: Research Triangle, NC, USA, 1995. [Google Scholar]
- Ärzén, K.E. An Architecture for Expert System Based Feedback Control. Automatica 1989, 25, 813–827. [Google Scholar] [CrossRef] [Green Version]
- Äström Karl, J.; Anton, J.J. Expert Control. IFAC Proc. Vol. 1984, 17, 2579–2584. [Google Scholar] [CrossRef]
- Äström Karl, J.; Anton, J.J.; Ärzén, K.E. Expert Control. Automatica 1986, 22, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Moore, R.L.; Hawkinson, L.B.; Knickerbocker, C.G.; Churchman, L.M. Expert systems applications in industry. In Proceedings of the ISA International Conference, Houston, TX, USA, 22 October 1984; pp. 22–25. [Google Scholar]
- Shirley, R.S. Some lessons learned using expert systems for process control. IEEE Control Syst. Mag. 1987, 7, 11–15. [Google Scholar] [CrossRef]
- Ünal, M.; Ak, A.; Topuz, V.; Erdal, H. Optimization of PID Controllers Using ant Colony and Genetic Algorithms, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kofinas, P.; Dounis, A.I.; Papadakis, G.; Assimakopoulos, M. An Intelligent MPPT controller based on direct neural control for partially shaded PV system. Energy Build. 2015, 90, 51–64. [Google Scholar] [CrossRef]
- Thangaraju, I.; Muruganandam, M.; Madheswaran, M. Performance Analysis and Experimental Verification of Buck Converter fed DC Series Motor using Hybrid Intelligent Controller with Stability Analysis and Parameter Variations. J. Electr. Eng. Technol. 2015, 10, 518–528. [Google Scholar] [CrossRef] [Green Version]
- Al-saedi, M.I.; Wu, H.; Handroos, H. Intelligent controller of a flexible hybrid robot machine for ITER assembly and maintenance. Fusion Eng. Des. 2014, 89, 1795–1803. [Google Scholar] [CrossRef]
- Mishra, P.; Kumar, V.; Rana, K. A novel intelligent controller for combating stiction in pneumatic control valves. Control Eng. Pract. 2014, 33, 94–104. [Google Scholar] [CrossRef]
- Liu, B.; Ding, Y.; Gao, N.; Zhang, X. A bio-system inspired nonline ar intelligent controller with application to bio-reactor system. Neurocomputing 2015, 168, 1065–1075. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, G. Intelligent vibration control for high-speed spinning beam based on fuzzy self-tuning PID controller. Shock Vib. 2015, 2015, 1–8. [Google Scholar] [CrossRef]
- Azali, S.; Sheikhan, M. Intelligent control of photovoltaic system using BPSO-GSA-optimized neural network and fuzzy-based PID for maximum power point tracking. Appl. Intell. 2016, 44, 88–110. [Google Scholar] [CrossRef]
- Babu, V.S.; Kumar, U.A.; Priyadharshini, R.; Premkumar, K.; Nithin, S. An intelligent controller for smart home. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 2654–2657. [Google Scholar]
- Rahmanian, E.; Akbari, H.; Sheisi, G.H. Maximum power point tracking in grid connected wind plant by using intelligent controller and switched reluctance generator. IEEE Trans. Sustain. Energy 2017, 8, 1313–1320. [Google Scholar] [CrossRef]
- Jafari, M.; Xu, H.; Carrillo, L.R.G. Brain emotional learning-based intelligent controller for flocking of multi-agent systems. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 1996–2001. [Google Scholar]
- Bigdeli, N.; Ziazi, H.A. Design of fractional robust adaptive intelligent controller for uncertain fractional-order chaotic systems based on active control technique. Nonlinear Dyn. 2017, 87, 1703–1719. [Google Scholar] [CrossRef]
- Han, H.G.; Wu, X.L.; Liu, Z.; Qiao, J.F. Design of self-organizing intelligent controller using fuzzy neural network. IEEE Trans. Fuzzy Syst. 2017, 26, 3097–3111. [Google Scholar] [CrossRef]
- Golshannavaz, S.; Khezri, R.; Esmaeeli, M.; Siano, P. A two-stage robust-intelligent controller design for efficient LFC based on Kharitonov theorem and fuzzy logic. J. Ambient Intell. Humaniz. Comput. 2018, 9, 1445–1454. [Google Scholar] [CrossRef]
- Adhvaryu, A.D.; Adarsh, S.; Ramchandran, K. Design of fuzzy based intelligent controller for autonomous mobile robot navigation. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; pp. 841–846. [Google Scholar]
- Saxena, A.; Kumar, J.; Deolia, V.K. Design a Robust Intelligent Controller for Rigid Robotic Manipulator System having Two Links and Payloads. In Proceedings of the 2020 International Conference on Power Electronics & IoT Applications in Renewable Energy and its Control (PARC), Mathura, India, 28–29 February 2020; pp. 159–163. [Google Scholar]
- Chiu, C.H.; Wu, C.Y. Bicycle Robot Balance Control Based on a Robust Intelligent Controller. IEEE Access 2020, 8, 84837–84849. [Google Scholar] [CrossRef]
- Heij, C.; Ran, A.C.; van Schagen, F. Introduction to Mathematical Systems Theory: Linear Systems, Identification and Control, 1st ed.; Birkhäuser Verlag: Basel, Switzerland, 2007. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Coley, D.A. An Introduction to Genetic Algorithms for Scientists and Engineers, 1st ed.; World Scientific: Hackensack, NJ, USA, 1999. [Google Scholar]
- Abonyi, J.; Feil, B. Cluster Analysis for Data Mining and System Identification, 1st ed.; Birkhäuser Verlag AG: Berlin, Germany, 2007. [Google Scholar]
- Chu, S.R.; Shoureshi, R.; Tenorio, M. Neural networks for system identification. IEEE Control Syst. Mag. 1990, 10, 31–35. [Google Scholar] [CrossRef]
- Nelles, O. Nonlinear System Identification: From Classical Approaches to Neural Networks and Fuzzy Models, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Nowaková, J.; Pokornỳ, M. Double Expert System for Monitoring and Re-adaptation of PID Controllers. In Innovations in Bio-inspired Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2014; pp. 85–93. [Google Scholar]
- Nowaková, J.; Pokornỳ, M.; Pieš, M. Conventional controller design based on Takagi–Sugeno fuzzy models. J. Appl. Log. 2015, 13, 148–155. [Google Scholar] [CrossRef]
- Yazdanbakhsh, O.; Dick, S. A systematic review of complex fuzzy sets and logic. Fuzzy Sets Syst. 2018, 338, 1–22. [Google Scholar] [CrossRef]
- Jager, R. Fuzzy Logic in Control, 1st ed.; Kluwer Academic Publishers: Delft, The Netherlands, 1995. [Google Scholar]
- Doerr, B.; Le, H.P.; Makhmara, R.; Nguyen, T.D. Fast genetic algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference, Berlin, Germany, 15–19 July 2017; pp. 777–784. [Google Scholar]
- Hu, B.G.; Mann, G.K. A Systematic Study of Fuzzy PID Controllers - Function-Based Evaluation Approach, IEEE Trans. Fuzzy Syst. 2001, 9, 699–712. [Google Scholar]
- Farsi, M.; Karam, K.; Abdalla, H. Intelligent multi-controller assessment using fuzzy logic. Fuzzy Sets Syst. 1996, 79, 25–41. [Google Scholar] [CrossRef]
- Nilsson, N.J. Principles of Artificial Intelligence, 2nd ed.; Morgan Kaufmann: Burlington, MA, USA, 2014. [Google Scholar]
- Zou, L.; Wen, X.; Wang, Y. Linguistic truth-valued intuitionistic fuzzy reasoning with applications in human factors engineering. Inf. Sci. 2016, 327, 201–216. [Google Scholar] [CrossRef]
- Yager, R.R.; Zadeh, L.A. An Introduction to Fuzzy Logic Applications in Intelligent Systems, 2nd ed.; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Cornelis, C.; De Cock, M.; Kerre, E.E. The generalized modus ponens in a fuzzy set theoretical framework. In Fuzzy If-Then Rules in Computational Intelligence; Springer: Boston, MA, USA, 2000; pp. 37–59. [Google Scholar]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Nowakova, J.; Platos, J.; Snasel, V. Automatic power system identification using genetic algorithms. In Proceedings of the 2014 International Conference on Intelligent Networking and Collaborative Systems, Salerno, Italy, 10–12 September 2014; pp. 133–137. [Google Scholar]
- Nowakova, J.; Platos, J.; Hasal, M. System identification acceleration and improvement with genetic programming usage. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–7. [Google Scholar]
- Chambers, L.D. Practical Handbook of Genetic Algorithms: Complex Coding Systems; CRC Press: Boca Raton, FL, USA, 2019; Volume 3. [Google Scholar]
- Miller, F.P.; Vandome, A.F.; McBrewster, J. Nyquist-Shannon Sampling Theorem, 1st ed.; Alphascript Publishing: San Carlos, CA, USA, 2010. [Google Scholar]
- O’Dwyer, A. Handbook of PI and PID Controller Tuning Rules, 3rd ed.; World Scientific: Singapore, 2009. [Google Scholar]
- Zhao, Z.Y.; Tomizuka, M. Fuzzy Gain Scheduling of PID Controllers. IEEE Trans. Syst. Man Cybern. 1993, 23, 1392–1398. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Yang, T. A New Type of Computational Verb Gain-scheduling PID Controller. In Proceedings of the 2010 International Conference on Anti-Counterfeiting Security and Identification in Communication (ASID), Chengdu, China, 18–20 July 2010; pp. 235–238. [Google Scholar]
- Nowaková, J. Knowledge-Based Adaptation of Controllers. 2017. Available online: https://dspace.vsb.cz/handle/10084/122038 (accessed on 9 August 2020).
- Collette, Y. Crossover GA Default Function. Available online: https://help.scilab.org/docs/6.1.0/en_US/crossover_ga_default.html (accessed on 15 July 2020).



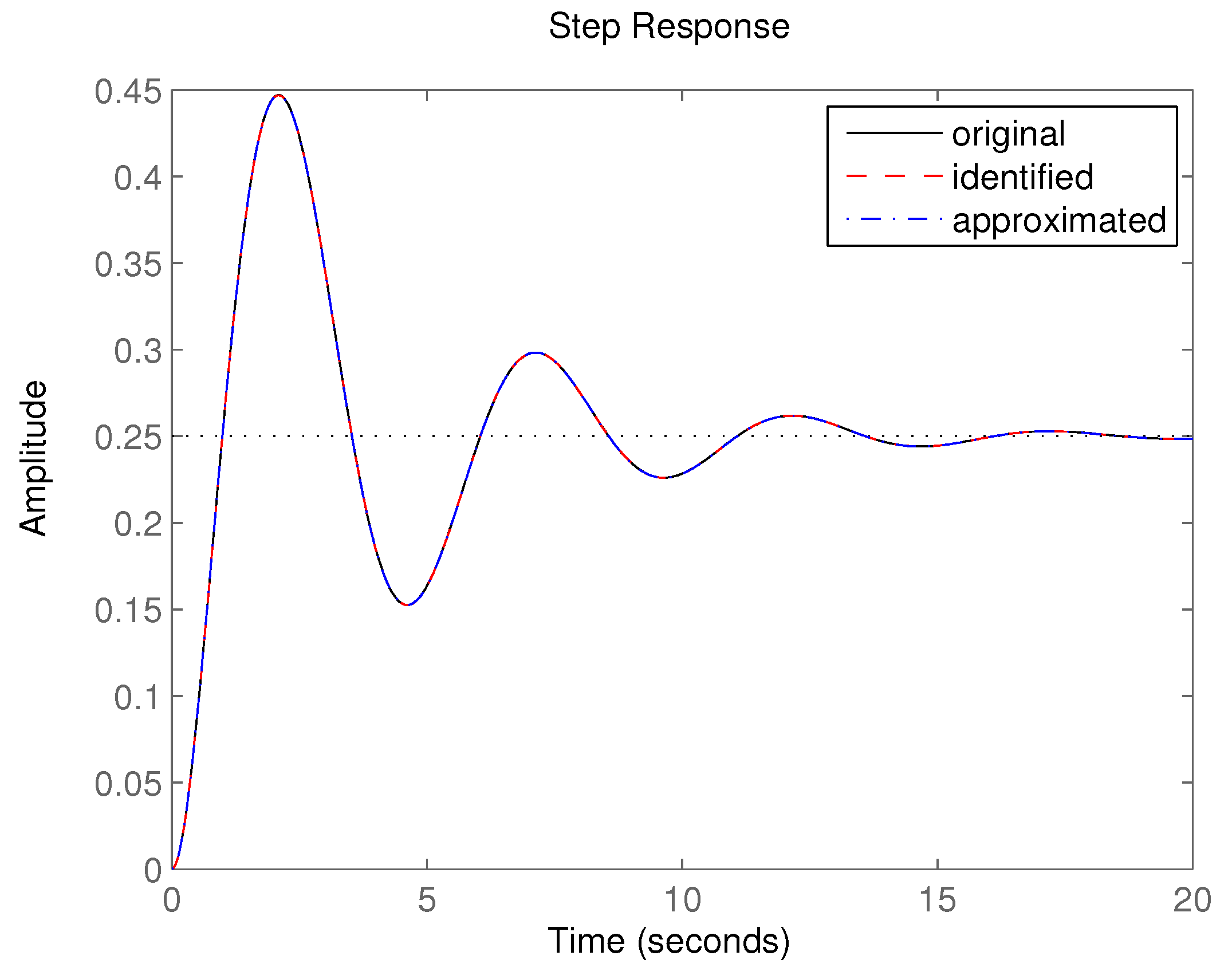
| original | −2.31816 | 1.83381 | −0.472367 | ||
| mean | −2.31318 | 1.82481 | −0.467787 | ||
| median | −2.31390 | 1.82610 | −0.468444 | ||
| identified | std | 0.00341 | 0.00618 | 0.003142 | |
| min | −2.31769 | 1.79844 | −0.471932 | ||
| max | −2.29859 | 1.83297 | −0.454380 | ||
| Fitness Function Value | |||||
| original | 0.0264792 | 0.00182614 | −0.0174828 | ||
| mean | 0.0262743 | 0.00210919 | −0.0174222 | ||
| median | 0.0263552 | 0.00203472 | −0.0174471 | ||
| identified | std | 0.0002218 | 0.00023706 | 0.0001634 | |
| min | 0.0252438 | 0.00182211 | −0.0180518 | ||
| max | 0.0266417 | 0.00311891 | −0.0168724 |
| Design Method | Overshoot (%) | Settling Time (2% Standard) (s) | |
|---|---|---|---|
| ZN step response method | classic | 58.69 | 2.5934 |
| expert | 34.60 | 1.6355 | |
| Combination of ZN methods | classic | 25.72 | 5.4623 |
| expert | 1.345 | 2.4214 | |
| CHR method | classic | 15.86 | 1.6975 |
| expert | 4.482 | 2.1660 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nowaková, J.; Pokorný, M. Intelligent Controller Design by the Artificial Intelligence Methods. Sensors 2020, 20, 4454. https://doi.org/10.3390/s20164454
Nowaková J, Pokorný M. Intelligent Controller Design by the Artificial Intelligence Methods. Sensors. 2020; 20(16):4454. https://doi.org/10.3390/s20164454
Chicago/Turabian StyleNowaková, Jana, and Miroslav Pokorný. 2020. "Intelligent Controller Design by the Artificial Intelligence Methods" Sensors 20, no. 16: 4454. https://doi.org/10.3390/s20164454
APA StyleNowaková, J., & Pokorný, M. (2020). Intelligent Controller Design by the Artificial Intelligence Methods. Sensors, 20(16), 4454. https://doi.org/10.3390/s20164454





