Detection of Transmitted Power Violation Based on Geolocation Spectrum Database in Satellite-Terrestrial Integrated Networks
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Related Work
1.3. Contributions
- Formulate a generalized model for spectrum sharing in the satellite-terrestrial integrated networks, where the terrestrial base station can apply to the geolocation spectrum database for the available spectrum of the satellite.
- Propose a detection framework based on geolocation spectrum database, which specifies the tasks and roles of the satellite-terrestrial integrated network, surveillance network, and geolocation spectrum database no matter when the terrestrial base station operates at the single power level or multiple power level.
- Analyze the optimization problem under both single and multiple transmitted power level scenarios, and further the AaN detector is derived.
- Provide comprehensive simulations under various parameter configurations, which represent that the superiority and effectiveness of the proposed detecting framework.
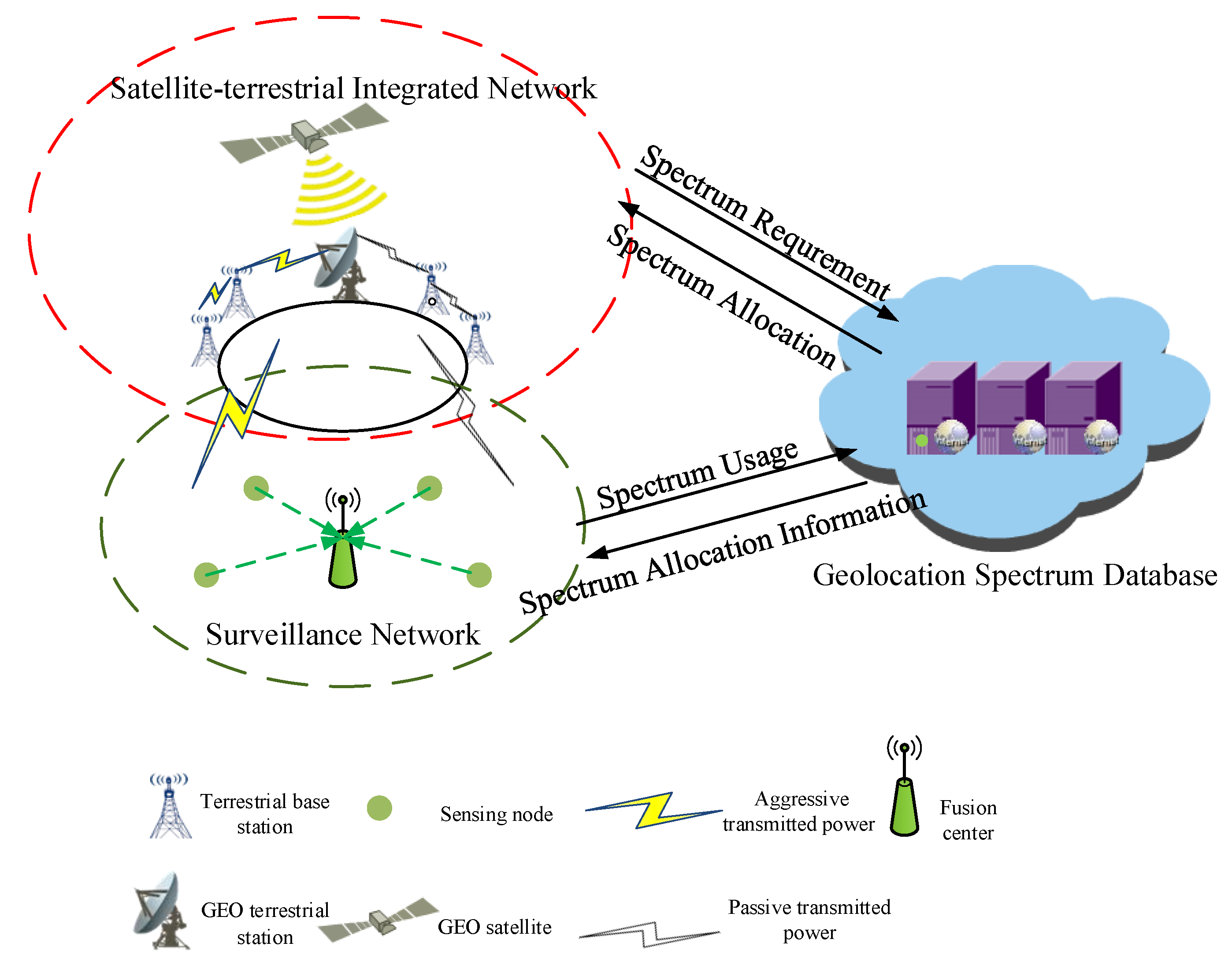
2. System Model
2.1. Database-Based Detection Framework
2.2. Hybrid Hypothesis Testing Model
3. Detection of TPV under Heterogeneous False Alarm Constraint
3.1. Detection Criteria under Heterogeneous False Alarm Constraint
3.2. Hybrid Hypothesis Testing Model
3.2.1. Single-Node Detection under Heterogeneous False-Alarm Constraint
- When the SNR is small, . At this time, the introduced function only holds one solution. Therefore, . To satisfy two false alarm constraints, .
- When the SNR is large, , , where are the three solutions of the introduced function . At this point, the two false alarm probabilities and reach the upper limit, respectively, which satisfies .
3.2.2. Multi-Node Detection under Heterogeneous False-Alarm Constraint
3.3. Detection of TPV at Multiple Power Levels
3.3.1. Generalized Maximum Likelihood Detection
3.3.2. The AaN Detector
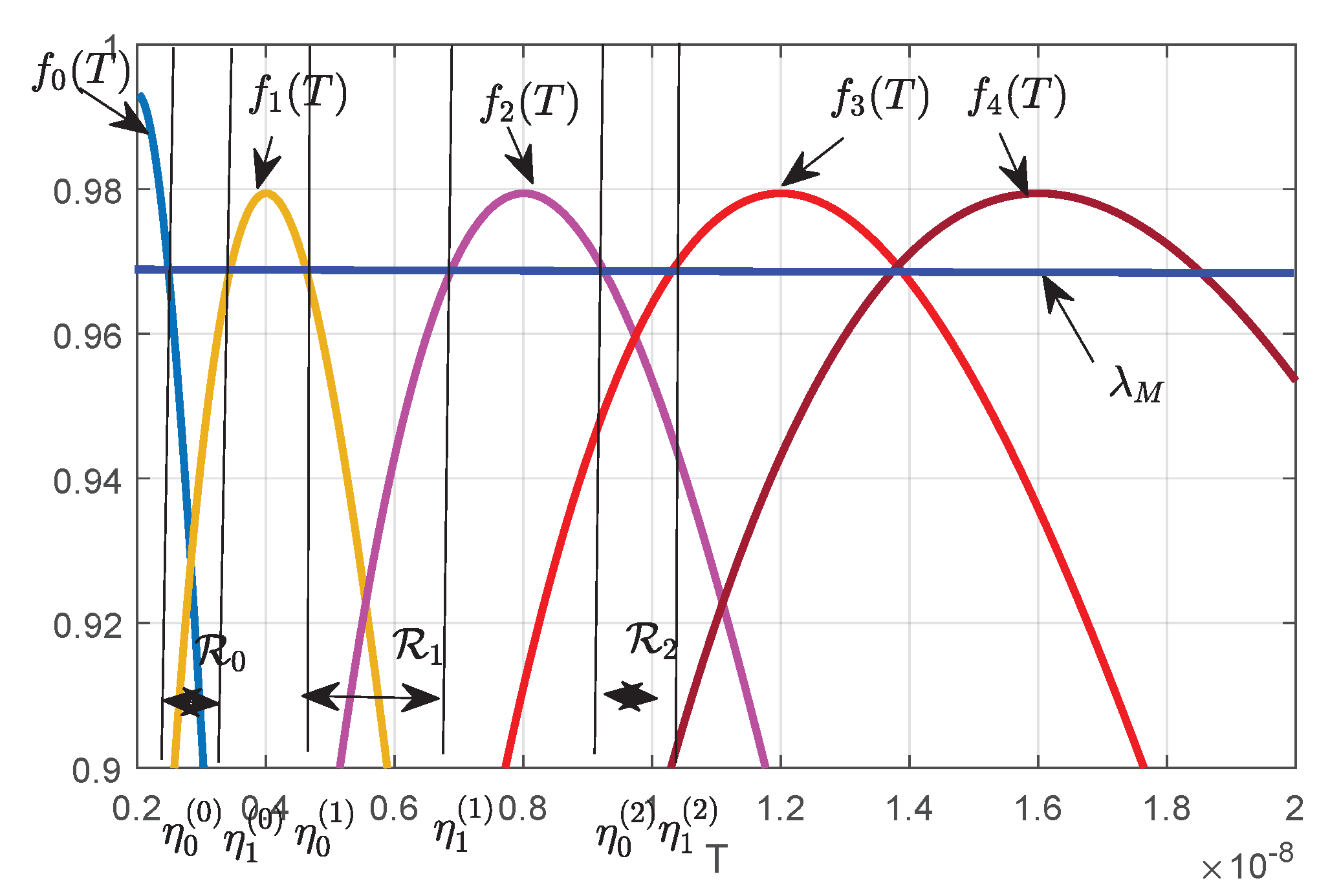
3.3.3. Threshold Setting
- , when the terrestrial user is working, its actual transmitted power . The variance of the observed quantity must be greater than , so the estimated variance of the observed data should be greater than ;
- , because when , is monotonically decreasing. Therefore, there is such that for all , it satisfies , i.e., is true.
- N is determined by the false alarm constraint.
- is the peak point of , where , ;
- When the number of samples M is large enough, approaches 1;
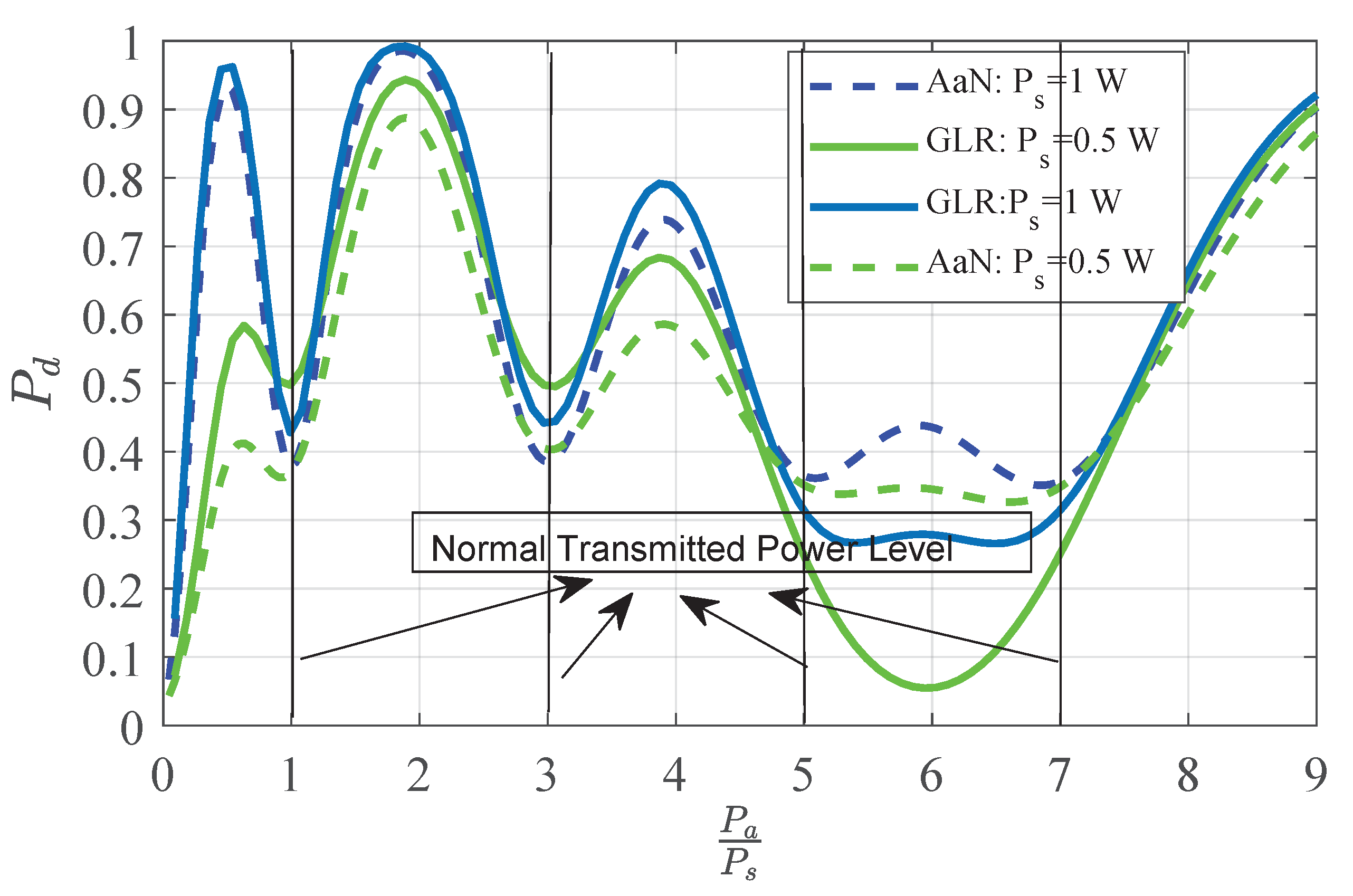
- The distance between each power level is always reasonably set so that each power level can be distinguished. Finally, between the two adjacent peak points, namely, in the interval , the detector can be approximated as
4. Simulation Results
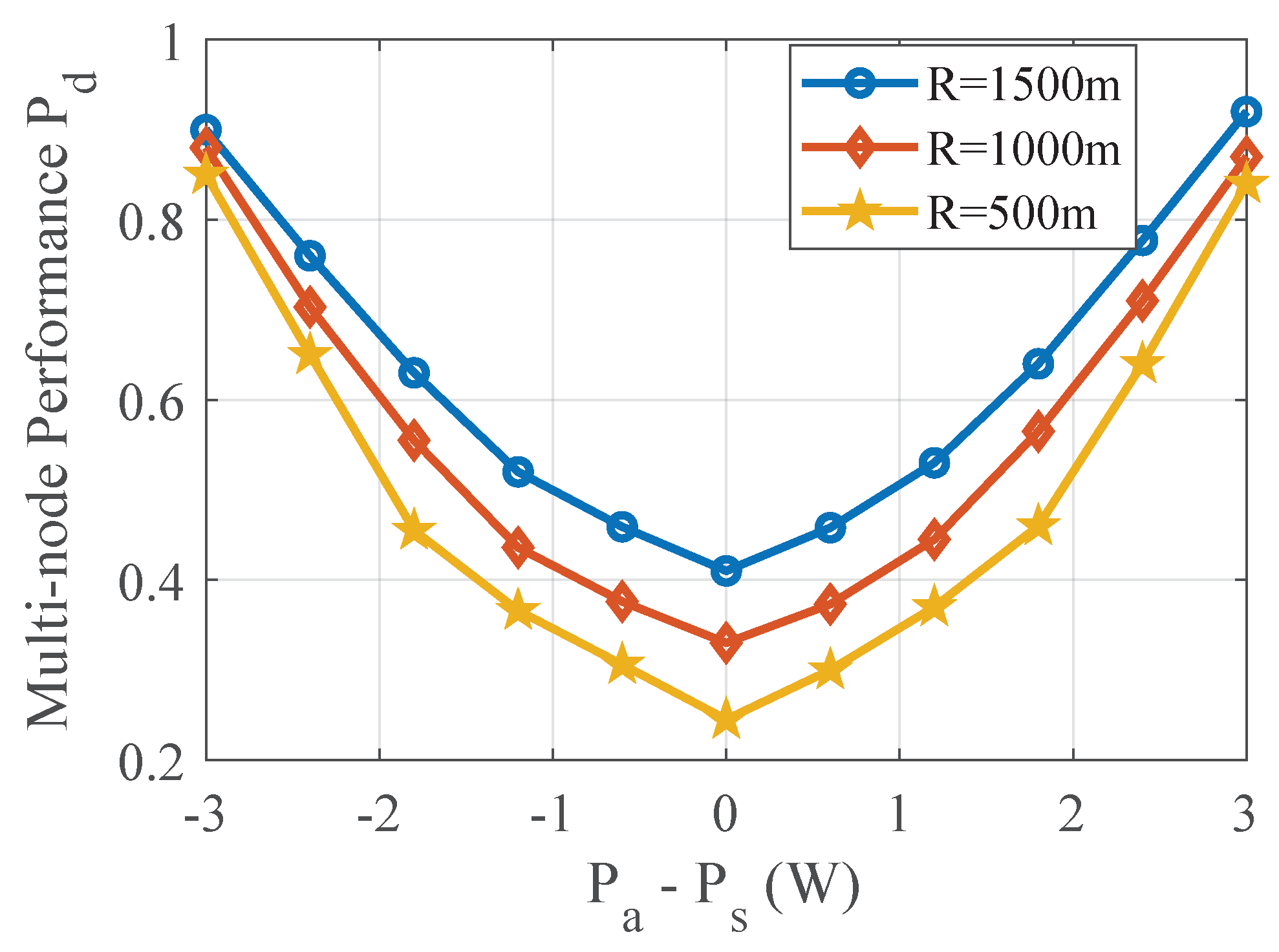
4.1. Performance of TPV Detection with Power Level L = 1
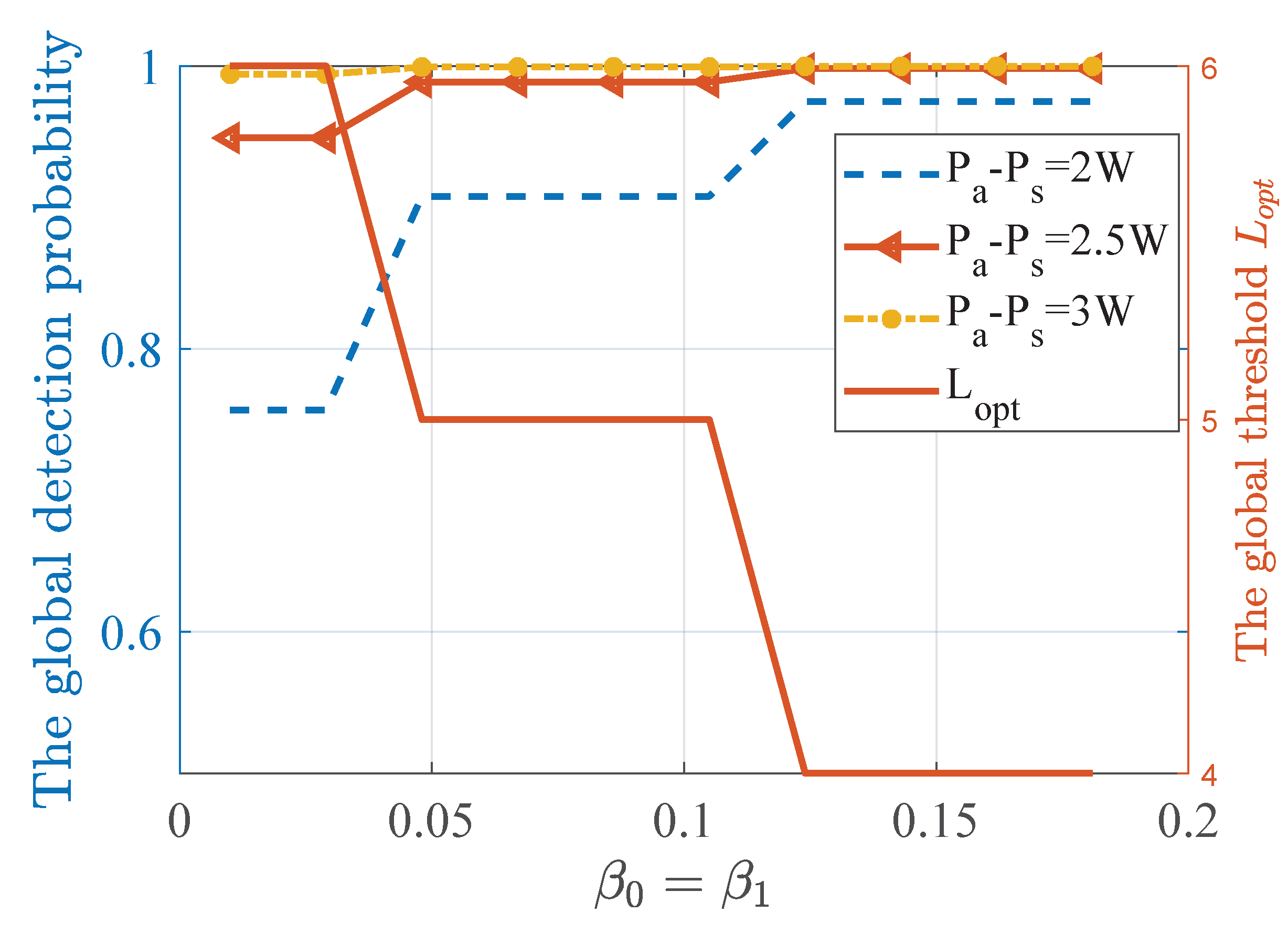
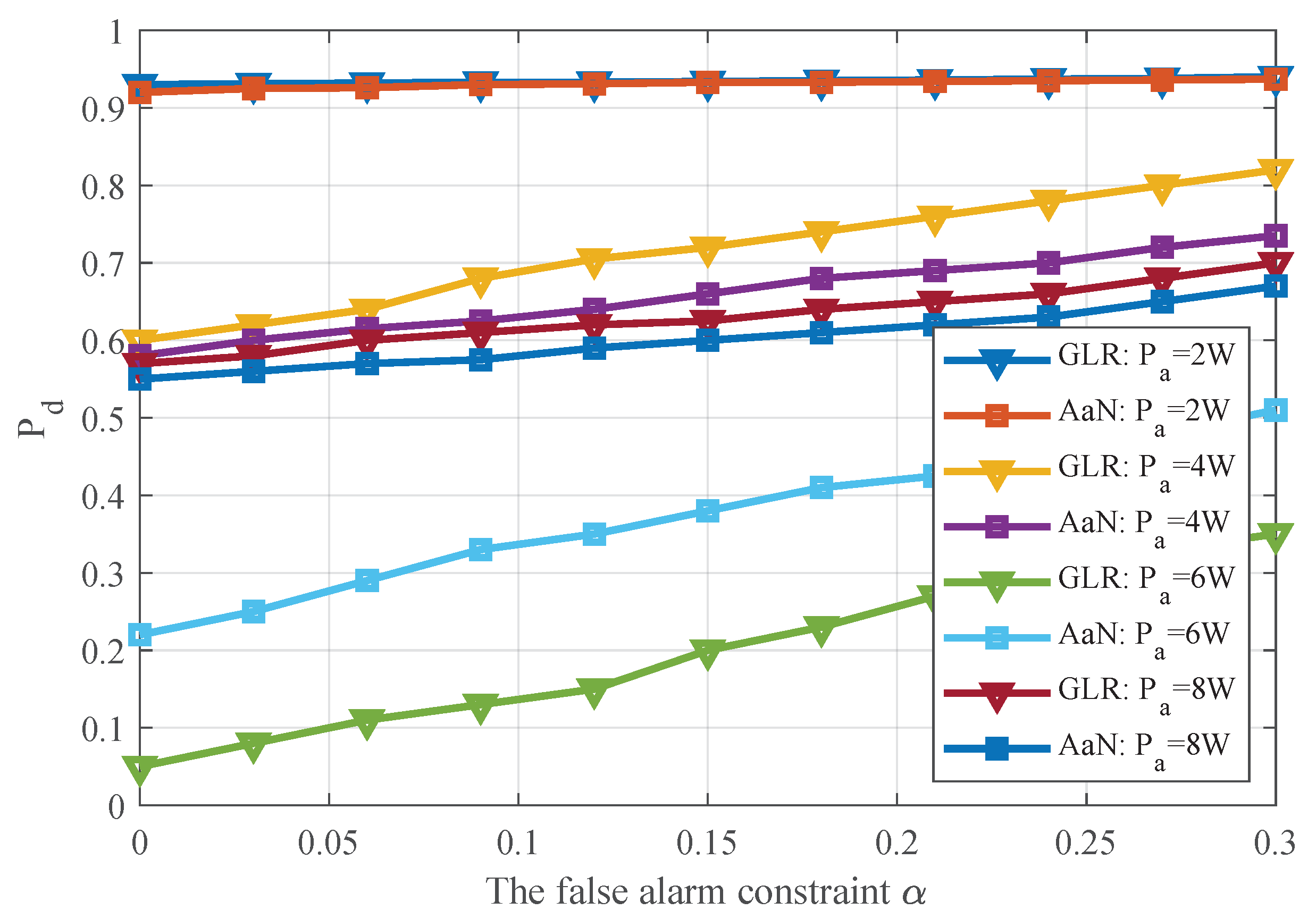
4.2. Performance of TPV Detection with Multiple Power Levels.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| TPV | transmitted power violation |
| GMNP | generalized multi-hypothesis Neyman–Pearson |
| PUEA | primary user emulation attack |
| PU-T | primary user’s transmitter |
| SU-T | secondary user’s transmitter |
| GLR | generalized likelihood ratio |
| AaN | Abnormal after Normal |
References
- Haykin, S. Cognitive radio: Brain-empowered wireless communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Mitola, J.; Maguire, J.G.Q. Cognitive radio: Making software radios more personal. IEEE Pers. Commun. 1999, 6, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Niyato, D.; Hossain, E.; Han, Z. Dynamic spectrum access in IEEE 802.22- based cognitive wireless networks: A game theoretic model for competitive spectrum bidding and pricing. IEEE Wireless Commun. 2009, 16, 16–23. [Google Scholar] [CrossRef]
- Li, H.; Guo, Q.; Li, Q. Satellite-based multi-resolution compressive spectrum detection in cognitive radio networks. In Proceedings of the 2nd International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 8–10 December 2012; pp. 1081–1085. [Google Scholar]
- Li, Z.; Wang, D.; Qi, P.; Hao, B. Maximum eigenvalue based sensing and power recognition for multi-antenna cognitive radio system. IEEE Trans. Veh. Technol. 2016, 65, 8218–8229. [Google Scholar] [CrossRef]
- Ju, M.; Kang, K.-M. Cognitive radio networks with secondary network selection. IEEE Trans. Veh. Technol. 2015, 65, 966–972. [Google Scholar] [CrossRef]
- Chi, Z.; Jiang, C.; Jin, J.; Wu, S.; Kuang, L.; Guo, S. Spectrum sensing and recognition in satellite systems. IEEE Trans. Veh. Technol. 2019, 68, 2502–2516. [Google Scholar]
- Zhang, C.; Jiang, C.; Kuang, L.; Jin, J.; He, Y.; Han, Z. Spatial spectrum sharing for satellite and terrestrial communication networks. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1075–1089. [Google Scholar] [CrossRef]
- Murty, R.; Chandra, R.; Moscibroda, T. Senseless: A databased-driven white spaces network. IEEE Trans. Mob. Comput. 2012, 11, 189–203. [Google Scholar] [CrossRef]
- Ding, G.; Wang, J.; Wu, Q. Cellular-based-station assisted device-to-device communications in TV white space. IEEE J. Sel. Areas Commun. 2016, 34, 107–121. [Google Scholar] [CrossRef] [Green Version]
- Höyhtyä, M.; Mämmelä, A.; Chen, X.; Hulkkonen, A.; Dunat, J.-C.; Gardey, J. Database-assisted spectrum sharing in satellite communications: A survey. IEEE Access 2017, 5, 25322–25341. [Google Scholar] [CrossRef]
- Yang, N.; Li, P.; Guo, D.; Zhang, L.; Ding, G. Detection of Interference Constraint Violation Based on Heterogeneous Data Fusion in Satellite-Earth Integrated Networks. IEEE Access 2020, 8, 37645–37656. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, B.; Guo, D.; Zhang, L.; Zhao, B.; Ding, G. Detection of Spectrum Misuse Behavior in Satellite-Terrestrial Spectrum Sensing Based on Multi-Hypothesis Tests. IEEE Access 2020, 8, 50399–50413. [Google Scholar] [CrossRef]
- Costello, D.J.; Forney, G.D. Channel coding: The road to channel capacity. Proc. IEEE 2007, 95, 1150–1177. [Google Scholar] [CrossRef] [Green Version]
- Ding, G.; Wang, J.; Wu, Q.; Song, F.; Chen, Y. Spectrum sensing in opportunity-heterogeneous cognitive sensor networks: How to cooperate? IEEE Sens. J. 2013, 13, 4247–4255. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, G.; Wu, Q.; Han, Z. Spectrum sensing under spectrum misuse behaviors: A multi-hypothesis test perspective. IEEE Trans. Inf. Forensics Secur. 2018, 13, 993–1007. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Ding, G.; Wu, Q. Detecting Abnormal Power Emission for Orderly Spectrum Usage. IEEE Trans. Veh. Technol. 2019, 68, 1989–1992. [Google Scholar] [CrossRef]
- Chen, C.; Cheng, H.; Yao, Y.-D. Cooperative spectrum sensing in cognitive radio networks in the presence of the primary user emulation attacks. IEEE Trans. Wirel. Commun. 2011, 10, 2135–2141. [Google Scholar] [CrossRef] [Green Version]
- Menon, R.; Buehrer, R.; Reed, J. Outage probability based comparison of underlay and overlay spectrum sharing techniques. In Proceeding of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN), Baltimore, MD, USA, 8–11 November 2005; pp. 101–109. [Google Scholar]
- Sithamparanathan, K.; De Nardis, L.; Di Benedetto, M.G.; Guidotti, A.; Corazza, G.E. Cognitive satellite terrestrial radios. In Proceedings of the IEEE Global Telecommunications Conference GLOBECOM, Miami, FL, USA, 6–10 December 2010. [Google Scholar]
- Sharma, S.K.; Symeon, C.; Bjorn, O. Satellite cognitive communications: Interference modeling and techniques selection. In Proceedings of the 6th Advanced Satellite Multimedia Systems Conference (ASMS) and 12th Signal Processing for Space Communications Workshop (SPSC), Baiona, Spain, 5–7 September 2012. [Google Scholar]
- ITU-R. P.526-8, Propagation by diffraction. 2003. Available online: https://www.itu.int/rec/R-REC-P.526-8-200304-S/en (accessed on 9 August 2020).
- Dissanayake, A.; Allnutt, J.; Haidara, F. A prediction model that combines rain attenuation and other propagation impairments along earthsatellite paths. IEEE Trans. Antennas Propag. 1997, 45, 1546–1558. [Google Scholar] [CrossRef]
- Dissanayake, A. Ka-band propagation modeling for fixed satellite applications. Online J. Space Commun. 2002, 2, 1–5. [Google Scholar]
- ITU-R. P.618, Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems. 2007. Available online: https://www.itu.int/rec/R-REC-P.618-9-200708-S/en (accessed on 9 August 2020).
- ITU-R. P.676-4, Attenuation by Atmospheric Gases. 1999. Available online: https://www.itu.int/rec/R-REC-P.676-4-199910-S/en (accessed on 9 August 2020).
- ITU-R. P.840-3, Attenuation Due to Clouds and Fog. 1999. Available online: https://www.itu.int/rec/R-REC-P.840-3-199910-S/en (accessed on 9 August 2020).
- ITU-R. S.672-4, Satellite Antenna Radiation Pattern for Use as a Design Objective in the Fixed-Satellite Service Employing Geostationary Satellites. 1997. Available online: https://www.itu.int/rec/R-REC-S.672-4-199709-I/en (accessed on 9 August 2020).


| The Notation | Physical Meaning | Value |
|---|---|---|
| Frequency band | ||
| h | Satellite height | 35,786 Km |
| Satellite EIRP | ||
| Desired side-lobe level relative to peak gain | ||
| Max satellite antenna gain | ||
| The path fading factor | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, N.; Li, P.; Guo, D.; Zhang, L.; Ding, G. Detection of Transmitted Power Violation Based on Geolocation Spectrum Database in Satellite-Terrestrial Integrated Networks. Sensors 2020, 20, 4462. https://doi.org/10.3390/s20164462
Yang N, Li P, Guo D, Zhang L, Ding G. Detection of Transmitted Power Violation Based on Geolocation Spectrum Database in Satellite-Terrestrial Integrated Networks. Sensors. 2020; 20(16):4462. https://doi.org/10.3390/s20164462
Chicago/Turabian StyleYang, Ning, Pinghui Li, Daoxing Guo, Linyuan Zhang, and Guoru Ding. 2020. "Detection of Transmitted Power Violation Based on Geolocation Spectrum Database in Satellite-Terrestrial Integrated Networks" Sensors 20, no. 16: 4462. https://doi.org/10.3390/s20164462
APA StyleYang, N., Li, P., Guo, D., Zhang, L., & Ding, G. (2020). Detection of Transmitted Power Violation Based on Geolocation Spectrum Database in Satellite-Terrestrial Integrated Networks. Sensors, 20(16), 4462. https://doi.org/10.3390/s20164462





