Adaptive Fine Distortion Correction Method for Stereo Images of Skin Acquired with a Mobile Phone
Abstract
:1. Introduction
- We propose the distortion correction method for mobile images as a pre-processing step for the 3D evaluation and analysis of stereo skin surface images captured using a mobile phone.
- Unlike prior studies that correct the mobile image of the human face, environment, etc., we correct the distortion of skin surface images with a complex structure to demonstrate the usability of mobile cameras in the field of biometric signals, which requires precision at the µm level.
- Most studies deal with the correction for barrel distortion, which appears strongly over a wide area, such as in fish-eye lens images. Contrastingly, our study proposes a correcting method for fine pincushion distortion in close-up images.
- We employ the division model using a single parameter rather than the camera calibration approach, which is a complicated and time-consuming method, to correct the mobile image in real time. Additionally, we generate a pixel-by-pixel distortion correction matrix containing different degrees of distortion in the left and right regions of the image to increase the precision of distortion correction.
2. Materials and Methods
2.1. Image Acquisition
2.2. The Vertical Line Pattern
2.3. Proposing the Distortion Correction Matrix (DCM)
2.4. Interpolation of the Corrected Image
2.5. Regression Analysis of the Relationship between the Distortion Ratio and Different Angle Images
3. Results
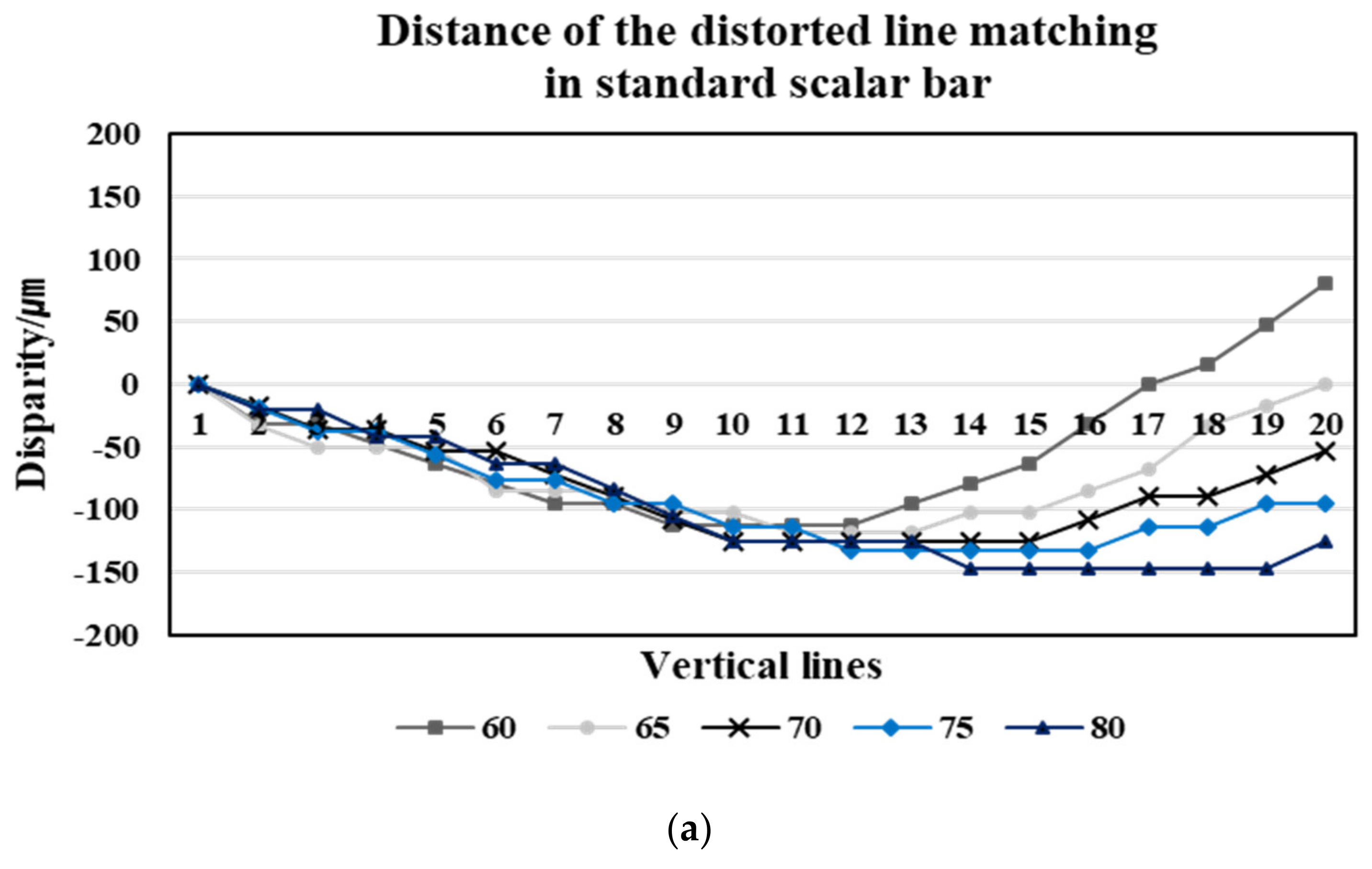
3.1. Comparing the before-and-after Distortion Correction for Vertical Line Pattern
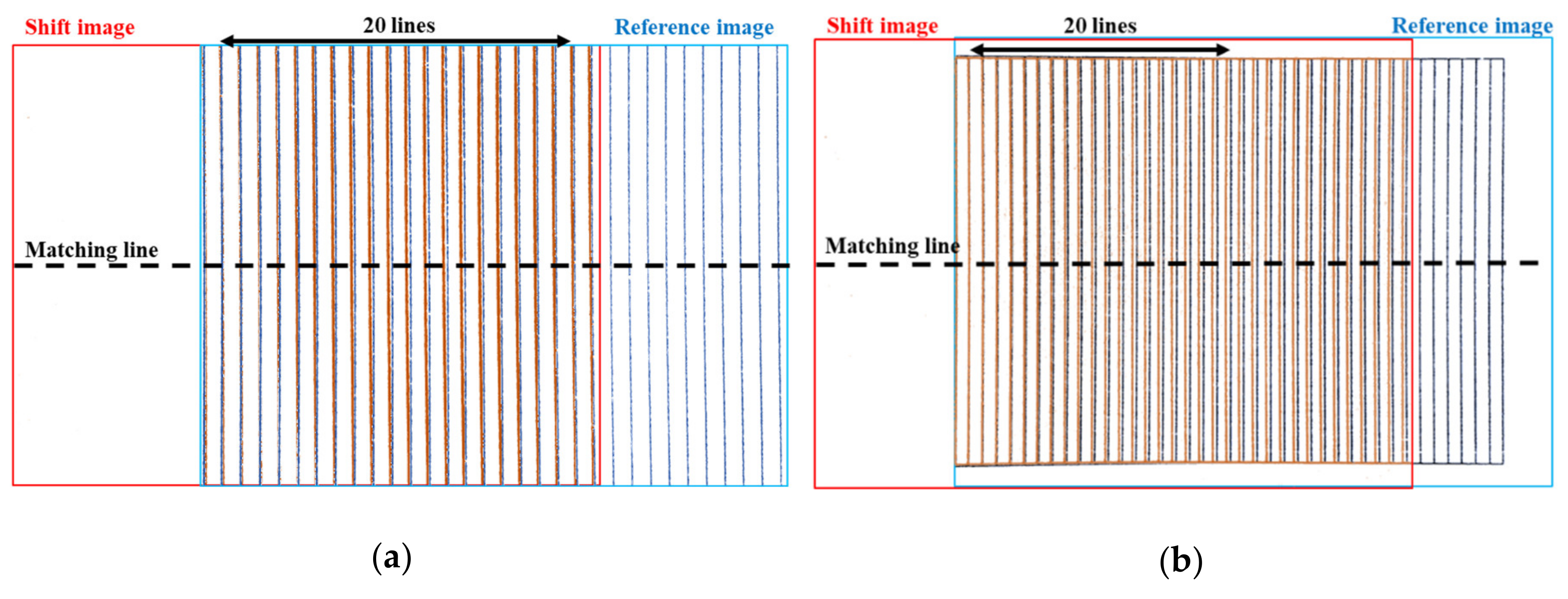
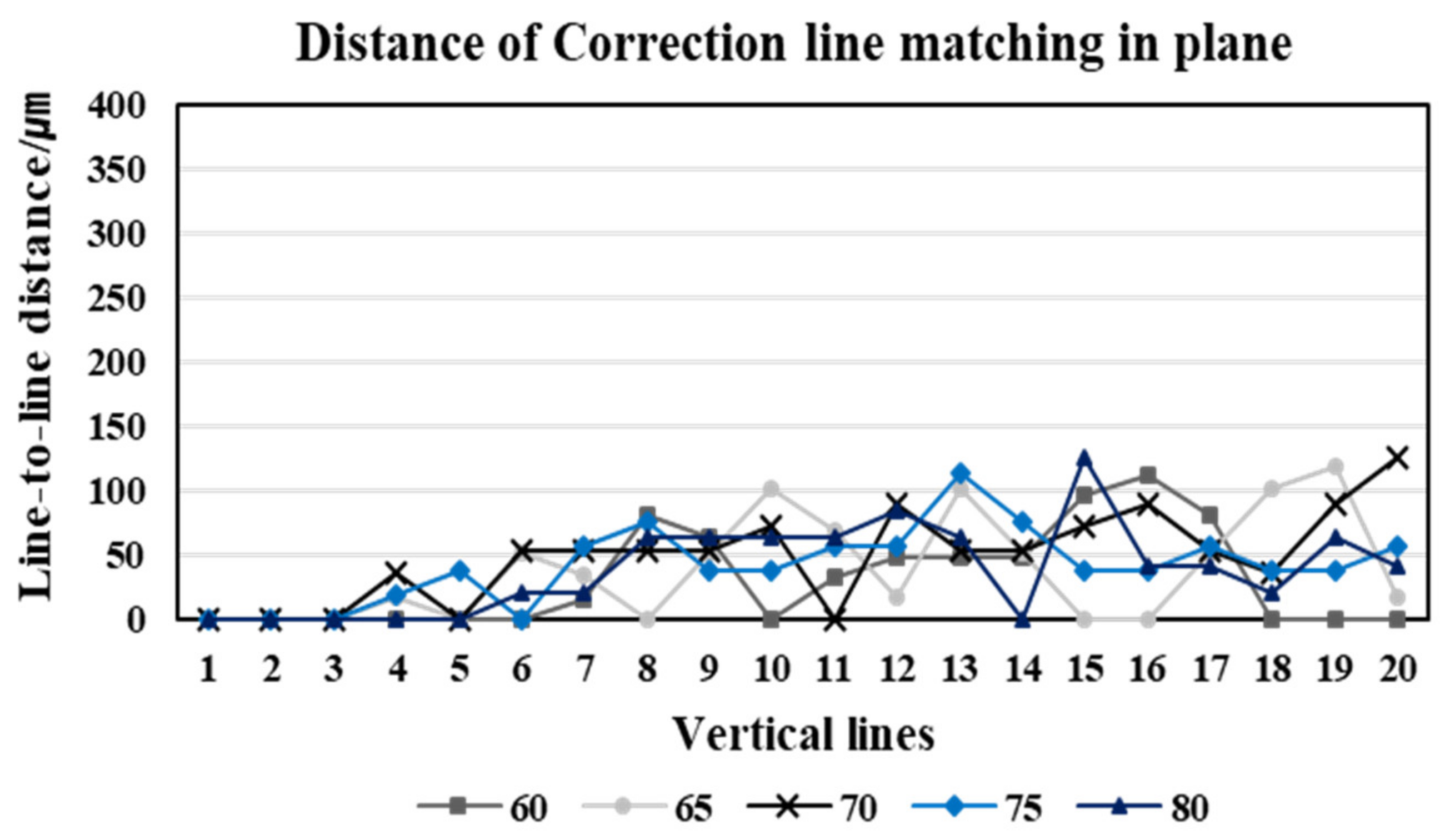
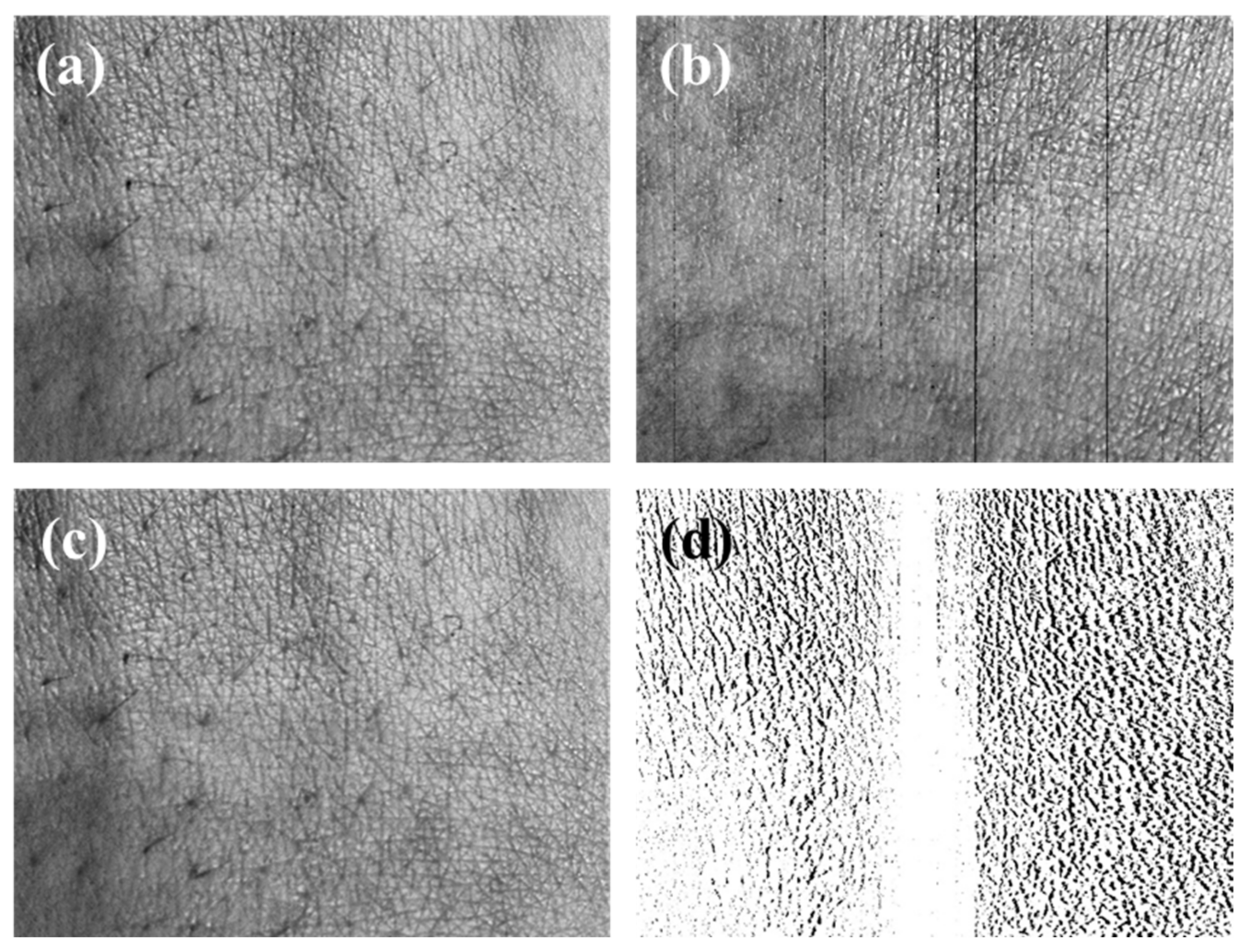
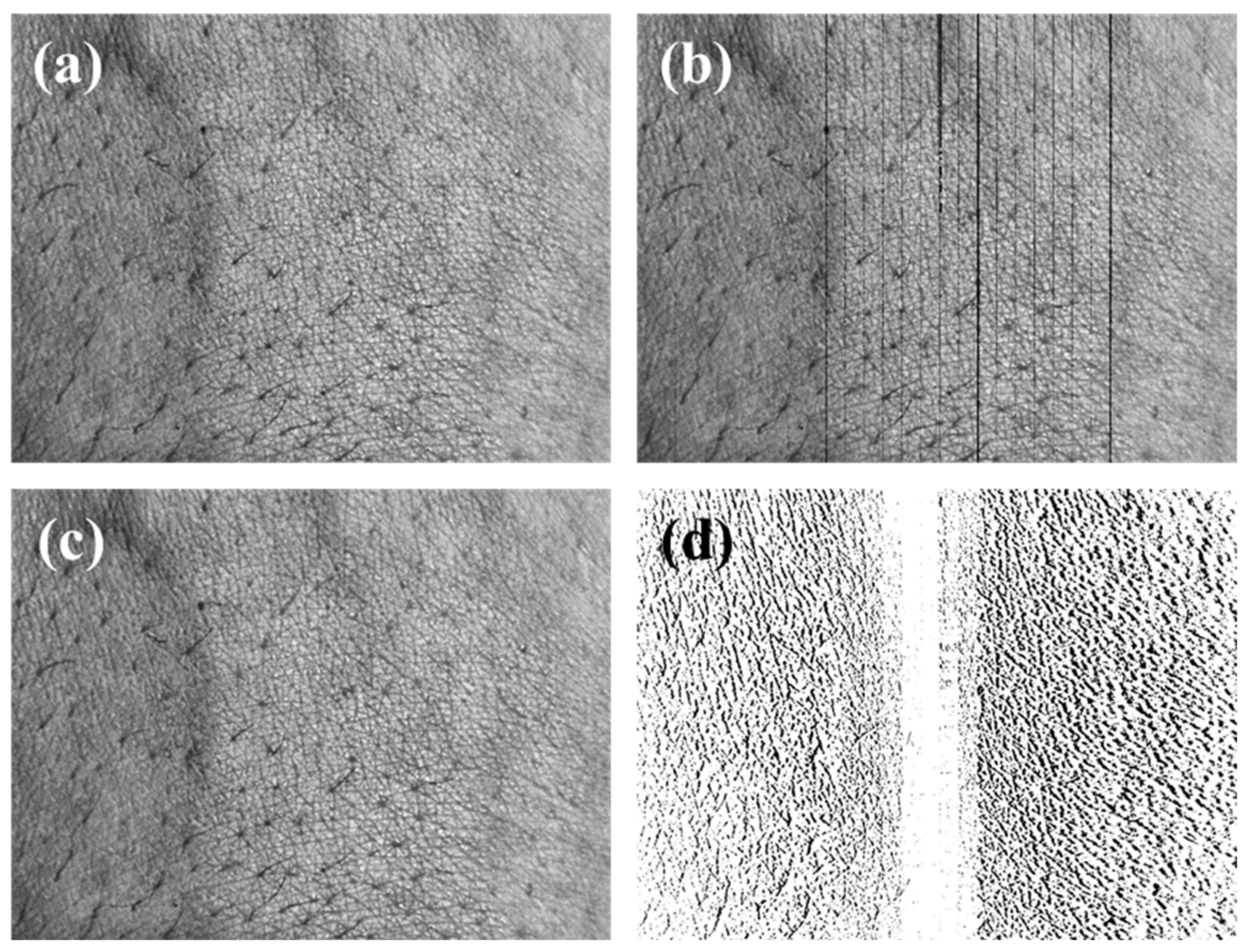
3.2. Comparing before-and-after Distortion Correction for Mobile Stereo Pattern Images in-Plane
3.3. Comparing before-and-after Distortion Correction for Mobile Stereo Pattern Images Containing Depth
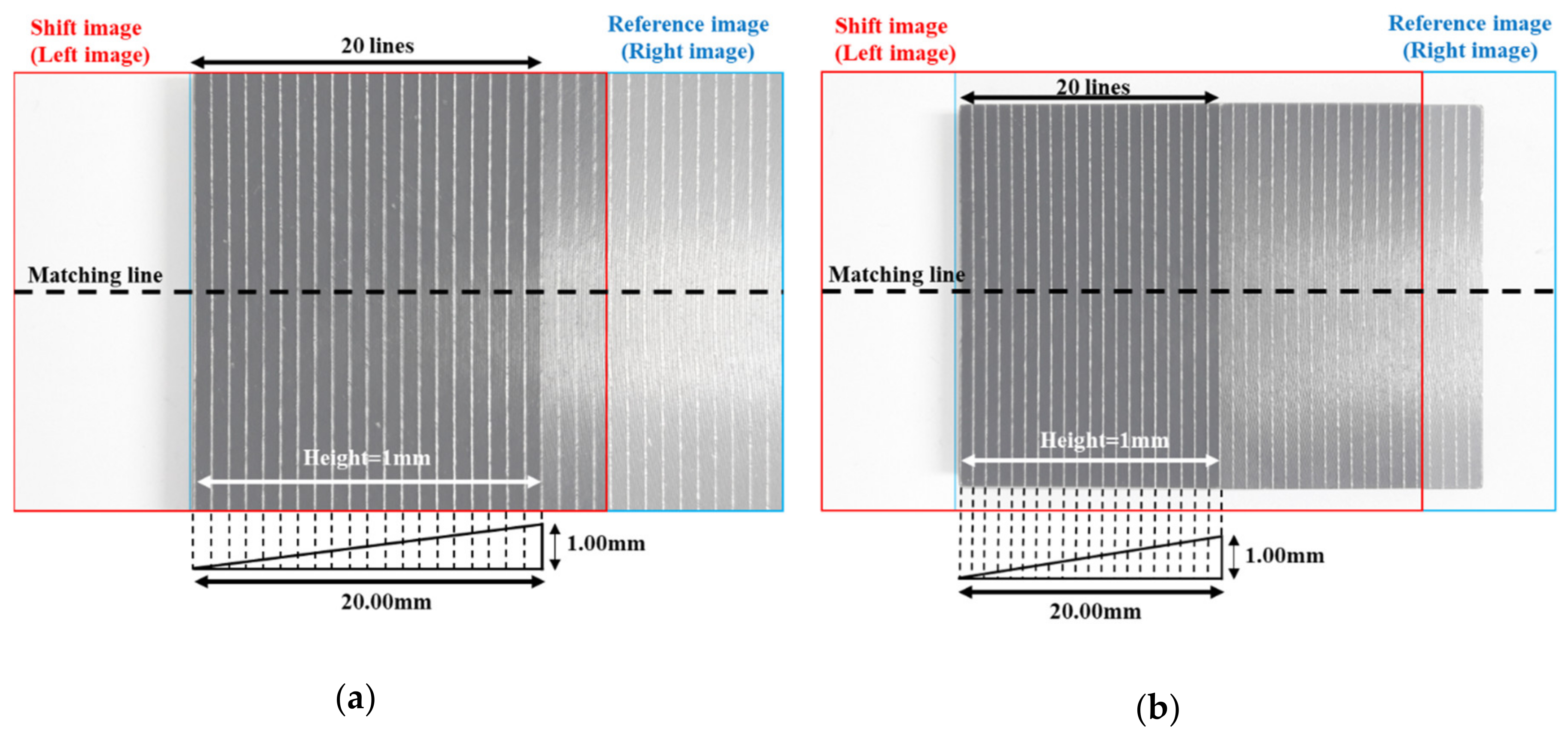
3.4. The Correcting Distortion Result of the Mobile Skin Image
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rew, J.; Choi, Y.-H.; Kim, H.; Hwang, E. Skin Aging Estimation Scheme Based on Lifestyle and Dermoscopy Image Analysis. Appl. Sci. 2019, 9, 1228. [Google Scholar] [CrossRef] [Green Version]
- Hong, G.; Lee, O. Three-Dimensional Reconstruction of Skin Disease Using Multi-View Mobile Images. Ski. Res. Technol. 2019, 25, 434–439. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, Y.; Chen, B. Out-of-Focus Projector Calibration Method with Distortion Correction on the Projection Plane in the Structured Light Three-Dimensional Measurement System. Sensors 2017, 17, 2963. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, L.; Wang, Y.; Yu, H.; Zhu, J. Automatic Camera Calibration Using Active Displays of a Virtual Pattern. Sensors 2017, 17, 685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Catherwood, T.E.; Winder, J.A.; McIntosh, S.A.; Winder, R.J. 3D Stereophotogrammetry: Post-Processing and Surface Integration. Imaging Sci. J. 2014, 63, 95–102. [Google Scholar] [CrossRef]
- Ko, M.; Kim, N.; Kim, K. Accurate Depth Estimation of Skin Surface Using a Light-Field Camera Toward Dynamic Haptic Palpation. Ski. Res. Technol. 2019, 25, 469–481. [Google Scholar] [CrossRef] [PubMed]
- Lee, O.; Lee, G.; Oh, J.; Kim, M.; Oh, C. An Optimized In Vivo Multiple-Baseline Stereo Imaging System for Skin Wrinkles. Opt. Commun. 2010, 283, 4840–4845. [Google Scholar] [CrossRef]
- Lee, O.; Lee, G.; Kim, M.; Kim, S.-K.; Baek, Y.; Oh, C. Multimodal Evaluation of Xenograft Tumors in Mice with an In-Vivo Stereo Imaging System and Small-Animal PET/CT. Melanoma Res. 2013, 23, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Freire-Obregón, D.; Narducci, F.; Barra, S.; Castrillón-Santana, M. Deep Learning for Source Camera Identification on Mobile Devices. Pattern Recognit. Lett. 2019, 126, 86–91. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Ding, H.; Yu, Z.; Zhang, Z.; Liu, W.; Chen, X. Joint Space-time Coding and Power Domain Non-orthogonal Multiple Access for Future Wireless System. KSII Trans. Internet Inf. Syst. 2020, 14, 93–113. [Google Scholar] [CrossRef]
- Moon, C.-I.; Lee, O. Age-Dependent Skin Texture Analysis and Evaluation Using Mobile Camera Image. Ski. Res. Technol. 2018, 24, 490–498. [Google Scholar] [CrossRef] [PubMed]
- Shih, Y.; Lai, W.-S.; Liang, C.-K. Distortion-Free Wide-Angle Portraits on Camera Phones. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Wei, H.; Wang, X. Correction of Image Radial Distortion Based on Division Model. Opt. Eng. 2017, 56, 13108. [Google Scholar] [CrossRef] [Green Version]
- Layek, A.; Chung, T.; Huh, E.-N. Remote Distance Measurement from a Single Image by Automatic Detection and Perspective Correction. KSII Trans. Internet Inf. Syst. 2019, 13, 3981–4004. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Zhou, Q. Real-Time Multi-Target Localization from Unmanned Aerial Vehicles. Sensors 2016, 17, 33. [Google Scholar] [CrossRef] [PubMed]
- Benligiray, B.; Topal, C. Blind Rectification of Radial Distortion by Line Straightness. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 28 August–2 September 2016; pp. 938–942. [Google Scholar]
- Wu, R.Q.; Liu, J.; Chen, W.; Gu, Q.S. Adaptive Wide-Lens Distortion Correction Based on Piecewise Polynomial Optimization. Procedia Comput. Sci. 2019, 154, 573–580. [Google Scholar] [CrossRef]
- Zheng, B.; Dong, Y.; Mullany, B.; Morse, E.; Davies, A. An Optical Positioning Sensor by Combining Optical Projection and a Virtual Camera Model. In Proceedings of the Remote Sensing System Engineering V, San Diego, CA, USA, 3 October 2014; p. 92230J. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Fitzgibbon, A.W. Simultaneous Linear Estimation of Multiple View Geometry and Lens Distortion. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2001, Kauai, HI, USA, 8–14 December 2001; p. I. [Google Scholar]
- Lee, M.; Kim, H.; Paik, J. Correction of Barrel Distortion in Fisheye Lens Images Using Image-Based Estimation of Distortion Parameters. IEEE Access 2019, 7, 45723–45733. [Google Scholar] [CrossRef]
- Qiao, N. Distortion correction of photoelectric image acquired by CCD camera. In Proceedings of the Sixth International Conference on Optical and Photonic Engineering (icOPEN 2018), Shanghai, China, 2 August 2018; p. 1082717. [Google Scholar]
- Park, J.; Byun, S.-C.; Lee, B.-U. Lens Distortion Correction Using Ideal Image Coordinates. IEEE Trans. Consum. Electron. 2009, 55, 987–991. [Google Scholar] [CrossRef]





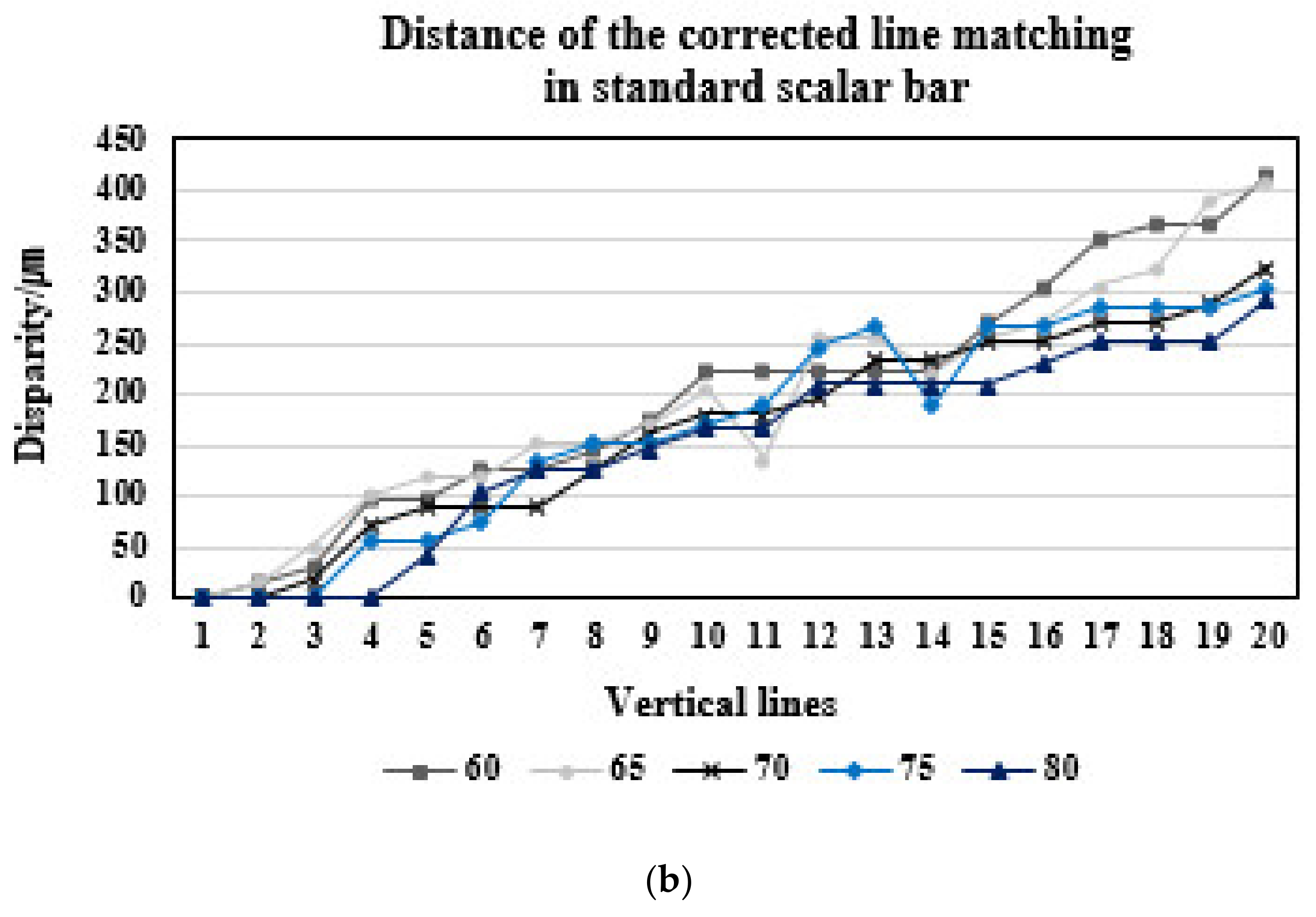

| Working Distance (mm) | Average Correction Rate (%) | Maximum of Error Distance before Correction (mm) | Maximum of Error Distance after Correction (mm) |
|---|---|---|---|
| 60 | 84.6% | 0.24 | 0.11 |
| 65 | 82.7% | 0.27 | 0.12 |
| 70 | 80.7% | 0.32 | 0.13 |
| 75 | 81.7% | 0.34 | 0.11 |
| 80 | 86.3% | 0.38 | 0.13 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, C.-I.; Lee, O. Adaptive Fine Distortion Correction Method for Stereo Images of Skin Acquired with a Mobile Phone. Sensors 2020, 20, 4492. https://doi.org/10.3390/s20164492
Moon C-I, Lee O. Adaptive Fine Distortion Correction Method for Stereo Images of Skin Acquired with a Mobile Phone. Sensors. 2020; 20(16):4492. https://doi.org/10.3390/s20164492
Chicago/Turabian StyleMoon, Cho-I, and Onseok Lee. 2020. "Adaptive Fine Distortion Correction Method for Stereo Images of Skin Acquired with a Mobile Phone" Sensors 20, no. 16: 4492. https://doi.org/10.3390/s20164492
APA StyleMoon, C.-I., & Lee, O. (2020). Adaptive Fine Distortion Correction Method for Stereo Images of Skin Acquired with a Mobile Phone. Sensors, 20(16), 4492. https://doi.org/10.3390/s20164492





