Short-Range Water Temperature Profiling in a Lake with Coastal Acoustic Tomography
Abstract
1. Introduction
2. Methods
2.1. Inversion Method
2.2. Experimental Settings
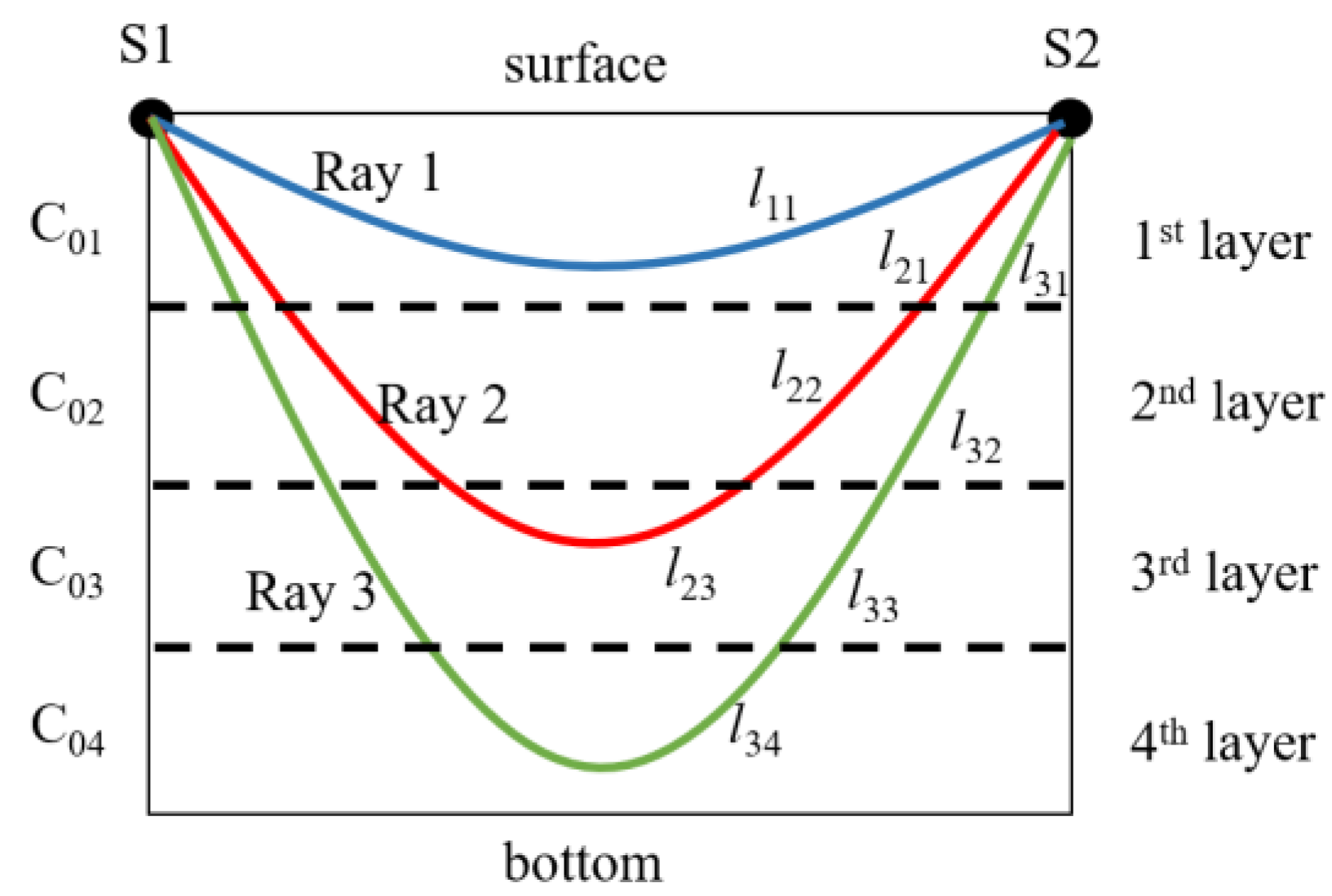
2.3. Ray Simulation
3. Results
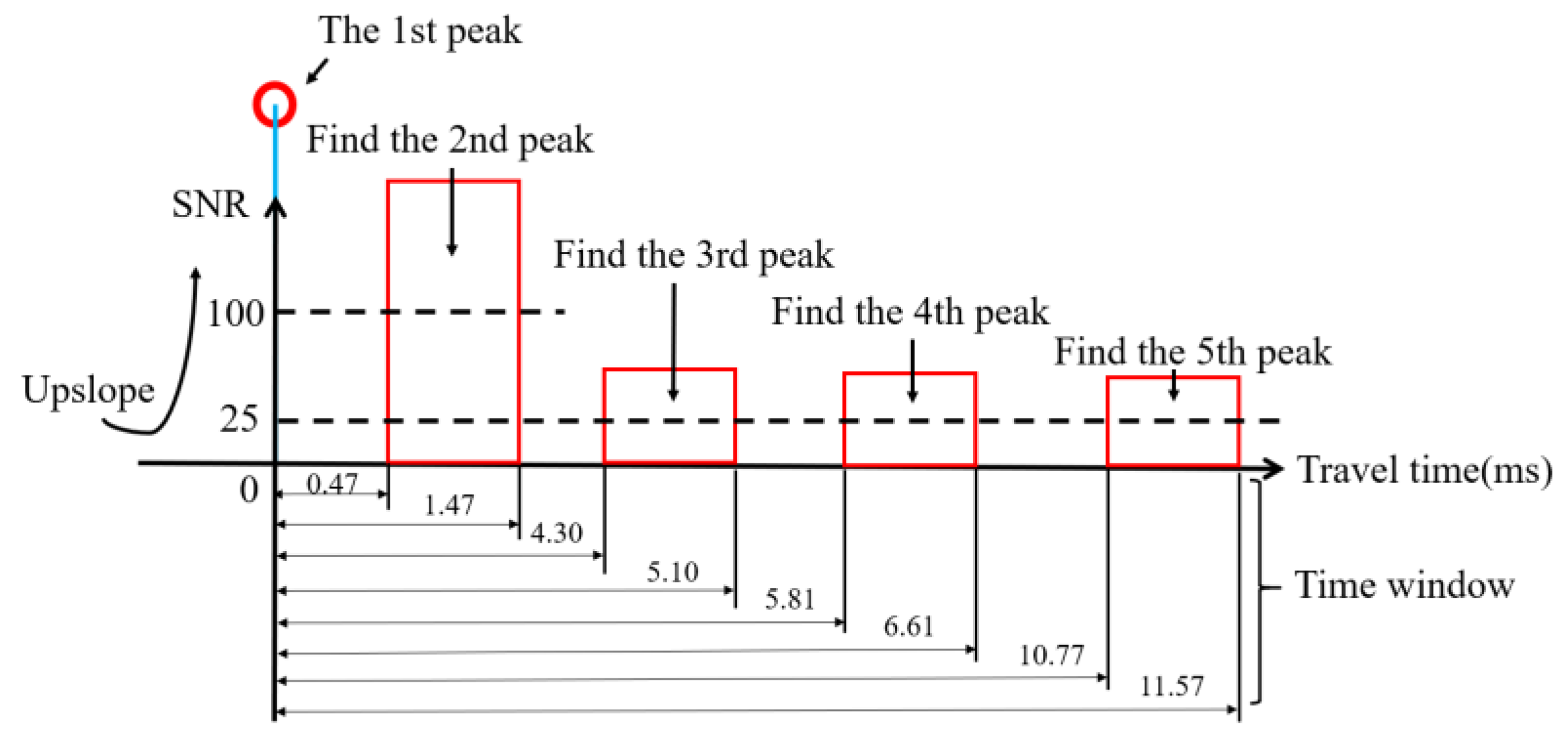
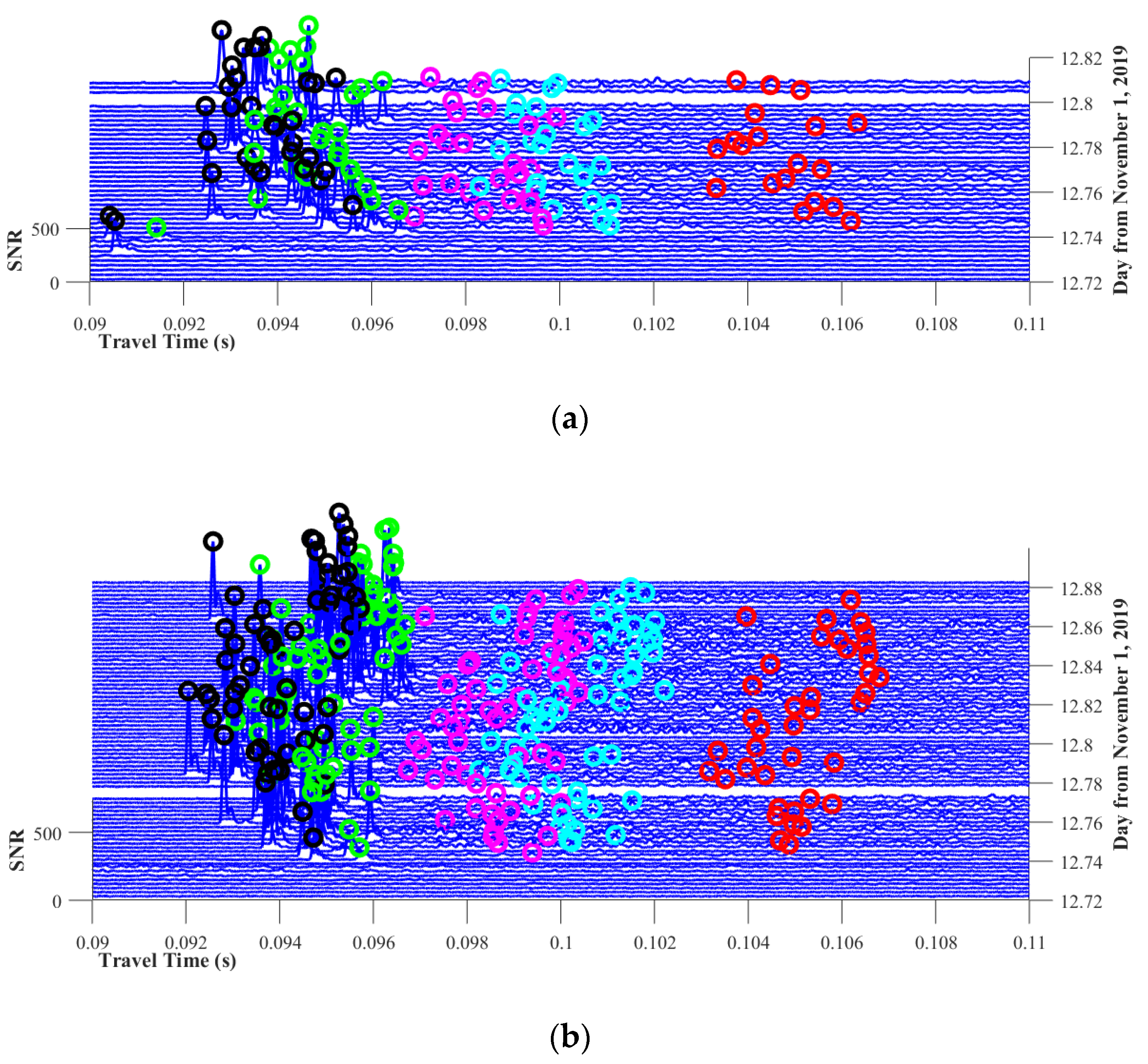
3.1. Correlation and Multi-Path Arrival Peak Identification
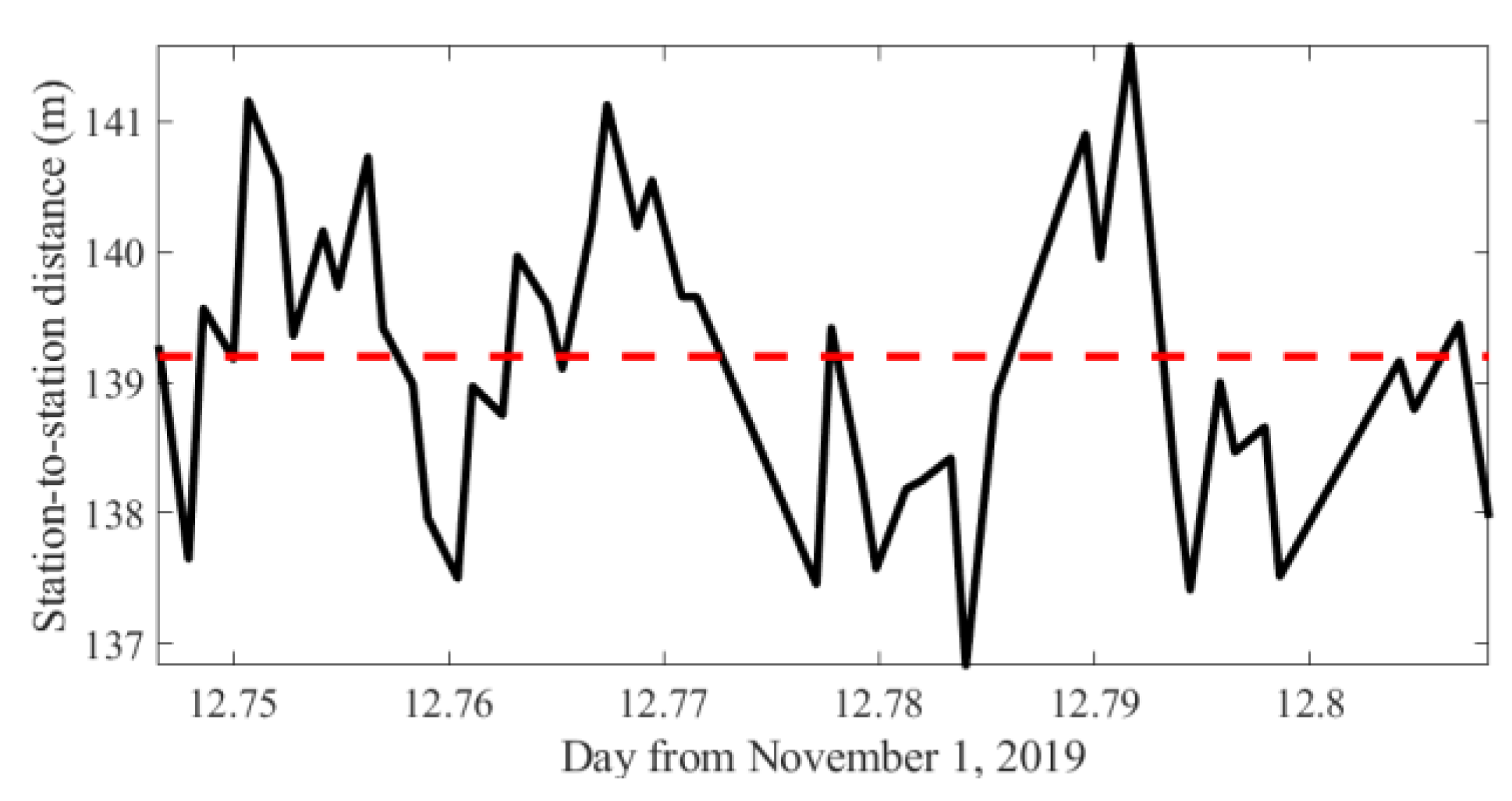
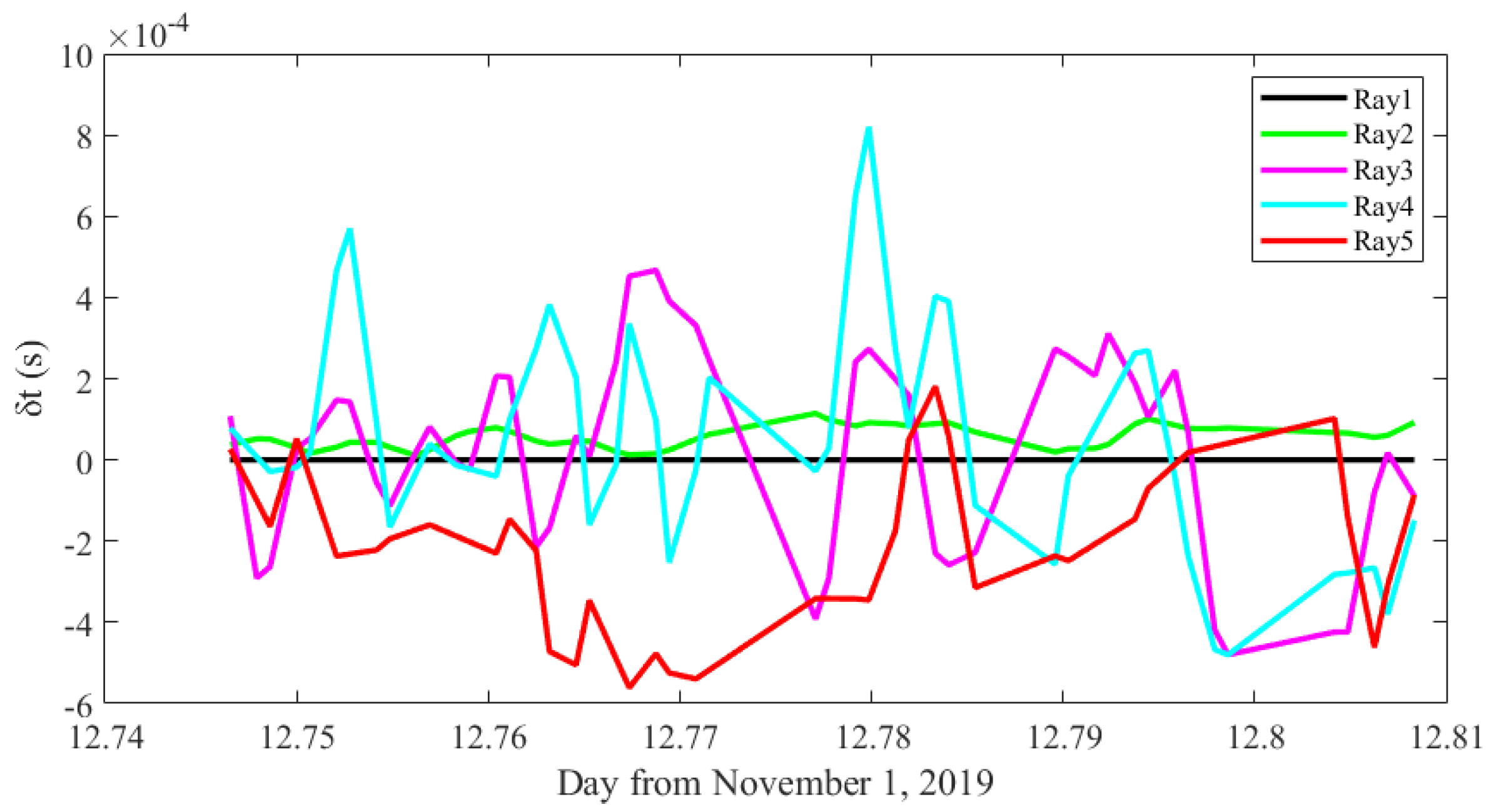
3.2. Position Drifting and Travel Time Correction
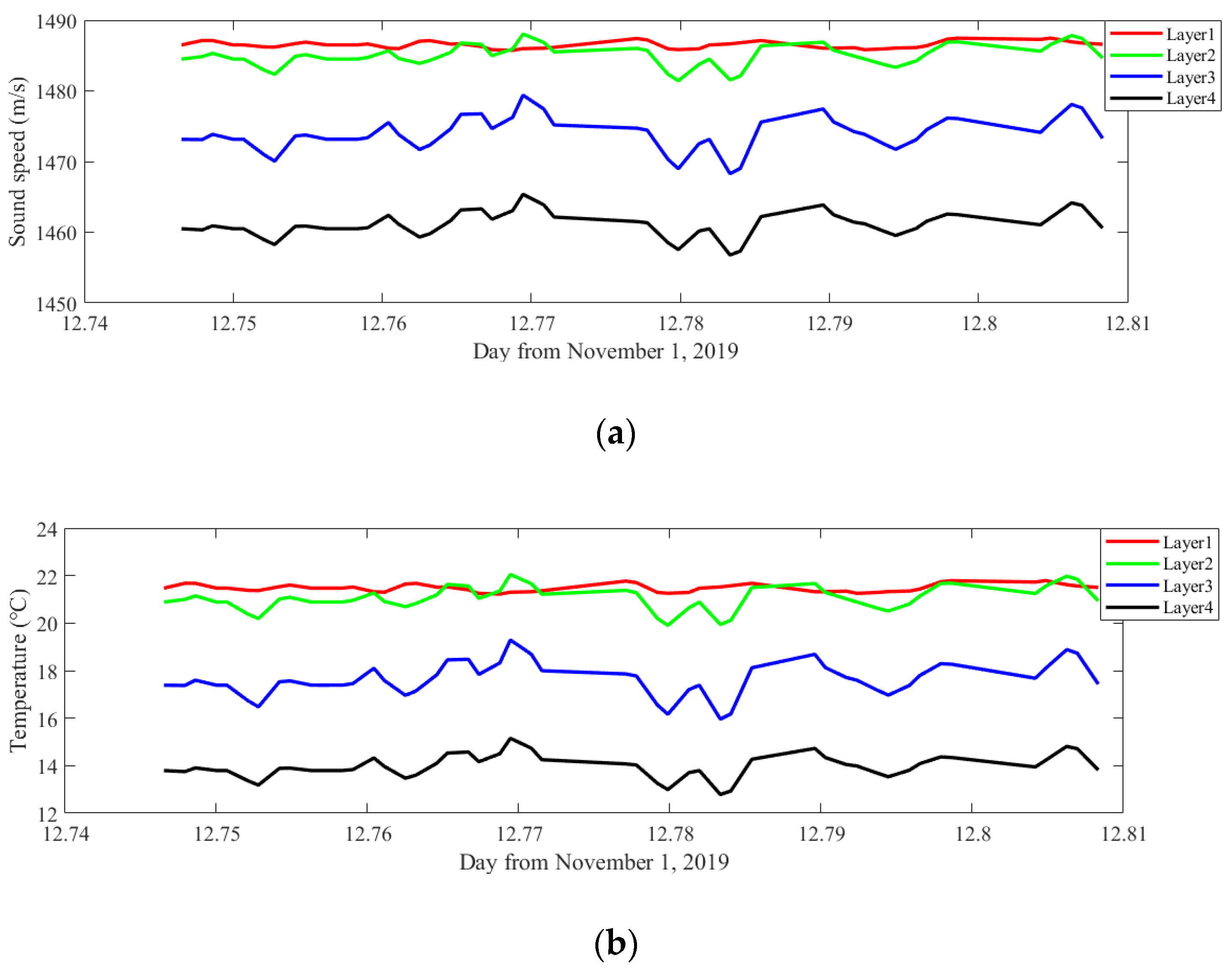
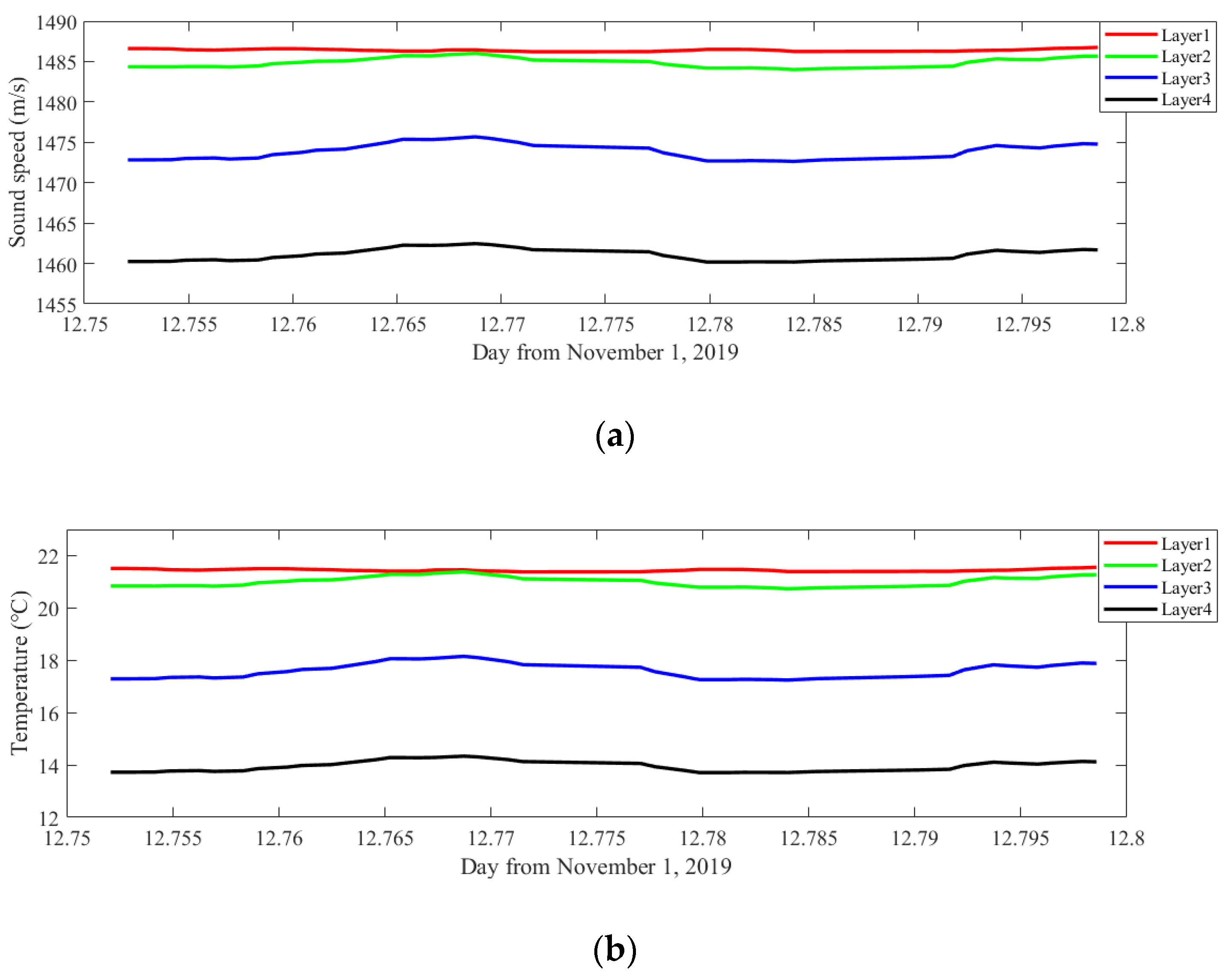
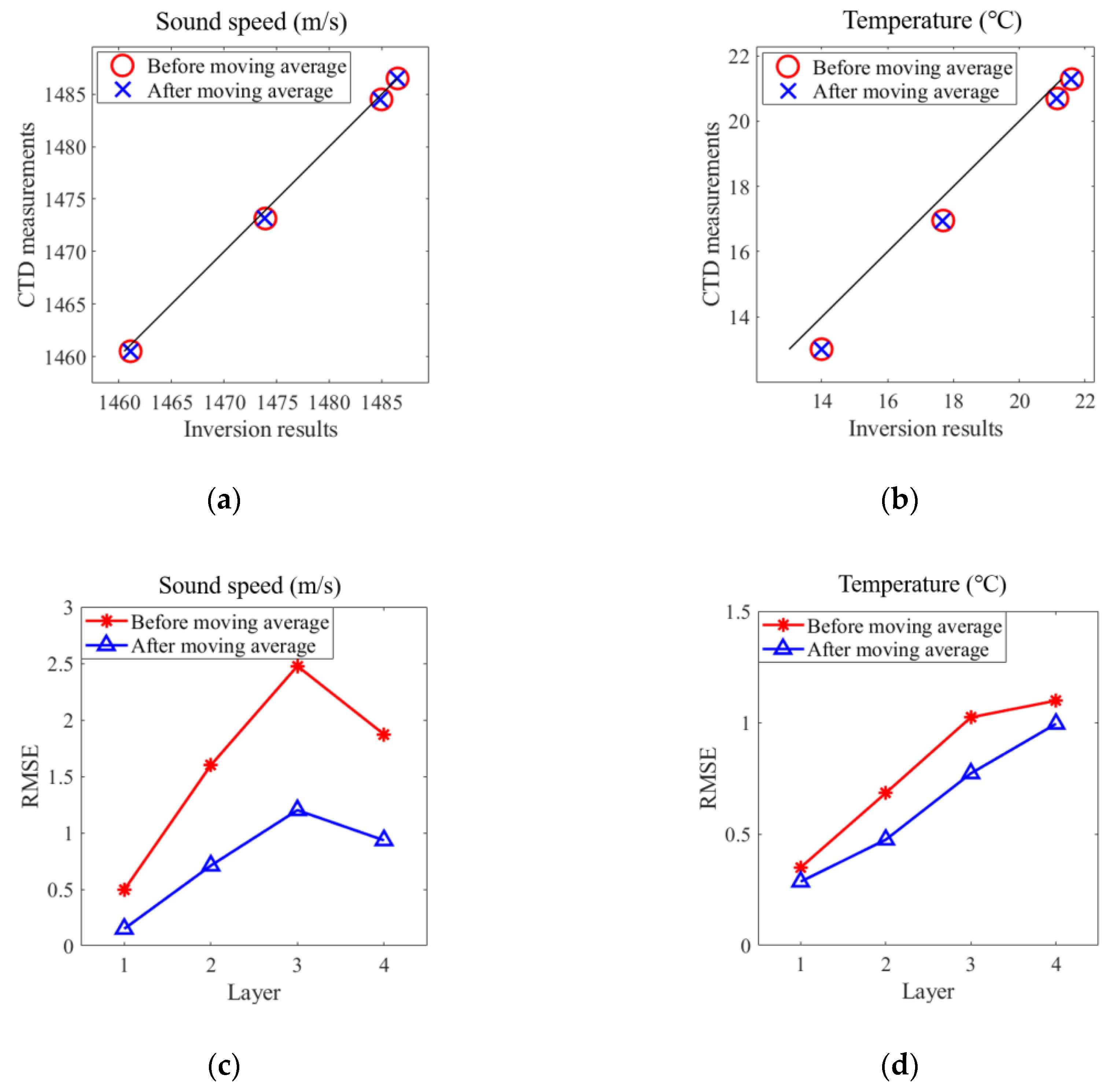
3.3. Inverted Temperature Profiling
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, L.; Wang, Y.; Wang, J.; Li, F. A High Spatial Resolution FBG Sensor Array for Measuring Ocean Temperature and Depth. Photonic Sens. 2020, 10, 57–66. [Google Scholar] [CrossRef]
- Pivato, M.; Carniello, L.; Viero, D.P.; Soranzo, C.; Defina, A.; Silvestri, S. Remote Sensing for Optimal Estimation of Water Temperature Dynamics in Shallow Tidal Environments. Remote Sens. 2020, 12, 51. [Google Scholar] [CrossRef]
- Munk, W.; Wunsch, C. Ocean acoustic tomography: A scheme for large scale monitoring. Deep Sea Res. Part A Oceanogr. Res. Pap. 1979, 26, 123–161. [Google Scholar] [CrossRef]
- Munk, W.; Forbes, A.M. Global Ocean Warming: An Acoustic Measure? J. Phys. Oceanogr. 1989, 19, 1765–1778. [Google Scholar] [CrossRef]
- Dushaw, B.D.; Worcester, P.F.; Munk, W.H.; Spindel, R.C.; Mercer, J.A.; Howe, B.M.; Metzger, K., Jr.; Birdsall, T.G.; Andrew, R.K.; Dzieciuch, M.A.; et al. A decade of acoustic thermometry in the North Pacific Ocean. J. Geophys. Res. 2009. [Google Scholar] [CrossRef]
- Zhao, Z. Internal tide oceanic tomography. Geophys. Res. Lett. 2016, 43, 9157–9164. [Google Scholar] [CrossRef]
- Worcester, P.F.; Lynch, J.F.; Morawitz, W.M.L.; Cornuelle, B.D.; Sutton, P.J.; Pawlowicz, R. Evolution of the large-scale temperature field in the Greenland Sea during 1988–1989 from tomographic measurements. J. Acoust. Soc. Am. 1995, 97, 2211–2214. [Google Scholar]
- Skarsoulis, E.K. Multi-section matched-peak tomographic inversion with a moving source. J. Acoust. Soc. Am. 2001, 110, 786–797. [Google Scholar] [CrossRef]
- Yamoaka, H.; Kaneko, A.; Park, J.H.; Zheng, H.; Gohda, N.; Takano, T.; Zhu, X.H.; Takasugi, Y. Coastal acoustic tomography system and its field application. IEEE J. Ocean. Eng. 2002, 27, 283–295. [Google Scholar] [CrossRef]
- Kaneko, A.; Zhu, X.H. Range-Average Measurement. In Coastal Acoustic Tomography; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Taniguchi, N.; Huang, C.F.; Arai, M.; Howe, B.M. Variation of residual current in the Seto Inland Sea driven by sea level difference between the Bungo and Kii Channels. J. Geophys. Res. Ocean. 2018, 123, 2921–2933. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, X.H.; Zhao, R. Near 7-day response of ocean bottom pressure to atmospheric surface pressure and winds in the northern South China Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2018, 132, 6–15. [Google Scholar] [CrossRef]
- Zhu, Z.N.; Zhu, X.H.; Guo, X.; Fan, X.; Zhang, C. Assimilation of coastal acoustic tomography data using an unstructured triangular grid ocean model for water with complex coastlines and islands. J. Geophys. Res. Ocean. 2017, 122, 7013–7030. [Google Scholar] [CrossRef]
- Chen, M.; Kaneko, A.; Lin, J.; Zhang, C. Mapping of a typhoon-driven coastal upwelling by assimilating coastal acoustic tomography data. J. Geophys. Res. Ocean. 2017, 122, 7822–7837. [Google Scholar] [CrossRef]
- Huang, H.; Guo, Y.; Wang, Z.; Shen, Y.; Wei, Y. Water Temperature Observation by Coastal Acoustic Tomography in Artificial Upwelling Area. Sensors 2019, 19, 2655. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Kaneko, A.; Zhu, X.H.; Gohda, N. Tomographic mapping of a coastal upwelling and the associated diurnal internal tides in Hiroshima Bay, Japan. J. Geophys. Res. Ocean. 2015, 120, 4288–4305. [Google Scholar] [CrossRef]
- Syamsudin, F.; Chen, M.; Kaneko, A.; Adityawarman, Y.; Zheng, H.; Mutsuda, H.; Hanifa, A.D.; Zhang, C.; Auger, G.; Wells, J.C.; et al. Profiling measurement of internal tides in Bali Strait by reciprocal sound transmission. Acoust. Sci. Technol. 2017, 38, 246–253. [Google Scholar] [CrossRef]
- Zhang, C.; Kaneko, A.; Zhu, X.H.; Howe, B.M.; Gohda, N. Acoustic measurement of the net transport through the Seto Inland Sea. Acoust. Sci. Technol. 2016, 37, 10–20. [Google Scholar] [CrossRef]
- Fan, W.; Chenm, Y.; Pan, H.; Ye, Y.; Cai, Y.; Zhang, Z. Experimental study on underwater acoustic imaging of 2-D temperature distribution around hot springs on floor of Lake Qiezishan, China. Exp. Therm. Fluid Sci. 2010, 34, 1334–1345. [Google Scholar] [CrossRef]
- Li, G.; Ingram, D.; Kaneko, A.; Chen, M.; Gohda, N.; Polydorides, N. Vertical underwater acoustic tomography in an experimental basin. J. Acoust. Soc. Am. 2017, 141, 3656. [Google Scholar] [CrossRef]
- Chen, M.; Syamsudin, F.; Kaneko, A.; Gohda, N.; Howe, B.M.; Mutsuda, H.; Dinan, A.H.; Zheng, H.; Huang, C.F.; Taniguchi, N.; et al. Real-time offshore coastal acoustic tomography enabled with mirror-transpond functionality. IEEE J. Ocean. Eng. 2018. [Google Scholar] [CrossRef]
- Kaneko, A.; Zhu, X.H. Inversion on a vertical slice. In Coastal Acoustic Tomography; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Mackenzie, K.V. Nine-term equation for sound speed in the oceans. J. Acoust. Soc. Am. 1981, 70, 807–812. [Google Scholar] [CrossRef]
- Porter, M.B. The Bellhop Manual and User’s Guide: Preliminary Draft; Heat, Light, and Sound Research, Inc.: La Jolla, CA, USA, 2011. [Google Scholar]
- Liu, W.; Zhu, X.; Zhu, Z.; Fan, X.; Dong, M.; Zhang, Z. A coastal acoustic tomography experiment in the Qiongzhou Strait. In Proceedings of the 2016 IEEE/OES China Ocean Acoustics (COA), Harbin, China, 9–11 January 2016. [Google Scholar] [CrossRef]





| Item | Value |
|---|---|
| Central frequency | 50 kHz |
| Transducer depth | 10 m |
| Order of M sequence | 12 |
| Repeat number | 8 |
| Q 1 | 3 |
| Station distance 2 | 140 m |
| Start and end time | 17:30–21:00 |
| round intervals 3 | 90 s |
| Layer Length (m) | Ray 1 | Ray 2 | Ray 3 | Ray 4 | Ray 5 | C0 (m/s) | T0 (°C) |
|---|---|---|---|---|---|---|---|
| Layer 1 | 139.20 1 | 140.63 | 146.19 | 63.83 | 91.49 | 1486.5 | 21.29 |
| Layer 2 | 0 | 0 | 0 | 30.64 | 22.73 | 1484.5 | 20.70 |
| Layer 3 | 0 | 0 | 0 | 28.82 | 22.04 | 1473.2 | 16.95 |
| Layer 4 | 0 | 0 | 0 | 24.41 | 18.98 | 1460.5 | 13.01 |
| Total | 139.20 | 140.63 | 146.19 | 147.69 | 155.23 | \ | \ |
| Travel time 2(s) | 0.093643 | 0.094606 | 0.098343 | 0.099852 | 0.104811 | \ | \ |
| Ray 1 | Ray 2 | Ray 3 | Ray 4 | Ray 5 | |
|---|---|---|---|---|---|
| Travel time(s) | 0.093643 | 0.094606 | 0.098343 | 0.099852 | 0.104811 |
| Time window 1(ms) | \ | 0.47–1.47 | 4.30–5.10 | 5.81–6.61 | 10.77–11.57 |
| SNR ((Signal-to-noise ratio) threshold | 100 | 100 | 25 | 25 | 25 |
| Item | Layer 1 | Layer 2 | Layer 3 | Layer 4 |
|---|---|---|---|---|
| Average C 1 before MA 2 | 1486.5 | 1485.0 | 1473.9 | 1461.1 |
| RMSE-C before MA | 0.4945 | 1.5984 | 2.4765 | 1.8721 |
| Average T 3 before MA | 21.60 | 21.16 | 17.69 | 13.99 |
| RMSE-T before MA | 0.3494 | 0.6838 | 1.0236 | 1.0985 |
| Average C after MA | 1486.4 | 1484.9 | 1473.9 | 1461.1 |
| RMSE-C after MA | 0.1502 | 0.7101 | 1.2004 | 0.9340 |
| Average T after MA | 21.57 | 21.13 | 17.67 | 13.98 |
| RMSE-T after MA | 0.2858 | 0.4742 | 0.7719 | 0.9945 |
| CTD-C 4 | 1486.5 | 1484.5 | 1473.2 | 1460.5 |
| CTD-T 5 | 21.29 | 20.69 | 16.95 | 13.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Guo, Y.; Li, G.; Arata, K.; Xie, X.; Xu, P. Short-Range Water Temperature Profiling in a Lake with Coastal Acoustic Tomography. Sensors 2020, 20, 4498. https://doi.org/10.3390/s20164498
Huang H, Guo Y, Li G, Arata K, Xie X, Xu P. Short-Range Water Temperature Profiling in a Lake with Coastal Acoustic Tomography. Sensors. 2020; 20(16):4498. https://doi.org/10.3390/s20164498
Chicago/Turabian StyleHuang, Haocai, Yong Guo, Guangming Li, Kaneko Arata, Xinyi Xie, and Pan Xu. 2020. "Short-Range Water Temperature Profiling in a Lake with Coastal Acoustic Tomography" Sensors 20, no. 16: 4498. https://doi.org/10.3390/s20164498
APA StyleHuang, H., Guo, Y., Li, G., Arata, K., Xie, X., & Xu, P. (2020). Short-Range Water Temperature Profiling in a Lake with Coastal Acoustic Tomography. Sensors, 20(16), 4498. https://doi.org/10.3390/s20164498





