Heart Rate Variability Analysis on Electrocardiograms, Seismocardiograms and Gyrocardiograms on Healthy Volunteers
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Set
2.2. Signal Processing
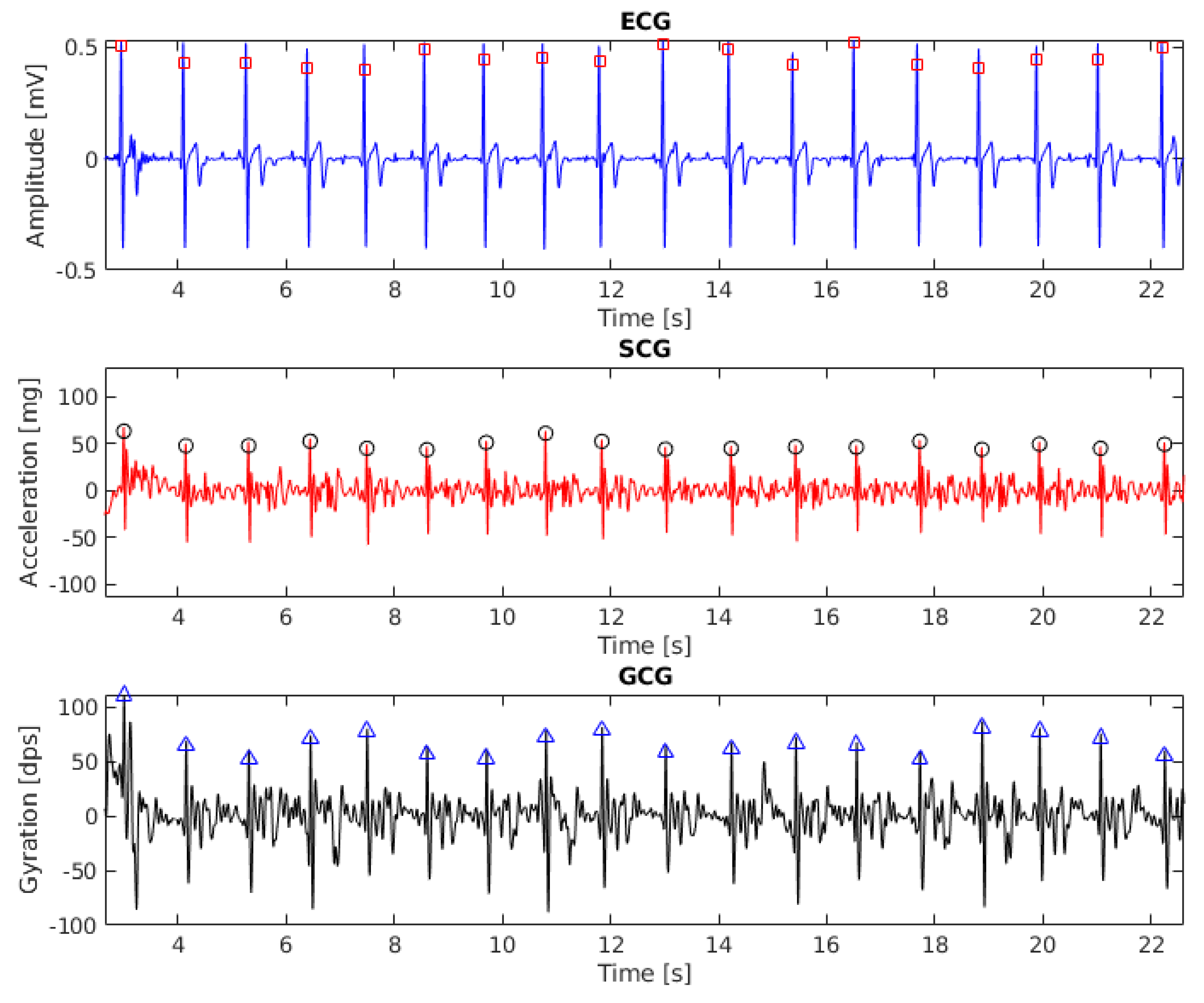
2.2.1. Heartbeat Detection in ECG
2.2.2. Heartbeat Detection in SCG and GCG
2.3. HRV Analysis
Poincaré Maps
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HRV | Heart rate variability |
| ECG | Electrocardiography, electrocardiogram |
| SCG | Seismocardiography |
| GCG | Gyrocardiography |
| MEMS | Microelectromechanical systems |
| MRI | Magnetic Resonance Imaging |
| EMD | Empirical Mode Decomposition |
| IMF | Intrinsic Mode Function |
| NN | The interval between consecutive normal heartbeats |
| FIR | Fininte impulse response [filter] |
| AO | Aortic valve opening [wave] |
| RSA | Respiratory sinus arrhythmia |
| SNR | Signal-to-noise [ratio] |
| AVNN | Mean inter-beat interval |
| SDNN | Standard deviation of all interbeat intervals |
| RMSSD | Root mean square of differences (RMSSD) of successive inter-beat intervals |
| pNN50 | The proportion of the number of pairs of successive differences greater than 50 ms divided by total number of normal inter-beat intervals |
| VLF | The power of very low frequency band (0.0033–0.04 Hz) of HRV spectrum |
| LF | The power of low frequency band (0.04–0.15 Hz) of HRV spectrum |
| HF | The power of high frequency band (0.15–0.4 Hz) of HRV spectrum |
| LF/HF | LF/HF ratio |
| TP | Total power of HRV spectrum (up to 0.4 Hz) |
| The width of the ellipse which containes the scatter points of Poincaré map | |
| The length of the ellipse which containes the scatter points of Poincaré map | |
| to ratio | |
| EA | The area of the ellipse which containes the scatter points of Poincaré map |
| VAI | Vector angular index |
| VLI | Vector length index |
| Pearson’s linear correlation coefficient |
References
- Montano, N.; Porta, A.; Cogliati, C.; Costantino, G.; Tobaldini, E.; Casali, K.R.; Iellamo, F. Heart rate variability explored in the frequency domain: A tool to investigate the link between heart and behavior. Neurosci. Biobehav. Rev. 2009, 33, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Pumprla, J.; Howorka, K.; Groves, D.; Chester, M.; Nolan, J. Functional assessment of heart rate variability: Physiological basis and practical applications. Int. J. Cardiol. 2002, 84, 1–14. [Google Scholar] [CrossRef]
- Laurin, A.; Blaber, A.; Tavakolian, K. Seismocardiograms return valid heart rate variability indices. In Proceedings of the Computing in Cardiology 2013, Zaragoza, Spain, 22–25 September 2013; pp. 413–416. [Google Scholar]
- Tadi, M.J.; Lehtonen, E.; Koivisto, T.; Pänkäälä, M.; Paasio, A.; Teräs, M. Seismocardiography: Toward heart rate variability (HRV) estimation. In Proceedings of the 2015 IEEE International Symposium on Medical Measurements and Applications (MeMeA) Proceedings, Turin, Italy, 7–9 May 2015; pp. 261–266. [Google Scholar] [CrossRef]
- Zanetti, J.M.; Tavakolian, K. Seismocardiography: Past, present and future. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 7004–7007. [Google Scholar] [CrossRef]
- Jaakkola, J.; Jaakkola, S.; Lahdenoja, O.; Hurnanen, T.; Koivisto, T.; Pänkäälä, M.; Knuutila, T.; Kiviniemi, T.O.; Vasankari, T.; Airaksinen, K.J. Mobile Phone Detection of Atrial Fibrillation With Mechanocardiography. Circulation 2018, 137, 1524–1527. [Google Scholar] [CrossRef] [PubMed]
- Tadi, M.J.; Lehtonen, E.; Pankäälä, M.; Saraste, A.; Vasankari, T.; Terás, M.; Koivisto, T. Gyrocardiography: A new non-invasive approach in the study of mechanical motions of the heart. Concept, method and initial observations. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 2034–2037. [Google Scholar] [CrossRef]
- Tadi, M.J.; Lehtonen, E.; Saraste, A.; Tuominen, J.; Koskinen, J.; Teräs, M.; Airaksinen, J.; Pänkäälä, M.; Koivisto, T. Gyrocardiography: A New Non-invasive Monitoring Method for the Assessment of Cardiac Mechanics and the Estimation of Hemodynamic Variables. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Zanetti, J.M.; Salerno, D.M. Seismocardiography: A technique for recording precordial acceleration. In Proceedings of the Computer-Based Medical Systems, Fourth Annual IEEE Symposium, Baltimore, MD, USA, 12–14 May 1991; pp. 4–9. [Google Scholar] [CrossRef]
- Castiglioni, P.; Faini, A.; Parati, G.; di Rienzo, M. Wearable Seismocardiography. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 3954–3957. [Google Scholar] [CrossRef]
- Castiglioni, P.; Meriggi, P.; Rizzo, F.; Vaini, E.; Faini, A.; Parati, G.; Merati, G.; di Rienzo, M. Cardiac sounds from a wearable device for sternal seismocardiography. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 4283–4286. [Google Scholar] [CrossRef]
- di Rienzo, M.; Vaini, E.; Castiglioni, P.; Meriggi, P.; Rizzo, F. Beat-to-beat estimation of LVET and QS2 indices of cardiac mechanics from wearable seismocardiography in ambulant subjects. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 7017–7020. [Google Scholar] [CrossRef]
- Ramos-Castro, J.; Moreno, J.; Miranda-Vidal, H.; García-González, M.A.; Fernández-Chimeno, M.; Rodas, G.; Capdevila, L. Heart rate variability analysis using a seismocardiogram signal. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 5642–5645. [Google Scholar] [CrossRef]
- Tavakolian, K.; Khosrow-Khavar, F.; Kajbafzadeh, B.; Marzencki, M.; Rohani, S.; Kaminska, B.; Menon, C. Seismocardiographic adjustment of diastolic timed vibrations. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 3797–3800. [Google Scholar] [CrossRef]
- Tadi, M.J.; Koivisto, T.; Pänkäälä, M.; Paasio, A. Accelerometer-Based Method for Extracting Respiratory and Cardiac Gating Information for Dual Gating during Nuclear Medicine Imaging. Int. J. Biomed. Imaging 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Martinek, R.; Brablik, J.; Kolarik, J.; Ladrova, M.; Nedoma, J.; Jaros, R.; Soustek, L.; Kahankova, R.; Fajkus, M.; Vojtisek, L.; et al. A Low-Cost System for Seismocardiography-Based Cardiac Triggering: A Practical Solution for Cardiovascular Magnetic Resonance Imaging at 3 Tesla. IEEE Access 2019, 7, 118608–118629. [Google Scholar] [CrossRef]
- Landreani, F.; Morri, M.; Martin-Yebra, A.; Casellato, C.; Pavan, E.; Frigo, C.; Caiani, E.G. Ultra-short-term heart rate variability analysis on accelerometric signals from mobile phone. In Proceedings of the 2017 E-Health and Bioengineering Conference (EHB), Sinaia, Romania, 22–24 June 2017; pp. 241–244. [Google Scholar] [CrossRef]
- Landreani, F.; Faini, A.; Martin-Yebra, A.; Morri, M.; Parati, G.; Caiani, E.G. Assessment of Ultra-Short Heart Variability Indices Derived by Smartphone Accelerometers for Stress Detection. Sensors 2019, 19, 3729. [Google Scholar] [CrossRef]
- Siecinski, S.; Tkacz, E.J.; Kostka, P.S. Comparison of HRV indices obtained from ECG and SCG signals from CEBS database. Biomed. Eng. Online 2019, 18. [Google Scholar] [CrossRef]
- Sieciński, S.; Kostka, P.; Piaseczna, N.; Wadas, M. Comparison of Indices Derived from Poincaré Maps on Electrocardiograms and Seismocardiograms. In Current Trends in Biomedical Engineering and Bioimages Analysis. Proceedings of the 21st Polish Conference on Biocybernetics and Biomedical Engineering; Korbicz, J., Maniewski, R., Patan, K., Kowal, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 15–24. [Google Scholar] [CrossRef]
- Jafari Tadi, M.; Mehrang, S.; Kaisti, M.; Lahdenoja, O.; Hurnanen, T.; Jaakkola, J.; Jaakkola, S.; Vasankari, T.; Kiviniemi, T.; Airaksinen, J.; et al. Comprehensive Analysis of Cardiogenic Vibrations for Automated Detection of Atrial Fibrillation Using Smartphone Mechanocardiograms. IEEE Sens. J. 2019, 19, 2230–2242. [Google Scholar] [CrossRef]
- Mehrang, S.; Lahdenoja, O.; Kaisti, M.; Tadi, M.J.; Hurnanen, T.; Airola, A.; Knuutila, T.; Jaakkola, J.; Jaakkola, S.; Vasankari, T.; et al. Classification of Atrial Fibrillation and Acute Decompensated Heart Failure Using Smartphone Mechanocardiography: A Multilabel Learning Approach. IEEE Sens. J. 2020, 20, 7957–7968. [Google Scholar] [CrossRef]
- Yang, C.; Aranoff, N.D.; Green, P.; Tavassolian, N. A Binary Classification of Cardiovascular Abnormality Using Time-Frequency Features of Cardio-mechanical Signals. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 5438–5441. [Google Scholar] [CrossRef]
- Inan, O.T.; Migeotte, P.F.; Park, K.S.; Etemadi, M.; Tavakolian, K.; Casanella, R.; Zanetti, J.; Tank, J.; Funtova, I.; Prisk, G.K.; et al. Ballistocardiography and Seismocardiography: A Review of Recent Advances. IEEE J. Biomed. Health Inform. 2015, 19, 1414–1427. [Google Scholar] [CrossRef] [PubMed]
- Tadi, M.J.; Lehtonen, E.; Hurnanen, T.; Koskinen, J.; Eriksson, J.; Pänkäälä, M.; Teräs, M.; Koivisto, T. A real-time approach for heart rate monitoring using a Hilbert transform in seismocardiograms. Physiol. Meas. 2016, 37, 1885–1909. [Google Scholar] [CrossRef] [PubMed]
- Korzeniowska-Kubacka, I.; Bilińska, M.; Piotrowicz, R. Usefulness of Seismocardiography for the Diagnosis of Ischemia in Patients with Coronary Artery Disease. Ann. Noninvasive Electrocardiol. 2005, 10, 281–287. [Google Scholar] [CrossRef] [PubMed]
- Meriheinä, U.; Juppo, M.; Koivisto, T.; Mikko, P.; Sairanen, K.; Grönholm, M. Heart Monitoring System. WIPO Patent WO 2015/036925 A1, 19 March 2015. [Google Scholar]
- Lahdenoja, O.; Hurnanen, T.; Kaisti, M.; Koskinen, J.; Tuominen, J.; Vähä-Heikkilä, M.; Parikka, L.; Wiberg, M.; Koivisto, T.; Pänkäälä, M. Cardiac monitoring of dogs via smartphone mechanocardiography: A feasibility study. Biomed. Eng. Online 2019, 18, 47. [Google Scholar] [CrossRef]
- Hernandez, J.E.; Cretu, E. Simple Heart Rate Monitoring System with a MEMS Gyroscope for Sleep Studies. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 61–67. [Google Scholar] [CrossRef]
- Yang, C.; Tavassolian, N. Combined Seismo- and Gyro-Cardiography: A More Comprehensive Evaluation of Heart-Induced Chest Vibrations. IEEE J. Biomed. Health Inform. 2018, 22, 1466–1475. [Google Scholar] [CrossRef]
- D’Mello, Y.; Skoric, J.; Xu, S.; Roche, P.J.R.; Lortie, M.; Gagnon, S.; Plant, D.V. Real-Time Cardiac Beat Detection and Heart Rate Monitoring from Combined Seismocardiography and Gyrocardiography. Sensors 2019, 19, 3472. [Google Scholar] [CrossRef]
- Iftikhar, Z.; Lahdenoja, O.; Tadi, M.J.; Hurnanen, T.; Vasankari, T.; Kiviniemi, T.; Airaksinen, J.; Koivisto, T.; Pänkäälä, M. Multiclass Classifier based Cardiovascular Condition Detection Using Smartphone Mechanocardiography. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef]
- Lahdenoja, O.; Hurnanen, T.; Iftikhar, Z.; Nieminen, S.; Knuutila, T.; Saraste, A.; Kiviniemi, T.; Vasankari, T.; Airaksinen, J.; Pänkäälä, M.; et al. Atrial Fibrillation Detection via Accelerometer and Gyroscope of a Smartphone. IEEE J. Biomed. Health Inform. 2018, 22, 108–118. [Google Scholar] [CrossRef]
- Mehrang, S.; Jafari Tadi, M.; Kaisti, M.; Lahdenoja, O.; Vasankari, T.; Kiviniemi, T.; Airaksinen, J.; Koivisto, T.; Pänkäälä, M. Machine Learning Based Classification of Myocardial Infarction Conditions Using Smartphone-Derived Seismo- and Gyrocardiography. In Proceedings of the 2018 Computing in Cardiology Conference (CinC), Maastricht, The Netherlands, 23–26 September 2018; Volume 45, pp. 1–4. [Google Scholar] [CrossRef]
- Friedrich, D.; Aubert, X.L.; Führ, H.; Brauers, A. Heart rate estimation on a beat-to-beat basis via ballistocardiography—A hybrid approach. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 4048–4051. [Google Scholar] [CrossRef]
- Siecinski, S.; Kostka, P.S.; Tkacz, E.J. Heart Rate Variability Analysis on CEBS Database Signals. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Honolulu, HI, USA, 18–21 July 2018; pp. 5697–5700. [Google Scholar] [CrossRef]
- Siecinski, S.; Kostka, P.S.; Tkacz, E.J.; Piaseczna, N.; Wadas, M. Heart Rate Variability Analysis on Reference Heart Beats and Detected Heart Beats of Smartphone Seismocardiograms. In International Conference on Information Technologies in Biomedicine, Proceedings of the ITIB 2019: Information Technology in Biomedicine, Kamień Śląski, Poland, 18–20 June 2019; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2019; Volume 1011, pp. 473–480. [Google Scholar] [CrossRef]
- Siecinski, S.; Kostka, P.S.; Tkacz, E.J. Influence of Empirical Mode Decomposition on Heart Rate Variability Indices Obtained from Smartphone Seismocardiograms. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 4913–4916. [Google Scholar] [CrossRef]
- Lahdenoja, O.; Hurnanen, T.; Tadi, M.J.; Pänkäälä, M.; Koivisto, T. Heart Rate Variability Estimation with Joint Accelerometer and Gyroscope Sensing. In Proceedings of the Computing in Cardiology, Vancouver, BC, Canada, 11–14 September 2016; Volume 43, pp. 717–720. [Google Scholar]
- Kaisti, M.; Tadi, M.J.; Lahdenoja, O.; Hurnanen, T.; Saraste, A.; Pankaala, M.; Koivisto, T. Stand-Alone Heartbeat Detection in Multidimensional Mechanocardiograms. IEEE Sens. J. 2019, 19, 234–242. [Google Scholar] [CrossRef]
- Kaisti, M.; Tadi, M.J.; Lahdenoja, O.; Hurnanen, T.; Pänkäälä, M.; Koivisto, T. Mechanocardiograms with ECG reference. IEEE DataPort 2018. [Google Scholar] [CrossRef]
- Pan, N.; Mang, V.; Un, M.P.; hang, P.S. Accurate Removal of Baseline Wander in ECG Using Empirical Mode Decomposition. In Proceedings of the 2007 Joint Meeting of the 6th International Symposium on Noninvasive Functional Source Imaging of the Brain and Heart and the International Conference on Functional Biomedical Imaging, Hangzhou, China, 12–14 October 2007; pp. 177–180. [Google Scholar] [CrossRef]
- MathWorks, Inc. Empirical Mode Decomposition—MATLAB Emd. Available online: https://www.mathworks.com/help/wavelet/ref/emd.html (accessed on 31 August 2019).
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, BME-32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Wedekind, D. Qrsdetector. Available online: https://github.com/danielwedekind/qrsdetector (accessed on 27 August 2019).
- Christov, I.I. Real time electrocardiogram QRS detection using combined adaptive threshold. Biomed. Eng. Online 2004, 3, 28. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, K.; Schmidt, S.E.; Jensen, A.S.; Søgaard, P.; Struijk, J.J. Definition of Fiducial Points in the Normal Seismocardiogram. Sci. Rep. 2018, 8, 15455. [Google Scholar] [CrossRef] [PubMed]
- Paukkunen, M.; Linnavuo, M.; RE, S. A Portable Measurement System for the Superior-Inferior Axis of the Seismocardiogram. J. Bioeng. Biomed. Sci. 2013, 3, 1–4. [Google Scholar] [CrossRef]
- Pandia, K.; Inan, O.T.; Kovacs, G.T.A.; Giovangrandi, L. Extracting respiratory information from seismocardiogram signals acquired on the chest using a miniature accelerometer. Physiol. Meas. 2012, 33, 1643–1660. [Google Scholar] [CrossRef]
- Vest, A.N.; Poian, G.D.; Li, Q.; Liu, C.; Nemati, S.; Shah, A.J.; Clifford, G.D. An open source benchmarked toolbox for cardiovascular waveform and interval analysis. Physiol. Meas. 2018, 39, 105004. [Google Scholar] [CrossRef]
- PhysioNet Cardiovascular Signal Toolbox. Available online: https://archive.physionet.org/physiotools/physionet-cardiovascular-signal-toolbox/ (accessed on 26 August 2019).
- Task Force of the European Society of Cardiology the North American Society of Pacing Electrophysiology. Heart Rate Variability. Standards of Measurement, Physiological Interpretation, and Clinical Use. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef]
- Acharya, U.R.; Joseph, K.P.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart rate variability: A review. Med. Biol. Eng. Comput. 2006, 44, 1031–1051. [Google Scholar] [CrossRef]
- Hon, E.; Lee, S.T. Electronic evaluations of the fetal heart rate patterns preceding fetal death: Further observations. Am. J. Obstet. Gynecol. 1965, 87, 814–826. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Waldman, L.K.; Fung, Y.C.; Covell, J.W. Transmural myocardial deformation in the canine left ventricle. Normal in vivo three-dimensional finite strains. Circ. Res. 1985, 57, 152–163. [Google Scholar] [CrossRef] [PubMed]
- Brennan, M.; Palaniswami, M.; Kamen, P. Do existing measures of Poincare plot geometry reflect nonlinear features of heart rate variability? IEEE Trans. Biomed. Eng. 2001, 48, 1342–1347. [Google Scholar] [CrossRef] [PubMed]
- Kitlas Golińska, A. Poincaré Plots in Analysis of Selected Biomedical Signals. Stud. Log. Gramm. Rhetor. 2013, 35, 117–127. [Google Scholar] [CrossRef]
- İşler, Y.; Kuntalp, M. Combining classical HRV indices with wavelet entropy measures improves to performance in diagnosing congestive heart failure. Comput. Biol. Med. 2007, 37, 1502–1510. [Google Scholar] [CrossRef] [PubMed]
- Karmakar, C.K.; Gubbi, J.; Khandoker, A.H.; Palaniswami, M. Analyzing temporal variability of standard descriptors of Poincaré plots. J. Electrocardiol. 2010, 43, 719–724. [Google Scholar] [CrossRef]
- Ruan, X.; Liu, C.; Liu, C.; Wang, X.; Li, P. Automatic detection of atrial fibrillation using R-R interval signal. In Proceedings of the 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; Volume 2, pp. 644–647. [Google Scholar] [CrossRef]
- Biala, T.; Dodge, M.; Schlindwein, F.S.; Wailoo, M. Heart rate variability using Poincaré plots in 10 year old healthy and intrauterine growth restricted children with reference to maternal smoking habits during pregnancy. In Proceedings of the 2010 Computing in Cardiology, Belfast, UK, 26–29 September 2010; pp. 971–974. [Google Scholar]
- Kozak, M. What is Strong Correlation? Teach. Stat. 2009, 31, 85–86. [Google Scholar] [CrossRef]
- Shlyk, N.I.; Sapozhnikova, E.N.; Kirillova, T.G.; Semenov, V.G. Typoloagical characteristics of the functional state of regulatory systems in schoolchildren and young athletes (According to Heart Rate Variability Data). Hum. Physiol. 2009, 35, 730. [Google Scholar] [CrossRef]
- Keet, S.W.M.; Bulte, C.S.E.; Garnier, R.P.; Boer, C.; Bouwman, R.A. Short-term heart rate variability in healthy adults. Anaesthesia 2013, 68, 775–777. [Google Scholar] [CrossRef][Green Version]
- Corrales, M.M.; de la Cruz Torres, B.; Esquivel, A.G.; Salazar, M.A.G.; Orellana, J.N. Normal values of heart rate variability at rest in a young, healthy and active Mexican population. Health 2012, 4, 377–385. [Google Scholar] [CrossRef]
- Charlier, P.; Cabon, M.; Herman, C.; Benouna, F.; Logier, R.; Houfflin-Debarge, V.; Jeanne, M.; De Jonckheere, J. Comparison of multiple cardiac signal acquisition technologies for heart rate variability analysis. J. Clin. Monit. Comput. 2019. [Google Scholar] [CrossRef] [PubMed]
- Migeotte, P.F.; Mucci, V.; Delière, Q.; Lejeune, L.; van de Borne, P. Multi-dimensional Kineticardiography a New Approach for Wearable Cardiac Monitoring Through Body Acceleration Recordings. In XIV Mediterranean Conference on Medical and Biological Engineering and Computing 2016; Kyriacou, E., Christofides, S., Pattichis, C.S., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 1125–1130. [Google Scholar] [CrossRef]
- Achi’ldiev, V.; Bedro, N.; Uspenckiy, V.; Gruzevich, Y.; Komarova, M.; Rulev, M.; Evseeva, Y. Gyrocardiography Unit for Non-Invasive Human Diseases Diagnosis. In Proceedings of the 2020 27th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), Saint Petersburg, Russia, 25–27 May 2020; pp. 1–7. [Google Scholar]
- Zanetti, J.M.; Poliac, M.O.; Crow, R.S. Seismocardiography: Waveform identification and noise analysis. In Proceedings of the [1991] Proceedings Computers in Cardiology, Venice, Italy, 23–26 September 1991; pp. 49–52. [Google Scholar] [CrossRef]

| Subject Number | Length of Recording | Remarks |
|---|---|---|
| 1 | 3 min | Breathing: 2 min normal, 30 s holding a breath, 30 s normal |
| 2 | 3 min | Breathing: 2 min normal, 30 s holding a breath, 30 s normal |
| 3 | 3 min | Breathing: 2 min normal, 30 s holding a breath, 30 s normal |
| 4 | 3 min | Breathing: 2 min normal, 30 s holding a breath, 30 s normal |
| 5 | 3 min | Breathing: 2 min normal, 30 s holding a breath, 30 s normal |
| 6 | 3 min | Breathing: 2 min normal, 30 s holding a breath, 30 s normal. |
| Sensor not strictly secured on chest because of body hair. | ||
| 7 | 3 min | Breathing: 2 min normal, 30 s holding a breath, 30 s normal |
| 8 | 3 min | In supine position |
| 9 | 10 min | In supine position |
| 10 | 10 min | In supine position |
| 11 | 30 min | In supine position |
| 12 | 10 min | In supine position |
| 13 | 10 min | In supine position |
| 14 | 10 min | In supine position |
| 15 | 10 min | In supine position |
| 16 | 10 min | In supine position |
| 17 | 10 min | In supine position |
| 18 | 10 min | In supine position |
| 19 | 10 min | In supine position |
| 20 | 10 min | In supine position |
| 21 | 10 min | In supine position |
| 22 | 10 min | In supine position; sensor loose in the end. |
| 23 | 10 min | |
| 24 | 10 min | In supine position |
| 25 | 9 min | In supine position |
| 26 | 10 min | In supine position |
| 27 | 10 min | |
| 28 | 10 min | In supine position |
| 29 | 10 min | In supine position |
| HRV Index | ECG | SCG | GCG |
|---|---|---|---|
| Mean (SD) | Mean (SD) | Mean (SD) | |
| AVNN [ms] | 954.90 (113.36) | 954.88 (113.36) | 954.91 (113.37) |
| SDNN [ms] | 84.18 (33.41) | 86.7100 (31.60) | 86.96 (33.42) |
| RMSSD [ms] | 75.84 (41.16) | 83.68 (36.37) | 77.7177 (36.37) |
| pNN50 | 0.30 (0.19) | 0.37 (0.17) | 0.31 (0.19) |
| VLF [ms2] | 1860.90 (1369.11) | 1861.44 (1371.98) | 1864.24 (1371.98) |
| LF [ms2] | 2570.18 (2251.61) | 2609.14 (2245.32) | 2601.45 (2293.06) |
| HF [ms2] | 2774.35 (2378.19) | 2909.42 (2259.84) | 2867.19 (2398.12) |
| LF/HF | 1.2659 (0.8454) | 1.0993 (0.7743) | 1.2048 (0.8065) |
| TP [ms2] | 8042.73 (5466.70) | 8216.96 (5340.56) | 8170.00 (5545.13) |
| SD1 [ms] | 53.70 (29.16) | 59.25 (25.7694) | 55.0292 (28.95) |
| SD2 [ms] | 105.35 (39.73) | 106.66 (38.58) | 105.9665 (39.79) |
| SD1/SD2 | 0.49 (0.15) | 0.55 (0.14) | 0.50 (0.15) |
| EA [ms2] | 20,738.45 (16,359.85) | 22,364.41 (15,599.28) | 21,252.91 (16,489.52) |
| VAI [] | 1.39 (0.64) | 1.61 (0.57) | 1.4442 (0.65) |
| VLI [ms] | 104.85 (39.71) | 106.04 (38.73) | 105.48 (39.79) |
| HRV Index | ECG | SCG | GCG |
|---|---|---|---|
| Mean (SD) | Mean (SD) | Mean (SD) | |
| AVNN [ms] | 941.23 (110.08) | 941.0472 (110.00) | 941.3313 (110.08) |
| SDNN [ms] | 64.94 (22.09) | 67.4271 (21.28) | 65.6358 (22.32) |
| RMSSD [ms] | 52.55 (23.89) | 60.01 (22.51) | 54.09 (23.25) |
| pNN50 | 0.27 (0.19) | 0.34 (0.17) | 0.28 (0.18) |
| VLF [ms2] | 1645.09 (1505.34) | 1646.89 (1514.59) | 1663.31 (1554.52) |
| LF [ms2] | 1575.98 (1131.11) | 1617.99 (1162.03) | 1608.56 (1176.83) |
| HF [ms2] | 1343.52 (1024.29) | 1493.9831 (1015.87) | 1386.01 (1024.23) |
| LF/HF | 1.70 (1.38) | 1.41 (1.11) | 1.57 (1.18) |
| TP [ms2] | 4845.82 (3090.72) | 5039.4577 (3093.67) | 4941.80 (3195.36) |
| SD1 [ms] | 37.26 (16.95) | 42.55 (15.97) | 38.35 (16.50) |
| SD2 [ms] | 83.30 (28.22) | 84.63 (27.77) | 83.9605 (28.64) |
| SD1/SD2 | 0.44 (0.14) | 0.5101 (0.1534) | 0.46 (0.13) |
| EA [ms2] | 10,835.40 (7491.69) | 12,246.36 (7433.61) | 11,192.33 (7649.02) |
| VAI [] | 1.18 (0.49) | 1.38 (0.48) | 1.2156 (0.47) |
| VLI [ms] | 82.97 (28.03) | 84.28 (27.59) | 83.61 (28.45) |
| HRV Index | ECG-SCG | ECG-GCG |
|---|---|---|
| Mean (SD) | Mean (SD) | |
| AVNN [ms] | 0.00 (0.00) | 0.00 (0.00) |
| SDNN [ms] | 0.05 (0.09) | 0.01 (0.01) |
| RMSSD [ms] | 0.22 (0.36) | 0.06 (0.13) |
| pNN50 | 2.87 (12.38) | 0.88 (4.26) |
| VLF [ms2] | 0.01 (0.01) | 0.00 (0.00) |
| LF [ms2] | 0.05 (0.07) | 0.02 (0.02) |
| HF [ms2] | 0.24 (0.45) | 0.05 (0.06) |
| LF/HF | 0.12 (0.16) | 0.07 (0.09) |
| TP [ms2] | 0.06 (0.12) | 0.02 (0.01) |
| SD1 [ms] | 0.22 (0.36) | 0.06 (0.13) |
| SD2 [ms] | 0.02 (0.04) | 0.01 (0.01) |
| SD1/SD2 | 0.19 (0.29) | 0.05 (0.12) |
| EA [ms2] | 0.26 (0.44) | 0.06 (0.13) |
| VAI [] | 0.25 (0.38) | 0.06 (0.14) |
| VLI [ms] | 0.02 (0.04) | 0.01 (0.01) |
| HRV Index | ECG-SCG | ECG-GCG |
|---|---|---|
| Mean (SD) | Mean (SD) | |
| AVNN [ms] | 0.00 (0.00) | 0.00 (0.00) |
| SDNN [ms] | 0.06 (0.09) | 0.02 (0.02) |
| RMSSD [ms] | 0.24 (0.40) | 0.08 (0.23) |
| pNN50 | 0.81 (2.90) | 0.15 (0.69) |
| VLF [ms2] | 0.03 (0.05) | 0.01 (0.03) |
| LF [ms2] | 0.08 (0.08) | 0.03 (0.04) |
| HF [ms2] | 0.28 (0.53) | 0.11 (0.25) |
| LF/HF | 0.16 (0.16) | 0.08 (0.10) |
| TP [ms2] | 0.08 (0.12) | 0.03 (0.03) |
| SD1 [ms] | 0.24 (0.40) | 0.08 (0.23) |
| SD2 [ms] | 0.03 (0.04) | 0.01 (0.01) |
| SD1/SD2 | 0.20 (0.33) | 0.08 (0.22) |
| EA [ms2] | 0.28 (0.48) | 0.09 (0.24) |
| VAI [] | 0.24 (0.38) | 0.07 (0.18) |
| VLI [ms] | 0.03 (0.04) | 0.01 (0.01) |
| HRV Index | (Full Signals) | (Signals Divided into 179 s Windows) |
|---|---|---|
| AVNN | 1.000 | 1.000 |
| SDNN | 0.993 | 0.979 |
| RMSSD | 0.965 | 0.886 |
| pNN50 | 0.852 | 0.858 |
| VLF | 1.000 | 0.998 |
| LF | 0.997 | 0.973 |
| HF | 0.994 | 0.970 |
| LF/HF | 0.947 | 0.870 |
| TP | 0.998 | 0.989 |
| 0.965 | 0.887 | |
| 0.998 | 0.993 | |
| 0.767 | 0.732 | |
| EA | 0.990 | 0.958 |
| VAI | 0.861 | 0.798 |
| VLI | 0.998 | 0.993 |
| HRV Index | (Full Signals) | (Signals Divided into 179 s Windows) |
|---|---|---|
| AVNN | 1.000 | 1.000 |
| SDNN | 1.000 | 0.998 |
| RMSSD | 0.998 | 0.990 |
| pNN50 | 0.997 | 0.993 |
| VLF | 1.000 | 0.998 |
| LF | 1.000 | 0.996 |
| HF | 0.998 | 0.995 |
| LF/HF | 0.987 | 0.937 |
| TP | 1.000 | 0.998 |
| 0.998 | 0.990 | |
| 1.000 | 0.999 | |
| 0.984 | 0.957 | |
| EA | 0.999 | 0.995 |
| VAI | 0.995 | 0.991 |
| VLI | 1.000 | 0.999 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sieciński, S.; Kostka, P.S.; Tkacz, E.J. Heart Rate Variability Analysis on Electrocardiograms, Seismocardiograms and Gyrocardiograms on Healthy Volunteers. Sensors 2020, 20, 4522. https://doi.org/10.3390/s20164522
Sieciński S, Kostka PS, Tkacz EJ. Heart Rate Variability Analysis on Electrocardiograms, Seismocardiograms and Gyrocardiograms on Healthy Volunteers. Sensors. 2020; 20(16):4522. https://doi.org/10.3390/s20164522
Chicago/Turabian StyleSieciński, Szymon, Paweł S. Kostka, and Ewaryst J. Tkacz. 2020. "Heart Rate Variability Analysis on Electrocardiograms, Seismocardiograms and Gyrocardiograms on Healthy Volunteers" Sensors 20, no. 16: 4522. https://doi.org/10.3390/s20164522
APA StyleSieciński, S., Kostka, P. S., & Tkacz, E. J. (2020). Heart Rate Variability Analysis on Electrocardiograms, Seismocardiograms and Gyrocardiograms on Healthy Volunteers. Sensors, 20(16), 4522. https://doi.org/10.3390/s20164522






