A Deep Learning Approach for Estimating Traffic Density Using Data Obtained from Connected and Autonomous Probes
Abstract
:1. Introduction
2. Preliminary
2.1. Specification of a Radar Sensor-Equipped Probe
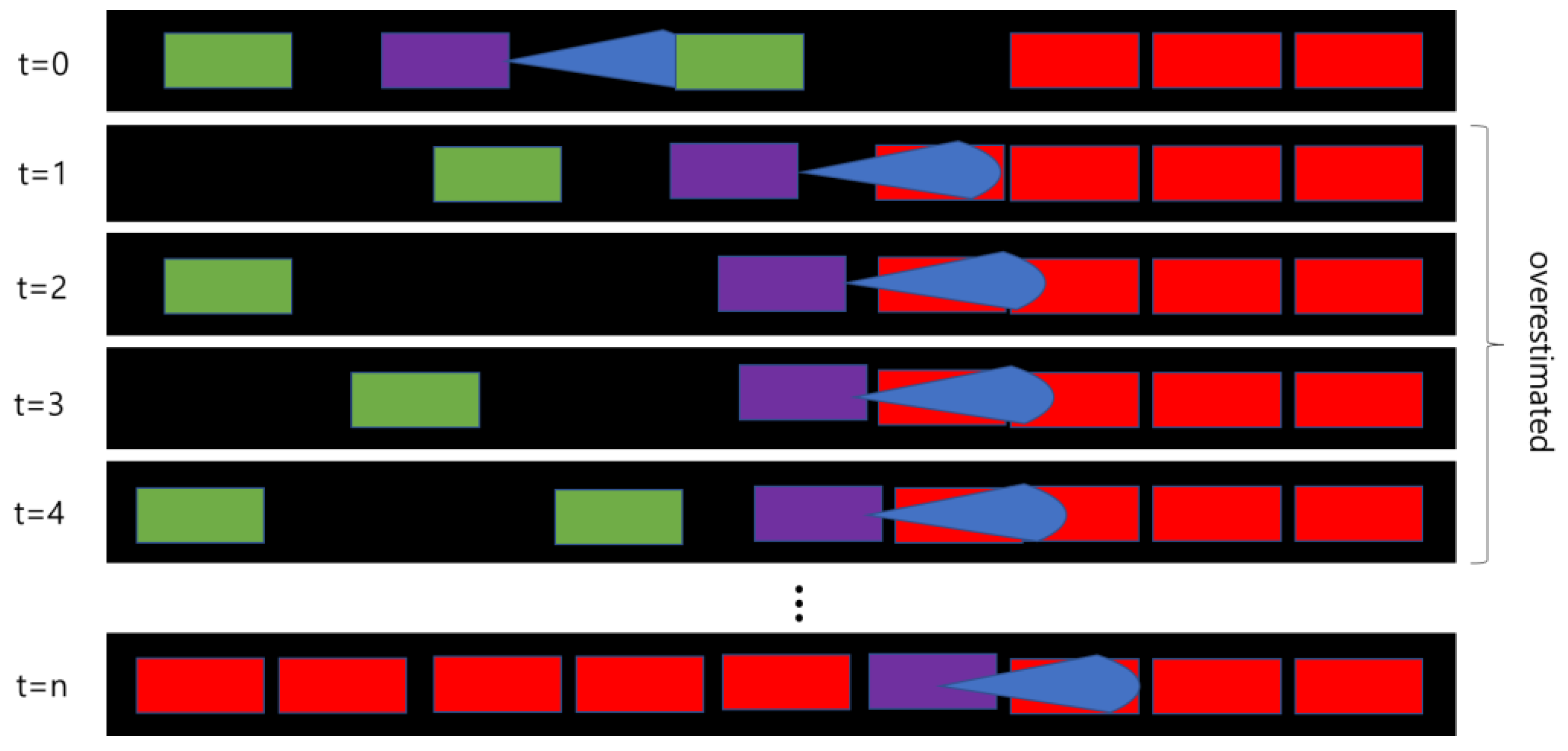
2.2. Traffic Density Estimation and Its Limitations on the CAPs Application
3. Deep Learning-Based Traffic Density Estimation
- Input vector at t
- : a hidden vector of previous time step
- : Input layer at t
- Cell state layer at t
- : Forget gate layer at t
- Estimated output at t
- : Activation function
- : Weights of a layer h (it plays a role in connecting perceptrons among layers)
- : Bias vector
4. Microscopic Simulation Based Evaluation
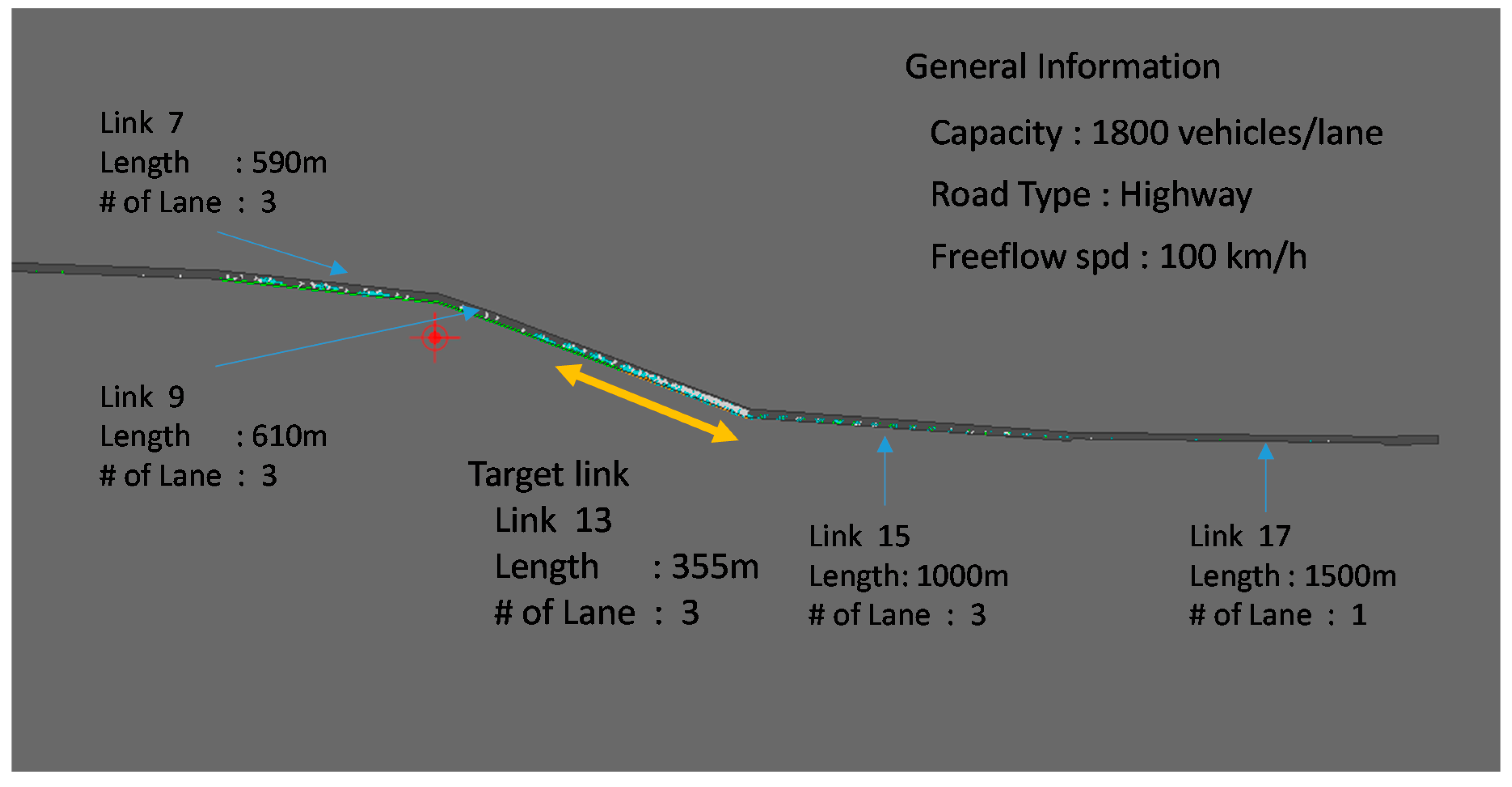
4.1. Simulation Environment
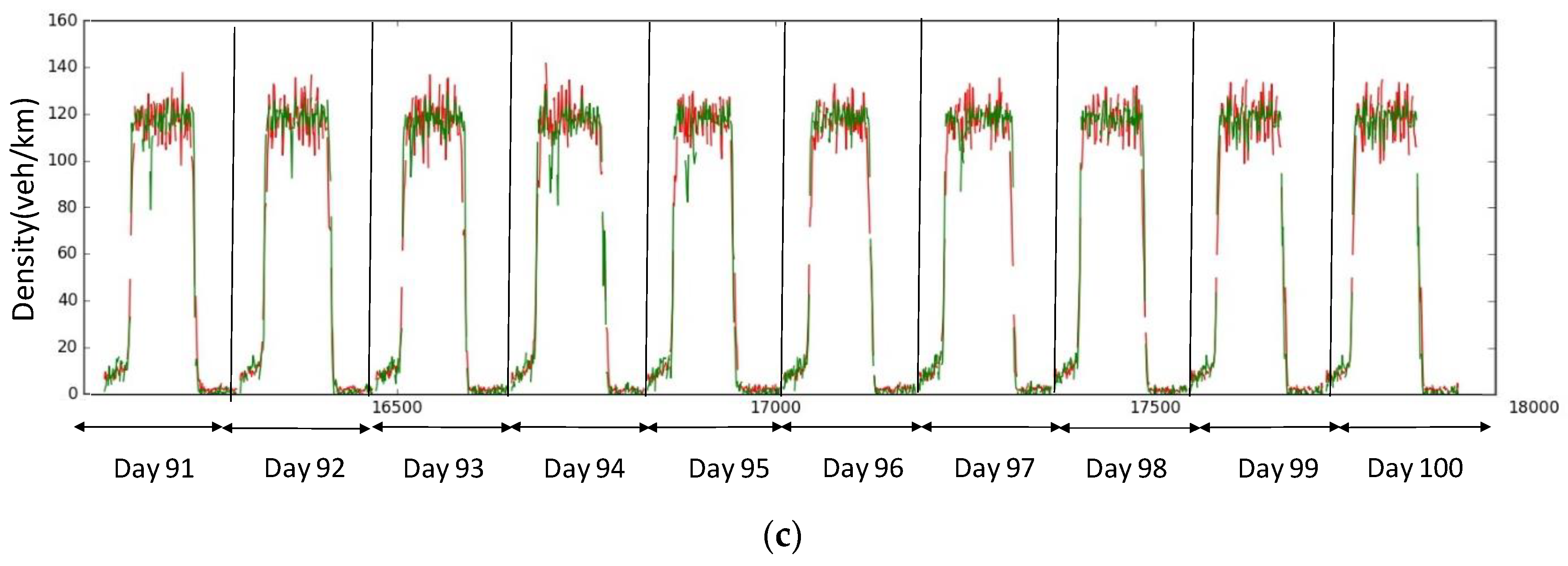
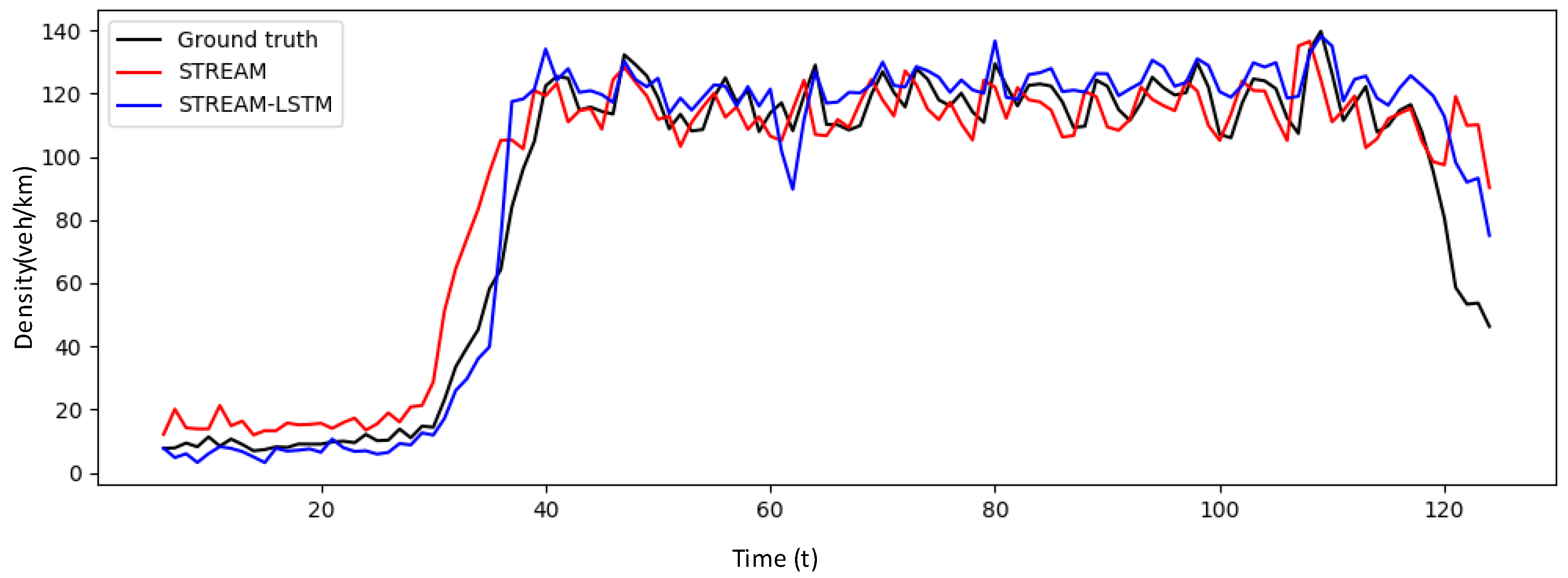
4.2. Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Aljamal, M.A.; Abdelghaffar, H.M.; Rakha, H.A. Estimation of traffic stream density using connected vehicle data: Linear and nonlinear filtering approaches. Sensors 2020, 20, 4066. [Google Scholar] [CrossRef] [PubMed]
- Aljamal, M.A.; Abdelghaffar, H.M.; Rakha, H.A. Developing a neural-kalman filtering approach for estimating traffic stream density using probe vehicle data. Sensors 2019, 19, 4325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanguesa, J.A.; Barrachina, J.; Fogue, M.; Garrido, P.; Martinez, F.J.; Cano, J.C.; Calafate, C.T.; Manzoni, P. Sensing traffic density combining V2V and V2I wireless communications. Sensors 2015, 15, 31794–31810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herring, R.; Hofleitner, A.; Abbeel, P.; Bayen, A. Estimating arterial traffic conditions using sparse probe data. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010. [Google Scholar]
- Seo, T.; Kusakabe, T.; Asakura, Y. Estimation of flow and density using probe vehicles with spacing measurement equipment. Transp. Res. Part C Emerg. Technol. 2015, 53, 134–150. [Google Scholar] [CrossRef] [Green Version]
- Al-Sobky, A.S.A.; Mousa, R.M. Traffic density determination and its applications using smartphone. Alex. Eng. J. 2016, 55, 513–523. [Google Scholar] [CrossRef] [Green Version]
- Seo, T.; Kusakabe, T. Probe vehicle-based traffic flow estimation method without fundamental diagram. Transp. Res. Procedia 2015, 9, 149–163. [Google Scholar] [CrossRef] [Green Version]
- Edie, L. Discussion of traffic stream measurements and definitions. In Proceedings of the Second International Symposium on the Theory of Traffic Flow, London, UK, 25–27 June 1963. [Google Scholar]
- Nam, D.; Lavanya, R.; Yang, I.; Jeon, W.H.; Jayakrishnan, R. Traffic density estimation using radar sensor data from probe vehicles. In Proceedings of the ITS World Congress, Montreal, QC, Canada, 29 October–2 November 2017. [Google Scholar]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Fluids Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Wang, Y.; Szeto, W.Y.; Han, K.; Friesz, T.L. Dynamic traffic assignment: A review of the methodological advances for environmentally sustainable road transportation applications. Transp. Res. Part B Methodol. 2018, 111, 370–394. [Google Scholar] [CrossRef]
- Szeto, M.W.; Gazis, D.C. Application of Kalman filtering to the surveillance and control of traffic systems. Transp. Sci. 1972, 6, 419–439. [Google Scholar] [CrossRef]
- Cremer, M. Flow variables: Estimation. In Concise Encyclopedia of Traffic & Transportation Systems; Pergamon: Amsterdam, The Netherlands, 1991; pp. 143–148. ISBN 978-0-08-036203-8. [Google Scholar]
- Papageorgiou, M. Application of Automatic Control Concepts to Traffic Flow Modeling and Control; Springer: New York, NY, USA, 1983. [Google Scholar]
- Kotsialos, A.; Papageorgiou, M. The importance of traffic flow modeling for motorway traffic control. Netw. Spat. Econ. 2001, 1, 179–203. [Google Scholar] [CrossRef]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transp. Res. Part C Emerg. Technol. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Tian, Y.; Pan, L. Predicting short-term traffic flow by long short-term memory recurrent neural network. In Proceedings of the 2015 IEEE International Conference on Smart City/SocialCom/SustainCom (SmartCity), Chengdu, China, 19–21 December 2015. [Google Scholar]
- Polson, N.; Sokolov, V. Deep learning for short-term traffic flow prediction. Transp. Res. Part C Emerg. Technol. 2016, 79, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Yi, H.; Jung, H.; Bae, S. Deep Neural Networks for traffic flow prediction. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju, Korea, 13–16 February 2017. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Graph Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- van Lint, J.W.C.; Hoogendoorn, S.P.; van Zuylen, H.J. Accurate freeway travel time prediction with state-space neural networks under missing data. Transp. Res. Part C Emerg. Technol. 2005, 13, 347–369. [Google Scholar] [CrossRef]
- Oh, C.; Ritchie, S.G.; Oh, J.S. Exploring the relationship between data aggregation and predictability to provide better predictive traffic information. Transp. Res. Rec. 2005, 1935, 28–36. [Google Scholar] [CrossRef]
- Liu, H.; Van Zuylen, H.; Van Lint, H.; Salomons, M. Predicting urban arterial travel time with state-space neural networks and Kalman filters. Transp. Res. Rec. 2006, 1968, 99–108. [Google Scholar] [CrossRef]
- Ji, B.; Hong, E.J. Deep-learning-based real-time road traffic prediction using long-term evolution access data. Sensors 2019, 19, 5327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]






| Sensor Code | Name | Target Angle (°) | Sensing Range (°) | Sensing Distance (m) |
|---|---|---|---|---|
| 1 | Forward Long | 0 | 10 | 30 |
| 2 | Forward Wide | 0 | 60 | 10 |
| 3 | Backward Left | 160 | 40 | 10 |
| 4 | Backward Right | 200 | 40 | 10 |
| 5 | Backward Long | 180 | 20 | 20 |
| Sensor Code | Name | Target Angle | Range | Distance |
|---|---|---|---|---|
| 1 | Front Long | 0 | 10 | 30 |
| 2 | Front Short | 0 | 60 | 10 |
| 3 | Rear Left | 160 | 40 | 10 |
| 4 | Rear Right | 200 | 40 | 10 |
| 5 | Rear Center | 180 | 20 | 20 |
| Type | Name | Configuration |
|---|---|---|
| Simulation | Simulation time | 1.5 h |
| Warm up time | First 0.25 h | |
| Analysis time | 1 h | |
| Updating time step of simulation | 0.1 s | |
| Demand profile | 5000 vehicles/1.5 h | |
| Vehicle compositions | -Sensor vehicle (1% to 10%) -Regular vehicle | |
| Generated samples | 100 days of morning peaks | |
| Density Estimation | Updating time step | 30 s |
| Congestion criteria | 80 km/hour | |
| Size of the moving horizon | 5-time step (2 min 30 sec) | |
| Dataset composition | Training: 70 days Test: 30 days |
| Penetration Rate | RMSE | Relative Error | ||||
|---|---|---|---|---|---|---|
| STREAM-LSTM | STREAM | Improve (%) | STREAM-LSTM | STREAM | Improve (%) | |
| 1% | 32.69 | 49.15 | 33.50 | 0.36 | 0.50 | 27.80 |
| 5% | 14.08 | 16.29 | 13.54 | 0.18 | 0.30 | 40.14 |
| 10% | 12.12 | 15.69 | 22.74 | 0.15 | 0.30 | 49.68 |
| 25% | 8.88 | 15.97 | 44.36 | 0.11 | 0.34 | 66.11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nam, D.; Lavanya, R.; Jayakrishnan, R.; Yang, I.; Jeon, W.H. A Deep Learning Approach for Estimating Traffic Density Using Data Obtained from Connected and Autonomous Probes. Sensors 2020, 20, 4824. https://doi.org/10.3390/s20174824
Nam D, Lavanya R, Jayakrishnan R, Yang I, Jeon WH. A Deep Learning Approach for Estimating Traffic Density Using Data Obtained from Connected and Autonomous Probes. Sensors. 2020; 20(17):4824. https://doi.org/10.3390/s20174824
Chicago/Turabian StyleNam, Daisik, Riju Lavanya, R. Jayakrishnan, Inchul Yang, and Woo Hoon Jeon. 2020. "A Deep Learning Approach for Estimating Traffic Density Using Data Obtained from Connected and Autonomous Probes" Sensors 20, no. 17: 4824. https://doi.org/10.3390/s20174824
APA StyleNam, D., Lavanya, R., Jayakrishnan, R., Yang, I., & Jeon, W. H. (2020). A Deep Learning Approach for Estimating Traffic Density Using Data Obtained from Connected and Autonomous Probes. Sensors, 20(17), 4824. https://doi.org/10.3390/s20174824





