On the Use of a Rotatable ECT Sensor to Investigate Dense Phase Flow: A Feasibility Study
Abstract
:1. Introduction
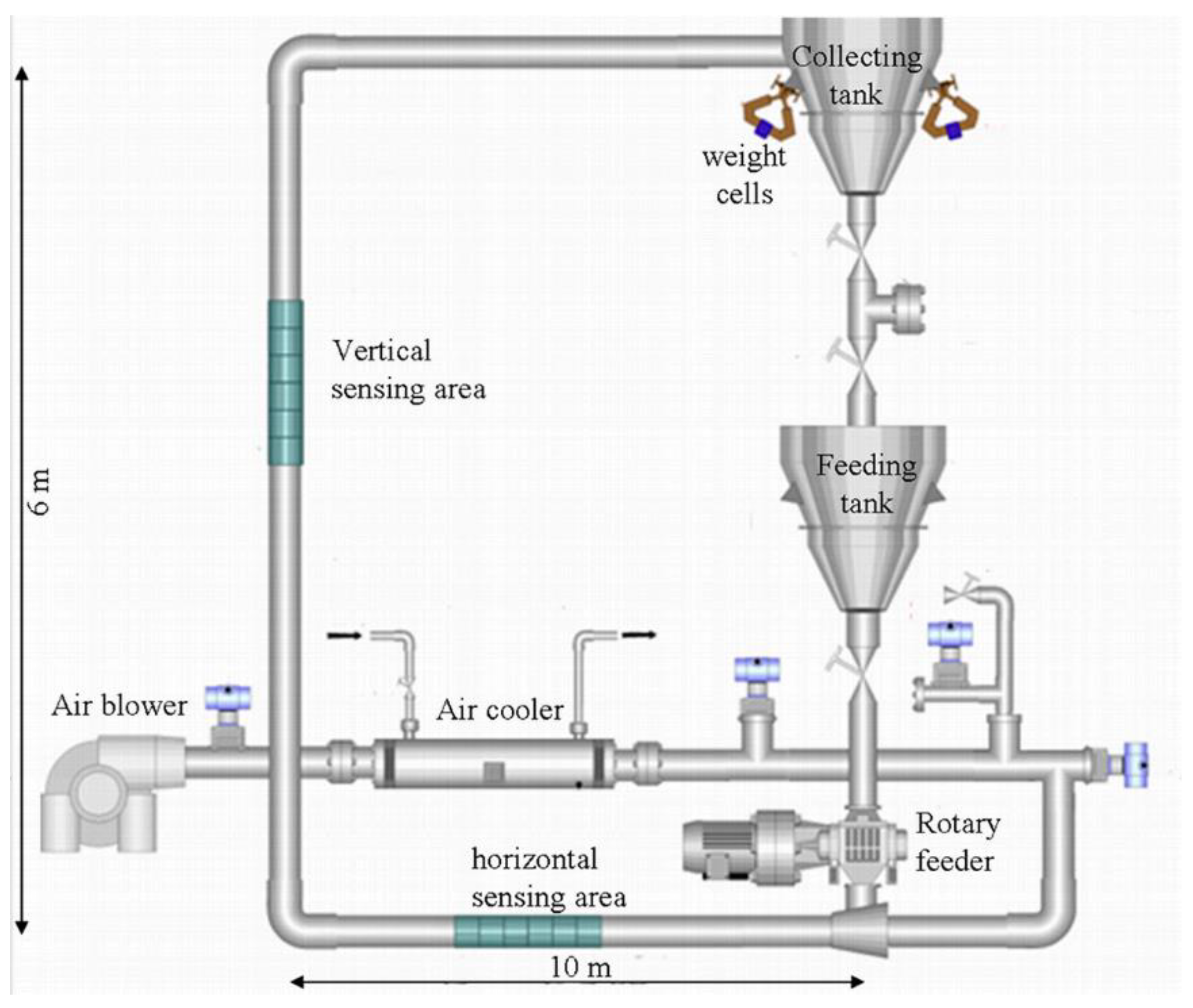
2. Experimental Setup
2.1. The Pneumatic Conveying Flow Loop
2.2. ECT Sensor and Acquisition Hardware
3. Image Reconstruction
- Set k = 0;
- Find an initial approximate image using an experimental set of capacitance data Cm and the LBP algorithm with an initial nodal sensitivity matrix calculated for homogeneous media with the normalized relative permittivity value of 0.5 (Equations (4) and (5)). The value of dielectric constant for simulating homogeneous sensor forward model was estimated due to the known minimum (1.0) and maximum (3.2) relative permittivity values of air and polyamide particle, respectively;
- Set k = k + 1;
- Find a forward solution as a new capacitance matrix and electric field distribution for each p positions (p = 1, 2, 3, 4) using ECT rotational FEM forward model and previously reconstructed image ;
- Normalize the new four capacitance sets (p = 1, 2, 3, 4);
- Combine the global rotation-based capacitance data set ;
- Calculate an updated sensitivity matrix using and nodal algorithm for each p positions (p = 1, 2, 3, 4);
- Combine the global matrix using four rotation-based sensitivity maps;
- Normalize the global sensitivity matrix ;
- Find the approximate image using an iterative optimization function that can be typically expressed as:
- Repeat steps 3–10 until k < desired number of iterations.
4. Results and Discussion
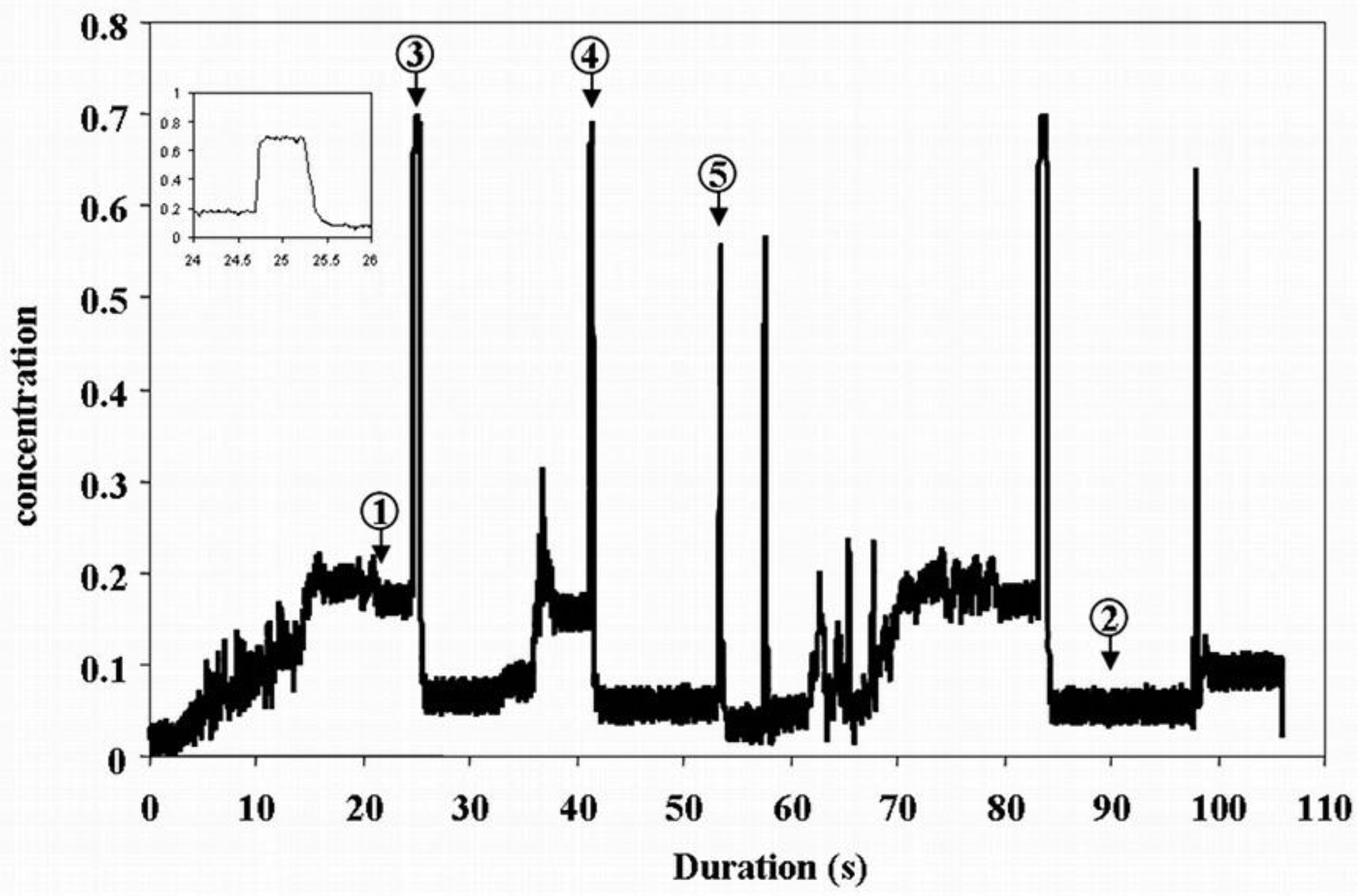
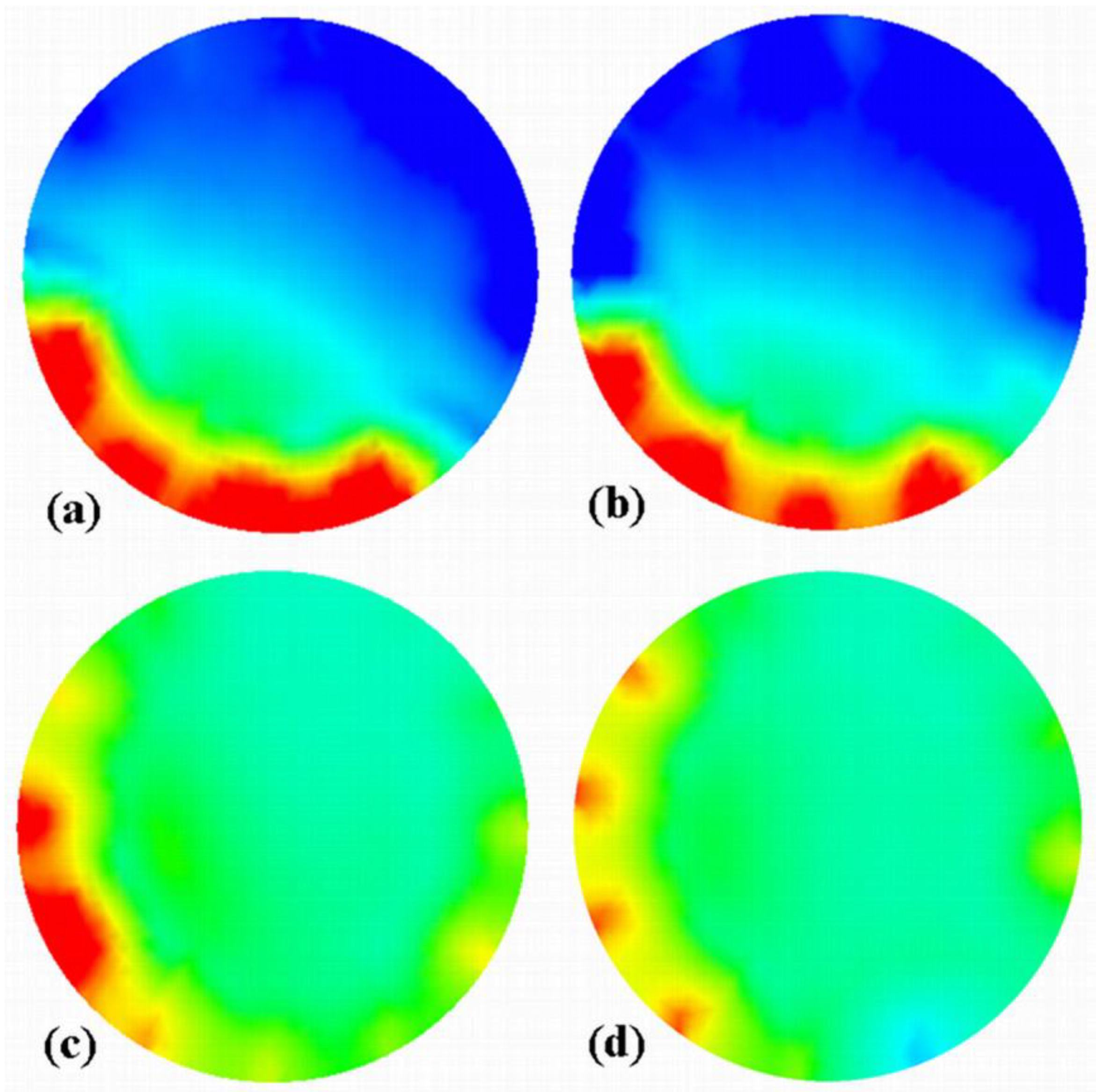
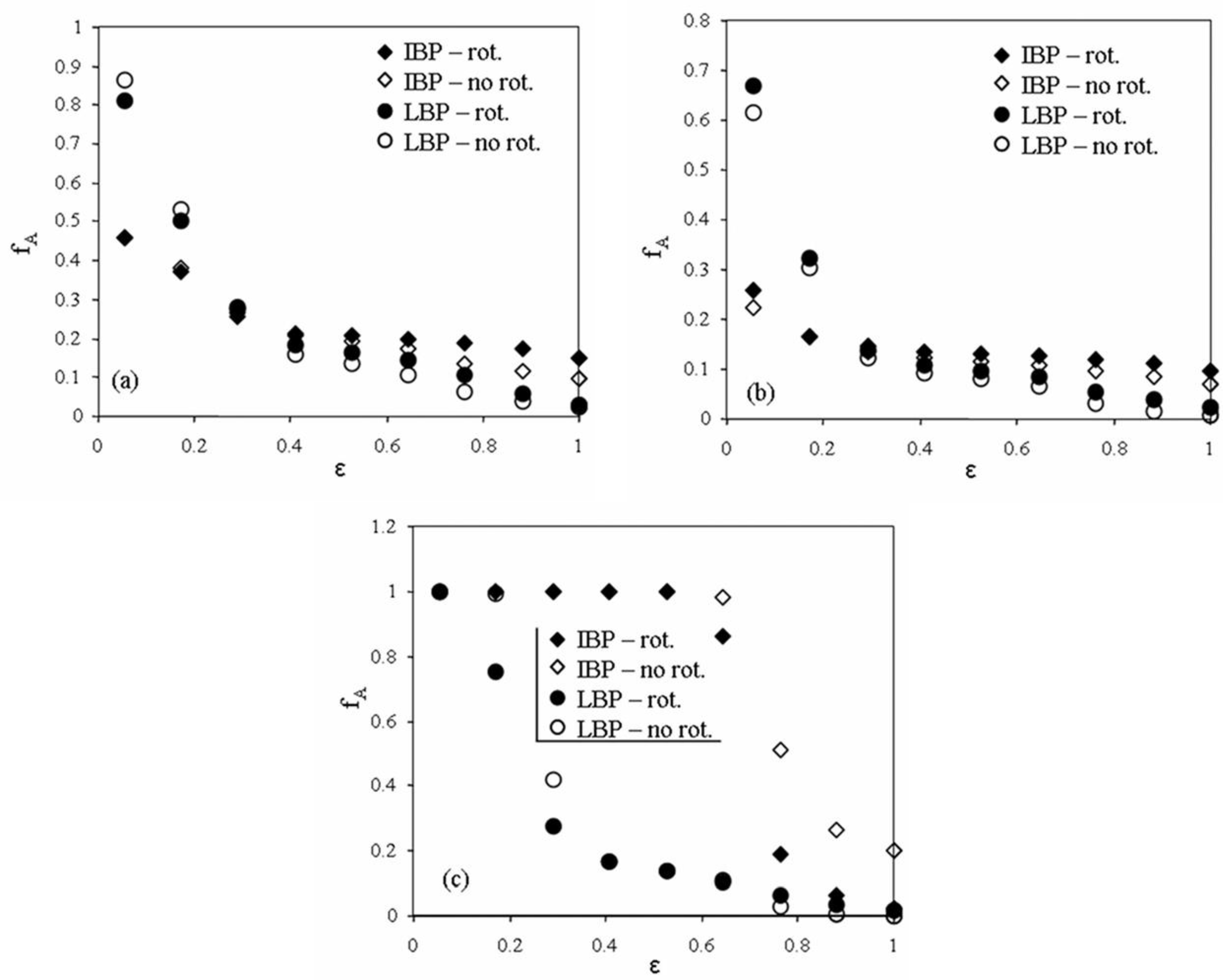
4.1. Experimental Results
4.2. Discussion
5. Conclusions
- The use of a rotatable sensor with 12 electrodes and 3 rotation steps achieves relatively satisfying results in terms of better surface delineation and solids concentration for the settled layer, despite the problems related to acquisition speed and noise.
- So far, the trend seems to show that the concentration level of settled layers and slugs are larger when rotation is used. Static tests on phantoms that simulate settled layers with known concentrations are necessary to attest if the improvement is verified.
- The current main drawbacks of the rotatable sensor are the rotation speed; also, the electromagnetic field that is generated by the stepper motor, which interferes with the capacitance measurements, is generating a significant drop in the SNR. Improvement of the sensor design is one of the main perspectives of work that is considered for the near future. This will also open the perspective of studying the applicability of the rotatable sensor for other types of flow regime.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mosorov, V.; Zych, M.; Hanus, R.; Sankowski, D.; Saoud, A. Improvement of Flow Velocity Measurement Algorithms Based on Correlation Function and Twin Plane Electrical Capacitance Tomography. Sensors 2020, 20, 306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Z.; Wu, F.; Yang, X.; Li, Y. Measurement of Gas-Oil Two-Phase Flow Patterns by Using CNN Algorithm Based on Dual ECT Sensors with Venturi Tube. Sensors 2020, 20, 1200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rymarczyk, T.; Tchorzewski, P.; Adamkiewicz, P.; Duda, K.; Szumowski, J.; Sikora, J. Practical Implementation of Electrical Tomography in a Distributed System to Examine the Condition of Objects. IEEE Sens. J. 2017, 17, 8166–8186. [Google Scholar] [CrossRef]
- Grudzien, K.; Romanowski, A.; Chaniecki, Z.; Niedostatkiewicz, M.; Sankowski, D. Description of the silo flow and bulk solid pulsation detection using ECT. Flow Meas. Instrum. 2010, 21, 198–206. [Google Scholar] [CrossRef]
- Garbaa, H.; Jackowska-Strumiłło, L.; Grudzień, K.; Romanowski, A. Application of electrical capacitance tomography and artificial neural networks to rapid estimation of cylindrical shape parameters of industrial flow structure. Arch. Electr. Eng. 2016, 65, 657–669. [Google Scholar] [CrossRef]
- Yang, W.Q.; Peng, L. Image reconstruction algorithms for electrical capacitance tomography. Meas. Sci. Technol. 2003, 14, R1–R13. [Google Scholar] [CrossRef]
- Wajman, R.; Fiderek, P.; Fidos, H.; Jaworski, T.; Nowakowski, J.; Sankowski, D.; Banasiak, R. Metrological evaluation of a 3D electrical capacitance tomography measurement system for two-phase flow fraction determination. Meas. Sci. Technol. 2013, 24, 065302. [Google Scholar] [CrossRef]
- Niderla, J.; Rymarczyk, T.; Sikora, J. Manufacturing planning and control system using tomographic sensors. Informatics Control Meas. Econ. Environ. Prot. 2018, 8, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Olmos, A.M.; Carvajal, M.A.; Morales, D.P.; García, A.; Palma, A.J. Development of an Electrical Capacitance Tomography system using four rotating electrodes. Sens. Actuators A Phys. 2008, 148, 366–375. [Google Scholar] [CrossRef]
- Huang, C.-N.; Yu, F.-M.; Chung, H.-Y. Rotational electrical impedance tomography. Meas. Sci. Technol. 2007, 18, 2958. [Google Scholar] [CrossRef]
- Murphy, S.C.; York, T.A. Electrical impedance tomography with non-stationary electrodes. Meas. Sci. Technol. 2006, 17, 3042. [Google Scholar] [CrossRef]
- Frounchi, J.; Bazzazi, A.-R. High Resolution Rotary Electrical Capacitance Tomography System. In Proceedings of the 3rd World Congress on IPT, Banff, AB, Canada, 2–5 September 2003; pp. 858–863. [Google Scholar]
- Liu, Z.; Babout, L.; Banasiak, R.; Sankowski, D. Effectiveness of rotatable sensor to improve image accuracy of ECT system. Flow Meas. Instrum. 2010, 21, 219–227. [Google Scholar] [CrossRef]
- Yang, W.Q.; Liu, S. Role of tomography in gas/solids flow measurement. Flow Meas. Instrum. 2000, 11, 237–244. [Google Scholar] [CrossRef]
- Jaworski, A.J.; Dyakowski, T. Investigations of flow instabilities within the dense pneumatic conveying system. In Proceedings of the Powder Technology; Elsevier: Amsterdam, The Netherlands, 2002; Volume 125, pp. 279–291. [Google Scholar]
- Ostrowski, K.L.; Luke, S.P.; Bennett, M.A.; Williams, R.A. Application of capacitance electrical tomography for on-line and off-line analysis of flow pattern in horizontal pipeline of pneumatic conveyer. Chem. Eng. J. 2000, 77, 43–50. [Google Scholar] [CrossRef]
- Zhu, K.; Madhusudana Rao, S.; Wang, C.H.; Sundaresan, S. Electrical capacitance tomography measurements on vertical and inclined pneumatic conveying of granular solids. Chem. Eng. Sci. 2003, 58, 4225–4245. [Google Scholar] [CrossRef]
- Dyakowski, T.; Luke, S.P.; Ostrowski, K.L.; Williams, R.A. On-line monitoring of dense phase flow using real time dielectric imaging. In Proceedings of the Powder Technology; Elsevier: Amsterdam, The Netherlands, 1999; Volume 104, pp. 287–295. [Google Scholar]
- Sun, M.; Liu, S.; Lei, J.; Li, Z. Mass flow measurement of pneumatically conveyed solids using electrical capacitance tomography. Meas. Sci. Technol. 2008, 19, 045503. [Google Scholar] [CrossRef]
- Kryszyn, J.; Smolik, W.T.; Radzik, B.; Olszewski, T.; Szabatin, R. Switchless charge-discharge circuit for electrical capacitance tomography. Meas. Sci. Technol. 2014, 25, 115009. [Google Scholar] [CrossRef]
- He, Y.B.; Wajman, R.; Banasiak, R.; Xu, M.S.D. Design of TCP/IP Based Flexible Three Dimensional Electrical Capacitance Tomography. In Proceedings of the 3rd International Workshop on Process Tomography, Tokyo, Japan, 17–19 April 2009. [Google Scholar]
- Łukasik, E.; Pańczyk, B.; Sikora, J. Calculation of the improper integrals for fourier boundary element method. Informatics Control Meas. Econ. Environ. Prot. 2013, 3, 7–10. [Google Scholar] [CrossRef]
- Sikora, J. Boundary Element Method for Impedance and Optical Tomography; Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 2007; ISBN 978-83-7207-728-8. [Google Scholar]
- Banasiak, R.; Wajman, R.; Soleimani, M. An efficient nodal Jacobian method for 3D electrical capacitance tomography image reconstruction. Insight Non-Destructive Test. Cond. Monit. 2009, 51, 36–38. [Google Scholar] [CrossRef]
- Majchrowicz, M.; Kapusta, P.; Jackowska-Strumiłło, L.; Banasiak, R.; Sankowski, D. Multi-GPU, Multi-Node Algorithms for Acceleration of Image Reconstruction in 3D Electrical Capacitance Tomography in Heterogeneous Distributed System. Sensors 2020, 20, 391. [Google Scholar] [CrossRef] [Green Version]
- Banasiak, R.; Wajman, R.; Sankowski, D.; Soleimani, M. Three-Dimensional Nonlinear Inversion of Electrical Capacitance Tomography Data Using a Complete Sensor Model. Prog. Electromagn. Res. Pier 2010, 100, 219–234. [Google Scholar] [CrossRef] [Green Version]
- Isaksen, Ø. A review of reconstruction techniques for capacitance tomography. Meas. Sci. Technol. 1996, 7, 325–337. [Google Scholar] [CrossRef]
- Soleimani, M. Computational aspects of low frequency electrical and electromagnetic tomography: A review study. Int. J. Numer. Anal. Model. 2008, 5, 407–440. [Google Scholar]
- Rymarczyk, T. Topological algorithms to solve inverse problem in electrical tomography. Informatics Control Meas. Econ. Environ. Prot. 2017, 7, 55–58. [Google Scholar] [CrossRef]
- Rymarczyk, T.; Kłosowski, G.; Kozłowski, E.; Tchórzewski, P. Comparison of Selected Machine Learning Algorithms for Industrial Electrical Tomography. Sensors 2019, 19, 1521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Q.; Meng, S.; Wang, D.; Zhao, Y.; Ye, M.; Yang, W.; Liu, Z. Investigation of gas-solid bubbling fluidized beds using ECT with a modified Tikhonov regularization technique. AIChE J. 2018, 64, 29–41. [Google Scholar] [CrossRef]
- Tortora, P.R.; Ceccio, S.L.; Trujillo, S.M.; O’Hern, T.J.; Shollenberger, K.A. Capacitance measurements of solid concentration in gas-solid flows. In Proceedings of the Powder Technology; Elsevier: Amsterdam, The Netherlands, 2004; Volume 148, pp. 92–101. [Google Scholar]
- Liu, S.; Chen, Q.; Wang, H.G.; Jiang, F.; Ismail, I.; Yang, W.Q. Electrical capacitance tomography for gas–solids flow measurement for circulating fluidized beds. Flow Meas. Instrum. 2005, 16, 135–144. [Google Scholar] [CrossRef]
- Mosorov, V.; Sankowski, D.; Mazurkiewicz, Ł.; Dyakowski, T. The “best-correlated pixels” method for solid mass flow measurements using electrical capacitance tomography. Meas. Sci. Technol. 2002, 13, 1810–1814. [Google Scholar] [CrossRef]
- Zhang, Y.; Lim, E.W.C.; Wang, C.H. Pneumatic transport of granular materials in an inclined conveying pipe: Comparison of computational fluid dynamics-discrete element method (CFD-DEM), electrical capacitance tomography (ECT), and particle image velocimetry (PIV) results. Ind. Eng. Chem. Res. 2007, 46, 6066–6083. [Google Scholar] [CrossRef]
- Paul, C.R. Introduction to Electromagnetic Compatibility, 2nd ed.; Wiley Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]


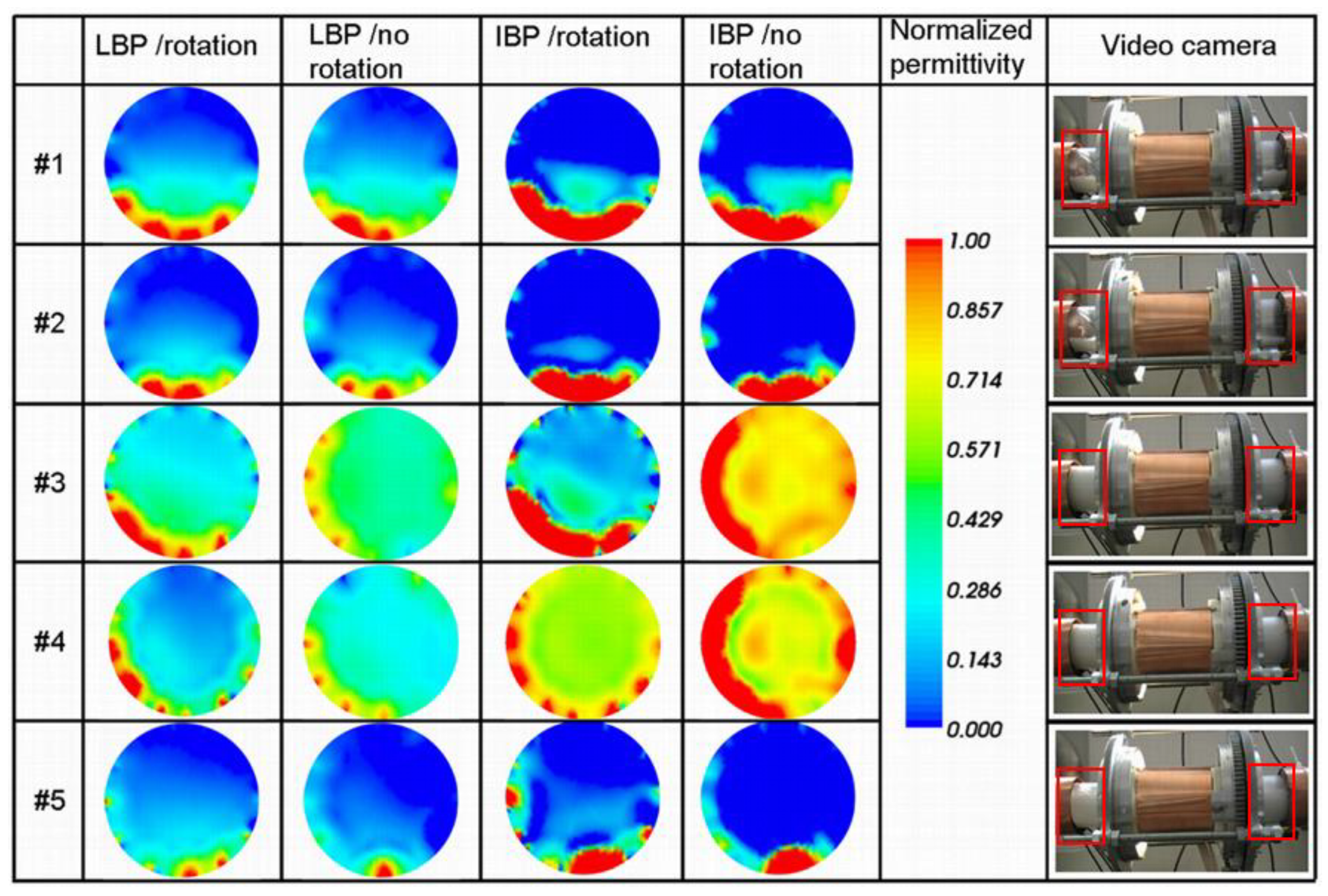


| Event | LBP Rotation | LBP No Rotation | IBP Rotation | IBP No Rotation | Estimated Concentration | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fA | Φ | fA | Φ | fA | Φ | fA | Φ | Φ* | |||||
| #1 | 0.63 | 0.28 | 0.2 | 0.55 | 0.278 | 0.18 | 0.828 | 0.256 | 0.225 | 0.706 | 0.265 | 0.208 | 0.177 |
| #2 | 0.69 | 0.136 | 0.105 | 0.63 | 0.123 | 0.089 | 0.89 | 0.146 | 0.135 | 0.85 | 0.135 | 0.121 | 0.06 |
| #4 | 0.52 | 1 | 0.62 | 0.466 | 1 | 0.566 | 0.566 | 1 | 0.66 | 0.878 | 1 | 0.915 | 0.69 |
| Event No. | Description | Size of Slug (Frames) | Time Lag (Frames) | Speed (ms−1) |
|---|---|---|---|---|
| #3 | Long slug/Moderate speed | 35 ± 1 | 11 ± 1 | 2.67 ± 0.24 |
| #4 | Long slug/Fast speed | 21 ± 1 | 6 ± 1 | 4.9 ± 0.82 |
| #5 | short slug/Fast speed | 4 ± 1 | 5 ± 1 | 5.88 ± 1.18 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wajman, R.; Banasiak, R.; Babout, L. On the Use of a Rotatable ECT Sensor to Investigate Dense Phase Flow: A Feasibility Study. Sensors 2020, 20, 4854. https://doi.org/10.3390/s20174854
Wajman R, Banasiak R, Babout L. On the Use of a Rotatable ECT Sensor to Investigate Dense Phase Flow: A Feasibility Study. Sensors. 2020; 20(17):4854. https://doi.org/10.3390/s20174854
Chicago/Turabian StyleWajman, Radosław, Robert Banasiak, and Laurent Babout. 2020. "On the Use of a Rotatable ECT Sensor to Investigate Dense Phase Flow: A Feasibility Study" Sensors 20, no. 17: 4854. https://doi.org/10.3390/s20174854
APA StyleWajman, R., Banasiak, R., & Babout, L. (2020). On the Use of a Rotatable ECT Sensor to Investigate Dense Phase Flow: A Feasibility Study. Sensors, 20(17), 4854. https://doi.org/10.3390/s20174854







