Near-Infrared Spectroscopy Coupled Chemometric Algorithms for Rapid Origin Identification and Lipid Content Detection of Pinus Koraiensis Seeds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Collection and Preparation
2.2. NIR Spectrometer and Spectral Acquisition
2.3. Lipid Content
2.4. Data Analysis
2.4.1. Discrete Wavelet Transformation
2.4.2. Wavelet Threshold Denoising and Compression Method
2.4.3. Principal Component Analysis (PCA)
2.4.4. Monte Carlo (MC) Combined with Uninformative Variable Elimination (UVE)
2.4.5. Partial Least-Square (PLS)
2.5. Origin and Lipid Content Calibration Models
2.6. Model Validation
3. Results
3.1. Quantitative Analysis of Lipid Content
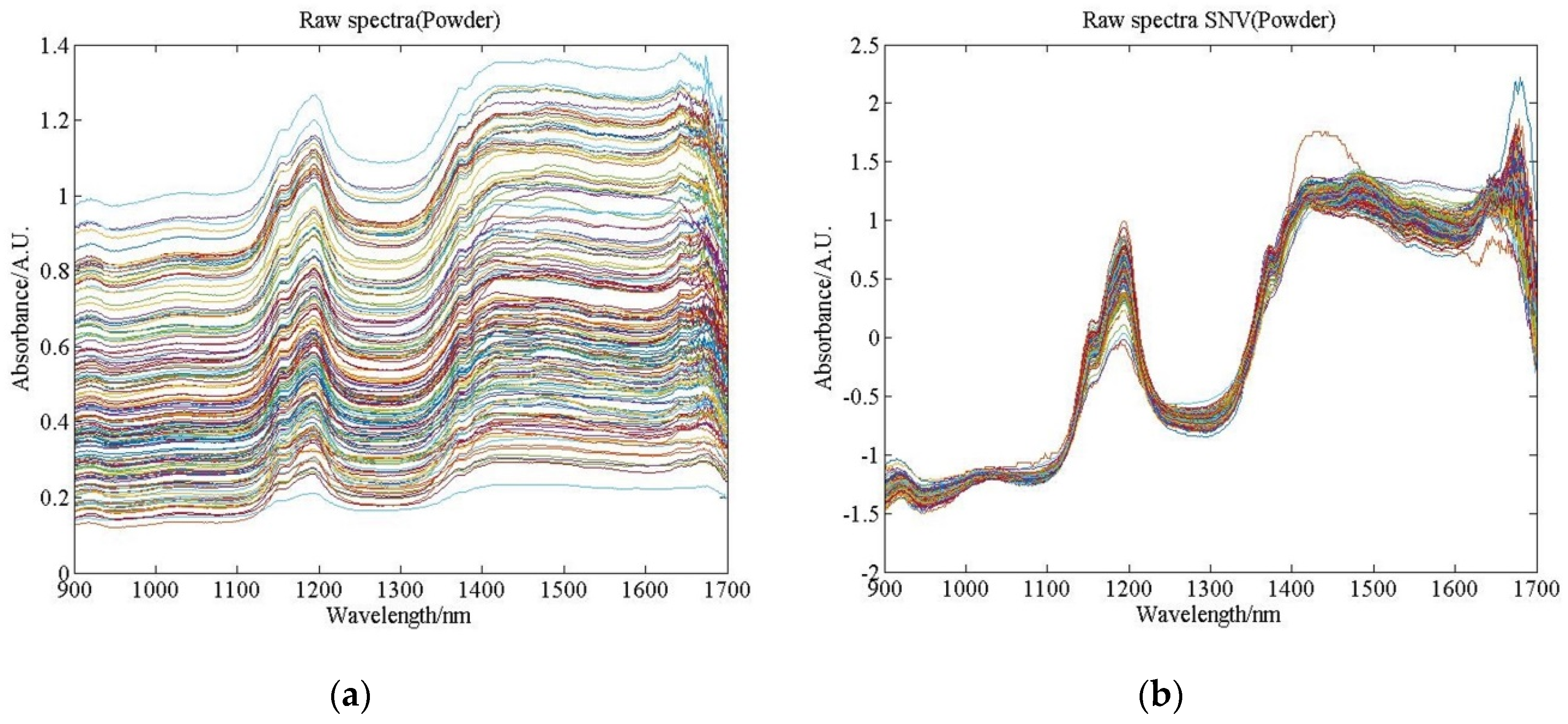
3.2. Spectral Data and Preprocessing Results
3.3. Results of Feature Selection
3.3.1. Results of Principal Component Analysis (PCA)
3.3.2. Results of Monte Carlo-Uninformative Variable Elimination (MCUVE)
3.4. Model Results and Analysis
3.4.1. Results of The Classification Model
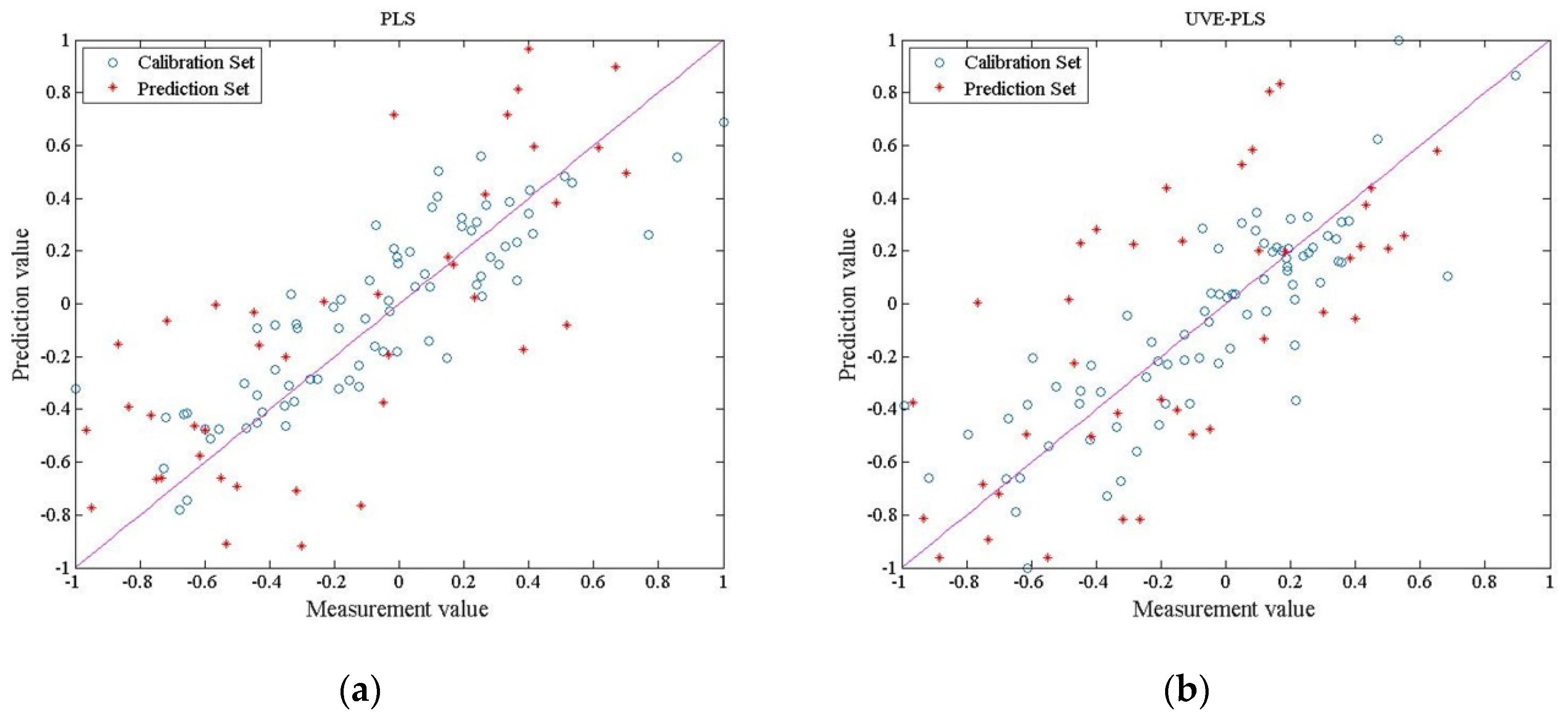
3.4.2. Results of the Regression Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ying, H.; Luo, C.; Pang, H.; Xue, L. Effect of Pinus koraiensis Seeds Stored on Seedling Growth from Different Areas. For. Prod. Spec. China 2009, 4, 5–6. [Google Scholar]
- Asset, G.L.; Staels, B.; Wolff, R.L.; Baugé, E.; Madj, Z.; Fruchart, J.C.; Dallongeville, J. Effects of Pinus pinaster and Pinus koraiensis seed oil supplementation on lipoprotein metabolism in the rat. Lipids 1999, 34, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhang, H.; Zhang, Y.; Zhao, H.; Wang, J. Analysis of the Essential Oils of Pine Cones of Pinus koraiensis Steb. Et Zucc. and P. sylvestris L. from China. J. Essent. Oil Res. 2010, 22, 446–448. [Google Scholar] [CrossRef]
- Loewe, V.; Navarro-Cerrillo, R.M.; García-Olmo, J.; Riccioli, C.; Sánchez-Cuesta, R. Discriminant analysis of Mediterranean pine nuts (Pinus pinea L.) from Chilean plantations by near infrared spectroscopy (NIRS). Food Control 2017, 73, 634–643. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, J.; Sun, L.; Chen, Q.; Zhou, F. Freshness measurement of eggs using near infrared (NIR) spectroscopy and multivariate data analysis. Innov. Food Sci. Emerg. Technol. 2011, 12, 182–186. [Google Scholar] [CrossRef]
- Kobori, H.; Inagaki, T.; Fujimoto, T.; Okura, T.; Tsuchikawa, S. Fast online NIR technique to predict MOE and moisture content of sawn lumber. Holzforschung 2015, 69, 329–335. [Google Scholar] [CrossRef]
- Tsuchikawa, S.; Kobori, H. A review of recent application of near infrared spectroscopy to wood science and technology. J. Wood Sci. 2015, 61, 213–220. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Ying, Y.; Ying, T.; Yu, H.; Fu, X. Discrimination of transgenic tomatoes based on visible/near-infrared spectra. Anal. Chim. Acta 2007, 584, 379–384. [Google Scholar] [CrossRef]
- Pannico, A.; Schouten, R.; Basile, B.; Romano, R.; Woltering, E.; Cirillo, C. Non-destructive detection of flawed hazelnut kernels and lipid oxidation assessment using NIR spectroscopy. J. Food Eng. 2015, 160, 42–48. [Google Scholar] [CrossRef]
- Han, Z.; Cai, S.; Zhang, X.; Qian, Q.; Huang, Y.; Dai, F.; Zhang, G. Development of predictive models for total phenolics and free p-coumaric acid contents in barley grain by near-infrared spectroscopy. Food Chem. 2017, 227, 342–348. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, H.; Chen, Q.; Huang, X.; Sun, Z.; Zhou, F. Identification of egg’s freshness using NIR and support vector data description. J. Food Eng. 2010, 98, 408–414. [Google Scholar] [CrossRef]
- Itoh, H.; Tomita, H.; Uno, Y.; Shiraishi, N. Development of method for non-destructive measurement of nitrate concentration in vegetable leaves by near-infrared spectroscopy. IFAC Proc. Vol. 2011, 44, 1773–1778. [Google Scholar] [CrossRef] [Green Version]
- Beghi, R.; Giovenzana, V.; Civelli, R.; Guidetti, R. Influence of packaging in the analysis of fresh-cut Valerianella locusta L. and Golden Delicious apple slices by visible-near infrared and near infrared spectroscopy. J. Food Eng. 2016, 171, 145–152. [Google Scholar] [CrossRef]
- Magwaza, L.S.; Naidoo, S.I.M.; Laurie, S.M.; Laing, M.D.; Shimelis, H. Development of NIRS models for rapid quantification of protein content in sweetpotato [Ipomoea batatas (L.) LAM.]. LWT-Food Sci. Technol. 2016, 72, 63–70. [Google Scholar] [CrossRef]
- Cortes, V.; Rodriguez, A.; Blasco, J.; Rey, B.; Besada, C.; Cubero, S.; Salvador, A.; Talens, P.; Aleixos, N. Prediction of the level of astringency in persimmon using visible and near-infrared spectroscopy. J. Food Eng. 2017, 204, 27–37. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi-Moghaddam, T.; Razavi, S.M.; Sazgarnia, A.; Taghizadeh, M. Predicting the moisture content and textural characteristics of roasted pistachio kernels using Vis/NIR reflectance spectroscopy and PLSR analysis. J. Food Meas. Charact. 2018, 12, 346–355. [Google Scholar] [CrossRef]
- Canneddu, G.; Júnior, L.C.C.; de Almeida Teixeira, G.H. Quality evaluation of shelled and unshelled macadamia nuts by means of near-infrared spectroscopy (NIR). J. Food Sci. 2016, 81, C1613–C1621. [Google Scholar] [CrossRef]
- Chen, J.-B.; Sun, S.-Q.; Zhou, Q. Chemical morphology of Areca nut characterized directly by Fourier transform near-infrared and mid-infrared microspectroscopic imaging in reflection modes. Food Chem. 2016, 212, 469–475. [Google Scholar] [CrossRef]
- Moscetti, R.; Monarca, D.; Cecchini, M.; Haff, R.P.; Contini, M.; Massantini, R. Detection of mold-damaged chestnuts by near-infrared spectroscopy. Postharvest Biol. Technol. 2014, 93, 83–90. [Google Scholar] [CrossRef]
- Hu, J.; Ma, X.; Liu, L.; Wu, Y.; Ouyang, J. Rapid evaluation of the quality of chestnuts using near-infrared reflectance spectroscopy. Food Chem. 2017, 231, 141–147. [Google Scholar] [CrossRef]
- Ghosh, S.; Mishra, P.; Mohamad, S.N.H.; de Santos, R.M.; Iglesias, B.D.; Elorza, P.B. Discrimination of peanuts from bulk cereals and nuts by near infrared reflectance spectroscopy. Biosyst. Eng. 2016, 151, 178–186. [Google Scholar] [CrossRef]
- American Oil Chemists’ Society. Official methods and recommended practices of the American Oil Chemists’ Society. AOCS 1998, 5, 2–93. [Google Scholar]
- Balabin, R.M.; Smirnov, S.V. Variable selection in near-infrared spectroscopy: Benchmarking of feature selection methods on biodiesel data. Anal. Chim. Acta 2011, 692, 63–72. [Google Scholar] [CrossRef]
- Bi, Y.; Yuan, K.; Xiao, W.; Wu, J.; Shi, C.; Xia, J.; Chu, G.; Zhang, G.; Zhou, G. A local pre-processing method for near-infrared spectra, combined with spectral segmentation and standard normal variate transformation. Anal. Chim. Acta 2016, 909, 30–40. [Google Scholar] [CrossRef]
- Cai, W.; Li, Y.; Shao, X. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra. Chemom. Intell. Lab. Syst. 2008, 90, 188–194. [Google Scholar] [CrossRef]
- Wu, D.; Chen, X.; Shi, P.; Wang, S.; Feng, F.; He, Y. Determination of α-linolenic acid and linoleic acid in edible oils using near-infrared spectroscopy improved by wavelet transform and uninformative variable elimination. Anal. Chim. Acta 2009, 634, 166–171. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.-T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef] [Green Version]
- Bruce, A.G.; Donoho, D.L.; Gao, H.Y.; Martin, R.D. Denoising and Robust Non-Linear Wavelet Analysis. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 15 March 1994; Volume 2242, pp. 325–336. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- He, Y.; Li, X.; Deng, X. Discrimination of varieties of tea using near infrared spectroscopy by principal component analysis and BP model. J. Food Eng. 2007, 79, 1238–1242. [Google Scholar] [CrossRef]
- Amorello, D.; Orecchio, S.; Pace, A.; Barreca, S. Discrimination of almonds (Prunus dulcis) geographical origin by minerals and fatty acids profiling. Nat. Prod. Res. 2016, 30, 2107–2110. [Google Scholar] [CrossRef]
- Malegori, C.; Marques, E.J.N.; de Freitas, S.T.; Pimentel, M.F.; Pasquini, C.; Casiraghi, E. Comparing the analytical performances of Micro-NIR and FT-NIR spectrometers in the evaluation of acerola fruit quality, using PLS and SVM regression algorithms. Talanta 2017, 165, 112–116. [Google Scholar] [CrossRef] [PubMed]
- Mehmood, T. PLS Modeling the Starch Contents of Corn Data Measured Through Different NIR Spectrometers. Int. J. Food Eng. 2019, 5, 132–135. [Google Scholar] [CrossRef]
- Yang, X.; Hong, H.; You, Z.; Cheng, F. Spectral and image integrated analysis of hyperspectral data for waxy corn seed variety classification. Sensors 2015, 15, 15578–15594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shetty, N.; Gislum, R.; Jensen, A.M.D.; Boelt, B. Development of NIR calibration models to assess year-to-year variation in total non-structural carbohydrates in grasses using PLSR. Chemom. Intell. Lab. Syst. 2012, 111, 34–38. [Google Scholar] [CrossRef]
- Jaya, S.; Chari, V.K.; Konda Naganathan, G.; Jeyam, S. Sensing of moisture content of in-shell peanuts by NIR reflectance spectroscopy. J. Sens. Technol. 2012, 2012, 1–7. [Google Scholar]
- Akpolat, H.; Barineau, M.; Jackson, K.A.; Akpolat, M.Z.; Francis, D.M.; Chen, Y.-J.; Rodriguez-Saona, L.E. High-Throughput Phenotyping Approach for Screening Major Carotenoids of Tomato by Handheld Raman Spectroscopy Using Chemometric Methods. Sensors 2020, 20, 3723. [Google Scholar] [CrossRef]
- Trygg, J.; Wold, S. PLS regression on wavelet compressed NIR spectra. Chemom. Intell. Lab. Syst. 1998, 42, 209–220. [Google Scholar] [CrossRef]
- Di Egidio, V.; Sinelli, N.; Giovanelli, G.; Moles, A.; Casiraghi, E. NIR and MIR spectroscopy as rapid methods to monitor red wine fermentation. Eur. Food Res. Technol. 2010, 230, 947–955. [Google Scholar] [CrossRef]
- Dos Santos Panero, P.; dos Santos Panero, F.; dos Santos Panero, J.; da Silva, H.E.B. Application of extended multiplicative signal correction to short-wavelength near infrared spectra of moisture in marzipan. J. Data Anal. Inf. Process. 2013, 1, 30–34. [Google Scholar] [CrossRef] [Green Version]
- Jensen, P.N.; Sørensen, G.; Engelsen, S.B.; Bertelsen, G. Evaluation of quality changes in walnut kernels (Juglans regia L.) by Vis/NIR spectroscopy. J. Agric. Food Chem. 2001, 49, 5790–5796. [Google Scholar] [CrossRef]







| Set | Mean | Min (b) | Max (c) | SD (d) | CV (e) |
|---|---|---|---|---|---|
| Yichun#1–40 | 63.01 | 62.60 | 63.40 | 0.27 | 0.41 |
| Heihe#41–80 | 61.17 | 60.30 | 62.20 | 0.52 | 0.85 |
| Changbai Mountain#81–120 | 60.90 | 59.70 | 62.30 | 0.76 | 1.26 |
| Calibration set (n (a) = 80) | 61.90 | 59.70 | 63.40 | 0.94 | 1.52 |
| Prediction set (n (a) = 40) | 60.75 | 60.10 | 62.20 | 0.71 | 1.16 |
| Total#120 | 61.70 | 59.70 | 63.40 | 1.09 | 1.77 |
| Wavelet Filter | Threshold Methods | Compression R (%) | PRD (a) (%) |
|---|---|---|---|
| db9 | Birge–Massart Strategy | 85.1519 | 0.28 |
| SURE Shrink Thresholding | 86.0656 | 0.36 | |
| Donoho Thresholding | 83.9738 | 0.23 | |
| Soft Thresholding | 86.0714 | 0.37 | |
| bior4.4 | Birge–Massart Strategy | 85.6925 | 0.28 |
| SURE Shrink Thresholding | 86.7016 | 0.39 | |
| Donoho Thresholding | 84.7487 | 0.21 | |
| Soft Thresholding | 86.7525 | 0.39 | |
| sym8 | Birge–Massart Strategy | 84.6819 | 0.27 |
| SURE Shrink Thresholding | 85.9911 | 0.36 | |
| Donoho Thresholding | 83.5233 | 0.20 | |
| Soft Thresholding | 86.1487 | 0.37 | |
| coif4 | Birge–Massart Strategy | 83.7562 | 0.26 |
| SURE Shrink Thresholding | 85.2497 | 0.37 | |
| Donoho Thresholding | 82.5347 | 0.20 | |
| Soft Thresholding | 85.5128 | 0.38 |
| Model | Input Dimensions | Calibration Set | Prediction Set | |||||
|---|---|---|---|---|---|---|---|---|
| Accuracy (%) | Time /s | Precision | Recall | F1 (a) | Accuracy (%) | Time /s | ||
| PLS (b) | 511 | 78.75 | 8.96 | 0.85 | 0.93 | 0.81 | 77.50 | 4.46 |
| SNV (c)–PLS | 511 | 88.75 | 8.13 | 0.93 | 0.95 | 0.92 | 87.50 | 3.32 |
| SNV–PCA (d)–PLS | 2 | 98.75 | 2.61 | 1.00 | 0.94 | 0.97 | 97.50 | 0.91 |
| 3 | 98.75 | 2.96 | 0.97 | 0.95 | 0.97 | 97.50 | 1.03 | |
| Model | Number of Features | Calibration Set (n (a) = 80) | Prediction Set (n (a) = 40) | ||
|---|---|---|---|---|---|
| RMSECV (b) | R2 (d) (Cal (e)) | RMSEP (c) | R2 (d) (Pre (f)) | ||
| PLS | 511 | 0.0407 | 0.8613 | 0.1396 | 0.7489 |
| UVE–PLS | 100 | 0.0159 | 0.9169 | 0.0875 | 0.8810 |
| MCUVE–PLS | 70 | 0.0449 | 0.8369 | 0.1556 | 0.6721 |
| WT–PLS | 154 | 0.0808 | 0.7284 | 0.1491 | 0.7595 |
| WT–MCUVE–PLS | 70 | 0.0098 | 0.9485 | 0.0390 | 0.9369 |
| PCR | 511 | 0.0467 | 0.7512 | 0.1357 | 0.7540 |
| PCA–PLS | 80 | 0.0284 | 0.8635 | 0.1693 | 0.7330 |
| SPA–PLS | 50 | 1.6666 | 0.8820 | 0.1538 | 0.8141 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Jiang, D.; Cao, J.; Zhang, D. Near-Infrared Spectroscopy Coupled Chemometric Algorithms for Rapid Origin Identification and Lipid Content Detection of Pinus Koraiensis Seeds. Sensors 2020, 20, 4905. https://doi.org/10.3390/s20174905
Li H, Jiang D, Cao J, Zhang D. Near-Infrared Spectroscopy Coupled Chemometric Algorithms for Rapid Origin Identification and Lipid Content Detection of Pinus Koraiensis Seeds. Sensors. 2020; 20(17):4905. https://doi.org/10.3390/s20174905
Chicago/Turabian StyleLi, Hongbo, Dapeng Jiang, Jun Cao, and Dongyan Zhang. 2020. "Near-Infrared Spectroscopy Coupled Chemometric Algorithms for Rapid Origin Identification and Lipid Content Detection of Pinus Koraiensis Seeds" Sensors 20, no. 17: 4905. https://doi.org/10.3390/s20174905
APA StyleLi, H., Jiang, D., Cao, J., & Zhang, D. (2020). Near-Infrared Spectroscopy Coupled Chemometric Algorithms for Rapid Origin Identification and Lipid Content Detection of Pinus Koraiensis Seeds. Sensors, 20(17), 4905. https://doi.org/10.3390/s20174905






