Real-Time Compact Environment Representation for UAV Navigation
Abstract
:1. Introduction
- Two novel algorithms, namely the vertical strip extraction algorithm and the plane adjustment algorithm, are proposed to effectively adapt to different obstacle shapes and different surface roughness, as well as to speed up the elimination of irrelevant environmental details by minimizing redundant information.
- The proposed OSAPE modeling scheme, which is the combination of the two proposed algorithms, can convert the normalized data into simplified prisms based on the size of the UAV in real time.
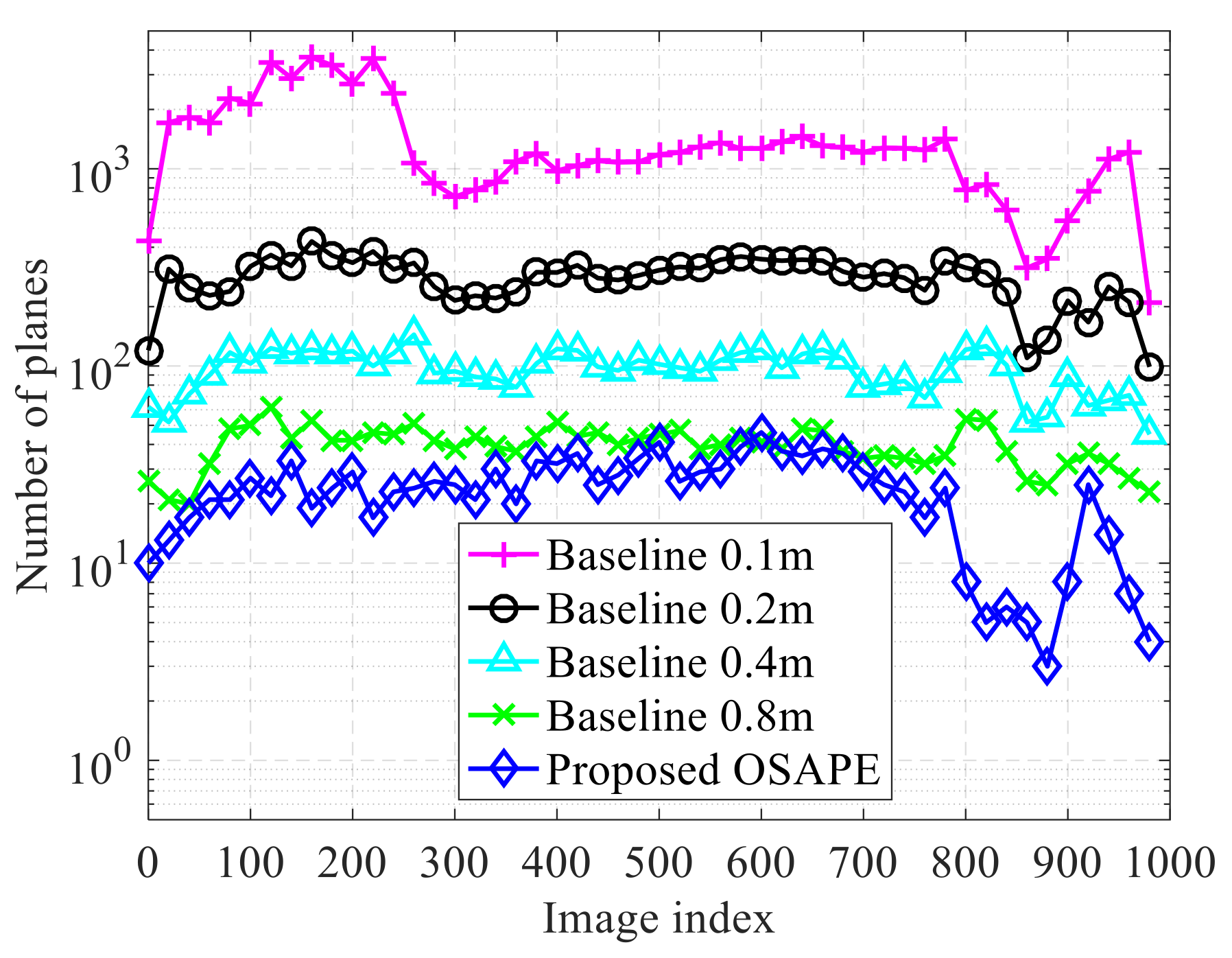
- By building a drone platform with a depth sensor, real-world experiments are conducted to demonstrate the advantage of the proposed scheme over the baseline.
2. Related Works
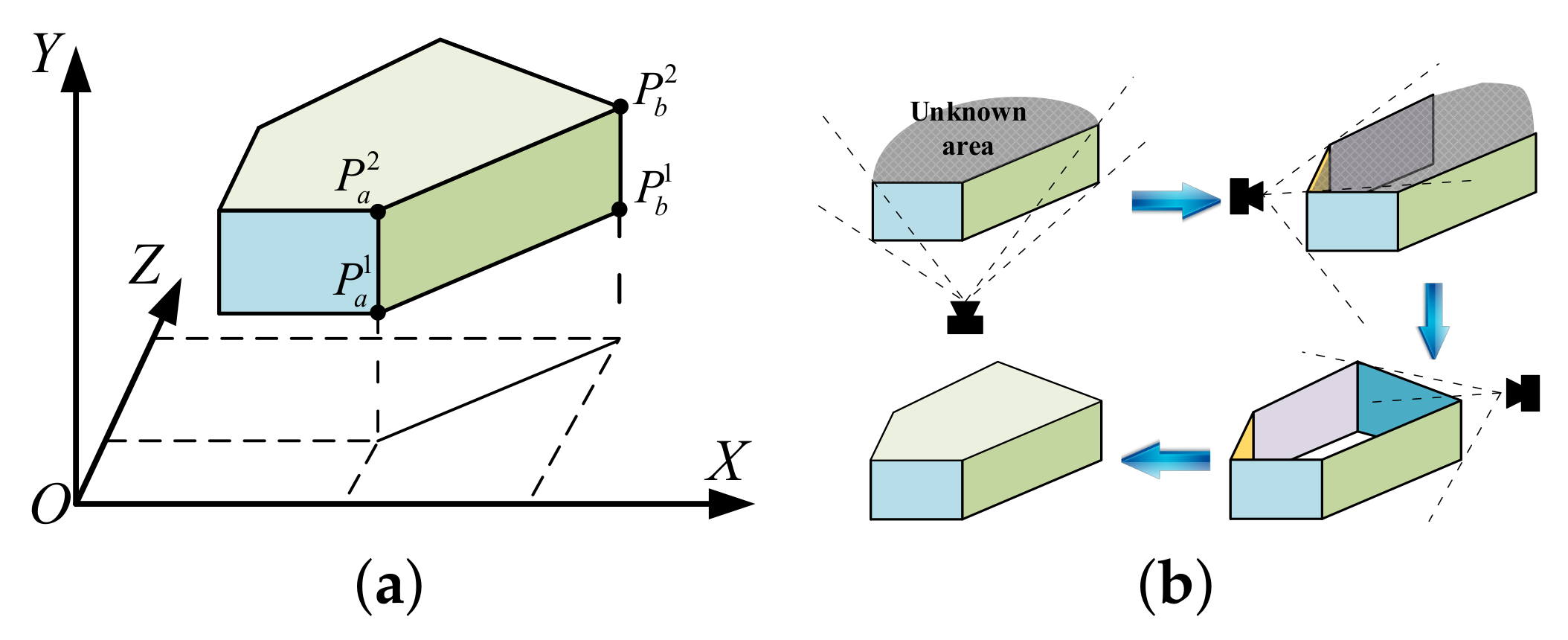
3. Adaptive Plane Extraction Model
4. The Proposed Vertical Strip Extraction Algorithm
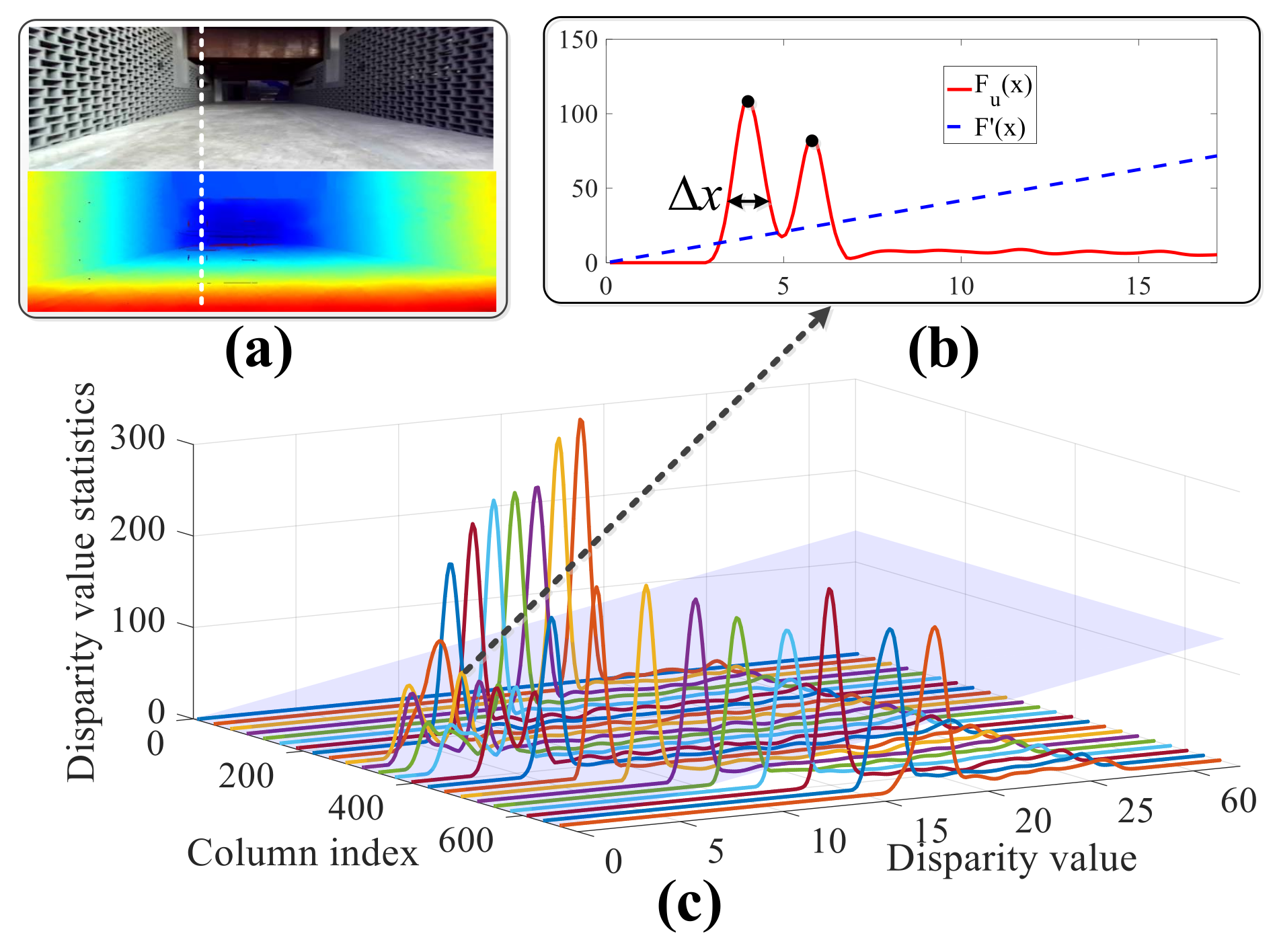
4.1. Statistical Estimation of Obstacles
4.2. Obstacle Identification with a Sliding Window
- The average of the disparity value in the sliding window is within the range and
- more than half of the pixels in the sliding window are within the range .
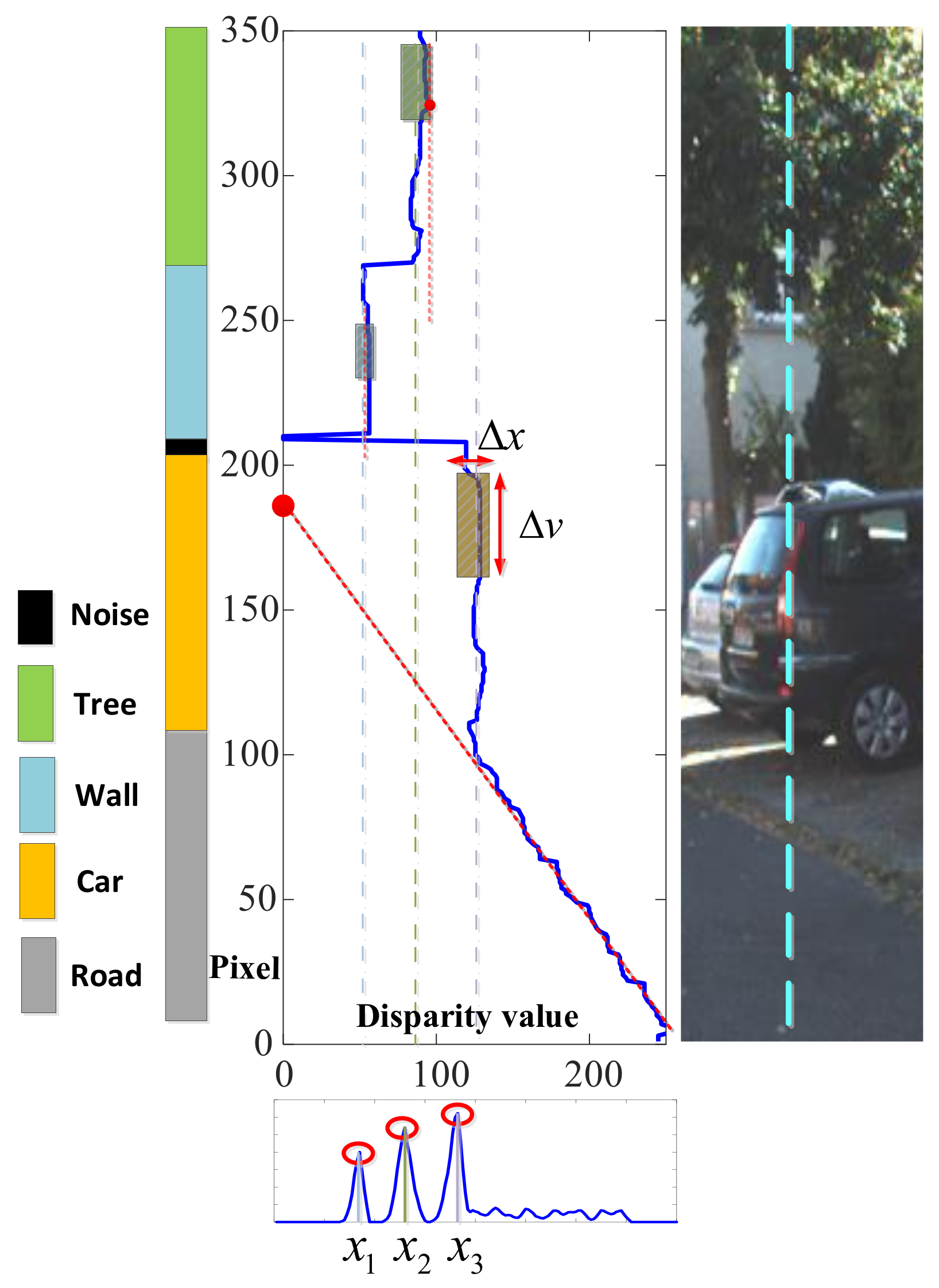
4.3. Irregular Object Processing
4.4. Vertical Strip Clustering
| Algorithm 1 Fast strip clustering algorithm. |
|
4.5. Computational Complexity
5. The Proposed Plane Adjustment Algorithm
5.1. Vertical Gap Filling
5.2. Concave Surface Converting
5.3. Adjacent Plane Refinement
- The angle between the two planes is less than the threshold and
- the distance between the boundaries of the adjacent sides is smaller than .
| Algorithm 2 Concave surface converting algorithm. |
|
5.4. Computational Complexity
6. Experiment and Analysis
6.1. AirSim Simulation
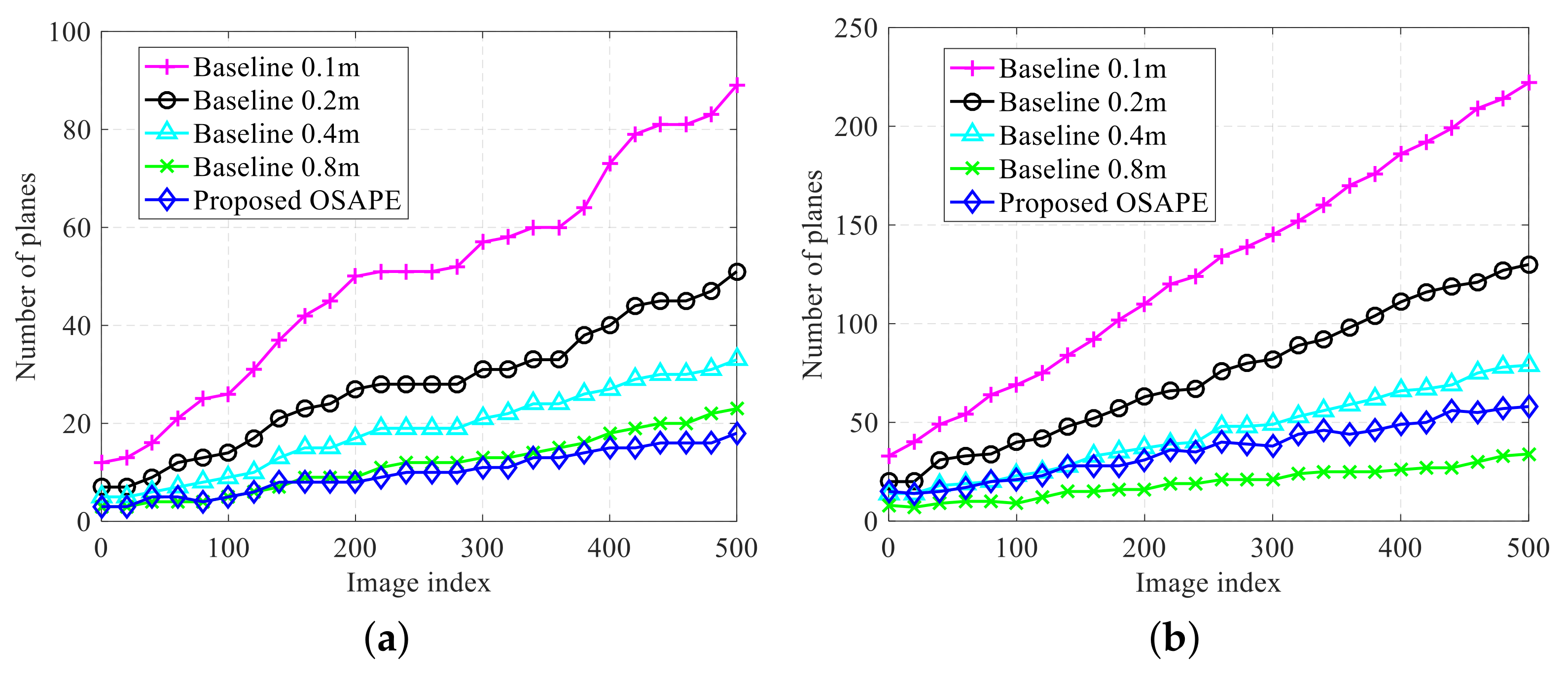
6.1.1. Compact Model
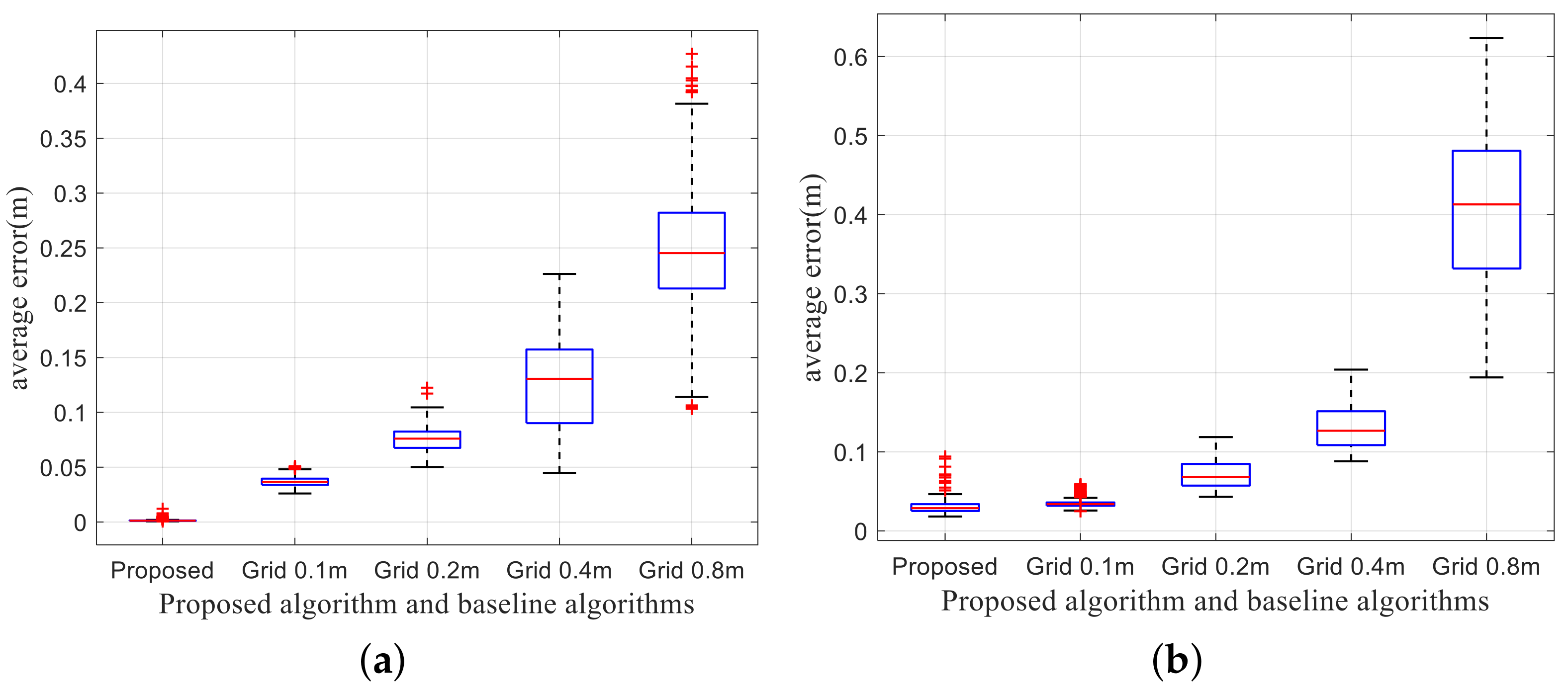
6.1.2. Memory Usage and Model Precision
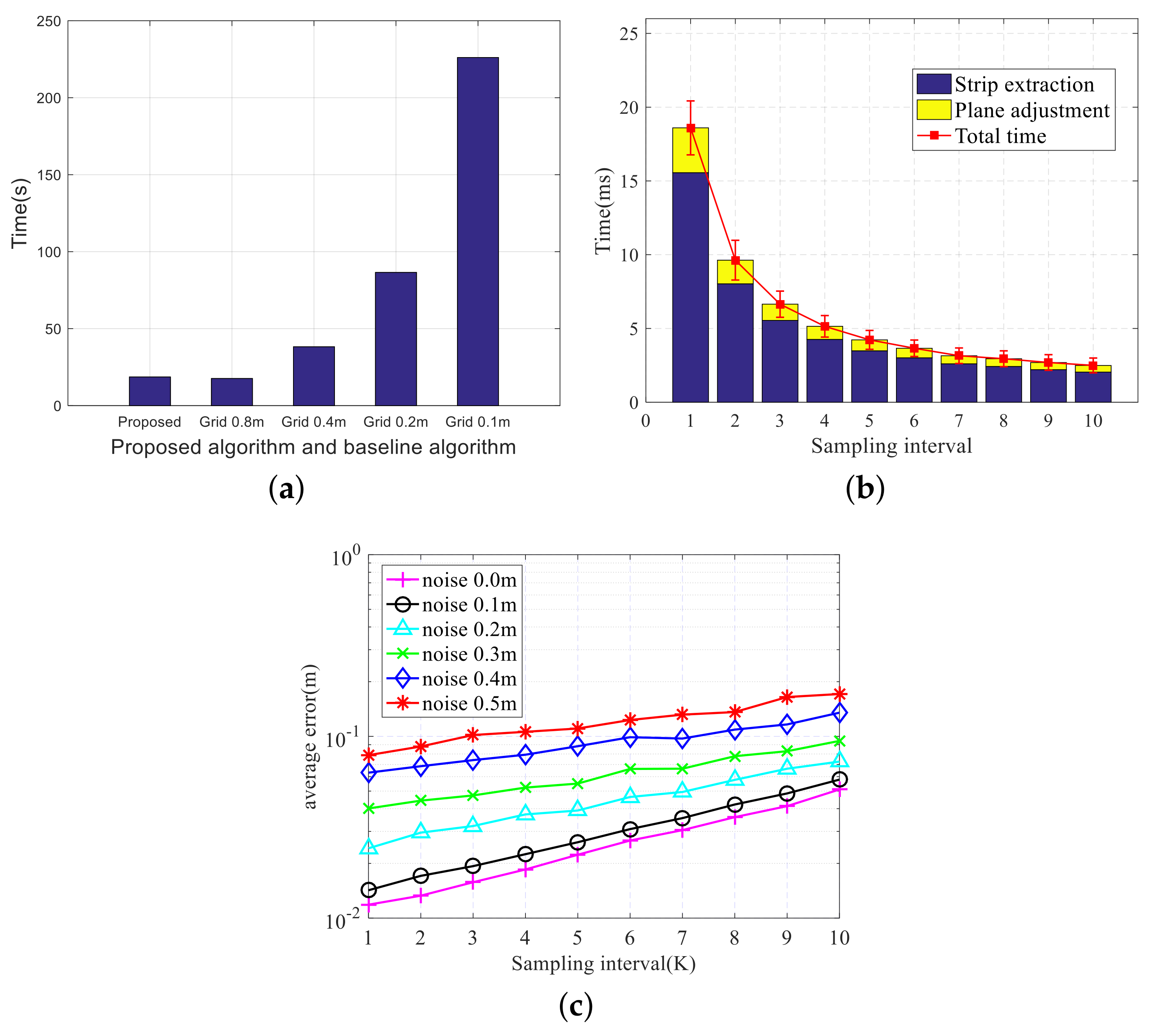
6.1.3. Processing Time
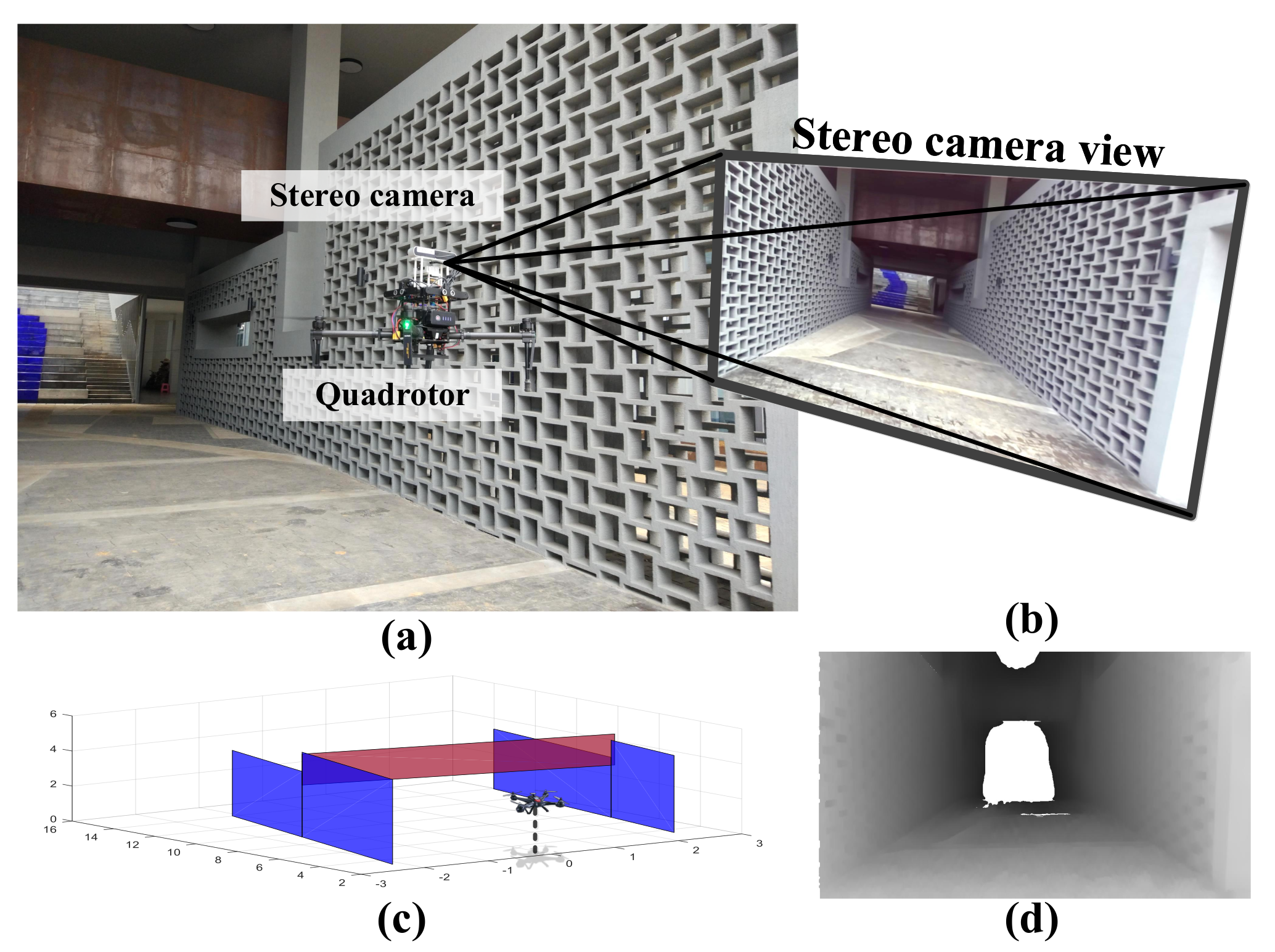
6.2. Experiment on the Developed Platform
6.3. Application
7. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
Appendix A. Prove of Lemma 1

References
- Zhong, Y.; Wang, X.; Xu, Y.; Wang, S.; Jia, T.; Hu, X.; Zhao, J.; Wei, L.; Zhang, L. Mini-UAV-Borne Hyperspectral Remote Sensing: From Observation and Processing to Applications. IEEE Geosci. Remote Sens. Mag. 2018, 6, 46–62. [Google Scholar] [CrossRef]
- Wu, Q.; Shen, X.; Jin, Y.; Chen, Z.; Li, S.; Khan, A.; Chen, D. Intelligent Beetle Antennae Search for UAV Sensing and Avoidance of Obstacles. Sensors 2019, 19, 1758. [Google Scholar] [CrossRef] [Green Version]
- Boonpook, W.; Tan, Y.; Ye, Y.; Torteeka, P.; Torsri, K.; Dong, S. A Deep Learning Approach on Building Detection from Unmanned Aerial Vehicle-Based Images in Riverbank Monitoring. Sensors 2018, 18, 3921. [Google Scholar] [CrossRef] [Green Version]
- Cao, T.; Xiang, Z.; Liu, J. Perception in Disparity: An Efficient Navigation Framework for Autonomous Vehicles With Stereo Cameras. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2935–2948. [Google Scholar] [CrossRef]
- Yang, S.; Yang, S.; Yi, X. An Efficient Spatial Representation for Path Planning of Ground Robots in 3D Environments. IEEE Access 2018, 6, 41539–41550. [Google Scholar] [CrossRef]
- Azevedo, F.; Dias, A.; Almeida, J.; Oliveira, A.; Ferreira, A.; Santos, T.; Martins, A.; Silva, E. LiDAR-Based Real-Time Detection and Modeling of Power Lines for Unmanned Aerial Vehicles. Sensors 2019, 19, 1812. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dinh, P.; Nguyen, T.M.; Sharafeddine, S.; Assi, C. Joint Location and Beamforming Design for Cooperative UAVs With Limited Storage Capacity. IEEE Trans. Commun. 2019, 67, 8112–8123. [Google Scholar] [CrossRef]
- Elfes, A. Using occupancy grids for mobile robot perception and navigation. Computer 1989, 22, 46–57. [Google Scholar] [CrossRef]
- Boucheron, L.E.; Creusere, C.D. Lossless wavelet-based compression of digital elevation maps for fast and efficient search and retrieval. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1210–1214. [Google Scholar] [CrossRef]
- Wurm, K.M.; Hornung, A.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: A probabilistic, flexible, and compact 3D map representation for robotic systems. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA) Workshop on Best Practice in 3D Perception And Modeling for Mobile Manipulation, Anchorage, Alaska, 4–8 May 2010; pp. 1210–1214. [Google Scholar]
- Fridovich-Keil, D.; Nelson, E.; Zakhor, A. AtomMap: A probabilistic amorphous 3D map representation for robotics and surface reconstruction. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3110–3117. [Google Scholar]
- Schreier, M.; Willert, V.; Adamy, J. Compact Representation of Dynamic Driving Environments for ADAS by Parametric Free Space and Dynamic Object Maps. IEEE Trans. Intell. Transp. Syst. 2016, 17, 367–384. [Google Scholar] [CrossRef]
- Wyeth, G.; Milford, M. Spatial cognition for robots. IEEE Robot. Automat. Mag. 2009, 16, 24–32. [Google Scholar] [CrossRef]
- Lindemann, S.R.; Lavalle, S.M. Simple and Efficient Algorithms for Computing Smooth, Collision-free Feedback Laws Over Given Cell Decompositions. Int. J. Rob. Res. 2009, 28, 600–621. [Google Scholar] [CrossRef] [Green Version]
- Mozaffari, M.; Taleb-Zadeh-Kasgari, A.; Saad, W.; Bennis, M.; Debbah, M. Beyond 5G With UAVs: Foundations of a 3D Wireless Cellular Network. IEEE Trans. Wireless Commun. 2019, 18, 357–372. [Google Scholar] [CrossRef] [Green Version]
- Falanga, D.; Kim, S.; Scaramuzza, D. How Fast Is Too Fast? The Role of Perception Latency in High-Speed Sense and Avoid. IEEE Robot. Autom. Lett. 2019, 4, 1884–1891. [Google Scholar] [CrossRef]
- Kumar, V.; Michael, N. Opportunities and challenges with autonomous micro aerial vehicles. Int. J. Robot. Res. 2012, 31, 1279–1291. [Google Scholar] [CrossRef]
- Petres, C.; Pailhas, Y.; Patron, P.; Petillot, Y.; Evans, J.; Lane, D. Path planning for autonomous underwater vehicles. IEEE Trans. Robot. 2007, 23, 331–341. [Google Scholar] [CrossRef]
- Ghosh, S.; Biswas, J. Joint perception and planning for efficient obstacle avoidance using stereo vision. In Proceedings of the 2017 International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1026–1031. [Google Scholar]
- Cordts, M.; Rehfeld, T.; Schneider, L.; Pfeiffer, D.; Enzweiler, M.; Roth, S.; Pollefeys, M.; Franke, U. The Stixel World: A medium-level representation of traffic scenes. Image. Vis. Comput. 2017, 68, 40–52. [Google Scholar] [CrossRef] [Green Version]
- Nashed, S.; Biswas, J. Curating Long-Term Vector Maps. In Proceedings of the 2016 International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4643–4648. [Google Scholar]
- Pham, H.H.; Le, T.L.; Vuillerme, N. Real-Time Obstacle Detection System in Indoor Environment for the Visually Impaired Using Microsoft Kinect Sensor. J. Sens. 2015, 2016, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Wu, H.; Xu, Z.; Min, H. Omni-Directional Obstacle Detection for Vehicles Based on Depth Camera. IEEE Access 2020, 8, 93733–93748. [Google Scholar] [CrossRef]
- Zhang, J.; Gui, M.; Wang, Q.; Liu, R.; Xu, J.; Chen, S. Hierarchical Topic Model Based Object Association for Semantic SLAM. IEEE Trans. Visual. Comput. Graphics 2019, 25, 3052–3062. [Google Scholar] [CrossRef]
- Andert, F.; Adolf, F.; Goormann, L.; Dittrich, J. Mapping and path planning in complex environments: An obstacle avoidance approach for an unmanned helicopter. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 745–750. [Google Scholar]
- Redondo, E.L.; Martinez-Marin, T. A compact representation of the environment and its frontiers for autonomous vehicle navigation. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gotenburg, Sweden, 11–14 June 2016; pp. 851–857. [Google Scholar]
- Liu, M.; Li, D.; Chen, Q.; Zhou, J.; Meng, K.; Zhang, S. Sensor Information Retrieval From Internet of Things: Representation and Indexing. IEEE Access 2018, 6, 36509–36521. [Google Scholar] [CrossRef]
- Ryde, J.; Dhiman, V.; Platt, R. Voxel planes: Rapid visualization and meshification of point cloud ensembles. In Proceedings of the 2013 International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 3731–3737. [Google Scholar]
- Pham, T.T.; Eich, M.; Reid, I.; Wyeth, G. Geometrically consistent plane extraction for dense indoor 3D maps segmentation. In Proceedings of the 2016 International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 4199–4204. [Google Scholar]
- Qian, X.; Ye, C. NCC-RANSAC: A Fast Plane Extraction Method for 3-D Range Data Segmentation. IEEE Trans. Cybern. 2014, 44, 2771–2783. [Google Scholar] [CrossRef]
- Ma, L.; Kerl, C.; Stückler, J.; Cremers, D. CPA-SLAM: Consistent plane-model alignment for direct RGB-D SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1285–1291. [Google Scholar]
- Ling, Y.; Shen, S. Building maps for autonomous navigation using sparse visual SLAM features. In Proceedings of the 2017 International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1374–1381. [Google Scholar]
- Wang, R.; Peethambaran, J.; Chen, D. LiDAR Point Clouds to 3-D Urban Models: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 606–627. [Google Scholar] [CrossRef]
- Shahzad, M.; Zhu, X.X. Automatic Detection and Reconstruction of 2-D/3-D Building Shapes From Spaceborne TomoSAR Point Clouds. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1292–1310. [Google Scholar] [CrossRef] [Green Version]
- Lafarge, F.; Keriven, R.; Brédif, M.; Vu, H. A Hybrid Multiview Stereo Algorithm for Modeling Urban Scenes. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 5–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nan, L.; Wonka, P. PolyFit: Polygonal Surface Reconstruction from Point Clouds. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2372–2380. [Google Scholar]
- Foix, S.; Alenya, G.; Torras, C. Lock-in Time-of-Flight (ToF) Cameras: A Survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, X.T.; Dinh, V.L.; Lee, H.; Kim, H. A High-Definition LIDAR System Based on Two-Mirror Deflection Scanners. IEEE Sens. J. 2018, 18, 559–568. [Google Scholar] [CrossRef]
- Jones, M.C.; Marron, J.S.; Sheather, S.J. A Brief Survey of Bandwidth Selection for Density Estimation. J. Am. Stat. Assoc. 1996, 91, 401–407. [Google Scholar] [CrossRef]
- Mallick, T.; Das, P.P.; Majumdar, A.K. Characterizations of Noise in Kinect Depth Images: A Review. IEEE Sens. J. 2014, 14, 1731–1740. [Google Scholar] [CrossRef]
- Nguyen, V.; Martinelli, A.; Tomatis, N.; Siegwart, R. A comparison of line extraction algorithms using 2D laser rangefinder for indoor mobile robotics. In Proceedings of the 2005 International Conference on Intelligent Robots and Systems (IROS), Edmonton, AB, Canada, 2–6 August 2005; pp. 1929–1934. [Google Scholar]
- Shah, S.; Dey, D.; Lovett, C.; Kapoor, A. AirSim: High-Fidelity visual and physical simulation for autonomous vehicles. In Proceedings of the 2017 International Conference on Field and Service Robotics, ETH Zürich, Switzerland, 12–15 September 2017; pp. 621–635.
- LaValle, S.M.; Kuffner, J.J. Rapidly-exploring Random Trees: Progress and prospects. In Proceedings of the Fourth Workshop on the Algorithmic Foundations of Robotics, Dartmouth, MA, USA, 16–18 March 2001; pp. 293–308. [Google Scholar]
- Kavraki, L.E.; Svestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Trans. Robot. Automat. 1996, 12, 566–580. [Google Scholar] [CrossRef] [Green Version]


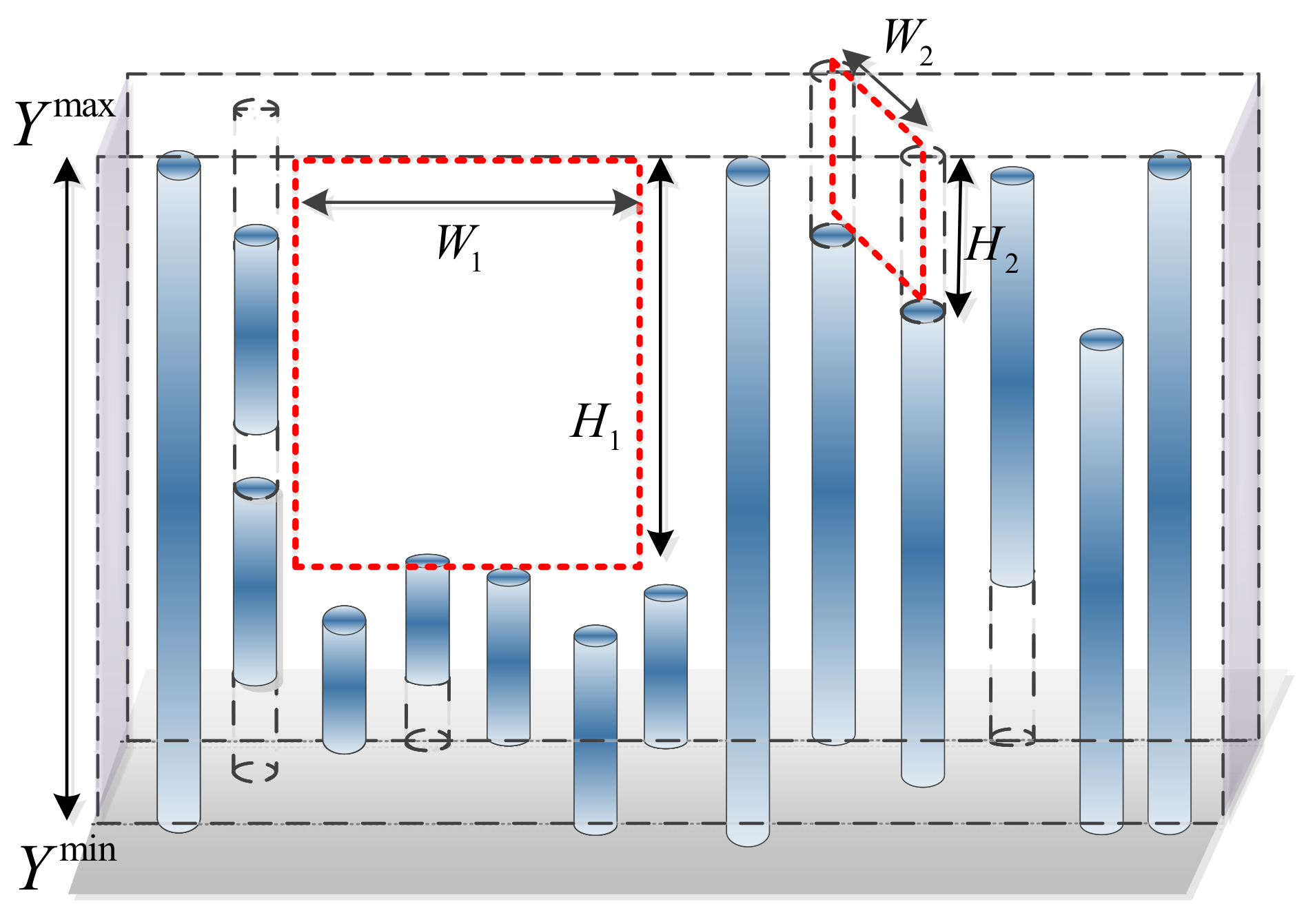





| Vertical rectangle | |
| The parameter of the rectangle | |
| , , and | The pitch, roll, and yaw angles |
| The normalized disparity data | |
| Focal length | |
| The Gaussian kernel function | |
| The probability density function in column u | |
| The minimum threshold of the probability density function | |
| The center of the ith peak | |
| The width of the ith sliding window | |
| The height of the ith sliding window | |
| The minimum recognizable obstacle height | |
| The minimum height to the passable region for the UAV | |
| The minimum width to the passable region for the UAV | |
| Estimated disparity value | |
| The rth cluster of the vertical strips |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng , K.; Li , D.; He , X.; Liu , M.; Song , W. Real-Time Compact Environment Representation for UAV Navigation. Sensors 2020, 20, 4976. https://doi.org/10.3390/s20174976
Meng K, Li D, He X, Liu M, Song W. Real-Time Compact Environment Representation for UAV Navigation. Sensors. 2020; 20(17):4976. https://doi.org/10.3390/s20174976
Chicago/Turabian StyleMeng , Kaitao, Deshi Li , Xiaofan He , Mingliu Liu , and Weitao Song . 2020. "Real-Time Compact Environment Representation for UAV Navigation" Sensors 20, no. 17: 4976. https://doi.org/10.3390/s20174976
APA StyleMeng , K., Li , D., He , X., Liu , M., & Song , W. (2020). Real-Time Compact Environment Representation for UAV Navigation. Sensors, 20(17), 4976. https://doi.org/10.3390/s20174976





