Bloch Surface Wave Resonance Based Sensors as an Alternative to Surface Plasmon Resonance Sensors
Abstract
:1. Introduction
2. Background
2.1. Optical Response Computation Method
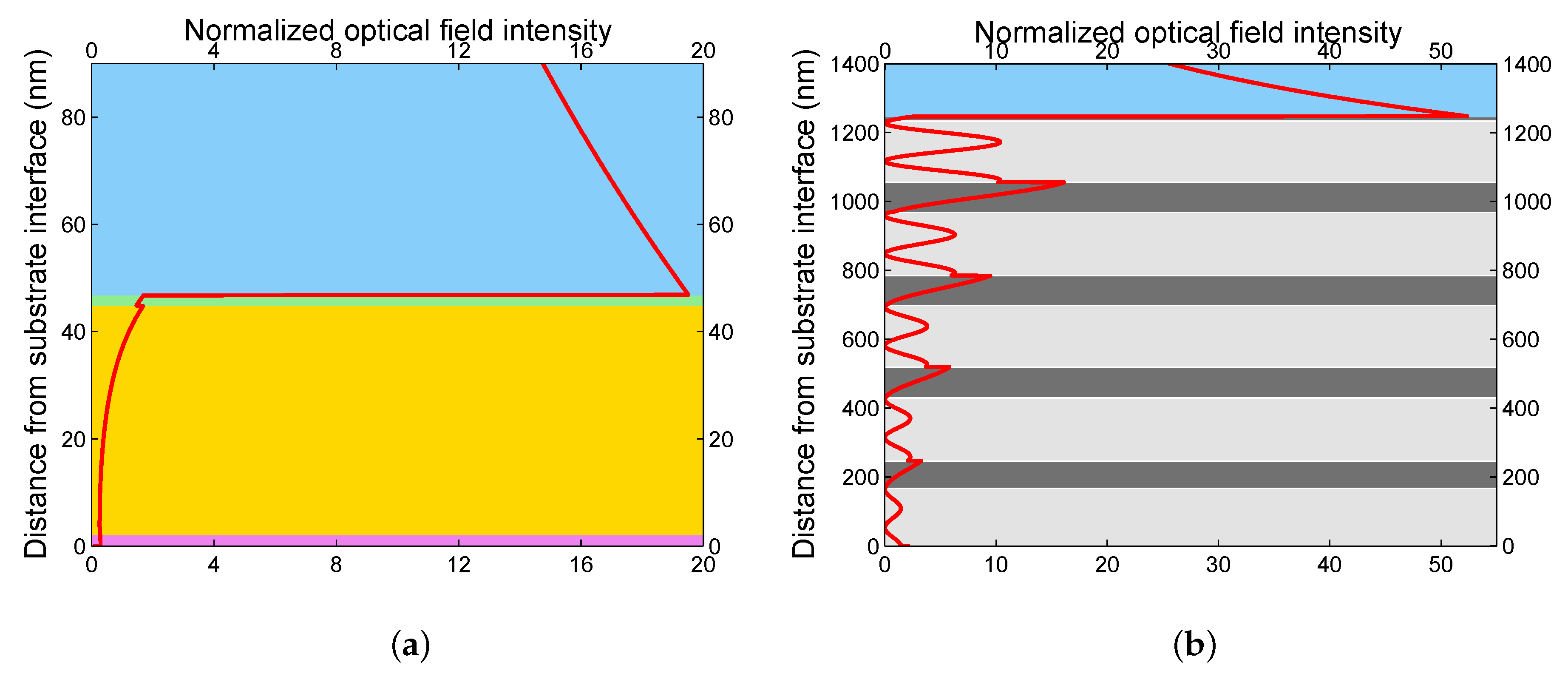
2.2. SPR Structure
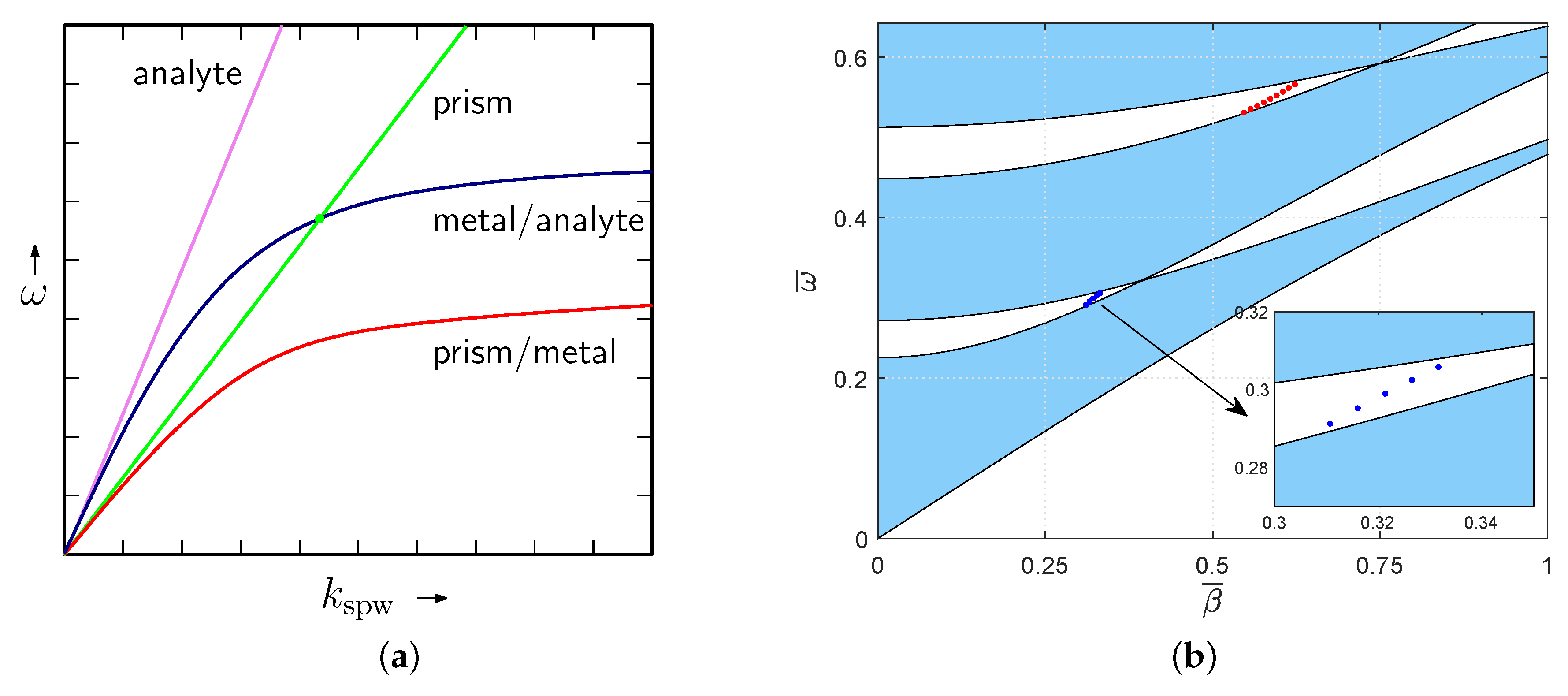
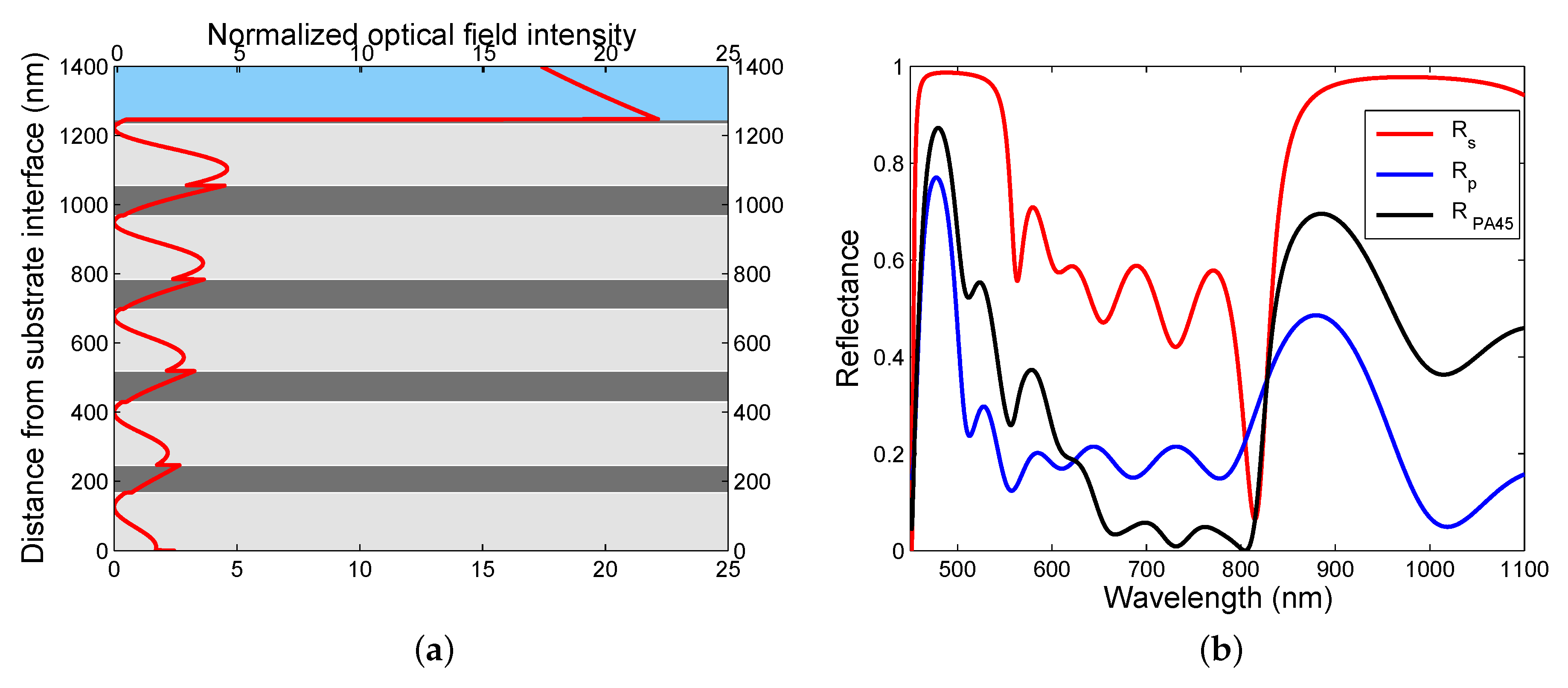
2.3. Periodic Multilayer Structure
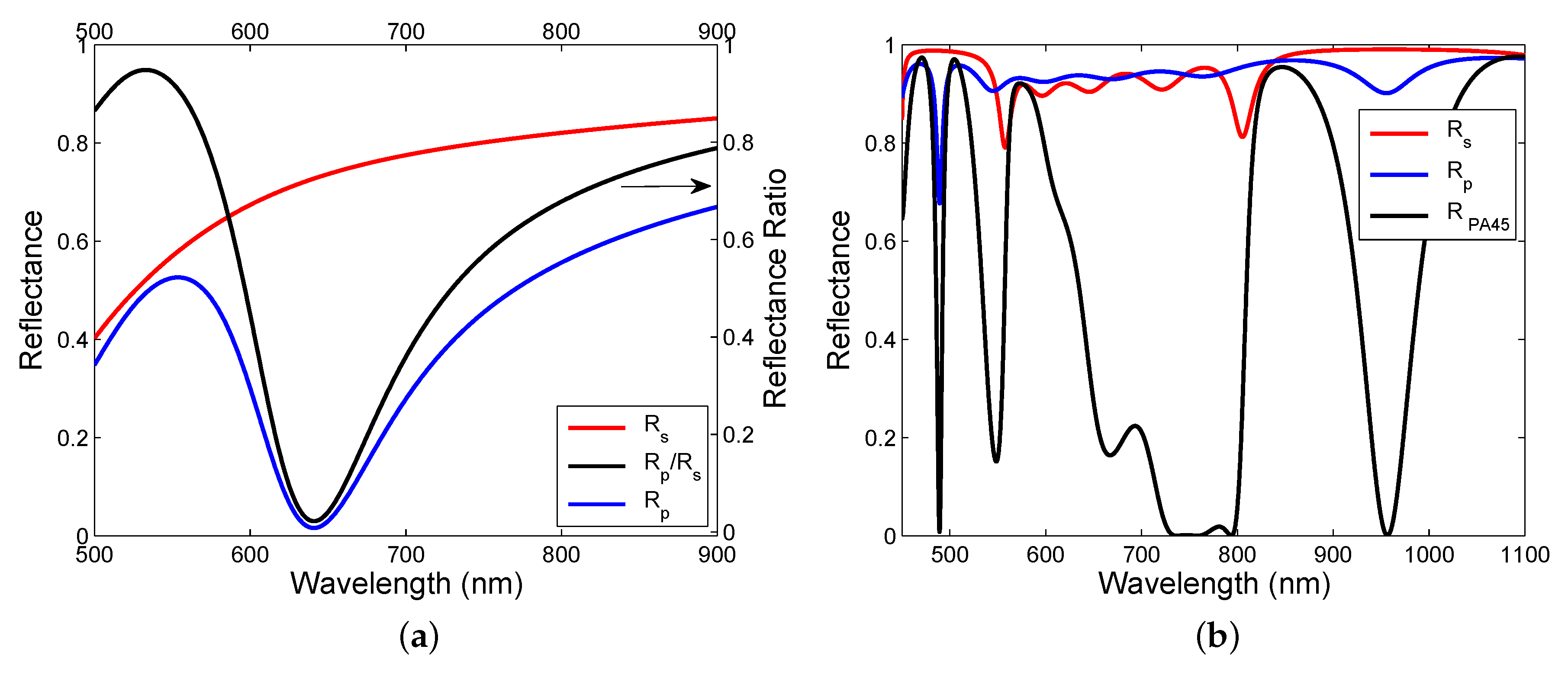
2.4. Reflectance Responses
3. Experimental Setup
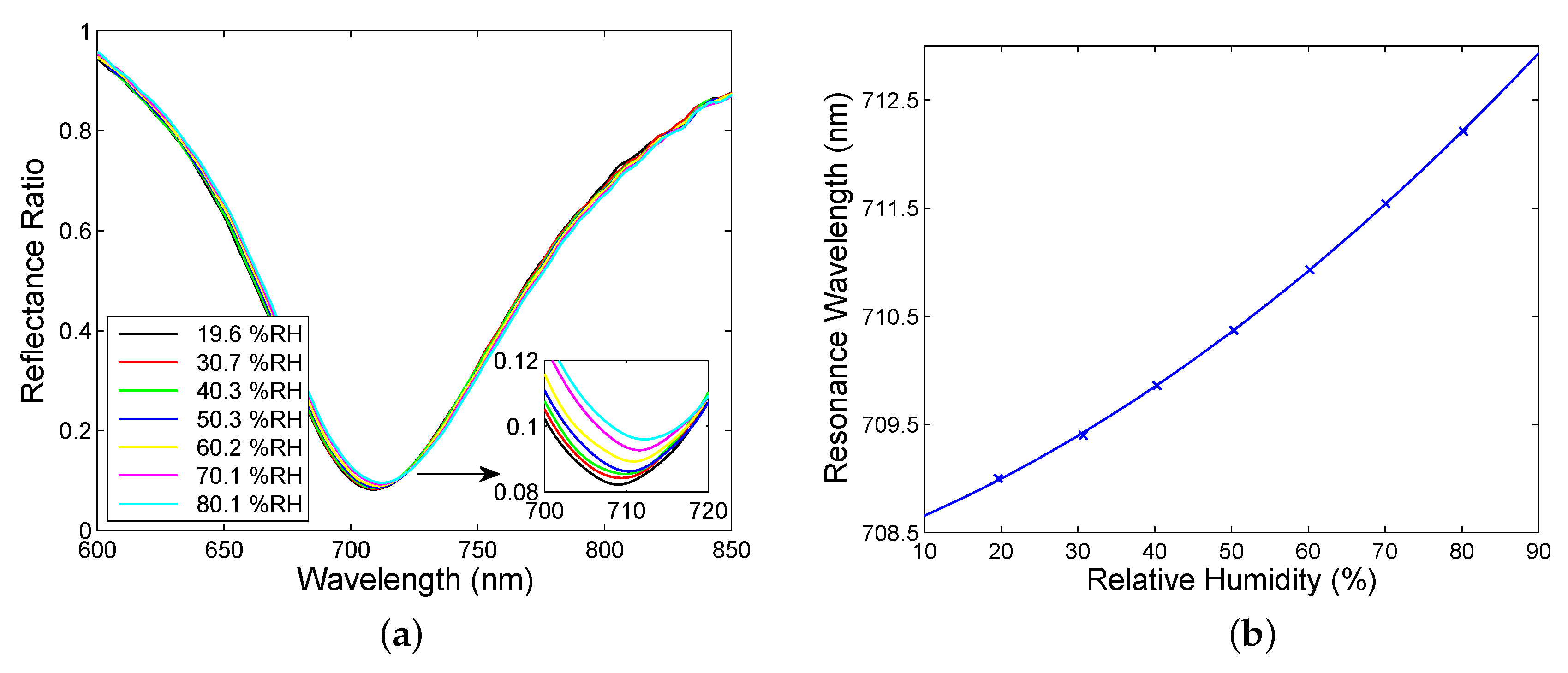
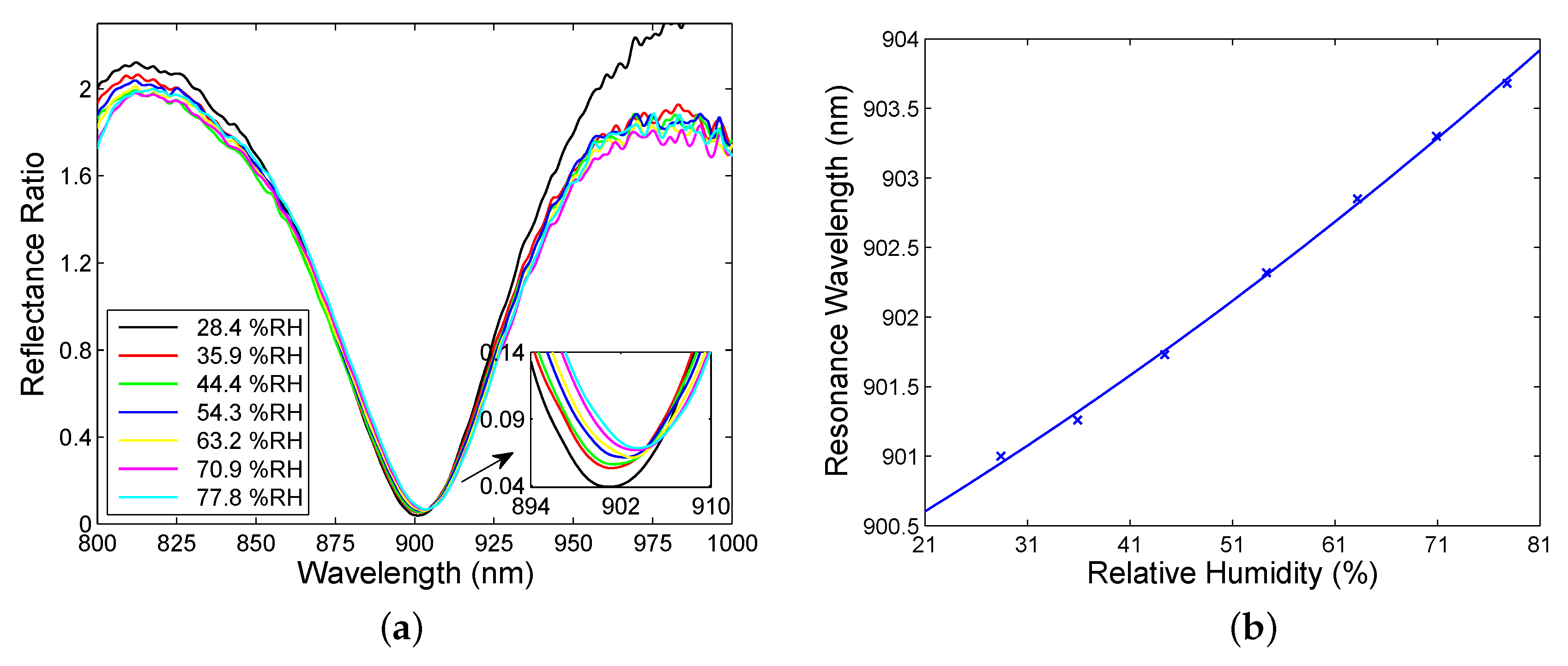
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kretschmann, E.; Raether, H. Radiative decay of nonradiative surface plasmons excited by light. Z. Naturforsch. 1968, A23, 2135–2136. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings; Springer: New York, NY, USA, 1988. [Google Scholar]
- Manuel, M.; Vidal, B.; Lopéz, R.; Alegret, S.; Alonso-Chamarro, J.; Garces, I.; Mateo, J. Determination of probable alcohol yield in musts by means of an SPR optical sensor. Sens. Actuators B Chem. 1993, 11, 455–459. [Google Scholar] [CrossRef]
- Homola, J. Surface Plasmon Resonance Based Sensors; Springer: New York, NY, USA, 2006. [Google Scholar]
- Abdulhalim, I.; Zourob, M.; Lakhtakia, A. Surface plasmon resonance sensors—A mini review. Electromagnetics 2008, 28, 213–242. [Google Scholar] [CrossRef]
- Gwon, H.R.; Lee, S.H. Spectral and angular responses of surface plasmon resonance based on the Kretschmann prism configuration. Mater. Trans. 2010, 51, 1150–1155. [Google Scholar] [CrossRef] [Green Version]
- Watad, I.; Abdulhalimn, I. Spectropolarimetric surface plasmon resonance sensor and the selection of the best polarimetric function. IEEE J. Sel. Top. Quant. Electron. 2017, 23, 4600609. [Google Scholar] [CrossRef]
- Pitarke, J.M.; Silkin, V.M.; Chulkov, E.V.; Echenique, P.M. Theory of surface plasmons and surface-plasmon polaritons. Rep. Prog. Phys. 2007, 70, 1–87. [Google Scholar] [CrossRef]
- Homola, J.; Yee, S.; Gauglitz, G. Surface plasmon resonance sensors: Review. Sens. Actuators B 1999, 54, 3–15. [Google Scholar] [CrossRef]
- Nikitin, P.; Beloglazov, A.; Kochergin, V.; Valeiko, M.; Ksenevich, T. Surface plasmon resonance interferometry for biological and chemical sensing. Sens. Actuators B Chem. 1999, 54, 43–50. [Google Scholar] [CrossRef]
- Deng, S.; Wang, P.; Yu, X. Phase-sensitive surface plasmon resonance sensors: Recent progress and future prospects. Sensors 2017, 17, 2819. [Google Scholar] [CrossRef] [Green Version]
- Liedberg, B.; Nylander, C.; Lundström, I. Principles of biosensing with an extended coupling matrix and surface plasmon resonance. Sens. Actuators B Chem. 1993, 11, 63–72. [Google Scholar] [CrossRef]
- Chiang, H.; Yeh, H.; Chen, C.; Wu, J.; Su, S.; Chang, R.; Wu, Y.; Tsai, D.; Jen, S.; Leung, P. Surface plasmon resonance monitoring of temperature via phase measurement. Opt. Commun. 2004, 241, 409–418. [Google Scholar] [CrossRef]
- Ho, H.; Law, W.; Wu, S.; Liu, X.; Wong, S.; Lin, C.; Kong, S.K. Phase-sensitive surface plasmon resonance biosensor using the photoelastic modulation technique. Sens. Actuators B Chem. 2006, 114, 80–84. [Google Scholar] [CrossRef]
- Dostálek, J.; Vaisocherova, H.; Homola, J. Multichannel surface plasmon resonance biosensor with wavelength division multiplexing. Sens. Actuators B Chem. 2005, 108, 758–764. [Google Scholar] [CrossRef]
- Yu, X.; Ding, X.; Liu, F.; Wei, X.; Wang, D. A surface plasmon resonance interferometer based on spatial phase modulation for protein array detection. Meas. Sci. Technol. 2008, 19, 015301. [Google Scholar] [CrossRef]
- Kabashin, A.; Patskovsky, S.; Grigorenko, A. Phase and amplitude sensitivities in surface plasmon resonance bio and chemical sensing. Opt. Express 2009, 17, 21191–21204. [Google Scholar] [CrossRef]
- Hsu, S.H.; Lin, Y.Y.; Lu, S.H.; Tsai, I.F.; Lu, Y.T.; Ho, H.T. Mycobacterium tuberculosis DNA detection dsing durface plasmon resonance modulated by telecommunication wavelength. Sensors 2014, 14, 458–467. [Google Scholar] [CrossRef] [Green Version]
- Ng, S.; Wu, C.; Wu, S.; Ho, H. White-light spectral interferometry for surface plasmon resonance sensing applications. Opt. Express 2011, 19, 4521–4527. [Google Scholar] [CrossRef]
- Shalabney, A.; Abdulhalim, I. Figure-of-merit enhancement of surface plasmon resonance sensors in the spectral interrogation. Opt. Lett. 2012, 37, 1175–1177. [Google Scholar] [CrossRef]
- Hlubina, P.; Duliakova, M.; Kadulova, M.; Ciprian, D. Spectral interferometry-based surface plasmon resonance sensor. Opt. Commun. 2015, 354, 240–245. [Google Scholar] [CrossRef]
- Hlubina, P.; Ciprian, D. Spectral phase shift of surface plasmon resonance in the Kretschmann configuration: Theory and experiment. Plasmonics 2017, 12, 1071–1078. [Google Scholar] [CrossRef]
- Rifat, A.A.; Rahmani, M.; Xu, L.; Miroshnichenko, A.E. Hybrid Metasurface Based Tunable Near-Perfect Absorber and Plasmonic Sensor. Materials 2018, 11, 1091. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chlebus, R.; Chylek, J.; Ciprian, D.; Hlubina, P. Surface plasmon resonance based measurement of the dielectric function of a thin metal film. Sensors 2018, 18, 3693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, D.; Loo, J.F.C.; Chen, J.; Yam, Y.; Chen, S.C.; He, H.; Kong, S.K.; Ho, H.P. Recent advances in surface plasmon resonance imaging sensors. Sensors 2019, 19, 1266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hlubina, P.; Urbancova, P.; Pudis, D.; Goraus, M.; Jandura, D.; Ciprian, D. Ultrahigh-sensitive plasmonic sensing of gas using a two-dimensional dielectric grating. Opt. Lett. 2019, 44, 5602–5605. [Google Scholar] [CrossRef] [PubMed]
- Roh, S.; Chung, T.; Lee, B. Overview of the characteristics of micro- and nanostructured surface plasmon resonance sensors. Sensors 2011, 11, 1565–1588. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klantsataya, E.; Jia, P.; Ebendorff-Heidepriem, H.; Monro, T.M.; François, A. Plasmonic Fiber Optic Refractometric Sensors: From Conventional Architectures to Recent Design Trends. Sensors 2017, 17, 12. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.K.; Pandey, A.K.; Kaur, B. A Review of advancements (2007–2017) in plasmonics-based optical fiber sensors. Opt. Fiber Technol. 2018, 43, 20–34. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]
- Ciprian, D.; Hlubina, P. Theoretical model of the influence of oxide overlayer thickness on the performance of a surface plasmon fibre-optic sensor. Meas. Sci. Technol. 2013, 24, 025105. [Google Scholar] [CrossRef]
- Hlubina, P.; Kadulova, M.; Ciprian, D.; Sobota, J. Reflection-based fibre-optic refractive index sensor using surface plasmon resonance. J. Europ. Opt. Soc. Rap. Publ. 2014, 9, 14033. [Google Scholar] [CrossRef] [Green Version]
- Yeh, P.; Yariv, A.; Cho, A.Y. Optical surface waves in periodic layered media. Appl. Phys. Lett. 1978, 32, 104–105. [Google Scholar] [CrossRef] [Green Version]
- Meade, R.D.; Brommer, K.D.; Rappe, A.M.; Joannopoulos, J.D. Electromagnetic Bloch waves at the surface of a photonic crystal. Phys. Rev. B 1991, 44, 10961–10964. [Google Scholar] [CrossRef] [PubMed]
- Robertson, W.M.; Arjavalingam, G.; Meade, R.D.; Brommer, K.D.; Rappe, A.M.; Joannopoulos, J.D. Observation of surface photons on periodic dielectric arrays. Opt. Lett. 1993, 18, 528–530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robertson, W.M.; May, M.S. Surface electromagnetic wave excitation on one-dimensional photonic band-gap arrays. Appl. Phys. Lett. 1999, 74, 1800–1802. [Google Scholar] [CrossRef]
- Ma, J.; Kang, X.B.; Wang, Z.G. Sensing performance optimization of the Bloch surface wave biosensor based on the Bloch impedance-matching method. Opt. Lett. 2019, 43, 5375–5378. [Google Scholar] [CrossRef]
- Guillermain, E.; Lysenko, V.; Orobtchouk, R.; Benyattou, T.; Roux, S.; Pillonnet, A.; Perriat, P. Bragg surface wave device based on porous silicon and its application for sensing. Appl. Phys. Lett. 2007, 90, 241116. [Google Scholar] [CrossRef]
- Konopsky, V.N.; Alieva, E.V. Photonic crystal surface waves for optical biosensors. Anal. Chem. 2007, 79, 4729–4735. [Google Scholar] [CrossRef]
- Giorgis, F.; Descrovi, E.; Summonte, C.; Dominici, L.; Michelotti, F. Experimental determination of the sensitivity of Bloch Surface Waves based sensors. Opt. Express 2010, 18, 8087–8093. [Google Scholar] [CrossRef]
- Danz, N.; Sinibaldi, A.; Michelotti, F.; Descrovi, E.; Munzert, P.; Schulz, U.; Sonntag, F. Improving the sensitivity of optical biosensors by means of Bloch surface waves. Biomed. Tech. 2012, 57, 584–587. [Google Scholar] [CrossRef]
- Konopsky, V.N.; Karakouza, T.; Alieva, E.V.; Vicario, C.; Sekatskii, S.K.; Dietler, G. Plasmonic Fiber Optic Refractometric Sensors: From Conventional Architectures to Recent Design Trends. Sensors 2013, 13, 2566–2578. [Google Scholar] [CrossRef] [Green Version]
- Sinibaldi, A.; Danz, N.; Descrovi, E.; Munzert, P.; Schulz, U.; Sonntag, F.; Dominici, L.; Michelotti, F. Direct comparison of the performance of Bloch surface wave and surface plasmon polariton sensors. Sens. Actuators B Chem. 2012, 174, 292–298. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, D.; Wang, P.; Ming, H.; Lakowicz, J.R. Strong Polarization Transformation of Bloch Surface Waves. Phys. Rev. Appl. 2018, 9, 024008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liscidini, M.; Sipe, J.E. Analysis of Bloch-surface-wave assisted diffraction-based biosensors. J. Opt. Soc. Am. B 2009, 26, 279–289. [Google Scholar] [CrossRef]
- Li, Y.; Yang, T.; Song, S.; Pang, Z.; Du, G. Phase properties of Bloch surface waves and their sensing applications. Appl. Phys. Lett. 2013, 103, 041116. [Google Scholar] [CrossRef]
- Sinibaldi, A.; Rizzo, R.; Figliozzi, G.; Descrovi, E.; Danz, N.; Munzert, P.; Anopchenko, A.; Michelotti, F. A full ellipsometric approach to optical sensing with Bloch surface waves on photonic crystals. Opt. Express 2013, 21, 23331–23344. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yang, T.; Pang, Z.; Du, G.; Song, S. Phase-sensitive Bloch surface wave sensor based on variable angle spectroscopic ellipsometry. Opt. Express 2014, 22, 21403–21410. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Zheng, Z.; Cheng, M.; Kong, W.; Liu, K. Polarimetric-Phase-Enhanced Intensity Interrogation Scheme for Surface Wave Optical Sensors with Low Optical Loss. Sensors 2018, 18, 3262. [Google Scholar] [CrossRef] [Green Version]
- Farmer, A.; Friedli, A.C.; Wright, S.M.; Robertson, W.M. Biosensing using surface electromagnetic waves in photonic band gap multilayers. Sens. Actuators B Chem. 2012, 173, 79–84. [Google Scholar] [CrossRef]
- Kong, W.; Zheng, Z.; Wan, Y.; Li, S.; Liu, J. High-sensitivity sensing based on intensity-interrogated Bloch surface wave sensors. Sens. Actuators B Chem. 2014, 193, 467–471. [Google Scholar] [CrossRef]
- Kanga, X.B.; Wen, L.; Wang, Z.G. Design of guided Bloch surface wave resonance bio-sensors with high sensitivity. Opt. Commun. 2017, 383, 531–536. [Google Scholar] [CrossRef]
- Kovalevich, T.; Belharet, D.; Robert, L.; Ulliac, G.; Kim, M.S.; Herzig, H.P.; Grosjean, T.; Bernal, M.P. Bloch surface waves at the telecommunicationwavelength with Lithium Niobate as top layer forintegrated optics. Appl. Opt. 2019, 58, 1757–1762. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.L.; Song, J.F.; Li, X.B.; Feng, J.; Sun, H.B. Optical Tamm states enhanced broad-band absorption of organic solar cells. Appl. Phys. Lett. 2012, 101, 243901. [Google Scholar] [CrossRef] [Green Version]
- Auguié, B.; Fuertes, M.C.; Angelomié, P.C.; Abdala, N.L.; Illia, G.J.A.A.S.; Fainstein, A. Tamm Plasmon Resonance in Mesoporous Multilayers: Toward a Sensing Application. ACS Photonics 2014, 9, 775–780. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, K.; Giannini, V.; Li, X. Planar Hot-Electron Photodetection with Tamm Plasmons. ACS Nano 2017, 19, 1719–1727. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lereu, A.L.; Zerrad, M.; Passian, A.; Amra, C. Surface plasmons and Bloch surface waves: Towards optimized ultra-sensitive optical sensors. Appl. Phys. Lett. 2017, 111, 011107. [Google Scholar] [CrossRef]
- Qiao, H.; Guan, B.; Gooding, J.J.; Reece, P.J. Protease detection using a porous silicon based Bloch surface wave optical biosensor. Opt. Express 2010, 18, 15174–15182. [Google Scholar] [CrossRef]
- Rodriguez, G.A.; Ryckman, J.D.; Jiao, Y.; Weiss, S.M. A size selective porous silicon grating-coupled Bloch surface and sub-surface wave biosensor. Biosens. Bioelectron. 2014, 53, 486–493. [Google Scholar] [CrossRef]
- Gryga, M.; Vala, D.; Kolejak, P.; Gembalova, L.; Ciprian, D.; Hlubina, P. One-dimensional photonic crystal for Bloch surface waves and radiation modes based sensing. Opt. Mater. Express 2019, 9, 4009–4022. [Google Scholar] [CrossRef]
- Deng, C.Z.; Ho, Y.L.; Lee, Y.C.; Wang, Z.; Tai, Y.H.; Zyskowski, M.; Daiguji, H.; Delaunay, J.J. Two-pair multilayer Bloch surface wave platform in the near- and mid-infrared regions. Appl. Phys. Lett. 2019, 115, 091102. [Google Scholar] [CrossRef]
- Gryga, M.; Ciprian, D.; Hlubina, P. Sensing concept based on Bloch surface waves and wavelength interrogation. Opt. Lett. 2020, 45, 1096–1099. [Google Scholar] [CrossRef]
- Gan, S.; Wang, H.; Liang, J.; Dai, X.; Xiang, Y. Ultra-Sensitive Refractive Index Sensors Based on Bloch Surface Waves with Transition Metal Dichalcogenides. IEEE Sens. J. 2019, 19, 8675–8680. [Google Scholar] [CrossRef]
- Balevicius, Z.; Baskys, A. Optical Dispersions of Bloch Surface Waves and Surface Plasmon Polaritons: Towards Advanced Biosensors. Materials 2019, 12, 3147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, G.S.; Xiong, X.; Hu, S.; Shi, W.; Chen, Y.; Zhu, W.; Zheng, H.; Yu, J.; Azeman, N.H.; Luo, Y.; et al. Photonic cavity enhanced high-performance surface plasmon resonance biosensor. Photonics Res. 2020, 8, 448–456. [Google Scholar] [CrossRef]
- Tu, T.; Panf, F.; Zhu, S.; Cheng, J.; Liu, H.; Wen, J.; Wang, T. Excitation of Bloch surface wave on tapered fiber coated with one-dimensional photonic crystal for refractive index sensing. Opt. Express 2017, 25, 9019–9027. [Google Scholar] [CrossRef] [PubMed]
- Tan, X.J.; Zhu, X.S. Optical fiber sensor based on Bloch surface wave in photonic crystals. Opt. Express 2016, 24, 16016–16026. [Google Scholar] [CrossRef]
- Scaravilli, M.; Micco, A.; Castaldi, G.; Coppola, G.; Gioffre, M.; Iodice, M.; Ferrara, V.L.; Galdi, V.; Cusano, A. Excitation of Bloch Surface Waves on an Optical Fiber Tip. Adv. Opt. Mater. 2018, 2018, 1800477. [Google Scholar] [CrossRef]
- Gonzalez-Valencia, E.; Herrera, R.A.; Torres, P. Bloch surface wave resonance in photonic crystal fibers: Towards ultra-wide range refractive index sensors. Opt. Express 2019, 27, 8236–8545. [Google Scholar] [CrossRef]
- Bethune, D.S. Optical harmonic generation and mixing in multilayer media: Analysis using optical transfer matrix techniques. J. Opt. Soc. Am. B 1989, 6, 910–916. [Google Scholar] [CrossRef]
- Pettersson, L.A.A.; Roman, L.S.; Inganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; John Wiley and Sons: Somerset, NJ, USA, 2005. [Google Scholar]
- Di Palma, P.; Sansone, L.; Taddei, C.; Campopiano, S.; Iadiciccoi, A. Fiber optic probe based on self-assembled photonic crystal for relative humidity sensing. J. Lightwave Technol. 2019, 37, 4610–4618. [Google Scholar] [CrossRef]
- Kolpakov, S.A.; Gordon, N.T.; Mou, C.; Zhou, K. Toward a New Generation of Photonic Humidity Sensors. Sensors 2014, 14, 3986–4013. [Google Scholar] [CrossRef] [PubMed]
- Ascorbe, J.; Corres, J.M.; Arregu, F.J.; Matias, I.R. Recent developments in fiber optics humidity sensors. Sensors 2017, 17, 893. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehrabani, S.; Kwong, P.; Gupta, M.; Arman, A. Hybrid microcavity humidity sensor. Appl. Phys. Lett. 2013, 102, 241101. [Google Scholar] [CrossRef]
- Lee, K.J.; Wawro, D.; Priambodo, P.S.; Magnusson, R. Agarose-gel based guided-mode resonance humidity sensor. IEEE Sens. J. 2007, 7, 409–414. [Google Scholar] [CrossRef]
- Peng, J.; Wang, W.; Qu, Y.; Sun, T.; Lv, D.; Dai, J.; Yang, M. Thin films based one-dimensional photonic crystal for humidity detection. Sens. Actuators A Phys. 2017, 263, 209–215. [Google Scholar] [CrossRef]
- Fuentes, O.; Corres, J.M.; Matias, I.R.; Villar, I. Generation of Lossy Mode Resonances in Planar Waveguides Toward Development of Humidity Sensors. J. Lightwave Technol. 2019, 37, 2300–2306. [Google Scholar] [CrossRef]
- Bohorquez, D.L.; Villar, I.; Corres, J.M.; Matias, I.R. Thin films based one-dimensional photonic crystal for humidity detection. Sens. Actuators B Chem. 2020, 325, 128795. [Google Scholar]
- Bönsch, G.; Potulski, E. Measurement of the refractive index of air and comparison with modified Edlén’s formulae. Metrologia 1998, 35, 133–139. [Google Scholar] [CrossRef]
- Mathar, R.J. Refractive Index of Humid Air in the Infrared: Model Fits. J. Opt. A Pure Appl. Opt. 2007, 9, 470–477. [Google Scholar] [CrossRef]
- Alvarez-Herrero, A.; Fort, A.; Guerrero, H.; Bernabeu, E. Ellipsometric characterization and influence of relative humidity on TiO2 layers optical properties. Thin Solid Film 1999, 349, 212–219. [Google Scholar] [CrossRef]
- Robertson, W.M.; Wright, S.M.; Friedli, A.; Summers, J.; Kaszynski, A. Design and characterization of an ultra- low-cost 3D-printed optical sensor based on Bloch surface wave resonance. Biosens. Bioelectron. 2020, 5, 100049. [Google Scholar] [CrossRef]





| Drude Term | Value | Oscillator 1 | Value | Oscillator 2 | Value |
|---|---|---|---|---|---|
| Parameter | Parameter | Parameter | |||
| 1 | 8.88 | 1.70 | |||
| (nm) | 130.77 | (nm) | 255.5 | (nm) | 660.67 |
| (nm) | 6608.3 | (nm) | −29.73 | (nm) | −819.68 |
| Material | Method | RH Range | Sensitivity (nm/%RH) | Ref. |
|---|---|---|---|---|
| polymer coating | whispering gallery mode resonance | 0–60% | 0.013 | [77] |
| agarose gel | guided mode resonance | 20–80% | 0.150 | [78] |
| porous thin film | photonic crystal mode resonance | 11–84% | 0.296 | [79] |
| indium tin oxide | lossy mode resonance | 65–90% | 0.212 | [80] |
| copper oxide | lossy mode resonance | 30–90% | 0.636 | [81] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gryga, M.; Ciprian, D.; Hlubina, P. Bloch Surface Wave Resonance Based Sensors as an Alternative to Surface Plasmon Resonance Sensors. Sensors 2020, 20, 5119. https://doi.org/10.3390/s20185119
Gryga M, Ciprian D, Hlubina P. Bloch Surface Wave Resonance Based Sensors as an Alternative to Surface Plasmon Resonance Sensors. Sensors. 2020; 20(18):5119. https://doi.org/10.3390/s20185119
Chicago/Turabian StyleGryga, Michal, Dalibor Ciprian, and Petr Hlubina. 2020. "Bloch Surface Wave Resonance Based Sensors as an Alternative to Surface Plasmon Resonance Sensors" Sensors 20, no. 18: 5119. https://doi.org/10.3390/s20185119
APA StyleGryga, M., Ciprian, D., & Hlubina, P. (2020). Bloch Surface Wave Resonance Based Sensors as an Alternative to Surface Plasmon Resonance Sensors. Sensors, 20(18), 5119. https://doi.org/10.3390/s20185119





