Measuring Effects of Two-Handed Side and Anterior Load Carriage on Thoracic-Pelvic Coordination Using Wearable Gyroscopes
Abstract
:1. Introduction
2. Experiment 1
2.1. Materials and Methods
2.1.1. Participants
2.1.2. Experiment Procedure
2.1.3. Instrumentation
2.1.4. Data Processing and Dependent Measures
2.1.5. Statistical Analyses
2.2. Results
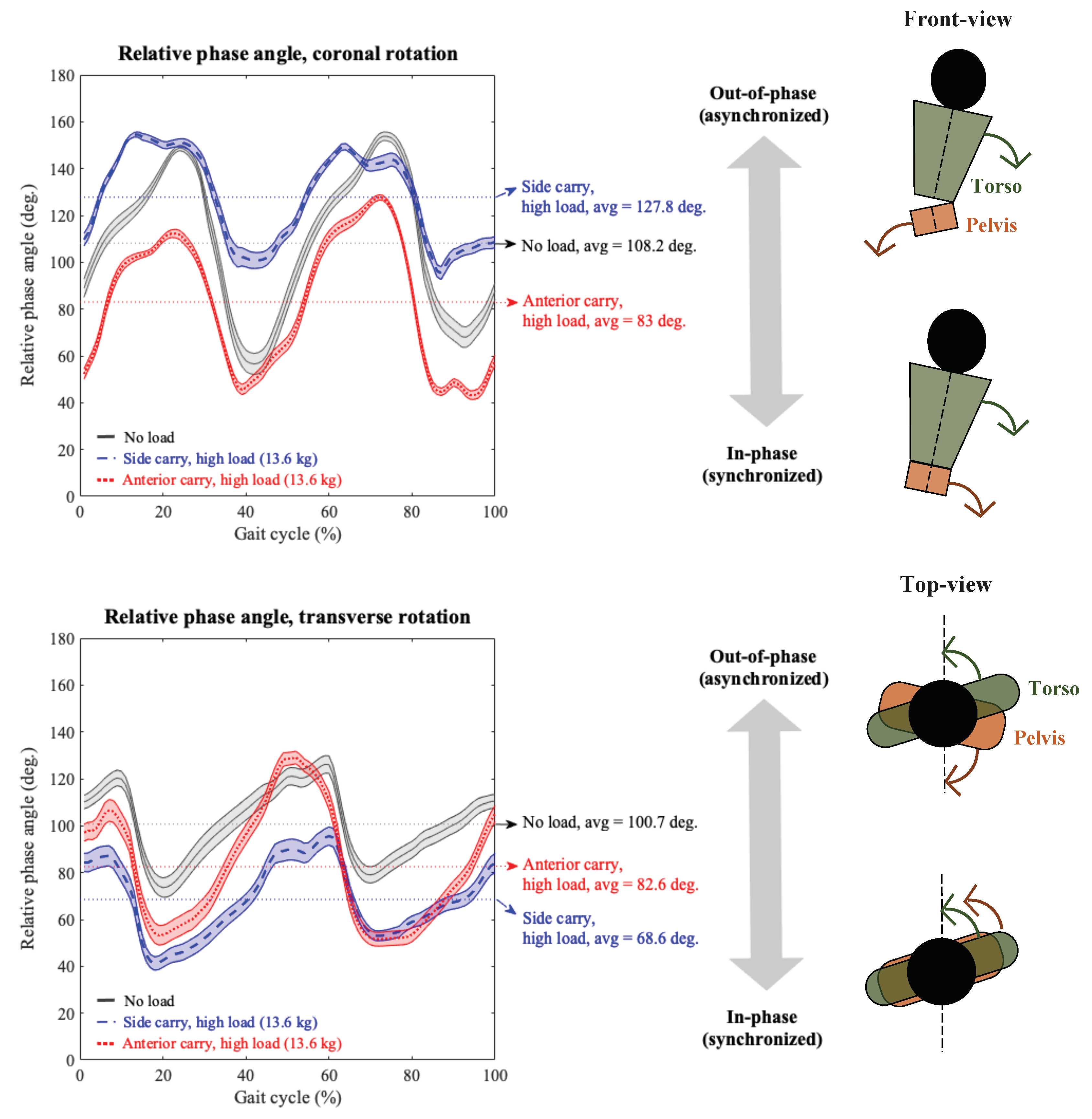
2.2.1. Torso and Pelvis Sway and Coordination in the Coronal Plane
2.2.2. Torso and Pelvis Sway and Coordination in the Transverse Plane
2.2.3. Torso and Pelvis Sway and Coordination in the Sagittal Plane
3. Experiment 2
3.1. Materials and Methods
3.1.1. Participants
3.1.2. Experiment Procedure
3.1.3. Instrumentation
3.1.4. Data Processing, Dependent Measures, and Statistical Analysis
3.2. Results
3.2.1. Torso and Pelvis Sway and Coordination in the Coronal Plane
3.2.2. Torso and Pelvis Sway and Coordination in the Transverse Plane
3.2.3. Torso and Pelvis Sway and Coordination in the Sagittal Plane
4. General Discussion
4.1. Analysis of Two-Handed Side Carry
4.2. Analysis of Two-Handed Anterior Carry
4.3. Study Contributions and Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Ethical Statement
Abbreviations
| IMU | Inertial Measurement Units |
| MMH | Manual Material Handling |
| MSD | Musculoskeletal Disorders |
| COM | Center of Mass |
Appendix A. Computing Temporal Gait Parameters Using Angular Velocity from a Shank-Mounted Gyroscope

Appendix B. Estimating Stride Length from Angular Velocity of the Right Shank and Thigh Recorded by Gyroscopes

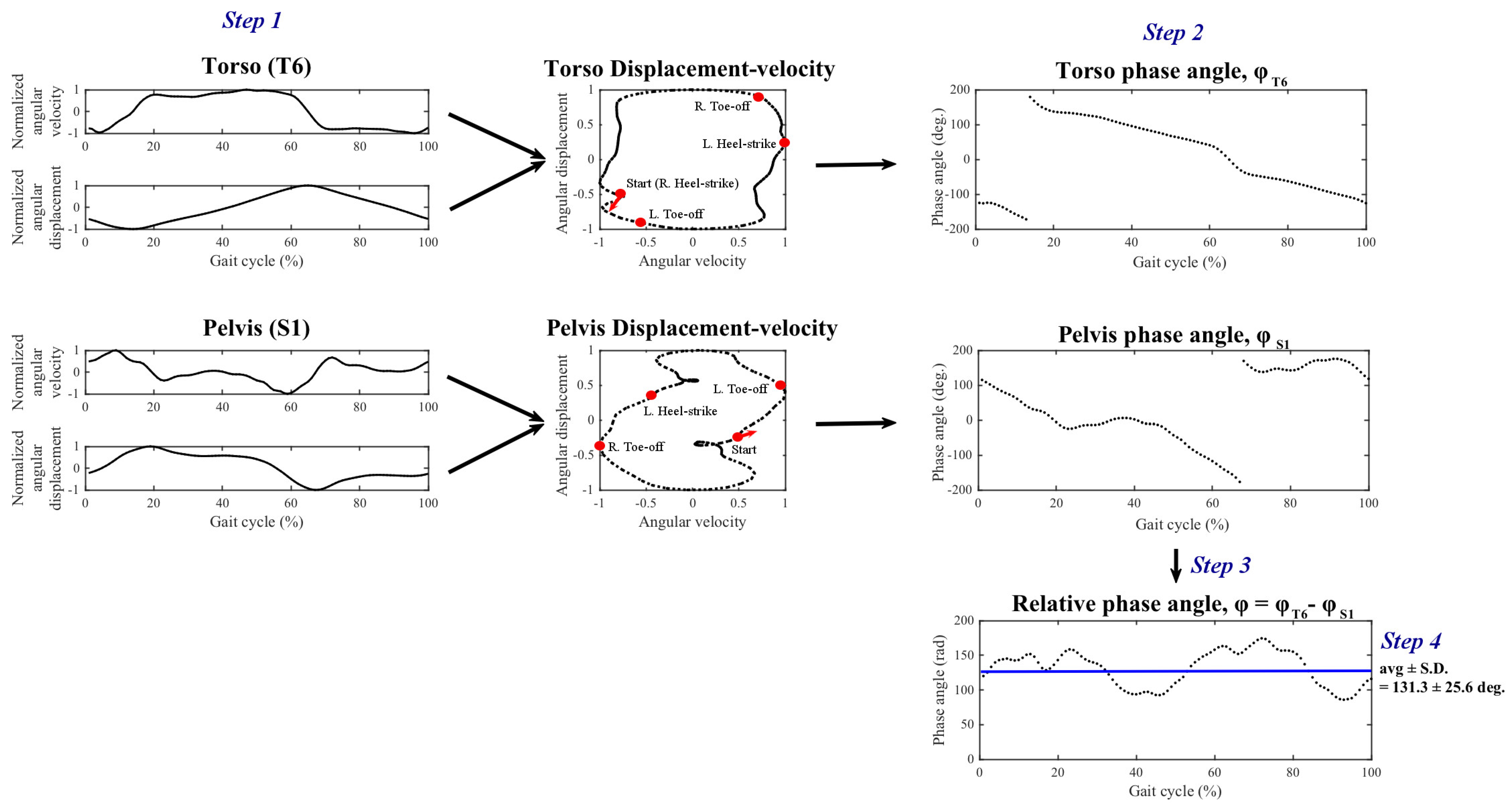
Appendix C. Algorithm for Calculating the Mean Thoracic-Pelvic Relative Phase Angle
References
- Orr, R.M.; Pope, R.R. Load Carriage: An Integrated Risk Management Approach. J. Strength Cond. Res. 2015, 29, S119–S128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, K.; Hur, P.; Rosengren, K.S.; Horn, G.P.; Hsiao-Wecksler, E.T. Effect of load carriage on gait due to firefighting air bottle configuration. Ergonomics 2010, 53, 882–891. [Google Scholar] [CrossRef] [PubMed]
- Anderson, A.; Meador, K.; McClure, L.; Makrozahopoulos, D.; Brooks, D.; Mirka, G. A biomechanical analysis of anterior load carriage. Ergonomics 2007, 50, 2104–2117. [Google Scholar] [CrossRef] [PubMed]
- Deros, B.M.; Daruis, D.D.; Ismail, A.R.; Sawal, N.A.; Ghani, J.A. Work-related musculoskeletal disorders among workers’ performing manual material handling work in an automotive manufacturing company. Am. J. Appl. Sci. 2010, 7, 1087. [Google Scholar] [CrossRef] [Green Version]
- Waters, T.R.; Putz-Anderson, V.; Baron, S. Methods for assessing the physical demands of manual lifting: A review and case study from warehousing. Am. Ind. Hyg. Assoc. J. 1998, 59, 871–881. [Google Scholar] [CrossRef]
- Lavender, S.A.; Marras, W.S.; Ferguson, S.A.; Splittstoesser, R.E.; Yang, G. Developing physical exposure-based back injury risk models applicable to manual handling jobs in distribution centers. J. Occup. Environ. Hyg. 2012, 9, 450–459. [Google Scholar] [CrossRef]
- Marras, W.S.; Lavender, S.A.; Ferguson, S.A.; Splittstoesser, R.E.; Yang, G. Quantitative biomechanical workplace exposure measures: Distribution centers. J. Electromyogr. Kinesiol. 2010, 20, 813–822. [Google Scholar] [CrossRef]
- Ciriello, V.M.; Snook, S.H.; Hashemi, L.; Cotnam, J. Distributions of manual materials handling task parameters. Int. J. Ind. Ergon. 1999, 24, 379–388. [Google Scholar] [CrossRef]
- Putz-Anderson, V.; Bernard, B.P.; Burt, S.E.; Cole, L.L.; Fairfield-Estill, C.; Fine, L.J.; Grant, K.A.; Gjessing, C.C.; Jenkins, L.; Hurrell, J.J., Jr. Musculoskeletal Disorders and Workplace Factors; National Institute for Occupational Safety and Health (NIOSH): Cincinnati, OH, USA, 1997.
- Bigos, S.J.; Spengler, D.; Martin, N.A.; Zeh, J.; Fisher, L.; Nachemson, A.; Wang, M. Back injuries in industry: A retrospective study. II. Injury factors. Spine 1986, 11, 246–251. [Google Scholar] [CrossRef]
- Simpson, K.M.; Munro, B.J.; Steele, J.R. Effect of load mass on posture, heart rate and subjective responses of recreational female hikers to prolonged load carriage. Appl. Ergon. 2011, 42, 403–410. [Google Scholar] [CrossRef]
- Bernard, B.P.; Putz-Anderson, V. Musculoskeletal Disorders and Workplace Factors; A Critical Review of Epidemiologic Evidence for Work-Related Musculoskeletal Disorders of the Neck, Upper Extremity, and Low Back; National Institute for Occupational Safety and Health, US Department of Health and Human Services: Washington, DC, USA, 1997.
- Van Vuuren, B.J.; Becker, P.J.; Van Heerden, H.J.; Zinzen, E.; Meeusen, R. Lower back problems and occupational risk factors in a South African steel industry. Am. J. Ind. Med. 2005, 47, 451–457. [Google Scholar] [CrossRef] [PubMed]
- LaFiandra, M.; Holt, K.G.; Wagenaar, R.C.; Obusek, J.P. Transverse plane kinetics during treadmill walking with and without a load. Clin. Biomech. 2002, 17, 116–122. [Google Scholar] [CrossRef]
- Nottrodt, J.W.; Manley, P. Acceptable loads and locomotor patterns selected in different carriage methods. Ergonomics 1989, 32, 945–957. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, T.; Hashimoto, M.; Koyanagi, M.; Hashizume, K. Asymmetric load-carrying in young and elderly women: Relationship with lower limb coordination. Gait Posture 2008, 28, 517–520. [Google Scholar] [CrossRef]
- Neumann, D.A.; Cook, T.M.; Sholty, R.L.; Sobush, D.C. An electromyographic analysis of hip abductor muscle activity when subjects are carrying loads in one or both hands. Phys. Ther. 1992, 72, 207–217. [Google Scholar] [CrossRef] [PubMed]
- DeVita, P.; Hong, D.; Hamill, J. Effects of asymmetric load carrying on the biomechanics of walking. J. Biomech. 1991, 24, 1119–1129. [Google Scholar] [CrossRef]
- Cook, T.M.; Neumann, D.A. The effects of load placement on the EMG activity of the low back muscles during load carrying by men and women. Ergonomics 1987, 30, 1413–1423. [Google Scholar] [CrossRef]
- McGill, S.M.; Marshall, L.; Andersen, J. Low back loads while walking and carrying: Comparing the load carried in one hand or in both hands. Ergonomics 2013, 56, 293–302. [Google Scholar] [CrossRef]
- Marras, W.S.; Granata, K.P. Changes in trunk dynamics and spine loading during repeated trunk exertions. Spine (Phila Pa 1976) 1997, 22, 2564–2570. [Google Scholar] [CrossRef]
- Rose, J.D.; Mendel, E.; Marras, W.S. Carrying and spine loading. Ergonomics 2013, 56, 1722–1732. [Google Scholar] [CrossRef]
- Zhang, X.A.; Ye, M.; Wang, C.T. Effect of unilateral load carriage on postures and gait symmetry in ground reaction force during walking. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Rohlmann, A.; Zander, T.; Graichen, F.; Schmidt, H.; Bergmann, G. How does the way a weight is carried affect spinal loads? Ergonomics 2014, 57, 262–270. [Google Scholar] [CrossRef] [PubMed]
- LaFiandra, M.; Wagenaar, R.C.; Holt, K.G.; Obusek, J.P. How do load carriage and walking speed influence trunk coordination and stride parameters? J. Biomech. 2003, 36, 87–95. [Google Scholar] [CrossRef]
- Goh, J.H.; Thambyah, A.; Bose, K. Effects of varying backpack loads on peak forces in the lumbosacral spine during walking. Clin. Biomech. 1998, 13, S26–S31. [Google Scholar] [CrossRef]
- Hong, Y.; Cheung, C.K. Gait and posture responses to backpack load during level walking in children. Gait Posture 2003, 17, 28–33. [Google Scholar] [CrossRef]
- Kinoshita, H. Effects of different loads and carrying systems on selected biomechanical parameters describing walking gait. Ergonomics 1985, 28, 1347–1362. [Google Scholar] [CrossRef]
- Qu, X.; Yeo, J.C. Effects of load carriage and fatigue on gait characteristics. J. Biomech. 2011, 44, 1259–1263. [Google Scholar] [CrossRef]
- Majumdar, D.; Pal, M.S.; Majumdar, D. Effects of military load carriage on kinematics of gait. Ergonomics 2010, 53, 782–791. [Google Scholar] [CrossRef]
- Pau, M.; Kim, S.; Nussbaum, M.A. Does load carriage differentially alter postural sway in overweight vs. normal-weight schoolchildren? Gait Posture 2012, 35, 378–382. [Google Scholar] [CrossRef]
- Cottalorda, J.; Rahmani, A.; Diop, M.; Gautheron, V.; Ebermeyer, E.; Belli, A. Influence of school bag carrying on gait kinetics. J. Pediatr. Orthop. B 2003, 12, 357–364. [Google Scholar]
- Ghori, G.M.U.; Luckwill, R.G. Responses of the lower limb to load carrying in walking man. Eur. J. Appl. Physiol. Occup. Physiol. 1985, 54, 145–150. [Google Scholar] [CrossRef] [PubMed]
- Burgess-Limerick, R.; Abernethy, B.; Neal, R.J. Relative phase quantifies interjoint coordination. J. Biomech. 1993, 26, 91–94. [Google Scholar] [CrossRef]
- Seay, J.F.; Van Emmerik, R.E.A.; Hamill, J. Low back pain status affects pelvis-trunk coordination and variability during walking and running. Clin. Biomech. 2011, 26, 572–578. [Google Scholar] [CrossRef] [PubMed]
- Van Emmerik, R.E.A.; Wagenaar, R.C. Effects of walking velocity on relative phase dynamics in the trunk in human walking. J. Biomech. 1996, 29, 1175–1184. [Google Scholar] [CrossRef]
- Whittle, M.W.; Levine, D. Three-dimensional relationships between the movements of the pelvis and lumbar spine during normal gait. Hum. Mov. Sci. 1999, 18, 681–692. [Google Scholar] [CrossRef]
- Graham, R.B.; Smallman, C.L.W.; Miller, R.H.; Stevenson, J.M. A dynamical systems analysis of assisted and unassisted anterior and posterior hand-held load carriage. Ergonomics 2015, 58, 480–491. [Google Scholar] [CrossRef]
- Mayagoitia, R.E.; Lotters, J.C.; Veltink, P.H.; Hermens, H. Standing balance evaluation using a triaxial accelerometer. Gait Posture 2002, 16, 55–59. [Google Scholar] [CrossRef]
- Faber, G.S.; Chang, C.C.; Rizun, P.; Dennerlein, J.T. A novel method for assessing the 3D orientation accuracy of inertial/magnetic sensors. J. Biomech. 2013, 46, 2745–2751. [Google Scholar] [CrossRef]
- Sabatini, A.M. Estimating three-dimensional orientation of human body parts by inertial/magnetic sensing. Sensors 2011, 11, 1489–1525. [Google Scholar] [CrossRef] [Green Version]
- Aminian, K.; Najafi, B.; Büla, C.; Leyvraz, P.F.; Robert, P. Spatio-temporal parameters of gait measured by an ambulatory system using miniature gyroscopes. J. Biomech. 2002, 35, 689–699. [Google Scholar] [CrossRef]
- Djuric, M. Automatic recognition of gait phases from accelerations of leg segments. In Proceedings of the 2008 9th Symposium on Neural Network Applications in Electrical Engineering, Belgrade, Serbia, 25–27 September 2008; pp. 121–124. [Google Scholar]
- Hanlon, M.; Anderson, R. Real-time gait event detection using wearable sensors. Gait Posture 2009, 30, 523–527. [Google Scholar] [CrossRef] [PubMed]
- Jasiewicz, J.M.; Allum, J.H.J.; Middleton, J.W.; Barriskill, A.; Condie, P.; Purcell, B.; Li, R.C.T. Gait event detection using linear accelerometers or angular velocity transducers in able-bodied and spinal-cord injured individuals. Gait Posture 2006, 24, 502–509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.W.; Mase, K.; Kogure, K. Detection of spatio-temporal gait parameters by using wearable motion sensors. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2005; pp. 6836–6839. [Google Scholar]
- Lim, S.; D’Souza, C. A narrative review on contemporary and emerging uses of inertial sensing in occupational ergonomics. Int. J. Ind. Ergon. 2020, 76, 102937. [Google Scholar] [CrossRef]
- Cohen, A.L.; Gjessing, C.C.; Fine, L.J.; Bernard, B.P.; McGlothlin, J.D. Elements of Ergonomics Programs: A Primer Based on Workplace Evaluations of Musculoskeletal Disorders; DIANE Publishing: Darby, PA, USA, 1997; Volume 97. [Google Scholar]
- Waters, T.R.; Putz-Anderson, V.; Garg, A. Applications Manual for the Revised NIOSH Lifting Equation; National Institute for Occupational Safety and Health, US Department of Health and Human Services: Washington, DC, USA, 1994.
- Madinei, S.; Ning, X. Effects of the weight configuration of hand load on trunk musculature during static weight holding. Ergonomics 2018, 61, 831–838. [Google Scholar] [CrossRef] [PubMed]
- Williamson, R.; Andrews, B.J. Detecting Absolute Human Knee Angle. Med Biol. Eng. Comput. 2001, 39, 294–302. [Google Scholar] [CrossRef]
- Moon, Y.; McGinnis, R.S.; Seagers, K.; Motl, R.W.; Sheth, N.; Wright, J.A., Jr.; Ghaffari, R.; Sosnoff, J.J. Monitoring gait in multiple sclerosis with novel wearable motion sensors. PLoS ONE 2017, 12, e0171346. [Google Scholar] [CrossRef] [PubMed]
- Salarian, A.; Russmann, H.; Vingerhoets, F.J.; Burkhard, P.R.; Aminian, K. Ambulatory monitoring of physical activities in patients with Parkinson’s disease. IEEE Trans. Biomed. Eng. 2007, 54, 2296–2299. [Google Scholar] [CrossRef]
- Snijders, T.A.B.; Bosker, R.J. Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling; Sage: Thousand Oaks, CA, USA, 1999. [Google Scholar]
- Maxwell Donelan, J.; Kram, R.; Arthur, D.K. Mechanical and metabolic determinants of the preferred step width in human walking. Proc. R. Soc. London. Ser. B Biol. Sci. 2001, 268, 1985–1992. [Google Scholar] [CrossRef] [Green Version]
- Dames, K.D.; Smith, J.D. Effects of load carriage and footwear on lower extremity kinetics and kinematics during overground walking. Gait Posture 2016, 50, 207–211. [Google Scholar] [CrossRef]
- Al-Obaidi, S.; Wall, J.C.; Al-Yaqoub, A.; Al-Ghanim, M. Basic gait parameters: A comparison of reference data for normal subjects 20 to 29 years of age from Kuwait and Scandinavia. J. Rehabil. Res. Dev. 2003, 40, 361–366. [Google Scholar] [CrossRef]
- Grieve, D.; Gear, R.J. The relationships between length of stride, step frequency, time of swing and speed of walking for children and adults. Ergonomics 1966, 9, 379–399. [Google Scholar] [CrossRef] [PubMed]
- Hirokawa, S. Normal gait characteristics under temporal and distance constraints. J. Biomed. Eng. 1989, 11, 449–456. [Google Scholar] [CrossRef]
- Wagenaar, R.C.; Beek, W.J. Hemiplegic gait: A kinematic analysis using walking speed as a basis. J. Biomech. 1992, 25, 1007–1015. [Google Scholar] [CrossRef]
- Sun, R.; Moon, Y.; McGinnis, R.S.; Seagers, K.; Motl, R.W.; Sheth, N.; Wright, J.A.; Ghaffari, R.; Patel, S.; Sosnoff, J.J. Assessment of postural sway in individuals with multiple sclerosis using a novel wearable inertial sensor. Digit. Biomark. 2018, 2, 1–10. [Google Scholar] [CrossRef]
- Elftman, H. The function of the arms in walking. Hum. Biol. 1939, 11, 529. [Google Scholar]
- Birrell, S.A.; Haslam, R.A. The influence of rifle carriage on the kinetics of human gait. Ergonomics 2008, 51, 816–826. [Google Scholar] [CrossRef]
- Martin, P.E.; Nelson, R.C. The effect of carried loads on the walking patterns of men and women. Ergonomics 1986, 29, 1191–1202. [Google Scholar] [CrossRef]
- Barbieri, F.A.; Dos Santos, P.C.R.; Lirani-Silva, E.; Vitório, R.; Gobbi, L.T.B.; Van Diëen, J.H. Systematic review of the effects of fatigue on spatiotemporal gait parameters. J. Back Musculoskelet. Rehabil. 2013, 26, 125–131. [Google Scholar] [CrossRef] [Green Version]
- Helbostad, J.L.; Leirfall, S.; Moe-Nilssen, R.; Sletvold, O. Physical fatigue affects gait characteristics in older persons. J. Gerontol. Ser. Biol. Sci. Med Sci. 2007, 62, 1010–1015. [Google Scholar] [CrossRef]
- Lamoth, C.J.; Meijer, O.G.; Wuisman, P.I.; van Dieën, J.H.; Levin, M.F.; Beek, P.J. Pelvis-thorax coordination in the transverse plane during walking in persons with nonspecific low back pain. Spine 2002, 27, E92–E99. [Google Scholar] [CrossRef]
- Lim, S.; D’Souza, C. Statistical prediction of load carriage mode and magnitude from inertial sensor derived gait kinematics. Appl. Ergon. 2019, 76, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Coley, B.; Najafi, B.; Paraschiv-Ionescu, A.; Aminian, K. Stair climbing detection during daily physical activity using a miniature gyroscope. Gait Posture 2005, 22, 287–294. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, A.M.; Martelloni, C.; Scapellato, S.; Cavallo, F. Assessment of walking features from foot inertial sensing. IEEE Trans. Biomed. Eng. 2005, 52, 486–494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, C.C.; Hsu, Y.L.; Shih, K.S.; Lu, J.M. Real-time gait cycle parameter recognition using a wearable accelerometry system. Sensors 2011, 11, 7314–7326. [Google Scholar] [CrossRef] [Green Version]
- Dejnabadi, H.; Jolles, B.M.; Aminian, K. A new approach to accurate measurement of uniaxial joint angles based on a combination of accelerometers and gyroscopes. IEEE Trans. Biomed. Eng. 2005, 52, 1478–1484. [Google Scholar] [CrossRef]
- Khandelwal, S.; Wickström, N. Evaluation of the performance of accelerometer-based gait event detection algorithms in different real-world scenarios using the MAREA gait database. Gait Posture 2017, 51, 84–90. [Google Scholar] [CrossRef]
- Kowalsky, D.B.; Rebula, J.R.; Ojeda, L.V.; Adamczyk, P.G.; Kuo, A.D. Human walking in the real world: Interactions between terrain type, gait parameters, and energy expenditure. bioRxiv 2019. [Google Scholar] [CrossRef] [Green Version]
- Williamson, J.R.; Dumas, A.; Ciccarelli, G.; Hess, A.R.; Telfer, B.A.; Buller, M.J. Estimating load carriage from a body-worn accelerometer. In Proceedings of the 2015 IEEE 12th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Cambridge, MA, USA, 9–12 June 2015; pp. 1–6. [Google Scholar]
- Benocci, M.; Bächlin, M.; Farella, E.; Roggen, D.; Benini, L.; Tröster, G. Wearable assistant for load monitoring: Recognition of on—Body load placement from gait alterations. In Proceedings of the 2010 4th International Conference on Pervasive Computing Technologies for Healthcare, Munich, Germany, 22–25 March 2010; pp. 1–8. [Google Scholar]
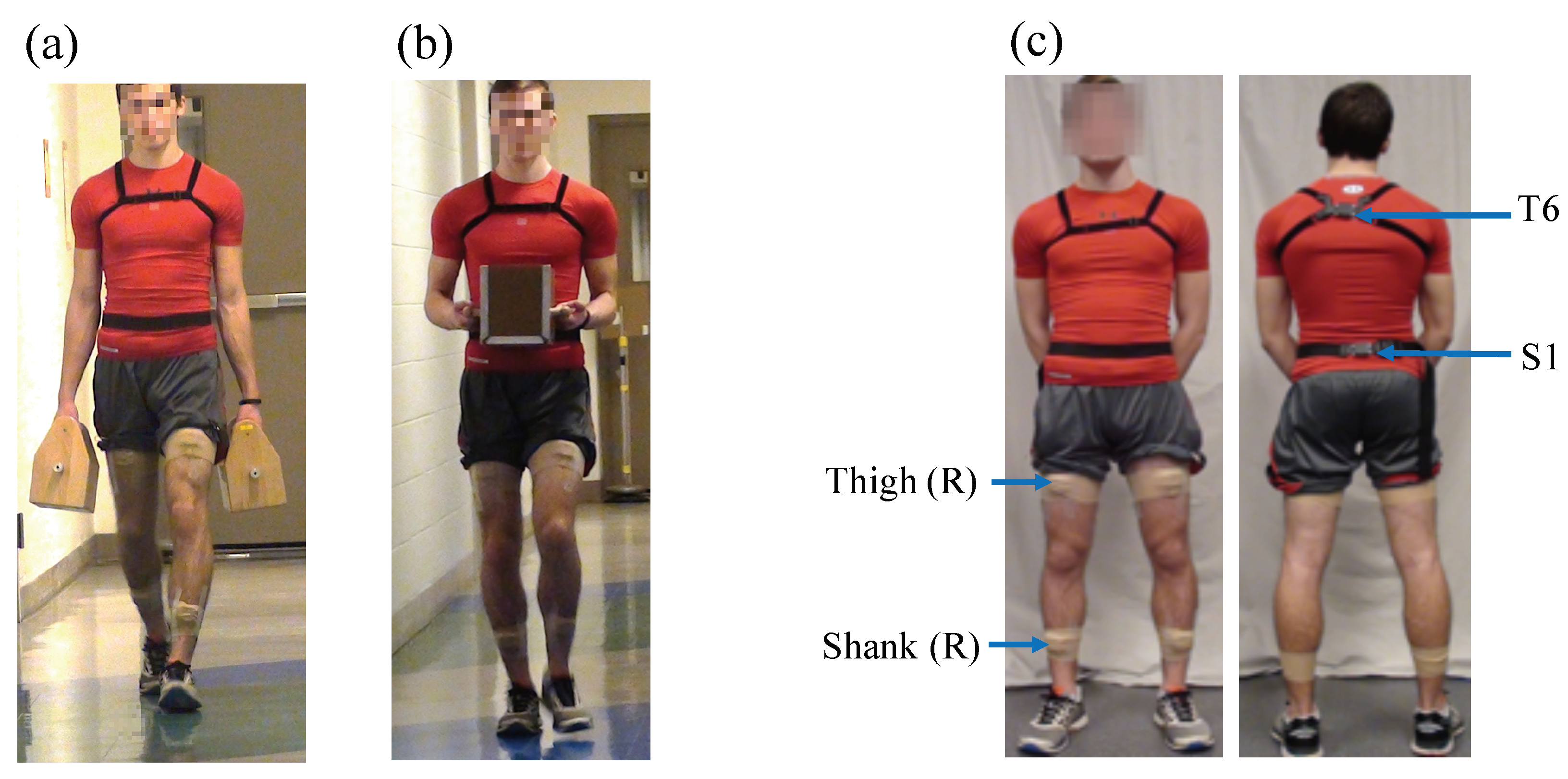
| Parameter | Definition | Inertial Sensor Location | Source | ||||
|---|---|---|---|---|---|---|---|
| T6 | S1 | R. Thigh | R. Shank | ||||
| Spatio-temporal parameters | |||||||
| 1 | Gait cycle duration (sec) | The duration of one gait cycle (one right plus left step duration calculated as the time between two consecutive right heel-strikes) | • | [42] | |||
| 2 | Stride length (cm) | The length moved from right heel-strike to the next right heel-strike during one gait cycle | • | • | [42] | ||
| Torso and pelvis postural sway | |||||||
| 3, 4 | Coronal ROM at T6 & S1 () | Range of rotation angle in coronal plane: Max (integrated angular velocity, z-axis) - min (integrated angular velocity, z-axis) | • | • | [25] | ||
| 5, 6 | Transverse ROM at T6 & S1 () | Same calculation as above in transverse plane: x-axis | • | • | |||
| 7, 8 | Sagittal ROM at T6 & S1 () | Same calculation as above in sagittal plane: y-axis | • | • | |||
| Thoracic-pelvic coordination | |||||||
| 9 | Coronal mean relative phase angle between T6 and S1 () | Average (pelvic phase angle - thoracic phase angle). Phase angle (t) = arctan (normalized angular velocity, z-axis (t)/normalized integrated angular velocity, z-axis (t)) | •——• | [25,34,60] | |||
| 10 | Transverse mean relative phase angle between T6 and S1 () | Same calculation as above in transverse plane: x-axis | •——• | ||||
| 11 | Sagittal mean relative phase angle between T6 and S1 () | Same calculation as above in sagittal plane: y-axis | •——• | ||||
| Carrying Mode | Load Level | Carrying Mode × Load Level | Relative Speed, Centered (s) | |
|---|---|---|---|---|
| Coronal plane | ||||
| ROM at T6 () | F(1, 114) = 0.24, p = 0.623 | F(3, 53) = 11.89, p < 0.001 * | F(3,53) = 0.15, p = 0.930 | F(1, 106) = 112.67, p < 0.001 * |
| (NL, L) > (M, H) | ||||
| ROM at S1 () | F(1, 130) = 0.02, p = 0.891 | F(3, 66) = 2.52, p = 0.066 | F(3, 66) = 0.11, p = 0.952 | F(1, 113) = 8.05, p = 0.005 * |
| Mean relative phase angle () | F(1, 101) = 96.96, p < 0.001 * | F(3, 71) = 1.72, p = 0.170 | F(3, 72) = 15.35, p < 0.001 * | F(1, 95) = 39.03, p < 0.001 * |
| Side > Anterior | Side: H > (M, L, NL) | |||
| Anterior: NL > (L, M, H) | ||||
| H, M, L: Side > Anterior | ||||
| Transverse plane | ||||
| ROM at T6 () | F(1, 118) = 1.65, p = 0.202 | F(3, 55) = 0.61, p = 0.612 | F(3, 55) = 1.17, p = 0.330 | F(1, 1) = 18.46, p = 1.0 |
| ROM at S1 () | F(1, 101) = 7.41, p = 0.008 * | F(3, 63) = 1.33, p = 0.272 | F(3, 63) = 1.47, p = 0.231 | F(1, 95) = 7.03, p = 0.009 * |
| Side > Anterior | ||||
| Mean relative phase angle () | F(1, 128) = 8.59, p = 0.004 * | F(3, 62) = 4.98, p = 0.004 * | F(3, 62) = 1.07, p = 0.371 | F(1, 110) = 0.04, p = 0.842 |
| Anterior > Side | (NL, L) > (M, H) | |||
| Sagittal plane | ||||
| ROM at T6 () | F(1, 113) = 28.55, p < 0.001 * | F(3, 60) = 0.58, p = 0.630 | F(3, 60) = 3.11, p = 0.033 * | F(1, 91) = 0.08, p = 0.775 |
| Side > Anterior | H, M, L: Side > Anterior | |||
| ROM at S1 () | F(1, 128) = 2.95, p = 0.088 | F(3, 65) = 2.07, p = 0.113 | F(3, 65) = 0.69, p = 0.565 | F(1, 1) = 16.35, p = 1.0 |
| Mean relative phase angle () | F(1, 122) = 7.14, p = 0.009 * | F(3, 57) = 0.53, p = 0.664 | F(3, 57) = 1.30, p = 0.284 | F(1, 103) = 7.24, p = 0.008 * |
| Side > Anterior | ||||
| Side Carry | Anterior Carry | ||||||
|---|---|---|---|---|---|---|---|
| No-Load | Low (4.5 kg) | Medium (9.1 kg) | High (13.6 kg) | Low (4.5 kg) | Medium (9.1 kg) | High (13.6 kg) | |
| Coronal plane | |||||||
| ROM at T6 () | 5.6 ± 0.3 | - | −1.7 ± 0.3 | −1.8 ± 0.4 | - | −1.7 ± 0.3 | −1.8 ± 0.4 |
| ROM at S1 () | 7.5 ± 0.4 | - | - | - | - | - | - |
| Mean relative phase angle () | 109.5 ± 5.2 | +5.0 ± 7.0 | +8.4 ± 6.0 | +23.6 ± 5.9 | −22.2 ± 6.0 | −22.9 ± 6.5 | −30.2 ± 6.1 |
| Transverse plane | |||||||
| ROM at T6 () | 5.6 ± 0.4 | - | - | - | - | - | - |
| ROM at S1 () | 7.4 ± 0.4 | [ - - - - - - - - - - - - +1.7 ± 0.6 - - - - - - - - - - - - - - ] | - | - | - | ||
| Mean relative phase angle () | 102.2 ± 7.6 | −30.5 ± 10.7 | −30.4 ± 10.5 | −33.8 ± 9.1 | - | −11.6 ± 10.3 | −18.8 ± 10.6 |
| Sagittal plane | |||||||
| ROM at T6 () | 2.9 ± 0.2 | +0.5 ± 0.3 | +0.5 ± 0.3 | +0.6 ± 0.3 | −0.2 ± 0.2 | −0.5 ± 0.2 | −0.3 ± 0.2 |
| ROM at S1 () | 3.8 ± 0.7 | - | - | - | - | - | - |
| Mean relative phase angle () | 81.7 ± 3.5 | [ - - - - - - - - - - - - +1.8 ± 4.5 - - - - - - - - - - - - - - ] | [ - - - - - - - - - - - - - −9.0 ± 4.5 - - - - - - - - - - - - - - ] | ||||
| Carrying Mode | Load Level | Carrying Mode × Load Level | Relative Speed, Centered (s) | |
|---|---|---|---|---|
| Coronal plane | ||||
| ROM at T6 () | F(1, 123) = 0.02, p = 0.896 | F(3, 79) = 6.48, p = 0.001 * | F(3, 78) = 0.69, p = 0.558 | F(1, 93) = 48.81, p < 0.001 * |
| NL > (M, H), L > M | ||||
| ROM at S1 () | F(1, 149) = 5.16, p = 0.025 * | F(3, 72) = 0.91, p = 0.442 | F(3, 71) = 0.71, p = 0.548 | F(1, 124) = 24.91, p < 0.001 * |
| Side > Anterior | ||||
| Mean relative phase angle () | F(1, 125) = 28.52, p < 0.001 * | F(3, 76) = 1.12, p = 0.346 | F(3, 75) = 3.91, p = 0.012 * | F(1, 122) = 5.01, p = 0.027 * |
| Side > Anterior | Anterior: NL > H | |||
| H, M, L: Side > Anterior | ||||
| Transverse plane | ||||
| ROM at T6 () | F(1, 86) = 5.96, p = 0.017 * | F(3, 46) = 2.24, p = 0.096 | F(3, 46) = 1.44, p = 0.242 | F(1, 68) = 13.88, p < 0.001 * |
| Side > Anterior | ||||
| ROM at S1 () | F(1, 84) = 20.12, p < 0.001 * | F(3, 41) = 0.64, p = 0.595 | F(3, 41) = 3.12, p = 0.036 * | F(1, 55) = 47.64, p < 0.001 * |
| Side > Anterior | H, M, L: Side > Anterior | |||
| Mean relative phase angle () | F(1, 122) = 0.07, p = 0.794 | F(3, 60) = 5.23, p = 0.003 * | F(3, 59) = 0.40, p = 0.752 | F(1, 86) = 2.17, p = 0.145 |
| NL > (L, M, H) | ||||
| Sagittal plane | ||||
| ROM at T6 () | F(1, 130) = 47.34, p < 0.001 * | F(3, 64) = 1.01, p = 0.393 | F(3, 62) = 6.67, p = 0.001 * | F(1, 100) = 3.34, p = 0.071 |
| Side > Anterior | Side: (H, M) > NL | |||
| H, M, L: Side > Anterior | ||||
| ROM at S1 () | F(1, 120) = 0.287, p = 0.593 | F(3, 58) = 0.12, p = 0.947 | F(3, 57) = 0.36, p = 0.779 | F(1, 112) = 0.79, p = 0.378 |
| Mean relative phase angle () | F(1, 103) = 3.59, p = 0.061 | F(3, 49) = 0.81, p = 0.493 | F(3, 48) = 0.76, p = 0.523 | F(1, 1) = 0.69, p = 1.0 |
| Side Carry | Anterior Carry | ||||||
|---|---|---|---|---|---|---|---|
| No-Load | Low (4.5 kg) | Medium (9.1 kg) | High (13.6 kg) | Low (4.5 kg) | Medium (9.1 kg) | High (13.6 kg) | |
| Coronal plane | |||||||
| ROM at T6 () | 4.3 ± 0.2 | −0.4 ± 0.3 | −1.1 ± 0.3 | −1.0 ± 0.3 | −0.4 ± 0.3 | −1.1 ± 0.3 | −1.0 ± 0.3 |
| ROM at S1 () | 8.3 ± 6.6 | [ - - - - - - - - - - - - +0.3 ± 0.4 - - - - - - - - - - - - - - ] | [ - - - - - - - - - - - - −0.6 ± 0.4 - - - - - - - - - - - - - - ] | ||||
| Mean relative phase angle () | 118.7 ± 6.2 | +1.8 ± 7.1 | +7.4 ± 7.1 | +5.9 ± 7.1 | −11.4 ± 7.7 | −21.3 ± 8.0 | −24.7 ± 7.8 |
| Transverse plane | |||||||
| ROM at T6 () | 5.2 ± 0.3 | [ - - - - - - - - - - - - +1.0 ± 0.3 - - - - - - - - - - - - - - ] | [ - - - - - - - - - - - - +0.2 ± 0.3 - - - - - - - - - - - - - - ] | ||||
| ROM at S1 () | 7.1 ± 0.6 | +1.3 ± 1.0 | +2.5 ± 1.1 | +2.3 ± 1.2 | −0.7 ± 0.7 | −0.9 ± 0.6 | −0.9 ± 0.6 |
| Mean relative phase angle () | 66.1 ± 4.4 | −18.1 ± 5.8 | −20.7 ± 5.4 | −17.8 ± 6.4 | −18.1 ± 5.8 | −20.7 ± 5.4 | −17.8 ± 6.4 |
| Sagittal plane | |||||||
| ROM at T6 () | 2.7 ± 0.1 | +0.3 ± 0.2 | +0.5 ± 0.2 | +0.5 ± 0.2 | −0.4 ± 0.2 | −0.5 ± 0.2 | −0.2 ± 0.1 |
| ROM at S1 () | 3.5 ± 0.3 | - | - | - | - | - | - |
| Mean relative phase angle () | 52.9 ± 3.3 | - | - | - | - | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, S.; D'Souza, C. Measuring Effects of Two-Handed Side and Anterior Load Carriage on Thoracic-Pelvic Coordination Using Wearable Gyroscopes. Sensors 2020, 20, 5206. https://doi.org/10.3390/s20185206
Lim S, D'Souza C. Measuring Effects of Two-Handed Side and Anterior Load Carriage on Thoracic-Pelvic Coordination Using Wearable Gyroscopes. Sensors. 2020; 20(18):5206. https://doi.org/10.3390/s20185206
Chicago/Turabian StyleLim, Sol, and Clive D'Souza. 2020. "Measuring Effects of Two-Handed Side and Anterior Load Carriage on Thoracic-Pelvic Coordination Using Wearable Gyroscopes" Sensors 20, no. 18: 5206. https://doi.org/10.3390/s20185206
APA StyleLim, S., & D'Souza, C. (2020). Measuring Effects of Two-Handed Side and Anterior Load Carriage on Thoracic-Pelvic Coordination Using Wearable Gyroscopes. Sensors, 20(18), 5206. https://doi.org/10.3390/s20185206





