Accuracy of Solid-State Residential Water Meters under Intermittent Flow Conditions
Abstract
:1. Introduction
2. Materials and Methods
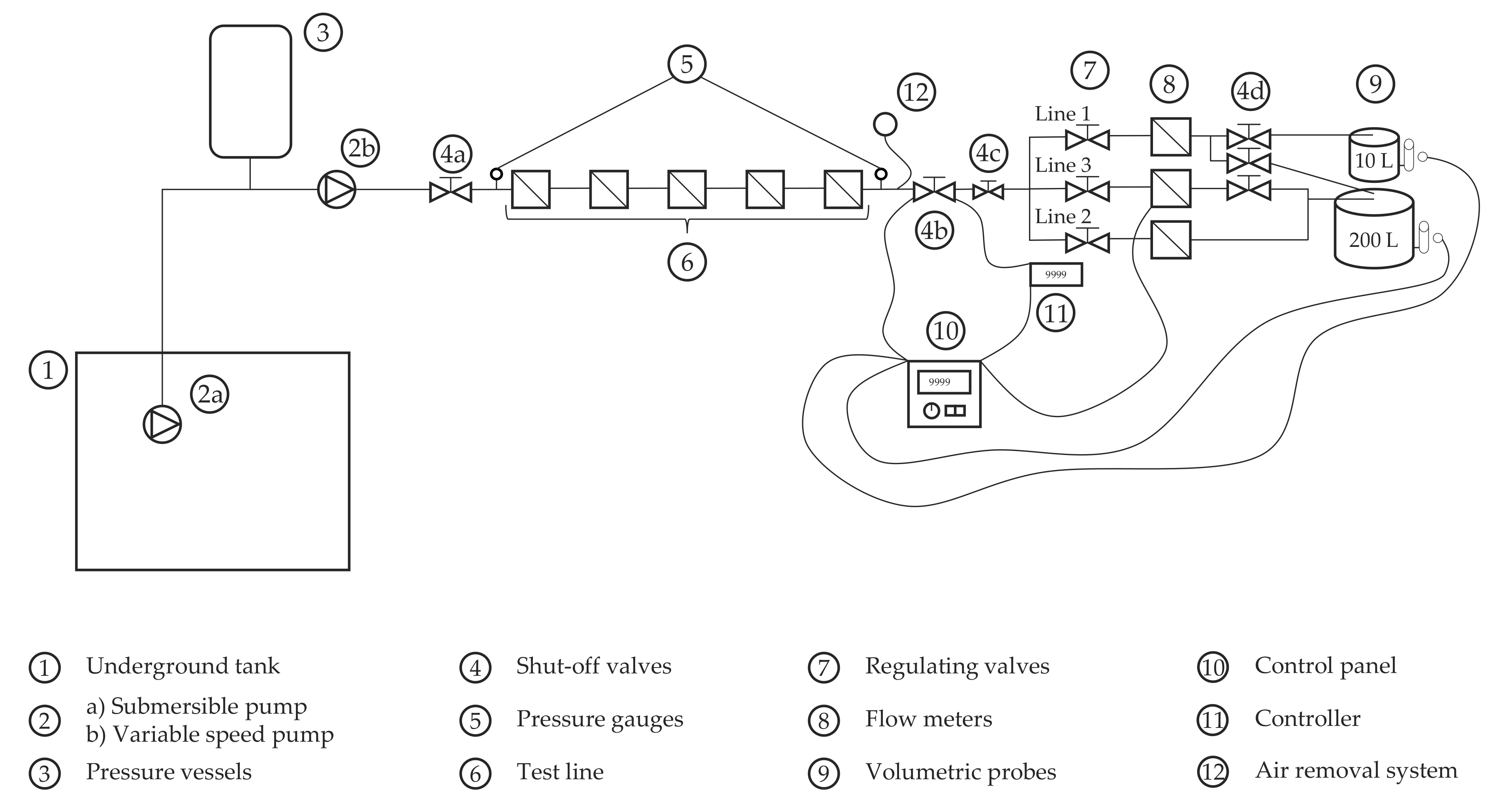
2.1. Test Bench Description
2.2. Sample Description
- (i)
- Manufacturers of solid-state water meters ensure minimal tolerances during production. In addition, variations detected between units are later corrected in the calibration process. Consequently, potential differences in the behavior of a solid-state water meter under steady and intermittent flow conditions are mainly due to the firmware and/or the signal processing algorithm, which are identical for all meters of a certain type and manufacturer.
- (ii)
- The present study aims to detect whether the processing algorithms used by each meter type show any significant fault that impedes a correct measure of water consumption under intermittent flow conditions.
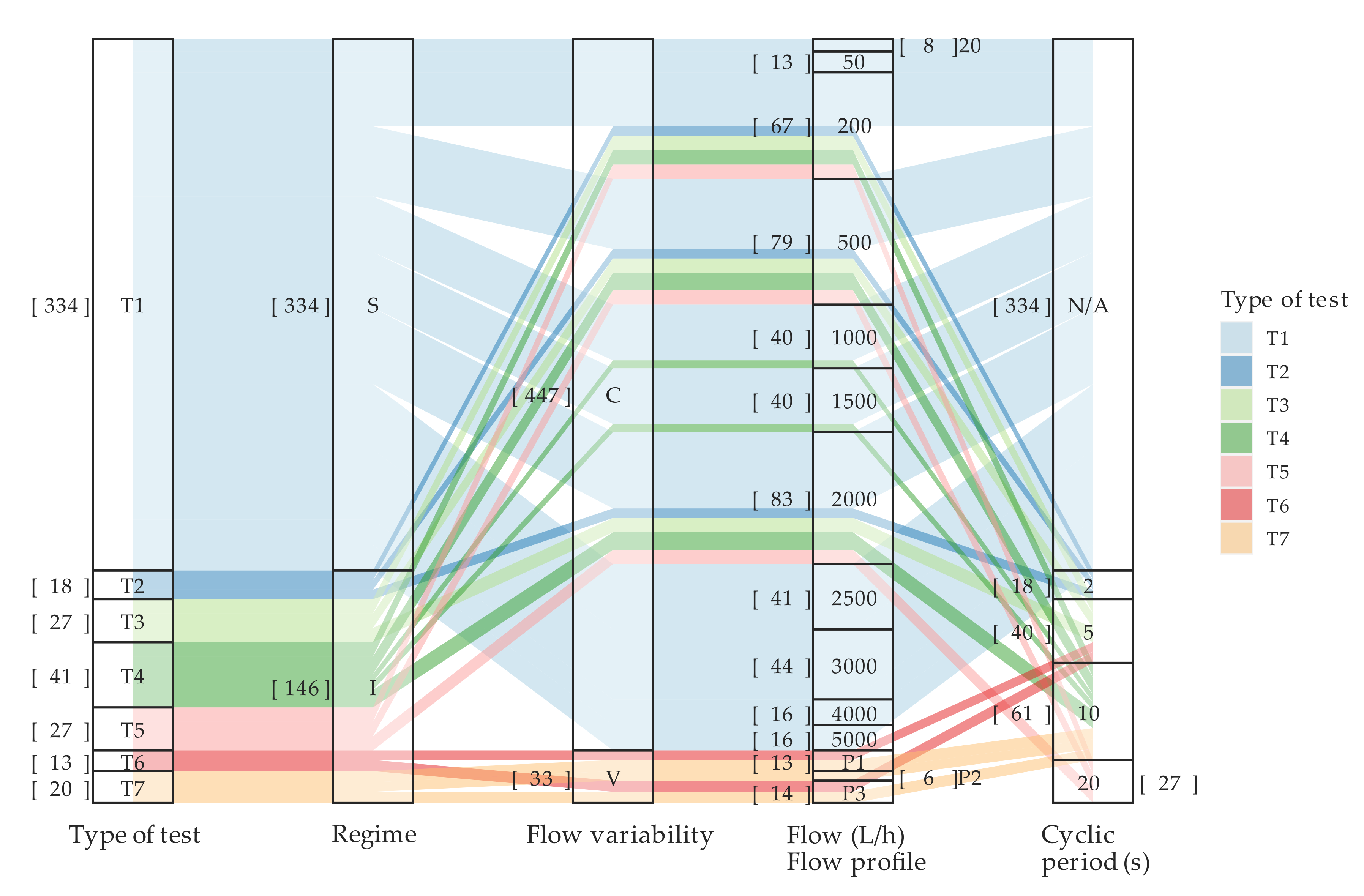
2.3. Test Programme Description
2.4. Analysis Methods Overview
3. Results and Discussion
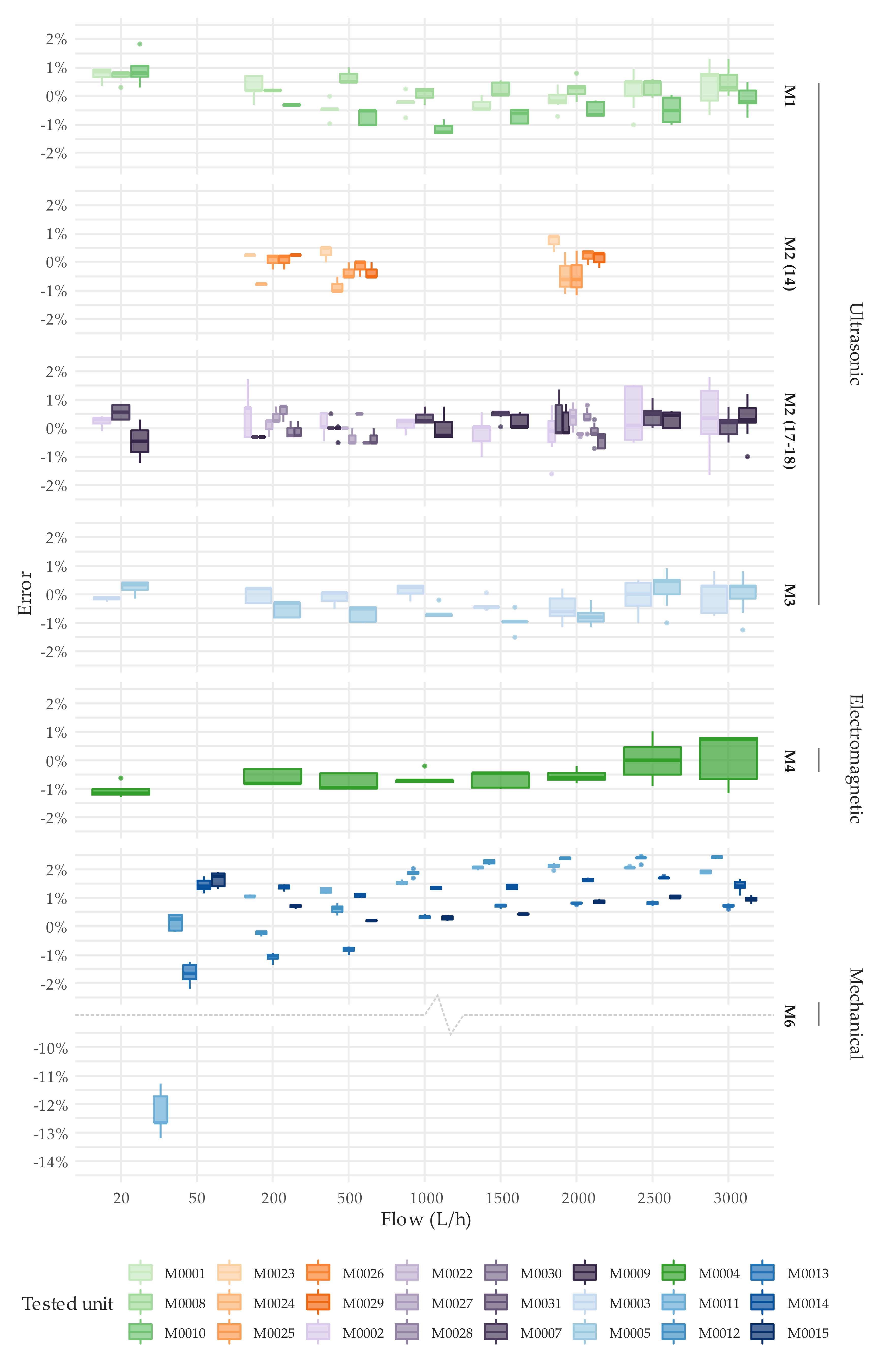
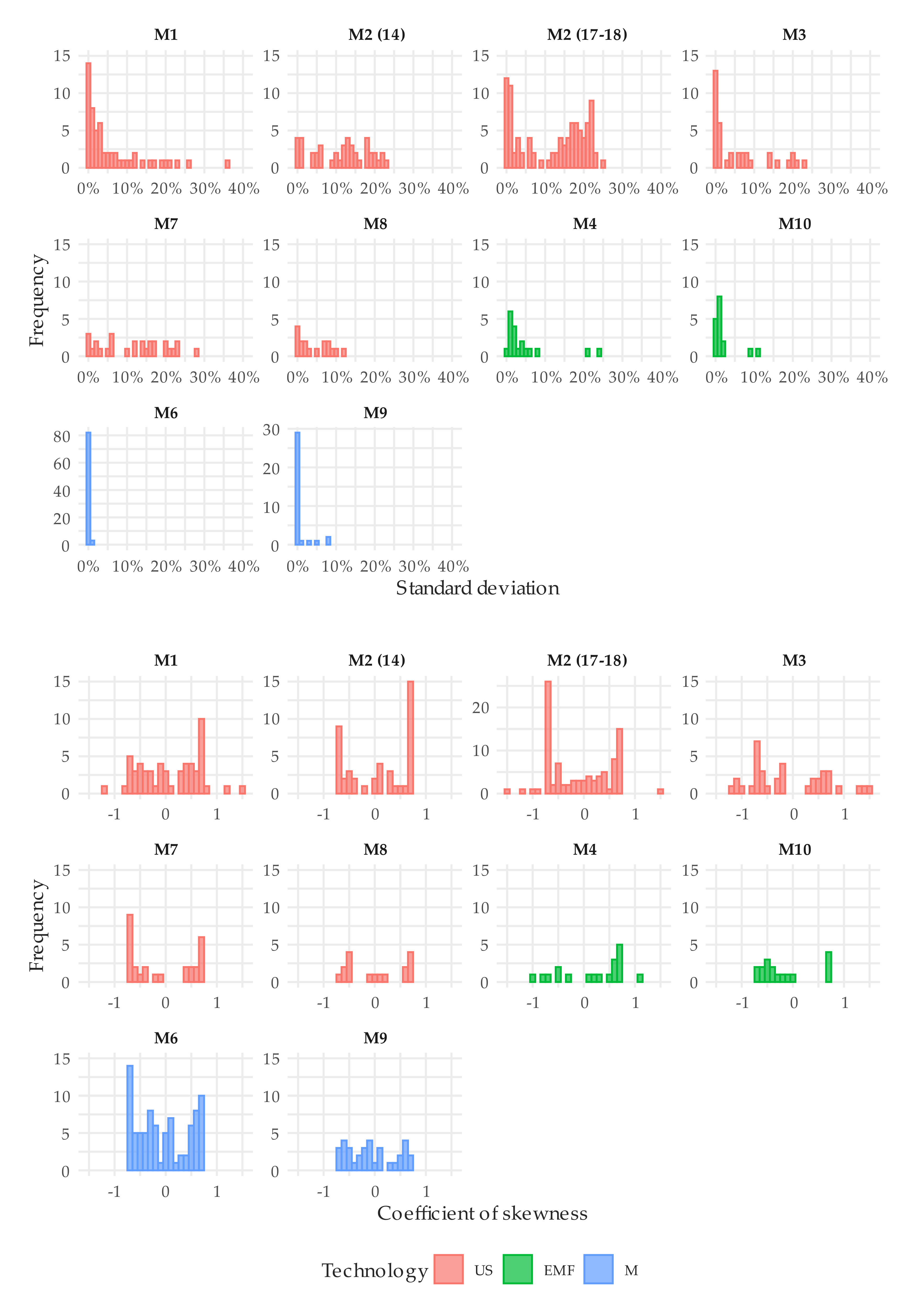
3.1. Metrological Performance under Steady Flow Conditions
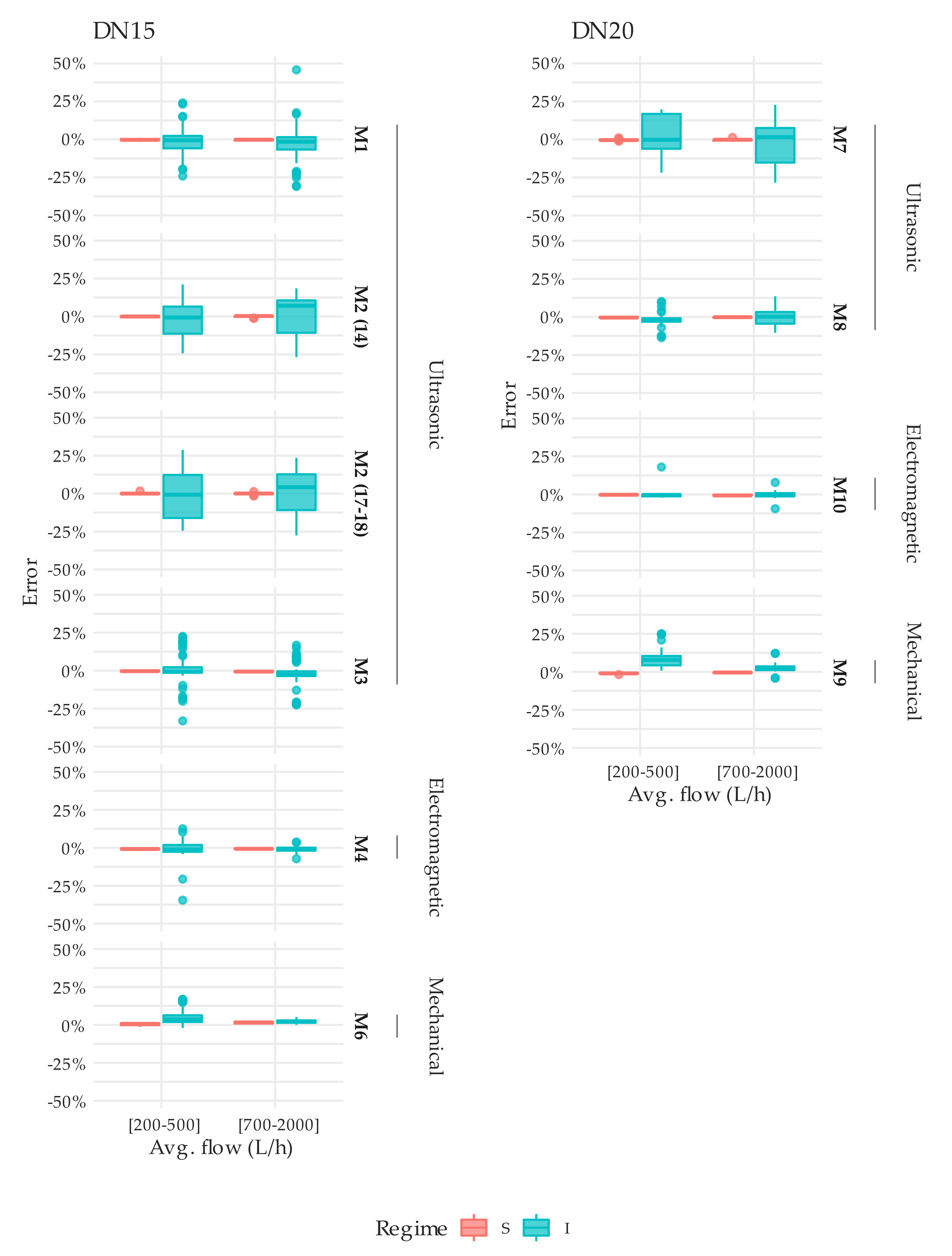
3.2. Metrological Performance under Intermittent Flow Conditions
4. Conclusions
- (i)
- Test under steady flow conditions. The error of the meters is obtained by means of standing start and stop test method conducted in a volumetric test bench. These errors are taken as a reference for the results obtained in the next stage.
- (ii)
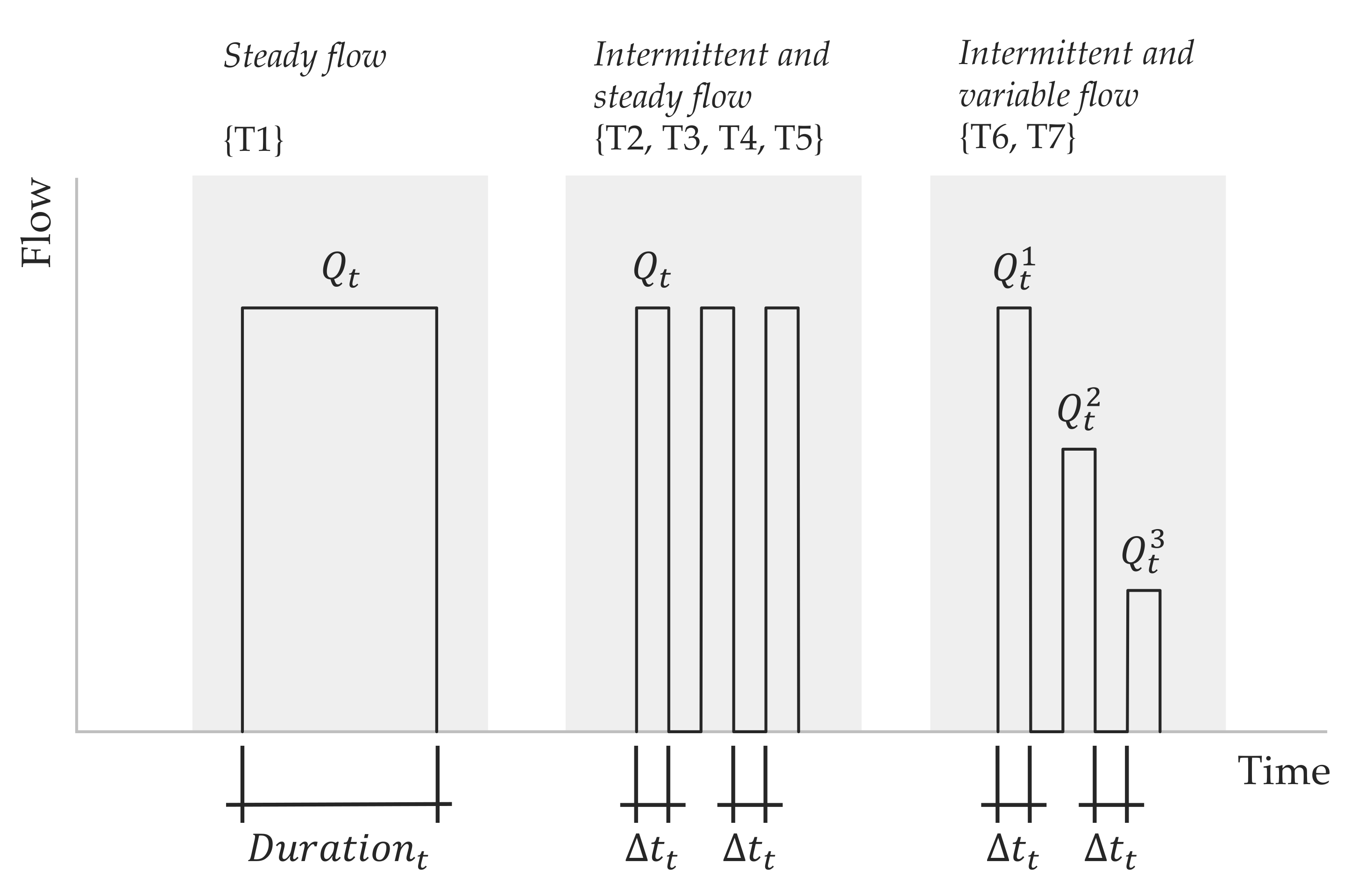
- Test under intermittent flow conditions. The designed programme includes different levels of both constant and variable flow rate, as well as different consumption durations.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Díaz, I.; Flores, J. Accurate Assessment of under Metering in MADRID Water Supply. In Proceedings of the 5th IWA Specialist Conference on Efficient Use and Management of Urban Water, Sydney, Australia, 25–28 October 2009. [Google Scholar]
- Szilveszter, S.; Beltran, R.; Fuentes, A. Performance analysis of the domestic water meter park in water supply network of Ibarra, Ecuador. Urban Water J. 2017, 14, 85–96. [Google Scholar] [CrossRef]
- Arregui, F.; Cabrera, E.; Cobacho, R.; García-Serra, J. Reducing Apparent Losses Caused By Meters Inaccuracies. Water Pract. Technol. 2006, 1. [Google Scholar] [CrossRef] [Green Version]
- Richards, G.L.; Johnson, M.C.; Barfuss, S.L. Apparent losses caused by water meter inaccuracies at ultralow flows. J. Water Around World 2010, 102, 123–132. [Google Scholar] [CrossRef]
- Barfuss, S.L.; Johnson, M.C.; Neilsen, M.A. Accuracy of In-Service Water Meters at Low and High Flow Rates; The Water Resarch Foundation: Denver, CO, USA, 2011. [Google Scholar]
- Mbabazi, D.; Banadda, N.; Kiggundu, N.; Mutikanga, H.; Babu, M. Determination of domestic water meter accuracy degradation rates in Uganda. J. Water Supply Res. Technol. AQUA 2015, 64, 486–492. [Google Scholar] [CrossRef]
- Bowen, P.T.; Harp, J.F.; Entwistle, J.; Shoeleh, M. Evaluating Residential Water Meter Performance; AWWA Research Foundation and American Water Works Association: Denver, CO, USA, 1991. [Google Scholar]
- Mutikanga, H.E.; Sharma, S.K.; Vairavamoorthy, K. Investigating water meter performance in developing countries: A case study of Kampala, Uganda. Water SA 2011, 37, 567–574. [Google Scholar] [CrossRef] [Green Version]
- Stoker, D.M.; Barfuss, S.L.; Johnson, M.C. Flow measurement accuracies of in-service residential water meters. J. Am. Water Work Assoc. 2012, 104, E637–E642. [Google Scholar] [CrossRef]
- Arregui, F.; Gavara, F.; Soriano, J.; Pastor-Jabaloyes, L. Performance Analysis of Ageing Single-Jet Water Meters for Measuring Residential Water Consumption. Water 2018, 10, 612. [Google Scholar] [CrossRef] [Green Version]
- ISO - ISO 4064-1:2014 - Water Meters for Cold Potable Water and Hot Water—Part 1: Metrological and Technical Requirements. Available online: https://www.iso.org/standard/55371.html (accessed on 5 August 2020).
- Mello, E.J. As perdas não físicas e o posicionamento do medidor de água. In Proceedings of the XXVII Congresso Interamericano de Engenharia Sanitária e Ambiental, Porto Alegre, Brazil, 25–29 September 2009. [Google Scholar]
- Buck, B.S.; Johnson, M.C.; Barfuss, S.L. Effects of particulates on water meter accuracy through expected life. J. Am. Water Work. Assoc. 2012, 104, E231–E242. [Google Scholar] [CrossRef] [Green Version]
- Deoreo, W.B.; Mayer, P.W. Residential End Uses of Water; American Water Works Association Research Foundation: Denver, CO, USA, 1999. [Google Scholar]
- Blokker, E.; Vreeburg, J.; van Dijk, J. Simulating residential water demand with a stochastic end-use model. J. Water Resour. Plan. Manag. 2009, 136, 19–26. [Google Scholar] [CrossRef]
- Beal, C.; Stewart, R.A. South East Queensland Residential End Use Study: Final Report; Urban Water Security Research Alliance: City East, Australia, 2011. [Google Scholar]
- Deoreo, W.B.; Mayer, P.W. Residential End Uses of Water Study; American Water Works Association Research Foundation: Denver, CO, USA, 2013. [Google Scholar]
- Roberts, P.; Athuraliya, A.; Brown, A. Residential Water Use Study, Volume 1—Winter 2010; Yarra Valley Water: Melbourne, Australia, 2011. [Google Scholar]
- ISO - ISO 4064-2:2014 - Water Meters for Cold Potable Water and Hot Water—Part 2: Test Methods. Available online: https://www.iso.org/standard/55383.html (accessed on 5 August 2020).
- Chadwick, J.R.; Barfuss, S.L.; Johnson, M.C. Accuracy of residential water meters in response to short. intermittent flows. AWWA Water Sci. 2019, 1. [Google Scholar] [CrossRef] [Green Version]
- Hovany, L. Error in Water Meter Measuring Due to Shorter Flow and Consumption Shorter Than the Time the Meter was Calibrated. Water Supply Syst. Anal. Sel. Top. 2012. [Google Scholar] [CrossRef] [Green Version]
- Yaniv, S. Reduction of apparent losses using the UFR (Unmeasured-flow reducer): Case studies. In Proceedings of the 5th IWA Specialist Conference on Efficient Water Use and Management, Sydney, Australia, 25–29 October 2009. [Google Scholar]
- Team R.C. R: A Language and Environment for Statistical Computing 2019. Available online: https://www.R-project.org/ (accessed on 17 September 2020).
- OIML—OIML R 49-1:2013—Water Meters for Cold Potable Water and Hot Water—Part 1: Metrological and Technical Requirements. Available online: https://www.oiml.org/en/files/pdf_r/r049-1-e13.pdf (accessed on 5 August 2020).
- Wickham, H.; Navarro, D.; Pedersen, T.L. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Arregui, F.J.; Balaguer, M.; Soriano, J.; García-Serra, J. Quantifying measuring errors of new residential water meters considering different customer consumption patterns. Urban Water J. 2016, 13, 463–475. [Google Scholar] [CrossRef] [Green Version]
- Buchberger, S.G.; Wu, L. Model for Instantaneous Residential Water Demands. J. Hydraul. Eng. 1995, 121, 232–246. [Google Scholar] [CrossRef]
- Buchberger, S.G.; Wells, G.J. Intensity, Duration, and Frequency of Residential Water Demands. J. Water Resour. Plan. Manag. 1996, 122, 11–19. [Google Scholar] [CrossRef]
- Guercio, R.; Magini, R.; Pallavicini, I. Instantaneous residential water demand as stochastic point process. Water Resour. Mznagernent. 2001, 48, 129–138. [Google Scholar]
- Alvisi, S.; Franchini, M.; Marinelli, A. A stochastic model for representing drinking water demand at residential level. Water Resour. Manag. 2003, 17, 197–222. [Google Scholar] [CrossRef]
- García, V.J.; García-Bartual, R.; Cabrera, E.; Arregui, F.; García-Serra, J. Stochastic model to evaluate residential water demands. J. Water Resour. Plan. Manag. 2004, 130, 386–394. [Google Scholar] [CrossRef]
- Alcocer-Yamanaka, V.H.; Tzatchkov, V.G.; Arreguin-Cortes, F.I. Modeling of drinking water distribution networks using stochastic demand. Water Resour. Manag. 2012, 26, 1779–1792. [Google Scholar] [CrossRef]


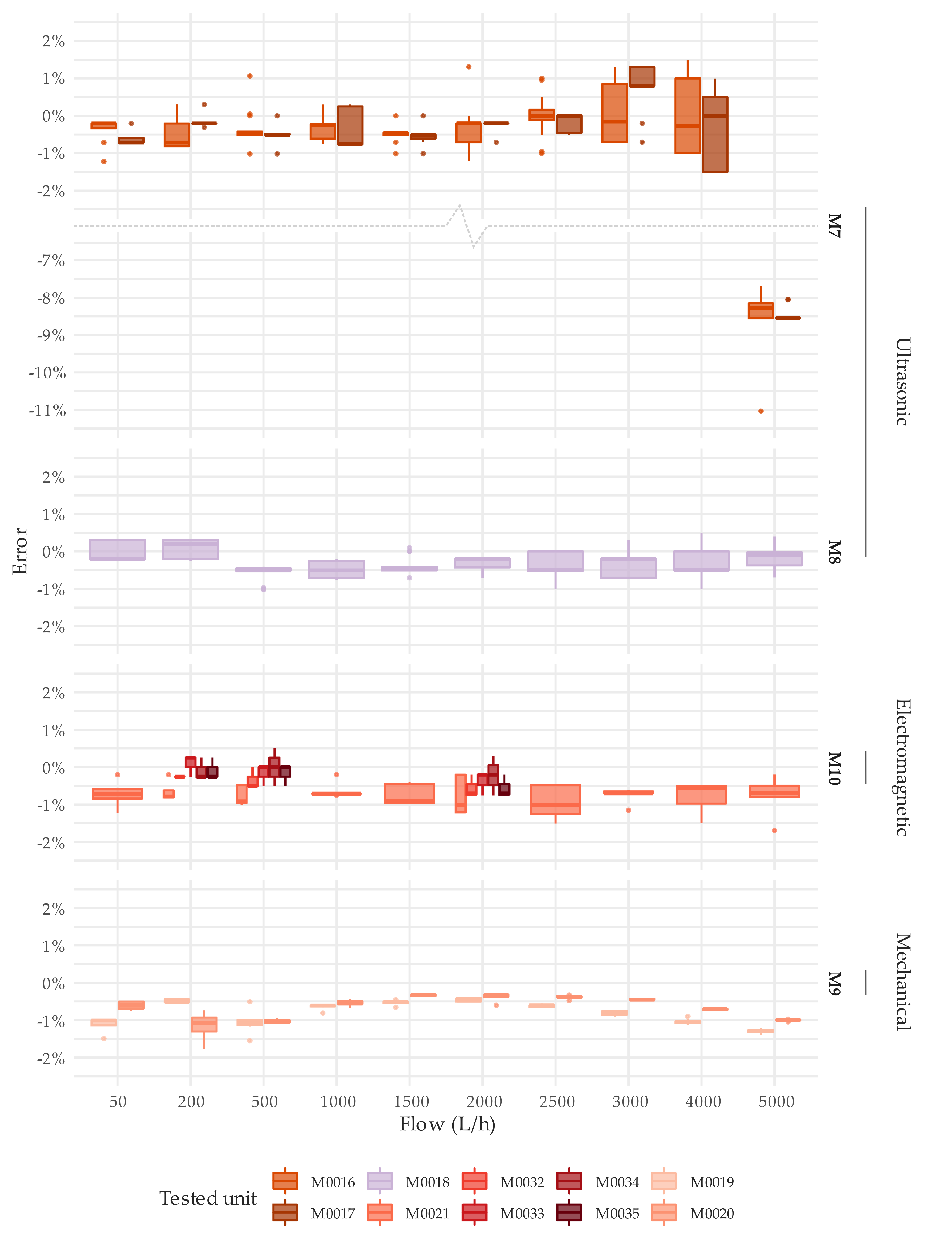


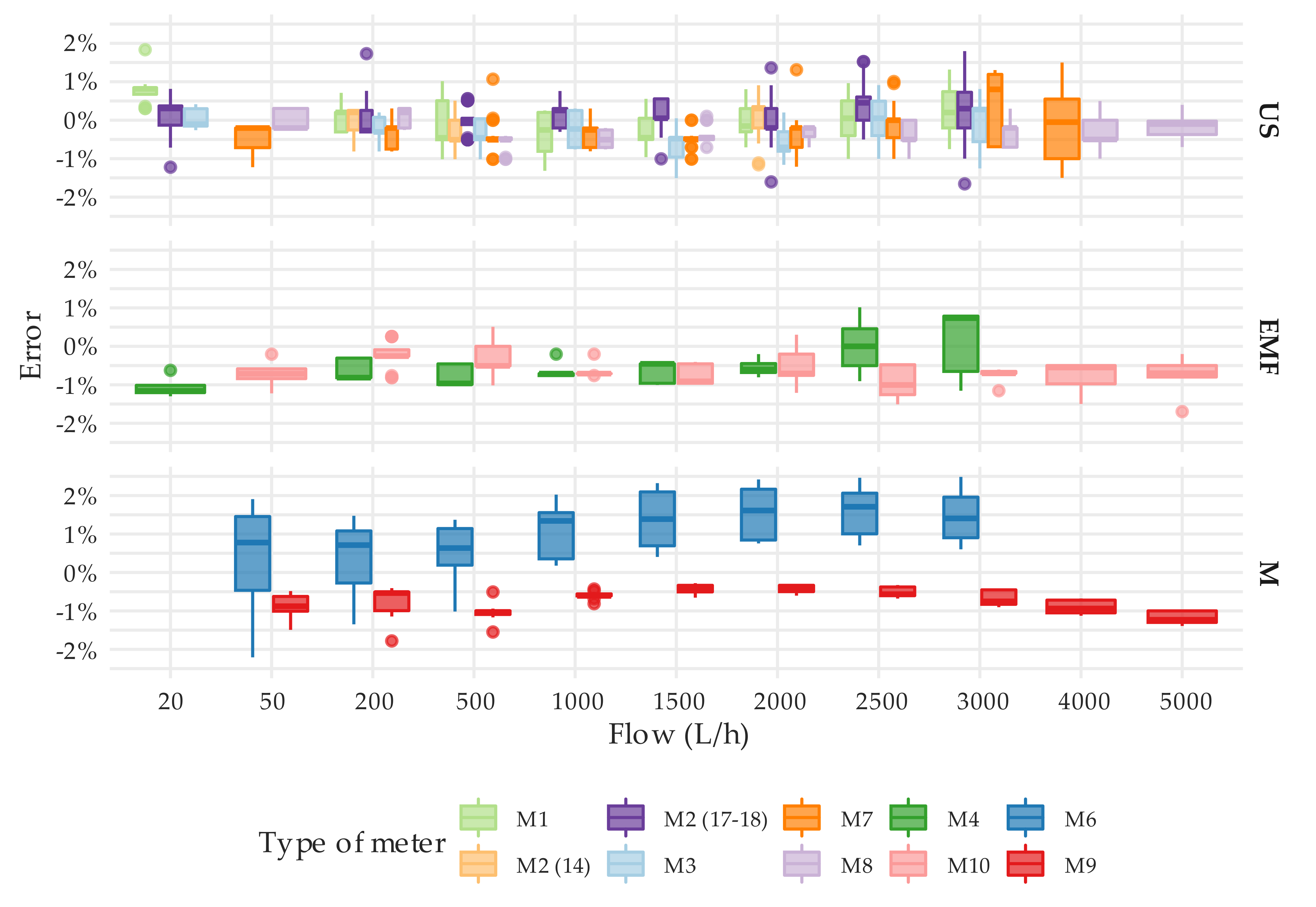
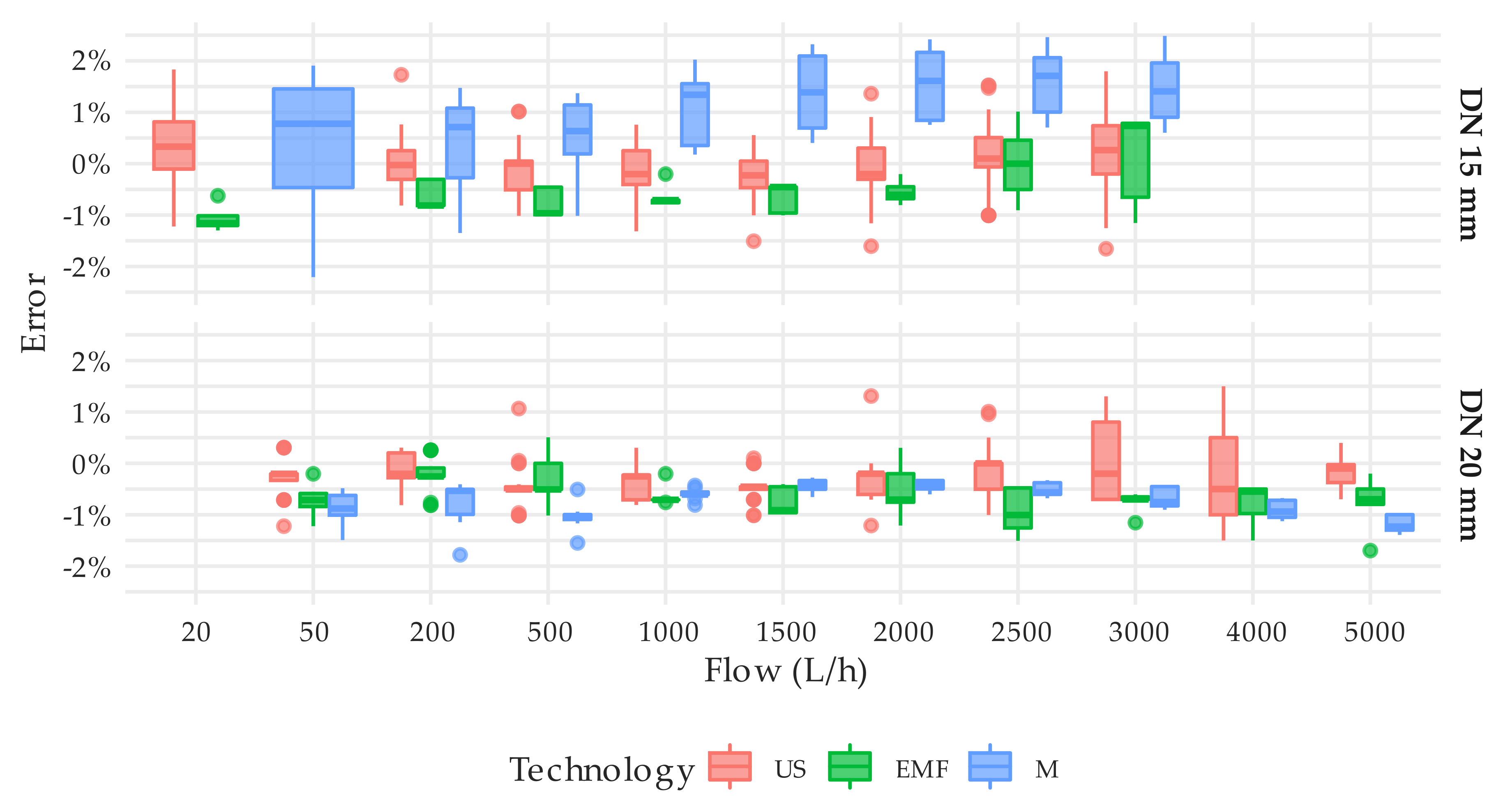
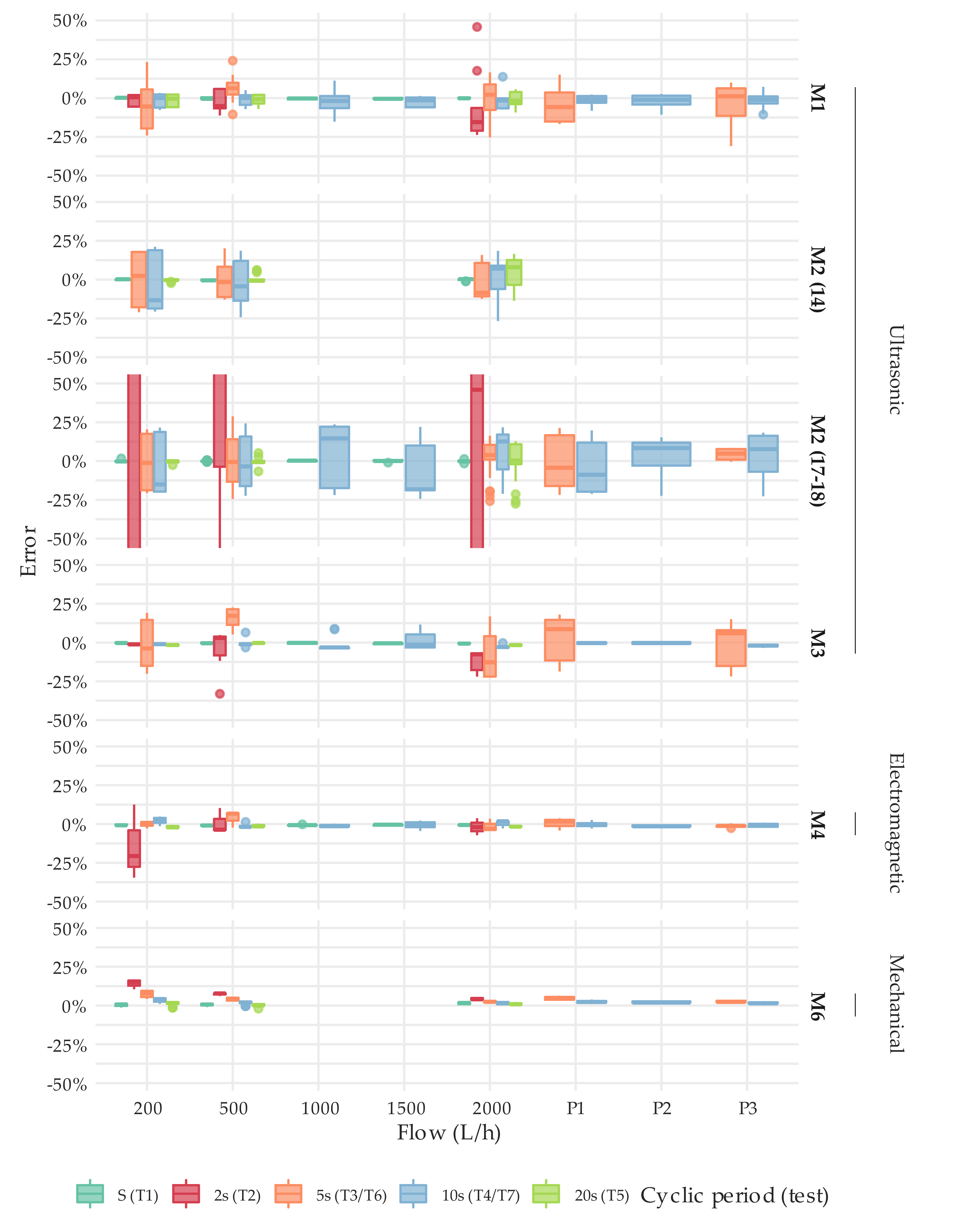

| Manufacturer | Type of Meter | Num. of Units | Technology | DN | Metrological Class (Q3/Q1) | Q1 (L/h) | Q2 (L/h) | Q3 (m3/h) | Q4 (m3/h) |
|---|---|---|---|---|---|---|---|---|---|
| B3 | M1 | 3 | US | 15 | 400 | 6.25 | 10 | 2.5 | 3.125 |
| B5 | M2 (14)(*) | 5 | US | 15 | 160 | 10 | 16 | 1.6 | 2.0 |
| B5 | M2 (17–18)(*) | 8 | US | 15 | 160 | 10 | 16 | 1.6 | 2.0 |
| B1 | M3 | 2 | US | 15 | 400 | 6.25 | 10 | 2.5 | 3.125 |
| B4 | M4 | 1 | EMF | 15 | 800 | 3.125 | 5 | 2.5 | 3.125 |
| B7 | M5 | 1 | US | 15 | 800 | 3.125 | 5 | 2.5 | 3.125 |
| B2 | M6 | 5 | M | 15 | 125 | 20 | 32 | 2.5 | 3.125 |
| B5 | M7 | 2 | US | 20 | 250 | 10 | 16 | 2.5 | 3.125 |
| B6 | M8 | 1 | US | 20 | 400 | 10 | 16 | 4.0 | 5.0 |
| B4 | M9 | 2 | M | 20 | 160 | 25 | 40 | 4.0 | 5.0 |
| B4 | M10 | 5 | EMF | 20 | 800 | 5 | 8 | 4.0 | 5.0 |
| Type of Meter | Age (Years) | Accumulated Volume (m3) | Default Resolution | Resolution Change |
|---|---|---|---|---|
| M1 | 1 | 3.8 | L | Available |
| M2 | 3.6 | 2611.8 | L | Available |
| M3 | 1.0 | 1.4 | L | Available |
| M4 | 5.0 | 0.2 | L | Available |
| M5 | 2.0 | 12.7 | L | Available |
| M6 | 4 | 2289.5 | dL | Not available |
| M7 | 0.5 | 1.2 | L | Available |
| M8 | 0 | 0.1 | L | Available |
| M9 | 0 | 0.7 | dL | Not available |
| M10 | 0 | 0.4 | L | Available |
| Type of Test | Avg. Duration (min) | Avg. Volume (L) | Reading Uncertainty |
|---|---|---|---|
| T1 | 32 | 195 | 1.02% |
| T2 | 80 | 504 | 0.40% |
| T3 | 72 | 396 | 0.50% |
| T4 | 69 | 486 | 0.41% |
| T5 | 73 | 388 | 0.52% |
| T6 | 98 | 790 | 0.25% |
| T7 | 106 | 734 | 0.27% |
| Technology | Type of Meter | ID Meter | Test | Time Frame (s) |
|---|---|---|---|---|
| US | M2 | M0002 | T2 | 2 |
| M0007 | T2 | 2 | ||
| M0009 | T2 | 2 | ||
| M7 | M0016 | T2 | 2 | |
| M0017 | T2 | 2 |
| Tech. | Diam. | Type of Meter | Meter | |||||
|---|---|---|---|---|---|---|---|---|
| US | DN15 | M1 | M0001 | −148% | 0.518% | 1.952% | 8.202% | 2.100% |
| M0008 | 0.470% | 0.296% | −1.957% | 7.171% | −2.426% | |||
| M0010 | −0.546% | 0.296% | −4.145% | 7.347% | −3.599% | |||
| Avg. M1 | −0.075% | 0.512% | −1.383% | 3.088% | −1.308% | |||
| M2 (14) | M0002 | 0.318% | 0.609% | 5.103% | 16.020% | 4.785% | ||
| M0007 | −0.081% | 0.243% | −0.834% | 14.756% | −0.753% | |||
| M0009 | −0.165% | 0.190% | −3.597% | 13.740% | −3.432% | |||
| M0022 | 0.034% | 0.208% | −1.962% | 12.691% | −1.995% | |||
| M0027 | 0.039% | 0.491% | 0.841% | 14.658% | 0.803% | |||
| M0028 | 0.546% | 0.200% | 2.059% | 13.504% | 1.512% | |||
| M0030 | −0.300% | 0.296% | −2.871% | 13.640% | −2.571% | |||
| M0031 | −0.216% | 0.298% | −6.307% | 12.172% | −6.091% | |||
| Avg. M2 (14) | 0.022% | 0.285% | −0.946% | 3.572% | −0.968% | |||
| M2 (17–18) | M0023 | 0.288% | 0.194% | −2.206% | 13.511% | −2.494% | ||
| M0024 | −0.813% | 0.190% | 2.480% | 11.103% | 3.293% | |||
| M0025 | −0.135% | 0.340% | −2.151% | 10.559% | −2.016% | |||
| M0026 | −0.051% | 0.287% | −0.252% | 12.483% | −0.201% | |||
| M0029 | −0.046% | 0.370% | −2.430% | 12.721% | −2.383% | |||
| Avg. M2 (17–18) | −0.040% | 0.318% | −0.934% | 2.866% | −0.894% | |||
| M3 | M0003 | −0.063% | 0.259% | 1.466% | 9.085% | 1.529% | ||
| M0005 | −0.614% | 0.279% | −0.267% | 10.202% | 0.346% | |||
| Avg. M3 | −0.339% | 0.389% | 0.599% | 1.226% | 0.938% | |||
| DN20 | M7 | M0016 | −0.389% | 0.443% | 0.067% | 13.139% | 0.456% | |
| M0017 | −0.343% | 0.326% | 3.635% | 14.761% | 3.978% | |||
| Avg. M7 | −0.366% | 0.033% | 1.851% | 2.523% | 2.217% | |||
| M8 | M0018 | −0.322% | 0.410% | −1.800% | 5.430% | −1.478% | ||
| EM | DN15 | M4 | M0004 | −0.699% | 0.281% | −1.113% | 8.121% | −0.415% |
| DN20 | M10 | M0021 | −0.716% | 0.267% | −0.004% | 3.498% | 0.712% | |
| M0032 | −0.296% | 0.191% | - | - | - | |||
| M0033 | −0.042% | 0.297% | - | - | - | |||
| M0034 | −0.042% | 0.374% | - | - | - | |||
| M0035 | −0.127% | 0.267% | - | - | - | |||
| Avg. M10 | −0.245% | 0.283% | −0.004% | - | 0.241% | |||
| M | DN15 | M6 | M0011 | 1.169% | 0.127% | 3.873% | 2.773% | 2.705% |
| M0012 | 0.218% | 0.452% | 2.916% | 4.242% | 2.698% |
| Tech. | Diam. | Type of Meter | Meter | |||||
|---|---|---|---|---|---|---|---|---|
| US | DN15 | M1 | M0001 | −0.221% | 0.300% | 2.914% | 10.575% | 3.134% |
| M0008 | 0.190% | 0.286% | −1.886% | 6.899% | −2.076% | |||
| M0010 | −0.773% | 0.374% | −8.652% | 8.970% | −7.879% | |||
| Avg. M1 | −0.268% | 0.483% | −2.541% | 5.810% | −2.273% | |||
| M2 (14) | M0002 | −0.076% | 0.549% | 6.451% | 12.804% | 6.527% | ||
| M0007 | 0.383% | 0.400% | −0.614% | 15.668% | −0.997% | |||
| M0009 | 0.142% | 0.387% | 2.262% | 15.288% | 2.121% | |||
| M0022 | 0.387% | 0.530% | 1.460% | 10.937% | 1.073% | |||
| M0027 | −0.217% | 0.038% | −2.309% | 16.240% | −2.092% | |||
| M0028 | 0.362% | 0.330% | −0.049% | 16.749% | −0.410% | |||
| M0030 | −0.145% | 0.330% | 0.684% | 14.733% | 0.828% | |||
| M0031 | −0.434% | 0.260% | 2.455% | 14.996% | 2.889% | |||
| Avg. M2 (14) | 0.050% | 0.314% | 1.292% | 2.611% | 1.242% | |||
| M2 (17–18) | M0023 | 0.723% | 0.321% | −2.256% | 9.746% | −2.979% | ||
| M0024 | −0.454% | 0.743% | 0.610% | 10.563% | 1.064% | |||
| M0025 | −0.454% | 0.793% | 4.681% | 9.557% | 5.135% | |||
| M0026 | 0.219% | 0.278% | 2.807% | 15.606% | 2.588% | |||
| M0029 | 0.145% | 0.240% | 0.899% | 14.684% | 0.754% | |||
| Avg.M2 (17–18) | 0.045% | 0.360% | 1.312% | 2.397% | 1.267% | |||
| M3 | M0003 | −0.244% | 0.418% | −3.924% | 8.999% | −3.679% | ||
| M0005 | −0.798% | 0.297% | −1.357% | 7.395% | −0.559% | |||
| Avg. M3 | −0.521% | 0.391% | −2.640% | 1.815% | −2.119% | |||
| DN20 | M7 | M0016 | −0.295% | 0.571% | 1.753% | 10.762% | 2.048% | |
| M0017 | −0.274% | 0.191% | −5.312% | 16.424% | −5.039% | |||
| Avg. M7 | −0.284% | 0.015% | −1.780% | 4.996% | −1.495% | |||
| M8 | M0018 | −0.331% | 0.218% | −0.372% | 6.026% | −0.041% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arregui, F.J.; Pastor-Jabaloyes, L.; Mercedes, A.V.; Gavara, F.J. Accuracy of Solid-State Residential Water Meters under Intermittent Flow Conditions. Sensors 2020, 20, 5339. https://doi.org/10.3390/s20185339
Arregui FJ, Pastor-Jabaloyes L, Mercedes AV, Gavara FJ. Accuracy of Solid-State Residential Water Meters under Intermittent Flow Conditions. Sensors. 2020; 20(18):5339. https://doi.org/10.3390/s20185339
Chicago/Turabian StyleArregui, Francisco J., Laura Pastor-Jabaloyes, Angel V. Mercedes, and Francesc J. Gavara. 2020. "Accuracy of Solid-State Residential Water Meters under Intermittent Flow Conditions" Sensors 20, no. 18: 5339. https://doi.org/10.3390/s20185339
APA StyleArregui, F. J., Pastor-Jabaloyes, L., Mercedes, A. V., & Gavara, F. J. (2020). Accuracy of Solid-State Residential Water Meters under Intermittent Flow Conditions. Sensors, 20(18), 5339. https://doi.org/10.3390/s20185339







