New Insights into the Design and Application of a Passive Acoustic Monitoring System for the Assessment of the Good Environmental Status in Spanish Marine Waters
Abstract
:1. Introduction
2. Materials and Methods
2.1. SAMARUC as Passive Acoustic Monitoring Device
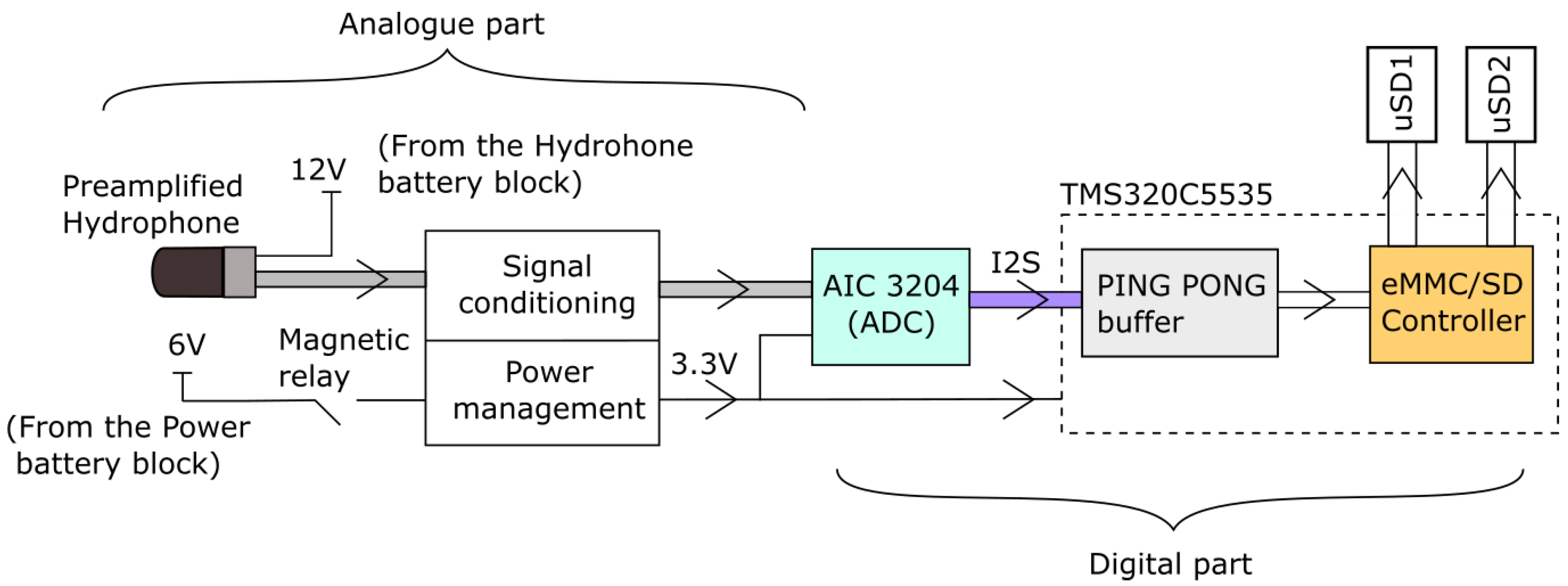
2.1.1. Specific Electronics
2.1.2. File System
2.1.3. Housing and Battery Blocks
2.1.4. Ringed Buoys and Hydrophone Protection
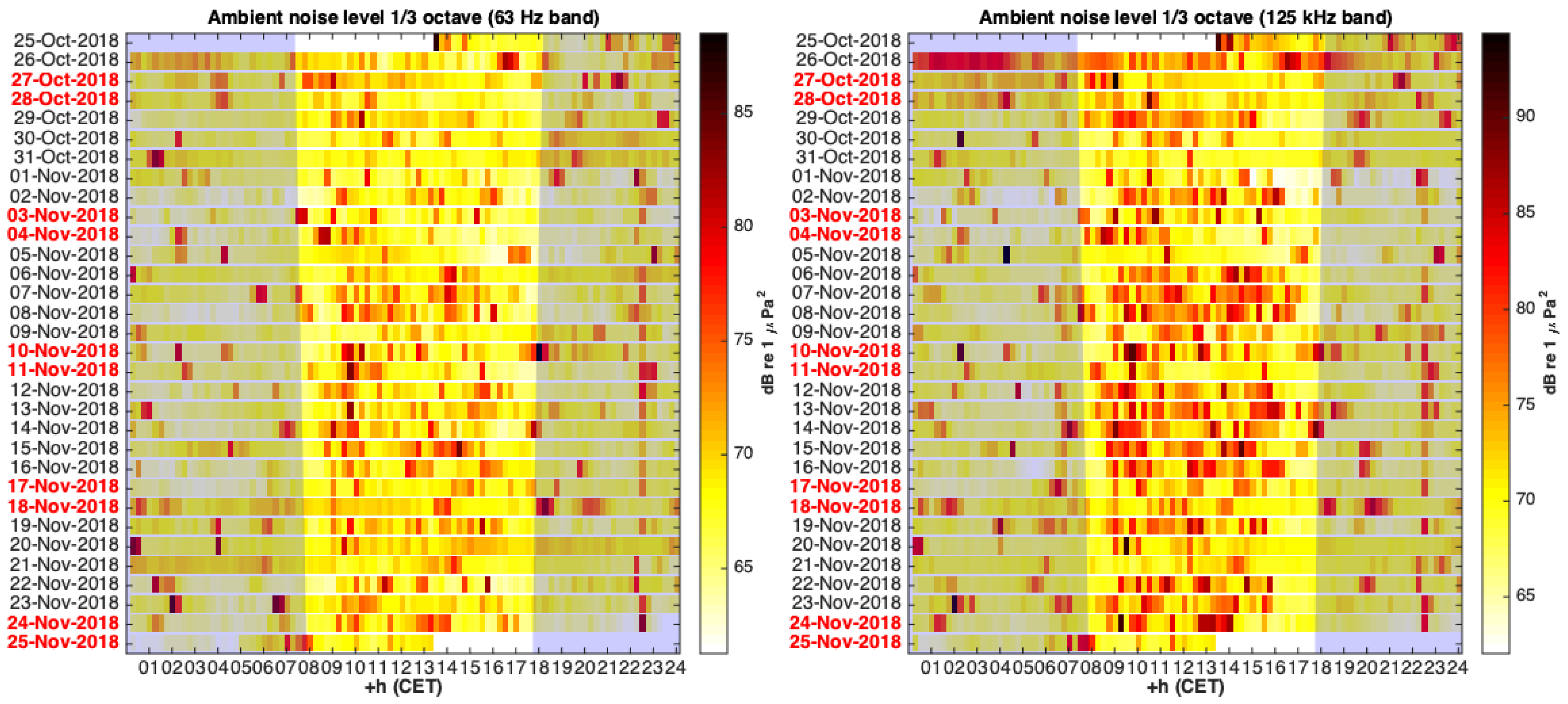
2.2. Data Acquisition and Study Area
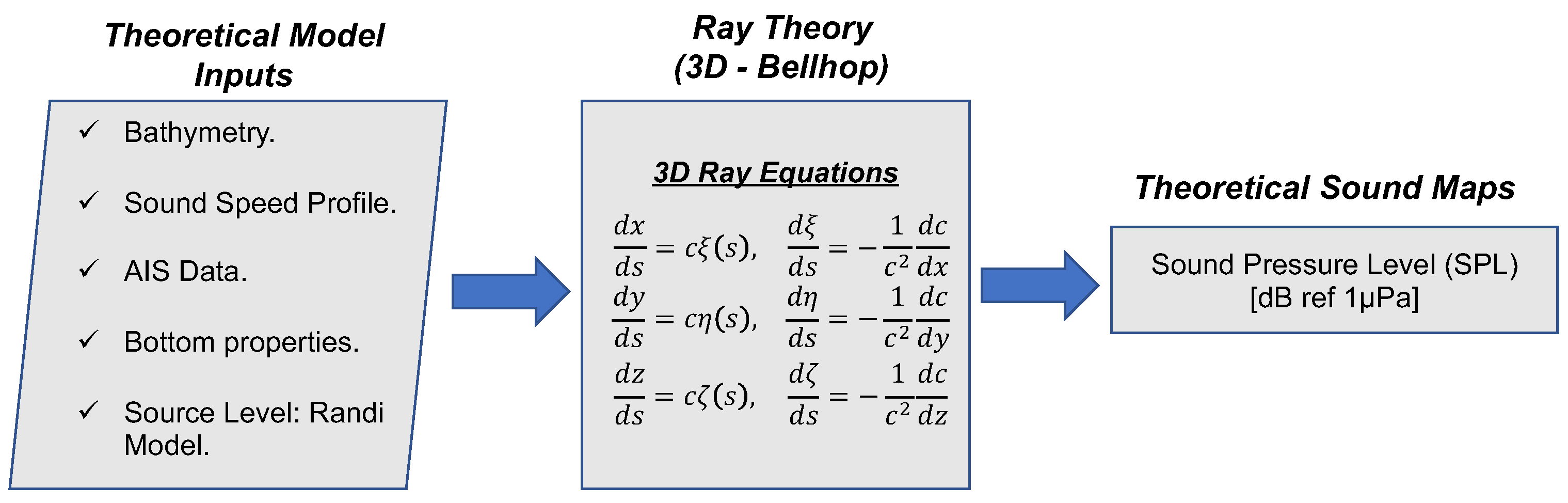
2.3. Numerical Modelling of Sound Propagation
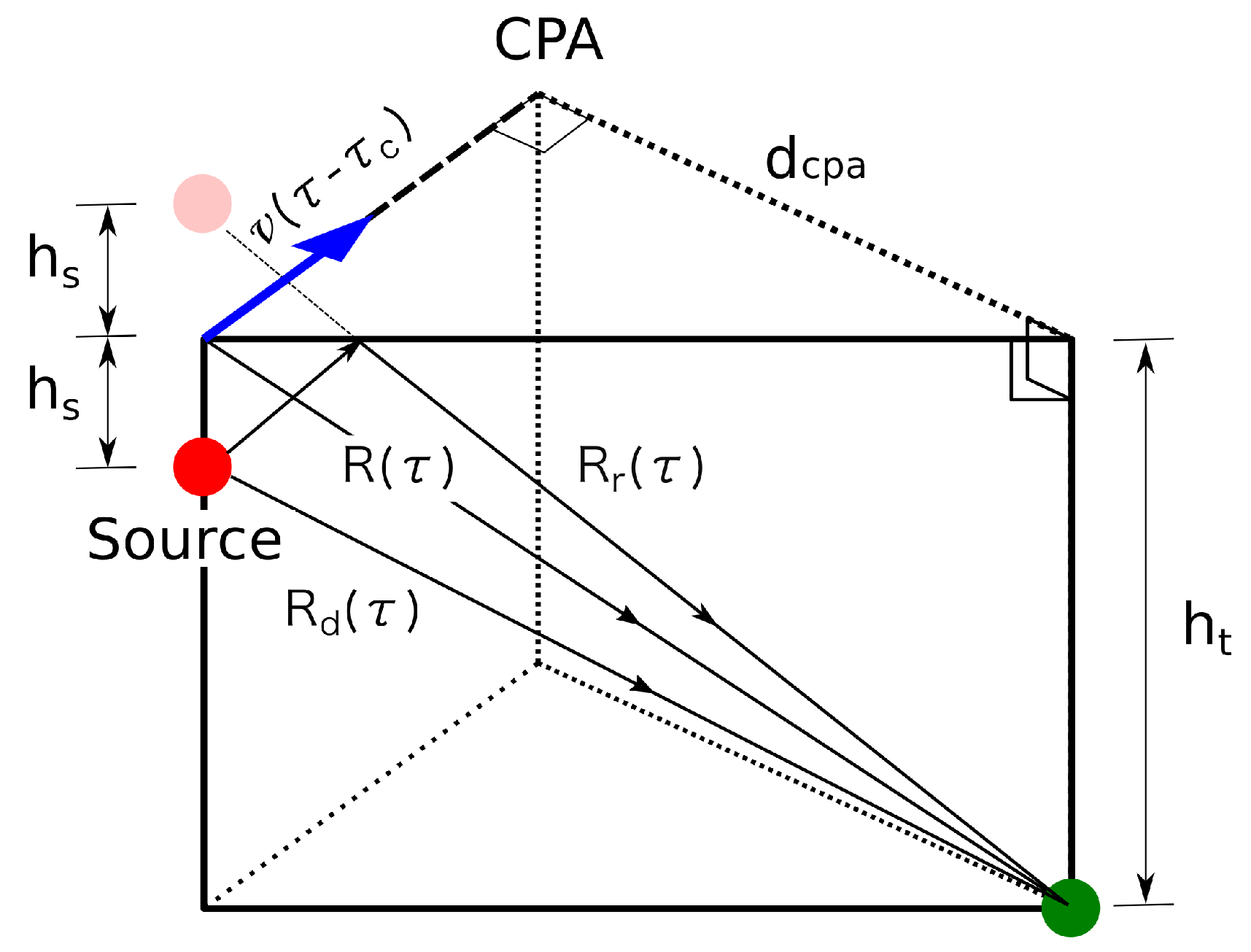
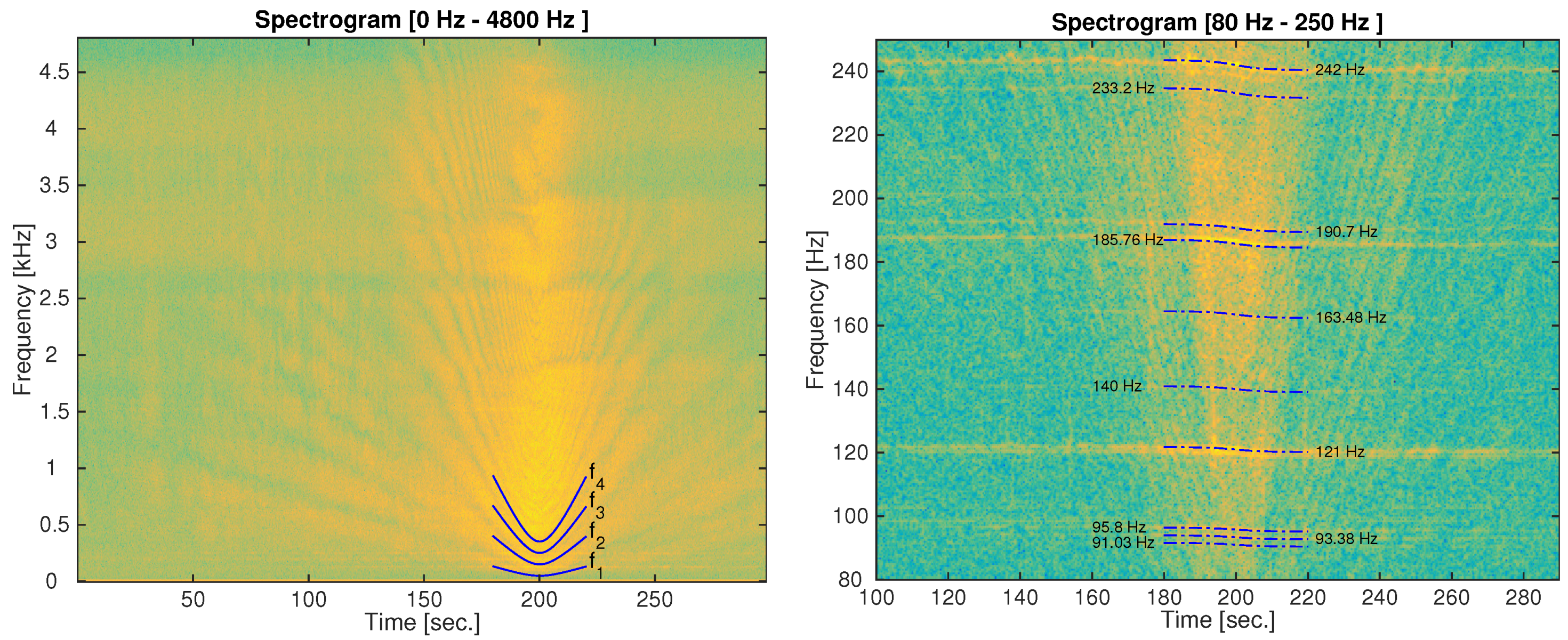
2.4. Tracking Ships Using Acoustic Signatures of Engine Propeller Noise
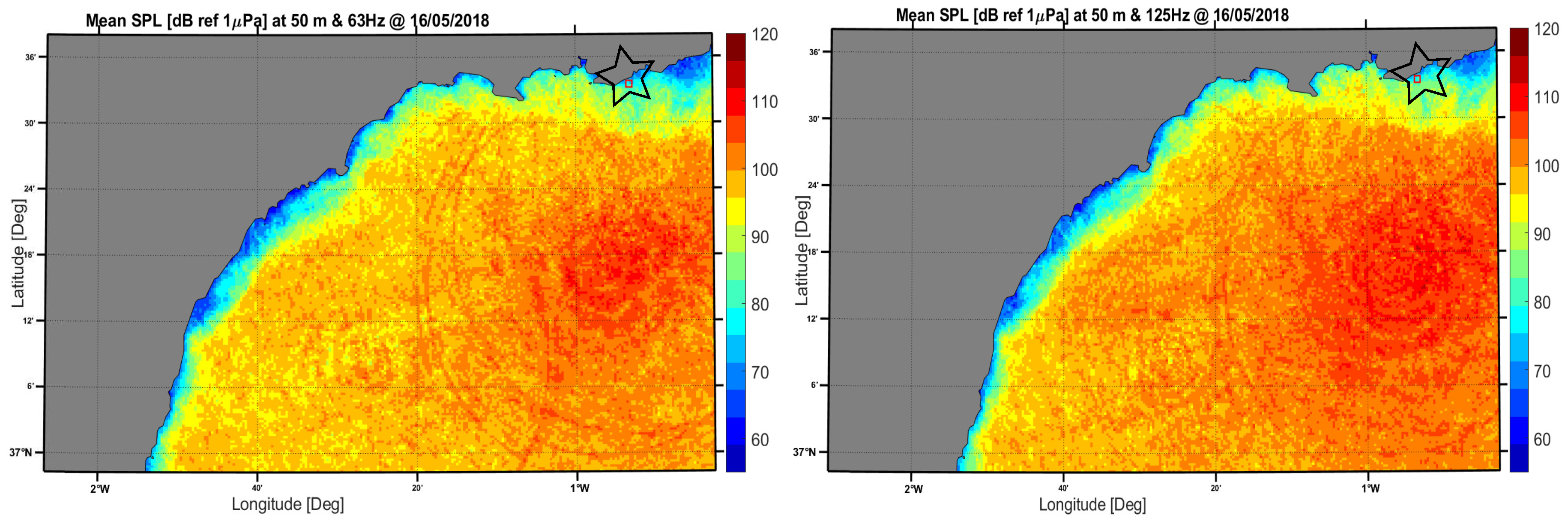
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TGNoise | Technical Group on Underwater Noise |
| PAM | Passive Acoustic Monitoring |
| MSFD | Marine Strategy Framework Directive |
| GES | Good Environmental Status |
| DSP | Digital Signal Processor |
| ADC | Analog to Digital Converter |
| EMC | Electromagnetic Compatibility |
| GEBCO | General Bathymetric Chart of the Oceans |
| PPT | Parts per Thousand |
| AIS | Automatic Identification System |
| SPL | Sound Pressure Level |
| V | Volts |
| CPA | Closest Point of Approach |
Appendix A
References
- Dekeling, R.; Tasker, M.; Van Der Graaf, S.; Ainslie, M.; Andersson, M.; André, M.; Borsani, J.; Brensing, K.; Castellote, M.; Cronin, D.; et al. Monitoring Guidance for Underwater noise in European Seas: Monitoring Guidance specifications, Part II: Monitoring Guidance Specifications. In JRC Scientific and Policy Report EUR 26555 EN; Publications Office of the European Union: Luxembourg, 2014; pp. 1–49. [Google Scholar]
- Lara, G.; Bou-Cabo, M.; Esteban, J.A.; Espinosa, V.; Miralles, R. Design and Application of a Passive Acoustic Monitoring System in the Spanish Implementation of the Marine Strategy Framework Directive. In Proceedings of the 6th International Electronic Conference on Sensors and Applications session Applications, Basel, Switzerland, 15–30 November 2019; MDPI: Basel, Switzerland. [Google Scholar] [CrossRef] [Green Version]
- SAMARUC Web. Available online: http://samaruc.webs.upv.es (accessed on 2 June 2020).
- Breeding, J.E.; Plug, L.A.; Bradley, E.L.; Walrod, M.H.; McBride, W. Research Ambient Noise Directionality (RANDI) 3.1—Physics Description; Technical Report NRL/FR/7176-95-9628; Naval Research Laboratory: Stennis Space Center, MS, USA, 8 August 1996. [Google Scholar]
- Explora (Patents and Software) UPV Web. Available online: https://aplicat.upv.es/exploraupv/ficha-tecnologia/patente_software/15065?busqueda=R-16202-2012 (accessed on 15 July 2020).
- Etter, P.C. Underwater Acoustic Modeling and Simulation, 5th ed.; CRC Press: Boca Raton, FL, USA, 2018; ISBN-10: 1138054925. [Google Scholar]
- Porter, M.B.; Liu, Y. Finite element Ray Tracing. In. J. Theor. Comput. Acous. 1994, 2, 947–956. [Google Scholar]
- Hovem, J.M. Ray Trace Modeling of Underwater Sound Propagation. In Modeling and Measurement Methods for Acoustic Waves and for Acoustic Microdevices; InTechOpen: London, UK, 2013; p. 22. [Google Scholar] [CrossRef]
- EMODnet. Oceans Physics at Your Fingertips. Available online: https://www.emodnet-physics.eu/Map/ (accessed on 9 September 2019).
- GEBCO. Gridded Bathymetric Data. Available online: https://www.gebco.net/data_and_products/gridded_bathymetry_data/ (accessed on 9 September 2019).
- Mackenzie, K.V. Nine-term equation for the sound speed in the oceans. In. J. Acoust. Soc. Am. 1981, 70, 807–812. [Google Scholar] [CrossRef]
- Ross, D.; Kuperman, W.A. Mechanics of Underwater Noise. J. Acoust. Soc. Am. 1989, 86, 1626. [Google Scholar] [CrossRef]
- Gervaise, C.; Kinda, B.G.; Bonnel, J.; Stéphan, Y.; Vallez, S. Passive geoacoustic inversion with a single hydrophone using broadband ship noise. In. J. Acoust. Soc. Am. 2012, 131, 1999–2010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crocker, S.E.; Nielsen, P.L.; Miller, J.H.; Siderius, M. Geoacoustic inversion of ship radiated noise in shallow water using data from a single hydrophone. In. J. Acoust. Soc. Am. 2014, 136, EL362–EL368. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.; Yang, K.; Duan, R.; Lei, Z. Joint Estimation of Source Range and Depth Using a Bottom-Deployed Vertical Line Array in Deep Water. Sensors 2017, 17, 1315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tong, J.; Hu, Y.; Bao, M.; Xie, W. Target tracking using acoustic signatures of light-weight aircraft propeller noise. In Proceedings of the 2013 IEEE China Summit and International Conference on Signal and Information Processing, Beijing, China, 6–10 July 2013; pp. 20–24. [Google Scholar] [CrossRef]
- Lo, K.W.; Perry, S.W.; Ferguson, B.G. Aircraft flight parameter estimation using acoustical Lloyd’s mirror effect. IEEE. Trans. Aerosp. Electron. Syst. 2002, 38, 137–151. [Google Scholar] [CrossRef]
- Commission Decision (EU) 2017/848. OJEU 2017, L 125, 43–74.
- Miralles, R.; Lara, G.; Gosalbez, J.; Bosch, I.; León, A. Improved visualization of large temporal series for the evaluation of good environmental status. In. Appl. Acoust. 2019, 148, 55–61. [Google Scholar] [CrossRef]



| Sensitivity of the pre-amplified hydrophone | −167 dB re 1 V/uPa (Cetacean Research C57) |
| # batteries used (with/without preamplification) | 36/28 (type D) |
| AIC3204 programmable gain | 0–30 dB |
| Storage capacity | Currenty: (1 + 1) Tbytes |
| Sampling rate | 192 kHz |
| System bandwidth ±3 dB | 10 Hz–96 kHz |
| Maximum depth | 500 m. (Housing and buoys) |
| Autonomy | Up to 4 months |
| Element | Functionality |
|---|---|
| File system | Increase the system storage capacity to 1 TByte (presently) |
| Specific electronics | Isolate the grounds. Use a second microSD card (storage capacity × 2) |
| Housing | 6082 aluminum, widely used in marine applications |
| Battery block | Maximize energy density according to the tube dimensions |
| Flotation buoys | Ease of handling and avoidance of acoustic shadows |
| Protection cage | Hydrophone protection |
| 16 May 2018 | 63 Hz | ||||
|---|---|---|---|---|---|
| Hours | 6:00–7:00 h | 14:00–15:00 h | 19:00–20:00 h | 23:00–00:00 h | Average |
| SAMARUC | 78 ± 13 | 85.3 ± 0.5 | 79.7 ± 0.7 | 83.1 ± 1.2 | 82 ± 6 |
| Theoretical results | 81 ± 3 | 91 ± 5 | 78 ± 3 | 84 ± 2 | 83 ± 5 |
| 125 Hz | |||||
| Hours | 6:00–7:00 h | 14:00–15:00 h | 19:00–20:00 h | 23:00–00:00 h | Average |
| SAMARUC | 85 ± 4 | 90 ± 2 | 83.8 ± 0.3 | 81 ± 2 | 85 ± 9 |
| Theoretical results | 83 ± 4 | 93 ± 3 | 81.4 ± 1.1 | 81 ± 4 | 85 ± 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lara, G.; Miralles, R.; Bou-Cabo, M.; Esteban, J.A.; Espinosa, V. New Insights into the Design and Application of a Passive Acoustic Monitoring System for the Assessment of the Good Environmental Status in Spanish Marine Waters. Sensors 2020, 20, 5353. https://doi.org/10.3390/s20185353
Lara G, Miralles R, Bou-Cabo M, Esteban JA, Espinosa V. New Insights into the Design and Application of a Passive Acoustic Monitoring System for the Assessment of the Good Environmental Status in Spanish Marine Waters. Sensors. 2020; 20(18):5353. https://doi.org/10.3390/s20185353
Chicago/Turabian StyleLara, Guillermo, Ramón Miralles, Manuel Bou-Cabo, José Antonio Esteban, and Víctor Espinosa. 2020. "New Insights into the Design and Application of a Passive Acoustic Monitoring System for the Assessment of the Good Environmental Status in Spanish Marine Waters" Sensors 20, no. 18: 5353. https://doi.org/10.3390/s20185353
APA StyleLara, G., Miralles, R., Bou-Cabo, M., Esteban, J. A., & Espinosa, V. (2020). New Insights into the Design and Application of a Passive Acoustic Monitoring System for the Assessment of the Good Environmental Status in Spanish Marine Waters. Sensors, 20(18), 5353. https://doi.org/10.3390/s20185353






