Vibration Analysis of Post-Buckled Thin Film on Compliant Substrates
Abstract
1. Introduction
2. Buckling Analysis
3. Vibration Analysis of Post-Buckled System
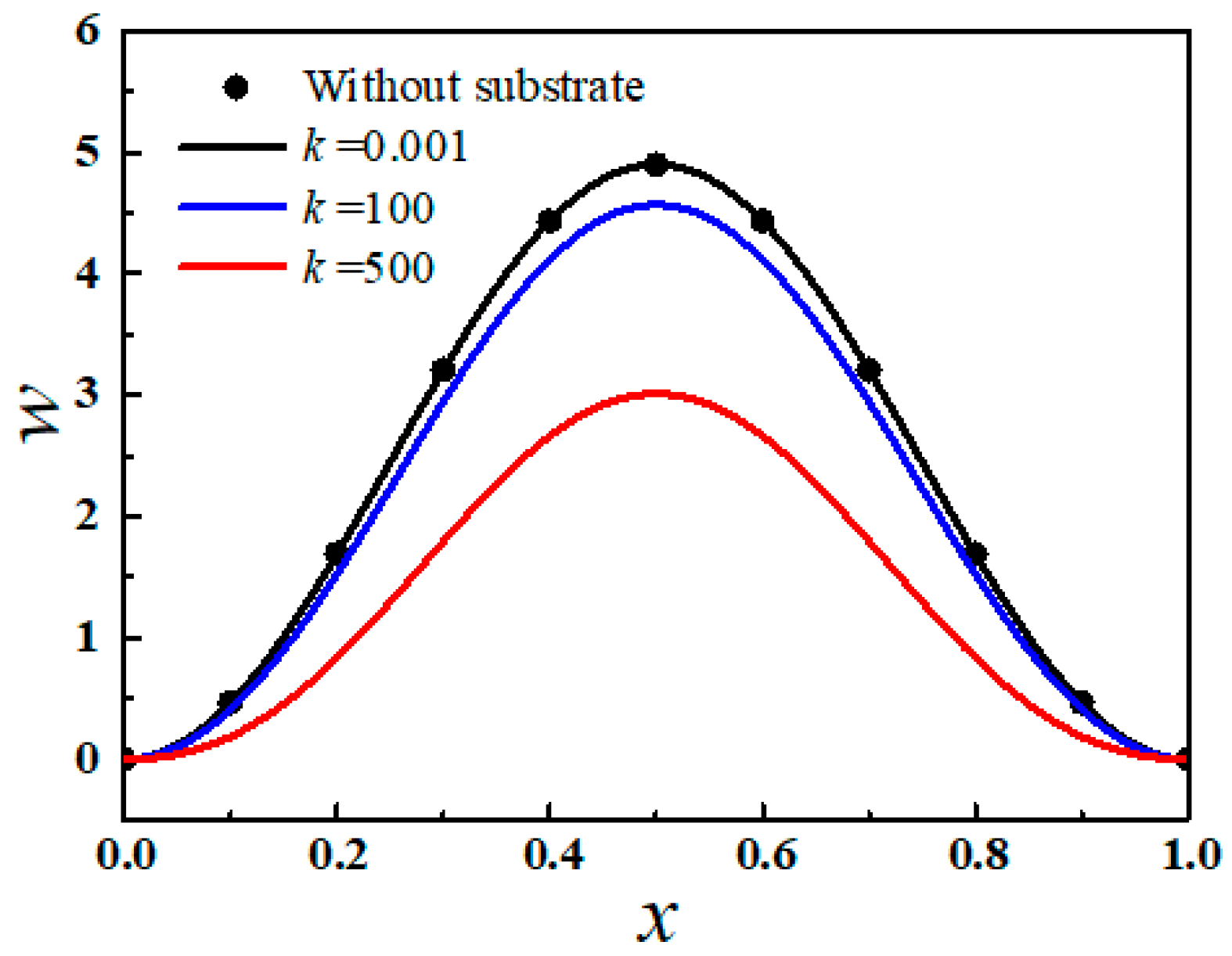
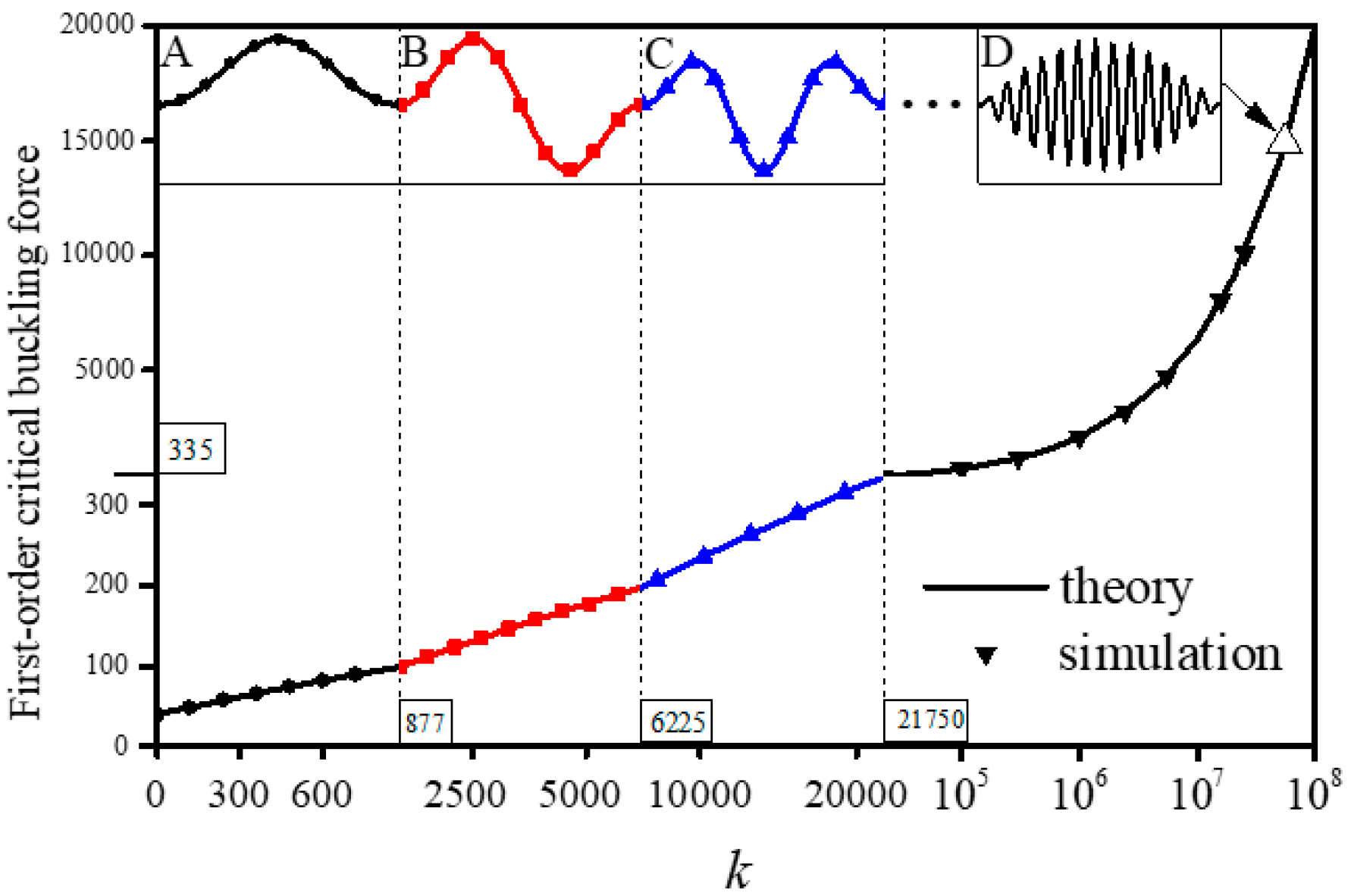
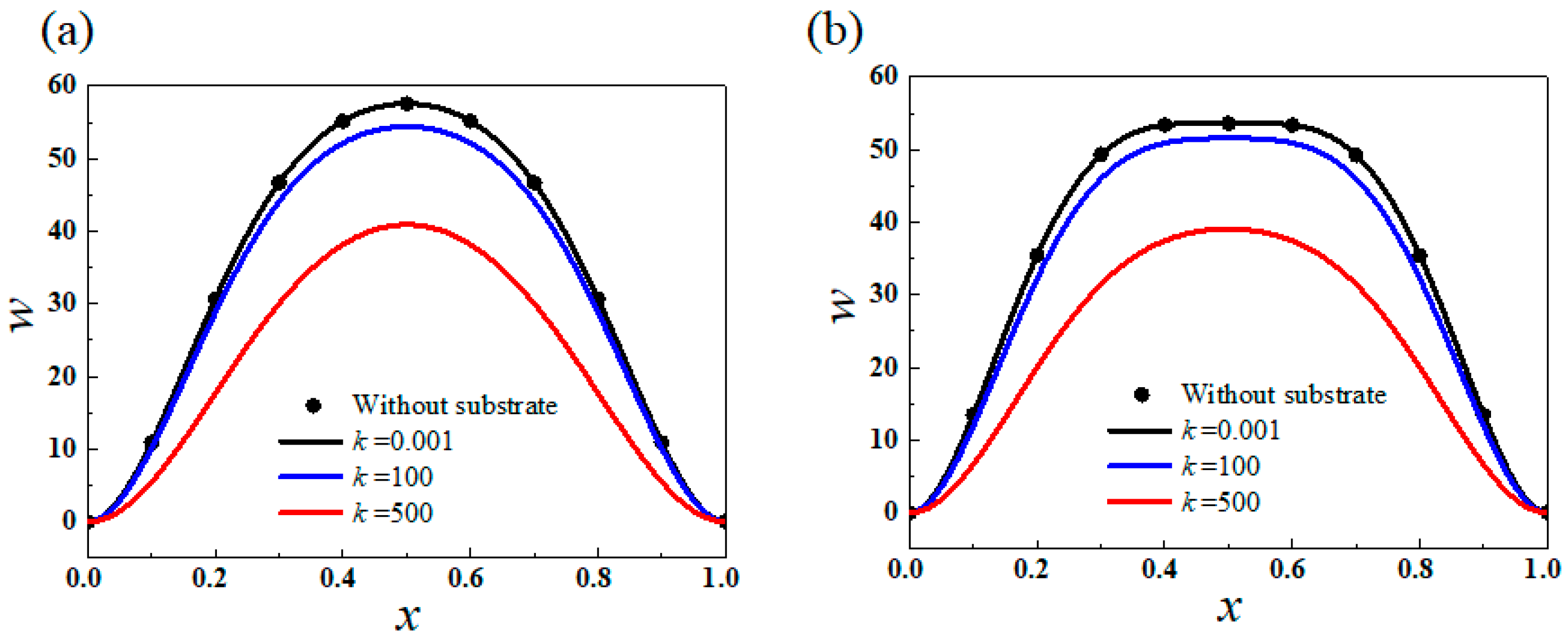
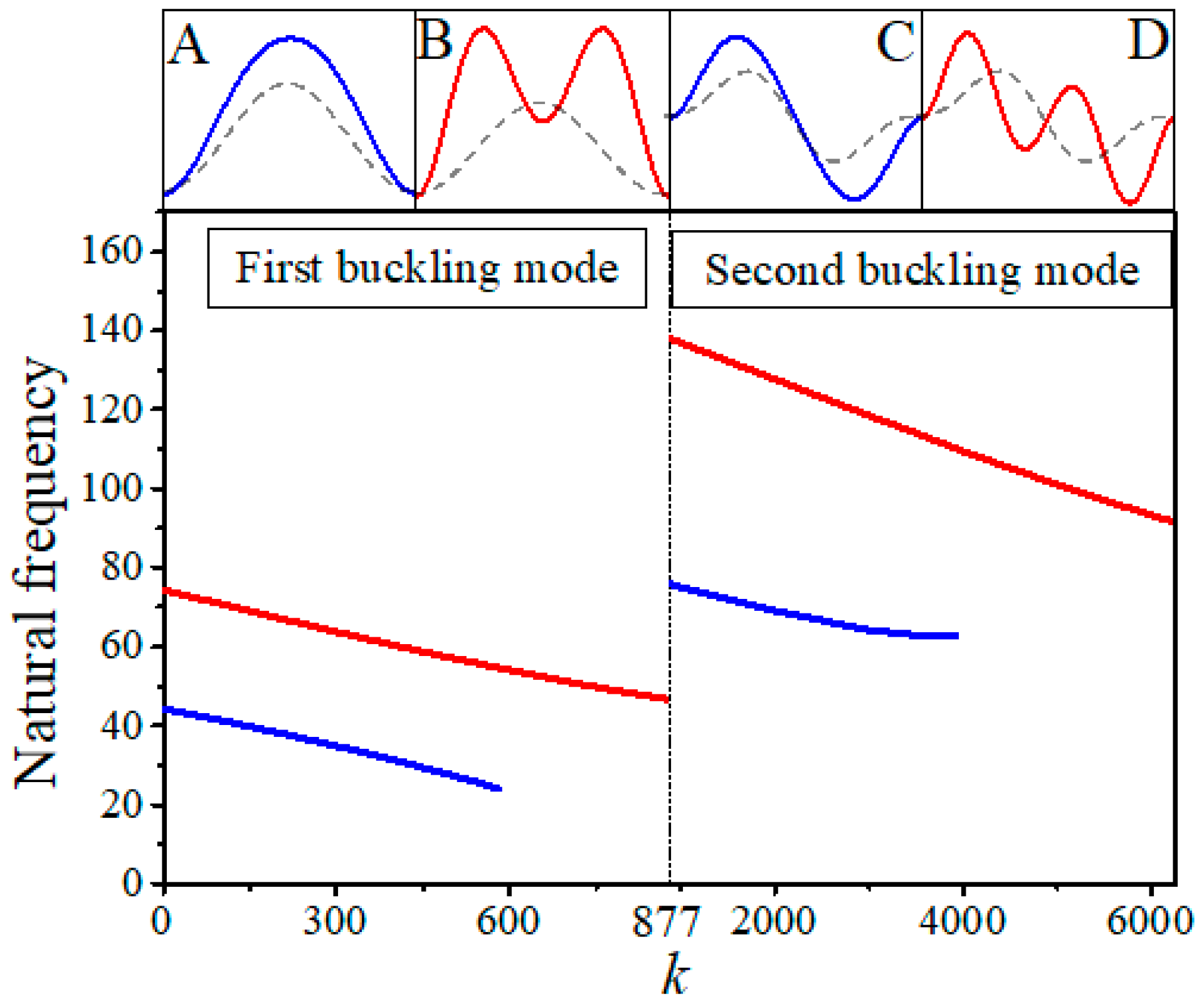
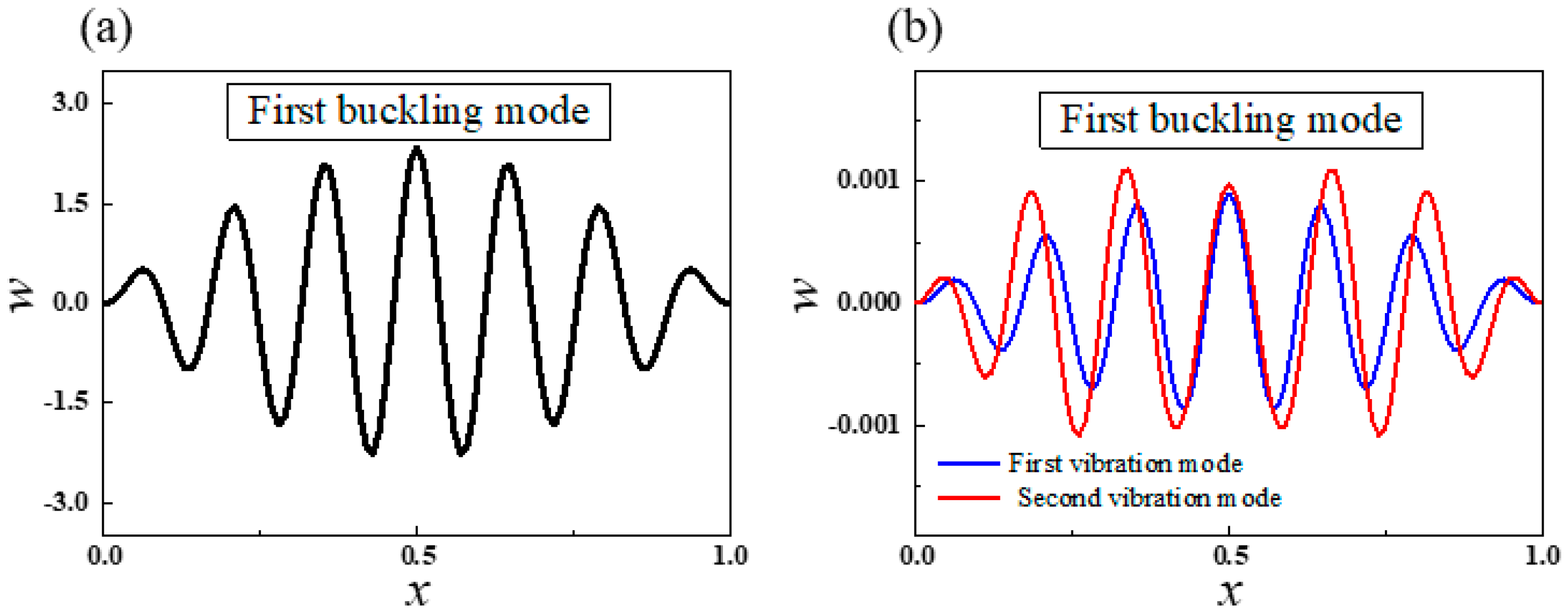
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rogers, J.A. Wearable Electronics Nanomesh on-skin electronics. Nat. Nanotechnol. 2017, 12, 839–840. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.H.; Huang, Y.G.; Rogers, J.A. Mechanics of stretchable batteries and supercapacitors. Curr. Opin. Solid State Mater. Sci. 2015, 19, 190–199. [Google Scholar] [CrossRef]
- Ma, Q.; Cheng, H.Y.; Jang, K.I.; Luan, H.W.; Hwang, K.C.; Rogers, J.A.; Huang, Y.G.; Zhang, Y.H. A nonlinear mechanics model of bio-inspired hierarchical lattice materials consisting of horseshoe microstructures. J. Mech. Phys. Solids 2016, 90, 179–202. [Google Scholar] [CrossRef] [PubMed]
- Song, J. Mechanics of stretchable electronics. Curr. Opin. Solid State Mater. Sci. 2015, 19, 160–170. [Google Scholar] [CrossRef]
- Song, J.Z.; Feng, X.; Huang, Y.G. Mechanics and thermal management of stretchable inorganic electronics. Natl. Sci. Rev. 2016, 3, 128–143. [Google Scholar] [CrossRef]
- Ma, Y.J.; Zhang, Y.C.; Cai, S.S.; Han, Z.Y.; Liu, X.; Wang, F.L.; Cao, Y.; Wang, Z.H.; Li, H.F.; Chen, Y.H.; et al. Flexible Hybrid Electronics for Digital Healthcare. Adv. Mater. 2020, 32, 1902062. [Google Scholar] [CrossRef]
- Yan, D.; Chang, J.; Zhang, H.; Liu, J.; Song, H.; Xue, Z.; Zhang, F.; Zhang, Y. Soft three-dimensional network materials with rational bio-mimetic designs. Nat. Commun. 2020, 11, 1180. [Google Scholar] [CrossRef]
- Wu, H.; Tian, Y.; Luo, H.B.; Zhu, H.; Duan, Y.Q.; Huang, Y.A. Fabrication Techniques for Curved Electronics on Arbitrary Surfaces. Adv. Mater. Technol. 2020, 5, 29. [Google Scholar] [CrossRef]
- Li, H.C.; Xu, Y.; Li, X.M.; Chen, Y.; Jiang, Y.; Zhang, C.X.; Lu, B.W.; Wang, J.; Ma, Y.J.; Chen, Y.H.; et al. Epidermal Inorganic Optoelectronics for Blood Oxygen Measurement. Adv. Healthc. Mater. 2017, 6, 1601063. [Google Scholar] [CrossRef]
- Wang, C.; Hwang, D.; Yu, Z.B.; Takei, K.; Park, J.; Chen, T.; Ma, B.W.; Javey, A. User-interactive electronic skin for instantaneous pressure visualization. Nat. Mater. 2013, 12, 899–904. [Google Scholar] [CrossRef]
- Webb, R.C.; Ma, Y.J.; Krishnan, S.; Li, Y.H.; Yoon, S.; Guo, X.G.; Feng, X.; Shi, Y.; Seidel, M.; Cho, N.H.; et al. Epidermal devices for noninvasive, precise, and continuous mapping of macrovascular and microvascular blood flow. Sci. Adv. 2015, 1, 1500701. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Zhang, Y.H.; Malyarchuk, V.; Jia, L.; Jang, K.I.; Webb, R.C.; Fu, H.R.; Shi, Y.; Zhou, G.Y.; Shi, L.K.; et al. Epidermal photonic devices for quantitative imaging of temperature and thermal transport characteristics of the skin. Nat. Commun. 2014, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Choi, J.; Hourlier-Fargette, A.; Xue, Y.; Chung, H.U.; Lee, J.Y.; Wang, X.; Xie, Z.; Kang, D.; Wang, H.; et al. Relation between blood pressure and pulse wave velocity for human arteries. Proc. Natl. Acad. Sci. USA 2018, 115, 11144–11149. [Google Scholar] [CrossRef] [PubMed]
- Someya, T.; Sekitani, T.; Iba, S.; Kato, Y.; Kawaguchi, H.; Sakurai, T. A large-area, flexible pressure sensor matrix with organic field-effect transistors for artificial skin applications. Proc. Natl. Acad. Sci. USA 2004, 101, 9966–9970. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, M.; Shim, H.J.; Ghaffari, R.; Cho, H.R.; Son, D.; Jung, Y.H.; Soh, M.; Choi, C.; Jung, S.; et al. Stretchable silicon nanoribbon electronics for skin prosthesis. Nat. Commun. 2014, 5, 1–11. [Google Scholar] [CrossRef]
- Yang, S.X.; Chen, Y.C.; Nicolini, L.; Pasupathy, P.; Sacks, J.; Su, B.; Yang, R.; Sanchez, D.; Chang, Y.F.; Wang, P.L.; et al. “Cut-and-Paste” Manufacture of Multiparametric Epidermal Sensor Systems. Adv. Mater. 2015, 27, 6423–6430. [Google Scholar] [CrossRef]
- Jin, H.C.; Abelson, J.R.; Erhardt, M.K.; Nuzzo, R.G. Soft lithographic fabrication of an image sensor array on a curved substrate. J. Vac. Sci. Technol. B 2004, 22, 2548–2551. [Google Scholar] [CrossRef]
- Ko, H.C.; Stoykovich, M.P.; Song, J.Z.; Malyarchuk, V.; Choi, W.M.; Yu, C.J.; Geddes, J.B.; Xiao, J.L.; Wang, S.D.; Huang, Y.G.; et al. A hemispherical electronic eye camera based on compressible silicon optoelectronics. Nature 2008, 454, 748–753. [Google Scholar] [CrossRef]
- Jung, I.W.; Xiao, J.L.; Malyarchuk, V.; Lu, C.F.; Li, M.; Liu, Z.J.; Yoon, J.; Huang, Y.G.; Rogers, J.A. Dynamically tunable hemispherical electronic eye camera system with adjustable zoom capability. Proc. Natl. Acad. Sci. USA 2011, 108, 1788–1793. [Google Scholar] [CrossRef]
- Harrison, C.; Stafford, C.M.; Zhang, W.H.; Karim, A. Sinusoidal phase grating created by a tunably buckled surface. ApPhL 2004, 85, 4016–4018. [Google Scholar] [CrossRef]
- Yang, D.; He, L.H. Photo-triggered wrinkling of glassy nematic films. SmMaS 2014, 23. [Google Scholar] [CrossRef]
- Li, Z.W.; Zhai, Y.; Wang, Y.; Wendland, G.M.; Yin, X.B.; Xiao, J.L. Harnessing Surface Wrinkling-Cracking Patterns for Tunable Optical Transmittance. Adv. Opt. Mater. 2017, 5, 170425. [Google Scholar] [CrossRef]
- Lee, E.; Zhang, M.L.; Cho, Y.; Cui, Y.; Van der Spiegel, J.; Engheta, N.; Yang, S. Tilted Pillars on Wrinkled Elastomers as a Reversibly Tunable Optical Window. Adv. Mater. 2014, 26, 4127–4133. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Jiang, H.; Liu, Z.J.; Khang, D.Y.; Huang, Y.; Rogers, J.A.; Lu, C.; Koh, C.G. Buckling of a stiff thin film on a compliant substrate in large deformation. IJSS 2008, 45, 3107–3121. [Google Scholar] [CrossRef]
- Wang, S.D.; Song, J.Z.; Kim, D.H.; Huang, Y.G.; Rogers, J.A. Local versus global buckling of thin films on elastomeric substrates. ApPhL 2008, 93, 023126. [Google Scholar] [CrossRef]
- Huck, W.T.S.; Bowden, N.; Onck, P.; Pardoen, T.; Hutchinson, J.W.; Whitesides, G.M. Ordering of spontaneously formed buckles on planar surfaces. Langmuir 2000, 16, 3497–3501. [Google Scholar] [CrossRef]
- Sharp, J.S.; Jones, R.A.L. Micro-buckling as a route towards surface Patterning. Adv. Mater. 2002, 14, 799–802. [Google Scholar] [CrossRef]
- Khang, D.Y.; Jiang, H.Q.; Huang, Y.; Rogers, J.A. A stretchable form of single-crystal silicon for high-performance electronics on rubber substrates. Science 2006, 311, 208–212. [Google Scholar] [CrossRef]
- Chen, X.; Hutchinson, J.W. Herringbone buckling patterns of compressed thin films on compliant substrates. J. Appl. Mech. Trans. ASME 2004, 71, 597–603. [Google Scholar] [CrossRef]
- Huang, Z.Y.; Hong, W.; Suo, Z. Nonlinear analyses of wrinkles in a film bonded to a compliant substrate. J. Mech. Phys. Solids 2005, 53, 2101–2118. [Google Scholar] [CrossRef]
- Su, Y.W.; Zhao, H.Y.; Liu, S.Y.; Li, R.; Wang, Y.H.; Wang, Y.Z.; Bian, J.; Huang, Y.A. Buckling of beams with finite prebuckling deformation. IJSS 2019, 165, 148–159. [Google Scholar] [CrossRef]
- Pang, W.; Cheng, X.; Zhao, H.; Guo, X.; Ji, Z.; Li, G.; Liang, Y.; Xue, Z.; Song, H.; Zhang, F.; et al. Electro-mechanically controlled assembly of reconfigurable 3D mesostructures and electronic devices based on dielectric elastomer platforms. Natl. Sci. Rev. 2020, 7, 342–354. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Emam, S.A. Exact solution and stability of postbuckling configurations of beams. Nonlinear Dyn. 2008, 54, 395–408. [Google Scholar] [CrossRef]
- Emam, S.A. Approximate analytical solutions for the nonlinear free vibrations of composite beams in buckling. CmpSt 2013, 100, 186–194. [Google Scholar] [CrossRef]
- Cristobal, G.; Irina, T.; Andrea, Z. The Effect of Polycaprolactone Nanofibers on the Dynamic and Impact Behavior of Glass Fibre Reinforced Polymer Composites. J. Compos. Sci. 2018, 2, 43. [Google Scholar]
- Neukirch, S.; Frelat, J.; Goriely, A.; Maurini, C. Vibrations of post-buckled rods: The singular inextensible limit. J. Sound Vibrat. 2012, 331, 704–720. [Google Scholar] [CrossRef][Green Version]
- Emam, S.A.; Nayfeh, A.H. Non-linear response of buckled beams to 1:1 and 3:1 internal resonances. Int. J. Non Linear Mech. 2013, 52, 12–25. [Google Scholar] [CrossRef]
- Ansari, R.; Ashrafi, M.A.; Pourashraf, T.; Hemmatnezhad, M. Vibration Analysis of a Postbuckled Microscale FG Beam Based on Modified Couple Stress Theory. SV 2014, 2014. [Google Scholar] [CrossRef]
- Shojaei, M.F.; Ansari, R.; Mohammadi, V.; Rouhi, H. Nonlinear forced vibration analysis of postbuckled beams. Arch. Appl. Mech. 2014, 84, 421–440. [Google Scholar] [CrossRef]
- Emam, S.A.; Eltaher, M.A.; Khater, M.E.; Abdalla, W.S. Postbuckling and Free Vibration of Multilayer Imperfect Nanobeams under a Pre-Stress Load. Appl. Sci. 2018, 8, 2238. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, X. Dynamic behaviors of controllably buckled thin films. ApPhL 2009, 95, 231915. [Google Scholar] [CrossRef]
- Wang, H.L.; Ning, X.; Li, H.B.; Luan, H.W.; Xue, Y.G.; Yu, X.G.; Fan, Z.C.; Li, L.M.; Rogers, J.A.; Zhang, Y.H.; et al. Vibration of mechanically-assembled 3D microstructures formed by compressive buckling. J. Mech. Phys. Solids 2018, 112, 187–208. [Google Scholar] [CrossRef] [PubMed]
- Tseng, W.Y.; Dugundji, J. Nonlinear Vibrations of a Buckled Beam Under Harmonic Excitation. J. Appl. Mech. 1971, 38, 467. [Google Scholar] [CrossRef]
- Huang, R. Kinetic wrinkling of an elastic film on a viscoelastic substrate. J. Mech. Phys. Solids 2005, 53, 63–89. [Google Scholar] [CrossRef]
- Sridhar, N.; Srolovitz, D.J.; Cox, B.N. Buckling and post-buckling kinetics of compressed thin films on viscous substrates. AcMat 2002, 50, 2547–2557. [Google Scholar] [CrossRef]
- Gioia, G.; DeSimone, A.; Ortiz, M.; Cuitino, A.M. Folding energetics in thin-film diaphragms. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2002, 458, 1223–1229. [Google Scholar] [CrossRef]
- Younesian, D.; Hosseinkhani, A.; Askari, H.; Esmailzadeh, E. Elastic and viscoelastic foundations: A review on linear and nonlinear vibration modeling and applications. Nonlinear Dyn. 2019, 97, 853–895. [Google Scholar] [CrossRef]
- Kounadis, A.N.; Mallis, J.; Sbarounis, A. Postbuckling analysis of columns resting on an elastic foundation. Arch. Appl. Mech. 2006, 75, 395–404. [Google Scholar] [CrossRef]
- Wen, C.Q.; Tang, L.; Yang, G.T. Buckling and post-buckling of pinned Euler beams on weakened Winkler foundation under thermal loading. JThSt 2020, 43, 529–542. [Google Scholar] [CrossRef]
- Akgoz, B.; Civalek, O. Bending analysis of FG microbeams resting on Winkler elastic foundation via strain gradient elasticity. CmpSt 2015, 134, 294–301. [Google Scholar] [CrossRef]
- Kim, D.; Shin, G.; Kang, Y.J.; Kim, W.; Ha, J.S. Fabrication of a Stretchable Solid-State Micro-Supercapacitor Array. ACS Nano 2013, 7, 7975–7982. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, Y.H.; Cho, J.; Lee, J.; Huang, X.; Jia, L.; Fan, J.A.; Su, Y.W.; Su, J.; Zhang, H.G.; et al. Stretchable batteries with self-similar serpentine interconnects and integrated wireless recharging systems. Nat. Commun. 2013, 4, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Xue, Y.H.; Roy, A.K.; Dai, L.M. Transparent and Stretchable High-Performance Supercapacitors Based on Wrinkled Graphene Electrodes. ACS Nano 2014, 8, 1039–1046. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Wang, C.Y.; Yue, Z.L.; Shu, K.W.; Wallace, G.G. Intrinsically Stretchable Supercapacitors Composed of Polypyrrole Electrodes and Highly Stretchable Gel Electrolyte. ACS Appl. Mater. Interfaces 2013, 5, 9008–9014. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Wang, Y.; Li, Y.; Fu, H. Vibration Analysis of Post-Buckled Thin Film on Compliant Substrates. Sensors 2020, 20, 5425. https://doi.org/10.3390/s20185425
Fan X, Wang Y, Li Y, Fu H. Vibration Analysis of Post-Buckled Thin Film on Compliant Substrates. Sensors. 2020; 20(18):5425. https://doi.org/10.3390/s20185425
Chicago/Turabian StyleFan, Xuanqing, Yi Wang, Yuhang Li, and Haoran Fu. 2020. "Vibration Analysis of Post-Buckled Thin Film on Compliant Substrates" Sensors 20, no. 18: 5425. https://doi.org/10.3390/s20185425
APA StyleFan, X., Wang, Y., Li, Y., & Fu, H. (2020). Vibration Analysis of Post-Buckled Thin Film on Compliant Substrates. Sensors, 20(18), 5425. https://doi.org/10.3390/s20185425




