Method for Remote Determination of Object Coordinates in Space Based on Exact Analytical Solution of Hyperbolic Equations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Linearization Method of Hyperbolic Equations
2.2. The Proposed Analytical Method for Determining the Coordinates of an Object in a Positioning System with 5 Base Stations
| Algorithm 1. Identifying of the true solution |
|
3. Results
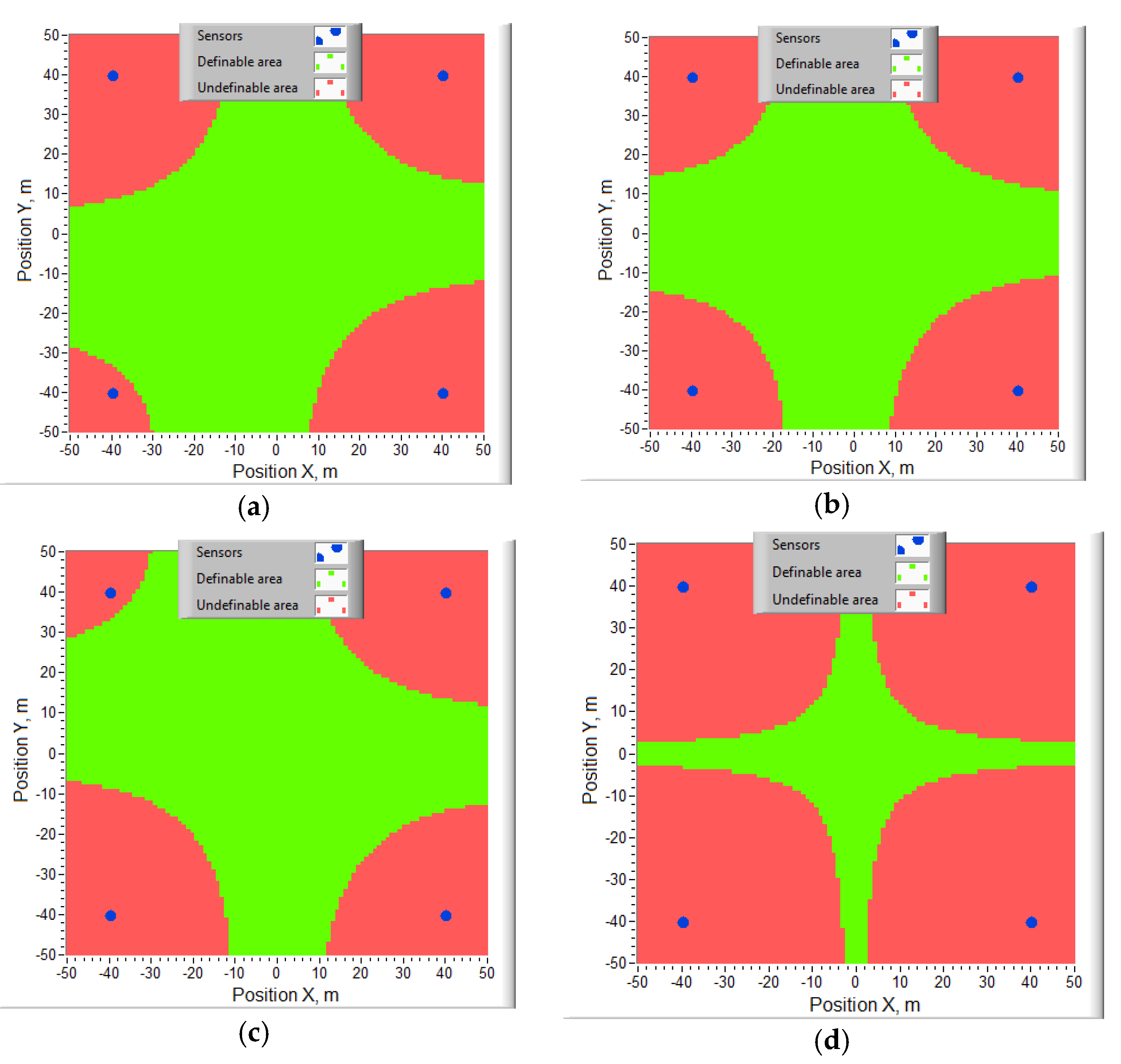
3.1. Spatial Ambiguity Problem
3.2. Influence of the TDoA Fluctuations on the Accuracy of Coordinate Estimation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weon, I.S.; Lee, S.G.; Ryu, J.K. Object Recognition Based Interpolation with 3D LIDAR and Vision for Autonomous Driving of an Intelligent Vehicle. IEEE Access 2020, 8, 65599–65608. [Google Scholar] [CrossRef]
- López-Sastre, R.J.; Herranz-Perdiguero, C.; Guerrero-Gómez-Olmedo, R.; Oñoro-Rubio, D.; Maldonado-Bascón, S. Boosting multi-vehicle tracking with a joint object detection and viewpoint estimation sensor. Sensors 2019, 19, 4062. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; So, A.M.C.; Li, Y. Robust convex approximation methods for TDOA-based localization under NLOS conditions. IEEE Trans. Signal Process. 2016, 64, 3281–3296. [Google Scholar] [CrossRef]
- Gan, Y.; Cong, X.; Sun, Y. Refinement of TOA localization with sensor position uncertainty in closed-form. Sensors 2020, 20, 390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, N.H.; Doğançay, K. Optimal geometry analysis for multistatic TOA localization. IEEE Trans. Signal Process. 2016, 64, 4180–4193. [Google Scholar] [CrossRef]
- Deak, G.; Curran, K.; Condell, J. A survey of active and passive indoor localisation systems. Comput. Commun. 2012, 35, 1939–1954. [Google Scholar] [CrossRef]
- Ferreira, A.F.G.; Fernandes, D.M.A.; Catarino, A.P.; Monteiro, J.L. Localization and positioning systems for emergency responders: A survey. IEEE Commun. Surv. Tutor. 2017, 19, 2836–2870. [Google Scholar] [CrossRef]
- Hashemi, A.; Cao, Y.; Casbeer, D.W.; Yin, G. Unmanned aerial vehicle circumnavigation using noisy range-based measurements without global positioning system information. J. Dyn. Syst. Meas. Control 2015, 137, 031009. [Google Scholar] [CrossRef]
- Gharghan, S.K.; Nordin, R.; Ismail, M.; Abd Ali, J. Accurate wireless sensor localization technique based on hybrid PSO-ANN algorithm for indoor and outdoor track cycling. IEEE Sens. J. 2015, 16, 529–541. [Google Scholar] [CrossRef]
- Sadowski, S.; Spachos, P. Rssi-based indoor localization with the internet of things. IEEE Access 2018, 6, 30149–30161. [Google Scholar] [CrossRef]
- Ramadhan, H.; Yustiawan, Y.; Kwon, J. Applying Movement Constraints to BLE RSSI-Based Indoor Positioning for Extracting Valid Semantic Trajectories. Sensors 2020, 20, 527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, N.H.; Doğançay, K. Instrumental variable based Kalman filter algorithm for three-dimensional AOA target tracking. IEEE Signal Process. Lett. 2018, 25, 1605–1609. [Google Scholar] [CrossRef]
- Mallick, M.; Arulampalam, S.; Yan, Y.; Ru, J. Three-Dimensional Tracking of an Aircraft Using Two-Dimensional Radars. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 585–600. [Google Scholar] [CrossRef]
- Talebi, S.P.; Werner, S. Distributed Kalman filtering and control through embedded average consensus information fusion. IEEE Trans. Autom. Control 2019, 64, 4396–4403. [Google Scholar] [CrossRef] [Green Version]
- Luo, J.A.; Pan, S.W.; Peng, D.L.; Wang, Z.; Li, Y.J. Source localization in acoustic sensor networks via constrained least-squares optimization using AOA and GROA measurements. Sensors 2018, 18, 937. [Google Scholar] [CrossRef] [Green Version]
- Kazmi, W.; Foix, S.; Alenyà, G.; Andersen, H.J. Indoor and outdoor depth imaging of leaves with time-of-flight and stereo vision sensors: Analysis and comparison. ISPRS J. Photogramm. Remote Sens. 2014, 88, 128–146. [Google Scholar] [CrossRef] [Green Version]
- Iliev, N.; Paprotny, I. Review and comparison of spatial localization methods for low-power wireless sensor networks. IEEE Sens. J. 2015, 15, 5971–5987. [Google Scholar] [CrossRef]
- Francis, S.L.; Anavatti, S.G.; Garratt, M. Real-time path planning module for autonomous vehicles in cluttered environment using a 3D camera. Int. J. Veh. Auton. Syst. 2018, 14, 40–61. [Google Scholar] [CrossRef]
- Surti, S.; Karp, J.S. Advances in time-of-flight PET. Phys. Medica 2016, 32, 12–22. [Google Scholar] [CrossRef] [Green Version]
- Paredes, J.A.; Álvarez, F.J.; Aguilera, T.; Aranda, F.J. Precise drone location and tracking by adaptive matched filtering from a top-view ToF camera. Expert Syst. Appl. 2020, 141, 112989. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, S.; Chen, C.P. TOA-based passive localization in quasi-synchronous networks. IEEE Commun. Lett. 2014, 18, 592–595. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, F.; Yang, L.; Jiang, W. Source localization using a moving receiver and noisy TOA measurements. Signal Process. 2016, 119, 185–189. [Google Scholar] [CrossRef]
- Xiong, H.; Peng, M.; Gong, S.; Du, Z. A novel hybrid RSS and TOA positioning algorithm for multi-objective cooperative wireless sensor networks. IEEE Sens. J. 2018, 18, 9343–9351. [Google Scholar] [CrossRef]
- Wei, Y.; Li, W.; Tang, Q.; Wei, P.; Zhang, H. A Closed-Form Location Algorithm Without Auxiliary Variables for Moving Target in Noncoherent Multiple-Input and Multiple-Output Radar System. IEEE Access 2020, 8, 69496–69508. [Google Scholar] [CrossRef]
- Wang, Y.; Ho, K.C. Unified near-field and far-field localization for AOA and hybrid AOA-TDOA positionings. IEEE Ttans. Wirel. Commun. 2017, 17, 1242–1254. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, G. Geolocation Algorithm of Interference Sources from FDOA Measurements Using Satellites Based on Taylor Series Expansion. In Proceedings of the IEEE Vehicular Technology Conference, Nanjing, China, 15–18 May 2016. [Google Scholar]
- Zhang, S.; Huang, Z.; Feng, X.; He, J.; Shi, L. Multi-Sensor Passive Localization Using Second Difference of Coherent Time Delays with Incomplete Measurements. IEEE Access 2019, 7, 43167–43178. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, H.; Wan, Q. An iterative method for moving target localization using TDOA and FDOA measurements. IEEE Access 2017, 6, 2746–2754. [Google Scholar] [CrossRef]
- Hmam, H. Optimal sensor velocity configuration for TDOA-FDOA geolocation. IEEE Trans. Signal Process. 2016, 65, 628–637. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, P.; Yang, Z.; Wei, F.; Wang, C. A novel estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of calibration emitters. IEEE Access 2019, 8, 1613–1643. [Google Scholar] [CrossRef]
- Kim, S.; Chong, J.W. An efficient TDOA-based localization algorithm without synchronization between base stations. Int. J. Distrib. Sens. Netw. 2015, 11, 832351. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Yin, J.; Tang, T.; Chen, X.; Wu, Z. Quadratic constrained weighted least-squares method for TDOA source localization in the presence of clock synchronization bias: Analysis and solution. Digit. Signal Process. 2018, 82, 237–257. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhang, H.; Wang, W.Q.; So, H.C. Source localization using TDOA and FDOA measurements based on semidefinite programming and reformulation linearization. J. Frankl. Inst. 2019, 356, 11817–11838. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Y. An efficient semidefinite relaxation algorithm for moving source localization using TDOA and FDOA measurements. IEEE Commun. Lett. 2016, 21, 80–83. [Google Scholar] [CrossRef]
- Hu, D.; Huang, Z.; Chen, X.; Lu, J. A moving source localization method using TDOA, FDOA and Doppler rate measurements. IEICE Trans. Commun. 2016, 99, 758–766. [Google Scholar] [CrossRef]
- Wennervirta, J.; Wigren, T. RTT positioning field performance. IEEE Trans. Veh. Technol. 2010, 59, 3656–3661. [Google Scholar] [CrossRef]
- Wigren, T. Fingerprinting localisation using round trip time and timing advance. IET Commun. 2012, 6, 419–427. [Google Scholar] [CrossRef]
- Guo, G.; Chen, R.; Ye, F.; Peng, X.; Liu, Z.; Pan, Y. Indoor Smartphone Localization: A Hybrid WiFi RTT-RSS Ranging Approach. IEEE Access 2019, 7, 176767–176781. [Google Scholar] [CrossRef]
- Tahat, A.; Kaddoum, G.; Yousefi, S.; Valaee, S.; Gagnon, F. A look at the recent wireless positioning techniques with a focus on algorithms for moving receivers. IEEE Access 2016, 4, 6652–6680. [Google Scholar] [CrossRef]
- Gezici, S. A survey on wireless position estimation. Wirel. Pers. Commun. 2008, 44, 263–282. [Google Scholar] [CrossRef]
- Stefanski, J.; Sadowski, J. TDOA versus ATDOA for wide area multilateration system. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 179. [Google Scholar] [CrossRef] [Green Version]
- Díez-González, J.; Álvarez, R.; González-Bárcena, D.; Sánchez-González, L.; Castejón-Limas, M.; Perez, H. Genetic Algorithm Approach to the 3D Node Localization in TDOA Systems. Sensors 2019, 19, 3880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ge, T.; Tharmarasa, R.; Lebel, B.; Florea, M.; Kirubarajan, T.T. A Multidimensional TDOA Association Algorithm for Joint Multitarget Localization and Multisensor Synchronization. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2083–2100. [Google Scholar] [CrossRef]
- Yaro, A.S.; Sha’ameri, A.Z.; Kamel, N. Position Estimation Error Performance Model for a Minimum Configuration 3-D Multilateration. Int. J. Electr. Eng. Inform. 2018, 10, 153–169. [Google Scholar] [CrossRef]
- Mao, G.; Fidan, B.; Anderson, B.D. Wireless sensor network localization techniques. Comput. Netw. 2007, 51, 2529–2553. [Google Scholar] [CrossRef]
- Ho, K.C. Bias reduction for an explicit solution of source localization using TDOA. IEEE Trans. Signal Process. 2012, 60, 2101–2114. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef] [Green Version]
- Okello, N.; Fletcher, F.; Musicki, D.; Ristic, B. Comparison of recursive algorithms for emitter localisation using TDOA measurements from a pair of UAVs. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1723–1732. [Google Scholar] [CrossRef]
- Díez-González, J.; Álvarez, R.; Sánchez-González, L.; Fernández-Robles, L.; Pérez, H.; Castejón-Limas, M. 3D Tdoa Problem Solution with Four Receiving Nodes. Sensors 2019, 19, 2892. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Ho, K.C.; Wan, Q. Solution and Analysis of TDOA Localization of a Near or Distant Source in Closed Form. IEEE Trans. Signal Process. 2019, 67, 320–335. [Google Scholar] [CrossRef]
- Peng, Z.; Li, C. Portable microwave radar systems for short-range localization and life tracking: A review. Sensors 2019, 19, 1136. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, S.I.; Kuptsov, V.D.; Fedotov, A.A. The signal processing algorithm of automotive FMCW radars with an extended range of speed estimation. J. Phys. Conf. Ser. 2019, 1236, 012081. [Google Scholar] [CrossRef]
- Kuptsov, V.D.; Ivanov, S.I.; Fedotov, A.A.; Badenko, V.L. Features of Multi-target Detection Algorithm for Automotive FMCW Radar. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11660, pp. 355–364. [Google Scholar]
- Kronauge, M.; Rohling, H. New chirp sequence radar waveform. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2870–2877. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P.; Poor, H.V. MIMO Radar for Advanced Driver-Assistance Systems and Autonomous Driving: Advantages and Challenges. IEEE Signal Process. Mag. 2020, 37, 98–117. [Google Scholar] [CrossRef]
- Ivanov, S.I.; Kuptsov, V.D.; Fedotov, A.A.; Badenko, V.L. CFAR multi-target detection based on non-central Chi-square distribution for FMCW. J. Phys. Conf. Ser. 2020, 1515, 032059. [Google Scholar] [CrossRef]
- Kuptsov, V.D.; Ivanov, S.I.; Fedotov, A.A.; Badenko, V.L. Multi-target method for small unmanned vehicles parameters remote determination by microwave radars. J. Phys. Conf. Ser. 2020, 1515, 032045. [Google Scholar] [CrossRef]
- Kutsov, V.D.; Ivanov, S.I.; Fedotov, A.A.; Badenko, V.L. Millimeter Wave Radar for Intelligent Transportation Systems: A Case Study of Multi-Target Problem Solution. E3S Web Conf. 2020, 157, 05011. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Ansari, N.; Hu, F.; Shao, Y.; Elikplim, N.R.; Li, L. A survey on fusion-based indoor positioning. IEEE Commun. Surv. Tutor. 2019, 22, 566–594. [Google Scholar] [CrossRef]
- Fang, B.T. Simple solutions for hyperbolic and related position fixes. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 748–753. [Google Scholar] [CrossRef]
- Al-Samahi, S.S.; Zhang, Y.; Ho, K.C. Elliptic and hyperbolic localizations using minimum measurement solutions. Signal Process. 2020, 167, 107273. [Google Scholar] [CrossRef]
- Malanowski, M.; Kulpa, K. Two methods for target localization in multistatic passive radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 572–580. [Google Scholar] [CrossRef]
- Shuster, S.; Sinclair, A.J.; Lovell, T.A. Initial Relative-Orbit Determination Using Heterogeneous TDOA. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017. [Google Scholar]
- Cameron, K.J.; Bates, D.J. Geolocation with FDOA Measurements via Polynomial Systems and RANSAC. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 0676–0681. [Google Scholar]
- Rui, L.; Ho, K.C. Elliptic localization: Performance study and optimum receiver placement. IEEE Trans. Signal Process. 2014, 62, 4673–4688. [Google Scholar] [CrossRef]
- Vesely, J.; Van Doan, S. Analytical Method Solving System of Hyperbolic Equations. In Proceedings of the 2015 25th International Conference Radioelektronika (RADIOELEKTRONIKA), Pardubice, Czech Republic, 21–22 April 2015; pp. 343–348. [Google Scholar]
- Van Doan, S.; Vesely, J. The Effectivity Comparison of TDOA Analytical Solution Methods. In Proceedings of the 2015 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; pp. 800–805. [Google Scholar]
- Van Doan, S.; Vesely, J.; Janu, P. The Measurement of TDOA Short Baseline. In Proceedings of the International Conference on Military Technologies (ICMT), Brno, Czech Republic, 19–21 May 2015; pp. 1–5. [Google Scholar]
- Kuptsov, V.D.; Ivanov, S.I.; Fedotov, A.A.; Badenko, V.L. High-precision analytical TDoA positioning algorithm for eliminating the ambiguity of coordinates determination. IOP Conf. Ser. Mater. Sci. Eng. 2020, 904, 012013. [Google Scholar] [CrossRef]
- Takahashi, Y.; Honma, N.; Sato, J.; Murakami, T.; Murata, K. Accuracy Comparison of Wireless Indoor Positioning Using Single Anchor: TOF only Versus TOF-DOA Hybrid Method. In Proceedings of the 2019 IEEE Asia-Pacific Microwave Conference (APMC), Singapore, 10–13 December 2019; pp. 1679–1681. [Google Scholar]
- Vashist, A.; Bhanushali, D.R.; Relyea, R.; Hochgraf, C.; Ganguly, A.; Manoj, S.; Ptucha, R.; Kwasinski, A.; Kuhl, M.E. Indoor Wireless Localization Using Consumer-Grade 60 GHz Equipment with Machine Learning for Intelligent Material Handling. In Proceedings of the 2020 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 4–6 January 2020. [Google Scholar]
- Piccinni, G.; Avitabile, G.; Coviello, G.; Talarico, C. Real-Time Distance Evaluation System for Wireless Localization. IEEE Trans. Circuits Syst. 2020, 1–11. [Google Scholar] [CrossRef]
- Avitabile, G.; Florio, A.; Coviello, G. Angle of Arrival Estimation through a Full-Hardware Approach for Adaptive Beamforming. IEEE Trans. Circuits Syst. 2020, 1. [Google Scholar] [CrossRef]
- Fokin, G.A.; Kireev, A.V.; Al-Odhari, A.H. TDOA Positioning Accuracy Performance Evaluation for Arc sensor Configuration. In Proceedings of the 2018 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 14–15 March 2018; pp. 1–5. [Google Scholar]
- Liu, Y.; Yang, L.; Li, J. Robust UWB Indoor Position Tracking Using TDOA Measurements. In Proceedings of the 2018 IEEE 4th International Conference on Computer and Communications, Chengdu, China, 7–10 December 2018; pp. 736–743. [Google Scholar]









| i = 1 | i = 2 | i = 3 | i = 4 | ||||
|---|---|---|---|---|---|---|---|
| L | → | R | → | U | → | D | |
| R | → | U | → | D | → | L | |
| U | → | D | → | L | → | R | |
| D | → | L | → | R | → | U | |
| E | → | F | → | G | → | H | |
| F | → | G | → | H | → | E | |
| G | → | H | → | E | → | F | |
| Deviation TDoA, ps | RMSmin, m | RMSmax, m |
|---|---|---|
| 0 | 0 | 5.56 × 10−13 |
| 10 | 0.0032 | 0.037 |
| 100 | 0.031 | 0.338 |
| 1000 | 0.328 | 3.3 |
| Deviation TDoA, ps | RMSmin, m. Analytical Method | RMSmin, m. Linear Method | RMSmax, m. Analytical Method | RMSmax, m. Linear Method |
|---|---|---|---|---|
| 0 | 0 | 1.91 × 10−9 | 1.013 × 10−6 | 8.80 × 10−5 |
| 1 | 0.029 | 0.166 | 0.055 | 0.318 |
| 10 | 0.29 | 1.67 | 0.552 | 3.17 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuptsov, V.; Badenko, V.; Ivanov, S.; Fedotov, A. Method for Remote Determination of Object Coordinates in Space Based on Exact Analytical Solution of Hyperbolic Equations. Sensors 2020, 20, 5472. https://doi.org/10.3390/s20195472
Kuptsov V, Badenko V, Ivanov S, Fedotov A. Method for Remote Determination of Object Coordinates in Space Based on Exact Analytical Solution of Hyperbolic Equations. Sensors. 2020; 20(19):5472. https://doi.org/10.3390/s20195472
Chicago/Turabian StyleKuptsov, Vladimir, Vladimir Badenko, Sergei Ivanov, and Alexander Fedotov. 2020. "Method for Remote Determination of Object Coordinates in Space Based on Exact Analytical Solution of Hyperbolic Equations" Sensors 20, no. 19: 5472. https://doi.org/10.3390/s20195472
APA StyleKuptsov, V., Badenko, V., Ivanov, S., & Fedotov, A. (2020). Method for Remote Determination of Object Coordinates in Space Based on Exact Analytical Solution of Hyperbolic Equations. Sensors, 20(19), 5472. https://doi.org/10.3390/s20195472








