Vital-Signs Detector Based on Frequency-Shift Keying Radar
Abstract
:1. Introduction
2. Vital-Signs Detection Using FSK Radar
2.1. Operating Principles for FSK Radar
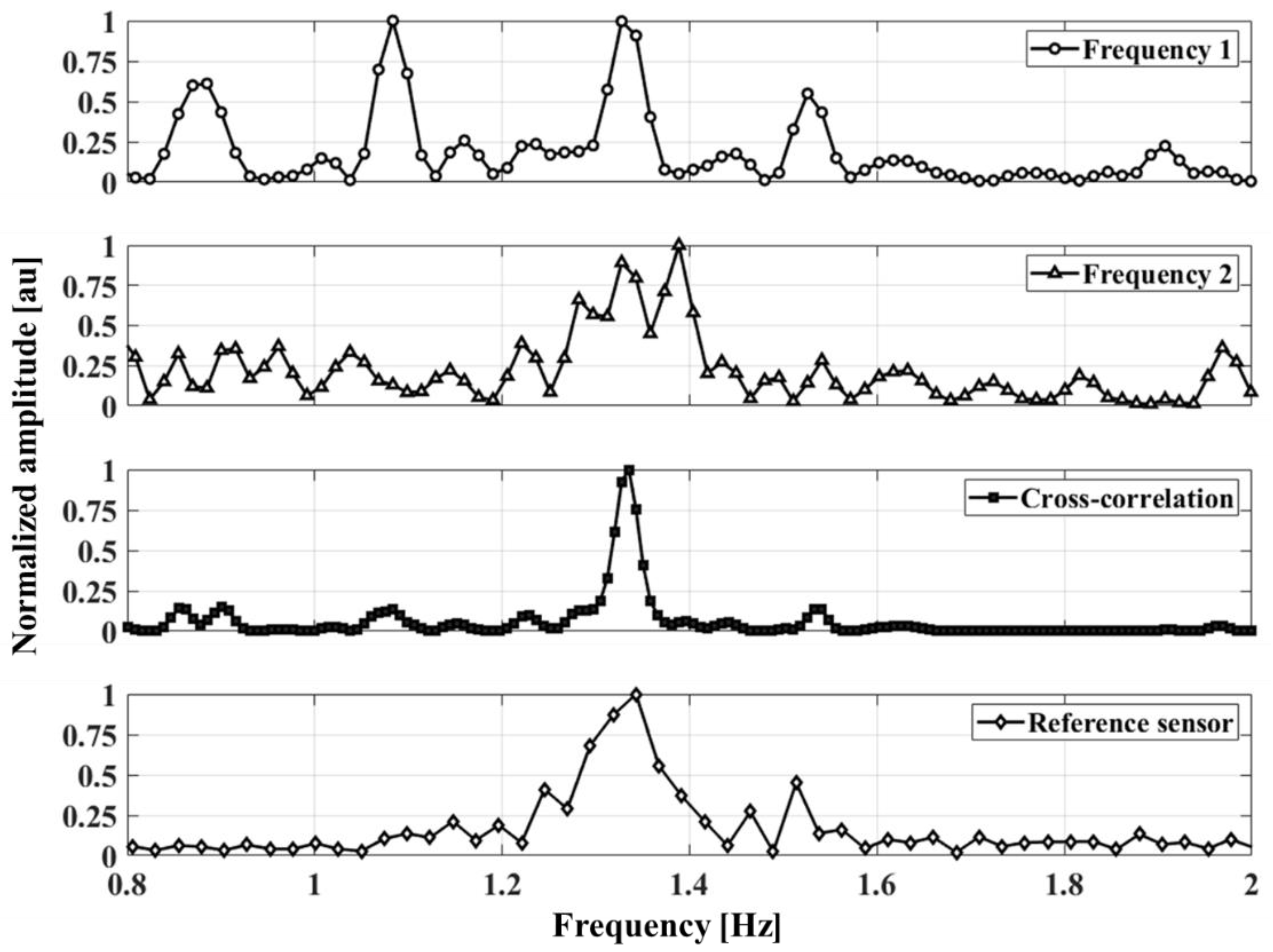
2.2. Cross-Correlation Method
2.3. Frequency Discrimination Using Envelope Detection for Proposed FSK Radar
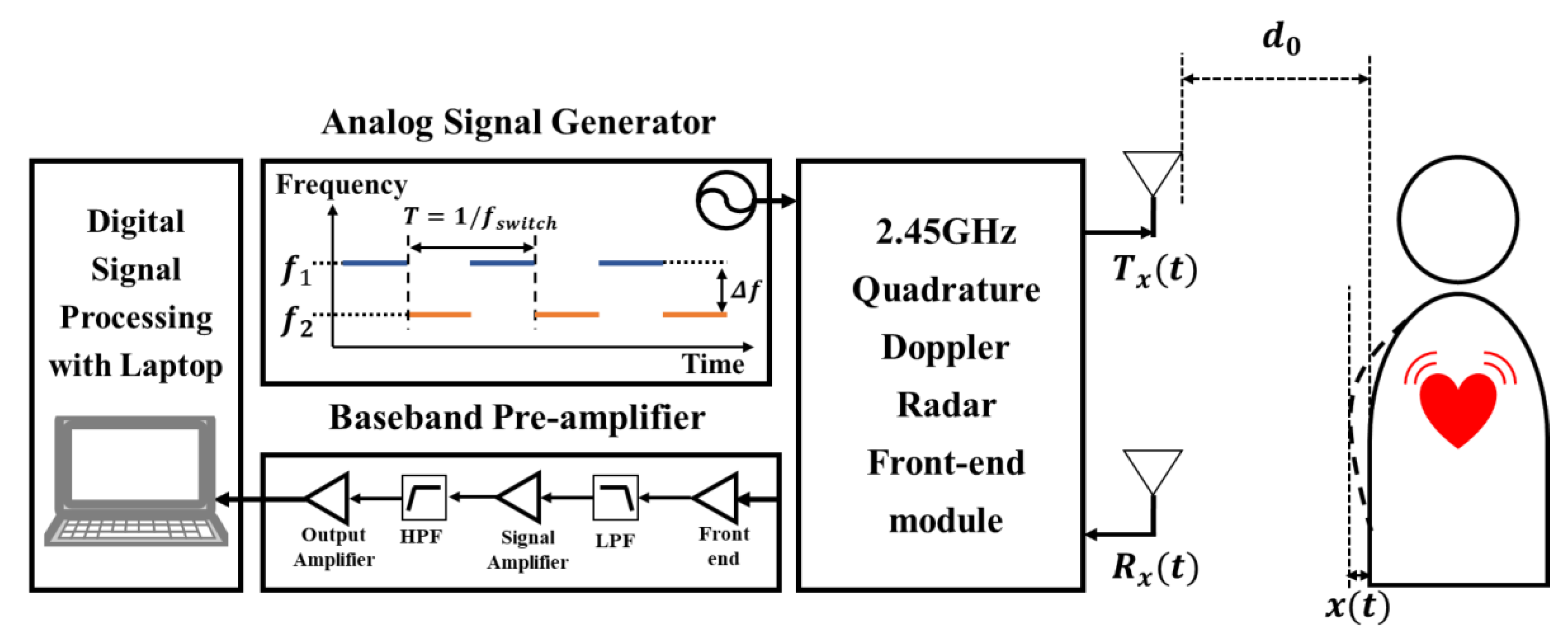
3. Implementation
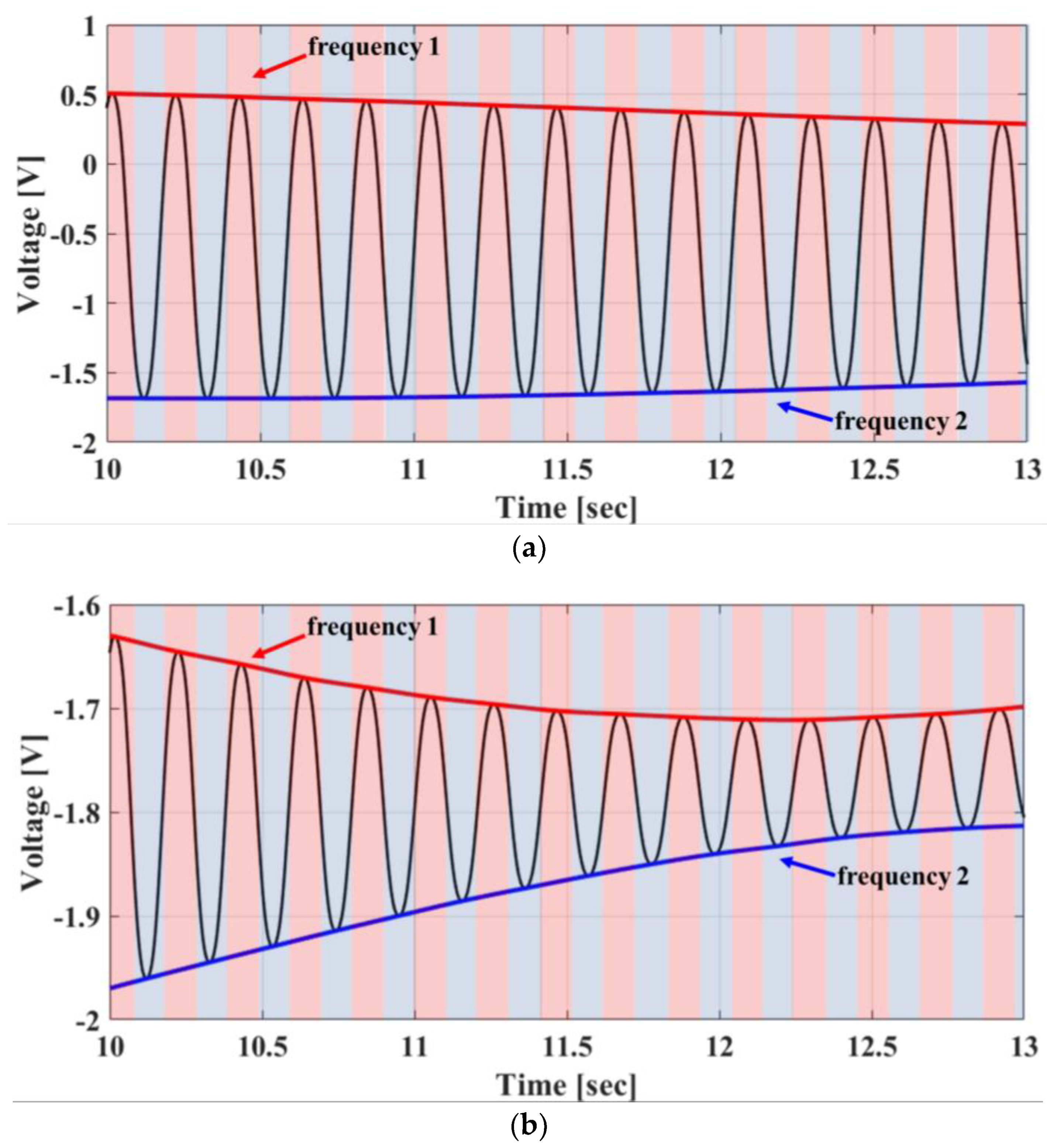
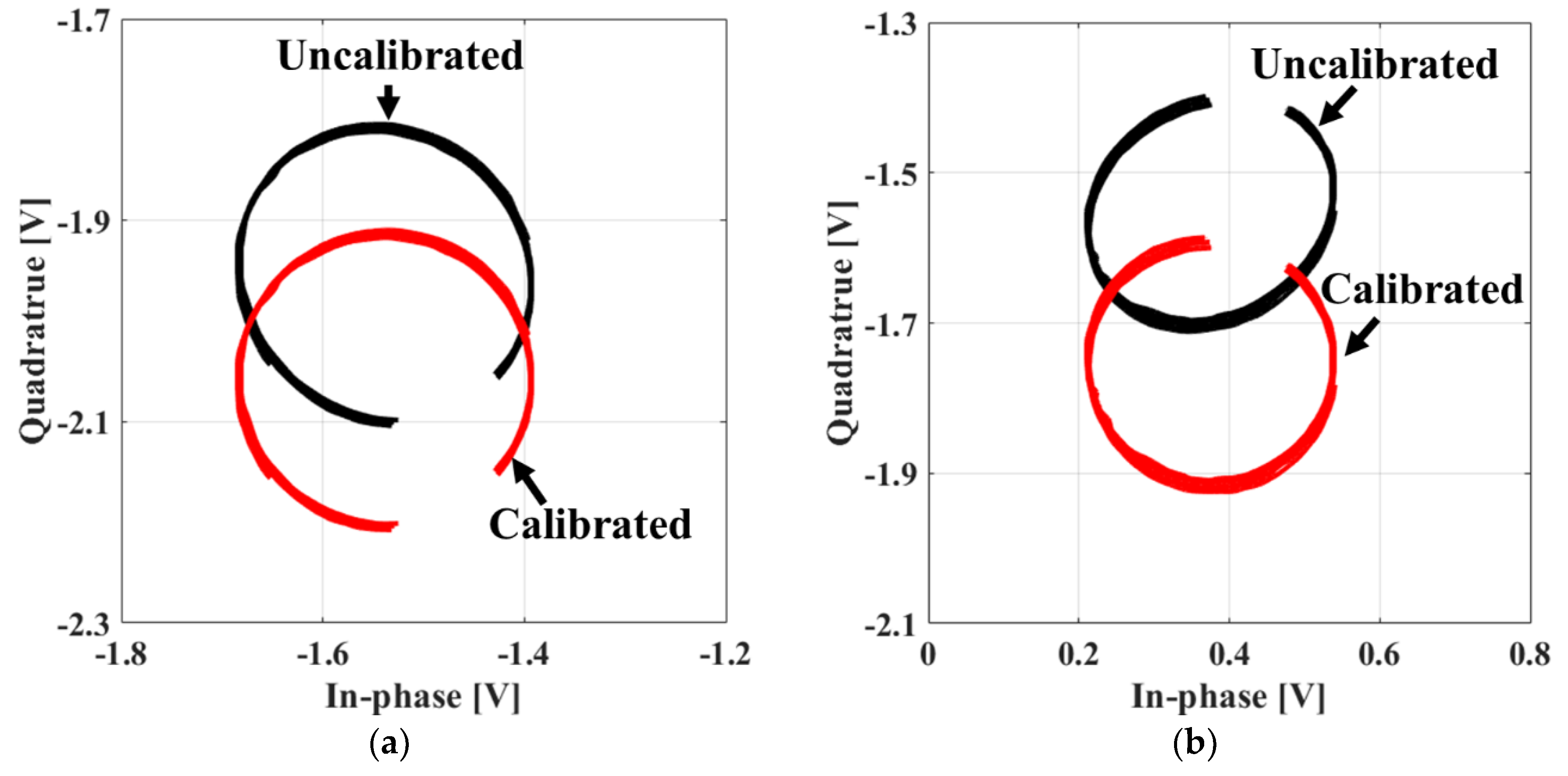
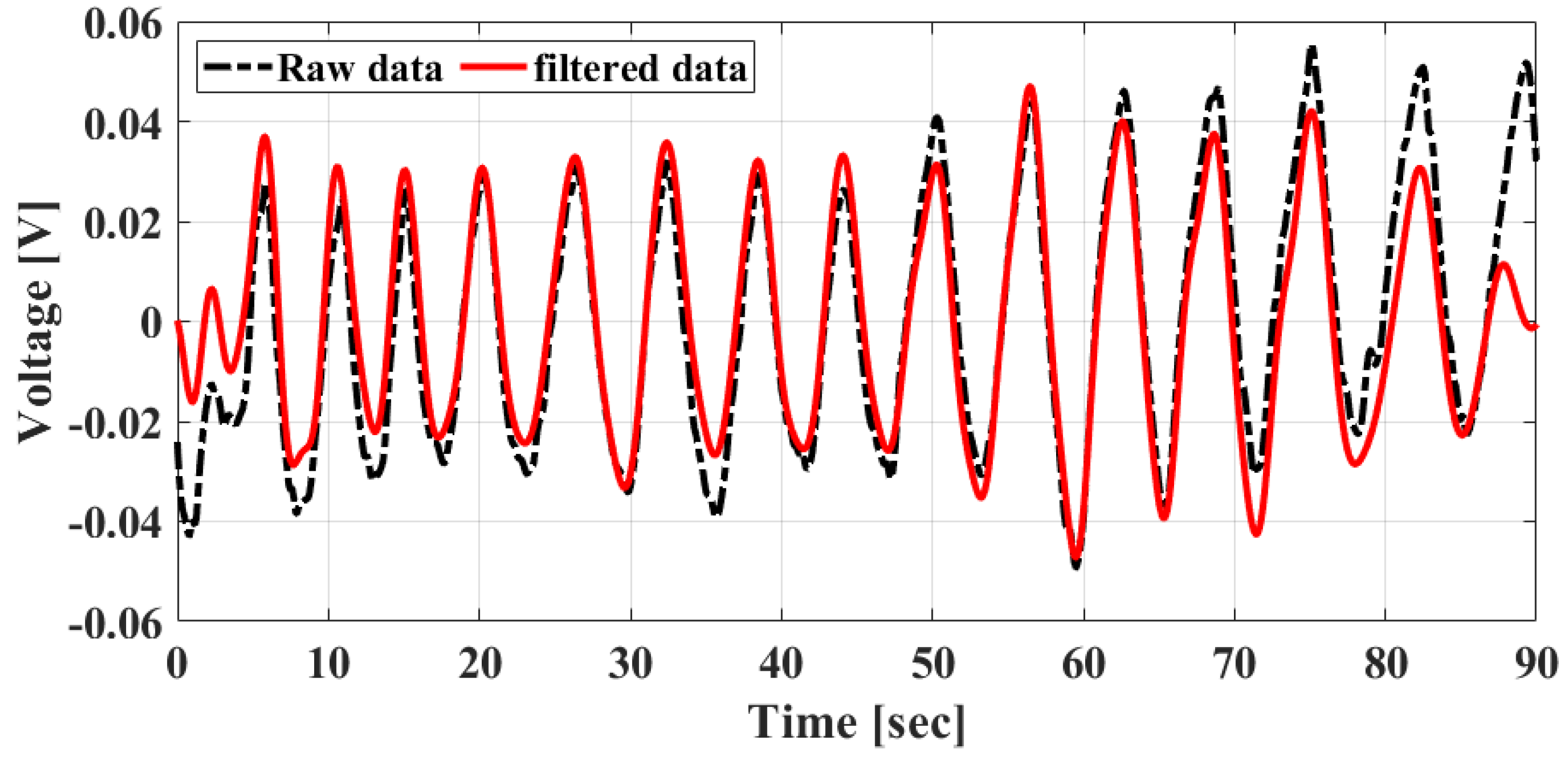
3.1. Digital Signal Processing
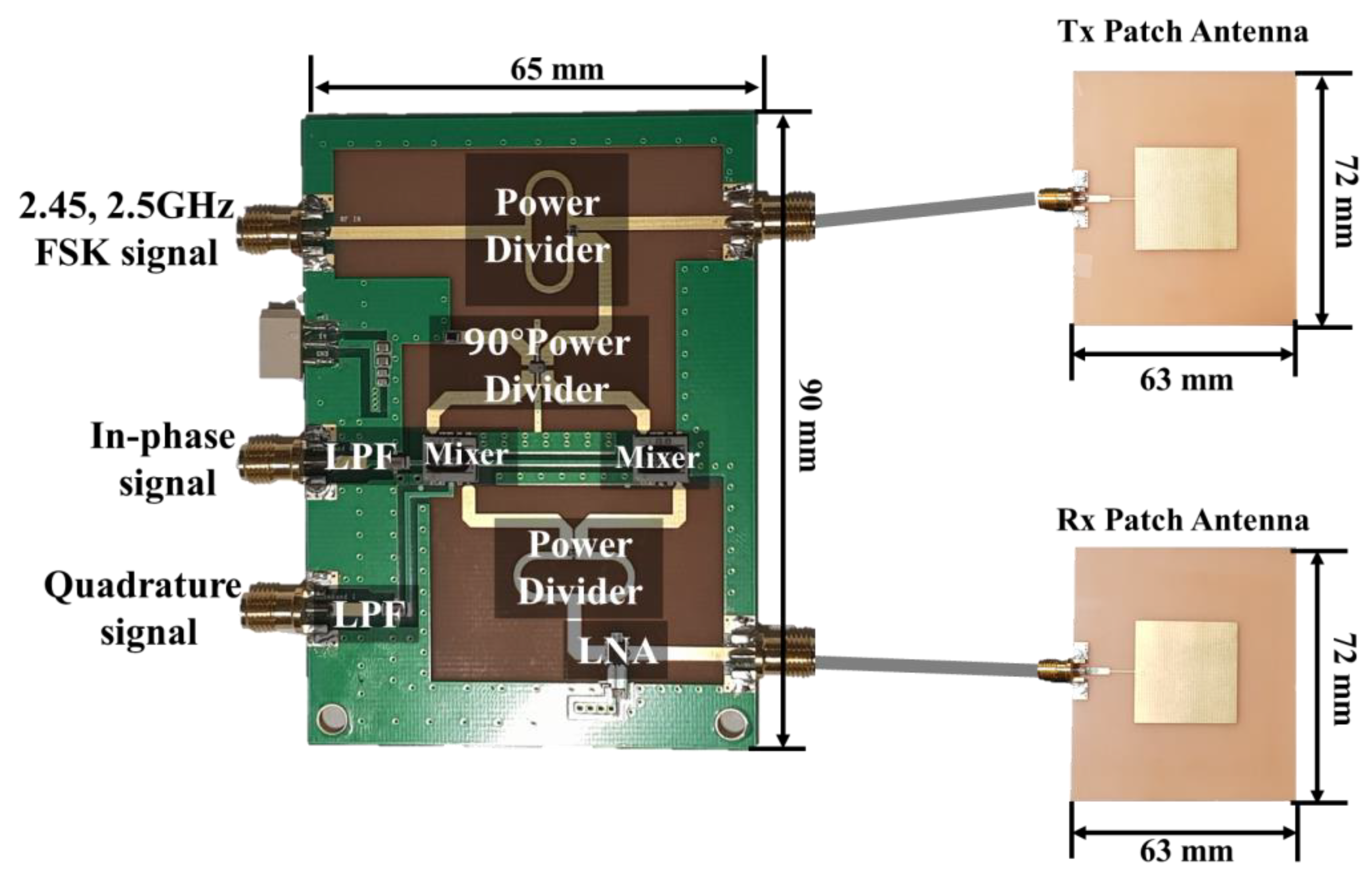
3.2. Implemented FSK Radar Module
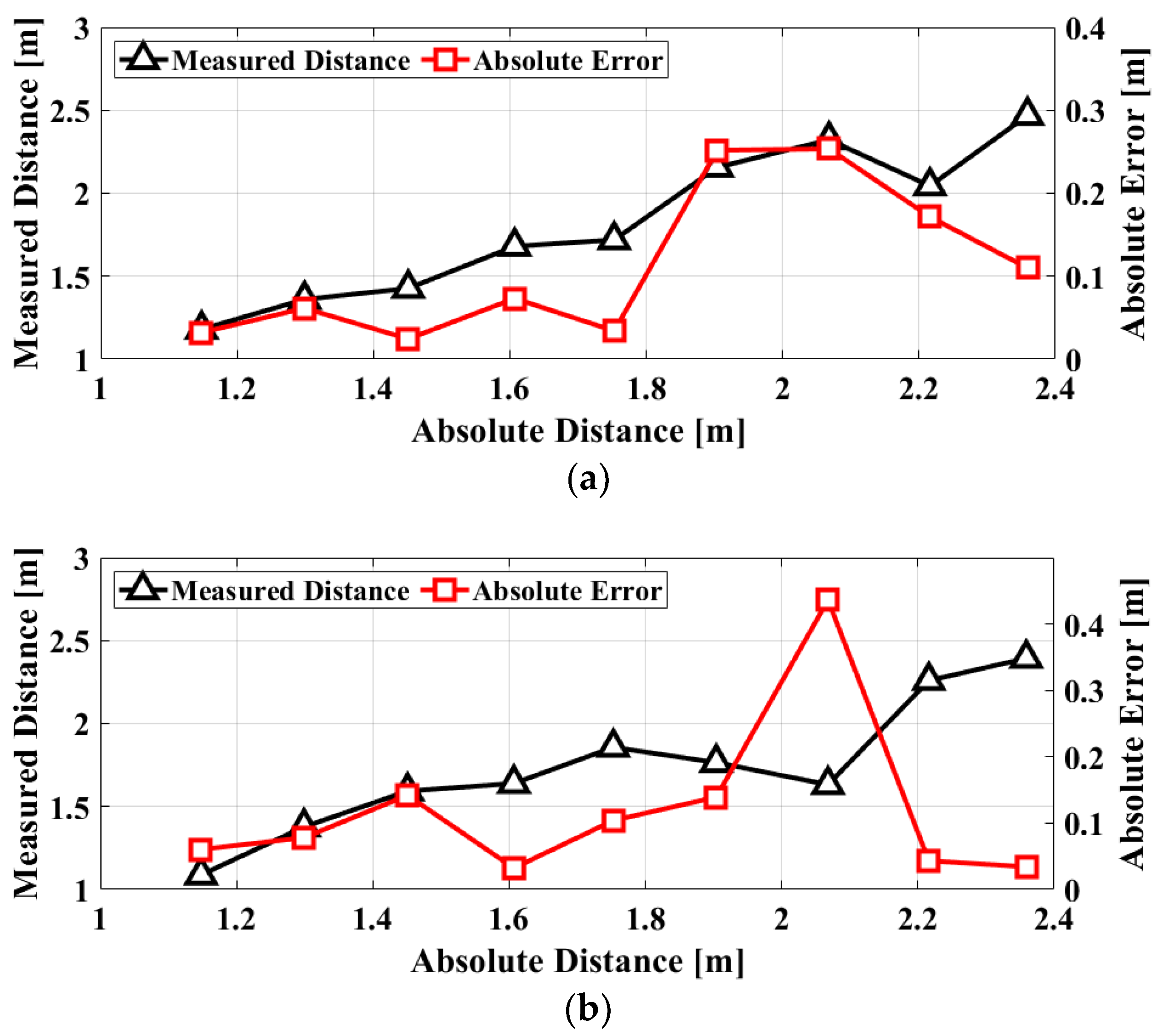
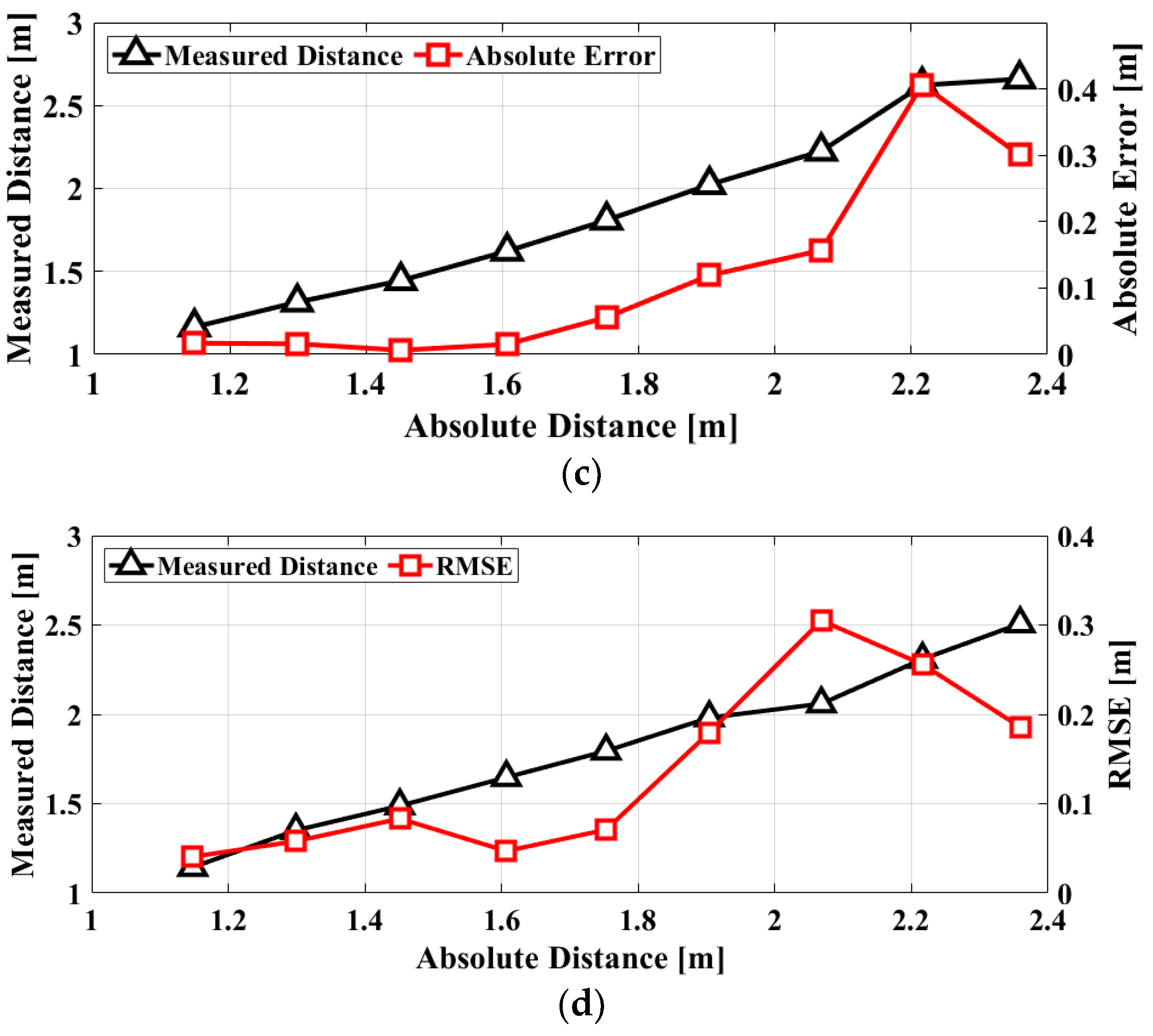
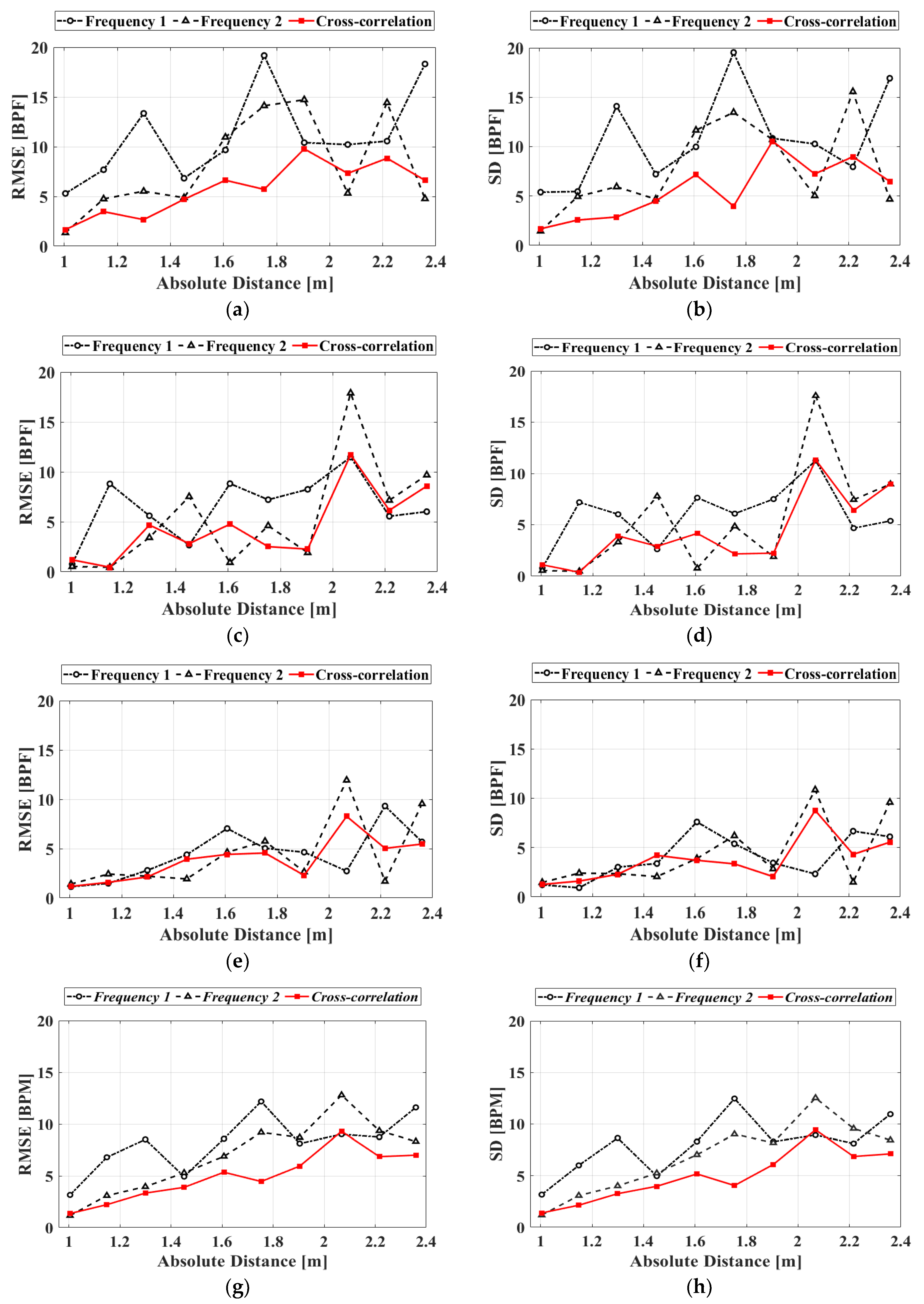
4. Measurement Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, J.C. Noninvasive microwave measurement of respiration. Proc. IEEE 1975, 63, 1530. [Google Scholar] [CrossRef]
- Chen, K.-M.; Misra, D.; Wang, H.; Chuang, H.-R.; Postow, E. An X-band microwave life-detection system. IEEE Trans. Biomed. Eng. 1986, 33, 697–701. [Google Scholar]
- Chen, K.-M.; Huang, Y.; Zhang, J.; Norman, A. Microwave life-detection systems for searching human subjects under earthquake rubble or behind barrier. IEEE Trans. Biomed. Eng. 2000, 47, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Zhuang, Y.; Song, C.; Wang, A.; Li, Y.; Gu, C.; Li, C.; Xu, W. SleepSense: A noncontact and cost-effective sleep monitoring system. IEEE Trans. Biomed. Circuits Syst. 2016, 11, 189–202. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Park, J.-H.; Jang, S.-Y.; Yang, J.-R. Peak detection algorithm for vital sign detection using Doppler radar sensors. Sensors 2019, 19, 1575. [Google Scholar] [CrossRef] [Green Version]
- Brüster, C.; Antink, C.H.; Wartzek, T. Ambient and unobtrusive cardiorespiratory monitoring techniques. IEEE Rev. Biomed. Eng. 2015, 8, 30–43. [Google Scholar] [CrossRef]
- Shang, N.; Xin, K.; Yu, C.; Wang, L. Design of direct wave cancellation system for high-frequency CW radar. J. Eng. 2019, 2019, 6660–6663. [Google Scholar] [CrossRef]
- De Groote, A.; Wantier, M.; Chéron, G.; Estenne, M.; Paiva, M. Chest wall motion during tidal breathing. J. Appl. Physiol. 1997, 83, 1531–1537. [Google Scholar] [CrossRef] [Green Version]
- Ramachandran, G.; Singh, M. Three-dimensional reconstruction of cardiac displacement patterns on the chest wall during the P, QRS and T-segments of the ECG by laser speckle interferometry. Med. Biol. Eng. Comput. 1989, 27, 525–530. [Google Scholar] [CrossRef]
- Park, J.-H.; Jeong, Y.-J.; Lee, G.-E.; Oh, J.-T.; Yang, J.-R. 915-MHz continuous-wave Doppler radar sensor for detection of vital signs. Electronics 2019, 8, 561. [Google Scholar] [CrossRef] [Green Version]
- Guanghao, S.; Matsui, T. Rapid and stable measurement of respiratory rate from Doppler radar signals using time domain autocorrelation model. In Proceedings of the 2015 37th Annual Int. Conf. of the IEEE Eng. in Medicine and Biology Society, Milan, Italy, 25–29 August 2015. [Google Scholar]
- Li, M.; Lin, J. Wavelet-transform-based data-length-variation technique for fast heart rate detection using 5.8-GHz CW Doppler radar. IEEE Trans. Microw. Theory Techn. 2018, 66, 568–576. [Google Scholar] [CrossRef]
- Iyer, B.; Garg, M.; Pathak, N.P.; Ghosh, D. Concurrent dual-band RF system for human respiration rate and heartbeat detection. In Proceedings of the 2013 IEEE Conf. on Information & Communication Technologies, Thuckalay, Tamil Nadu, India, 11–12 April 2013. [Google Scholar]
- Choi, C.-H.; Park, J.-H.; Lee, H.-N.; Yang, J.-R. Heartbeat detection using a Doppler radar sensor based on the scaling function of Wavelet transform. Microw. Opt. Techn. Lett. 2019, 61, 1792–1796. [Google Scholar] [CrossRef]
- Yang, J.-R.; Hong, S. A 24-GHz radar sensor with a six-port network for short-range detection. Microw. Opt. Techn. Lett. 2014, 56, 2634–2637. [Google Scholar] [CrossRef]
- Park, J.-H.; Yang, J.-R. Two-tone CW Doppler radar based on envelope detection method. Microw. Opt. Techn. Lett. 2020, 62, 3146–3150. [Google Scholar] [CrossRef]
- Hu, W.; Zhao, Z.; Wang, Y.; Zhang, H.; Lin, F. Noncontact accurate measurement of cardiopulmonary activity using a compact quadrature Doppler radar sensor. IEEE Trans. Biomed. Eng. 2014, 61, 725–735. [Google Scholar] [CrossRef] [PubMed]
- Droitcour, A.D.; Boric-Lubecke, O.; Lubecke, V.M.; Lin, J.; Kovacs, G.T. Range correlation and I/Q performance benefits in single-chip silicon Doppler radars for noncontact cardiopulmonary monitoring. IEEE Trans. Microw. Theory Techn. 2004, 52, 838–848. [Google Scholar] [CrossRef]
- Siddiq, K.; Hobden, M.K.; Pennock, S.R.; Watson, R.J. Phase noise in FMCW radar systems. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 70–81. [Google Scholar] [CrossRef]
- Smith, S. Digital Signal Processing: A Practical Guide for Engineers and Scientists; Newnes: Oxford, UK, 2003; pp. 136–140. [Google Scholar]
- Wang, J.; Wang, X.; Chen, L.; Huangfu, J.; Li, C.; Ran, L. Noncontact distance and amplitude-independent vibration measurement based on an extended DACM algorithm. IEEE Trans. Instrum. Meas. 2013, 63, 145–153. [Google Scholar] [CrossRef]
- Yang, J.-R.; Kim, D.-W.; Hong, S. A calibration method of a range finder with a six-port network. IEEE Microw. Wireless Compon. Lett. 2007, 17, 549–551. [Google Scholar] [CrossRef]
- Singh, A.; Gao, X.; Yavari, E.; Zakrzewski, M.; Cao, X.; Lubecke, V.; Boric-Lubecke, O. Data-based quadrature imbalance compensation for a CW Doppler radar system. IEEE Trans. Microw. Theory Techn. 2013, 61, 1718–1724. [Google Scholar] [CrossRef]
- Li, C.; Zhao, H.; Xi, F. Accurate DC offset calibration of Doppler radar via non-convex optimization. Electron. Lett. 2015, 51, 1282–1284. [Google Scholar]
- Pratt, V. Direct least-squares fitting of algebraic surfaces. ACM SIGGRAPH Comput. Graph. 1987, 21, 145–152. [Google Scholar] [CrossRef]
- Fan, T.; Ma, C.; Gu, Z.; Lv, Q.; Chen, J.; Ye, D.; Huangfu, J.; Sun, Y.; Li, C.; Ran, L. Wireless hand gesture recognition based on continuous-wave Doppler radar sensors. IEEE Trans. Microw. Theory Techn. 2016, 64, 4012–4020. [Google Scholar] [CrossRef]
- Li, C.; Lin, J. Complex signal demodulation and random body movement cancellation techniques for non-contact vital sign detection. In Proceedings of the 2008 IEEE Int. Microw. Symp., Atlanta, GA, USA, 15–20 June 2008; pp. 567–570. [Google Scholar]
- Wang, J.; Karp, T.; Muñoz-Ferreras, J.M.; Gómez-García, R.; Li, C. A spectrum-efficient FSK radar technology for range tracking of both moving and stationary human subjects. IEEE Trans. Microw. Theory Techn. 2019, 67, 5406–5416. [Google Scholar] [CrossRef]





| Subjects | Gender | Age | Weight | Height | BMI |
|---|---|---|---|---|---|
| A | Male | 25 | 90 | 177 | 28.73 |
| B | Male | 28 | 76 | 182 | 22.94 |
| C | Male | 25 | 83 | 172 | 28.06 |
| Subject | RMSE in BPM | SD in BPM | ||||
|---|---|---|---|---|---|---|
| 2.45 GHz | 2.5 GHz | CC 1 | 2.45 GHz | 2.5 GHz | CC 1 | |
| A | 11.970 | 9.347 | 6.260 | 11.814 | 9.324 | 6.264 |
| B | 7.160 | 7.478 | 5.599 | 7.032 | 7.524 | 5.640 |
| C | 5.037 | 5.609 | 4.393 | 5.034 | 5.550 | 4.422 |
| Average | 8.562 | 7.632 | 5.472 | 8.550 | 7.602 | 5.460 |
| [5] | [10] | [14] | This Work | |
|---|---|---|---|---|
| Type | CW | CW | CW | FSK |
| Operating Frequency (GHz) | 2.45 | 0.915 | 2.45 | 2.45 & 2.5 |
| Distance to target (m) | 0.4 | 0.2–1.4 | 1.0 | 1.0–2.4 |
| Signal Processing | Peak detection | Fast-Fourier transform | Wavelet transform | Cross-correlation |
| Detectable Information | Respiration, heartbeat | Respiration, heartbeat | Respiration, heartbeat | Respiration, heartbeat, distance |
| Mean absolute error in HR 1 (%) | 3.22 | 1.37 | 3.93 | 6.00 |
| Reference ECG sensor | Three-electrodes sensor manufactured by Vernier Software and Technology | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sim, J.Y.; Park, J.-H.; Yang, J.-R. Vital-Signs Detector Based on Frequency-Shift Keying Radar. Sensors 2020, 20, 5516. https://doi.org/10.3390/s20195516
Sim JY, Park J-H, Yang J-R. Vital-Signs Detector Based on Frequency-Shift Keying Radar. Sensors. 2020; 20(19):5516. https://doi.org/10.3390/s20195516
Chicago/Turabian StyleSim, Jae Young, Jae-Hyun Park, and Jong-Ryul Yang. 2020. "Vital-Signs Detector Based on Frequency-Shift Keying Radar" Sensors 20, no. 19: 5516. https://doi.org/10.3390/s20195516
APA StyleSim, J. Y., Park, J.-H., & Yang, J.-R. (2020). Vital-Signs Detector Based on Frequency-Shift Keying Radar. Sensors, 20(19), 5516. https://doi.org/10.3390/s20195516






