Application of Composite Spectrum in Agricultural Machines
Abstract
:1. Introduction
2. Materials and Methods
2.1. Equipment
2.2. Case Analyses by the Different Working Conditions and Speed of the Components of the Combine Harvester
2.3. Procedure of Vibration Data Acquisition
2.4. Composite Spectrum Calculation
2.4.1. Power Spectrum Density and Cross Power Spectrum Density
2.4.2. Non-Coherent CS
2.4.3. Coherent Cross Power Spectrum Density, Coherent Composite Fourier Transform and Coherent CS
2.4.4. Poly-Coherent CS
2.5. Statistical Analysis
3. Results
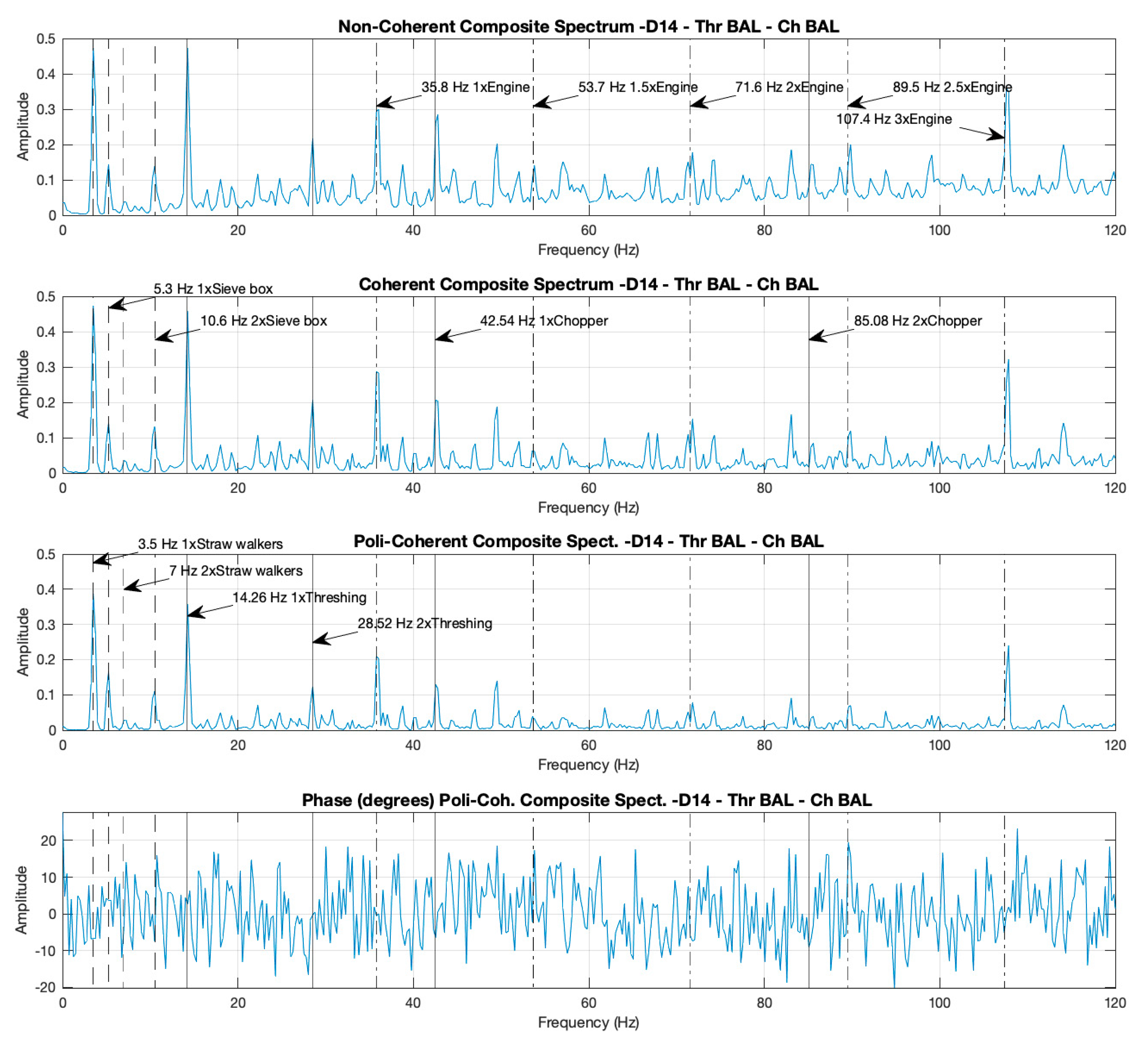
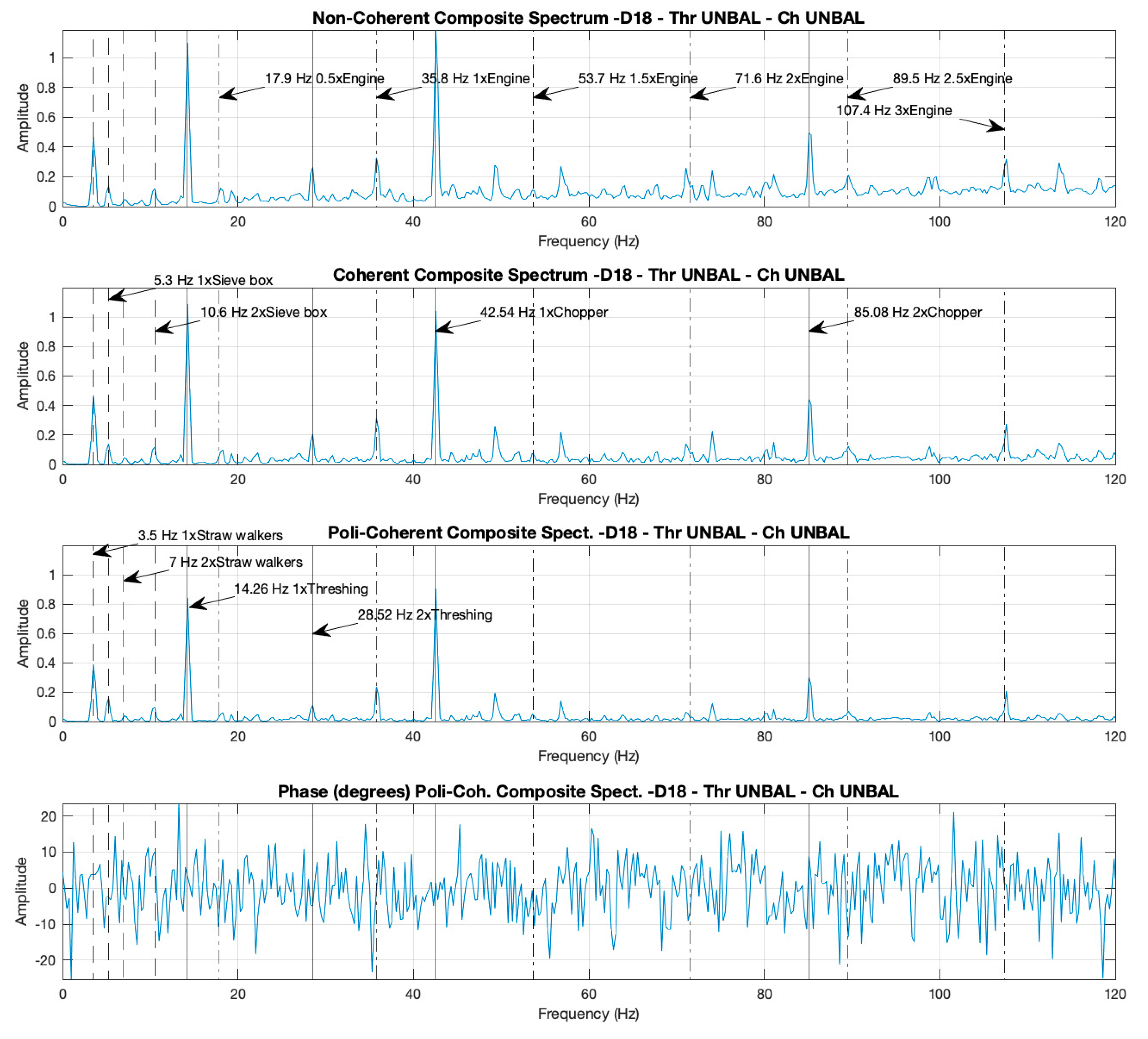
3.1. Analysis and Comparisons of Two Cases, with the Thresher and the Chopper, Both in Balanced (Case D14) and Unbalanced (Case D18) Conditions, and with the Motor at Maximum Rotational Speed
3.1.1. Individual Spectra: Identification of the Components by Their Peaks and Comparisons of the Amplitudes of the Peaks in the Four Spectra in Cases D14 and D18
3.1.2. Composite Spectra: Identification of the Components by Their Peaks and Comparisons of the Amplitudes of the Peaks in the Non-Coherent, Coherent, and Poly-Coherent CS for Cases D14 and D18
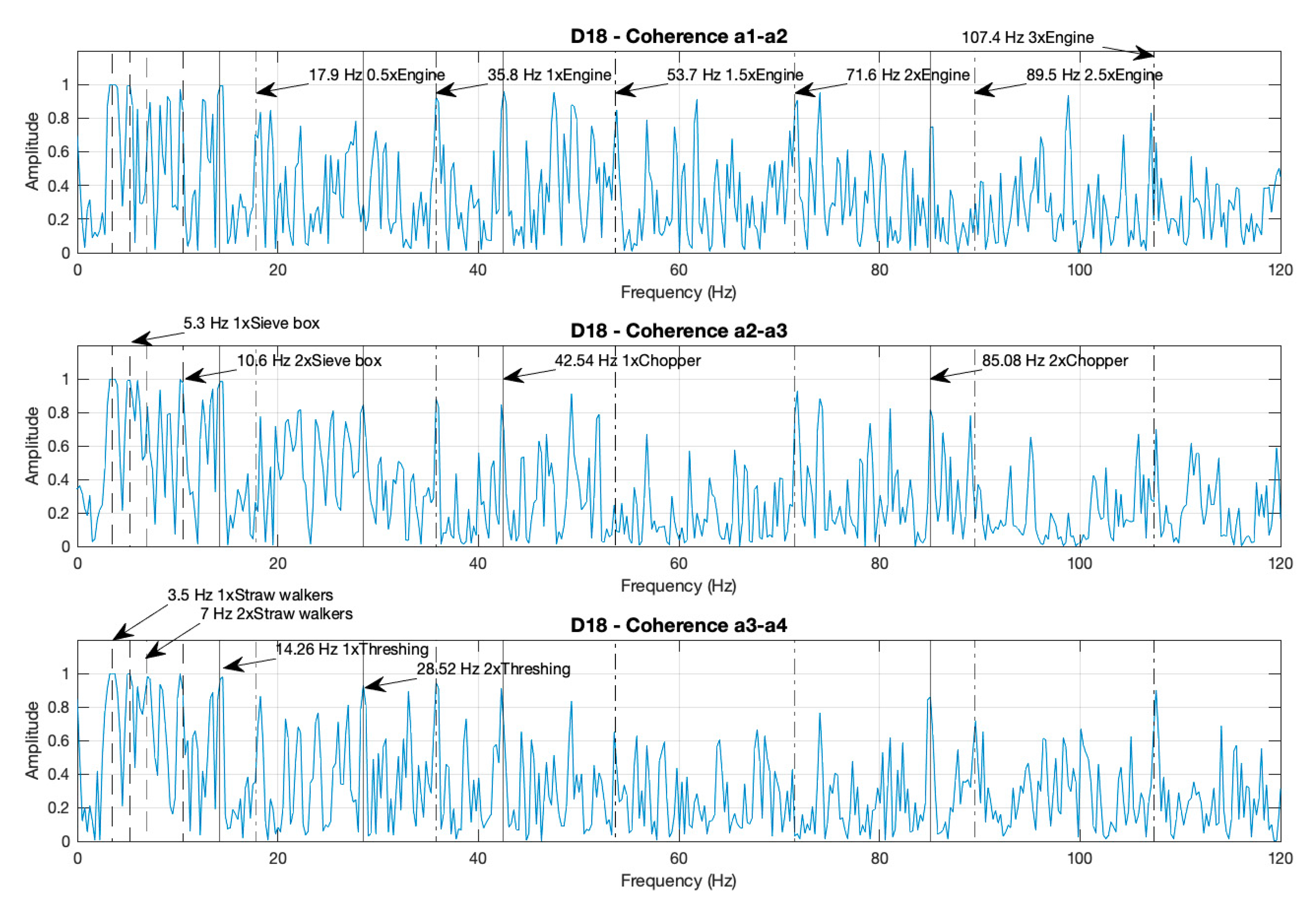
3.1.3. Coherence Functions for Case D18 and Noise–Data Comparisons between the Composite and Individual Spectra
3.2. Peak Amplitudes Comparison between the Different Spectra in all cases D1-D18
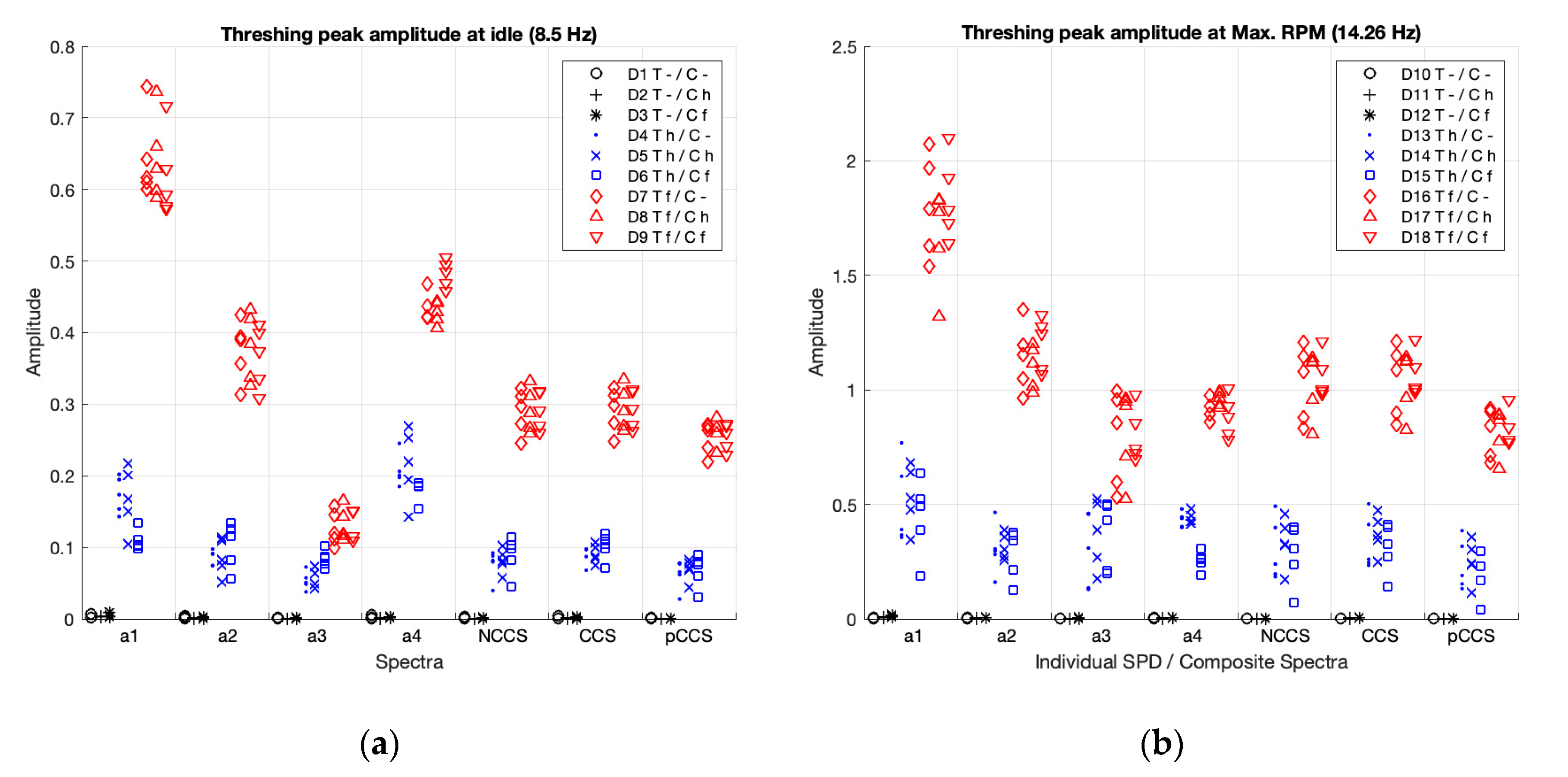
3.2.1. Peak Amplitudes with the Thresher in Deactivation, Activation, and Failure Working Conditions
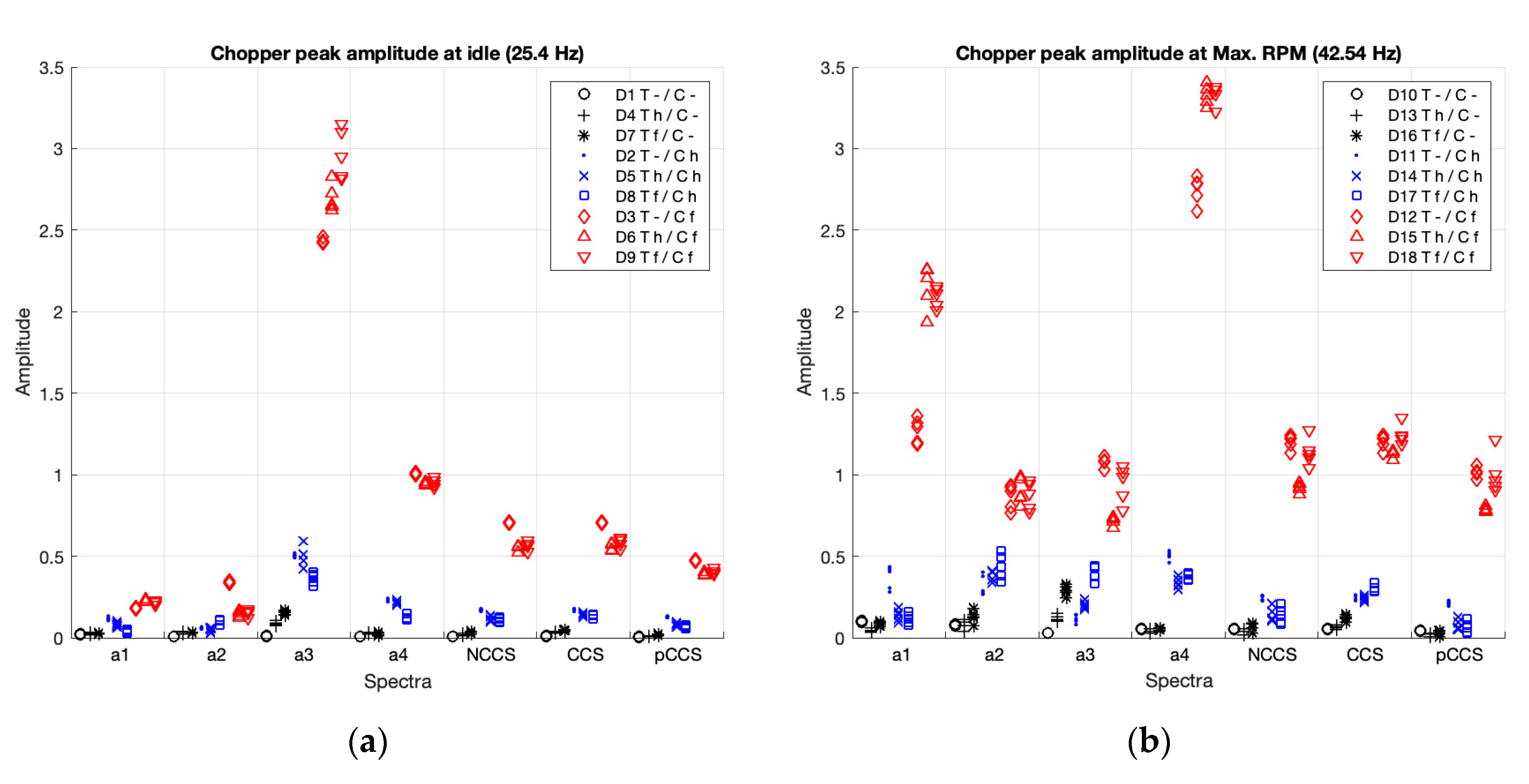
3.2.2. Peak Amplitudes with the Chopper in Deactivation, Activation, and Failure Working Conditions
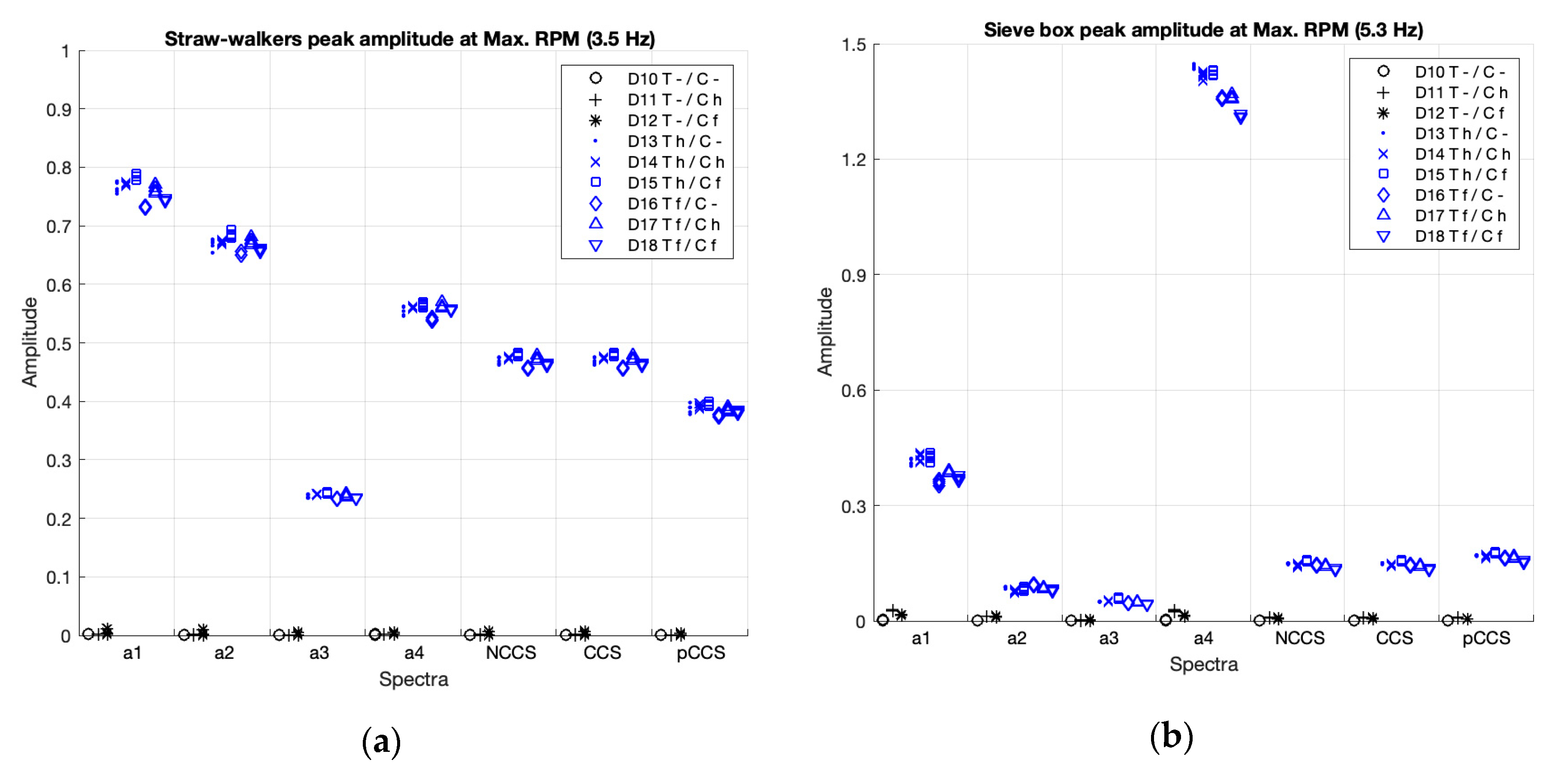
3.2.3. Peak Amplitudes with the Straw Walkers and Sieve Box in Deactivation and Activation Working Conditions
3.2.4. Summary of the Magnitude of the Differences of the Peak Amplitudes for Each Spectrum According to the Different Component Status
3.2.5. Area Under the Curve Comparisons in the Different Spectra (Individuals, Non-Coherent CS, Coherent CS, and Poly-Coherent CS) in all Cases (D1–D18)
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dieter Kutzbach, H. Trends in power and machinery. J. Agric. Eng. Res. 2000, 76, 237–247. [Google Scholar] [CrossRef]
- Craessaerts, G.; de Baerdemaeker, J.; Saeys, W. Fault diagnostic systems for agricultural machinery. Biosys. Eng. 2010, 106, 26–36. [Google Scholar] [CrossRef]
- Miu, P. Combine Harvesters Theory, Modeling, and Design; CRC Press: Boka Raton, FL, USA, 2014; ISBN 978-1-4822-8237-5. [Google Scholar]
- Amiama, C.; Bueno, J.; Álvarez, C.J.; Pereira, J.M. Design and field test of an automatic data acquisition system in a self-propelled forage harvester. Comput. Electron. Agri. 2008, 61, 192–200. [Google Scholar] [CrossRef]
- Bloch, H.P.; Geitner, F.K. Practical Machinery Management for Process Plants: Machinery Failure Analysis and Troubleshooting; Elsevier: Amsterdam, The Netherlands, 1997; Volume 2, ISBN 978-0-08-051058-3. [Google Scholar]
- Rao, B.K.N. The need for condition monitoring and maintenance management in industries. In Handbook of Condition Monitoring; Elsevier Science: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Higgs, P.A.; Parkin, R.; Jackson, M.; Al-Habaibeh, A.; Zorriassatine, F.; Coy, J. a survey on condition monitoring systems in industy. Am. Soc. Mech. Eng. Digital Collect. 2008, 41758, 163–178. [Google Scholar]
- Randall, R.B. Vibration signals from rotating and reciprocating machines. In Vibration-Based Condition Monitoring; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 25–62. ISBN 978-0-470-97766-8. [Google Scholar]
- Ahmad, R.; Kamaruddin, S. An overview of time-based and condition-based maintenance in industrial application. Comput. Ind. Eng. 2012, 63, 135–149. [Google Scholar] [CrossRef]
- Norton, M.P.; Karczub, D.G. Fundamentals of Noise and Vibration Analysis for Engineers; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Courrech, J.; Eshleman, R.L. Chapter condition monitoring of machinery. In Harris’ Shock and Vibration Handbook; Piersol, A.G., Harris, C.M., Eds.; McGraw-Hill: New York, NY, USA, 2002; pp. 16.1–16.25. [Google Scholar]
- Langer, T.H.; Ebbesen, M.K.; Kordestani, A. Experimental analysis of occupational whole-body vibration exposure of agricultural tractor with large square baler. Int. J. Ind. Ergonom. 2015, 47, 79–83. [Google Scholar] [CrossRef]
- Gomez-Gil, J.; Gomez-Gil, F.; Martin-de-Leon, R. The influence of tractor-seat height above the ground on lateral vibrations. Sensors 2014, 14, 19713–19730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pang, J.; Li, Y.; Ji, J.; Xu, L. Vibration excitation identification and control of the cutter of a combine harvester using triaxial accelerometers and partial coherence sorting. Biosyst. Eng. 2019, 185, 25–34. [Google Scholar] [CrossRef]
- Tint, P.; Tarmas, G.; Koppel, T.; Reinhold, K.; Kalle, S. Vibration and noise caused by lawn maintenance machines in association with risk to health. Agron. Res. 2012, 10, 251–260. [Google Scholar]
- Scarlett, A.J.; Price, J.S.; Stayner, R.M. Whole-body vibration: Evaluation of emission and exposure levels arising from agricultural tractors. J. Terramech. 2007, 44, 65–73. [Google Scholar] [CrossRef]
- Hostens, I.; Ramon, H. Descriptive analysis of combine cabin vibrations and their effect on the human body. J. Sound Vib. 2003, 266, 453–464. [Google Scholar] [CrossRef]
- Ruiz-Gonzalez, R.; Gomez-Gil, J.; Gomez-Gil, F.J.; Martínez-Martínez, V. An SVM-based classifier for estimating the state of various rotating components in agro-industrial machinery with a vibration signal acquired from a single point on the machine chassis. Sensors 2014, 14, 20713–20735. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Martínez, V.; Gomez-Gil, F.J.; Gomez-Gil, J.; Ruiz-Gonzalez, R. An artificial neural network based expert system fitted with genetic algorithms for detecting the status of several rotary components in agro-industrial machines using a single vibration signal. Expert Syst. Appl. 2015, 42, 6433–6441. [Google Scholar] [CrossRef]
- Khodabakhshian, R. Maintenance management of tractors and agricultural machinery: Preventive maintenance systems. Agric. Eng. Int. CIGR J. 2013, 15, 147–159. [Google Scholar]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Patricia Henriquez, J.B.A. Review of automatic fault diagnosis systems using audio and vibration signals. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 642–652. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal Process. 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Han, T.; Yang, B.S.; Choi, W.H.; Kim, J.S. Fault diagnosis system of induction motors based on neural network and genetic algorithm using stator current signals. Int. J. Rotating Mach. 2006, 2006, 1–13. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. A survey on deep learning based bearing fault diagnosis. Neurocomputing 2019, 335, 327–335. [Google Scholar] [CrossRef]
- Guo, S.; Yang, T.; Gao, W.; Zhang, C. A novel fault diagnosis method for rotating machinery based on a convolutional neural network. Sensors 2018, 18, 1429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, Y.; Liu, X. A deep adaptive learning method for rolling bearing fault diagnosis using immunity. Tinshhua Sci. Technol. 2019, 24, 750–762. [Google Scholar] [CrossRef]
- Elbhbah, K.; Sinha, J.K. Vibration-based condition monitoring of rotating machines using a machine composite spectrum. J. Sound Vib. 2013, 332, 2831–2845. [Google Scholar] [CrossRef]
- Sinha, J.K.; Elbhbah, K. A future possibility of vibration based condition monitoring of rotating machines. Mech. Syst. Signal Process. 2013, 34, 231–240. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. An improved data fusion technique for faults diagnosis in rotating machines. Measurement 2014, 58, 27–32. [Google Scholar] [CrossRef]
- Elbhbah, K.; Sinha, J.K.; Hahn, W.; Tasker, G. Application of composite spectrum in steam turbo-generator set. In Vibration Engineering and Technology of Machinery; Sinha, J.K., Ed.; Springer International Publishing: Berlin, Germany, 2015; pp. 139–144. ISBN 978-3-319-09917-0. [Google Scholar]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Nembhard, A.D. A novel fault diagnosis technique for enhancing maintenance and reliability of rotating machines. Struct. Health Monit. 2015, 14, 604–621. [Google Scholar] [CrossRef] [Green Version]
- Luwei, K.C.; Yunusa-Kaltungo, A.; Sha’aban, Y.A. Integrated fault detection framework for classifying rotating machine faults using frequency domain data fusion and artificial neural networks. Machines 2018, 6, 59. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Academic Press: Cambridge, MA, USA, 2013; ISBN 978-1-4832-7648-9. [Google Scholar]




| Thresher Status | Chopper Status | Idle | Max. RPM |
|---|---|---|---|
| Off (Deactivated) | Off | D1 | D10 |
| Balanced | D2 | D11 | |
| Unbalanced | D3 | D12 | |
| Balanced (on and Healthy) | Off | D4 | D13 |
| Balanced | D5 | D14 | |
| Unbalanced | D6 | D15 | |
| Unbalanced (on and Faulty) | Off | D7 | D16 |
| Balanced | D8 | D17 | |
| Unbalanced | D9 | D18 |
| Regime | Thresher | Chopper | Straw Walkers | Sieve Box | Engine |
|---|---|---|---|---|---|
| Idle | 8.5 Hz (508.3 RPM) | 25.4 Hz (1524 RPM) | 2 Hz (180 RPM) | 3 Hz (120 RPM) | 21.4 Hz (1280 RPM) |
| Max. RPM | 14.26 Hz (839.5 RPM) | 42.54 Hz (2517 RPM) | 3.5 Hz (318 RPM) | 5.3 Hz (210 RPM) | 35.8 Hz (2144 RPM) |
| Deactivated | Balanced | Unbalanced | Balanced vs. Deactivated | Unbalancedb vs. Balanced | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N = 15 M (SD) | N = 15 M (SD) | N = 15 M (SD) | t | p | d | t | p | d | ||
| a1 | Idle | 0.0043 (0.0021) | 0.1502 (0.0413) | 0.6340 (0.0562) | 9.61 | * | 5.2 | 31.23 | * | 9.8 |
| Max. | 0.0087 (0.0043) | 0.4934 (0.1566) | 1.7703 (0.2050) | 8.73 | * | 4.4 | 21.97 | * | 7.0 | |
| a2 | Idle | 0.0017 (0.0011) | 0.0915 (0.0244) | 0.3736 (0.0415) | 9.90 | * | 5.4 | 22.28 | * | 8.3 |
| Max. | 0.0045 (0.0011) | 0.3007 (0.0890) | 1.1472 (0.1200) | 9.19 | * | 4.7 | 25.13 | * | 8.0 | |
| a3 | Idle | 0.0010 (0.0004) | 0.0640 (0.0190) | 0.1286 (0.0210) | 9.16 | * | 4.9 | 9.62 | * | 3.2 |
| Max. | 0.0027 (0.0011) | 0.3460 (0.1471) | 0.8001 (0.1654) | 7.09 | * | 3.3 | 8.56 | * | 2.9 | |
| a4 | Idle | 0.0022 (0.0013) | 0.2008 (0.0342) | 0.4479 (0.0305) | 13.49 | * | 8.5 | 25.76 | * | 7.6 |
| Max. | 0.0048 (0.0012) | 0.3793 (0.0973) | 0.9146 (0.0667) | 10.18 | * | 5.4 | 18.89 | * | 6.4 | |
| nCCS | Idle | 0.0009 (0.0007) | 0.0822 (0.0209) | 0.2907 (0.0272) | 10.25 | * | 5.7 | 27.75 | * | 8.6 |
| Max. | 0.0015 (0.0008) | 0.3065 (0.1194) | 1.0376 (0.1286) | 7.58 | * | 3.6 | 19.21 | * | 5.9 | |
| CCS | Idle | 0.0015 (0.0008) | 0.0936 (0.0147) | 0.2928 (0.0268) | 14.26 | * | 9.2 | 23.45 | * | 9.2 |
| Max. | 0.0036 (0.0011) | 0.3377 (0.1012) | 1.0467 (0.1247) | 9.13 | * | 4.7 | 19.84 | * | 6.2 | |
| pCCS | Idle | 0.0006 (0.0006) | 0.0660 (0.0185) | 0.2538 (0.0195) | 9.61 | * | 5.2 | 35.53 | * | 9.9 |
| Max. | 0.0008 (0.0006) | 0.2308 (0.0969) | 0.8178 (0.0898) | 7.18 | * | 3.4 | 20.70 | * | 6.3 | |
| Deactivated | Balanced | Unbalanced | Balanced vs. Deactivated | Unbalance vs. Balanced | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N = 15 M (SD) | N = 15 M (SD) | N = 15 M (SD) | t | p | d | t | p | d | ||
| a1 | Idle | 0.0257 (0.0050) | 0.0788 (0.0344) | 0.2082 (0.0207) | 5.15 | * | 2.2 | 12.45 | * | 4.6 |
| Max. | 0.0780 (0.0239) | 0.2083 (0.1272) | 1.8377 (0.4242) | 3.62 | * | 1.4 | 11.08 | * | 5.2 | |
| a2 | Idle | 0.0272 (0.0112) | 0.0676 (0.0243) | 0.2133 (0.0933) | 5.58 | * | 2.2 | 5.25 | * | 2.1 |
| Max. | 0.0973 (0.0342) | 0.3802 (0.0743) | 0.8773 (0.0754) | 11.94 | * | 4.9 | 22.20 | * | 6.6 | |
| a3 | Idle | 0.0946 (0.0579) | 0.4571 (0.0775) | 2.6982 (0.2461) | 15.33 | * | 5.4 | 21.70 | * | 12.3 |
| Max. | 0.1457 (0.1142) | 0.2394 (0.1279) | 0.9128 (0.1658) | 2.14 | * | 0.8 | 13.68 | * | 4.5 | |
| a4 | Idle | 0.0224 (0.0094) | 0.1935 (0.0446) | 0.9699 (0.0310) | 10.68 | * | 5.5 | 65.42 | * | 20.2 |
| Max. | 0.0482 (0.0104) | 0.4060 (0.0770) | 3.1347 (0.2913) | 11.85 | * | 6.5 | 21.04 | * | 12.8 | |
| nCCS | Idle | 0.0227 (0.0120) | 0.1354 (0.0286) | 0.6069 (0.0760) | 12.19 | * | 5.3 | 17.08 | * | 8.2 |
| Max. | 0.0480 (0.0217) | 0.1745 (0.0640) | 1.0872 (0.1347) | 6.48 | * | 2.6 | 20.18 | * | 8.7 | |
| CCS | Idle | 0.0348 (0.0149) | 0.1466 (0.0206) | 0.6168 (0.0692) | 18.06 | * | 6.3 | 17.14 | * | 9.2 |
| Max. | 0.0807 (0.0325) | 0.2631 (0.0351) | 1.1912 (0.0669) | 17.32 | * | 5.4 | 41.06 | * | 17.4 | |
| pCCS | Idle | 0.0121 (0.0066) | 0.0934 (0.0279) | 0.4254 (0.0380) | 8.76 | * | 4.2 | 31.77 | * | 10.0 |
| Max. | 0.0283 (0.0164) | 0.1184 (0.0740) | 0.9342 (0.1289) | 4.22 | * | 1.7 | 20.56 | * | 7.8 | |
| Deactivated | Activated | Activated vs. Deactivated | ||||
|---|---|---|---|---|---|---|
| N = 15 M (SD) | N = 45 M (SD) | t | p | d | ||
| a1 | Idle | 0.0037 (0.0038) | 0.1620 (0.0019) | 47.87 | * | 47.3 |
| Max. | 0.0030 (0.0024) | 0.7594 (0.0178) | 735.19 | * | 73.0 | |
| a2 | Idle | 0.0027 (0.0027) | 0.1226 (0.0052) | 563.73 | * | 33.2 |
| Max. | 0.0020 (0.0022) | 0.6679 (0.0117) | 1391.65 | * | 96.2 | |
| a3 | Idle | 0.0019 (0.0014) | 0.0788 (0.0014) | 175.83 | * | 55.5 |
| Max. | 0.0012 (0.0010) | 0.2379 (0.0038) | 2547.26 | * | 102.4 | |
| a4 | Idle | 0.0057 (0.0033) | 0.0639 (0.0017) | 27.80 | * | 19.8 |
| Max. | 0.0024 (0.0010) | 0.5565 (0.0091) | 1049.58 | * | 105.2 | |
| nCCS | Idle | 0.0015 (0.0022) | 0.0989 (0.0016) | 75.13 | * | 48.3 |
| Max. | 0.0010 (0.0016) | 0.4692 (0.0080) | 1539.22 | * | 98.0 | |
| CCS | Idle | 0.0026 (0.0023) | 0.0992 (0.0018) | 75.11 | * | 44.4 |
| Max. | 0.0016 (0.0015) | 0.4692 (0.0080) | 1443.09 | * | 98.3 | |
| pCCS | Idle | 0.0009 (0.0016) | 0.0754 (0.0015) | 115.25 | * | 48.1 |
| data | 0.0006 (0.0008) | 0.3858 (0.0072) | 902.67 | * | 92.6 | |
| Deactivated | Activated | Activated vs. Deactivated | ||||
|---|---|---|---|---|---|---|
| N = 15 M (SD) | N = 45 M (SD) | t | p | d | ||
| a1 | Idle | 0.0101 (0.0106) | 0.1216 (0.0406) | 20.48 | * | 4.7 |
| Max. | 0.0156 (0.0113) | 0.3962 (0.0269) | 351.32 | * | 21.2 | |
| a2 | Idle | 0.0084 (0.0090) | 0.1449 (0.0337) | 36.32 | * | 6.9 |
| Max. | 0.0082 (0.0055) | 0.0848 (0.0058) | 69.58 | * | 13.7 | |
| a3 | Idle | 0.0039 (0.0042) | 0.1190 (0.0163) | 83.57 | * | 12.1 |
| Max. | 0.0018 (0.0010) | 0.0498 (0.0045) | 140.03 | * | 17.8 | |
| a4 | Idle | 0.0056 (0.0043) | 0.7263 (0.0395) | 222.33 | * | 33.2 |
| Max. | 0.0139 (0.0106) | 1.3857 (0.0460) | 669.05 | * | 49.6 | |
| nCCS | Idle | 0.0052 (0.0063) | 0.1716 (0.0313) | 50.11 | * | 9.4 |
| Max. | 0.0055 (0.0039) | 0.1455 (0.0065) | 559.51 | * | 28.6 | |
| CCS | Idle | 0.0060 (0.0063) | 0.1717 (0.0313) | 49.53 | * | 9.3 |
| Max. | 0.0058 (0.0038) | 0.1459 (0.0065) | 589.59 | * | 28.8 | |
| pCCS | Idle | 0.0032 (0.0038) | 0.1494 (0.0267) | 47.40 | * | 9.9 |
| Max. | 0.0051 (0.0038) | 0.1658 (0.0072) | 747.80 | * | 31.1 | |
| Thresher | Chopper | Straw Walkers | Sieve Box | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Balanced vs. Deactivated | Unbalanced vs. Balanced | Balanced vs. Off Status | Unbalanced vs. Balanced | Balanced vs. Deactivated | Balanced vs. Deactivated | |||||||
| Idle | Max RPM | Idle | Max RPM. | Idle | Max. RPM | idle | Max RPM | Idle | Max RPM | Idle | Max RPM | |
| a1 | A | A | A | A | C | C | A | A | A | A | A | A |
| a2 | A | A | A | A | C | A | C | A | A | A | A | A |
| a3 | A | B | B | B | A | C | A | A | A | A | A | A |
| a4 | A | A | A | A | A | A | A | A | A | A | A | A |
| nCCS | A | A | A | A | A | B | A | A | A | A | A | A |
| CCS | A | A | A | A | A | A | A | A | A | A | A | A |
| pCCS | A | B | A | A | A | C | A | A | A | A | A | A |
| Cases | AUC 1 Ratio | AUC Ratio Reduction | |||||
|---|---|---|---|---|---|---|---|
| pCCS | CCS | nCCS | Individual Spectra 3 | pCCS vs. CCS 2 | pCCS vs. nCCS | pCCS vs. Individual Spectra 3 | |
| D1 | 6.8% | 8.9% | 14.7% | 12.7% | 24.1% | 54.1% | 46.5% |
| D2 | 6.5% | 8.7% | 15.2% | 13.0% | 25.0% | 57.3% | 49.8% |
| D3 | 6.3% | 8.2% | 14.3% | 12.7% | 23.4% | 56.0% | 50.4% |
| D4 | 12.3% | 17.1% | 25.8% | 19.4% | 27.8% | 52.3% | 36.4% |
| D5 | 12.3% | 17.0% | 25.8% | 19.4% | 27.7% | 52.5% | 36.7% |
| D6 | 12.3% | 16.8% | 25.8% | 20.2% | 26.7% | 52.2% | 38.9% |
| D7 | 11.8% | 16.7% | 25.5% | 19.0% | 29.1% | 53.6% | 37.7% |
| D8 | 11.9% | 16.7% | 26.1% | 19.6% | 28.8% | 54.5% | 39.5% |
| D9 | 11.8% | 16.4% | 25.4% | 19.4% | 28.0% | 53.4% | 38.9% |
| D10 | 5.6% | 7.8% | 13.8% | 11.6% | 27.8% | 59.4% | 51.6% |
| D11 | 6.3% | 8.7% | 15.4% | 12.0% | 27.7% | 59.2% | 48.0% |
| D12 | 8.5% | 11.4% | 17.4% | 14.5% | 25.1% | 51.1% | 41.2% |
| D13 | 14.5% | 19.6% | 27.4% | 20.3% | 26.4% | 47.3% | 28.9% |
| D14 | 14.4% | 19.5% | 27.5% | 20.4% | 25.9% | 47.6% | 29.2% |
| D15 | 14.6% | 19.5% | 26.4% | 20.1% | 25.2% | 44.7% | 27.3% |
| D16 | 13.7% | 18.9% | 26.9% | 20.5% | 27.4% | 49.1% | 33.3% |
| D17 | 14.5% | 19.5% | 27.2% | 20.6% | 25.7% | 46.6% | 29.4% |
| D18 | 13.1% | 18.2% | 25.8% | 19.8% | 28.0% | 49.3% | 34.0% |
| Min. | 5.6% | 7.8% | 13.8% | 11.6% | 23.4% | 44.7% | 27.3% |
| Max. | 14.6% | 19.6% | 27.5% | 20.6% | 29.1% | 59.4% | 51.6% |
| Avg. | 11.0% | 15.0% | 22.6% | 17.5% | 26.7% | 52.2% | 38.8% |
| Std. Dev. | 3.3% | 4.6% | 5.5% | 3.5% | 1.6% | 4.2% | 7.8% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feijoo, F.; Gomez-Gil, F.J.; Gomez-Gil, J. Application of Composite Spectrum in Agricultural Machines. Sensors 2020, 20, 5519. https://doi.org/10.3390/s20195519
Feijoo F, Gomez-Gil FJ, Gomez-Gil J. Application of Composite Spectrum in Agricultural Machines. Sensors. 2020; 20(19):5519. https://doi.org/10.3390/s20195519
Chicago/Turabian StyleFeijoo, Fernando, Francisco Javier Gomez-Gil, and Jaime Gomez-Gil. 2020. "Application of Composite Spectrum in Agricultural Machines" Sensors 20, no. 19: 5519. https://doi.org/10.3390/s20195519
APA StyleFeijoo, F., Gomez-Gil, F. J., & Gomez-Gil, J. (2020). Application of Composite Spectrum in Agricultural Machines. Sensors, 20(19), 5519. https://doi.org/10.3390/s20195519





