Space-Borne GNSS-R Ionospheric Delay Error Elimination by Optimal Spatial Filtering
Abstract
:1. Introduction
2. Materials and Methods
2.1. Calculation of Space-Borne GNSS-R Ionospheric Delay
2.2. Spatial Filtering of Ionospheric Delay
3. Results
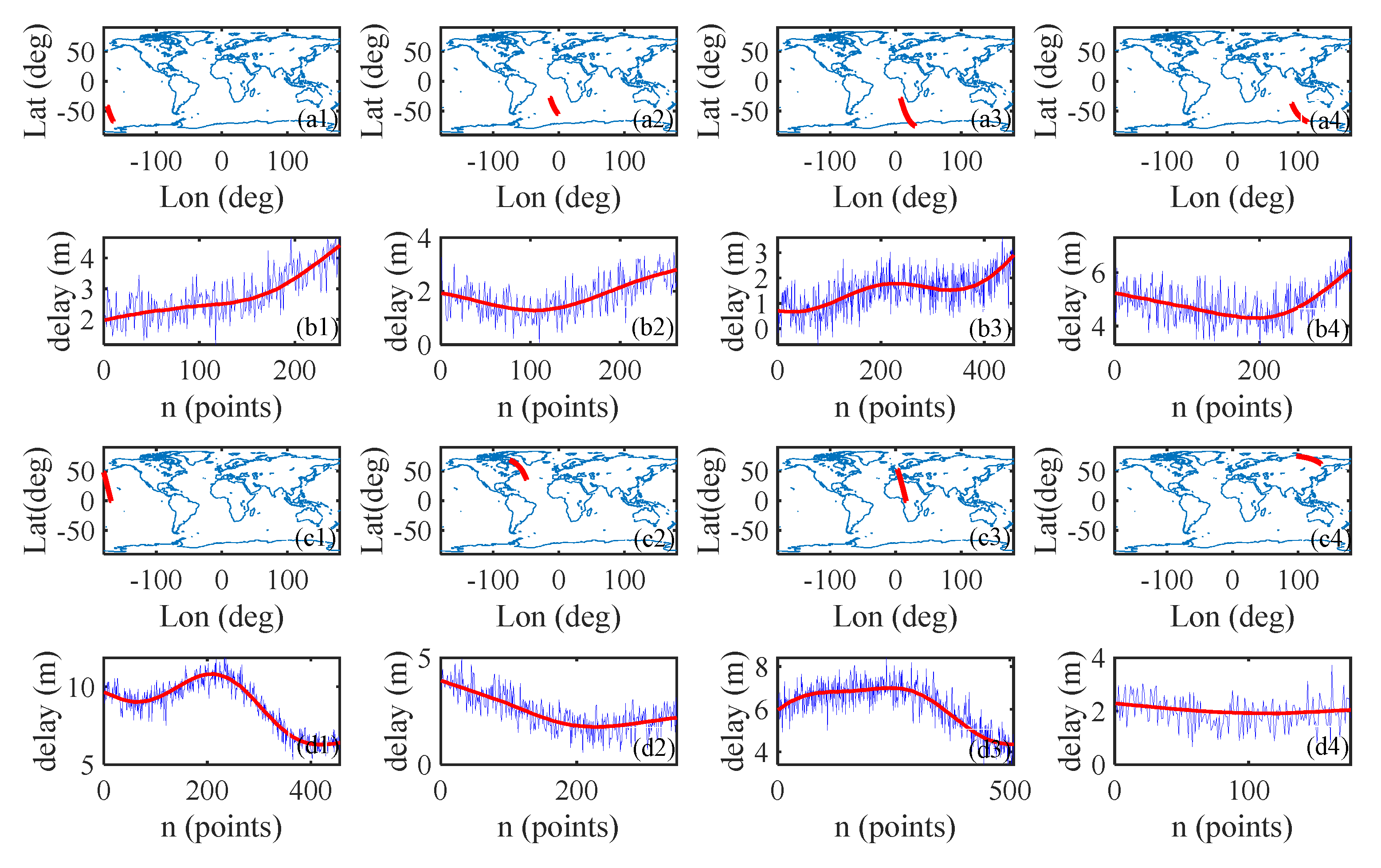
3.1. Ionospheric Delay from Simulated Orbital Data
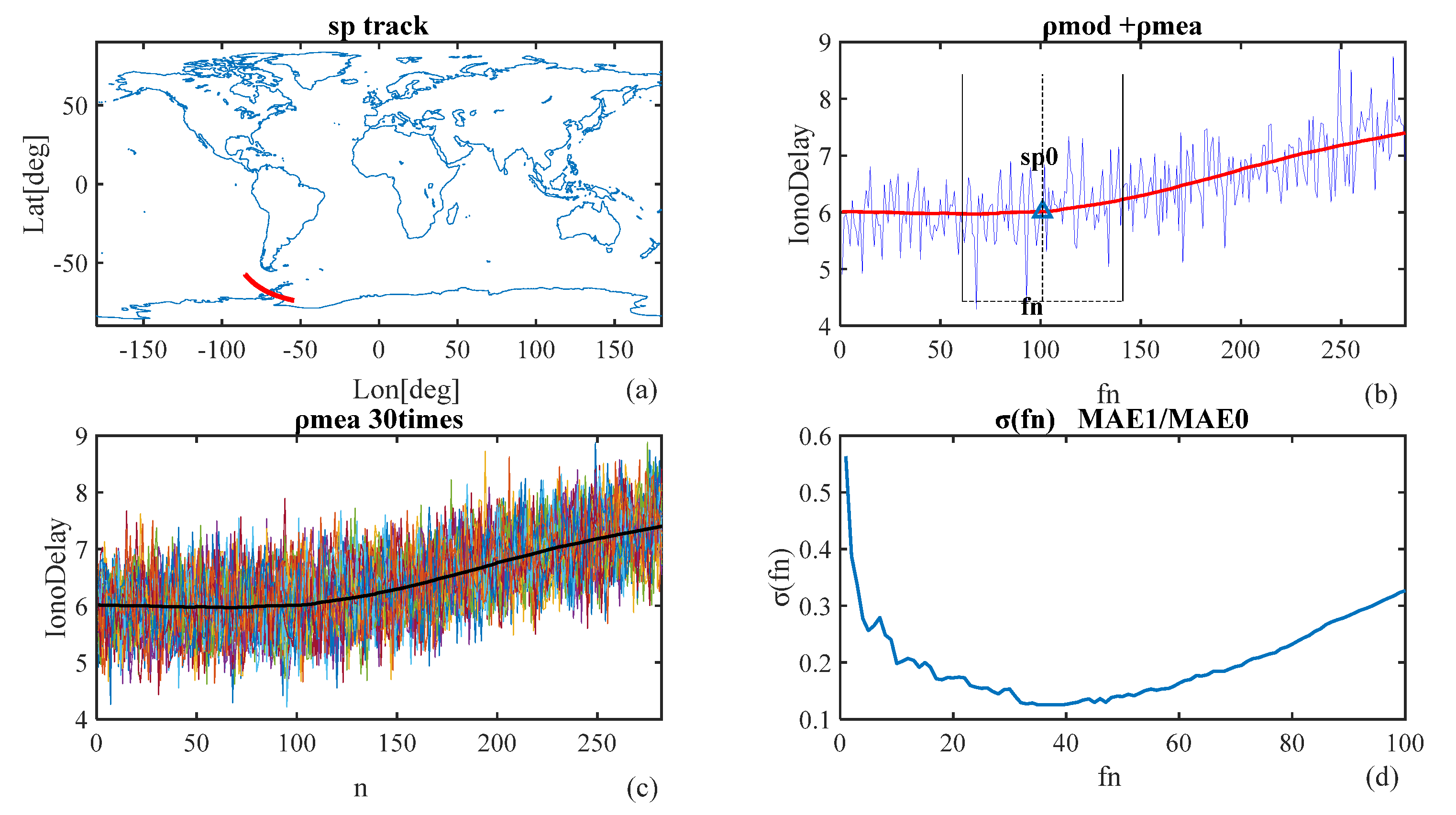
3.2. Spatial Filtering Method Results for Ionospheric Delay
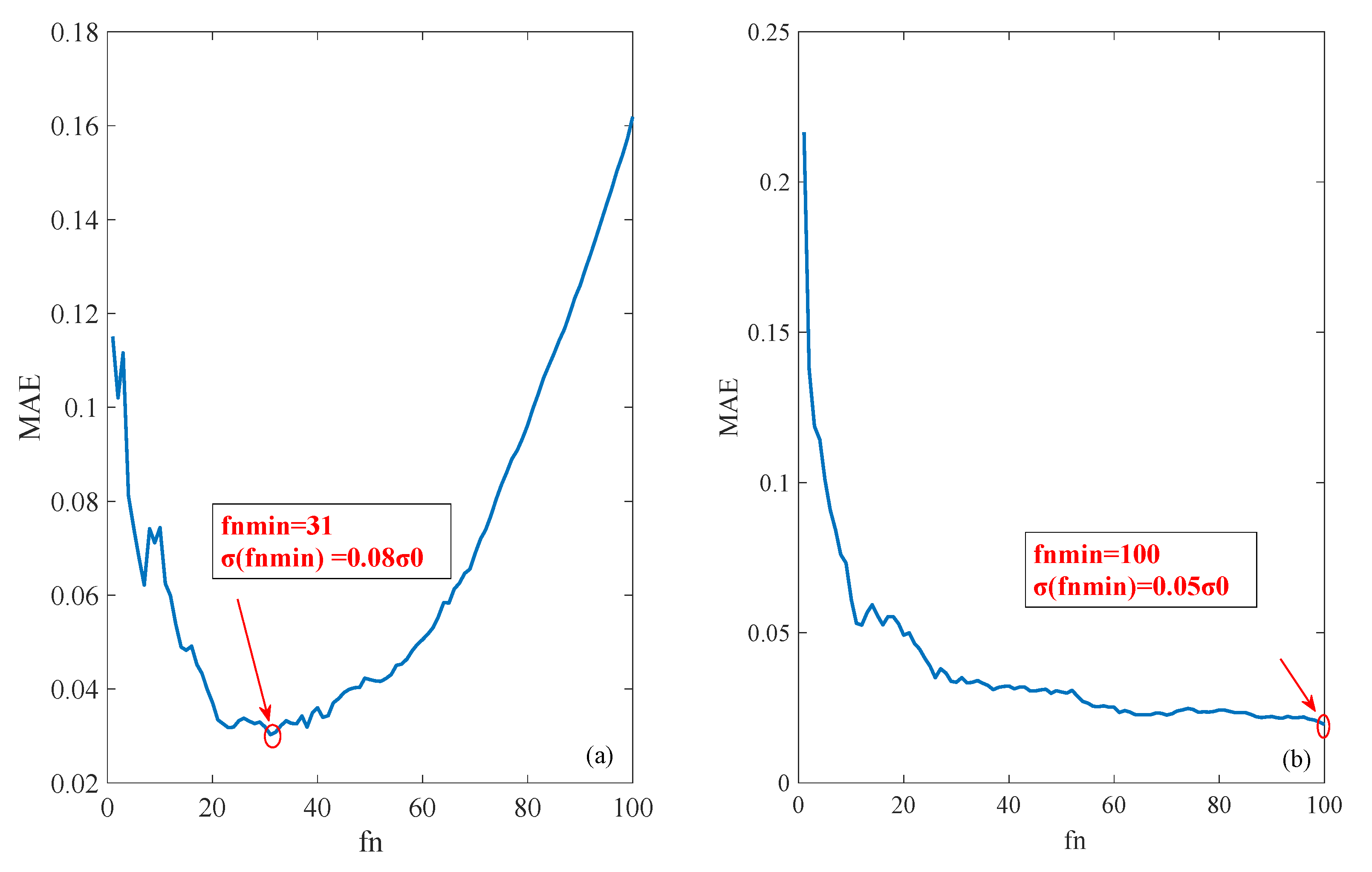
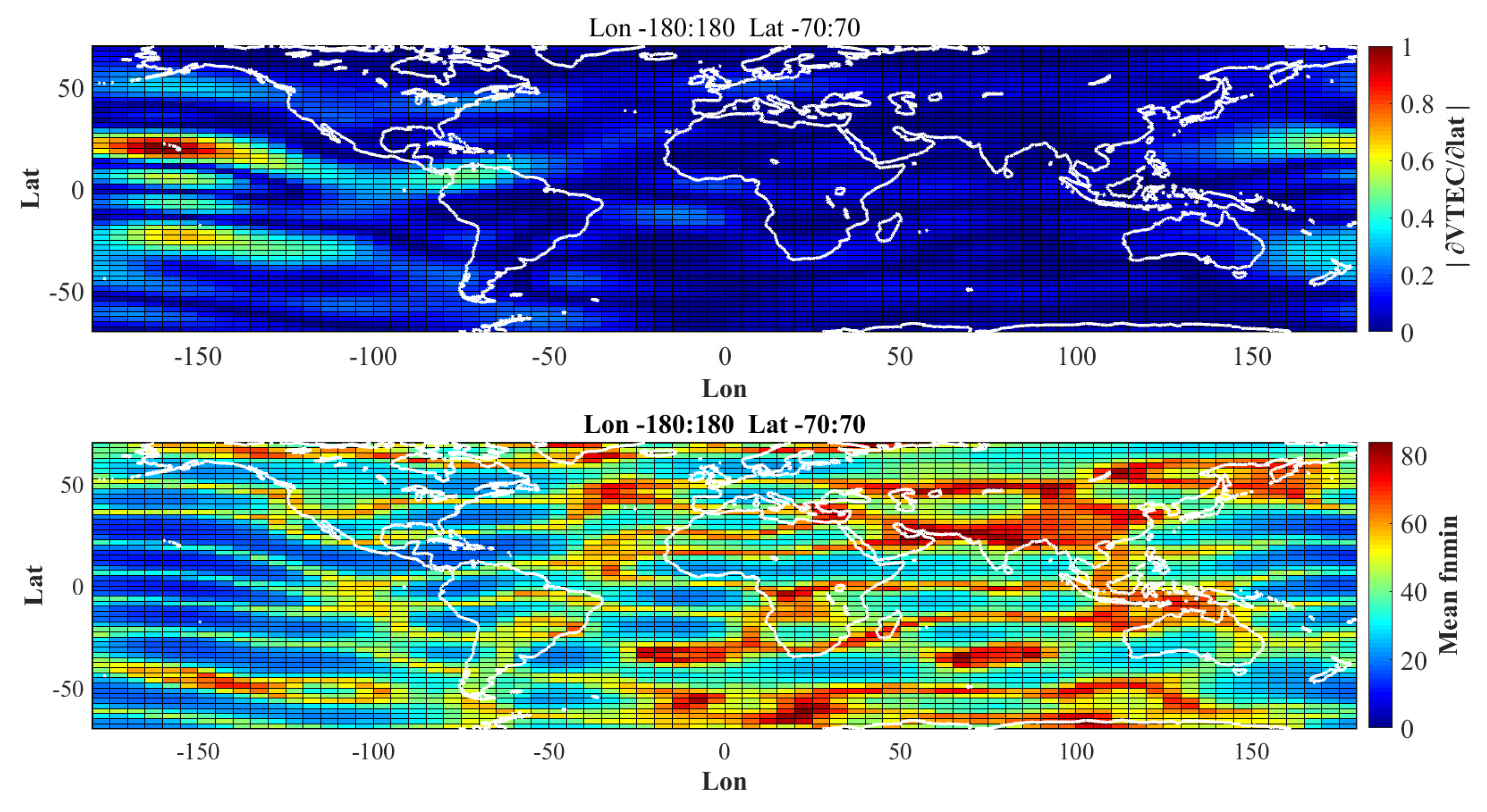
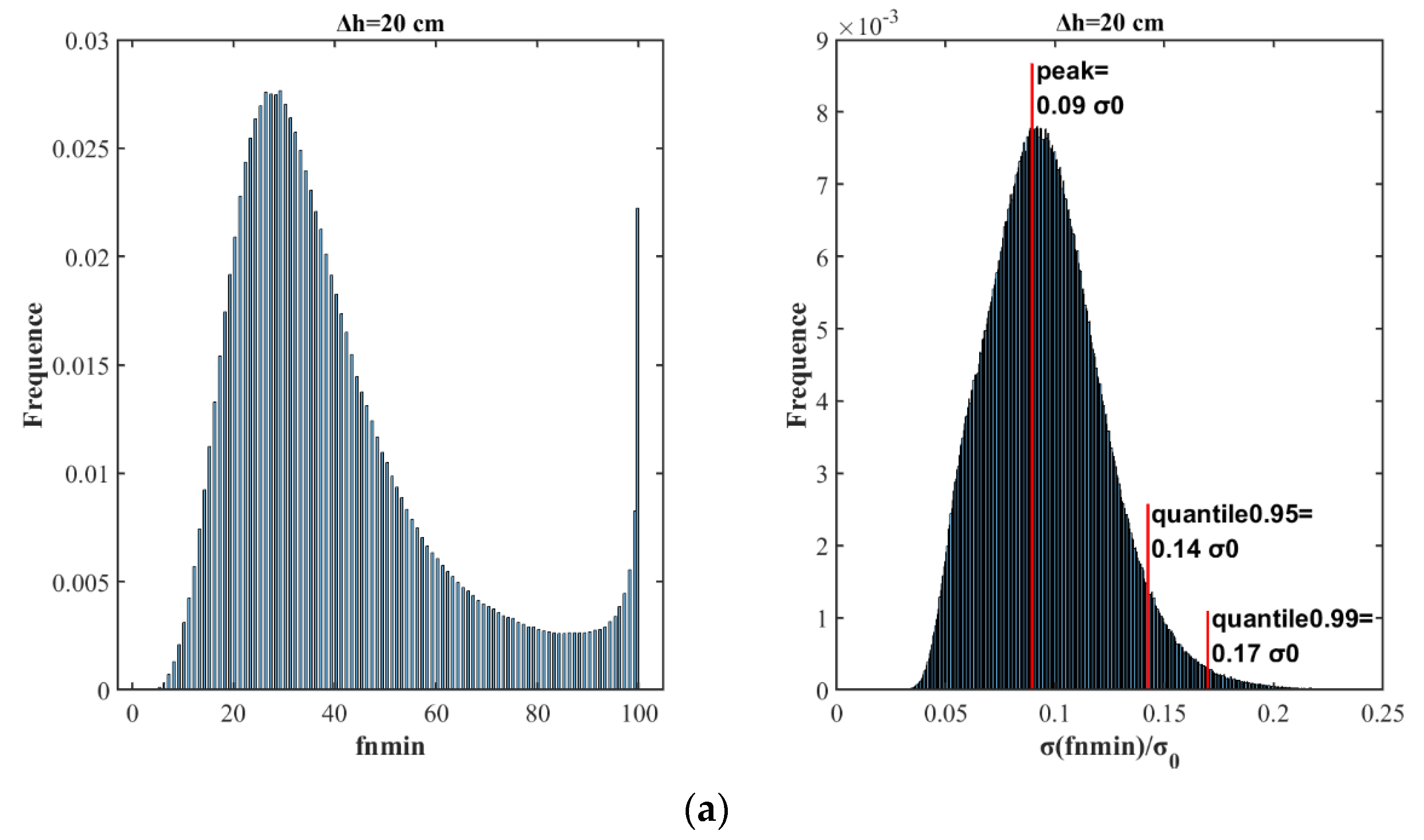
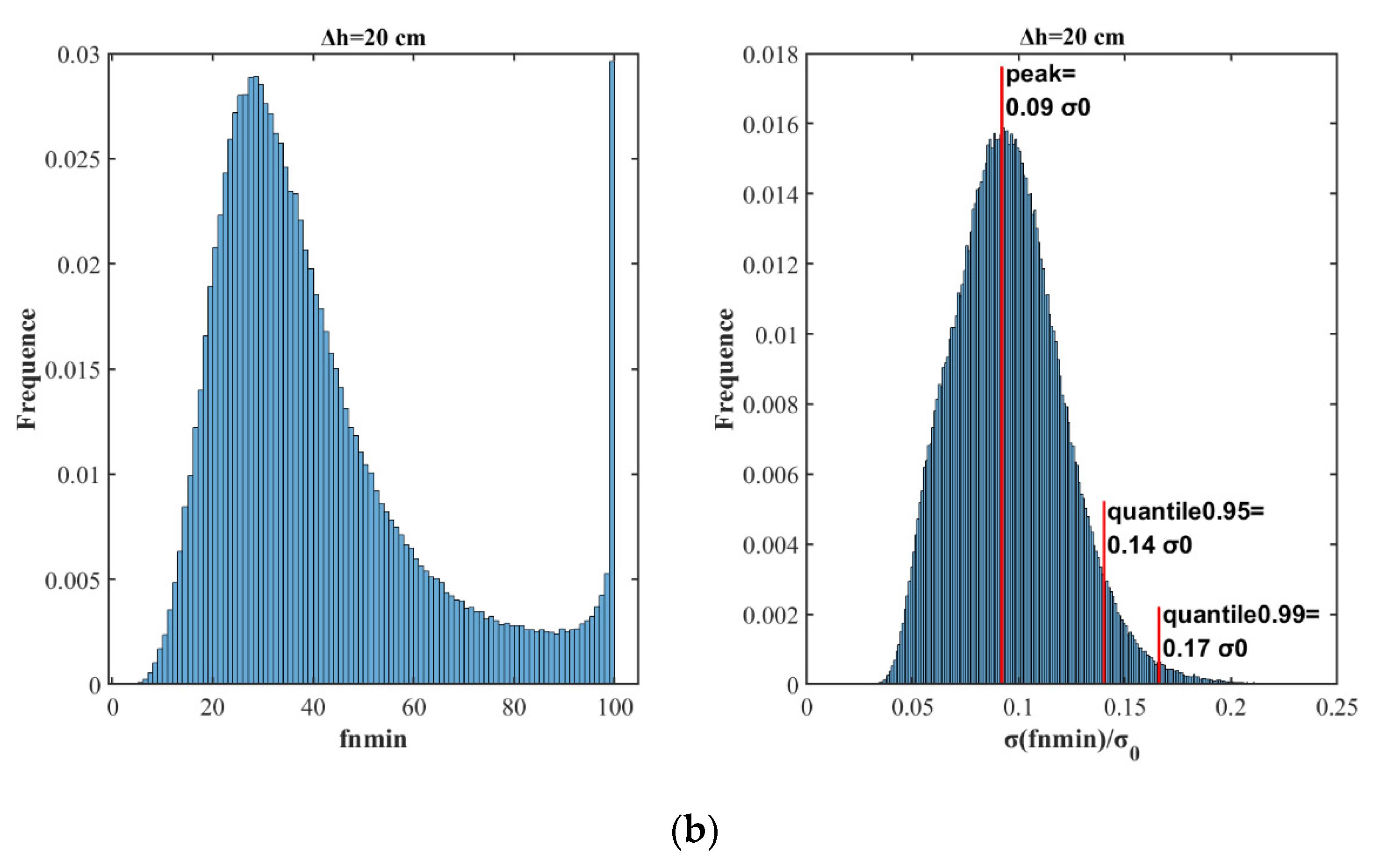
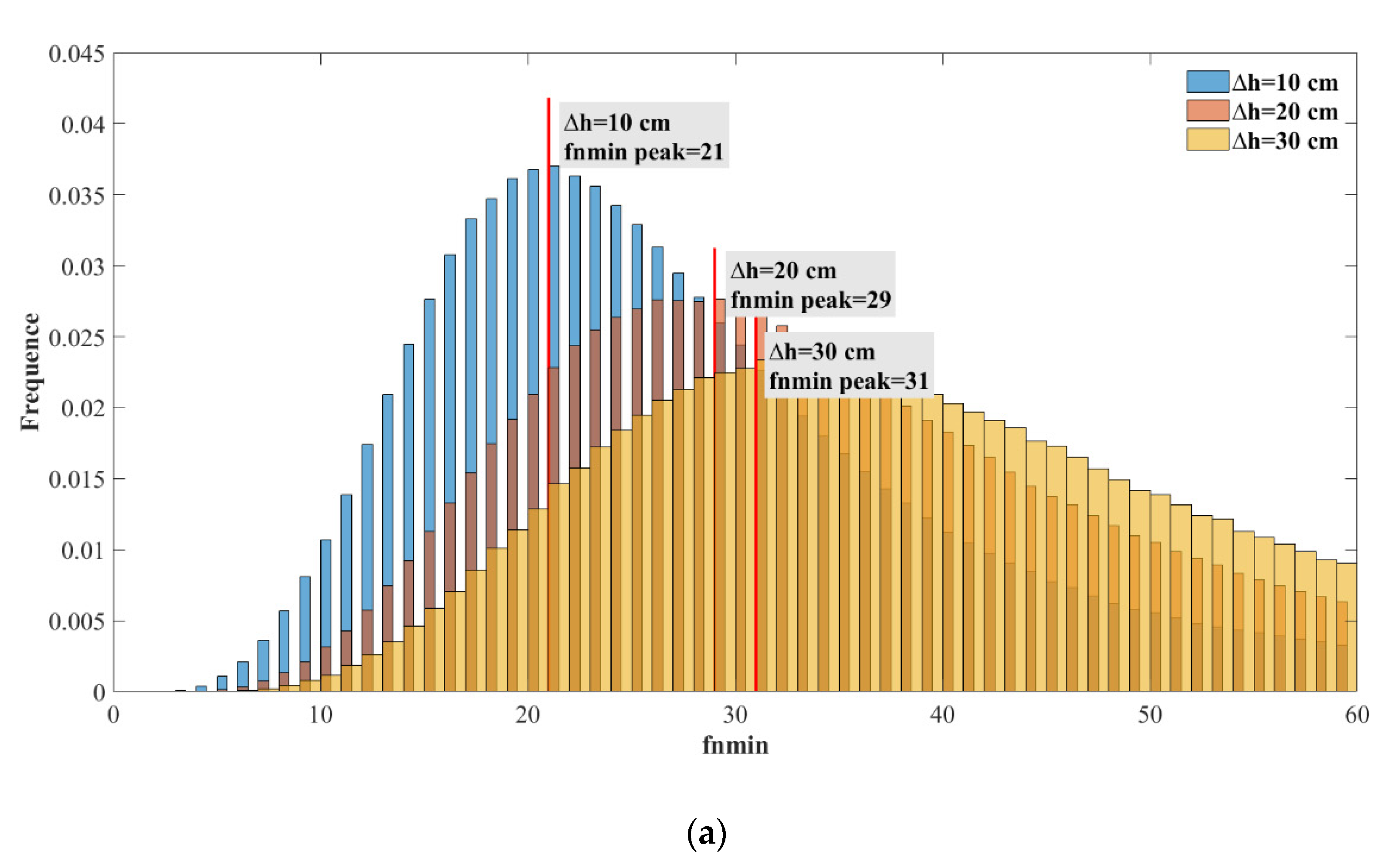
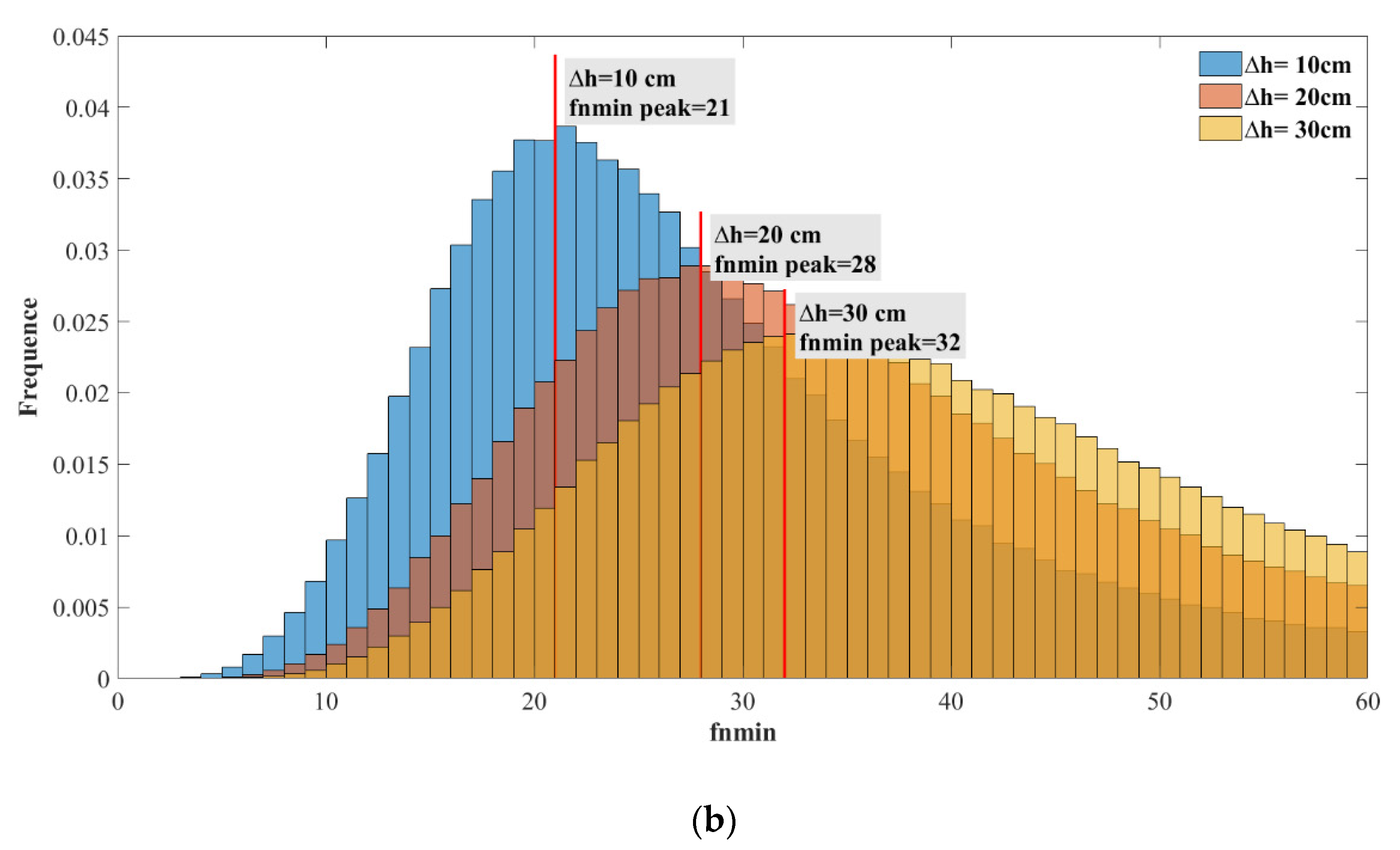
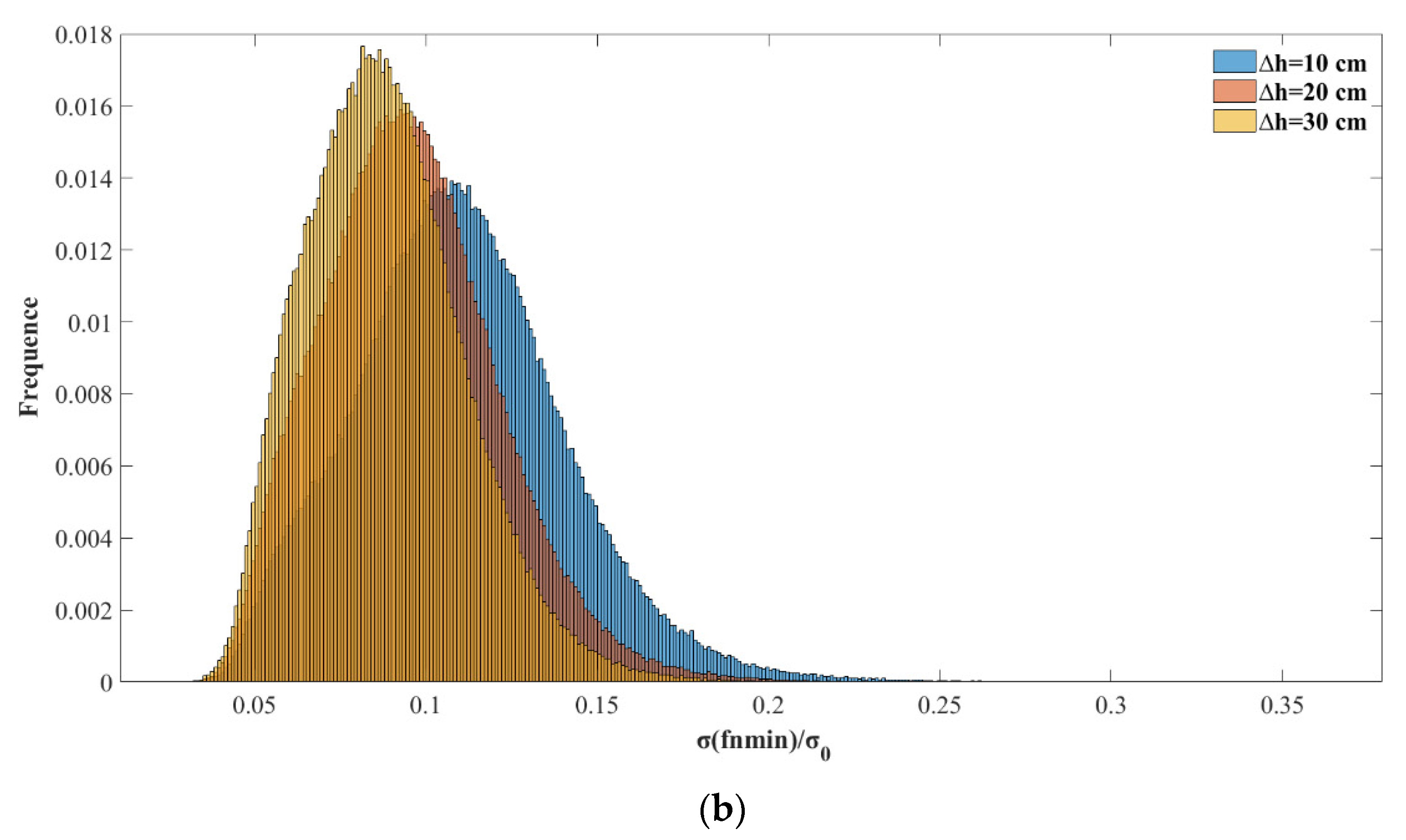
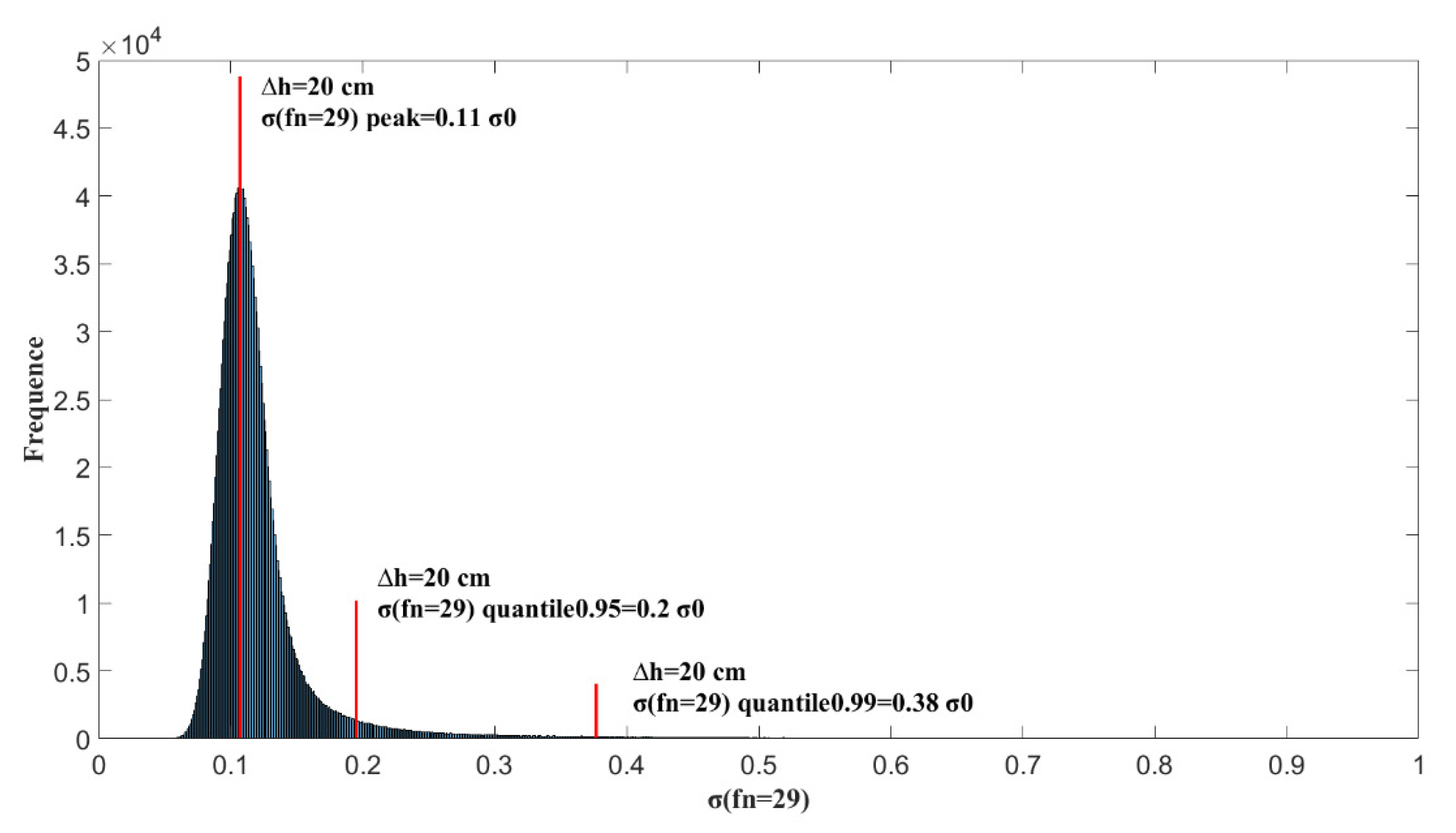
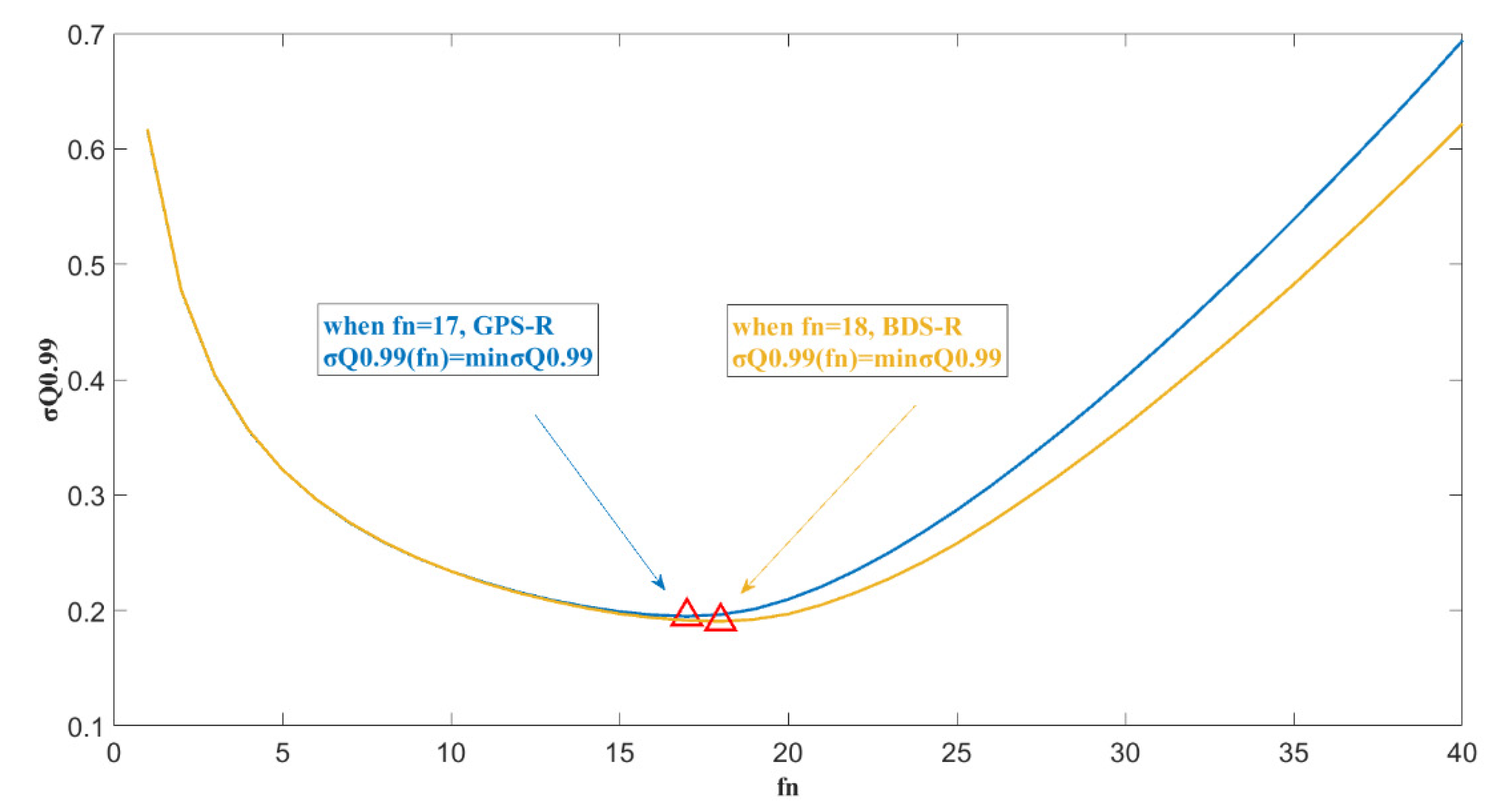
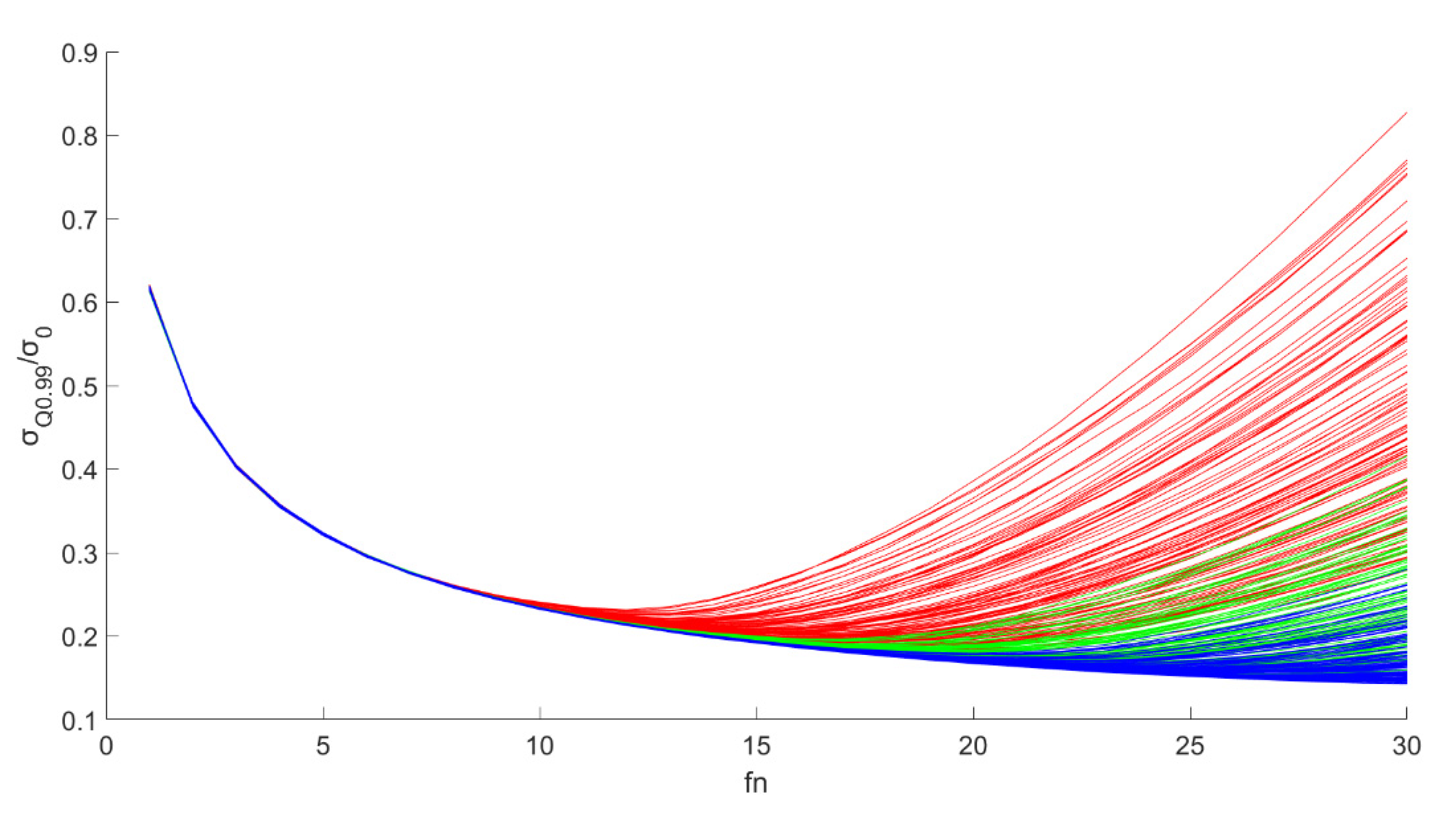
3.3. Statistical Analysis of the Spatial Filtering Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barrick, D.E. Relationship between slope probability density function and the physical optics integral in rough surface scattering. Proc. IEEE 1968, 56, 1728–1729. [Google Scholar] [CrossRef]
- Yu, K.; Rizos, C.; Burrage, D.; Dempster, A.G.; Zhang, K.; Markgraf, M. An overview of GNSS remote sensing. Eurasip J. Adv. Signal Process. 2014, 2014, 134. [Google Scholar] [CrossRef] [Green Version]
- Hajj, G.A.; Zuffada, C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal. Radio Sci. 2003, 38, 1089. [Google Scholar] [CrossRef]
- Lowe, S.T.; Zuffada, C.; Chao, Y.; Kroger, P.; Young, L.; LaBrecque, J. Five-cm-precision aircraft ocean altimetry using GPS reflections. Geophys. Res. Lett. 2002, 29, 1375. [Google Scholar] [CrossRef] [Green Version]
- Rius, A.; Cardellach, E.; Martín-Neira, M. Altimetric analysis of the sea-surface GPS-reflected signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2119–2127. [Google Scholar] [CrossRef]
- Jin, S.G.; Cardellach, E.; Xie, F. GNSS Remote Sensing: Theory, Methods and Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-Reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O. The DTU10 Gravity Field and Mean Sea Surface, in Second International Symposium of the Gravity Field of the Earth (IGFS2); University of Alaska-Fairbanks: Fairbanks, AL, USA, 2010. [Google Scholar]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. Global Ocean Altimetry with GNSS Reflections from TechDemoSat-1. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4088–4097. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Zuffada, C.; Loria, E.; O’Brien, A.; Haines, B. Improved GNSS-R Ocean Surface Altimetry with CYGNSS in the Seas of Indonesia. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6071–6087. [Google Scholar] [CrossRef]
- Xu, L.; Wan, W.; Chen, X.; Zhu, S.; Liu, B.; Hong, Y. Spaceborne GNSS-R Observation of Global Lake Level: First Results from the TechDemoSat-1 Mission. Remote Sens. 2019, 11, 1438. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Li, W.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.S.; Buontempo, C. First Precise Spaceborne Sea Surface Altimetry with GNSS Reflected Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 13, 102–112. [Google Scholar] [CrossRef]
- Ionospheric Propagation Data and Prediction Methods Required for the Design of Satellite Services and Systems. Recommendation ITU-R P.531-6. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-RECP.531-6-200102-S!!PDF-E.pdf (accessed on 17 November 2015).
- Camps, A.; Park, H.; Foti, G.; Gommenginger, C. Ionospheric Effects in GNSS-Reflectometry from Space. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5851–5861. [Google Scholar] [CrossRef]
- Martín-Neira, M.; D’Addio, S.; Buck, C.; Floury, N.; Prieto-Cerdeira, R. The PARIS Ocean Altimeter In-Orbit Demonstrator. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2209–2237. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J.; Jia, Y.; Fan, C.; Cui, W. Validation of Sentinel-3A/3B and Jason-3 Altimeter Wind Speeds and Significant Wave Heights Using Buoy and ASCAT Data. Remote Sens. 2020, 12, 2079. [Google Scholar] [CrossRef]
- Imel, D.A. Evaluation of the TOPEX/POSEIDON dual -frequency ionospheric correction. J. Geophys. Res. 1994, 99, 24895–24906. [Google Scholar] [CrossRef]
- Schaer, S.; Beutler, G.; Mervart, L.; Rothacher, M.; Wild, U. Global and regional ionosphere models using the GPS double difference phase observable. In Proceedings of the IGS Workshop on Special Topics on New Directions, Potsdam, Germany, 15–17 May 1995; pp. 77–92. [Google Scholar]
- Zi-Shen, L.I.; Ning-Bo, W.; Min, L.; Kai, Z.; Yun-Bin, Y.; Hong, Y. Evaluation and Analysis of the Global Ionospheric TEC Map in the Frame of International GNSS Service. Chin. J. Geophys. 2017, 60, 3718–3729. [Google Scholar]
- Yuan, Y. Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Iono-Sphere Based on GPS; Institude of Geodesy and Geophysics, China Academy of Sciences: Wuhan, China, 2002. [Google Scholar]
- Yue, X.; Schreiner, W.S.; Rocken, C.; Kuo, Y.-H. Validate the IRI2007 model by the COSMIC slant TEC data during the extremely solar minimum of 2008. Adv. Space Res. 2013, 51, 647–653. [Google Scholar] [CrossRef]
- Bona, P. Precision, Cross Correlation, and Time Correlation of GPS Phase and Code Observations. GPS Solut. 2000, 4, 3–13. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Liu, Y.; Xia, J. Space-Borne GNSS-R Ionospheric Delay Error Elimination by Optimal Spatial Filtering. Sensors 2020, 20, 5535. https://doi.org/10.3390/s20195535
Zhang Q, Liu Y, Xia J. Space-Borne GNSS-R Ionospheric Delay Error Elimination by Optimal Spatial Filtering. Sensors. 2020; 20(19):5535. https://doi.org/10.3390/s20195535
Chicago/Turabian StyleZhang, Qiuyang, Yang Liu, and Junming Xia. 2020. "Space-Borne GNSS-R Ionospheric Delay Error Elimination by Optimal Spatial Filtering" Sensors 20, no. 19: 5535. https://doi.org/10.3390/s20195535
APA StyleZhang, Q., Liu, Y., & Xia, J. (2020). Space-Borne GNSS-R Ionospheric Delay Error Elimination by Optimal Spatial Filtering. Sensors, 20(19), 5535. https://doi.org/10.3390/s20195535



