Angle-Sensitive Detector Based on Silicon-On-Insulator Photodiode Stacked with Surface Plasmon Antenna
Abstract
:1. Introduction
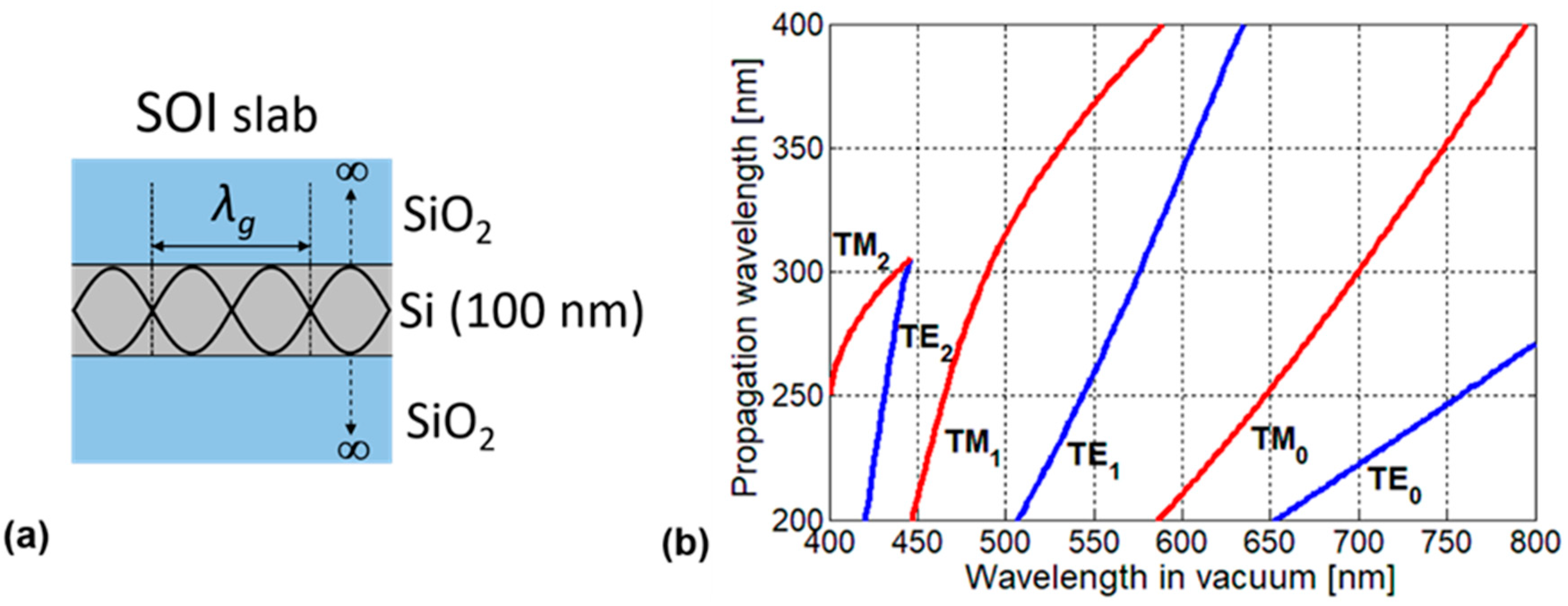
2. Device Structure and Fabrication Process
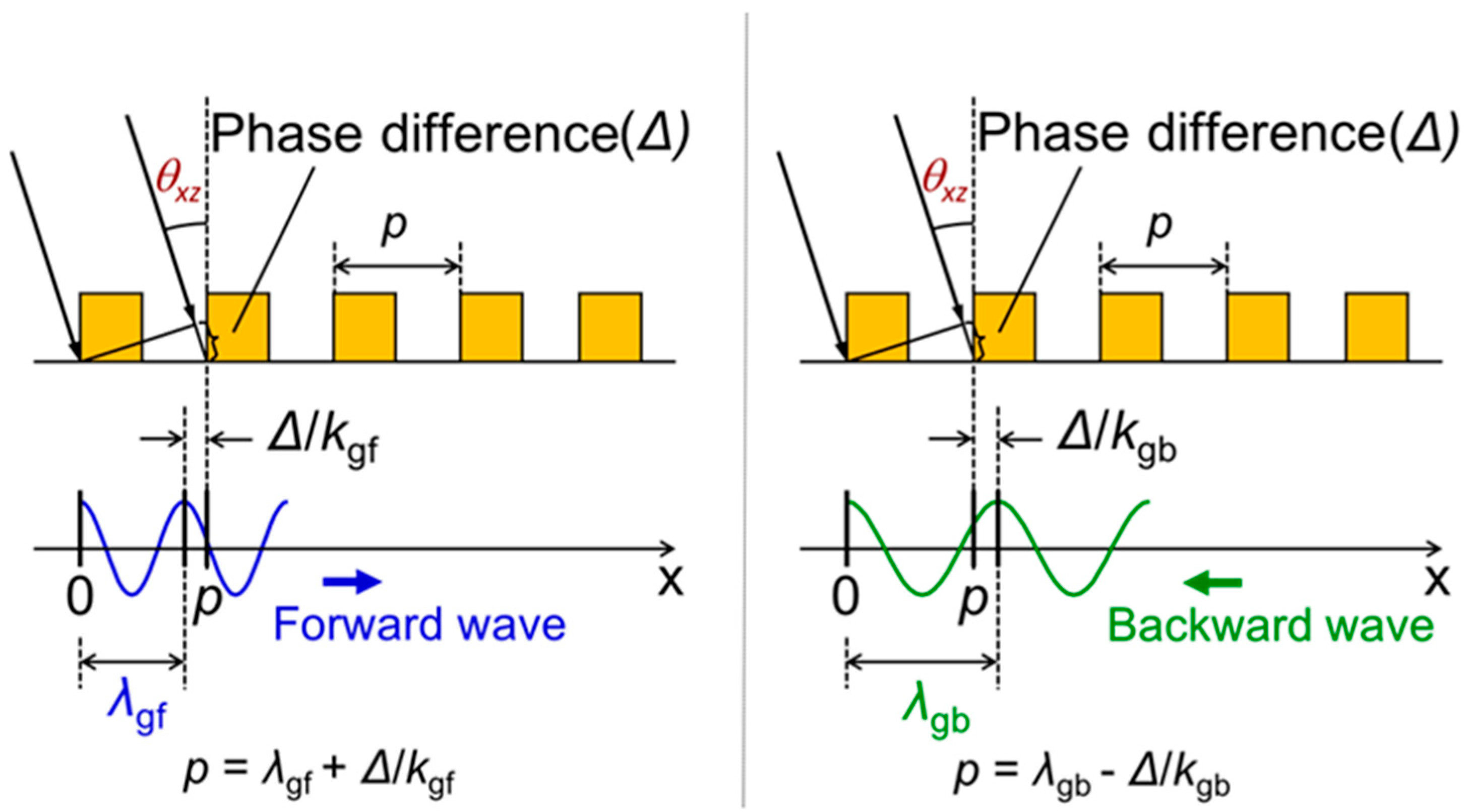
3. Principle of Angle Detection
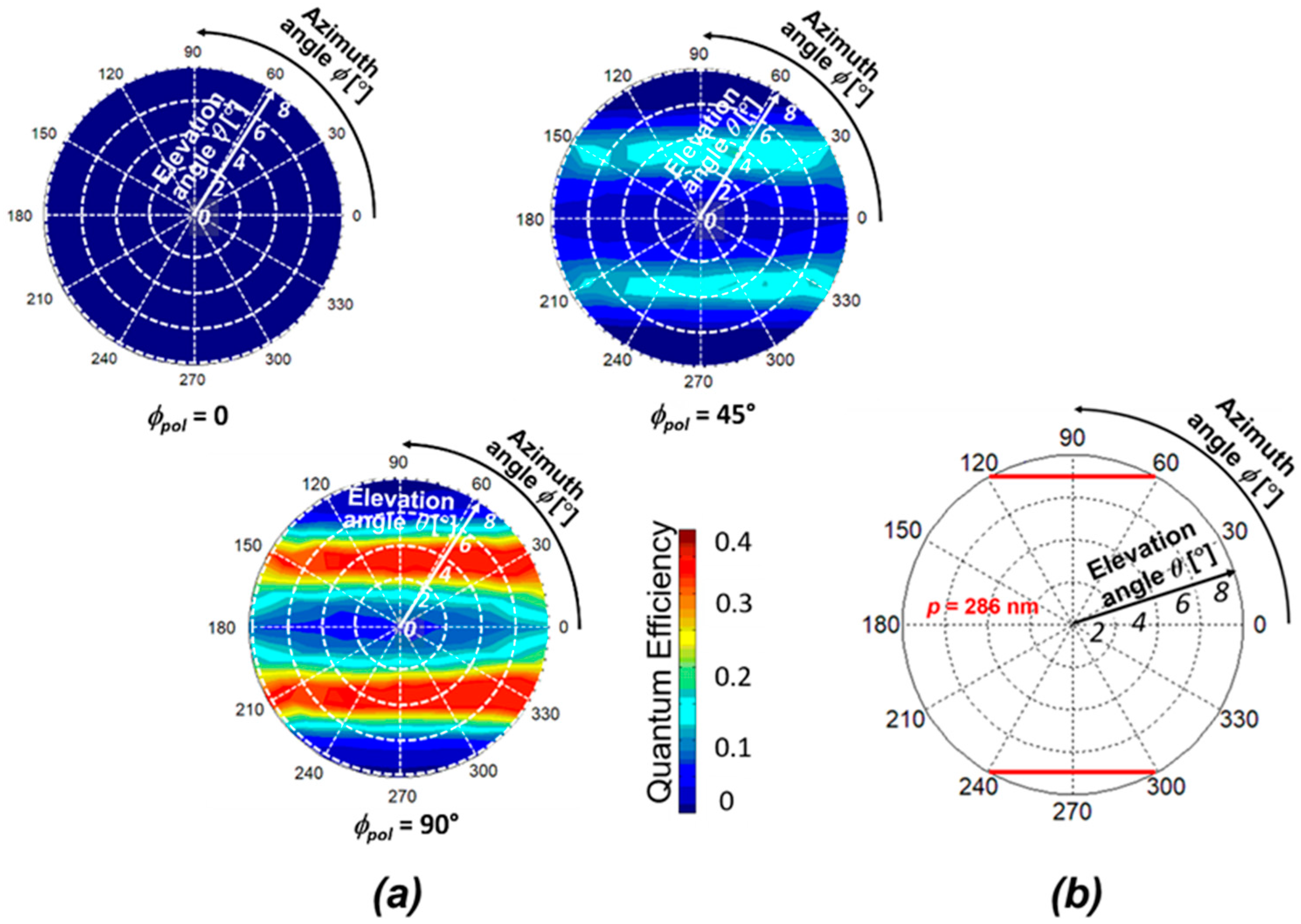
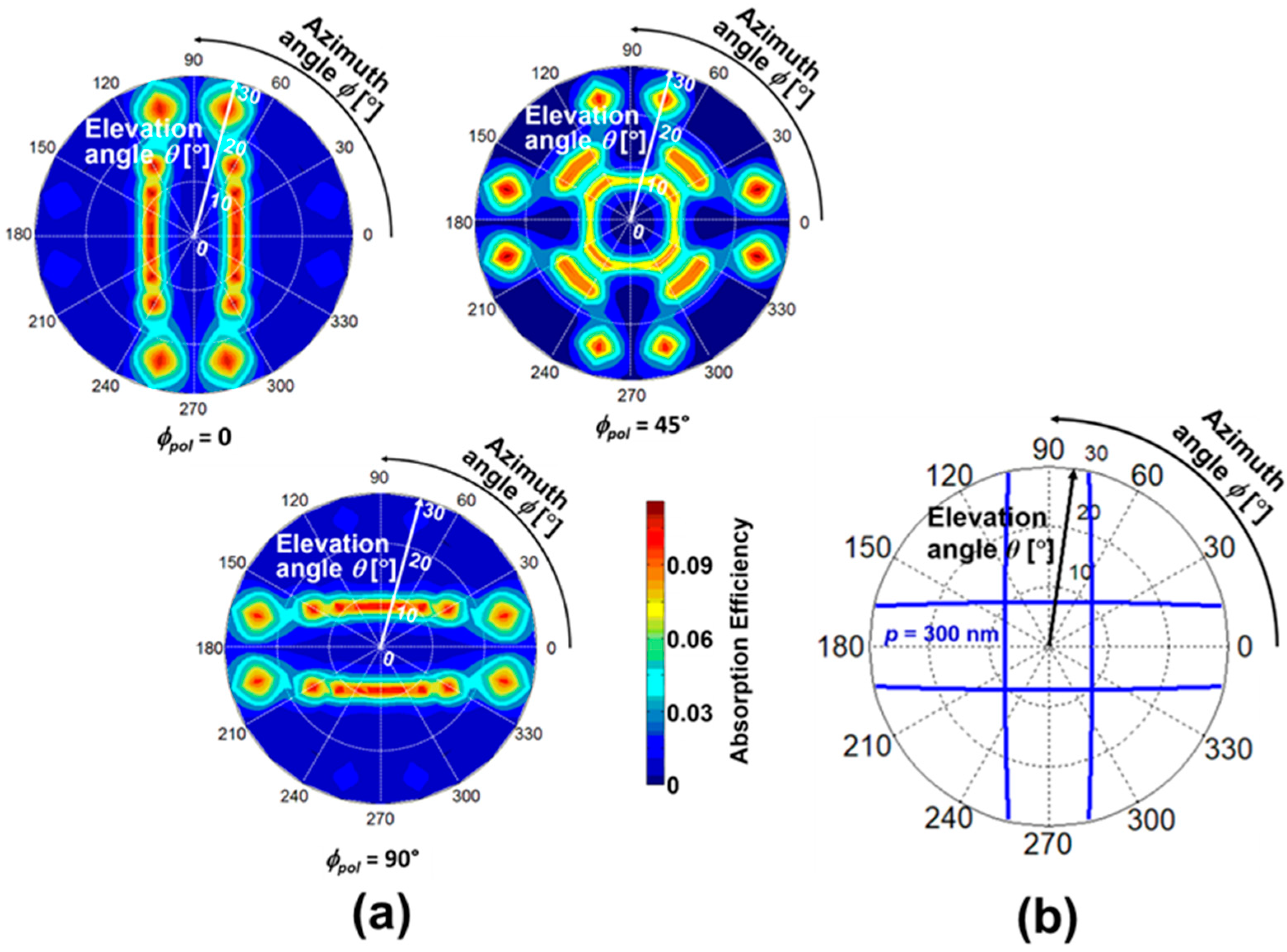
4. Results and Discussions
4.1. 1D L/S SP Antenna
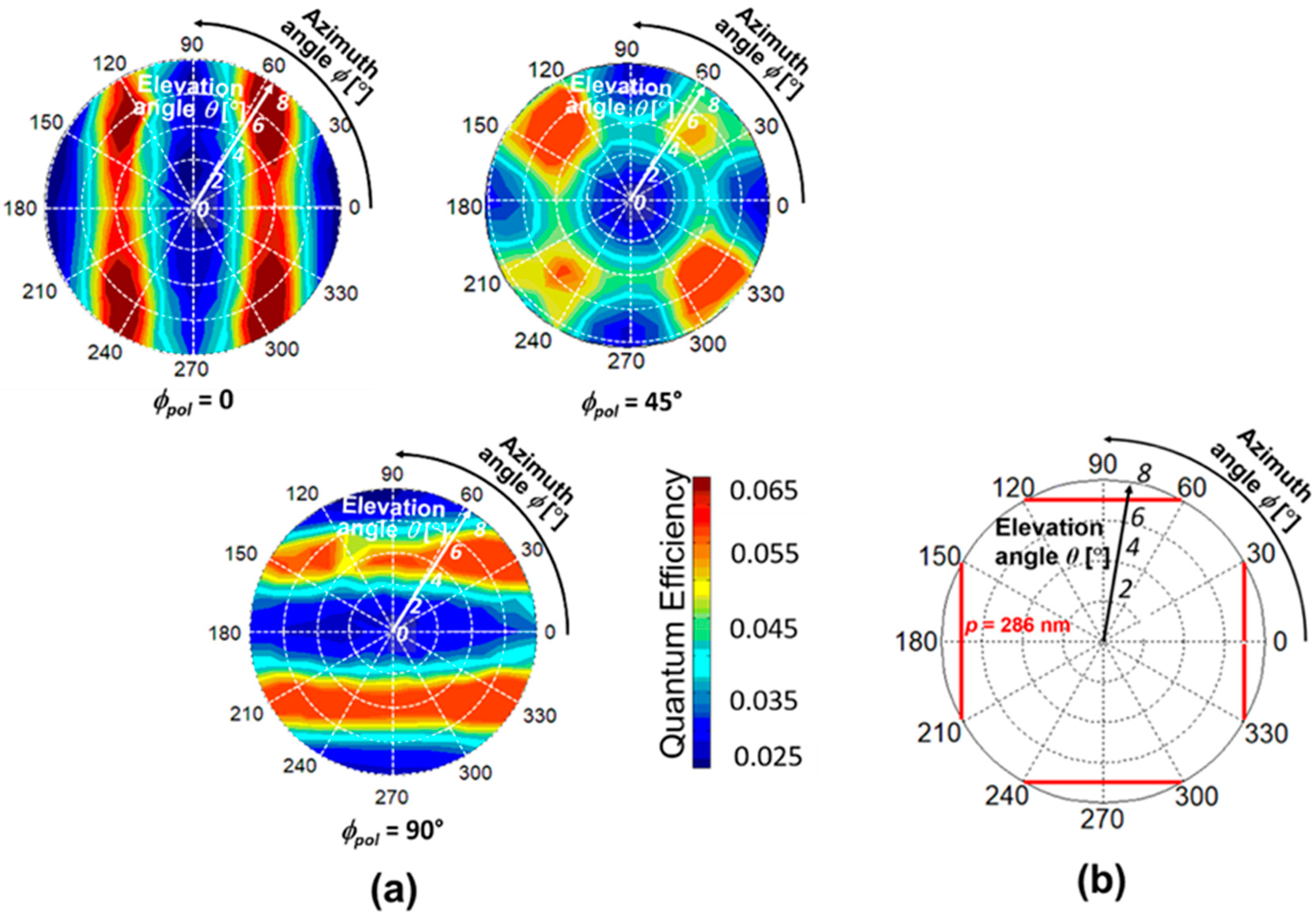
4.2. 2D Hole Array SP Antenna
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sivaramakrishnan, S.; Wang, A.; Gill, P.; Molnar, A. Design and characterization of enhanced angle sensitive pixels. IEEE Trans. Electron Devices 2016, 63, 113–119. [Google Scholar] [CrossRef]
- Papageorgiou, E.P.; Boser, B.E.; Anwar, M. An angle-selective CMOS imager with on-chip micro-collimators for blur reduction in near-field cell imaging. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shangai, China, 24–28 January 2016; pp. 337–340. [Google Scholar]
- Wang, P.; Menon, R. Computational snapshot angular-spectral lensless imaging. arXiv 2017, arXiv:1707.08104. [Google Scholar]
- Yi, S.; Zhou, M.; Yu, Z.; Fan, P.; Behdad, N.; Lin, D.; Wang, K.X.; Fan, S.; Brongersma, M. Subwavelength angle-sensing photodetectors inspired by directional hearing in small animals. Nat. Nanotechnol. 2018, 13, 1143–1147. [Google Scholar] [CrossRef] [PubMed]
- Adelson, E.H.; Bergen, J.R. The plenoptic function and the elements of early vision. Comput. Models Vis. Process. 1991, 3–20. [Google Scholar]
- Pereira, F.; Da Silva, E.A.B. Efficient plenoptic imaging representation: Why do we need it? In Proceedings of the 2016 IEEE International Conference on Multimedia and Expo (ICME), Seattle, WA, USA, 11–15 July 2016; pp. 1–6. [Google Scholar]
- Gershun, A. The Light Field. J. Math. Phys. 1939, 18, 51–151. [Google Scholar] [CrossRef]
- Fiss, J.; Curless, B.; Szeliski, R. Refocusing plenoptic images using depth-adaptive splatting. In Proceedings of the 2014 IEEE international conference on computational photography (ICCP), Santa Clara, CA, USA, 2–4 May 2014; pp. 1–9. [Google Scholar]
- Shroff, S.A.; Berkner, K. Image formation analysis and high resolution image reconstruction for plenoptic imaging systems. Appl. Opt. 2013, 52, D22–D31. [Google Scholar] [CrossRef] [PubMed]
- Wetzstein, G.; Ihrke, I.; Lanman, D.; Heidrich, W. Computational plenoptic imaging. Comput. Graph. Forum 2011, 30, 2397–2426. [Google Scholar] [CrossRef]
- Levoy, M. Light fields and computational imaging. Computer 2006, 39, 46–55. [Google Scholar] [CrossRef]
- McMillan, L.; Bishop, G. Plenoptic modeling: An image-based rendering system. In Proceedings of the 22nd annual conference on Computer graphics and interactive techniques, Los Angeles, California, USA, 6–11 August 1995; pp. 39–46. [Google Scholar]
- Radwell, N.; Selyem, A.; Mertens, L.; Edgar, M.P.; Padgett, M.J. Hybrid 3D ranging and velocity tracking system combining multi-view cameras and simple LiDAR. Sci. Rep. 2019, 9, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuo, G.; Antipa, N.; Ng, R.; Waller, L. DiffuserCam: Diffuser-based lensless cameras. In Proceedings of the Computational Optical Sensing and Imaging, San Francisco, California, USA, 26–29 June 2017; p. CTu3B-2. [Google Scholar]
- Stork, D.G.; Gill, P.R. Lensless Ultra-Miniature CMOS Computational imagers and sensors. In Proceedings of the Seventh International Conference on Sensor Technologies and Applications (SENSORCOMM 2013), Barcelona, Spain, 25–31 August 2013; pp. 186–190. [Google Scholar]
- Wang, A.; Molnar, A. A light-field image sensor in 180 nm CMOS. IEEE J. Solid-State Circuits 2012, 47, 257–271. [Google Scholar] [CrossRef]
- Satoh, H.; Inokawa, H. Surface plasmon antenna with gold line and space grating for enhanced visible light detection by a silicon-on-insulator metal-oxide-semiconductor photodiode. IEEE Trans. Nanotechnol. 2012, 11, 346–351. [Google Scholar] [CrossRef]
- Satoh, H.; Ono, A.; Inokawa, H. Enhanced visible light sensitivity by gold line-and-space grating gate electrode in thin silicon-on-insulator p-n junction photodiode. IEEE Trans. Electron Devices. 2013, 60, 812–818. [Google Scholar] [CrossRef] [Green Version]
- Satoh, H.; Kawakubo, K.; Ono, A.; Inokawa, H. Material Dependence of Metal Grating on SOI Photodiode for Enhanced Quantum Efficiency. IEEE Photon. Technol. Lett. 2013, 25, 1133–1135. [Google Scholar] [CrossRef] [Green Version]
- Inokawa, H.; Satoh, H.; Kawakubo, K.; Ono, A. Enhancement of SOI photodiode sensitivity by aluminium grating. ECS Transactions 2013, 53, 127. [Google Scholar] [CrossRef] [Green Version]
- Nagarajan, A.; Hara, S.; Satoh, H.; Panchanathan, A.P.; Inokawa, H. Directivity of SOI Photodiode with Gold Surface Plasmon Antenna. In Proceedings of the 2019 Silicon Nanoelectronics Workshop (SNW), Kyoto, Japan, 9–10 June 2019; pp. 121–122. [Google Scholar]
- Nagarajan, A.; Hara, S.; Satoh, H.; Panchanathan, A.P.; Inokawa, H. Polarization Dependence of Incident Angle Sensitivity in Soi Photodiode with 2d Hole Array Grating. In Proceedings of the 2020 Silicon Nanoelectronics Workshop (SNW), Honolulu, HI, USA, 13–14 June 2020; pp. 63–64. [Google Scholar]
- Nagarajan, A.; Hara, S.; Satoh, H.; Panchanathan, A.P.; Inokawa, H. Angular Selectivity of SOI Photodiode with Surface Plasmon Antenna. IEICE Electron. Expr. 2020, 17, 20200187. [Google Scholar] [CrossRef]
- Liu, J.M. Photonic Devices; Cambridge University Press: Cambridge, UK, 2005; pp. 95–99. [Google Scholar]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagarajan, A.; Hara, S.; Satoh, H.; Panchanathan, A.P.; Inokawa, H. Angle-Sensitive Detector Based on Silicon-On-Insulator Photodiode Stacked with Surface Plasmon Antenna. Sensors 2020, 20, 5543. https://doi.org/10.3390/s20195543
Nagarajan A, Hara S, Satoh H, Panchanathan AP, Inokawa H. Angle-Sensitive Detector Based on Silicon-On-Insulator Photodiode Stacked with Surface Plasmon Antenna. Sensors. 2020; 20(19):5543. https://doi.org/10.3390/s20195543
Chicago/Turabian StyleNagarajan, Anitharaj, Shusuke Hara, Hiroaki Satoh, Aruna Priya Panchanathan, and Hiroshi Inokawa. 2020. "Angle-Sensitive Detector Based on Silicon-On-Insulator Photodiode Stacked with Surface Plasmon Antenna" Sensors 20, no. 19: 5543. https://doi.org/10.3390/s20195543
APA StyleNagarajan, A., Hara, S., Satoh, H., Panchanathan, A. P., & Inokawa, H. (2020). Angle-Sensitive Detector Based on Silicon-On-Insulator Photodiode Stacked with Surface Plasmon Antenna. Sensors, 20(19), 5543. https://doi.org/10.3390/s20195543





