Method for Fault Diagnosis of Temperature-Related MEMS Inertial Sensors by Combining Hilbert–Huang Transform and Deep Learning
Abstract
:1. Introduction
- (1)
- We formulate the MEMS inertial sensor fault diagnosis method for deep learning problems. The proposed FD method uses the BLSTM-based HHT method to perform the feature extracting task and adopts a CNN to classify MEMS inertial sensor faults.
- (2)
- We propose a BLSTM-based HHT algorithm that performs a direct IMF computation method by introducing BLSTM to EMD, thereby improving the EMD efficiency by decreasing the number of iterations in obtaining IMFs. Additionally, we adopt noise assistance and frequent shifting to further improve the HHT performance.
- (3)
- We use the multiscale CNN (MS-CNN) to perform the fault classification task, in which Hilbert spectrums generated by the proposed BLSTM-based HHT are used as the input of the MS-CNN model.
2. Related Works
2.1. CNN-Based Fault Diagnosis
2.2. HHT-Based Fault Diagnosis
2.3. LSTM-Based Fault Diagnosis
3. Method for Fault Diagnosis of MEMS Inertial Sensors in Unmanned Aerial Vehicles by Combining Hilbert–Huang Transform and Deep Learning
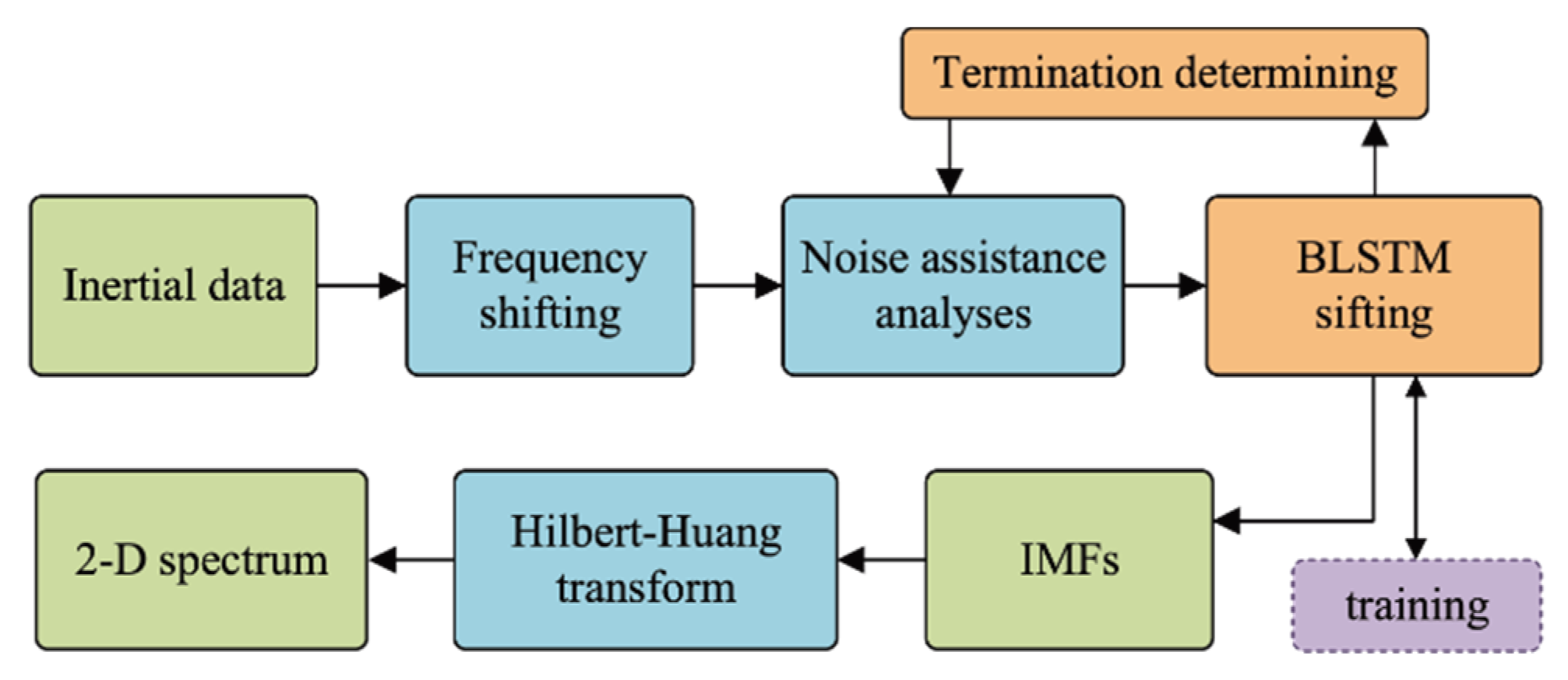
3.1. Overview
3.2. Proposed BLSTM-Based HHT
3.2.1. Modeling of End-to-End EMD
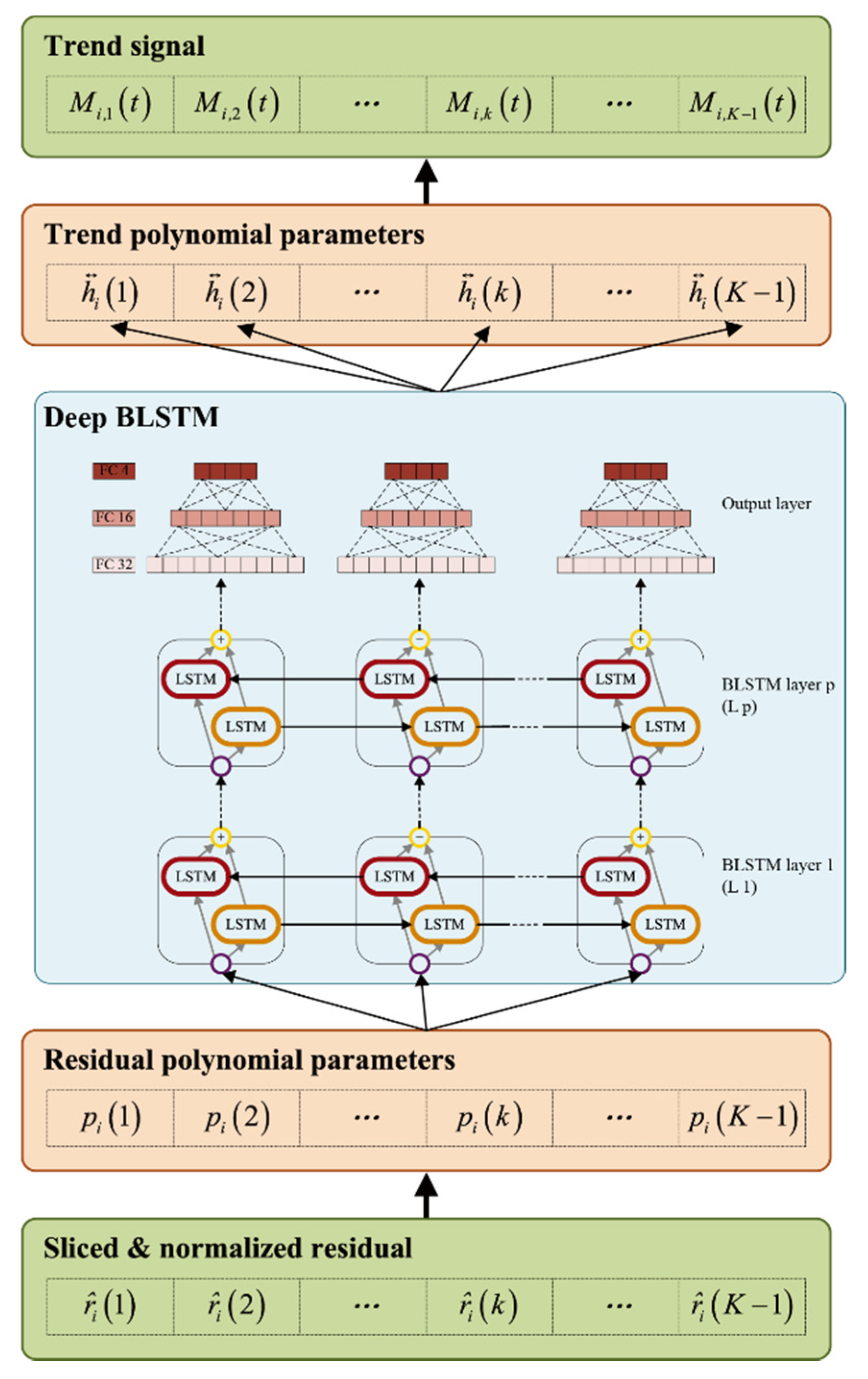
3.2.2. BLSTM-Based Sifting
3.2.3. BLSTM Training Strategy
3.2.4. IMF Computation
3.3. CNN Structure
| Algorithm 1: BLSTM-based EMD | |
| Requirement: Trained BLSTM-based EMD model by dataset in Figure 4. | |
| Input: Inertial measurement residual . | |
| Output:. | |
| Begin: | |
| 1: | Normalize residual: ; |
| 2: | Piecewise: ; |
| 3: | fordo: |
| 4: | Fitting : |
| 5: | ; |
| 6: | end for |
| 7: | Regress trend coefficient: |
| 8: | ; |
| 9: | fordo: |
| 10: | Compute piecewised trend signal: |
| ; | |
| 11: | end for |
| 12: | Compute trend signal:; |
| 13: | Compute IMF:; |
| 14: | Recover IMF: |
| ; | |
| 15: | Update : ; |
| 16: | End |
3.4. Summary of the Proposed FD Algorithm
| Algorithm 2: Proposed FD method | |
| Requirements: Trained BLSTM-based EMD model by dataset in Figure 4; Trained MS-CNN by Hilbert spectrums and corresponding fault labels. | |
| Input: Inertial measurement residual . | |
| Output: Fault classifications. | |
| Begin: | |
| 1: | Frequency shifting:; |
| 2: | fordo: |
| 3: | Compute according to Algorithm I with EEMD; |
| 4: | end for |
| 5: | Compute Hilbert spectrum by HT: ; |
| 6: | Classify fault by MS-CNN: ; |
| 7: | End. |
4. Experiments
4.1. Setting
4.2. BLSTM Comparison
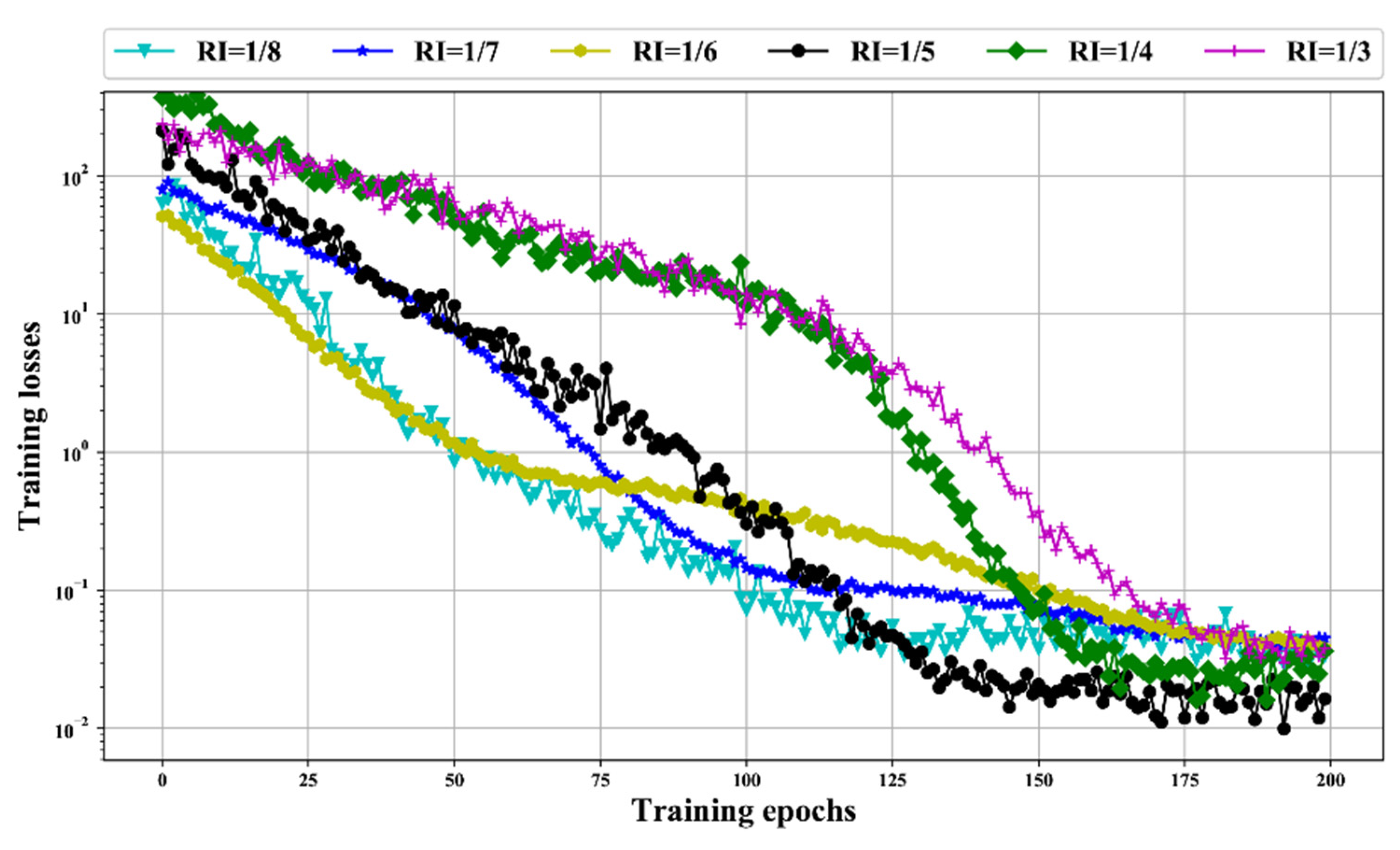
4.2.1. Comparison of Data Recording Strategies
4.2.2. BLSTM Structure Testing
4.3. EMD Performance Comparison
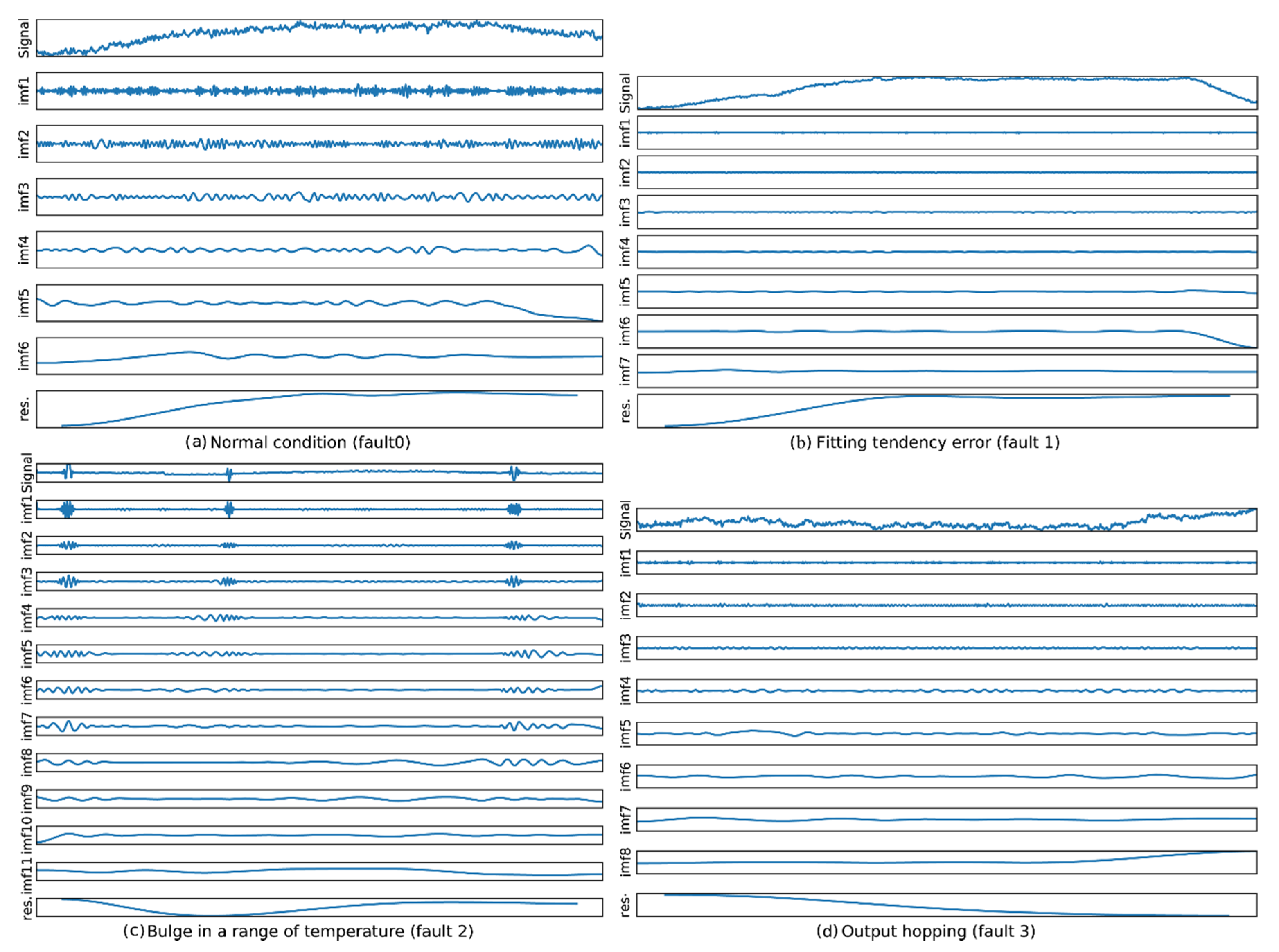
4.3.1. Evaluation of EMD Results
4.3.2. Comparison of EMD Efficiency
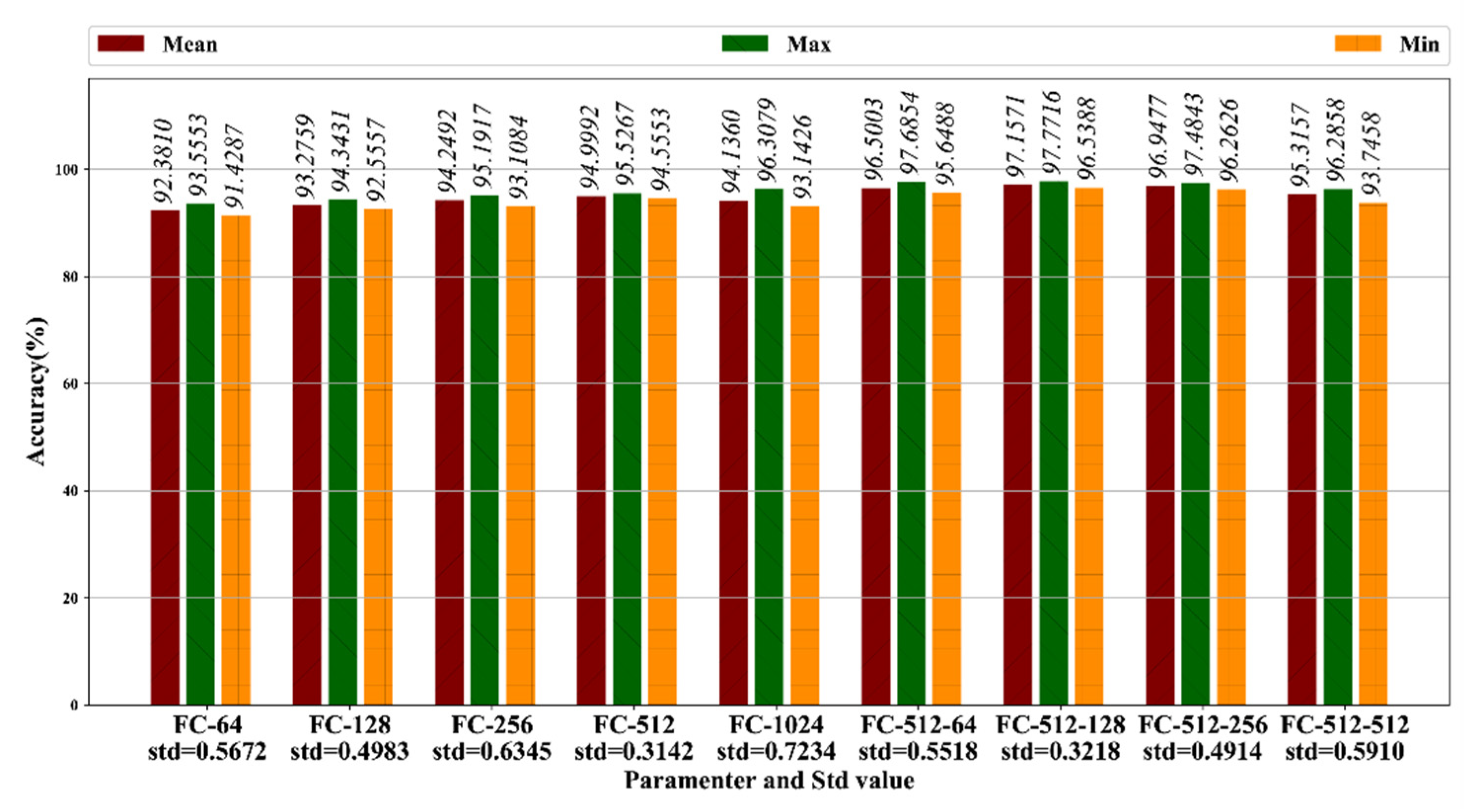
4.4. Multiscale CNN Comparison
4.5. FD Performance Comparison
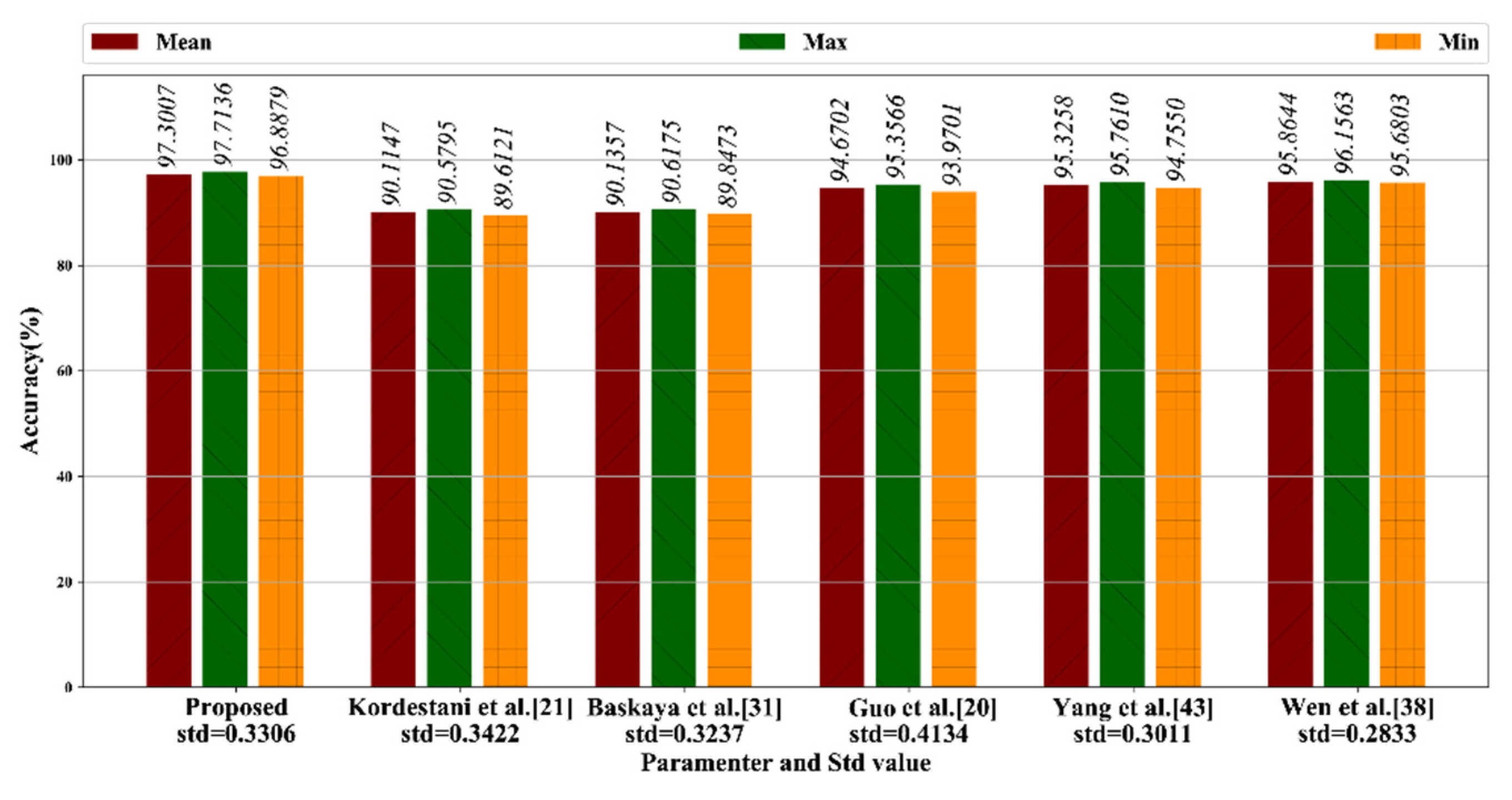
4.5.1. Comparison on Mean Accuracy
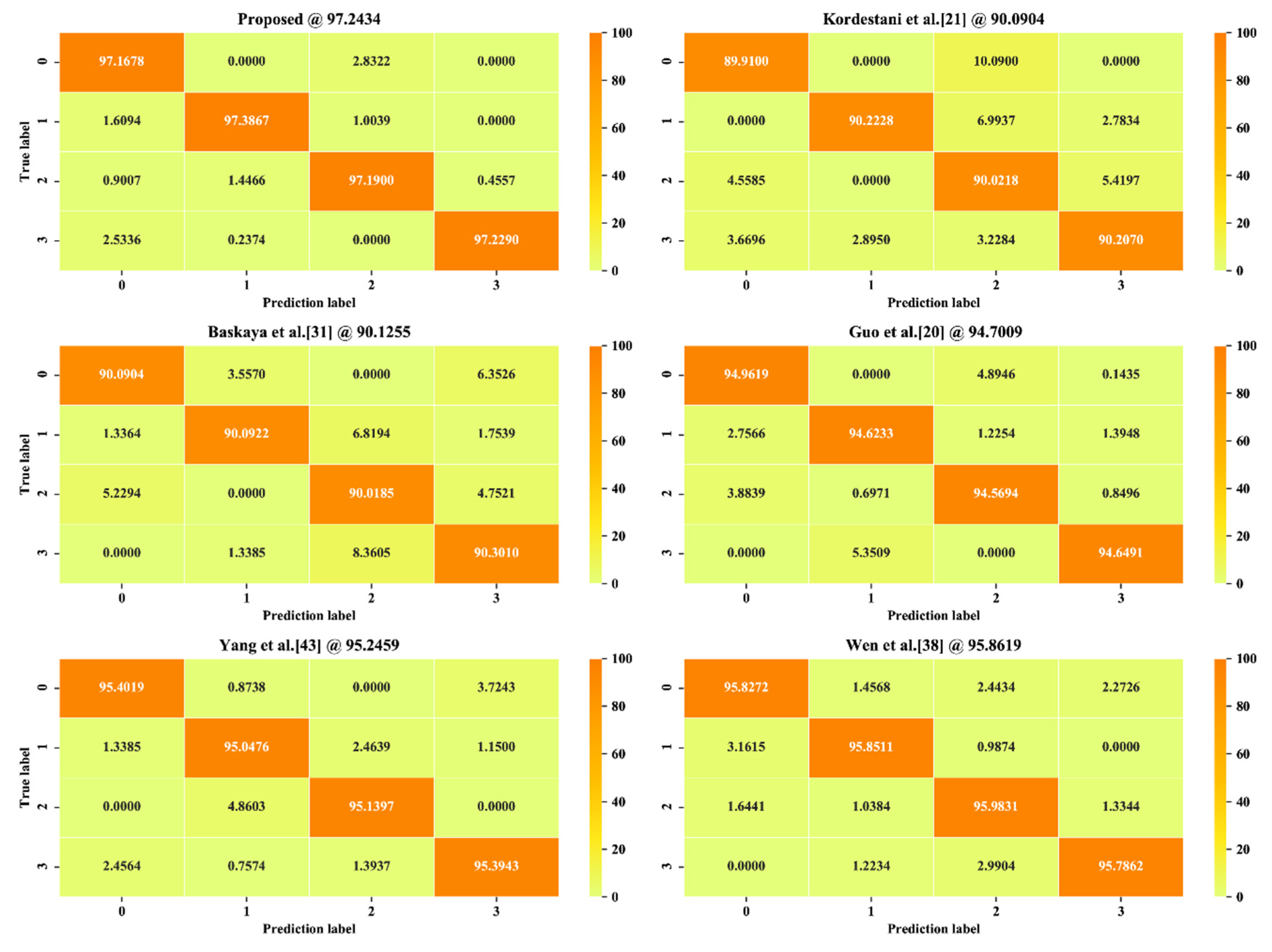
4.5.2. Comparison on Confusion Matrix
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rossi, M.; Brunelli, D. Autonomous Gas Detection and Mapping with Unmanned Aerial Vehicles. IEEE Trans. Instrum. Meas. 2016, 65, 765–775. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the use of unmanned aerial systems for environmental monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef] [Green Version]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Zhou, B.; Wang, L.; Xing, H.; Zhang, R. Lixin A Novel Tri-Axial MEMS Gyroscope Calibration Method over a Full Temperature Range. Sensors 2018, 18, 3004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, B.; Chu, H.; Sun, T.; Guo, L. Thermal calibration of a tri-axial MEMS gyroscope based on Parameter-Interpolation method. Sens. Actuators A Phys. 2017, 261, 103–116. [Google Scholar] [CrossRef]
- Araghi, G. Temperature compensation model of MEMS inertial sensors based on neural network. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 301–309. [Google Scholar]
- Mistry, P.; Lane, P.; Allen, P. Railway Point-Operating Machine Fault Detection Using Unlabeled Signaling Sensor Data. Sensors 2020, 20, 2692. [Google Scholar] [CrossRef]
- Luong, T.T.N.; Kim, J.M. The Enhancement of Leak Detection Performance for Water Pipelines through the Renovation of Training Data. Sensors 2020, 20, 2542. [Google Scholar] [CrossRef]
- Dong, L.I.; Shulin LI, U.; Zhang, H. A method of anomaly detection and fault diagnosis with online adaptive learning under small training samples. Pattern Recognit. 2017, 64, 374–385. [Google Scholar] [CrossRef]
- Kim, S.Y.; Kang, C.H.; Song, J.W. 1-point RANSAC UKF with Inverse Covariance Intersection for Fault Tolerance. Sensors 2020, 20, 353. [Google Scholar] [CrossRef] [Green Version]
- Qin, J.; Zhang, G.; Zheng, W.X.; Kang, Y. Neural Network-Based Adaptive Consensus Control for a Class of Nonaffine Nonlinear Multiagent Systems with Actuator Faults. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3633–3644. [Google Scholar] [CrossRef]
- Pan, J.; Luo, D.; Wu, L.; Zhang, J. FlexRay based treble-redundancy UAV flight control computer system. In Proceedings of the IEEE International Conference on Control & Automation, Ohrid, Macedonia, 3–6 July 2017. [Google Scholar]
- Pan, J.H.; Zhang, S.B.; Ma, H. Design of Flight Control System Bus Controller of UAV Based on Double CAN-Bus. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Baech, Switzerland, 2014; Volume 479, pp. 641–645. [Google Scholar]
- Najjar, N.; Gupta, S.; Hare, J.; Kandil, S.; Walthall, R. Optimal sensor selection and fusion for heat exchanger fouling diagnosis in aerospace systems. IEEE Sens. J. 2016, 16, 4866–4881. [Google Scholar] [CrossRef]
- Deckert, J.C.; Desai, M.; Deyst, J.; Willsky, A. F-8 DFBW sensor failure identification using analytic redundancy. IEEE Trans. Autom. Control 1977, 22, 795–803. [Google Scholar] [CrossRef]
- Chi, C.; Deng, P.; Zhang, J.; Pan, Z.; Li, T.; Wu, Z. A Fault Diagnosis Method of Temperature Sensor Based on Analytical Redundancy. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Paris), Paris, France, 2–5 May 2019; pp. 156–162. [Google Scholar]
- Lyu, P.; Lai, J.; Liu, J.; Liu, H.H.; Zhang, Q. A thrust model aided fault diagnosis method for the altitude estimation of a quadrotor. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 1008–1019. [Google Scholar] [CrossRef]
- Guo, D.; Zhong, M.; Zhou, D. Multisensor data-fusion-based approach to airspeed measurement fault detection for unmanned aerial vehicles. IEEE Trans. Instrum. Meas. 2017, 67, 317–327. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Yang, G. Distributed fault detection and isolation for multiagent systems: An interval observer approach. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 2220–2230. [Google Scholar] [CrossRef]
- Guo, D.; Zhong, M.; Ji, H.; Liu, Y.; Yang, R. A Hybrid Feature Model and Deep Learning Based Fault Diagnosis for Unmanned Aerial Vehicel Sensors. Neurocomputing 2018, 319, 155–163. [Google Scholar] [CrossRef]
- Kordestani, M.; Samadi, M.F.; Saif, M.; Khorasani, K. A New Fault Diagnosis of Multifunctional Spoiler System Using Integrated Artificial Neural Network and Discrete Wavelet Transform methods. IEEE Sens. J. 2018, 18, 4990–5001. [Google Scholar] [CrossRef]
- Zhu, T.B.; Lu, F. A Data-Driven Method of Engine Sensor on Line Fault Diagnosis and Recovery. Appl. Mech. Mater. 2014, 490, 1657–1660. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Y.; Lu, W.; Yang, Z. A bearing fault diagnosis method based on VMD-SVD and Fuzzy clustering. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1950018. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, W. A Fault Diagnosis Intelligent Algorithm Based on Improved BP Neural Network. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1959028. [Google Scholar] [CrossRef]
- Chen, B.; Huang, D.; Zhang, F. The Modeling Method of a Vibrating Screen Efficiency Prediction Based on KPCA and LS-SVM. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1950009. [Google Scholar] [CrossRef]
- Naderi, E.; Khorasani, K. Data-driven fault detection, isolation and estimation of aircraft gas turbine engine actuator and sensors. Mech. Syst. Signal Process. 2018, 100, 415–438. [Google Scholar] [CrossRef]
- Fravolini, M.L.; Napolitano, M.R.; Del Core, G.; Papa, U. Experimental interval models for the robust fault detection of aircraft air data sensors. Control Eng. Pract. 2018, 78, 196–212. [Google Scholar] [CrossRef]
- Xuyun, F.U.; Chen, H.; Zhang, G.; Tao, T. A New Point Anomaly Detection Method About Aero Engine Based on Deep Learning. In Proceedings of the 2018 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Xi’an, China, 15–17 August 2018; pp. 176–181. [Google Scholar]
- Gao, Z.; Ma, C.; Song, D.; Liu, Y. Deep quantum inspired neural network with application to aircraft fuel system fault diagnosis. Neurocomputing 2017, 238, 13–23. [Google Scholar] [CrossRef]
- He, Y.; Peng, Y.; Wang, S.; Liu, D.; Leong, P.H. A structured sparse subspace learning algorithm for anomaly detection in UAV flight data. IEEE Trans. Instrum. Meas. 2017, 67, 90–100. [Google Scholar] [CrossRef]
- Baskaya, E.; Bronz, M.; Delahaye, D. Fault detection & diagnosis for small uavs via machine learning. In Proceedings of the 2017 IEEE/AIAA 36th Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 17–21 September 2017; pp. 1–6. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, S.; Yang, S.; Gui, G. Learning attention representation with a multi-scale CNN for gear fault diagnosis under different working conditions. Sensors 2020, 20, 1233. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, Y.; Liu, W.; Ma, Z. A Novel Fault Diagnosis Approach for Chillers Based on 1-D Convolutional Neural Network and Gated Recurrent Unit. Sensors 2020, 20, 2458. [Google Scholar] [CrossRef]
- Chen, S.; Ge, H.; Li, J.; Pecht, M. Progressive Improved Convolutional Neural Network for Avionics Fault Diagnosis. IEEE Access 2019, 7, 177362–177375. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L.; Zhang, Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Chong, U.P. Signal model-based fault detection and diagnosis for induction motors using features of vibration signal in two-dimension domain. Stroj. Vestn. 2011, 57, 655–666. [Google Scholar]
- Zhong, D.; Guo, W.; He, D. An Intelligent Fault Diagnosis Method based on STFT and Convolutional Neural Network for Bearings Under Variable Working Conditions. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Qingdao), Qingdao, China, 25–27 October 2019. [Google Scholar]
- Chu, W.; Lin, C.; Kao, K. Fault Diagnosis of a Rotor and Ball-Bearing System Using DWT Integrated with SVM, GRNN, and Visual Dot Patterns. Sensors 2019, 19, 4806. [Google Scholar] [CrossRef] [Green Version]
- Cabrera, D.; Sancho, F.; Li, C.; Cerrada, M.; Sánchez, R.V.; Pacheco, F.; de Oliveira, J.V. Automatic Feature Extraction of Time-Series applied to Fault Severity Assessment of Helical Gearbox in Stationary and Non-Stationary Speed Operation. Appl. Soft Comput. 2017, 58, 53–64. [Google Scholar] [CrossRef]
- Yang, Q.; Ruan, J.; Zhuang, Z.; Huang, D. Condition Evaluation for Opening Damper of Spring-Operated High-Voltage Circuit Breaker Using Vibration Time-Frequency Image. IEEE Sens. J. 2019, 19, 8116–8126. [Google Scholar] [CrossRef]
- Lan, S.; Chen, M.J.; Chen, D.Y. A Novel HVDC Double-Terminal Non-Synchronous Fault Location Method Based on Convolutional Neural Network. IEEE Trans. Power Deliv. 2019, 34, 848–857. [Google Scholar] [CrossRef]
- Tabian, I.; Fu, H.; Sharif Khodaei, Z. A convolutional neural network for impact detection and characterization of complex composite structures. Sensors 2019, 19, 4933. [Google Scholar] [CrossRef] [Green Version]
- De Oliveira, M.A.; Monteiro, A.V.; Vieira Filho, J. A new structural health monitoring strategy based on PZT sensors and convolutional neural network. Sensors 2018, 18, 2955. [Google Scholar] [CrossRef] [Green Version]
- Pham, H.C.; Ta, Q.B.; Kim, J.T.; Ho, D.D.; Tran, X.L.; Huynh, T.C. Bolt-Loosening Monitoring Framework Using an Image-Based Deep Learning and Graphical Model. Sensors 2020, 20, 3382. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; Asadi, D. Detection of the ice assertion on aircraft using empirical mode decomposition enhanced by multi-objective optimization. Mech. Syst. Signal Process. 2017, 88, 9–24. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, J.; Duan, S. Flutter test data processing based on improved Hilbert-Huang transform. Math. Probl. Eng. 2018, 2018, 3496870. [Google Scholar] [CrossRef] [Green Version]
- Mokhtari, S.A.; Sabzehparvar, M. Application of Hilbert–Huang Transform with Improved Ensemble Empirical Mode Decomposition in Nonlinear Flight Dynamic Mode Characteristics Estimation. J. Comput. Nonlinear Dyn. 2019, 14, 011006. [Google Scholar] [CrossRef]
- Guo, M.F.; Yang, N.C.; Chen, W.F. Deep-Learning-Based Fault Classification Using Hilbert–Huang Transform and Convolutional Neural Network in Power Distribution Systems. IEEE Sens. J. 2019, 19, 6905–6913. [Google Scholar] [CrossRef]
- Han, B.; Yang, X.; Ren, Y.; Lan, W. Comparisons of different deep learning-based methods on fault diagnosis for geared system. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef]
- Xie, Y.; Xiao, Y.; Liu, X.; Liu, G.; Jiang, W.; Qin, J. Time-Frequency Distribution Map-Based Convolutional Neural Network (CNN) Model for Underwater Pipeline Leakage Detection Using Acoustic Signals. Sensors 2020, 20, 5040. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.R.; Lee, J.E.; Zeng, Y.M. Time Series Multiple Channel Convolutional Neural Network with Attention-Based Long Short-Term Memory for Predicting Bearing Remaining Useful Life. Sensors 2019, 20, 166. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Gu, H.; Shen, X.; You, D. Bayesian Long Short-Term Memory Model for Fault Early Warning of Nuclear Power Turbine. IEEE Access 2020, 8, 50801–50813. [Google Scholar] [CrossRef]
- Yin, A.; Yan, Y.; Zhang, Z.; Li, C.; Sánchez, R.V. Fault Diagnosis of Wind Turbine Gearbox Based on the Optimized LSTM Neural Network with Cosine Loss. Sensors 2020, 20, 2339. [Google Scholar] [CrossRef] [Green Version]
- Hoseinzadeh, M.S.; Khadem, S.E.; Sadooghi, M.S. Modifying the Hilbert-Huang transform using the nonlinear entropy-based features for early fault detection of ball bearings. Appl. Acoust. 2019, 150, 313–324. [Google Scholar] [CrossRef]
- Liang, K.; Qin, N.; Huang, D.; Fu, Y. Convolutional recurrent neural network for fault diagnosis of high-speed train bogie. Complexity 2018, 2018, 4501952. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Chen, J.; Liu, Y.; Cheng, J.; Yang, Y.; Kuanfang, H.; Wang, G.; Liu, Y. Roller Bearing Fault Diagnosis Based on Adaptive Sparsest Narrow-Band Decomposition and MMC-FCH. Shock Vib. 2019, 2019, 7585401. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.G.; Huang, H.Z.; Li, Y.F. A Bi-Directional LSTM prognostics method under multiple operational conditions. IEEE Trans. Ind. Electron. 2019, 66, 8792–8802. [Google Scholar] [CrossRef]
- Yang, J.; Guo, Y.; Zhao, W. Long short-term memory neural network based fault detection and isolation for electro-mechanical actuators. Neurocomputing 2019, 360, 85–96. [Google Scholar] [CrossRef]
- Miao, H.; Li, B.; Sun, C.; Liu, J. Joint Learning of Degradation Assessment and RUL Prediction for Aeroengines via Dual-Task Deep LSTM Networks. IEEE Trans. Ind. Inform. 2019, 15, 5023–5032. [Google Scholar] [CrossRef]
- Damaševičius, R.; Napoli, C.; Sidekerskienė, T.; Woźniak, M. IMF mode demixing in EMD for jitter analysis. J. Comput. Sci. 2017, 22, 240–252. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Gu, H.; Liu, X.; Zhao, B.; Zhou, H. The In-Operation Drift Compensation of MEMS Gyroscope Based on Bagging-ELM and Improved CEEMDAN. IEEE Sens. J. 2019, 19, 5070–5077. [Google Scholar] [CrossRef]
- Hosseini-Pishrobat, M.; Keighobadi, J. Robust Vibration Control and Angular Velocity Estimation of a Single-Axis MEMS Gyroscope Using Perturbation Compensation. J. Intell. Robot. Syst. 2019, 94, 61–79. [Google Scholar] [CrossRef]








| Layer | Name | Details |
|---|---|---|
| 1. | Conv1 | Conv (); stride: () |
| 2. | Conv2 | Conv (); stride: () |
| 3. | Pool 1 | Max pool (); stride: () |
| 4. | Conv3 | Conv (); stride: () |
| 5. | Pool 2 | Max pool (); stride: () |
| 6. | Conv4 | Conv (); stride: () |
| 7. | Pool 3 | Max pool (); stride: () |
| 8. | Multi | Concatenate features from layer 3 and 7 |
| 9. | FC1 | Fully connect 1 |
| 10. | FC2 | Fully connect 2 |
| 11. | Output | Soft max (4) |
| State | Size | Label | Label |
|---|---|---|---|
| Normal condition | 6000 | 0 | 1000 |
| Fitting tendency error | 6000 | 1 | 0100 |
| Bulge in a range of temperature | 6000 | 2 | 0010 |
| Output hopping | 6000 | 3 | 0001 |
| Parameter | Description | Selected Value |
|---|---|---|
| Batch size | Training samples in each training epoch | 16 |
| Dropout rate | Dropout probability | 0.25 |
| Training epochs | Number of training iterations | 200 |
| Unfold steps | Data length of each training sample in time steps | 256 |
| RI | Dataset | Name |
|---|---|---|
| RI () | ||
| RI () | ||
| RI () | ||
| RI () | ||
| RI () | ||
| RI () |
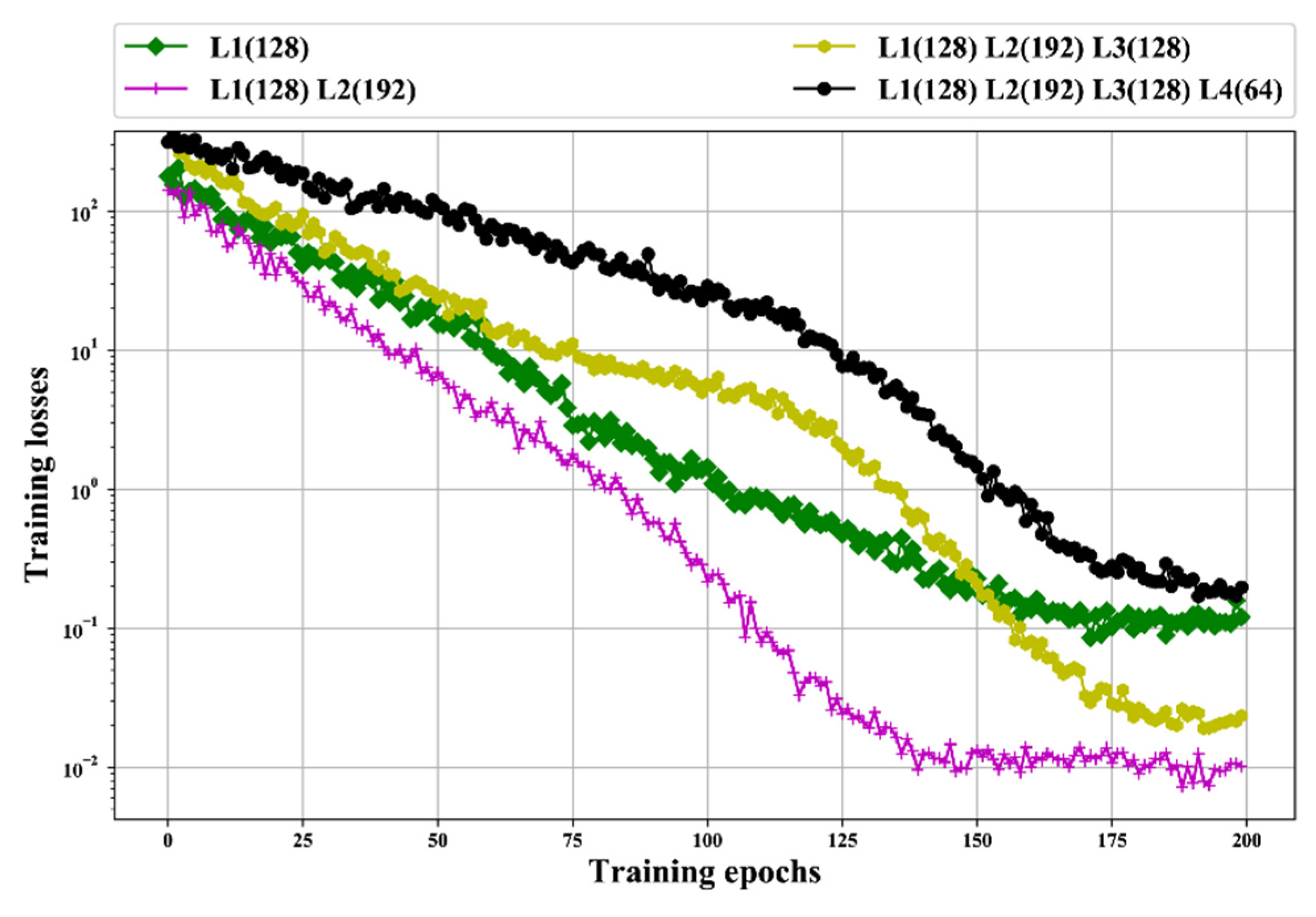
| Group | BLSTM Structure | Mean Loss |
|---|---|---|
| 1 layer | L1(64) | 0.5198 |
| L1(128) | 0.2109 | |
| L1(192) | 0.3917 | |
| L1(265) | 0.2392 | |
| 2 layers | L1(128) L2(64) | 0.0317 |
| L1(128) L2(128) | 0.0301 | |
| L1(128) L2(192) | 0.0258 | |
| L1(128) L2(256) | 0.0279 | |
| 3 layers | L1(128) L2(192) L3(64) | 0.0882 |
| L1(128) L2(192) L3(128) | 0.0791 | |
| L1(128) L2(192) L3(192) | 0.1003 | |
| L1(128) L2(192) L3(256) | 0.0932 | |
| 4 layers | L1(128) L2(192) L3(128) L4(64) | 0.4503 |
| L1(128) L2(192) L3(128) L4(128) | 0.8284 | |
| L1(128) L2(192) L3(128) L4(192) | 0.5017 | |
| L1(128) L2(192) L3(128) L4(256) | 0.6697 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, T.; Sheng, W.; Zhou, M.; Fang, B.; Luo, F.; Li, J. Method for Fault Diagnosis of Temperature-Related MEMS Inertial Sensors by Combining Hilbert–Huang Transform and Deep Learning. Sensors 2020, 20, 5633. https://doi.org/10.3390/s20195633
Gao T, Sheng W, Zhou M, Fang B, Luo F, Li J. Method for Fault Diagnosis of Temperature-Related MEMS Inertial Sensors by Combining Hilbert–Huang Transform and Deep Learning. Sensors. 2020; 20(19):5633. https://doi.org/10.3390/s20195633
Chicago/Turabian StyleGao, Tong, Wei Sheng, Mingliang Zhou, Bin Fang, Futing Luo, and Jiajun Li. 2020. "Method for Fault Diagnosis of Temperature-Related MEMS Inertial Sensors by Combining Hilbert–Huang Transform and Deep Learning" Sensors 20, no. 19: 5633. https://doi.org/10.3390/s20195633
APA StyleGao, T., Sheng, W., Zhou, M., Fang, B., Luo, F., & Li, J. (2020). Method for Fault Diagnosis of Temperature-Related MEMS Inertial Sensors by Combining Hilbert–Huang Transform and Deep Learning. Sensors, 20(19), 5633. https://doi.org/10.3390/s20195633






