Clustering-Based Component Fraction Estimation in Solid–Liquid Two-Phase Flow in Dredging Engineering
Abstract
:1. Introduction
- (1)
- Each dispersed phase is assumedly even-distributed in practice and thus can be presented by the same conductivity value [17]. However, solid and liquid objects are dynamically changeable and it is difficult to satisfy the assumption.
- (2)
- The ERT reconstruction of the detected field has natural limitations such as the ill-posed problem and ‘soft field’ effect [18,19]. These limitations make the CF estimation have uncertain, inconsistent, and incomplete characteristics. However, the MG method cannot really reflect these natural characteristics in the detected field, and thus the accuracy of the estimated CF value is not guaranteed.
- (3)
- The ERT image is of low spatial resolution that may make the detected objects have inevitable and random artifacts, and in most cases, objects with small size are undistinguishable at all. Consequently, the estimated CF value by MG may greatly deviate from the real one in practice.
2. Related Work
- (1)
- The f-FCM algorithm was used for the CF estimation process in the solid–liquid two-phase flow. The use of fuzzy clustering, rather than other clustering algorithms, aims to overcome uncertainty, uncompletedness, and inconsistency in the ERT imaging process.
- (2)
- All detected objects were categorized into distinguishable and undistinguishable sets by ERT, respectively. These distinguishable objects can be estimated by f-FCM, whereas undistinguishable objects are computed by prior information. In this paper, the prior information was perfectly determined and represented by an inquiring table that was constructed in advance.
3. Cluster-Based Component Fraction (CF) Estimation Method
3.1. Computation on Distinguishable Objects by the Fast Fuzzy Cluster Algorithm (f-FCM) Algorithm
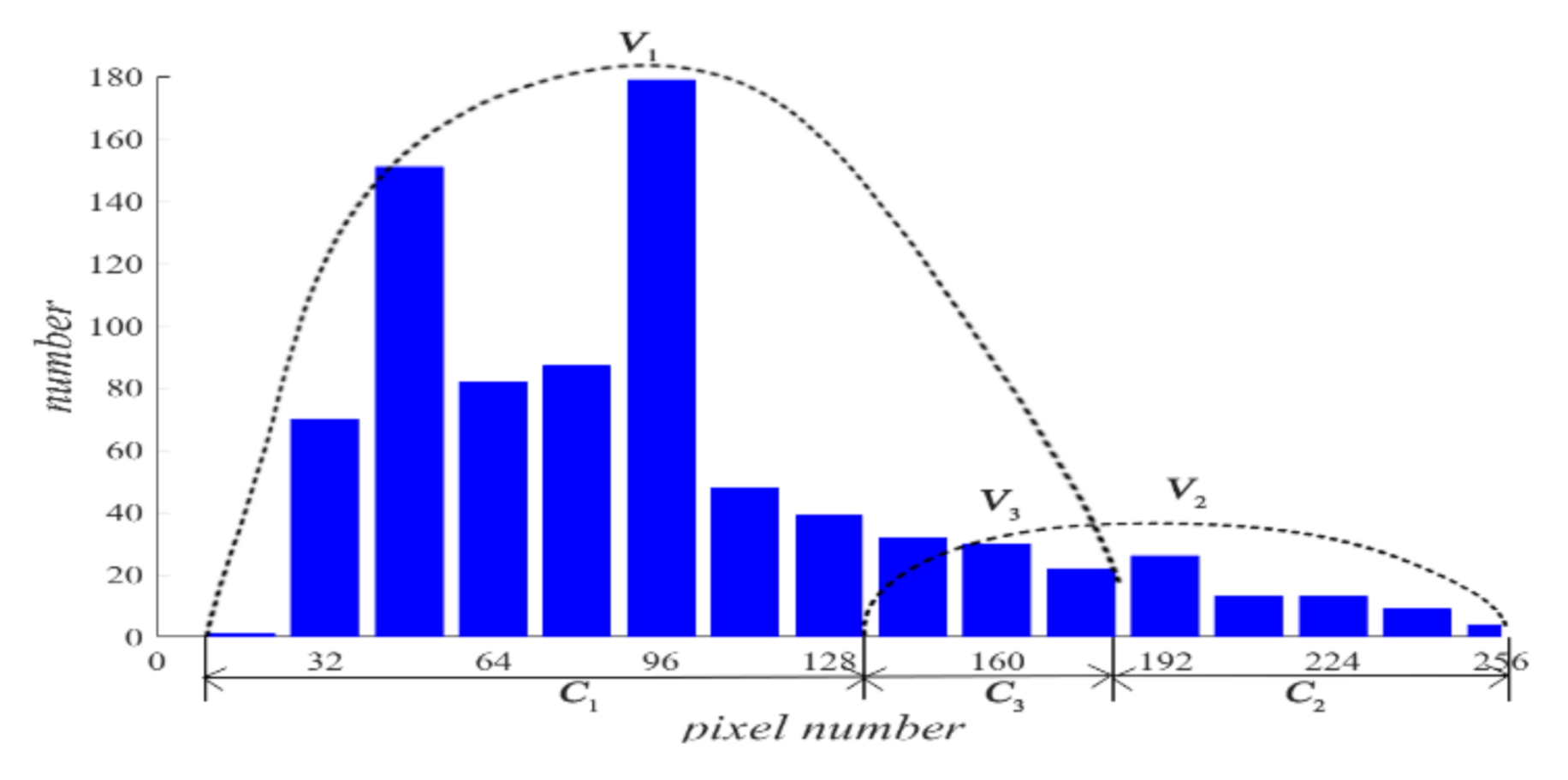
3.2. Computation on Undistinguishable Objects by Prior Information Inquiry
| Algorithm 1. The proposed CF estimation method. |
| Input: Boundary measurements and sensitivity matrix S Output: CF(1)
|
4. Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tapp, H.S.; Peyton, A.J.; Kemsley, E.K.; Wilson, R.H. Chemical engineering applications of electrical process tomography. Sens. Actuators B 2003, 92, 17–24. [Google Scholar] [CrossRef]
- Yang, L.; Yue, S.; Tan, Y. Solid Component Fraction in Multi-Phase Flows Using Electrical Resistance Tomography and Kalman Filter. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–30 July 2020; pp. 6313–6317. [Google Scholar]
- Beck, M.S.; Campogrande, E.; Morris, M.; Williams, R.A.; Waterfall, R.C. Tomographic Techniques for Process Design and Operation (Southampton: Computational Mechanics). Available online: https://www.researchgate.net/profile/Ramon_Pallas-Areny/publication/303689568_Multifrequency_electrical_impedance_tomography_as_an_alternative_to_absolute_imaging/links/574da8cd08ae82d2c6bdfd09/Multifrequency-electrical-impedance-tomography-as-an-alternative-to-absolute-imaging.pdf (accessed on 1 October 2020).
- Dyakowski, T.; Jaworski, A.J. Non-invasive process imaging—Principles and applications of industrial process tomography. Chem. Eng. Technol. 2003, 26, 697–706. [Google Scholar] [CrossRef]
- Guida, A.; Fan, X.; Parker, D.J.; Nienow, A.W.; Barigou, M. Positron emission particle tracking in a mechanically agitated solid–liquid suspension of coarse particles. Chem. Eng. Res. Design 2009, 87, 421–429. [Google Scholar] [CrossRef]
- Jaworski, A.J.; Meng, G. On-line measurement of separation dynamics in primary gas/oil/water separators: Challenges and technical solutions—A review. J. Pet. Sci. Eng. 2009, 68, 47–59. [Google Scholar] [CrossRef]
- Tan, Y.; Yue, S. Solid Concentration Estimation by Kalman Filter. Sensors 2020, 20, 2657. [Google Scholar] [CrossRef] [PubMed]
- McKenzie, G.; Record, P. Prognostic monitoring of aircraft wiring using electrical capacitive tomography Rev. Sci. Instrum. 2011, 82, 124705. [Google Scholar] [CrossRef]
- Ding, M.; Yue, S.; Song, K.; Wang, H. Fuzzy optimal solution of electric tomography imaging: Modelling and application. Flow Meas. Instrum. 2018, 59, 72–78. [Google Scholar] [CrossRef]
- Dong, F.; Xu, Y.; Hua, L.; Wang, H. Two Methods for Measurement of Gas-Liquid Flows in Vertical Upward Pipe Using Dual-Plane ERT System. IEEE Trans. Instrum. Meas. 2006, 55, 1576–1586. [Google Scholar] [CrossRef]
- Ismail, I.; Gamio, J.C.; Bukhari SF, A.; Yang, W.Q. Tomography for multi-phase flow measurement in the oil industry. Flow Meas. Instrum. 2005, 16, 145–155. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Q.; Xue, Q.; Fan, W.; Zhang, L.; Cao, Z.; Sun, B.; Wang, H.; Yang, W. A review on image reconstruction algorithms for electrical capacitance/resistance tomography. Sensor Rev. 2016, 36, 429–445. [Google Scholar] [CrossRef]
- Yang, C.; Wang, H.; Cui, Z. Application of electrical resistance tomography in bubble columns for volume fraction measurement. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference, Graz, Austria, 13–16 May 2012; pp. 1199–1203. [Google Scholar]
- Cui, Z.; Wang, H.; Xu, Y.; Zhang, L.; Yan, Y. An integrated ECT/ERT dual modality sensor. In Proceedings of the 2009 IEEE Instrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009; pp. 1434–1438. [Google Scholar]
- Hayes, D. Tomographic Flow Measurement by Combining Component Distribution and Velocity Profile Measurements in 2-Phase Oil/Gas Flows. Ph.D. Thesis, UMIST, Manchester, UK, 1994. [Google Scholar]
- Dong, F.; Jiang, Z.X.; Qiao, X.T.; Xu, L.A. Application of electrical resistance tomography to two-phase pipe flow parameters measurement. Flow Meas. Instrum. 2003, 14, 183–192. [Google Scholar] [CrossRef]
- Jia, J.J.; Wang, M.; Faraj, Y. Evaluation of EIT systems and algorithms for handling full void fraction range in two-phase flow measurement. Meas. Sci. Technol. 2015, 26, 015305. [Google Scholar] [CrossRef] [Green Version]
- Lewis, M.A.; Weber, D.F.; Moore, J.C. Dredging impact on an urbanized Florida bayou: Effects on benthos and algal-periphyton. Environ. Pollut. 2001, 115, 161–171. [Google Scholar] [CrossRef]
- Ding, M.; Yue, S.; Li, J.; Li, Q.; Wang, H. Optimal similarity norm for electrical tomography based on Bregman divergence. Rev. Sci. Instrum. 2020, 91, 033707. [Google Scholar] [CrossRef]
- Jin, H.; Lian, Y.; Yang, S.; He, G.; Guo, Z. The parameters measurement of air–water two phase flow using the electrical resistance tomography (ERT) technique in a bubble column. Flow Meas. Instr. 2013, 31, 55–60. [Google Scholar] [CrossRef]
- Wang Hx Xu, Y.B.; Dong, F. Electrical Tomography; Science Press: Beijing, China, 2013; pp. 9–73. [Google Scholar]
- Xu, Y.; Wang, H.; Cui, Z.; Dong, F. Application of electrical resistance tomography for slug flow measurement in gas/liquid flow of horizontal pipe. In Proceedings of the 2009 IEEE International Workshop on Imaging Systems and Techniques, Shenzhen, China, 11–12 May 2009; pp. 319–323. [Google Scholar]
- Ling, Y.; Zhang, H.; Pan, Y.; Wang, Q.; Shang, Z. Numerical Simulation for Phase Volume Fraction of solid-liquid Multiphase Flows in Horizontal Curved Pipe. Well Logging Technol. 2018, 42, 135–139. [Google Scholar]
- Xu, G. Theoretic and Applied Research of Electrical Impedance Tomography; Chongqing University, College of Electrical Engineering: Chongqing, China, 2004; pp. 40–95. [Google Scholar]
- Cao, Z.Z.; Zhou, J.; Liu, A.; Sun, D.; Yu, B.; Wei, J. A three dimensional coupled VOF and Level set (VOSET) method with and without phase change on general curvilinear grids, Chem. Eng. Sci. 2020, 223, 115705. [Google Scholar] [CrossRef]
- Sun, D.L.; Yu, S.; Yu, B.; Wang, P.; Liu, W. A VOSET method combined with IDEAL algorithm for 3D two-phase flows with large density and viscosity ratio. Int. J. Heat Mass Transfer. 2017, 114, 155–168. [Google Scholar] [CrossRef]
- Kong, L.; Zhang, S.; Wu, P.Z.; Yang, S.; Tao, W. A coupled volume-of-fluid and level-set method (VOSET) for capturing interface of two-phase flows in arbitrary polygon grid. Int. J. Heat Mass Transfer. 2019, 143, 118565. [Google Scholar]
- Boudraa, A.; Claryss, P. Fast fuzzy grey level image segmentation method. Med. Biol. Eng. Comput. 1997, 35, 686–693. [Google Scholar]
- Tang, L. Research on Image Reconstruction Algorithms and Design of Software for Electrical Impedance Tomography System; Tianjin University, School of Electrical Engineering and Automation: Tianjin, China, 2016; p. 930. [Google Scholar]
- Sun, B.Y.; Yue, S.H.; Cui, Z.Q.; Wang, H.X. A new linear back projection algorithm to electrical tomography based on measuring data decomposition. Meas. Sci. Tech. 2015, 26, 2234–2239. [Google Scholar] [CrossRef]
- Ding, M.L.; Yue, S.H.; Wang, H.X. Second-order sensitivity coefficient based electrical tomography imaging. Chem. Eng. Sci. 2019, 18, 40–49. [Google Scholar] [CrossRef]

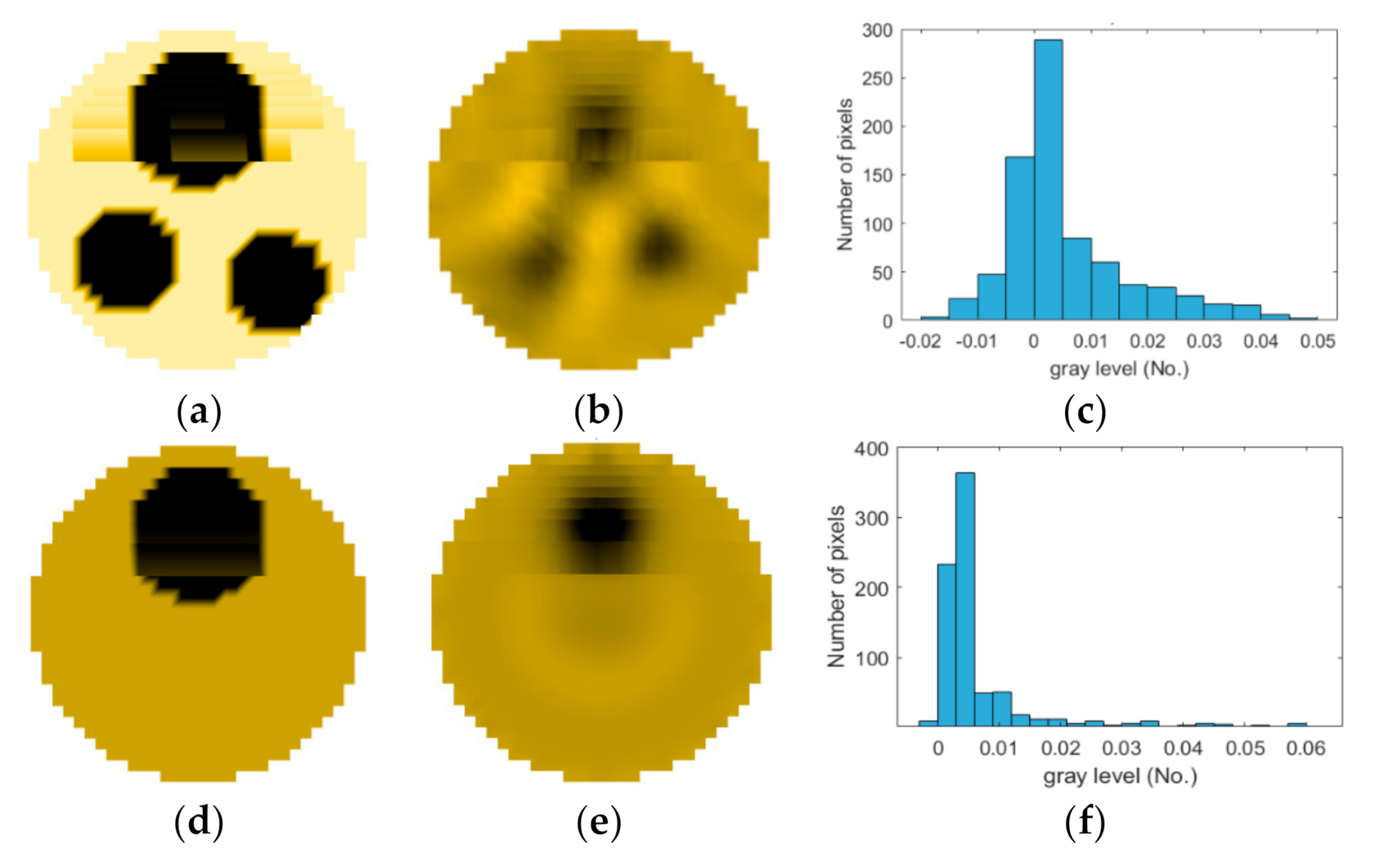

| CF | Model | ERT | Statistical Histogram | MG | Equation (12) |
|---|---|---|---|---|---|
| 10% |  |  | 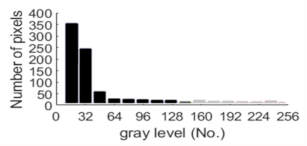 | 14.16% | 8.74% |
| 20% |  |  | 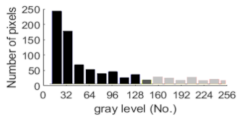 | 18.57% | 20.44% |
| 30% |  |  |  | 27.65% | 29.56% |
Legend:  background background  artifacts artifacts  object object | |||||
| Computed CF(1) | 0.358 | 0.366 | 0.310 | 0.225 | 0.096 |
|---|---|---|---|---|---|
| ERT image | 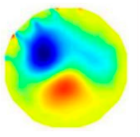 | 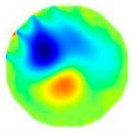 | 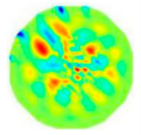 |  |  |
| Partitioned clusters |  |  |  |  |  |
| Pattern | Distribution | σ(Cu) | Pattern | Distribution | σ(Cu) |
|---|---|---|---|---|---|
| Model 1 | 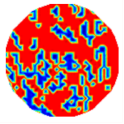 | −78.8 | Model 6 |  | −79.5 |
| Model 2 |  | −76.4 | Model 7 |  | −78.9 |
| Model 3 |  | −78.4 | Model 8 |  | −79 |
| Model 4 |  | −78.9 | Model 9 |  | −76 |
| Model 5 |  | −75.4 | Model 10 |  | −78.1 |
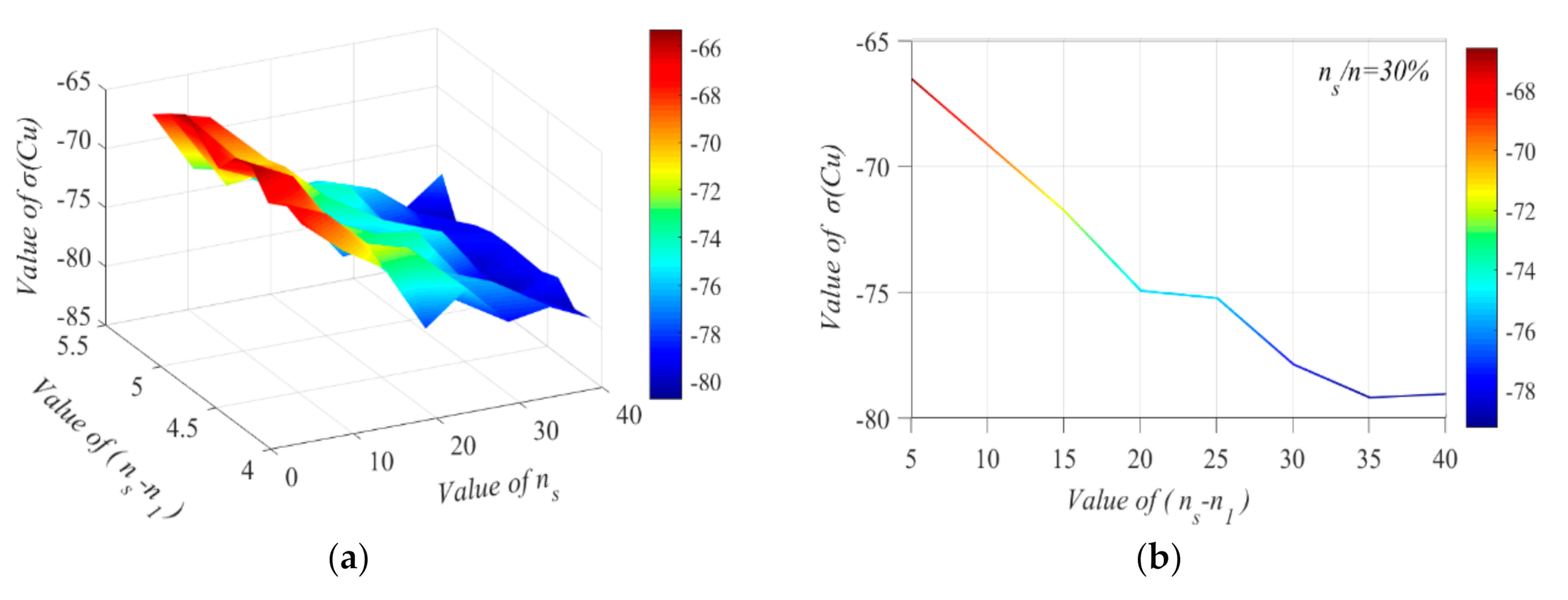
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5% | σ(Φ-y) | −67.2 | −66.6 | −67.6 | −65.5 | −65.8 | −67.8 | −66.5 | −65.3 | −66.3 | −67.4 |
| n1-ns | 3 | 0 | 3 | 2 | 0 | 3 | 3 | 2 | 0 | 3 | |
| 10% | σ(Φ-y) | −70.1 | −68 | −68.7 | −67 | −67.9 | −69.4 | −69.1 | −72 | −67.2 | −72.7 |
| n1-ns | 44 | 44 | 44 | 43 | 44 | 45 | 42 | 47 | 44 | 48 | |
| 15% | σ(Φ-y) | −72.3 | −71.3 | −72.5 | −72.3 | −72.7 | −72.8 | −70 | −70.5 | −71.4 | −73.5 |
| n1-ns | 84 | 84 | 86 | 87 | 87 | 86 | 81 | 84 | 83 | 86 | |
| 20% | σ(Φ-y) | −78.1 | −72.3 | −75.7 | −73.2 | −75.2 | −77.2 | −73.2 | −75 | −74.3 | −75.9 |
| n1-ns | 125 | 126 | 125 | 125 | 126 | 125 | 125 | 125 | 127 | 127 | |
| 25% | σ(Φ-y) | −75.3 | −77.2 | −75.8 | −73.6 | −75.7 | −74.8 | −76 | −74.1 | −74.8 | −75.7 |
| n1-ns | 167 | 169 | 166 | 165 | 166 | 167 | 166 | 165 | 165 | 167 | |
| 30% | σ(Φ-y) | −78.8 | −76.4 | −78.4 | −78.9 | −75.4 | −79.5 | −78.9 | −79 | −76 | −78.1 |
| n1-ns | 208 | 208 | 209 | 206 | 207 | 206 | 206 | 207 | 206 | 206 | |
| 35% | σ(Φ-y) | −78.2 | −78.6 | −79.4 | −80.5 | −79.7 | −80 | −78.6 | −79.3 | −78.7 | −79.7 |
| n1-ns | 247 | 247 | 249 | 247 | 247 | 247 | 248 | 247 | 247 | 247 | |
| 40% | σ(Φ-y) | −79.9 | −80.1 | −78.5 | −79 | −78.9 | −78.8 | −78.9 | −79.3 | −80.8 | −77.1 |
| n1-ns | 288 | 289 | 287 | 287 | 287 | 287 | 288 | 288 | 289 | 287 | |
| Real CF value | 0.305 | 0.332 | 0.342 | 0.367 | 0.381 | 0.406 |
| Identifiable object by ERT |  |  |  |  |  |  |
| Real CF value | 0.307 | 0.330 | 0.341 | 0.370 | 0.388 | 0.401 |
| Unidentifiable object by ERT |  |  |  |  |  |  |
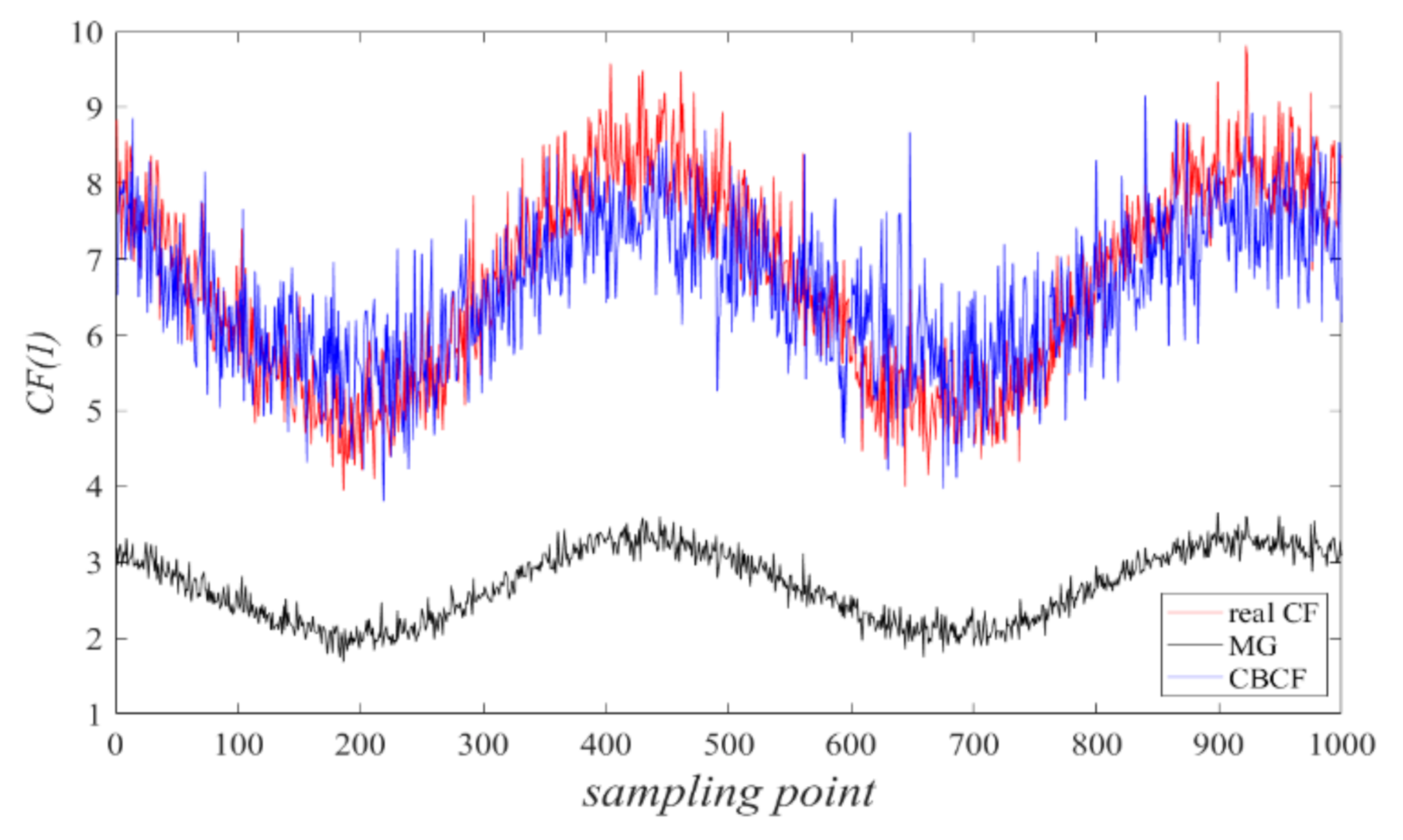
| Real CF | 7.00 | 5.28 | 5.48 | 7.52 | 8.24 | 6.86 | 5.19 | 5.66 | 7.58 | 8.13 |
|---|---|---|---|---|---|---|---|---|---|---|
| f-FCM | 2.96 | 2.73 | 2.72 | 3.01 | 3.02 | 2.90 | 2.92 | 2.81 | 2.90 | 2.95 |
| MG | 5.79 | 4.17 | 4.23 | 6.97 | 7.24 | 2.73 | 2.16 | 2.31 | 3.03 | 3.24 |
| CBCF | 6.66 | 5.75 | 5.76 | 6.99 | 7.44 | 6.60 | 5.89 | 5.97 | 7.10 | 7.48 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Yue, S.; Li, Q.; Wang, H. Clustering-Based Component Fraction Estimation in Solid–Liquid Two-Phase Flow in Dredging Engineering. Sensors 2020, 20, 5697. https://doi.org/10.3390/s20195697
Sun C, Yue S, Li Q, Wang H. Clustering-Based Component Fraction Estimation in Solid–Liquid Two-Phase Flow in Dredging Engineering. Sensors. 2020; 20(19):5697. https://doi.org/10.3390/s20195697
Chicago/Turabian StyleSun, Chang, Shihong Yue, Qi Li, and Huaxiang Wang. 2020. "Clustering-Based Component Fraction Estimation in Solid–Liquid Two-Phase Flow in Dredging Engineering" Sensors 20, no. 19: 5697. https://doi.org/10.3390/s20195697
APA StyleSun, C., Yue, S., Li, Q., & Wang, H. (2020). Clustering-Based Component Fraction Estimation in Solid–Liquid Two-Phase Flow in Dredging Engineering. Sensors, 20(19), 5697. https://doi.org/10.3390/s20195697






