Dynamic Response of PVDF Cantilever Due to Droplet Impact Using an Electromechanical Model
Abstract
:1. Introduction
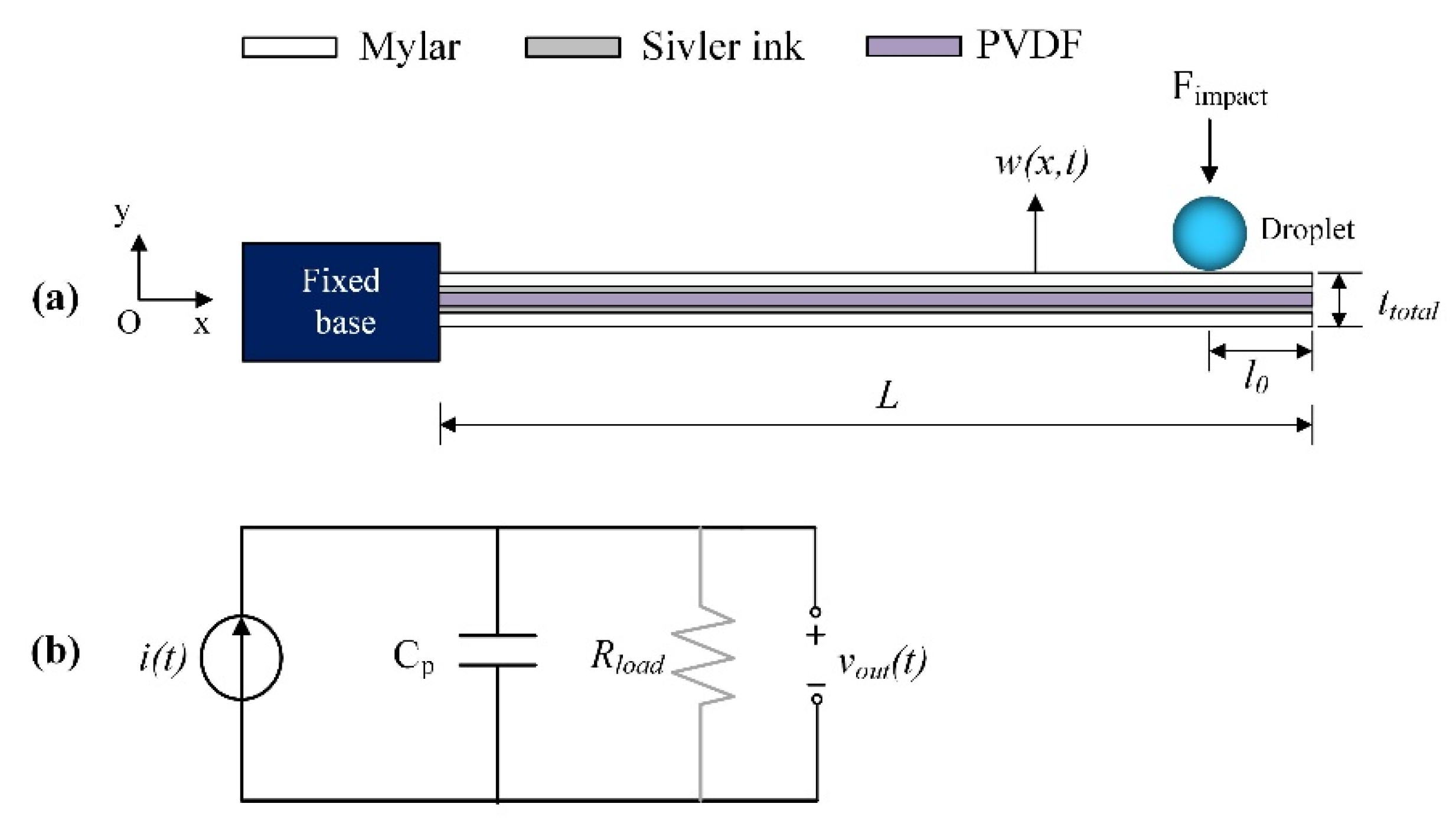
2. Modeling of the PVDF Cantilever Sensor
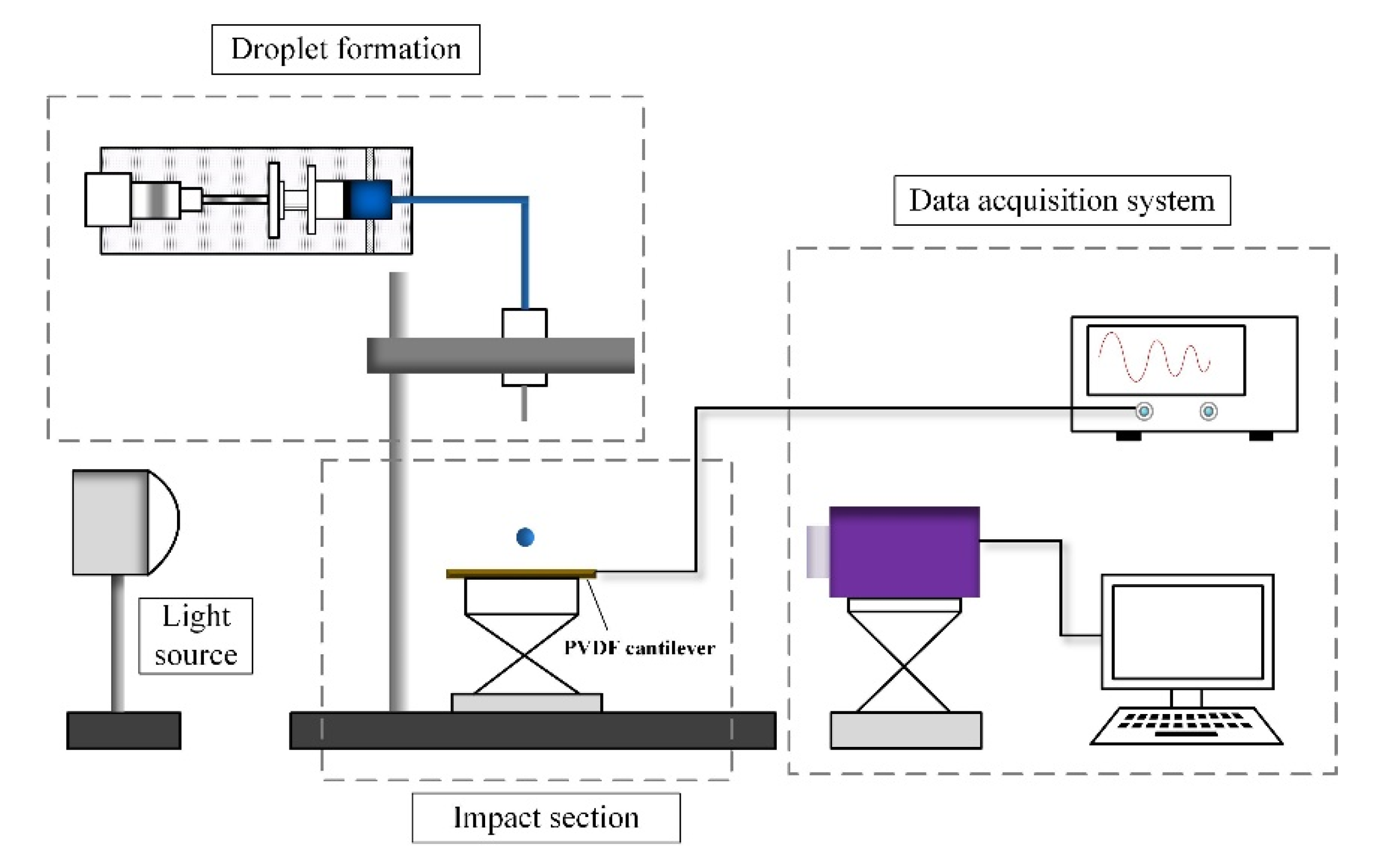
3. Experiment Setup
4. Discussion
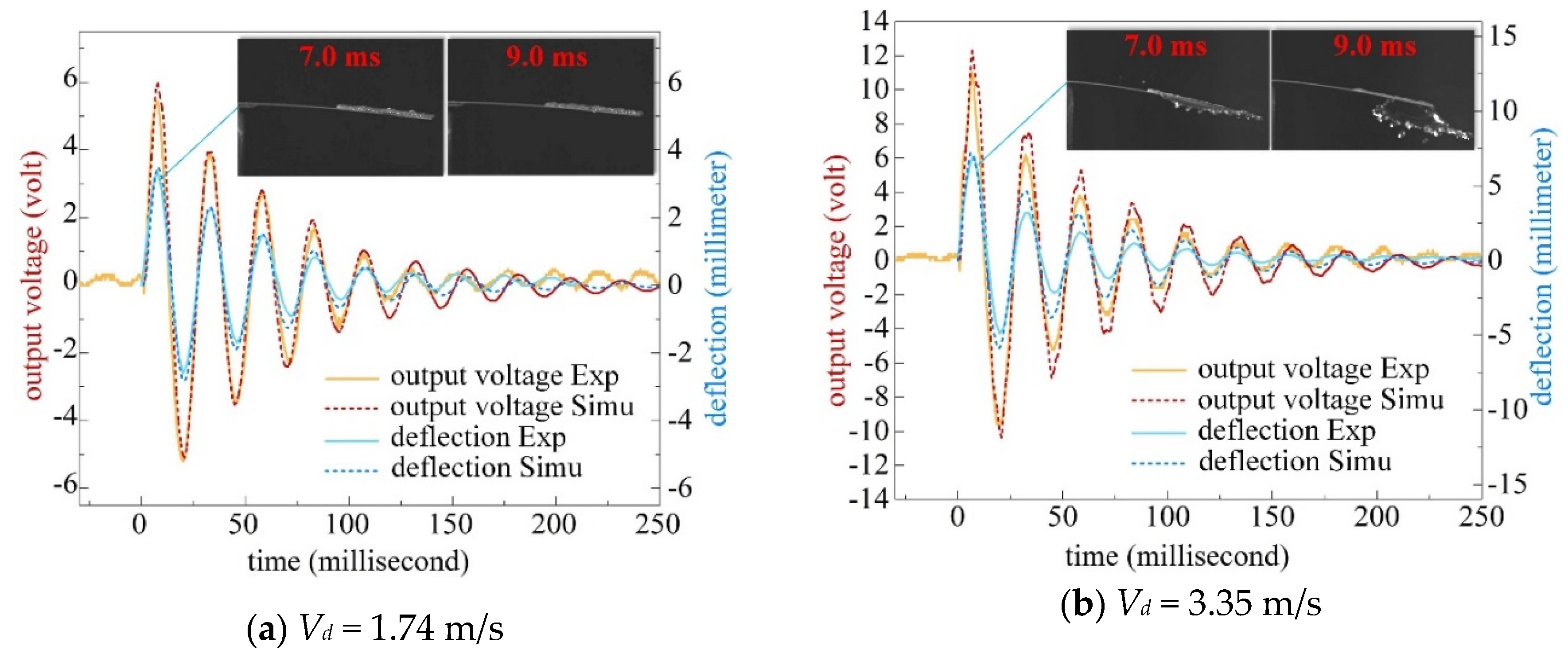
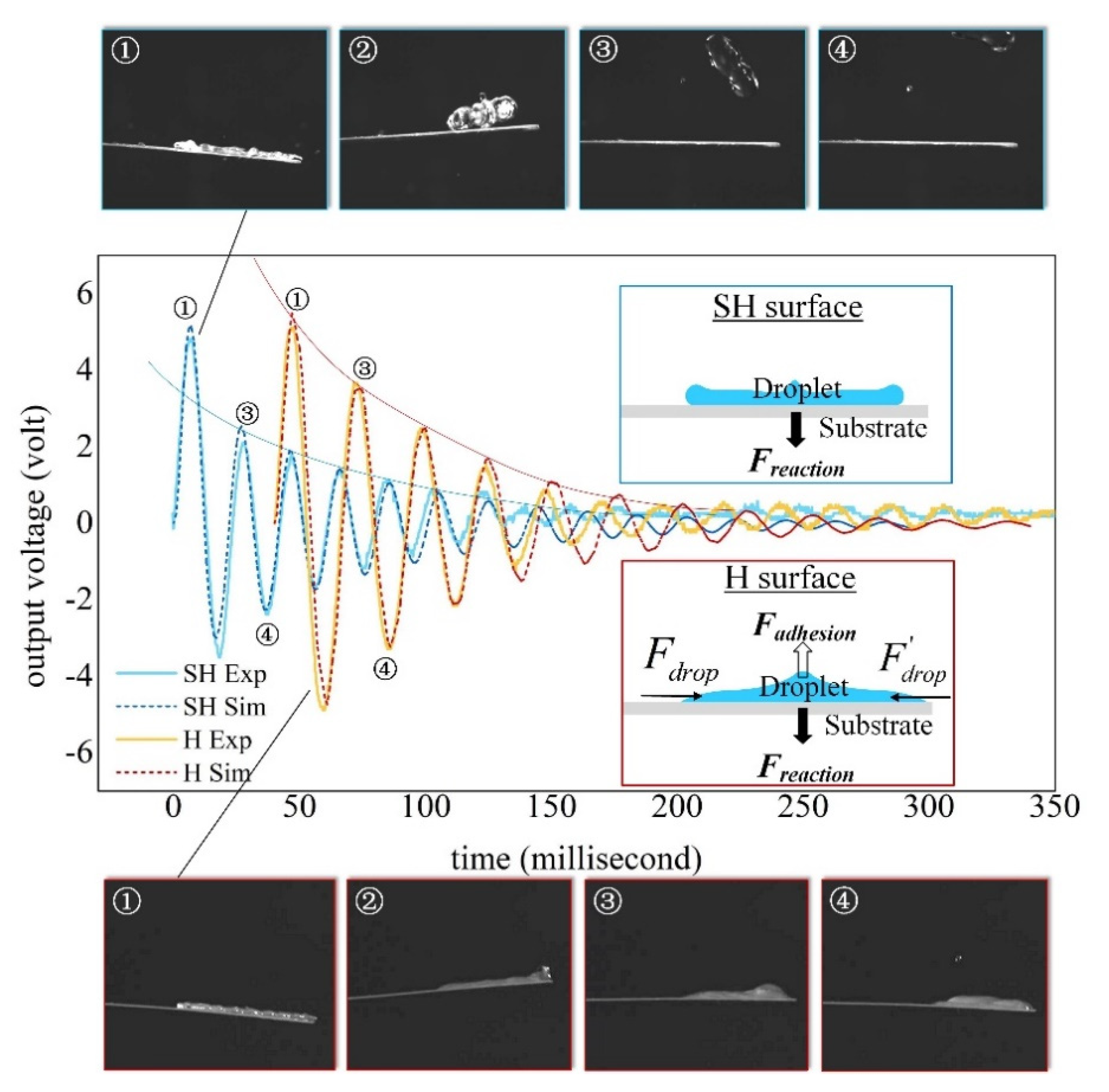
4.1. Impact on a Hydrophilic Beam
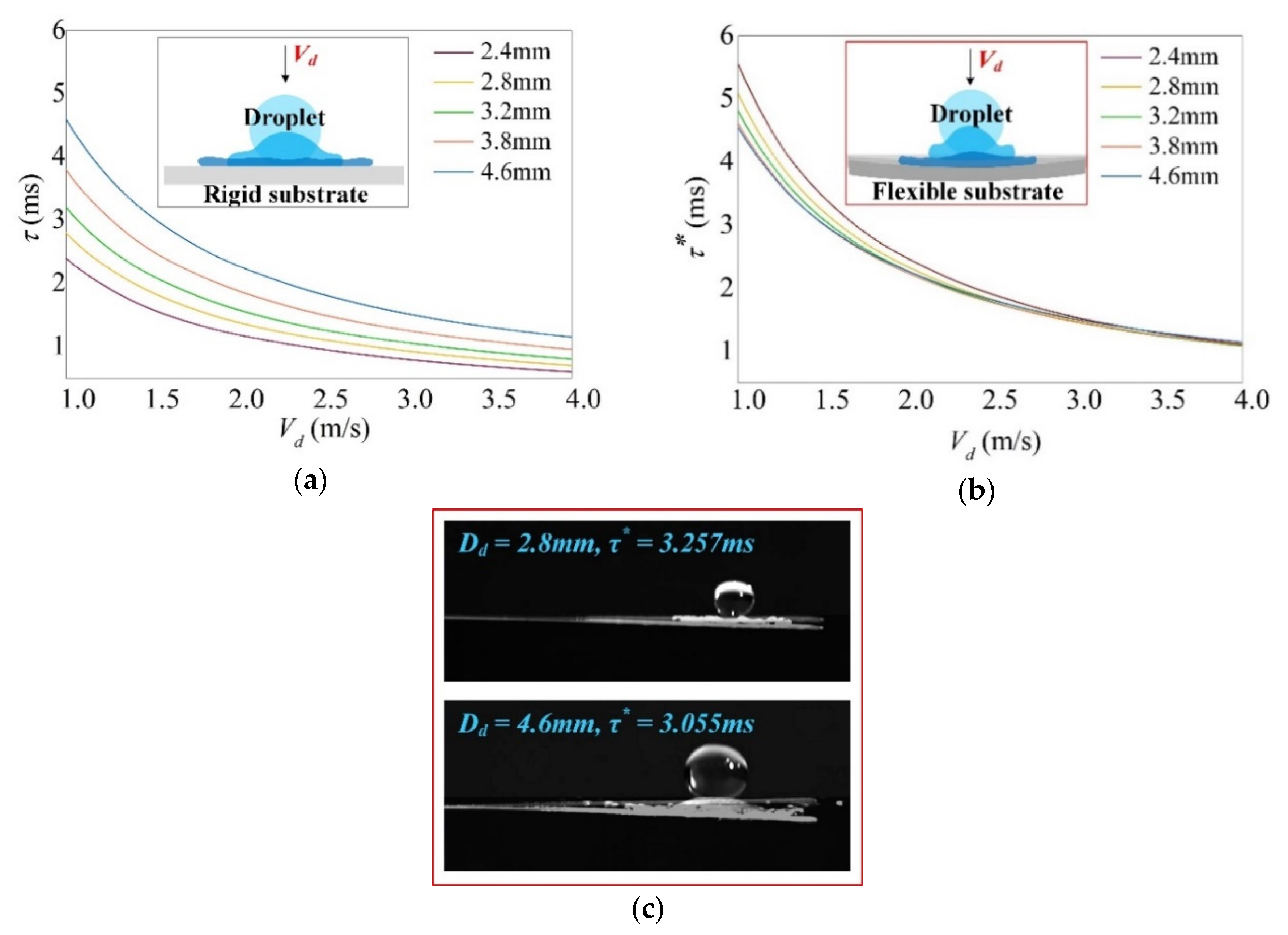
4.2. Droplet-Substrate Interaction Mechanisms
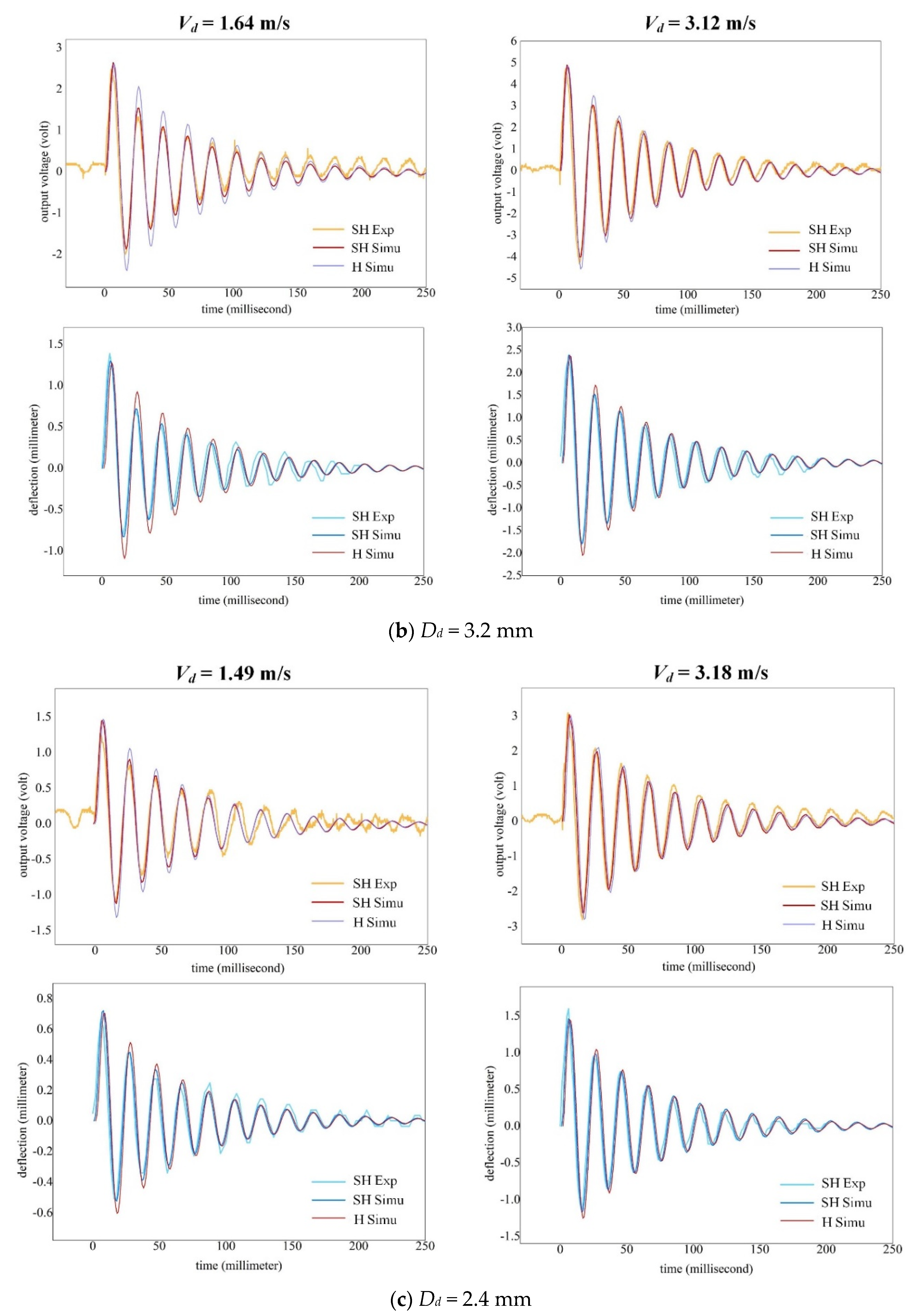
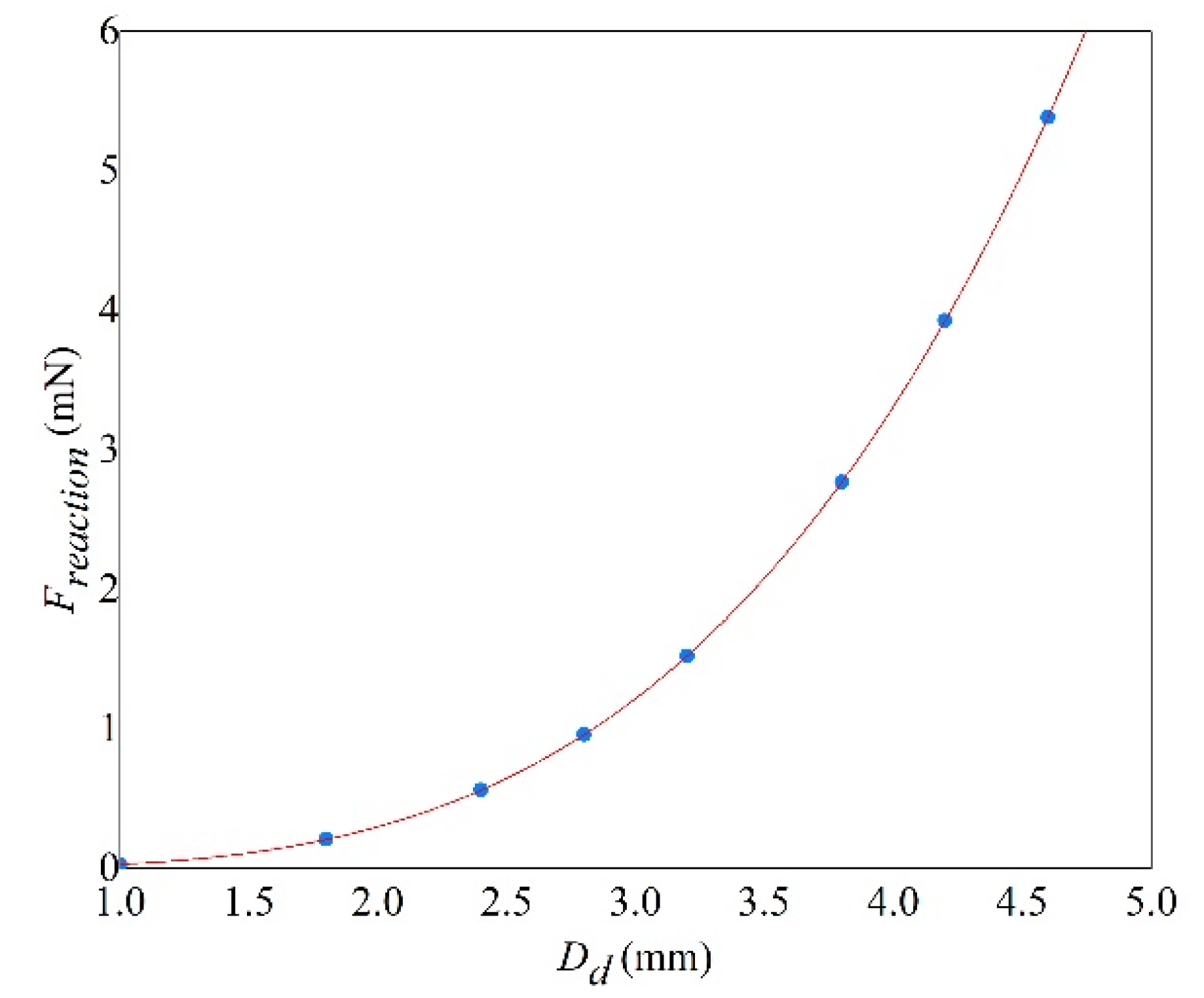
4.3. Impact on a Super-Hydrophobic Beam
4.3.1. Regime Transition of Droplet Impact Mechanism
4.3.2. Effect of Droplet Splash
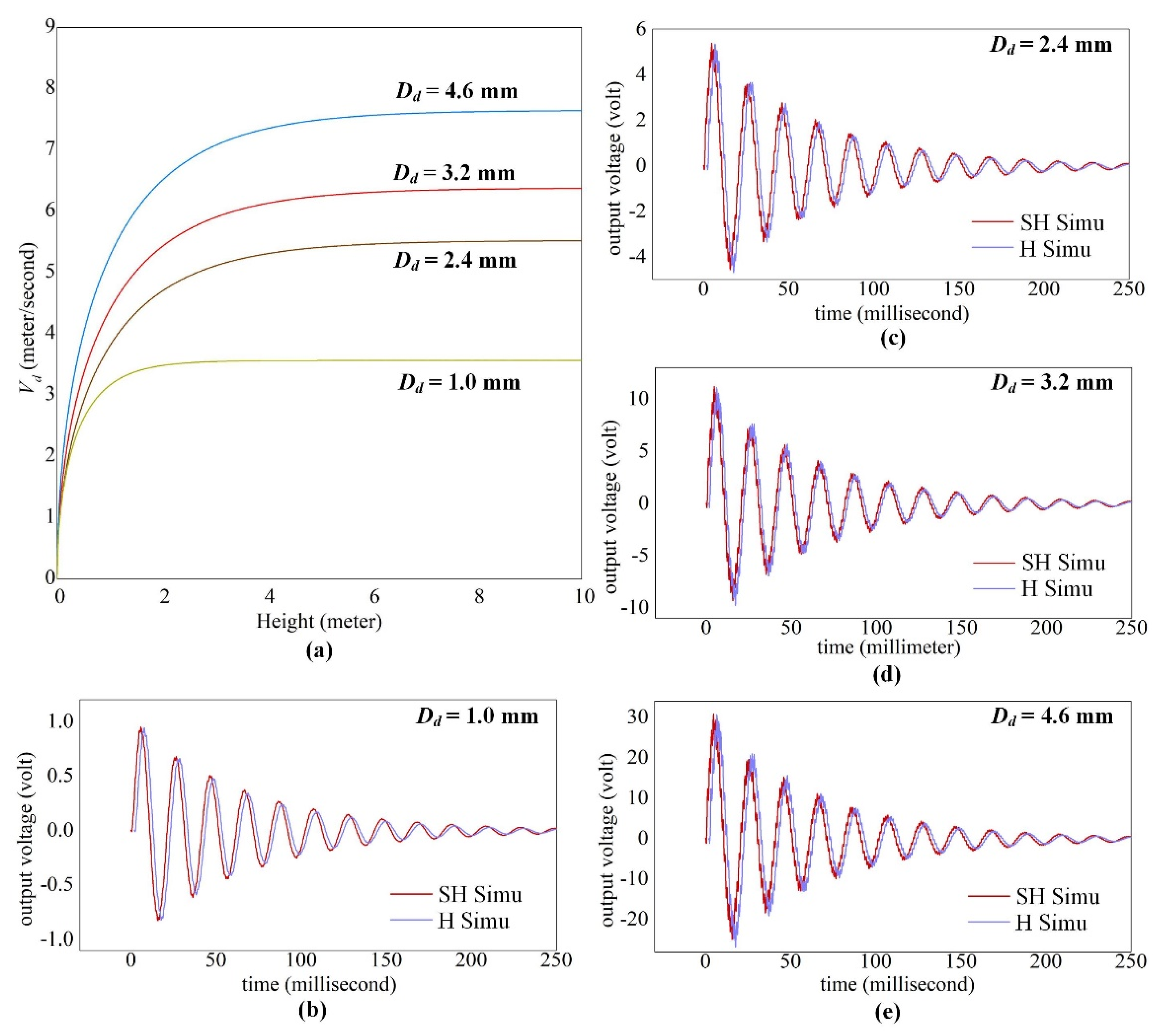
4.3.3. Dynamic Response under Excitation of Raindrops
4.4. Energy Collected from the SH and H Beams
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guigon, R.; Chaillout, J.-J.; Jager, T.; Despesse, G. Harvesting raindrop energy: Experimental study. Smart Mater. Struct. 2008, 17, 015039. [Google Scholar] [CrossRef]
- Guigon, R.; Chaillout, J.-J.; Jager, T.; Despesse, G. Harvesting raindrop energy: Theory. Smart Mater. Struct. 2008, 17, 015038. [Google Scholar] [CrossRef]
- Viola, F.; Romano, P.; Miceli, R.; Acciari, G.; Spataro, C. Piezoelectric model of rainfall energy harvester. In Proceedings of the 2014 Ninth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 25–27 March 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–7. [Google Scholar]
- Helseth, L.; Wen, H. Evaluation of the energy generation potential of rain cells. Energy 2017, 119, 472–482. [Google Scholar] [CrossRef]
- Fabio, V. Comparison among different rainfall energy harvesting structures. Appl. Sci. 2018, 8, 955. [Google Scholar]
- Doria, A.; Fanti, G.; Filipi, G.; Moro, F. Development of a Novel Piezoelectric Harvester Excited by Raindrops. Sensors 2019, 19, 3653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ong, Z.-Z.; Wong, V.-K.; Ho, J.-H. Performance enhancement of a piezoelectric rain energy harvester. Sensors Actuators A Phys. 2016, 252, 154–164. [Google Scholar] [CrossRef]
- Ilyas, M.A.; Swingler, J. Towards a prototype module for piezoelectric energy harvesting from raindrop impacts. Energy 2017, 125, 716–725. [Google Scholar] [CrossRef]
- Chua, K.G.; Hor, Y.F.; Lim, H.C. Raindrop kinetic energy piezoelectric harvesters and relevant interface circuits: Review, issues and outlooks. Sens. Transducers 2016, 200, 1–15. [Google Scholar]
- Wong, C.H.; Dahari, Z.; Jumali, M.H.; Mohamed, K.; Mohamed, J.J. Simulation and Fabrication of Wagon-Wheel-Shaped Piezoelectric Transducer for Raindrop Energy Harvesting Application. J. Electron. Mater. 2017, 46, 1587–1597. [Google Scholar] [CrossRef]
- Chin-Hong, W.; Dahari, Z.; Manaf, A.A.; Sidek, O.; Miskam, M.A.; Mohamed, J.J.; Miskam, M.A. Simulation of Piezoelectric Raindrop Energy Harvester. In Proceedings of the IEEE TENCON Spring Conference 2013, Sydney, Australia, 17–19 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 465–469. [Google Scholar]
- Vatansever, D.; Hadimani, R.L.; Shah, T.; Siores, E. An investigation of energy harvesting from renewable sources with PVDF and PZT. Smart Mater. Struct. 2011, 20, 055019. [Google Scholar] [CrossRef]
- Jellard, S.; Pu, S.-H.; Chen, S.; Yao, K.; White, N.M. Water droplet impact energy harvesting with P(VDF-TrFE) piezoelectric cantilevers on stainless steel substrates. Smart Mater. Struct. 2019, 28, 095002. [Google Scholar] [CrossRef]
- Patel, I.; Siores, E.; Shah, T. Utilisation of smart polymers and ceramic based piezoelectric materials for scavenging wasted energy. Sensors Actuators A Phys. 2010, 159, 213–218. [Google Scholar] [CrossRef]
- Ilyas, M.A.; Swingler, J. Piezoelectric energy harvesting from raindrop impacts. Energy 2015, 90, 796–806. [Google Scholar] [CrossRef]
- Wong, C.H.; Dahari, Z.; Manaf, A.A.; Miskam, M.A. Piezoelectric Beam Length Optimization for Raindrop Energy Harvesting Application. Appl. Mech. Mater. 2014, 705, 247–251. [Google Scholar] [CrossRef]
- Izrin, I.M.; Dahari, Z. Power Converter for Raindrop Energy Harvesting Application: Full-Wave Rectifier. In Proceedings of the 2017 IEEE 15th Student Conference on Research and Development (SCOReD), Putrajaya, MA, USA, 13–14 December 2017; IEEE: Piscataway, NJ, USA; pp. 327–331. [Google Scholar] [CrossRef]
- Acciari, G.; Caruso, M.; Miceli, R.; Riggi, L.; Romano, P.; Schettino, G.; Viola, F. Piezoelectric Rainfall Energy Harvester Performance by an Advanced Arduino-Based Measuring System. IEEE Trans. Ind. Appl. 2018, 54, 458–468. [Google Scholar] [CrossRef] [Green Version]
- Wong, V.-K.; Ho, J.-H.; Sam, H.-K. On accumulation of water droplets in piezoelectric energy harvesting. J. Intell. Mater. Syst. Struct. 2016, 28, 521–530. [Google Scholar] [CrossRef]
- Viola, F.; Romano, P.; Miceli, R.; Acciari, G. Harvesting Rainfall Energy by Means of Piezoelectric Transducer. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 634–639. [Google Scholar]
- Wong, V.-K.; Ho, J.-H.; Yap, E.H.; Chai, A.B. Dynamics of a piezoelectric energy harvester in a simulated rain environment. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 2642–2654. [Google Scholar] [CrossRef]
- Wong, V.-K.; Ho, J.-H.; Chai, A.B. Performance of a piezoelectric energy harvester in actual rain. Energy 2017, 124, 364–371. [Google Scholar] [CrossRef]
- Wong, C.H.; Dahari, Z. Development of Vibration-Based Piezoelectric Raindrop Energy Harvesting System. J. Electron. Mater. 2017, 46, 1869–1882. [Google Scholar] [CrossRef]
- Biswas, P.V.; Uddin, M.A. Harnessing raindrop energy in Banglagesh. In Proceedings of the International Conference on Mechanical Engineering 2009 (ICME2009), Dhaka, Bangladesh, 26–28 December 2009. [Google Scholar]
- Hassan, A.; Wong, C.H.; Dahari, Z. An Analytical Study of Output Voltage Profile Generated from Raindrop Energy; IEEE: Piscataway, NJ, USA, 2017; pp. 3775–3777. [Google Scholar]
- Perera, K.C.R.; Sampath, B.G.; Dassanayake, V.P.C. Harvesting of Kinetic Energy of the Raindrops. Int. J. Energy Power Eng. 2014, 8, 325–330. [Google Scholar]
- Mundo, C.; Sommerfeld, M.; Tropea, C. Droplet-wall collisions: Experimental studies of the deformation and breakup process. Int. J. Multiph. Flow 1995, 21, 151–173. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1142. [Google Scholar] [CrossRef] [Green Version]
- Erturk, A.; Inman, D. On Mechanical Modeling of Cantilevered Piezoelectric Vibration Energy Harvesters. J. Intell. Mater. Syst. Struct. 2008, 19, 1311–1325. [Google Scholar] [CrossRef]
- Sodano, H.A.; Park, G.; Inman, D.J. Estimation of Electric Charge Output for Piezoelectric Energy Harvesting. Strain 2004, 40, 49–58. [Google Scholar] [CrossRef]
- Wong, V.-K.; Ho, J.-H.; Yap, E. Dynamics of a piezoelectric beam subjected to water droplet impact with water layer formed on the surface. J. Intell. Mater. Syst. Struct. 2014, 26, 2170–2180. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. A Distributed Parameter Electromechanical Model for Cantilevered Piezoelectric Energy Harvesters. J. Vib. Acoust. 2008, 130, 041002. [Google Scholar] [CrossRef]
- Beeby, S.P.; O’Donnell, T.B. Energy Harvesting Technologies; Springer: Boston, MA, USA, 2009; pp. 47–49. [Google Scholar]
- Doria, A.; Fanti, G.; Moro, F. Response of a Piezoelectric Harvester to Impacts Generated by Rain-Drops. In Proceedings of the 2019 Fourteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 8–10 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–9. [Google Scholar]
- Soto, D.; De Larivière, A.B.; Boutillon, X.; Clanet, C.; Quéré, D. The force of impacting rain. Soft Matter 2014, 10, 4929–4934. [Google Scholar] [CrossRef]
- Imeson, A.; Vis, R.; De Water, E. The measurement of water-drop impact forces with a piezo-electric transducer. Catena 1981, 8, 83–96. [Google Scholar] [CrossRef]
- Range, K.; Feuillebois, F. Influence of Surface Roughness on Liquid Drop Impact. J. Colloid Interface Sci. 1998, 203, 16–30. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, G.; Dong, X.; Li, Z.; Liu, X. Dynamic Response of PVDF Cantilever Due to Droplet Impact Using an Electromechanical Model. Sensors 2020, 20, 5764. https://doi.org/10.3390/s20205764
Hao G, Dong X, Li Z, Liu X. Dynamic Response of PVDF Cantilever Due to Droplet Impact Using an Electromechanical Model. Sensors. 2020; 20(20):5764. https://doi.org/10.3390/s20205764
Chicago/Turabian StyleHao, Guannan, Xiangwei Dong, Zengliang Li, and Xiaoxiao Liu. 2020. "Dynamic Response of PVDF Cantilever Due to Droplet Impact Using an Electromechanical Model" Sensors 20, no. 20: 5764. https://doi.org/10.3390/s20205764



