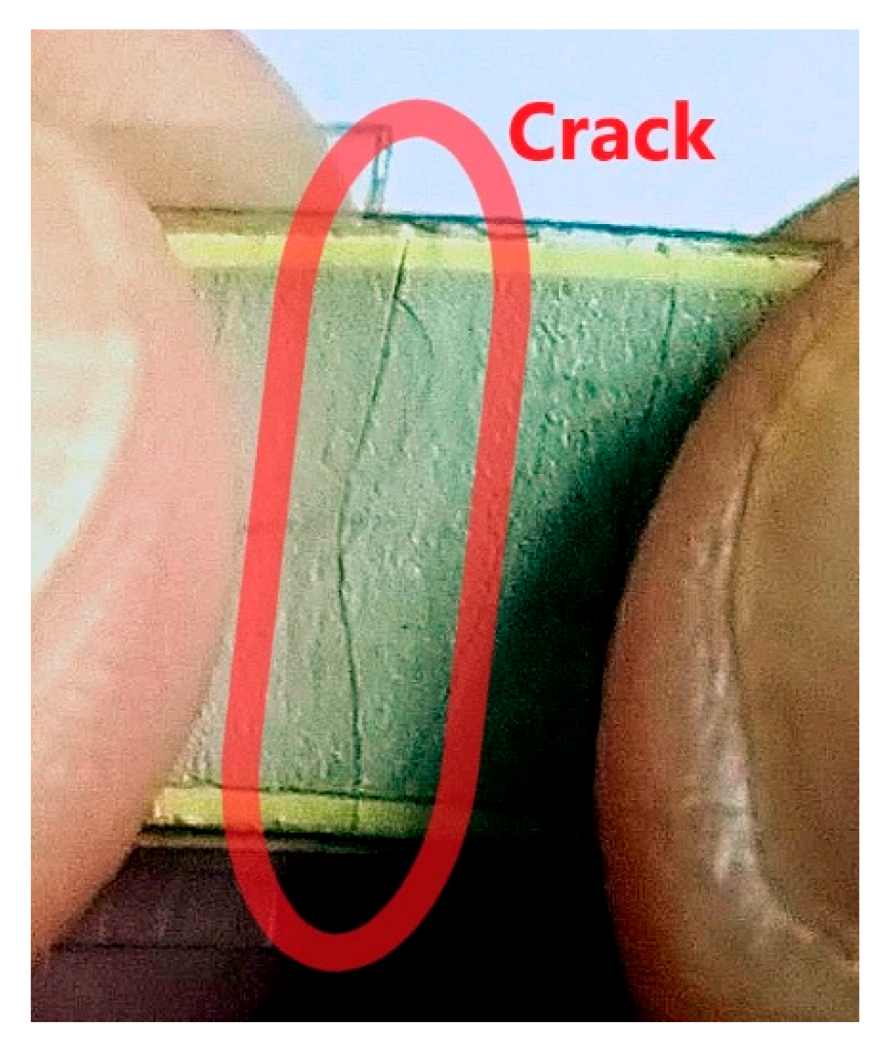
Crack Protective Layered Architecture of Lead-Free Piezoelectric Energy Harvester in Bistable Configuration
Abstract
:1. Introduction
2. Bimorph Cantilever Beam Design
2.1. Optimization of the Layer Configuration within the Proposed Multilayer Structure
3. 1DOF Model of Multilayer Piezoelectric Harvester
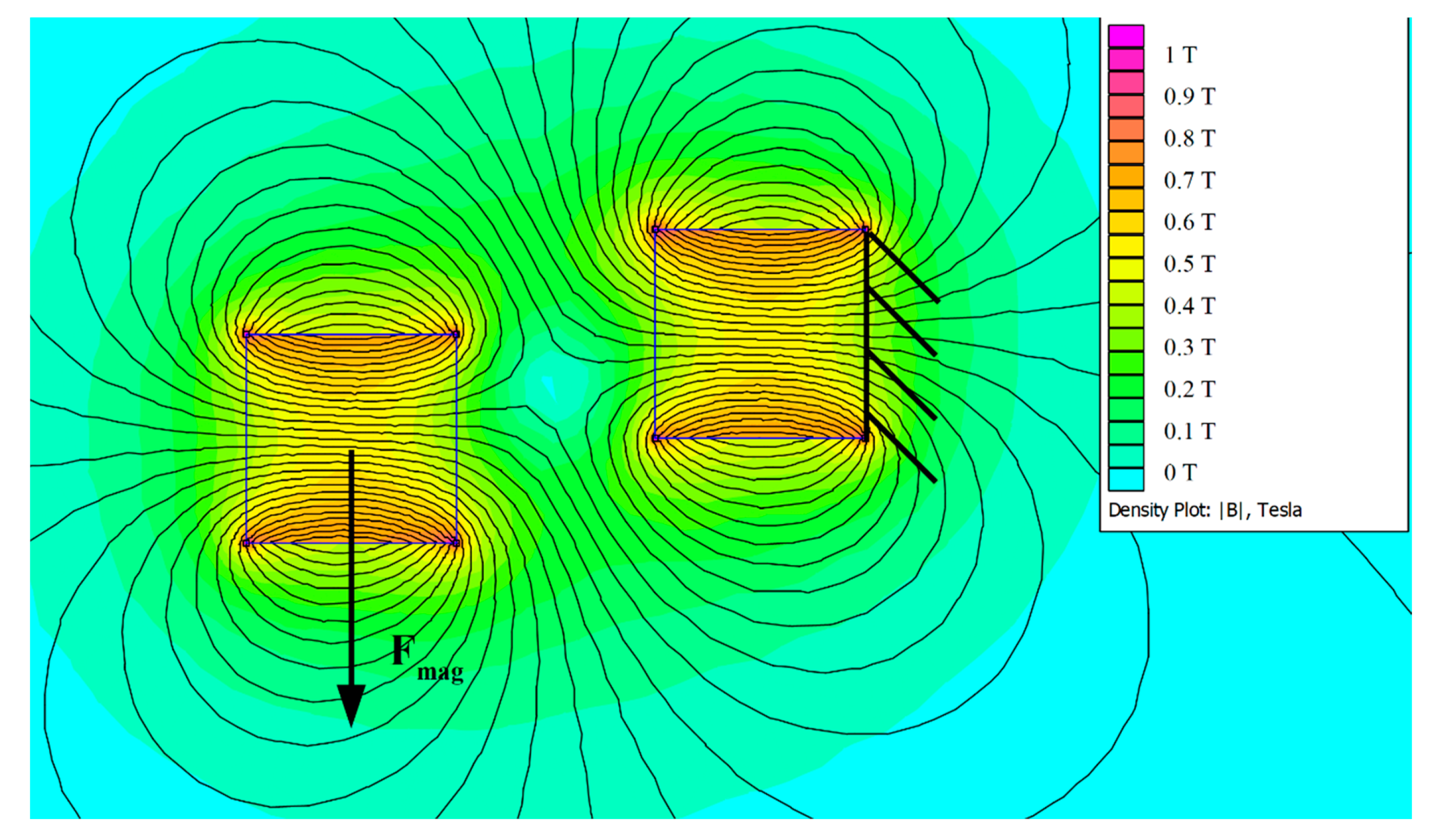
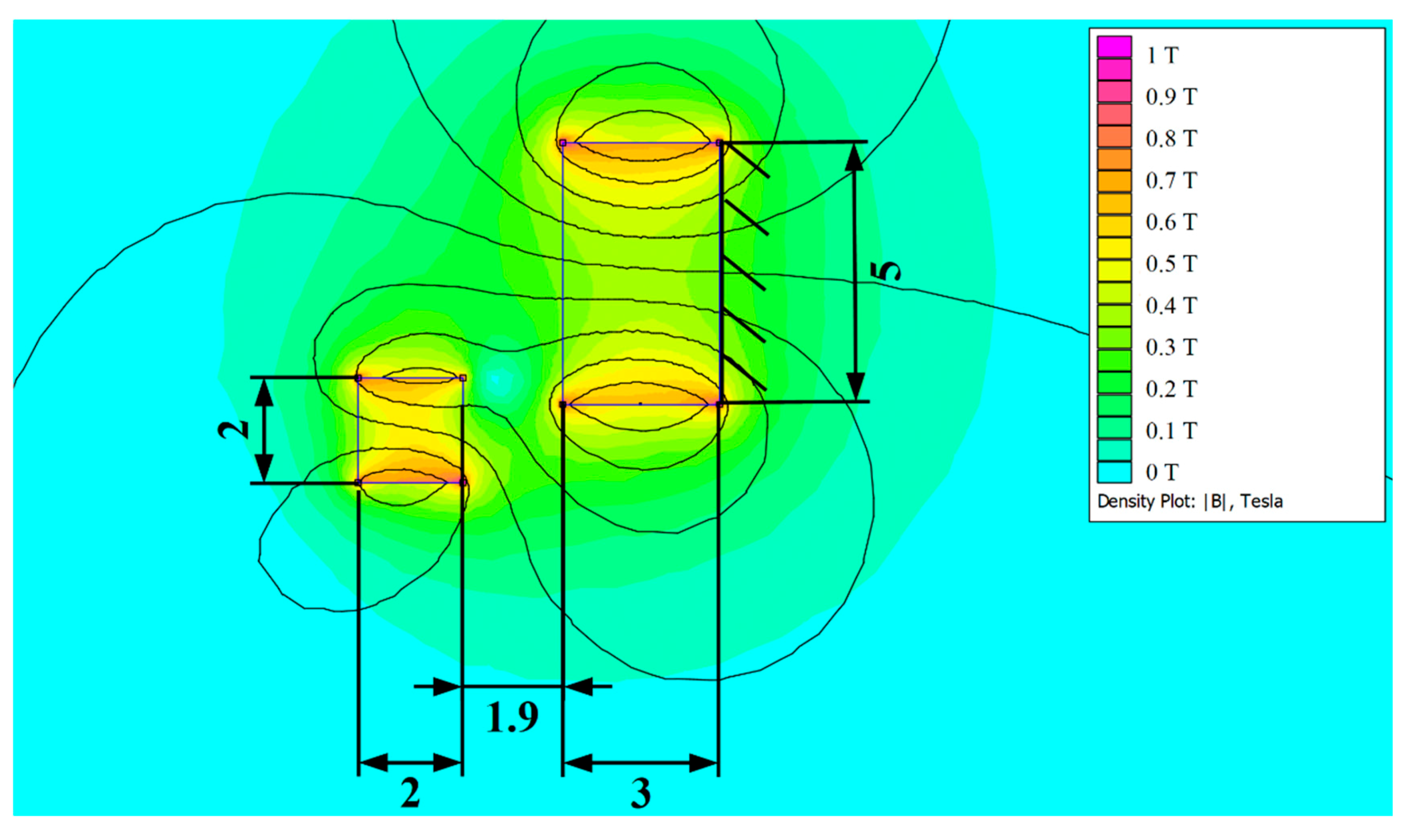
4. Design of Auxiliary Magnetic Spring and Model of Bistable Energy Harvester
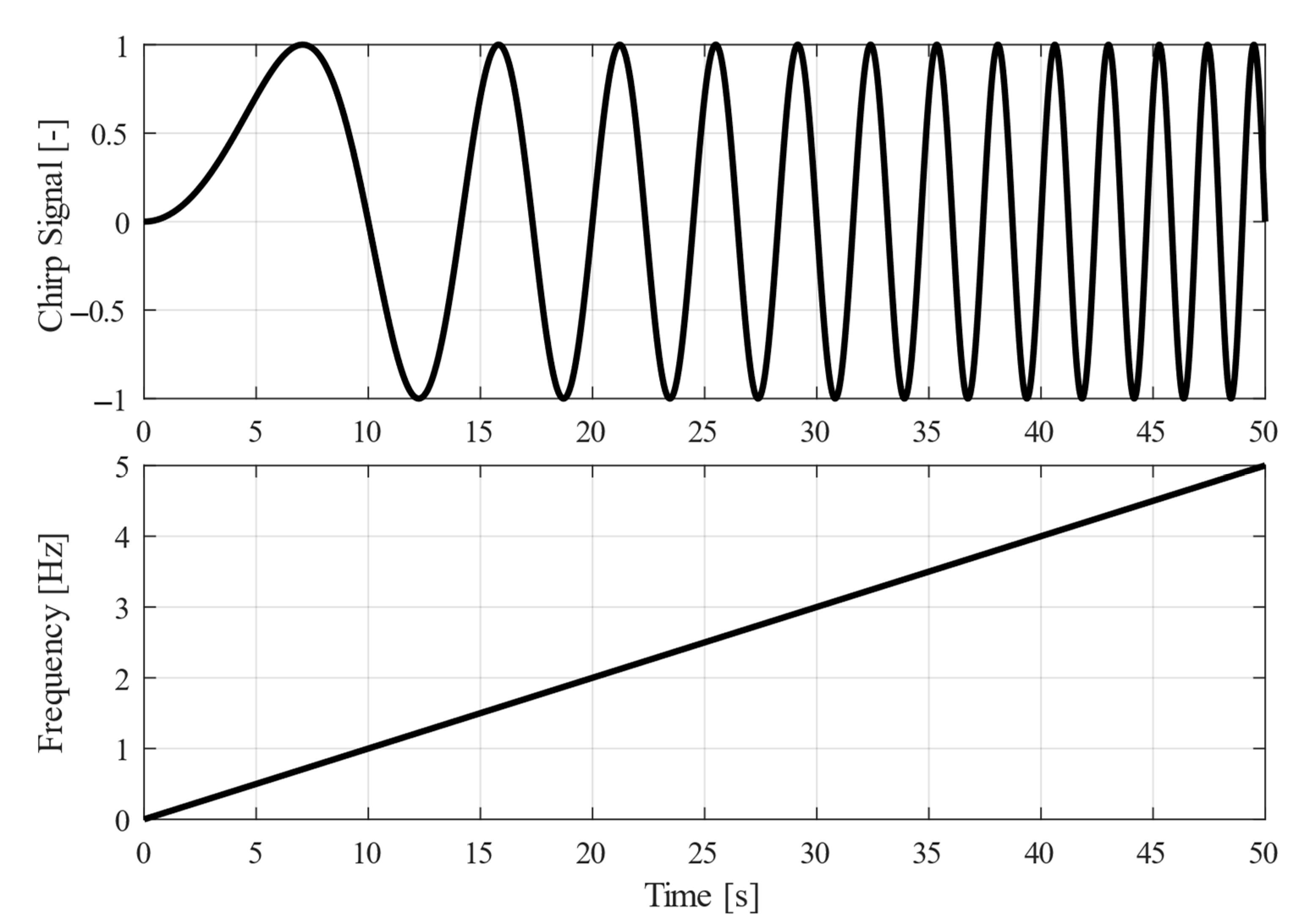
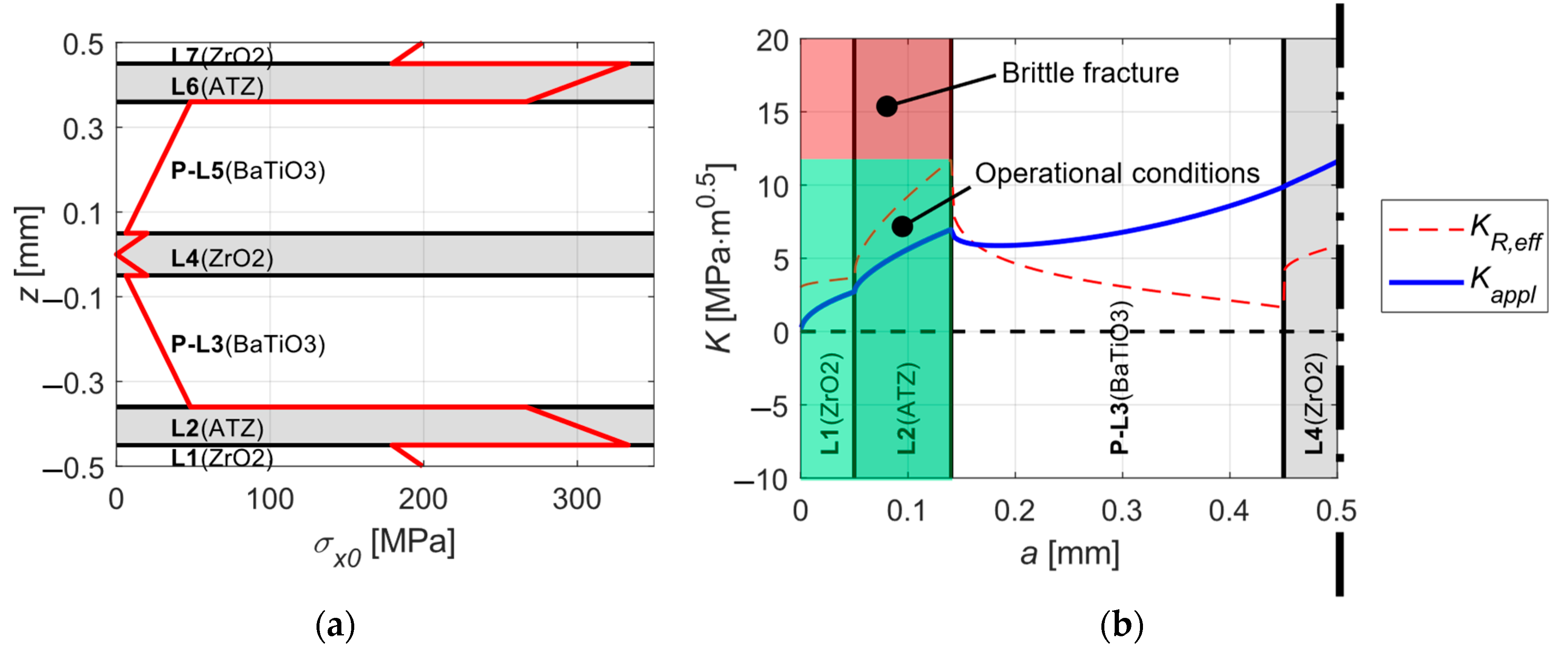
5. Simulation Results
6. Estimation of Critical Tip Displacement Amplitude
7. Discussion
7.1. Effect of the Protective Layers
7.2. PZT Solution vs. Proposed Lead-Free Design
7.3. Effect of the Auxiliary Magnets Producing Nonlinear Behaviour
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Caliò, R.; Rongala, U.; Camboni, D.; Milazzo, M.; Stefanini, C.; de Petris, G.; Oddo, C. Piezoelectric Energy Harvesting Solutions. Sensors 2014, 14, 4755–4790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bowen, C.R.; Kim, H.A.; Weaver, P.M.; Dunn, S. Piezoelectric and ferroelectric materials and structures for energy harvesting applications. Energy Environ. Sci. 2014, 7, 25. [Google Scholar] [CrossRef] [Green Version]
- Maurya, D.; Peddigari, M.; Kang, M.-G.; Geng, L.D.; Sharpes, N.; Annapureddy, V.; Palneedi, H.; Sriramdas, R.; Yan, Y.; Song, H.-C.; et al. Lead-free piezoelectric materials and composites for high power density energy harvesting. J. Mater. Res. 2018, 33, 2235–2263. [Google Scholar] [CrossRef] [Green Version]
- Tofel, P.; Machu, Z.; Chlup, Z.; Hadraba, H.; Drdlik, D.; Sevecek, O.; Majer, Z.; Holcman, V.; Hadas, Z. Novel layered architecture based on Al2O3/ZrO2/BaTiO3 for SMART piezoceramic electromechanical converters. Eur. Phys. J. Spec. Top. 2019, 228, 1575–1588. [Google Scholar] [CrossRef]
- Bai, Y.; Matousek, A.; Tofel, P.; Bijalwan, V.; Nan, B.; Hughes, H.; Button, T.W. (Ba,Ca)(Zr,Ti)O3 lead-free piezoelectric ceramics—The critical role of processing on properties. J. Eur. Ceram. Soc. 2015, 35, 3445–3456. [Google Scholar] [CrossRef]
- Sappati, K.K.; Bhadra, S. Piezoelectric polymer and paper substrates: A review. Sensors 2018, 18, 3605. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khaligh, A. Kinetic Energy Harvesting Using Piezoelectric and Electromagnetic Technologies—State of the Art. IEEE Trans. Ind. Electron. 2010, 57, 850–860. [Google Scholar] [CrossRef]
- Hadas, Z.; Smilek, J.; Rubes, O. Analyses of electromagnetic and piezoelectric systems for efficient vibration energy harvesting. In Proceedings of the Volume 10246, Smart Sensors, Actuators, and MEMS VIII, Barcelona, Spain, 8–10 May 2017; Fonseca, L., Prunnila, M., Peiner, E., Eds.; p. 1024619. [Google Scholar]
- Gljušćić, P.; Zelenika, S.; Blažević, D.; Kamenar, E. Kinetic energy harvesting for wearable medical sensors. Sensors 2019, 19, 4922. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Tofel, P.; Hadas, Z.; Smilek, J.; Losak, P.; Skarvada, P.; Macku, R. Investigation of a cantilever structured piezoelectric energy harvester used for wearable devices with random vibration input. Mech. Syst. Signal Process. 2018, 106, 303–318. [Google Scholar] [CrossRef] [Green Version]
- Qing, X.; Li, W.; Wang, Y.; Sun, H. Piezoelectric transducer-based structural health monitoring for aircraft applications. Sensors 2019, 19, 545. [Google Scholar] [CrossRef]
- Ambrosio, R.; Jimenez, A.; Mireles, J.; Moreno, M.; Monfil, K.; Heredia, H. Study of Piezoelectric Energy Harvesting System Based on PZT. Integr. Ferroelectr. 2011, 126, 77–86. [Google Scholar] [CrossRef]
- Rubes, O.; Brablc, M.; Hadas, Z. Verified nonlinear model of piezoelectric energy harvester. In Proceedings of the MATEC Web of Conferences, Wuhan, China, 10–12 November 2018; Volume 211. [Google Scholar]
- Sebald, G.; Kuwano, H.; Guyomar, D.; Ducharne, B. Experimental Duffing oscillator for broadband piezoelectric energy harvesting. Smart Mater. Struct. 2011, 20, 102001. [Google Scholar] [CrossRef]
- Litak, G.; Friswell, M.I.; Adhikari, S. Magnetopiezoelastic energy harvesting driven by random excitations. Appl. Phys. Lett. 2010, 96, 214103. [Google Scholar] [CrossRef]
- Rubes, O.; Hadas, Z. Designing, modelling and testing of vibration energy harvester with nonlinear stiffness. In Proceedings of the SPIE—The International Society for Optical Engineering, Anaheim, CA, USA, 9–13 April 2017; Volume 10246. [Google Scholar]
- Gao, Y.J.; Leng, Y.G.; Fan, S.B.; Lai, Z.H. Performance of bistable piezoelectric cantilever vibration energy harvesters with an elastic support external magnet. Smart Mater. Struct. 2014, 23, 095003. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Andò, B.; Baglio, S.; Trigona, C. Improved energy harvesting from wideband vibrations by nonlinear piezoelectric converters. Sensors Actuators A Phys. 2010, 162, 425–431. [Google Scholar] [CrossRef] [Green Version]
- Litak, G.; Friswell, M.I.; Adhikari, S. Regular and chaotic vibration in a piezoelectric energy harvester. Meccanica 2015, 51, 1017–1025. [Google Scholar] [CrossRef] [Green Version]
- Harne, R.L.; Wang, K.W. Prospects for Nonlinear Energy Harvesting Systems Designed Near the Elastic Stability Limit When Driven by Colored Noise. J. Vib. Acoust. 2014, 136, 021009. [Google Scholar] [CrossRef]
- Rubes, O.; Hadas, Z. Design and Simulation of Bistable Piezoceramic Cantilever for Energy Harvesting from Slow Swinging Movement. In Proceedings of the—2018 IEEE 18th International Conference on Power Electronics and Motion Control, PEMC 2018, Budapest, Hungary, 26–30 August 2018; pp. 663–668. [Google Scholar]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102–254105. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, W.; Zuo, M.; Tan, H.; Fan, H.; Mao, Q.; Wan, X. An arc-shaped piezoelectric bistable vibration energy harvester: Modeling and experiments. Sensors 2018, 18, 4472. [Google Scholar] [CrossRef] [Green Version]
- Majer, Z.; Ševeček, O.; Machů, Z.; Štegnerová, K.; Kotoul, M. Optimization of Design Parameters of Fracture Resistant Piezoelectric Vibration Energy Harvester; Trans Tech Publications Ltd.: Schwiz, Switzerland, 2018; Volume 774, ISBN 9783035713503. [Google Scholar]
- SGLAVO, V.; BERTOLDI, M. Design and production of ceramic laminates with high mechanical resistance and reliability. Acta Mater. 2006, 54, 4929–4937. [Google Scholar] [CrossRef]
- Maca, K.; Pouchly, V.; Drdlik, D.; Hadraba, H.; Chlup, Z. Dilatometric study of anisotropic sintering of alumina/zirconia laminates with controlled fracture behaviour. J. Eur. Ceram. Soc. 2017, 37, 4287–4295. [Google Scholar] [CrossRef]
- Chang, Y.; Bermejo, R.; Ševeček, O.; Messing, G.L. Design of alumina-zirconia composites with spatially tailored strength and toughness. J. Eur. Ceram. Soc. 2015, 35, 631–640. [Google Scholar] [CrossRef]
- Bermejo, M.R. Structural Integrity of Alumina-Zirconia Multilayered Ceramics. Ph.D. Thesis, Universitat Politecnica de Catalunya, Barcelona, Spain, 2006. [Google Scholar]
- MatWeb BaTiO3 Datasheet. 2019. Available online: http://www.matweb.com/search/datasheet.aspx?matguid=216d8486b52746f88d8aad6f667720a0&ckck=1 (accessed on 1 June 2019).
- Fett, T.; Diegele, E.; Munz, D.; Rizzi, G. Weight functions for edge cracks in thin surface layers. Int. J. Fract. 1996, 81, 205–215. [Google Scholar] [CrossRef]
- Bueckner, H.F. Novel principle for the computation of stress intensity factors. Z. Fuer Angew. Math. Mech. 1970, 50, 529. [Google Scholar]
- Sestakova, L.; Bermejo, R.; Chlup, Z.; Danzer, R. Strategies for fracture toughness, strength and reliability optimisation of ceramic-ceramic laminates. Int. J. Mater. Res. 2011, 102, 613–626. [Google Scholar] [CrossRef]
- Fett, T.; Munz, D.; Yang, Y.Y. Applicability of the extended Petroski–Achenbach weight function procedure to graded materials. Eng. Fract. Mech. 2000, 65, 393–403. [Google Scholar] [CrossRef]
- Ševeček, O.; Kotoul, M.; Leguillon, D.; Martin, E.; Bermejo, R. Understanding the edge crack phenomenon in ceramic laminates. Frat. Integrita Strutt. 2015, 9, 362–370. [Google Scholar]
- Erturk, A. Electromechanical Modeling of Piezoelectric Energy Harvesters; Virginia Tech: Blacksburg, VA, USA, 2009. [Google Scholar]
- Rubes, O.; Brablc, M.; Hadas, Z. Nonlinear vibration energy harvester: Design and oscillating stability analyses. Mech. Syst. Signal Process. 2018, 125, 170–184. [Google Scholar] [CrossRef]
- Rubes, O.; Brablc, M.; Hadas, Z. Verified Nonlinear Model of Piezoelectric Energy Harvester. In Proceedings of the VETOMAC 2018, Lisbon, Portugal, 10–13 September 2018. [Google Scholar]
- Hadraba, H.; Chlup, Z.; Drdlík, D.; Šiška, F. Characterisation of mechanical and fracture behaviour of Al2O3/ZrO2/BaTiO3 laminate by indentation. J. Eur. Ceram. Soc. 2020, 40, 4799–4807. [Google Scholar] [CrossRef]
- Drdlik, D.; Chlup, Z.; Hadraba, H.; Drdlikova, K. Surface roughness improvement of near net shaped alumina by EPD. J. Aust. Ceram. Soc. 2020, 56, 721–727. [Google Scholar] [CrossRef]










| Material | ρ (kg/m3) | E (GPa) | ν (–) | α (ppm/K) | Kc,0 (MPa·m0.5) | d31 (C/N) | (–) | |
|---|---|---|---|---|---|---|---|---|
 | ATZ | 4050 | 390 | 0.22 | 9.8 | 3.2 | – | – |
 | ZrO2 | 5680 | 210 | 0.31 | 10.3 | 3 | – | – |
 | BaTiO3 | 6020 | 70 | 0.22 | 11.5 | 0.7 | –58·10-12 | 1250 |
| meff (g) | beff (Ns/m) | keff (N/m) | macc (g) | Cp (nF) | θ (μN/V) | Rl (kΩ) |
|---|---|---|---|---|---|---|
| 6.3 | 3.75·10-2 | 555.8 | 7.1 | 75.6 | 245 | 45 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubes, O.; Machu, Z.; Sevecek, O.; Hadas, Z. Crack Protective Layered Architecture of Lead-Free Piezoelectric Energy Harvester in Bistable Configuration. Sensors 2020, 20, 5808. https://doi.org/10.3390/s20205808
Rubes O, Machu Z, Sevecek O, Hadas Z. Crack Protective Layered Architecture of Lead-Free Piezoelectric Energy Harvester in Bistable Configuration. Sensors. 2020; 20(20):5808. https://doi.org/10.3390/s20205808
Chicago/Turabian StyleRubes, Ondrej, Zdenek Machu, Oldrich Sevecek, and Zdenek Hadas. 2020. "Crack Protective Layered Architecture of Lead-Free Piezoelectric Energy Harvester in Bistable Configuration" Sensors 20, no. 20: 5808. https://doi.org/10.3390/s20205808
APA StyleRubes, O., Machu, Z., Sevecek, O., & Hadas, Z. (2020). Crack Protective Layered Architecture of Lead-Free Piezoelectric Energy Harvester in Bistable Configuration. Sensors, 20(20), 5808. https://doi.org/10.3390/s20205808







