Twelve-Year Analysis of NO2 Concentration Measurements at Belisario Station (Quito, Ecuador) Using Statistical Inference Techniques
Abstract
1. Introduction
- (1)
- Group the NO2 concentration measurements, taken from 1 January 2008 to 31 December 2019 at Belisario station, in sets of variables that represent the years, months, days of the week, and hours of the day.
- (2)
- Obtain estimates of the central tendency of the data and their dispersion, using classic, nonparametric, resampling, and robust methods.
- (3)
- Categorize the data and find confidence intervals that allow quantifying the differences between categories.
- (4)
- Find periodic behaviors in the variables.
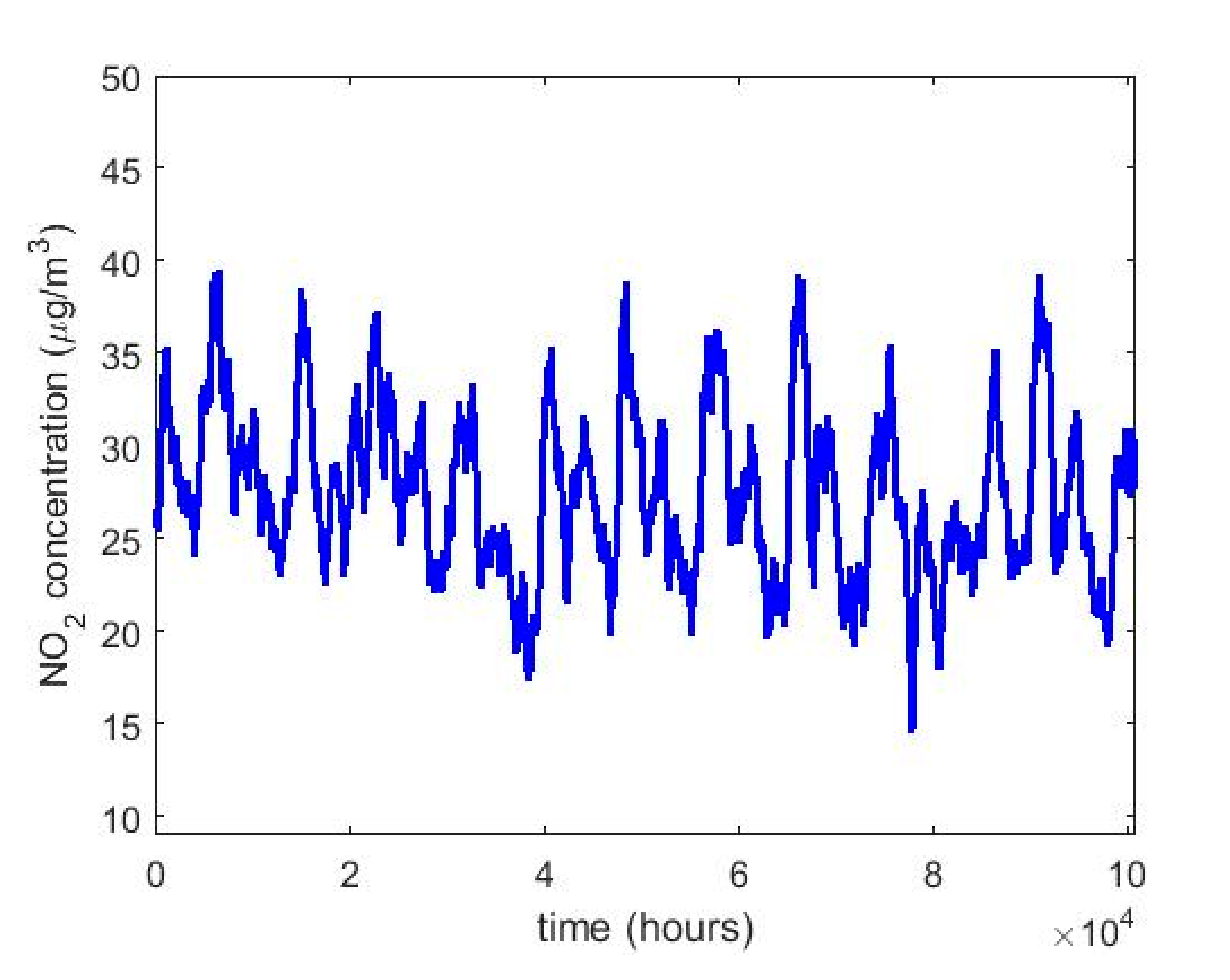
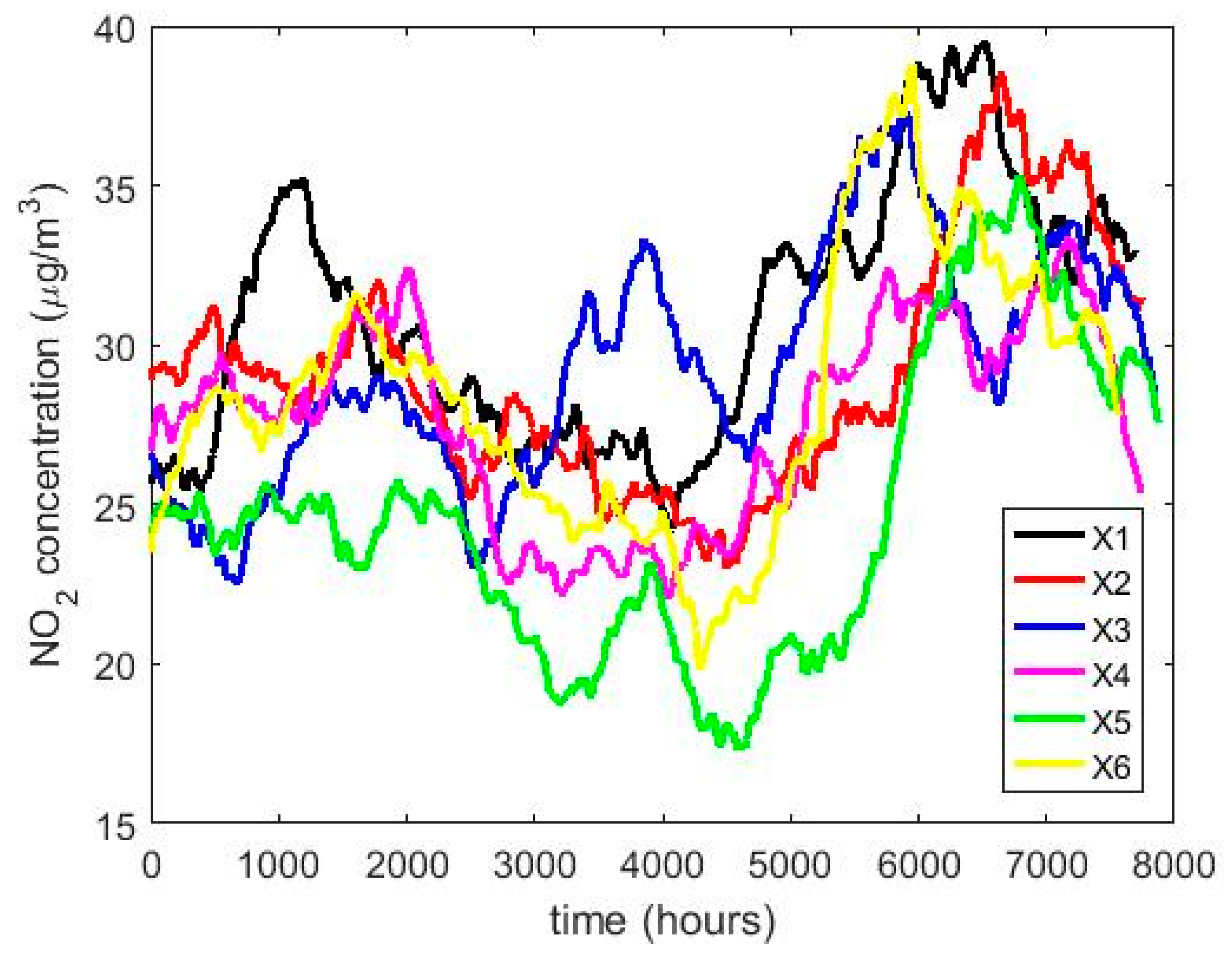
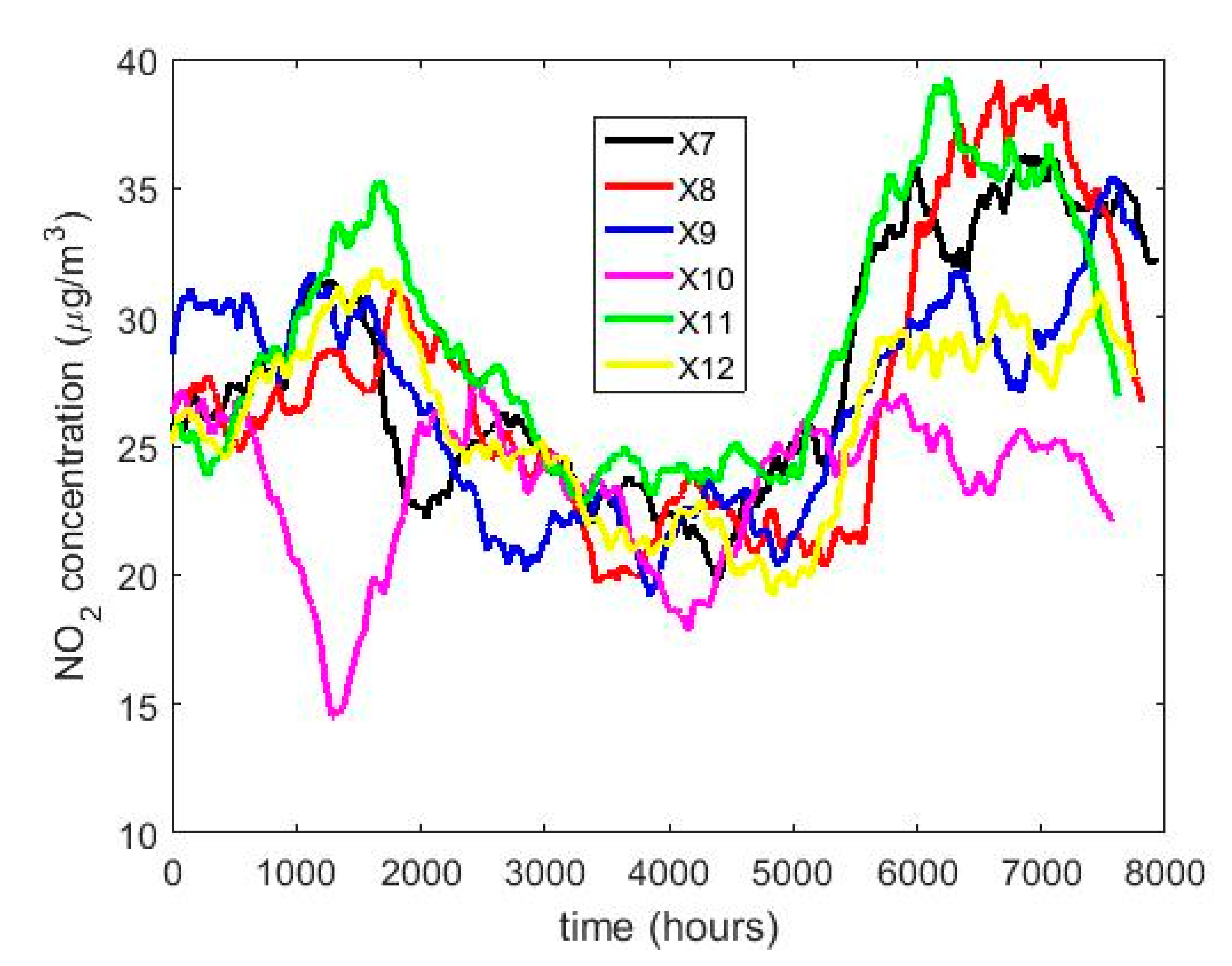
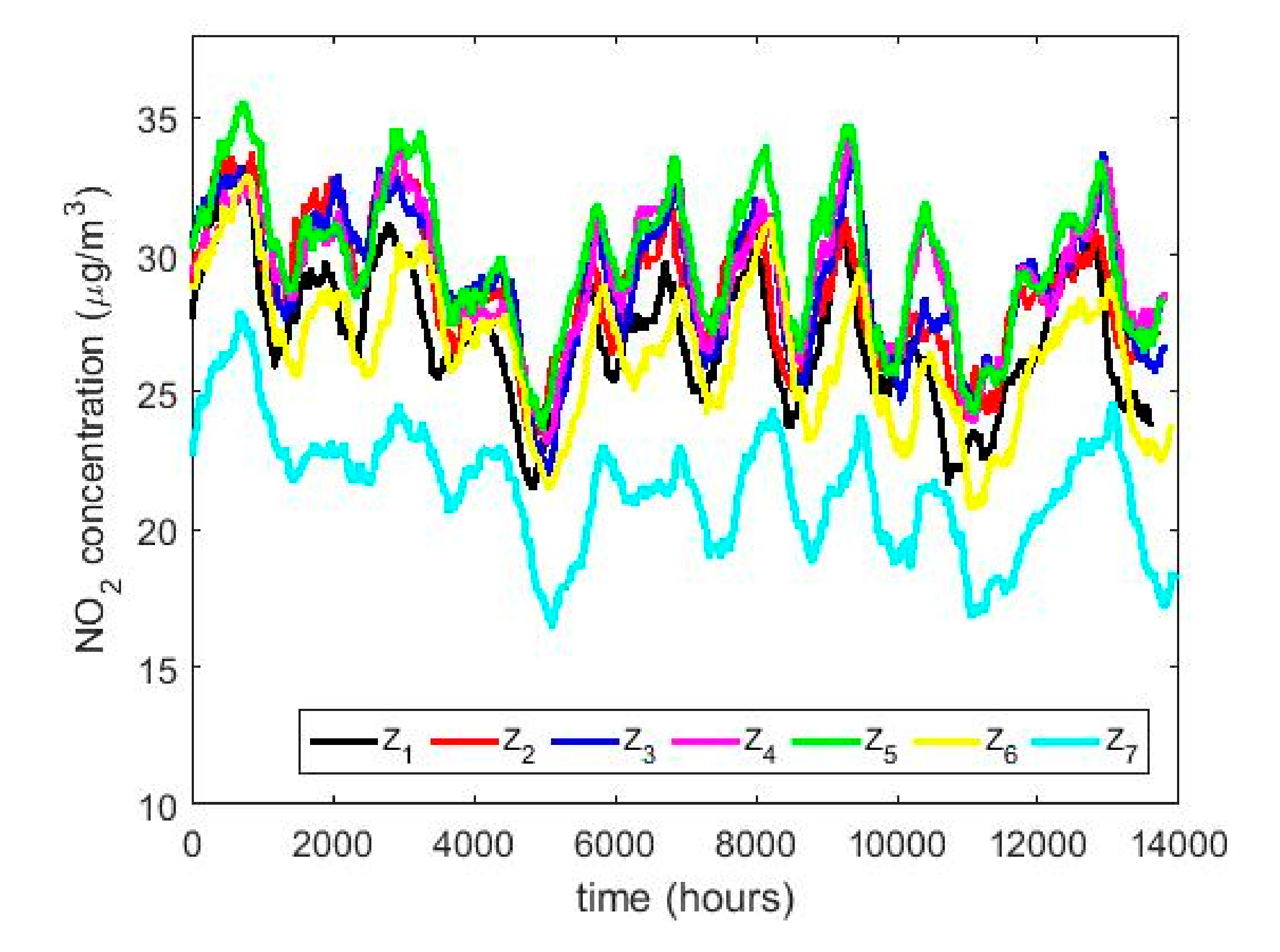
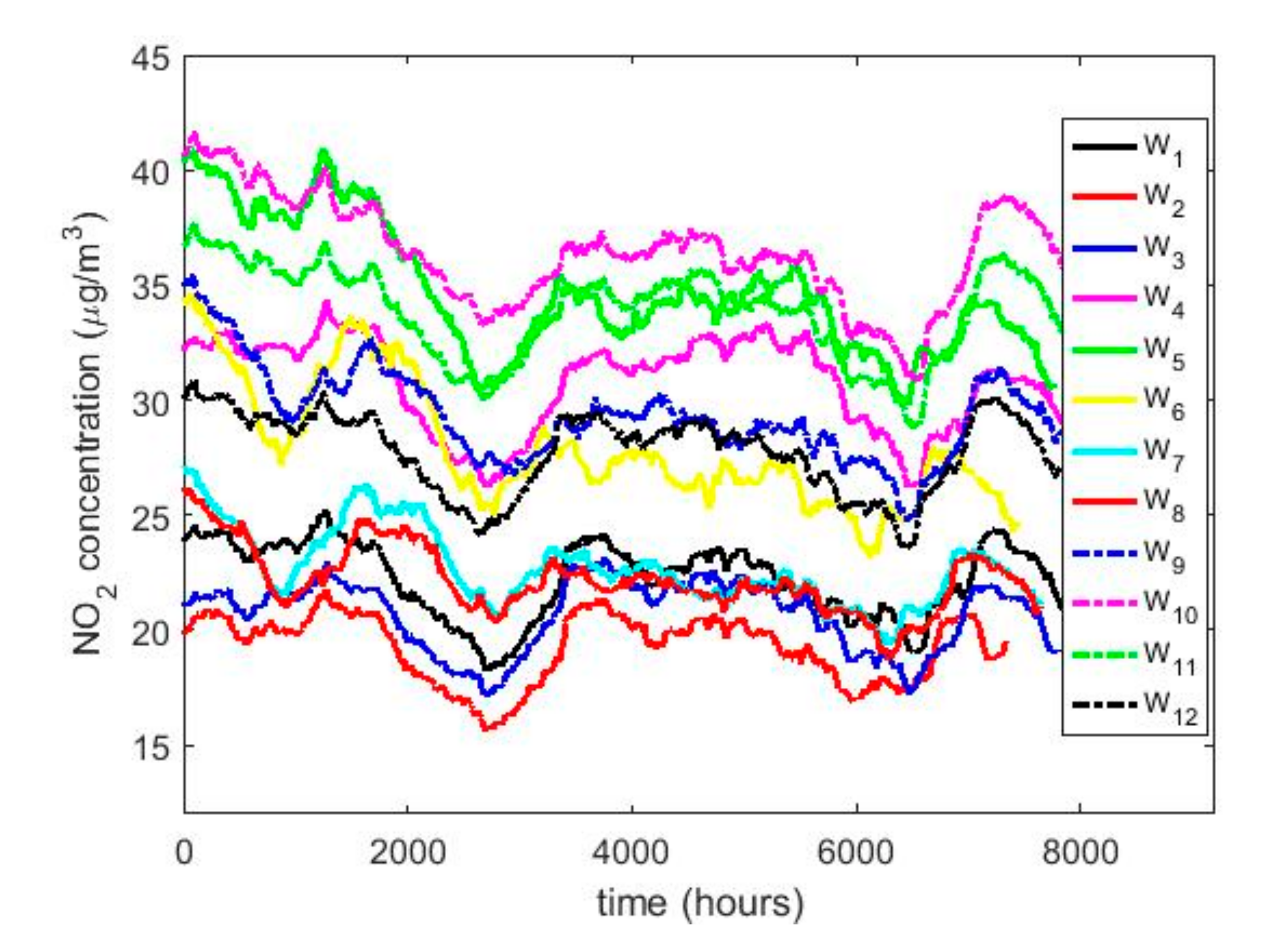
2. Summary Statistics of 12 Years of NO2 Concentration Measurements at Belisario Station
- , , stands for the set of samples collected in year .
- , , stands for the set of samples collected in the k-th month of the year.
- , , stands for the set of samples collected on the k-th day of the week.
- , , stands for the set of samples collected at each of the 24 h of the day but with hours in groups of 2 h.
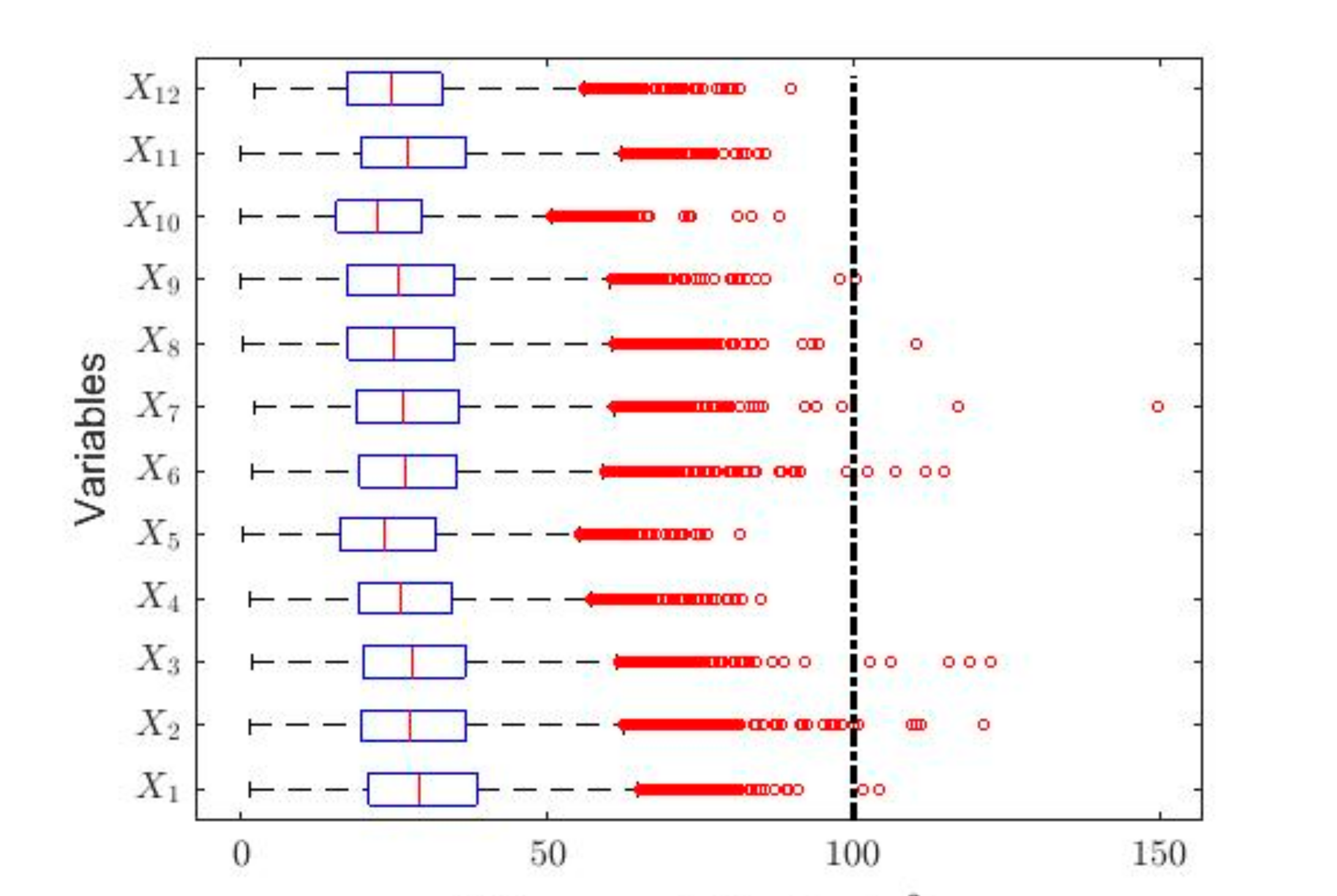
3. Analysis of NO2 Concentration Measurements Using Nonparametric Methods
4. Robust Analysis of the NO2 Concentration Measurements
4.1. Estimators of Central Tendency and Scale
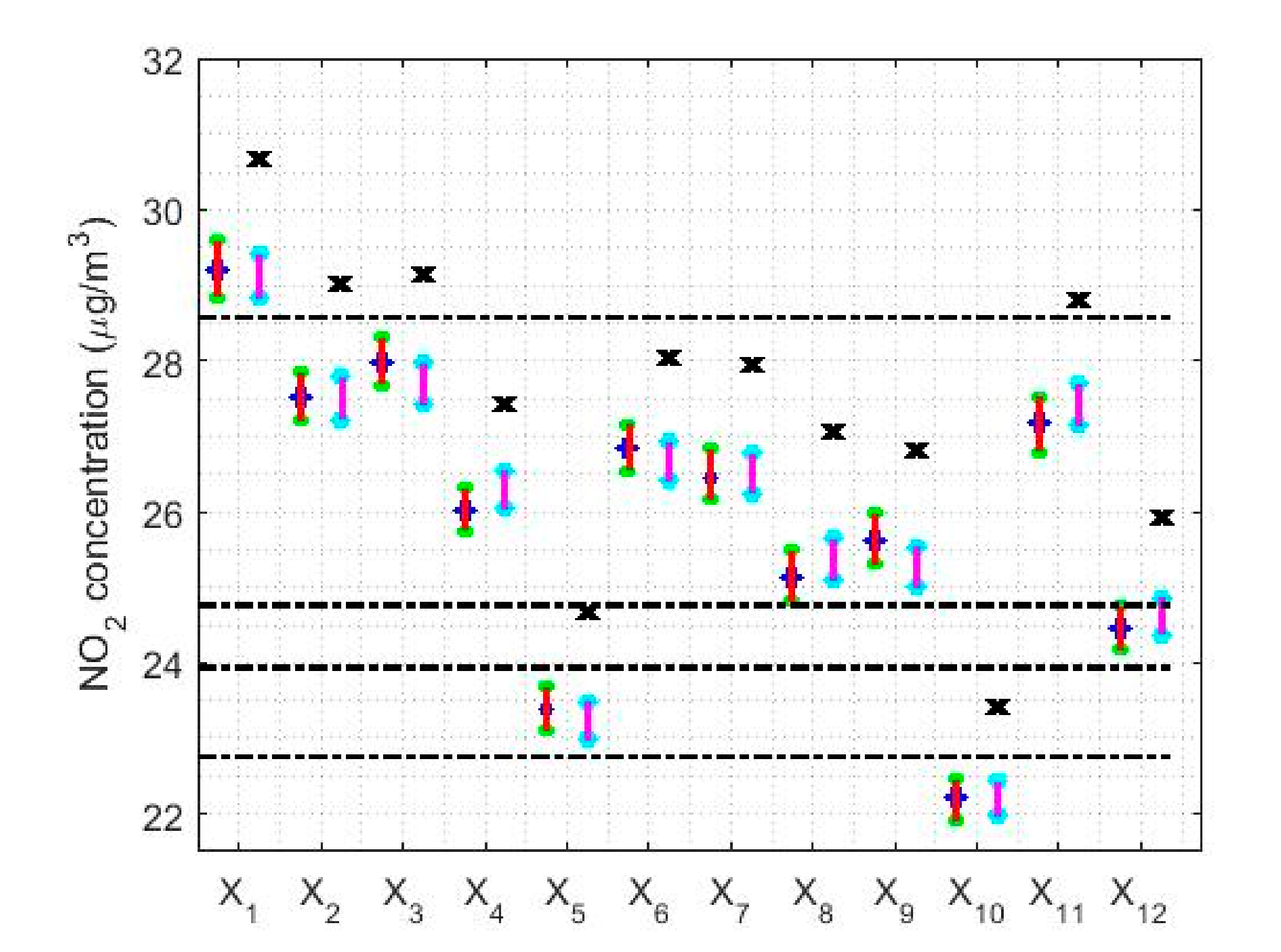
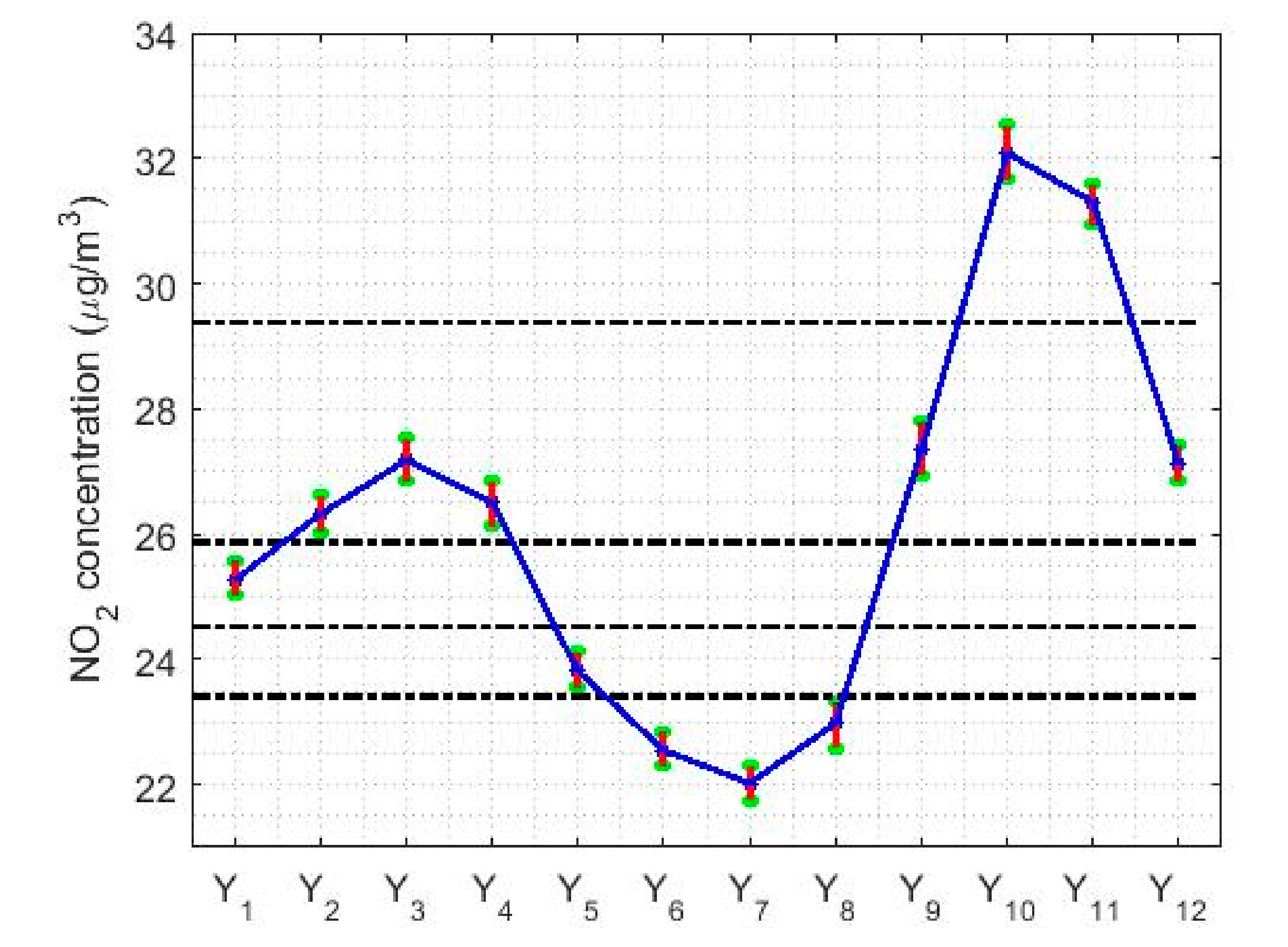
4.2. Confidence Intervals
- , where stands for the mean.
- , where stands for the median.
- , where stands for the interquartile range.
- .
- .
- .
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brown, T.L.; LeMay, H.E., Jr.; Bursten, B.E.; Murphy, C.J.; Woodward, P.M.; Stoltzfus, M.W.; Lufaso, M.W. Chemestry: The Central Science, 14th ed.; Pearson Education Limited: London, UK, 2018. [Google Scholar]
- Centers for Disease Control and Prevention. The National Institute for Occupational Safety and Health (NIOSH). Nitrogen Dioxide. Available online: https://www.cdc.gov/niosh/npg/npgd0454.html (accessed on 31 August 2020).
- Utell, M.J.; Frampton, M.W.; Roberts, N.J., Jr.; Finkelstein, J.N.; Cox, C.; Morrow, P.E. Mechanisms of Nitrogen Dioxide Toxicity in Humans; Research Report Number 43; Health Effect Institute: Monpelier, VT, USA, 1991. [Google Scholar]
- Hernandez, W.; Mendez, A.; Diaz-Marquez, A.M.; Zalakeviciute, R. Robust Analysis of PM2.5 Concentration Measurements in the Ecuadorian Park La Carolina. Sensors 2019, 19, 4648. [Google Scholar] [CrossRef]
- Hernandez, W.; Mendez, A.; Zalakeviciute, R.; Diaz-Marquez, A.M. Robust Confidence Intervals for PM2.5 Concentration Measurements in the Ecuadorian Park La Carolina. Sensors 2020, 20, 654. [Google Scholar] [CrossRef]
- Delgado-Saborit, J.M. Validación e Implementación de Técnicas de Captación Pasiva Para el Estudio de los Niveles y Efectos de Ozono Troposférico y Dióxido de Nitrógeno en un Área Costera Mediterránea. Ph.D. Thesis, Universitat Jaume I, Castelló, Spain, 2005. [Google Scholar]
- WHO Air Quality Guidelines for Particulate Matter, Ozone, Nitrogen Dioxide and Sulfur Dioxide. Global Update 2005. Summary of Risk Assessment. Available online: https://apps.who.int/iris/bitstream/handle/10665/69477/WHO_SDE_PHE_OEH_06.02_eng.pdf?sequence=1&isAllowed=y (accessed on 31 August 2020).
- Díaz, V. “Informe Calidad del Aire 2017,” Secretaría de Ambiente del Distrito Metropolitano de Quito. Available online: http://www.quitoambiente.gob.ec/ambiente/index.php/informes#informecalidad-del-aire-017 (accessed on 26 March 2020).
- Belisario, Quito Air Pollution: Real-time Air Quality Index (AQI). Available online: https://aqicn.org/city/ecuador/quito/belisario/www.quitoambiente.gob.ec (accessed on 6 October 2020).
- Datos Históricos REMMAQ Descarga 2004–2020. Available online: http://www.quitoambiente.gob.ec/ambiente/index.php/descarga-datos-historicos (accessed on 9 October 2020).
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference, 5th ed.; Chapman & Hall/CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2011. [Google Scholar]
- Hoaglin, D.C.; Mosteller, F.; Tukey, J.W. Understanding Robust and Exploratory Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Maronna, R.A.; Martin, R.D.; Yohai, V.J. Robust Statistics: Theory and Methods; John Wiley & Sons: Chichester, UK, 2006. [Google Scholar]
- Wilcox, R. Introduction to Robust Estimation and Hypothesis Testing, 3rd ed.; Academic Press: Waltham, MA, USA, 2012. [Google Scholar]
- Reece, S.; Williams, R.; Colón, M.; Southgate, D.; Huertas, E.; O’Shea, M.; Iglesias, A.; Sheridan, P. Spatial-Temporal Analysis of PM2.5 and NO2 Concentrations Collected Using Low-Cost Sensors in Peñuelas, Puerto Rico. Sensors 2018, 18, 4314. [Google Scholar] [CrossRef] [PubMed]
- Arnaudo, E.; Farasin, A.; Rossi, C. A Comparative Analysis for Air Quality Estimation from Traffic and Meteorological Data. Appl. Sci. 2020, 10, 4587. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Tan, X.; Fang, C. Analysis of NOx Pollution Characteristics in the Atmospheric Environment in Changchun City. Atmosphere 2020, 11, 30. [Google Scholar] [CrossRef]
- Kadiyala, A.; Kumar, A. An Examination of the Sensitivity of Sulfur Dioxide, Nitric Oxide, and Nitrogen Dioxide Concentrations to the Important Factors Affecting Air Quality Inside a Public Transportation Bus. Atmosphere 2012, 3, 266–287. [Google Scholar] [CrossRef]
- Hernandez, W.; Mendez, A.; González-Posadas, V.; Jiménez-Martín, J.L. Robust Analysis of the Information Obtained from a Set of 12 Years of SO2 Concentration Measurements. IEEE Access 2020, 8, 144976–144992. [Google Scholar] [CrossRef]
- Hernandez, W.; Mendez, A.M. Robust Estimation of Carbon Monoxide Measurements. Sensors 2020, 20, 4958. [Google Scholar] [CrossRef]
- Cavaliere, A.; Carotenuto, F.; Di Gennaro, F.; Gioli, B.; Gualtieri, G.; Martelli, F.; Matese, A.; Toscano, P.; Vagnoli, C.; Zaldei, A. Development of Low-Cost Air Quality Stations for Next Generation Monitoring Networks: Calibration and Validation of PM2.5 and PM10 Sensors. Sensors 2018, 18, 2843. [Google Scholar] [CrossRef]
- Rodríguez-Martín, M.; Rodríguez-Gonzálvez, P. Suitability of Automatic Photogrammetric Reconstruction Configurations for Small Archeological Remains. Sensors 2020, 20, 2936. [Google Scholar] [CrossRef]
- Lun Fung, P.; Zaidan, M.A.; Sillanpää, S.; Kousa, A.; Niemi, J.V.; Timonen, H.; Kuula, J.; Saukko, E.; Luoma, K.; Petäjä, T.; et al. Input-Adaptive Proxy for Black Carbon as a Virtual Sensor. Sensors 2020, 20, 182. [Google Scholar] [CrossRef] [PubMed]
- Hernandez, W.; Mendez, A.; Diaz-Marquez, A.M.; Zalakeviciute, R. PM2.5 concentration measurement analysis by using nonparametric statistical inference. IEEE Sens. J. 2020, 20, 1084–1094. [Google Scholar] [CrossRef]
- Hernandez, W.; Mendez, A.; Zalakeviciute, R.; Diaz-Marquez, A.M. Analysis of the information obtained from PM2.5 concentration measurements in an urban park. IEEE Trans. Instrum. Meas. 2020, 69, 6296–6311. [Google Scholar] [CrossRef]
- Mukherjee, A.; Brown, S.G.; McCarthy, M.C.; Pavlovic, N.R.; Stanton, L.G.; Lam Snyder, J.; D′Andrea, S.; Hafner, H.R. Measuring spatial and temporal PM2.5 variations in Sacramento, California, communities using a network of low-cost sensors. Sensors 2019, 19, 4701. [Google Scholar] [CrossRef]
- Borghi, F.; Spinazzè, A.; Campagnolo, D.; Rovelli, S.; Cattaneo, A.; Cavallo, D.M. Precision and accuracy of a direct-reading miniaturized monitor in PM2.5 exposure assessment. Sensors 2018, 18, 3089. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Van der A, R.J.; Stammes, P.; Wang, W.; Zhang, P.; Lu, N.; Fang, L. Carbon dioxide retrieval from TanSat observations and validation with TCCON measurements. Remote Sens. 2020, 12, 2204. [Google Scholar] [CrossRef]
- Shokr, M.; El-Tahan, M.; Ibrahim, A.; Steiner, A.; Gad, N. Long-term, high-resolution survey of atmospheric aerosols over egypt with NASA’s MODIS data. Remote Sens. 2017, 9, 1027. [Google Scholar] [CrossRef]
- Baire, M.; Melis, A.; Lodi, M.B.; Tuveri, P.; Dachena, C.; Simone, M.; Fanti, A.; Fumera, G.; Pisanu, T.; Mazzarella, G. A wireless sensors network for monitoring the carasau bread manufacturing process. Electronics 2019, 8, 1541. [Google Scholar] [CrossRef]
- Tang, C.-S.; Wu, T.-Y.; Chuang, K.-J.; Chang, T.-Y.; Chuang, H.-C.; Candice Lung, S.-C.; Chang, L.-T. Impacts of in-cabin exposure to size-fractionated particulate matters and carbon monoxide on changes in heart rate variability for healthy public transit commuters. Atmosphere 2019, 10, 409. [Google Scholar] [CrossRef]
- Model 42C NO-NO2-NOx Analyzer. Available online: http://www.thermo.com.cn/Resources/200802/productPDF_20998.pdf (accessed on 28 July 2020).
- Model 42i NO-NO2-NOx Analyzer. Available online: https://www.thermofisher.com/order/catalog/product/42I#/42I (accessed on 28 July 2020).
- U.S. Environmental Protection Agency. List of Designated Reference and Equivalent Methods; United States Environmental Protection Agency: Washington, DC, USA, 2020. [Google Scholar]
- EPA-454/B-17-001. Ambient Air Quality Monitoring Program. Quality Assurance Handbook for Air Pollution Measurement Systems; Environmental Protection Agency: Washington, DC, USA, 2017; Volume 2. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 5th ed.; Jhon Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bryson, M.C. Heavy-Tailed Distributions: Properties and Tests. Technometrics 1974, 16, 61–68. [Google Scholar] [CrossRef]
- Papoulis, A.; Unnikrishna Pillai, S. Probability, Random Variables, and Stochastic Processes, 4th ed.; McGraw-Hill Higher Education: New York, NY, USA, 2002. [Google Scholar]
- Hampel, F.R. The Influence Curve and its Role in Robust Estimation. J. Am. Stat. Assoc. 1974, 69, 383–393. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Rock, N.M.S. ROBUST: An Interactive FORTRAN-77 Package for Exploratory Data Analysis Using Parametric, Robust and Nonparametric Location and Scale Estimates, Data Transformations, Normality Tests, and Outlier Assessment. Comput. Geosci. 1987, 13, 463–494. [Google Scholar] [CrossRef]
- Croux, C.; Rouseeuw, P.J. A Class of High-Breakdown Scale Estimators Based on Subranges. Commun. Stat. Theory Methods 1992, 21, 1935–1951. [Google Scholar] [CrossRef]
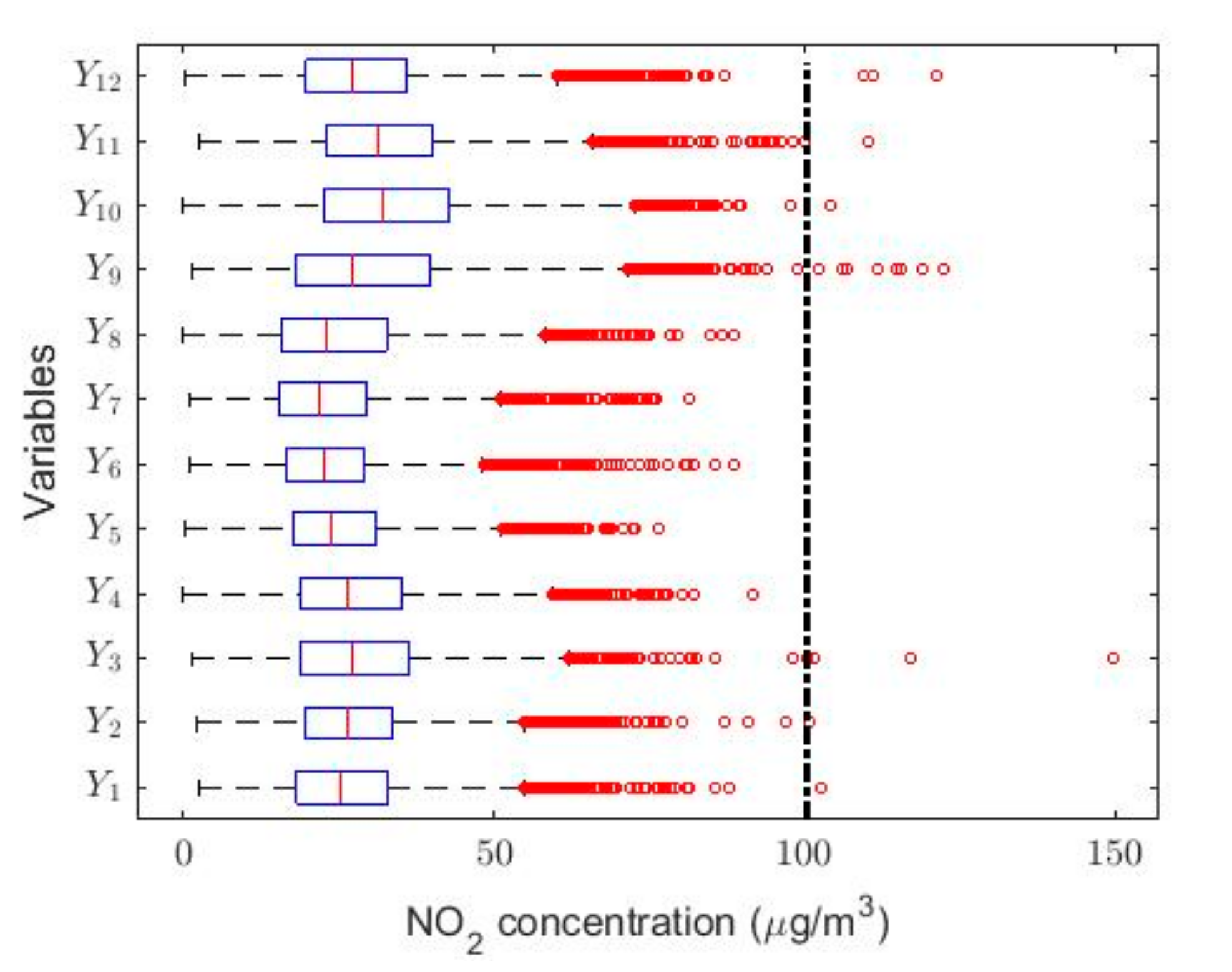
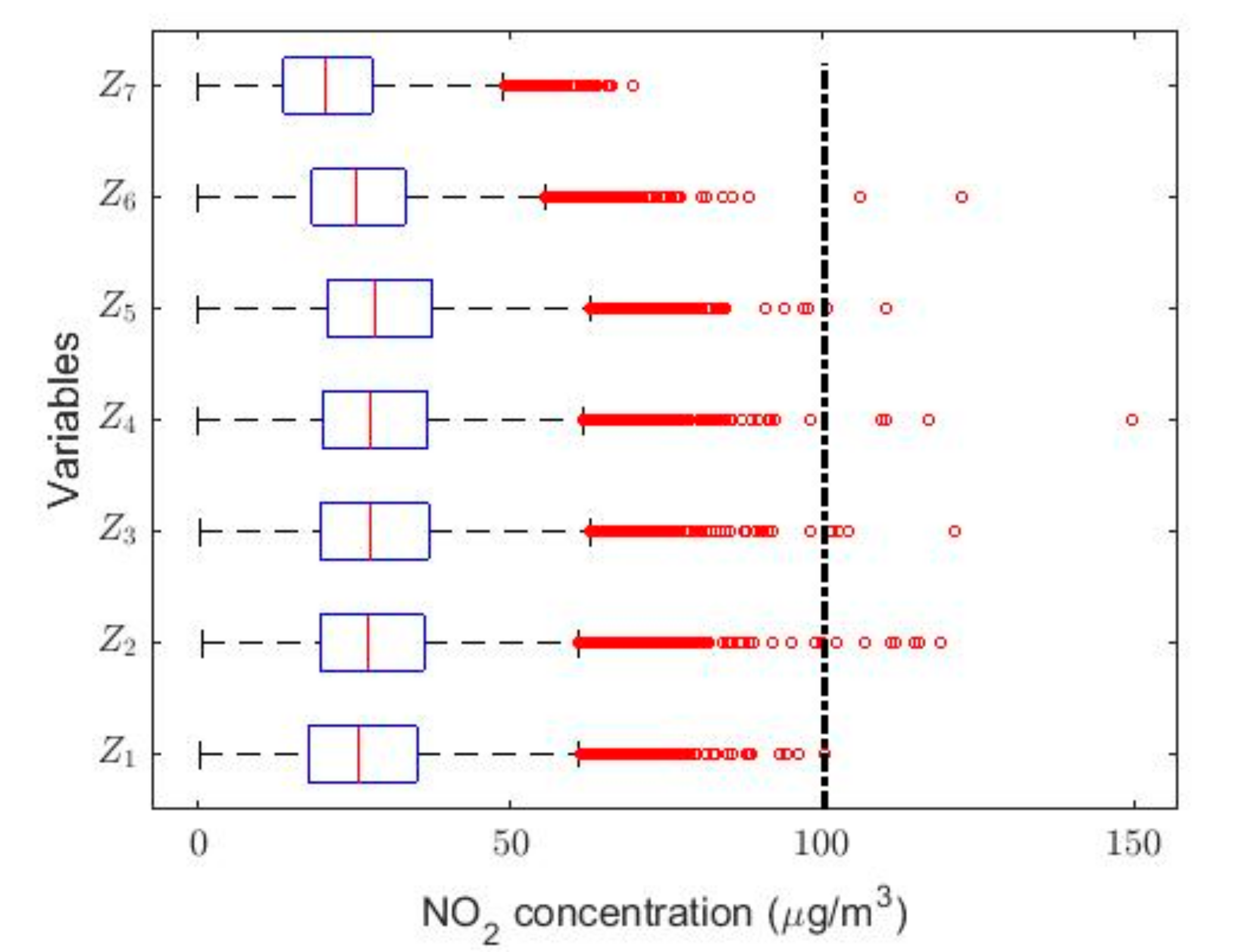
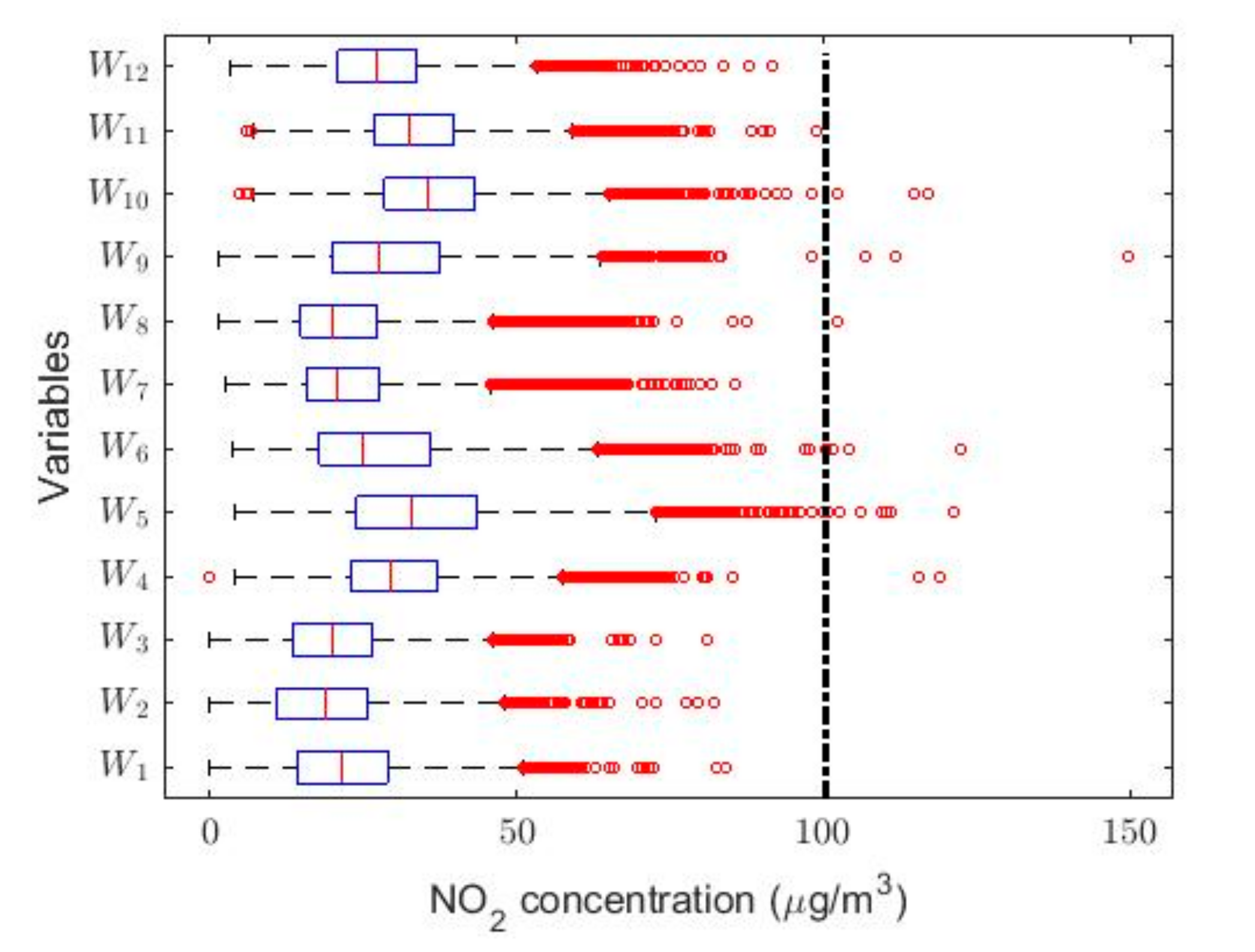
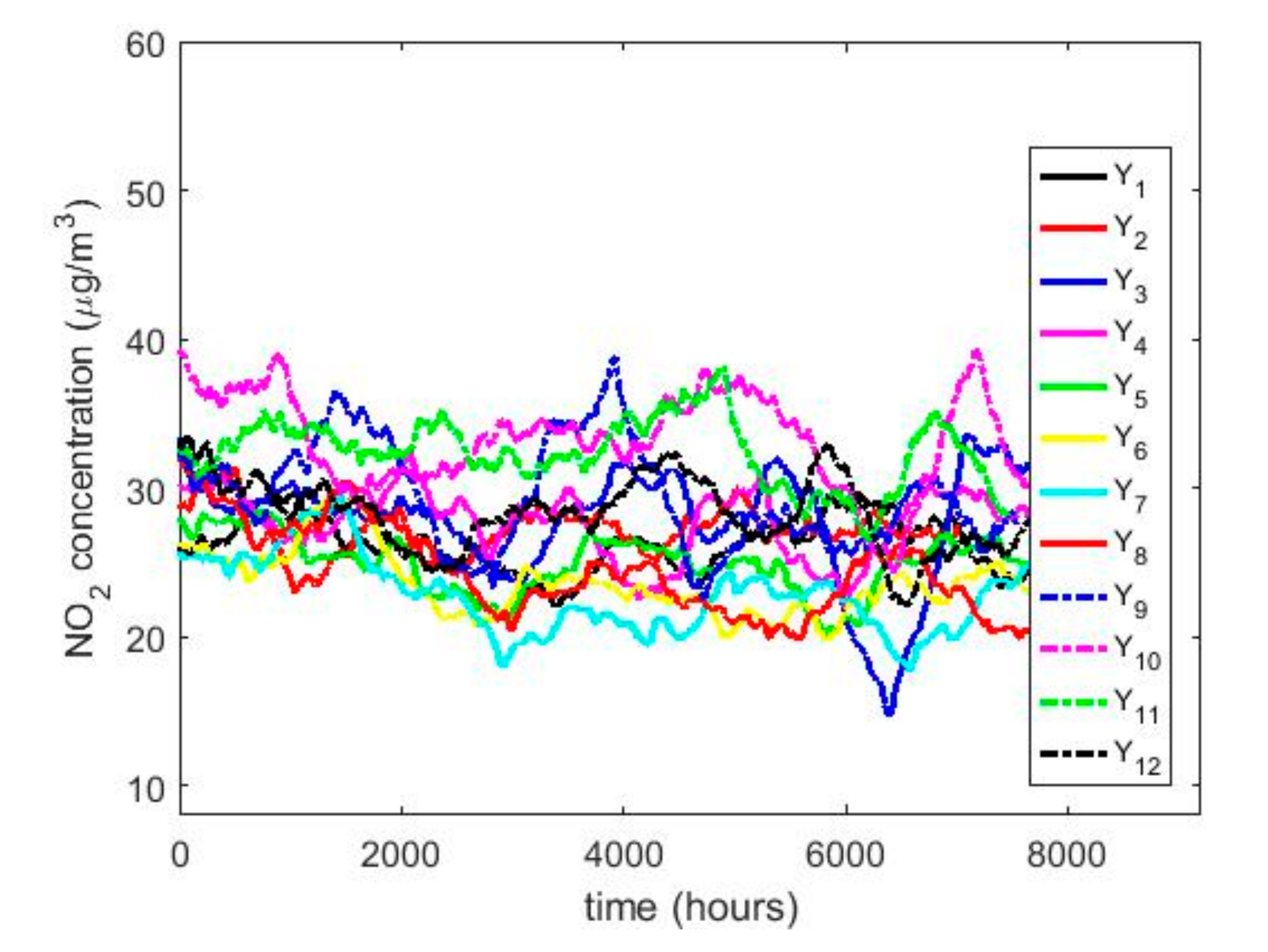
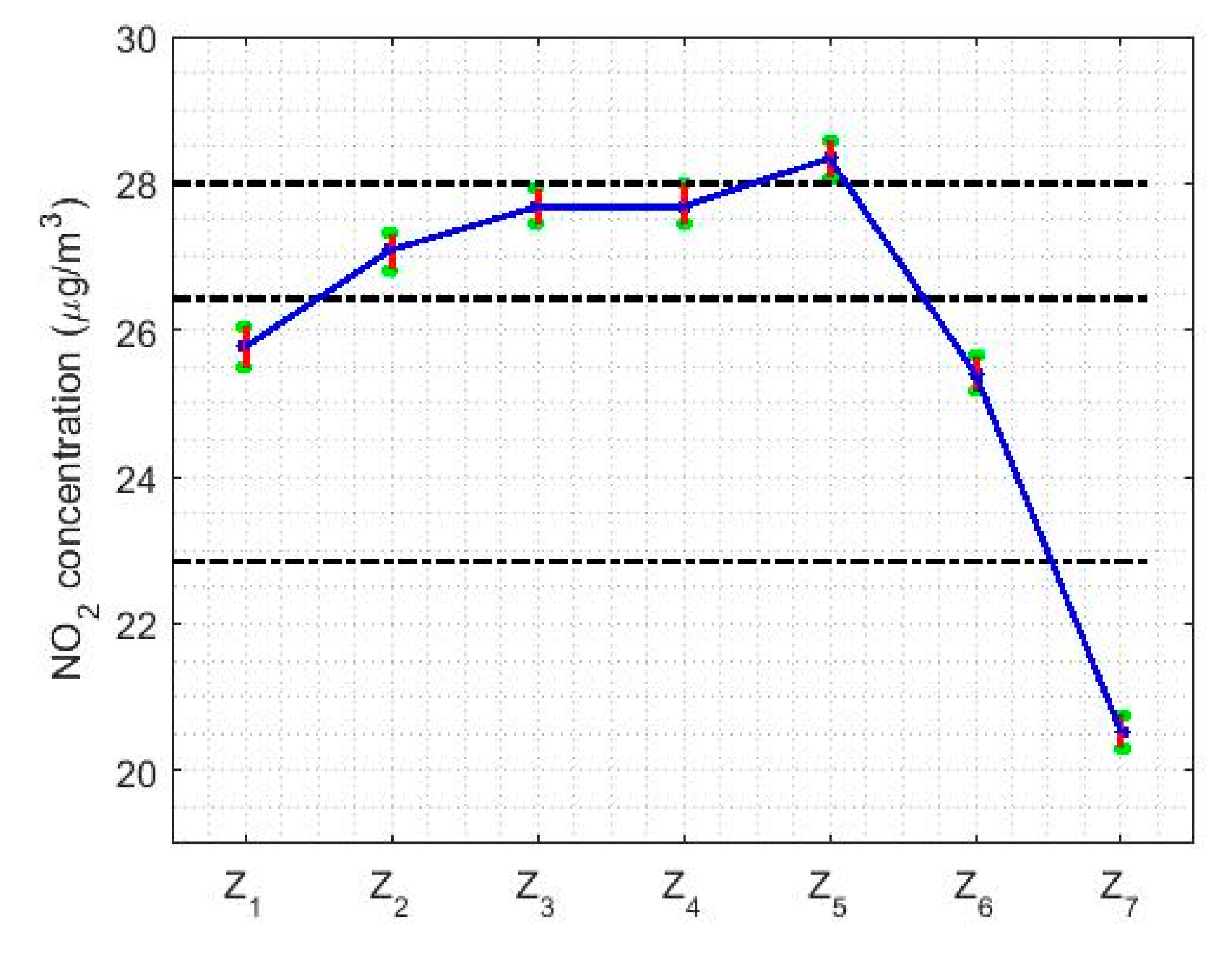
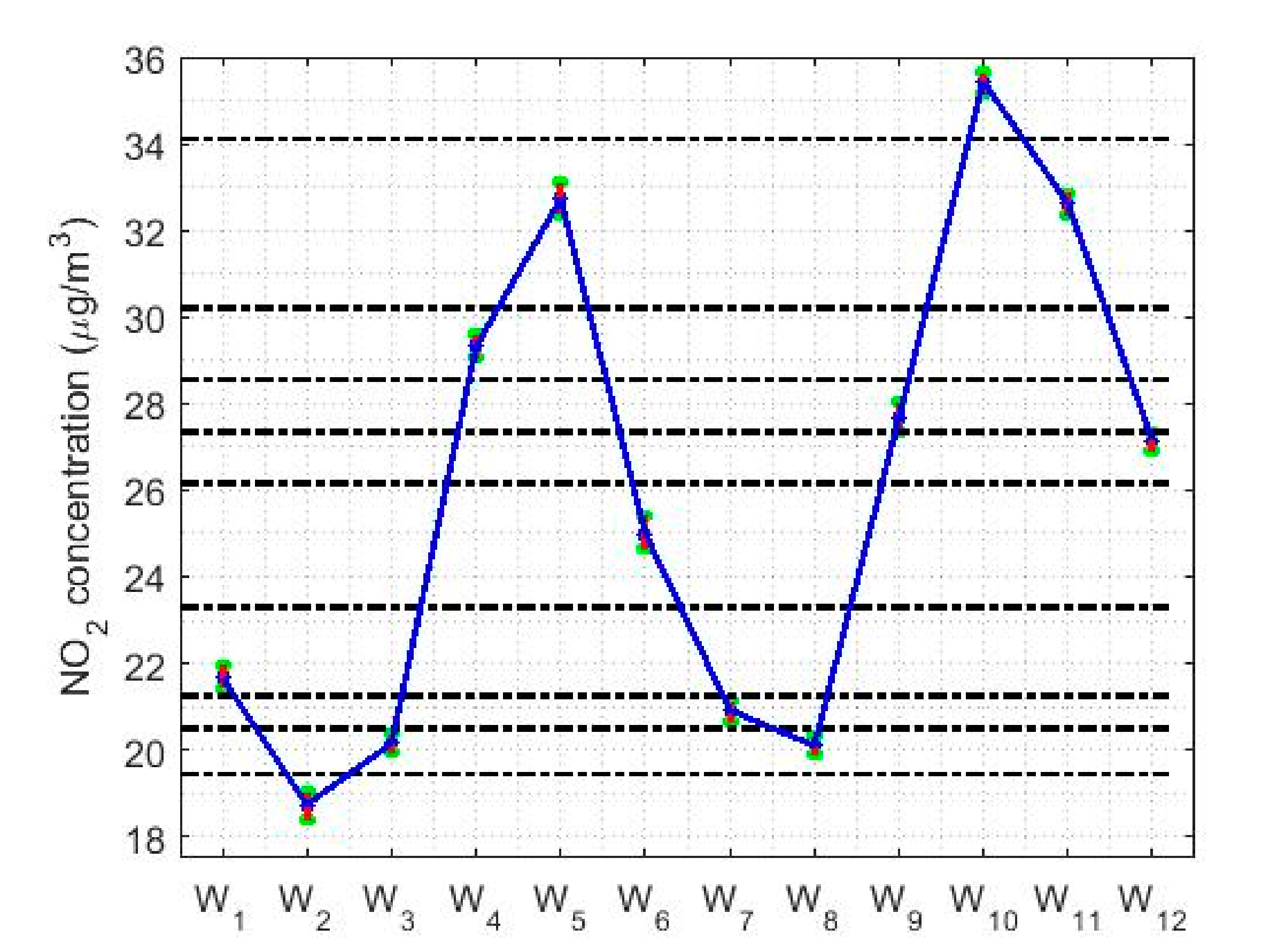
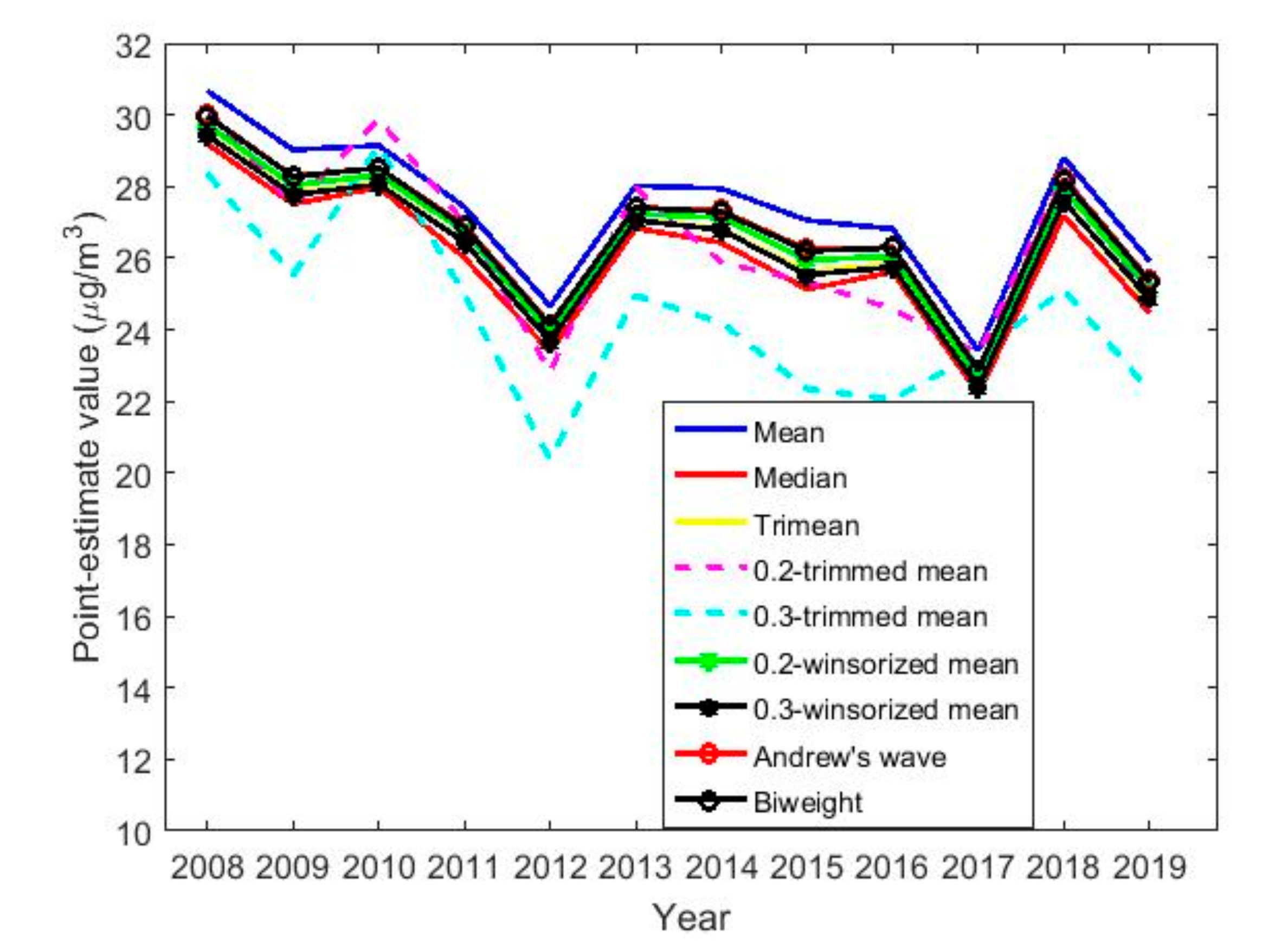
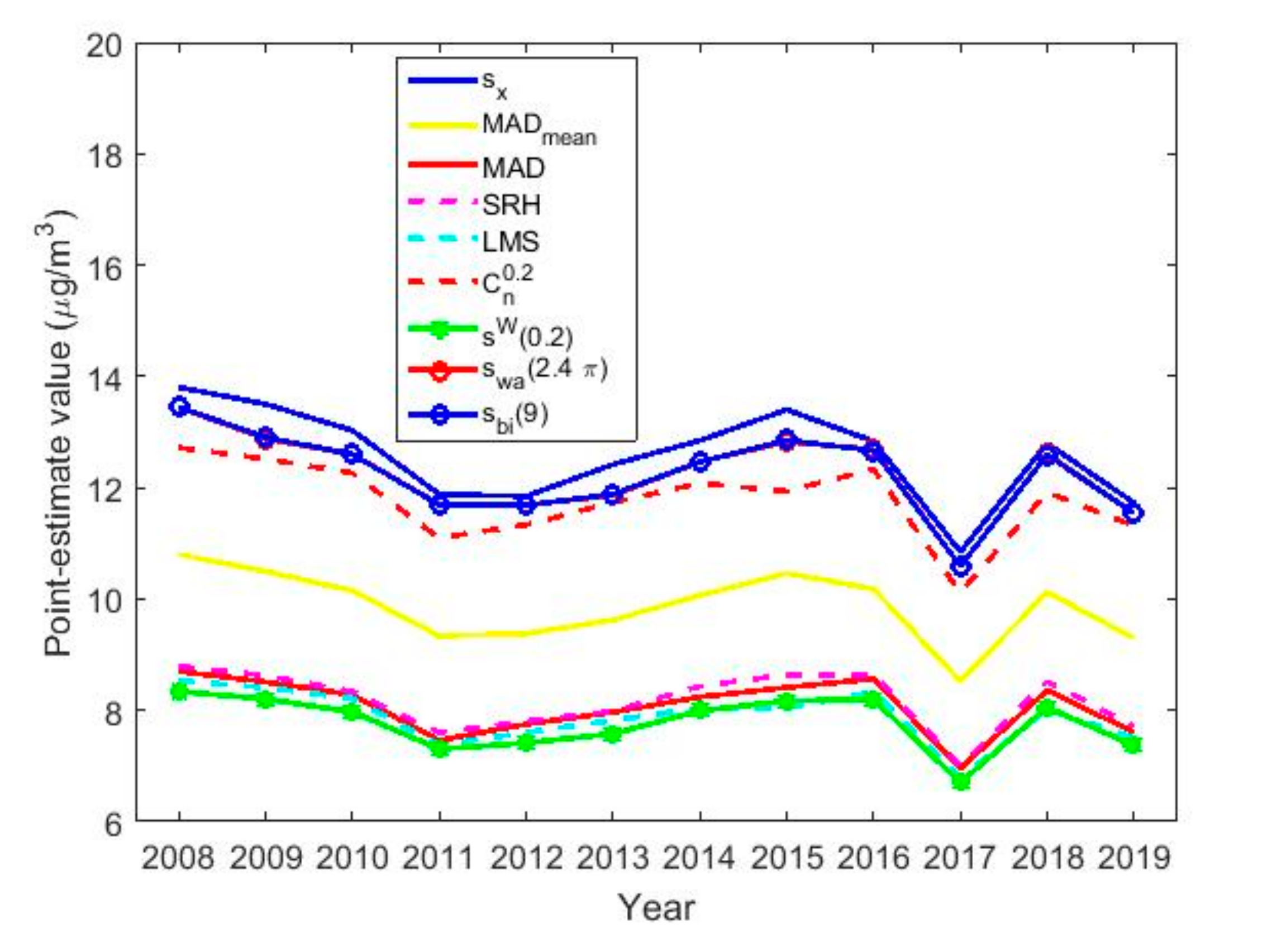
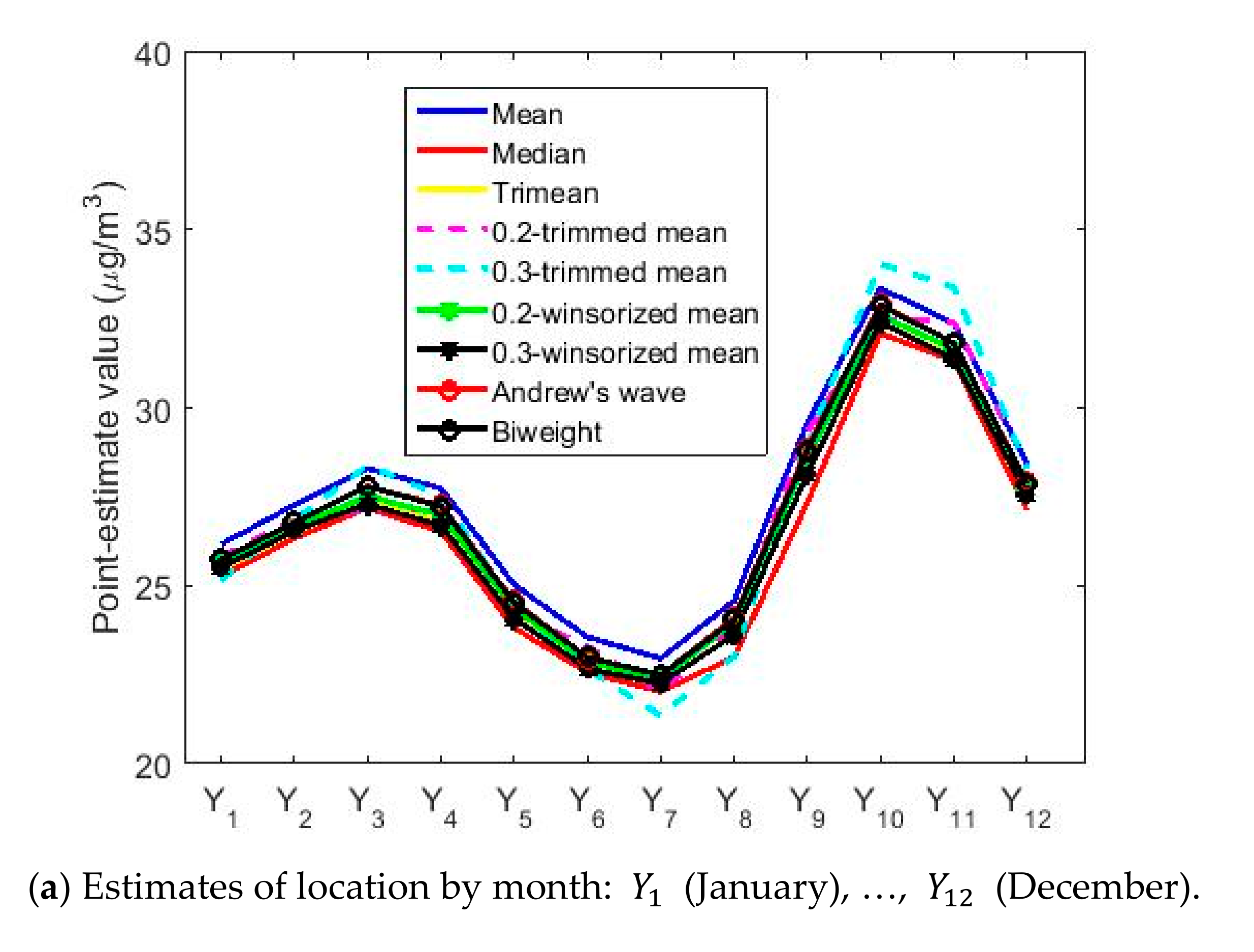

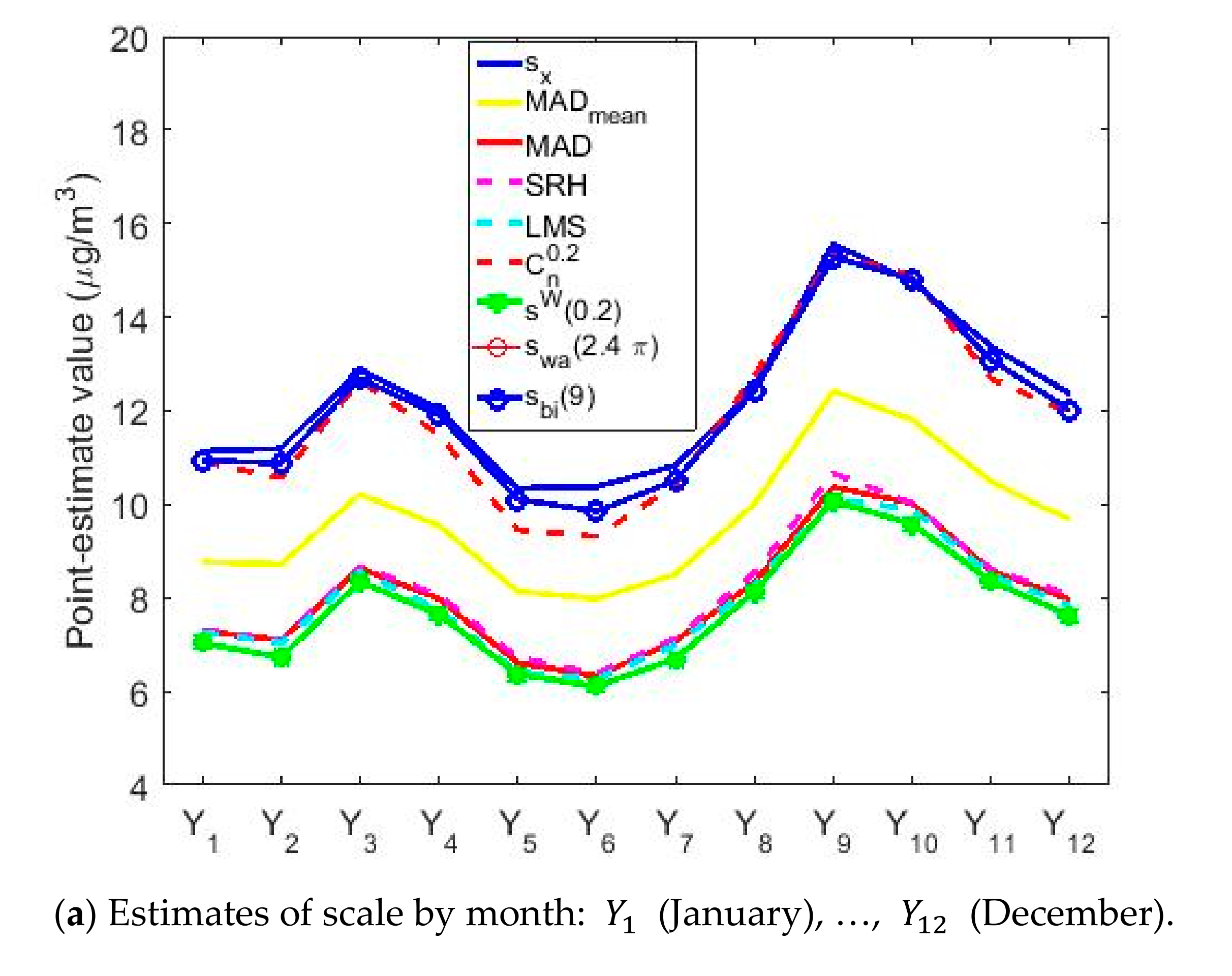
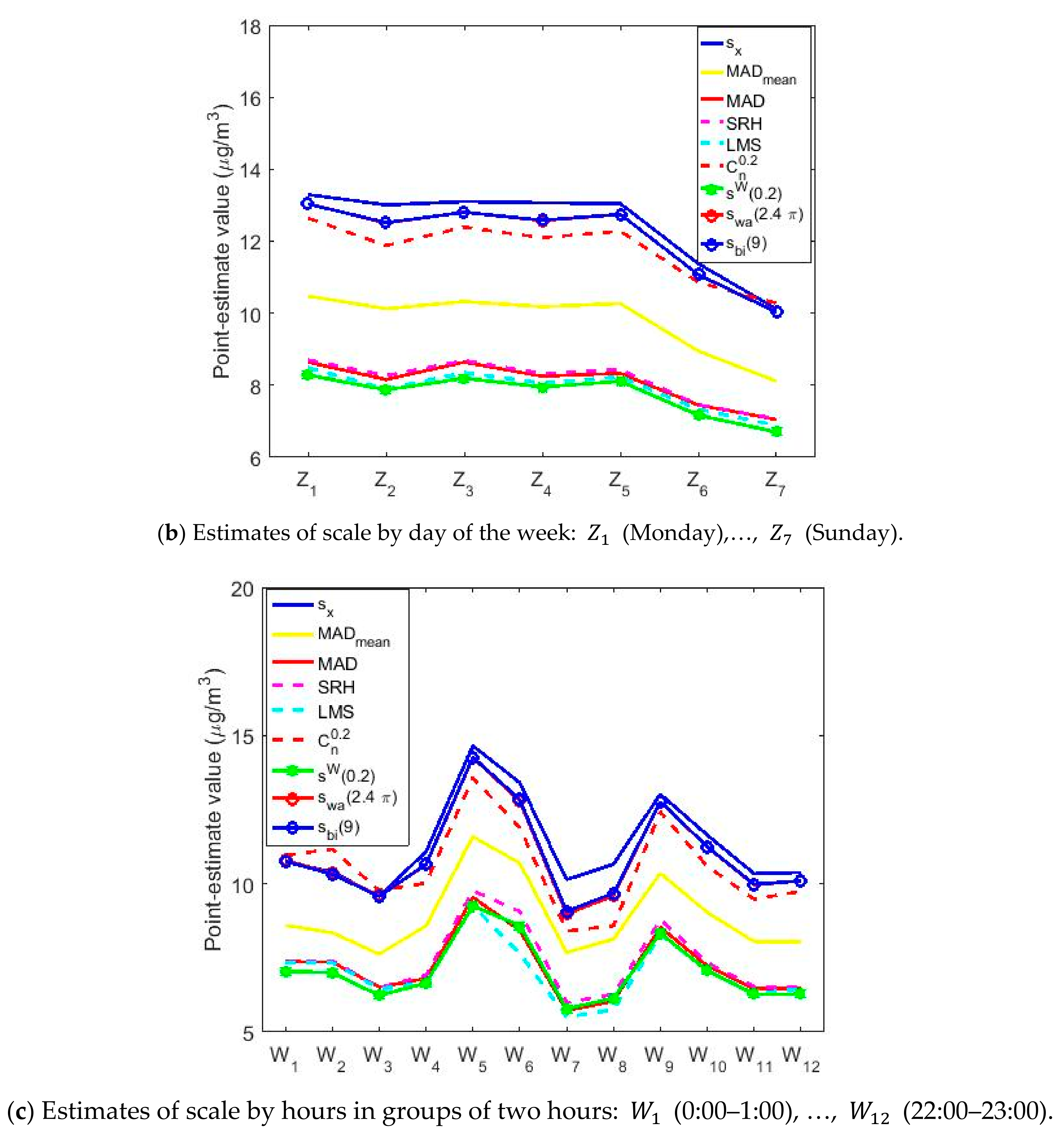
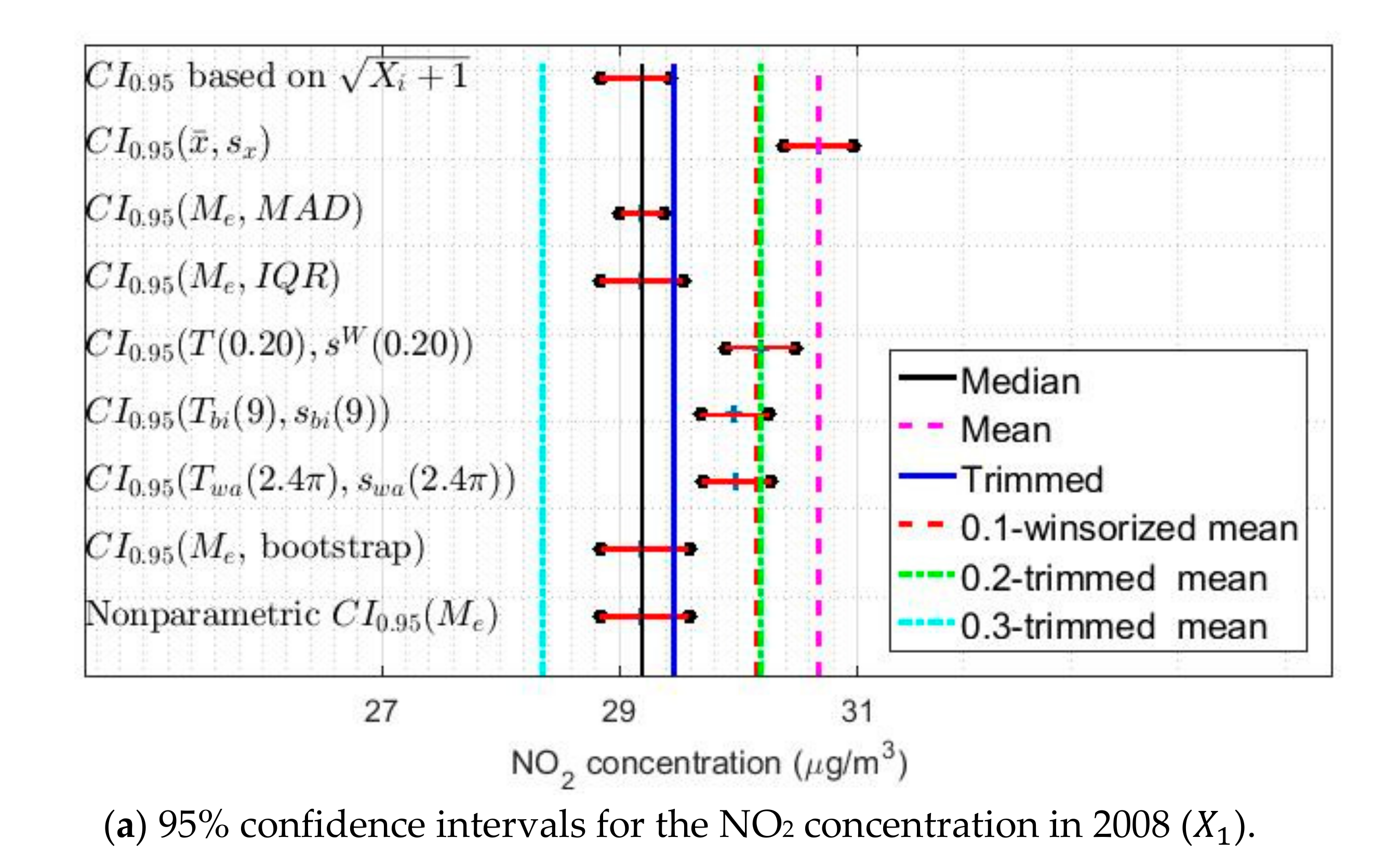
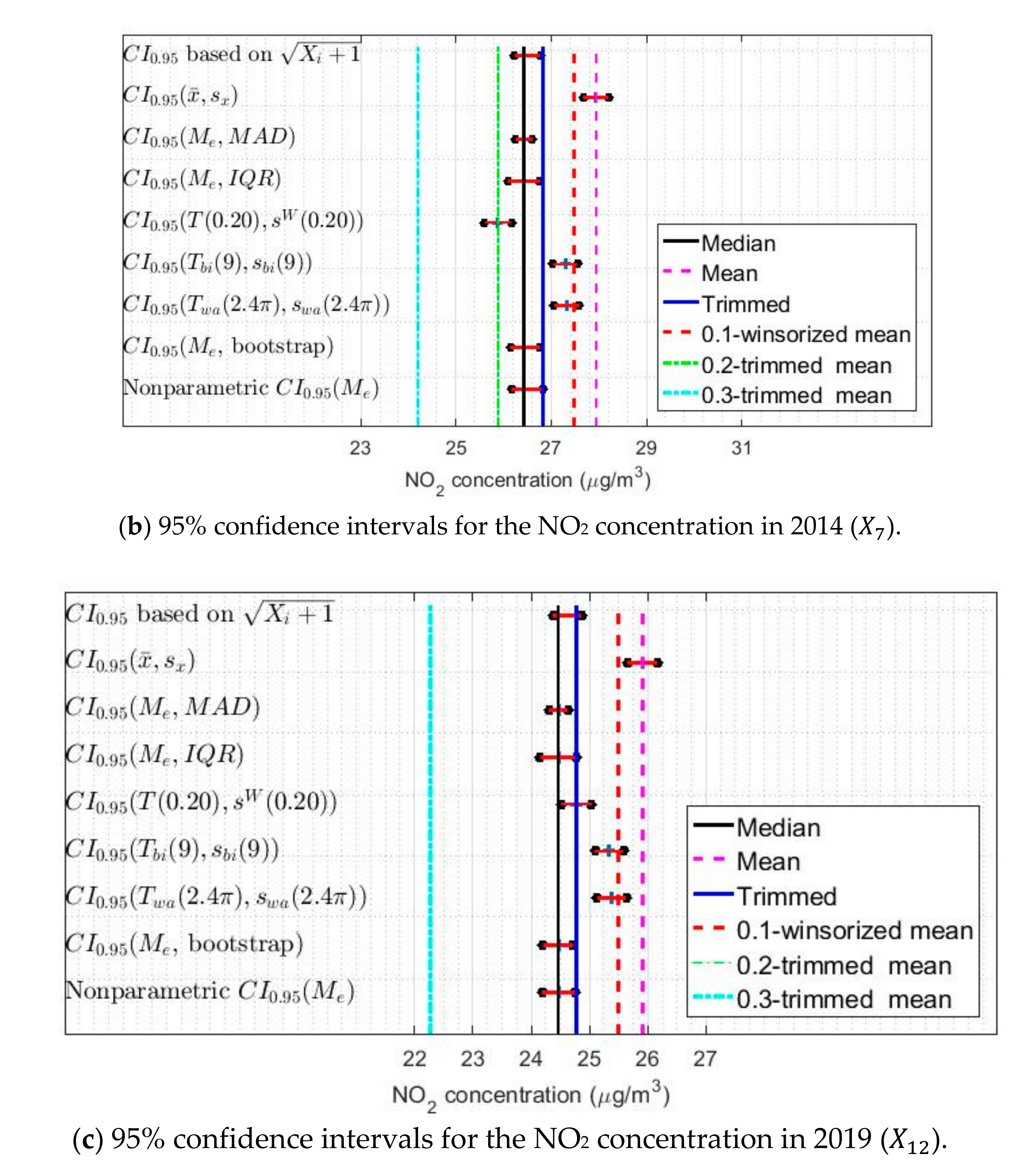
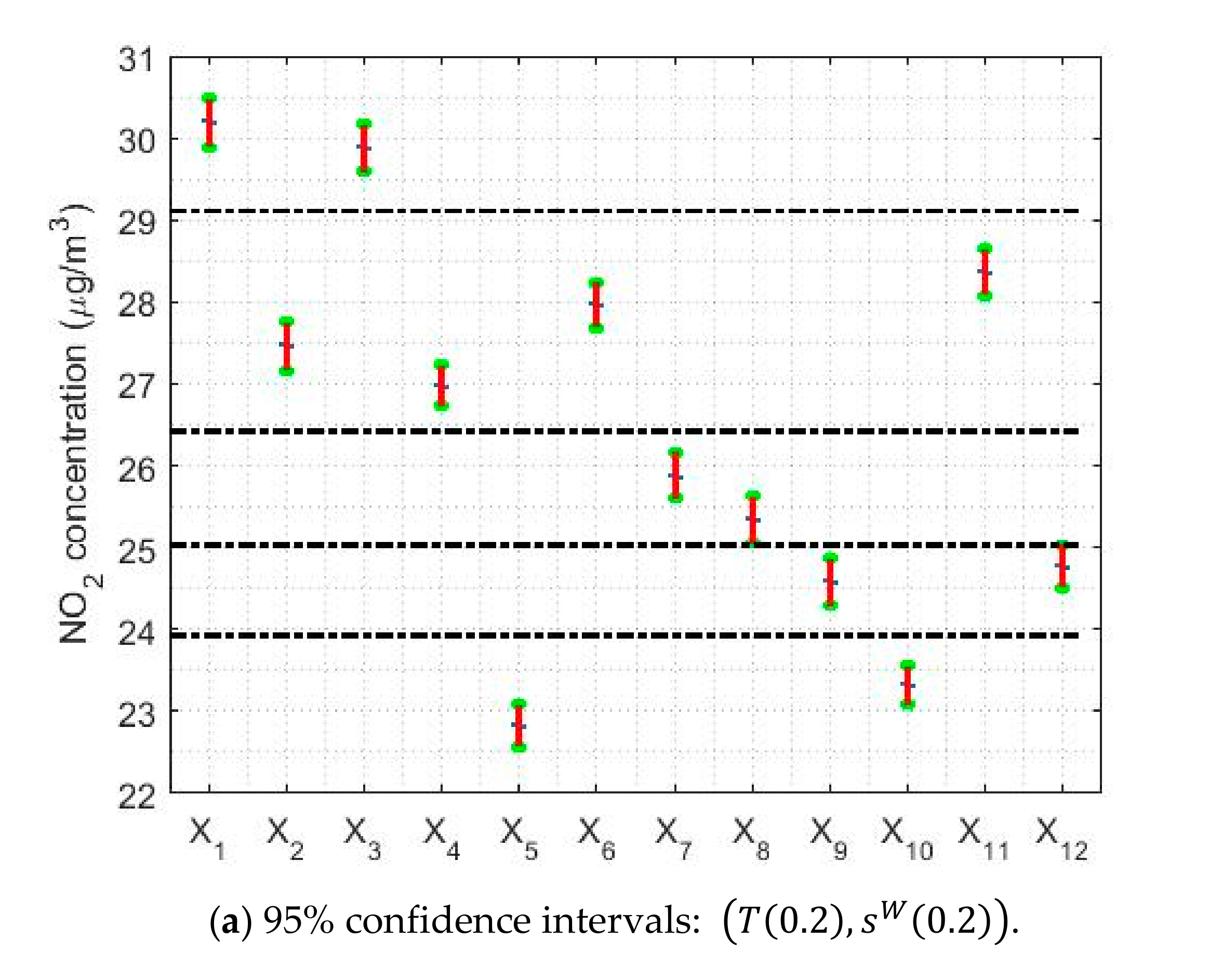
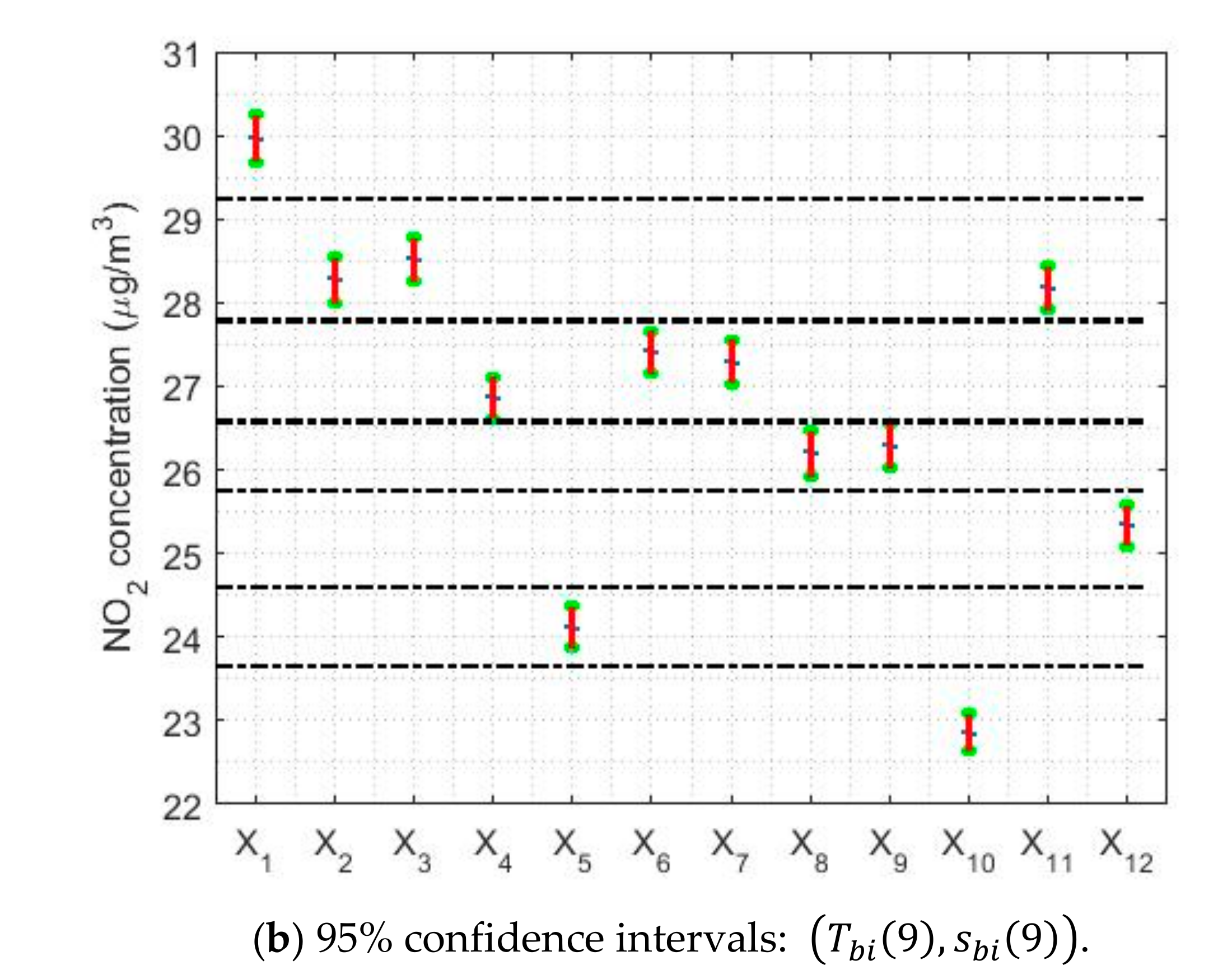
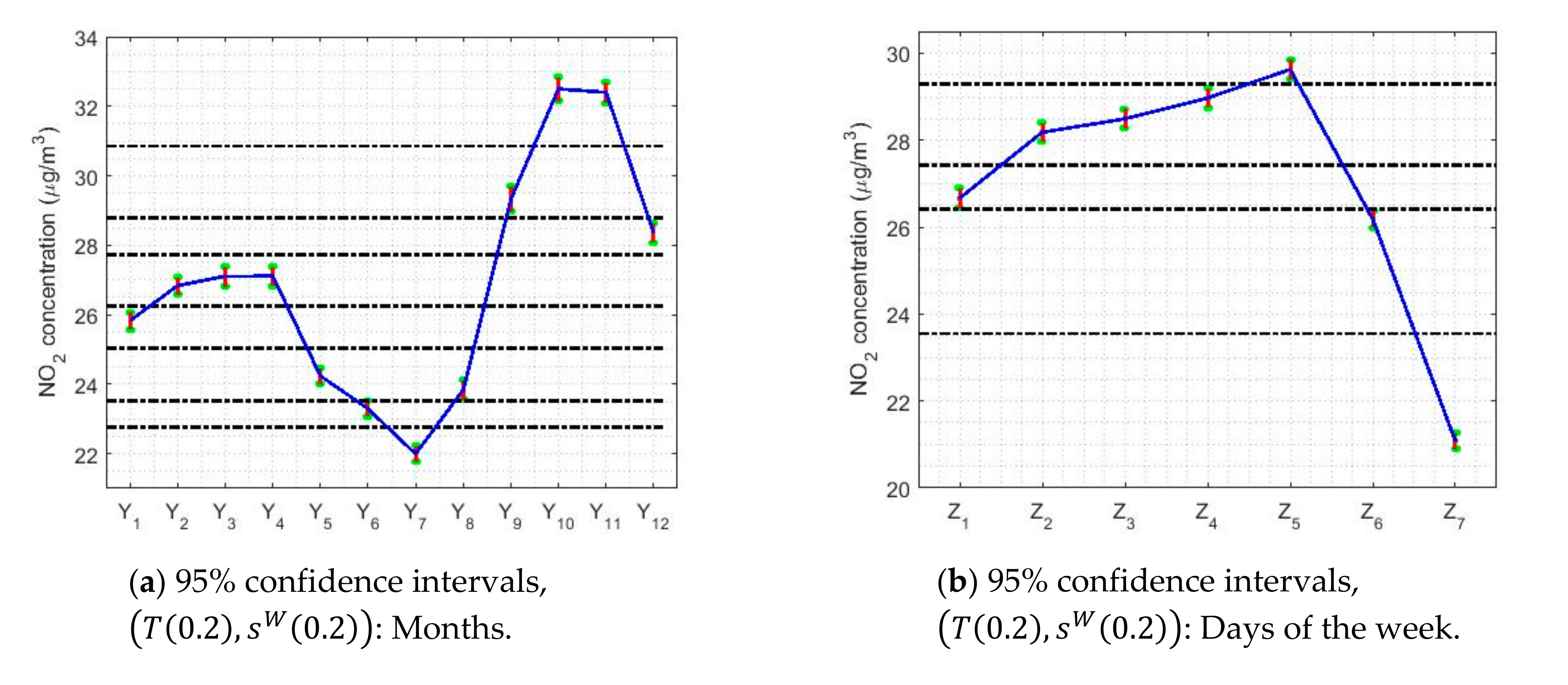
| Year | Count | Skewness | Kurtosis | Outliers % | |||||
|---|---|---|---|---|---|---|---|---|---|
| 8420 | 30.6714 | 29.190 | 13.8055 | 0.7028 | 3.7409 | 1.57 | 104.06 | 1.90 | |
| 8463 | 29.0274 | 27.510 | 13.5032 | 0.8793 | 4.7740 | 1.39 | 121.16 | 1.86 | |
| 8568 | 29.1409 | 27.970 | 13.0294 | 0.7802 | 4.5930 | 1.71 | 122.61 | 1.75 | |
| 8462 | 27.4369 | 26.010 | 11.8807 | 0.6098 | 3.5480 | 1.46 | 84.99 | 1.67 | |
| 8591 | 24.6597 | 23.380 | 11.8465 | 0.6422 | 3.4568 | 0.42 | 81.60 | 1.56 | |
| 8288 | 28.0209 | 26.835 | 12.4174 | 0.8509 | 5.0159 | 1.81 | 114.84 | 1.68 | |
| 8647 | 27.9431 | 26.430 | 12.8477 | 0.8255 | 4.9352 | 2.08 | 149.67 | 1.54 | |
| 8529 | 27.0562 | 25.130 | 13.4024 | 0.8700 | 4.1198 | 0.29 | 110.47 | 2.03 | |
| 8496 | 26.8132 | 25.610 | 12.8345 | 0.6392 | 3.6433 | 0 | 100.45 | 1.33 | |
| 8282 | 23.4152 | 22.220 | 10.8507 | 0.7390 | 3.8362 | 0 | 88.03 | 1.79 | |
| 8333 | 28.8103 | 27.180 | 12.7965 | 0.6763 | 3.5120 | 0 | 85.58 | 1.55 | |
| 8474 | 25.9156 | 24.465 | 11.7287 | 0.6842 | 3.6442 | 2.17 | 89.66 | 1.33 | |
| Total | 101,553 | 27.4108 | 25.950 | 12.7553 | 0.7747 | 4.2050 | 0 | 149.67 | 1.66 |
| Variable | ||
|---|---|---|
| 28.84 | 29.59 | |
| 27.21 | 27.86 | |
| 27.68 | 28.31 | |
| 25.75 | 26.32 | |
| 23.12 | 23.69 | |
| 26.55 | 27.16 | |
| 26.18 | 26.83 | |
| 24.82 | 25.48 | |
| 25.30 | 25.98 | |
| 21.91 | 22.47 | |
| 26.79 | 27.53 | |
| 24.19 | 24.75 |
| Year | Mean | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 30.6714 | 29.1900 | 29.4600 | 30.1907 | 28.3553 | 29.7156 | 29.4234 | 29.9821 | 29.9665 | |
| 29.0274 | 27.5100 | 27.8175 | 27.4588 | 25.5255 | 28.0363 | 27.7640 | 28.2836 | 28.2726 | |
| 29.1409 | 27.9700 | 28.1075 | 29.8856 | 29.1451 | 28.3203 | 28.0605 | 28.5222 | 28.5242 | |
| 27.4369 | 26.0100 | 26.4650 | 26.9828 | 24.9782 | 26.7571 | 26.4540 | 26.9136 | 26.8660 | |
| 24.6597 | 23.3800 | 23.6725 | 22.8323 | 20.3695 | 23.9037 | 23.6632 | 24.1463 | 24.1215 | |
| 28.0209 | 26.8350 | 27.0750 | 27.9641 | 24.9496 | 27.2365 | 27.0573 | 27.4127 | 27.4106 | |
| 28.0209 | 26.8350 | 27.0750 | 27.9641 | 24.9496 | 27.2365 | 27.0573 | 27.4127 | 27.4106 | |
| 27.9431 | 26.4300 | 26.8250 | 25.8820 | 24.2028 | 27.1266 | 26.7925 | 27.3246 | 27.2912 | |
| 27.0562 | 25.1300 | 25.6250 | 25.3397 | 22.3397 | 25.9492 | 25.5318 | 26.2370 | 26.1992 | |
| 26.8132 | 25.6100 | 25.8300 | 24.5848 | 22.0544 | 26.0465 | 25.7487 | 26.3029 | 26.2872 | |
| 23.4152 | 22.2200 | 22.4400 | 23.3262 | 23.3533 | 22.6466 | 22.3710 | 22.8758 | 22.8619 | |
| 28.8103 | 27.1800 | 27.6150 | 28.3698 | 25.1177 | 27.9231 | 27.5771 | 28.2248 | 28.1775 | |
| All years | 27.4108 | 25.9500 | 26.2850 | 27.0175 | 27.1500 | 26.5410 | 26.2272 | 26.7754 | 26.7526 |
| Year | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 13.8055 | 10.8025 | 8.7000 | 8.7900 | 8.5300 | 8.3386 | 13.4431 | 13.4482 | 12.7180 | |
| 13.5032 | 10.4953 | 8.5100 | 8.6250 | 8.4100 | 8.2029 | 12.8821 | 12.9066 | 12.5176 | |
| 13.0294 | 10.1525 | 8.2800 | 8.3350 | 8.2150 | 7.9726 | 12.6009 | 12.6008 | 12.2625 | |
| 11.8807 | 9.3367 | 7.4600 | 7.6000 | 7.3750 | 7.3040 | 11.7007 | 11.6932 | 11.0964 | |
| 11.8465 | 9.3780 | 7.7500 | 7.8050 | 7.6050 | 7.4137 | 11.6913 | 11.6828 | 11.3332 | |
| 12.4174 | 9.6233 | 7.9650 | 7.9850 | 7.8200 | 7.5782 | 11.8653 | 11.8836 | 11.7341 | |
| 12.8477 | 10.0650 | 8.2400 | 8.4300 | 8.0400 | 7.9912 | 12.4651 | 12.4657 | 12.0803 | |
| 13.4024 | 10.4634 | 8.4100 | 8.6400 | 8.0400 | 8.1693 | 12.8284 | 12.8536 | 11.9345 | |
| 12.8345 | 10.1818 | 8.5650 | 8.6400 | 8.3300 | 8.2007 | 12.6827 | 12.6662 | 12.3354 | |
| 10.8507 | 8.5253 | 6.9600 | 7.0100 | 6.7900 | 6.7041 | 10.5899 | 10.5901 | 10.1125 | |
| 12.7965 | 10.1228 | 8.3600 | 8.5200 | 8.0150 | 8.0536 | 12.5949 | 12.5894 | 11.9163 | |
| 11.7287 | 9.2944 | 7.6050 | 7.7100 | 7.5000 | 7.3684 | 11.5476 | 11.5364 | 11.3150 | |
| All years | 12.7553 | 9.9982 | 8.1800 | 8.2700 | 8.0250 | 7.8793 | 12.3747 | 12.3789 | 11.9345 |
| Variable | ||||
|---|---|---|---|---|
| 29.8938 | 30.4876 | 0.5938 | ||
| 29.6949 | 30.2693 | 0.5745 | ||
| 27.1675 | 27.7502 | 0.5827 | ||
| 28.0091 | 28.5581 | 0.5490 | ||
| 29.6042 | 30.1670 | 0.5628 | ||
| 28.2554 | 28.7891 | 0.5337 | ||
| 26.7233 | 27.2422 | 0.5189 | ||
| 26.6642 | 27.1629 | 0.4987 | ||
| 22.5709 | 23.0936 | 0.5227 | ||
| 23.8990 | 24.3935 | 0.4945 | ||
| 27.6921 | 28.2360 | 0.5440 | ||
| 27.1572 | 27.6682 | 0.5110 | ||
| 25.6012 | 26.1627 | 0.5616 | ||
| 27.0618 | 27.5874 | 0.5256 | ||
| 25.0507 | 25.6287 | 0.5780 | ||
| 25.9647 | 26.5093 | 0.5446 | ||
| 24.2941 | 24.8755 | 0.5814 | ||
| 26.0332 | 26.5726 | 0.5395 | ||
| 23.0855 | 23.5669 | 0.4814 | ||
| 22.6477 | 23.1040 | 0.4562 | ||
| 28.0815 | 28.6580 | 0.5765 | ||
| 27.9544 | 28.4953 | 0.5410 | ||
| 24.5174 | 25.0405 | 0.5231 | ||
| 25.1326 | 25.6244 | 0.4918 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernandez, W.; Mendez, A. Twelve-Year Analysis of NO2 Concentration Measurements at Belisario Station (Quito, Ecuador) Using Statistical Inference Techniques. Sensors 2020, 20, 5831. https://doi.org/10.3390/s20205831
Hernandez W, Mendez A. Twelve-Year Analysis of NO2 Concentration Measurements at Belisario Station (Quito, Ecuador) Using Statistical Inference Techniques. Sensors. 2020; 20(20):5831. https://doi.org/10.3390/s20205831
Chicago/Turabian StyleHernandez, Wilmar, and Alfredo Mendez. 2020. "Twelve-Year Analysis of NO2 Concentration Measurements at Belisario Station (Quito, Ecuador) Using Statistical Inference Techniques" Sensors 20, no. 20: 5831. https://doi.org/10.3390/s20205831
APA StyleHernandez, W., & Mendez, A. (2020). Twelve-Year Analysis of NO2 Concentration Measurements at Belisario Station (Quito, Ecuador) Using Statistical Inference Techniques. Sensors, 20(20), 5831. https://doi.org/10.3390/s20205831






