Dwell Time Allocation Algorithm for Multiple Target Tracking in LPI Radar Network Based on Cooperative Game
Abstract
:1. Introduction
2. Signal Model for Radar Networks
2.1. Target Motion Model
2.2. Received Signal Model
2.3. Schleher Intercept Factor
3. Dwell Time Allocation Algorithm for Radar Networks Based on a Cooperative Game Model
3.1. Optimization of Dwell Time Allocation Using Nash Bargaining Solution
3.2. Iterative Algorithm for Dwell Time Allocation
| Algorithm 1 Dwell time allocation algorithm based on the Nash bargaining solution (NBS) |
| Step 1: Parameter initialization: At the time instant, for , set the parameter initial values , and , Lagrangian multipliers and , the number of iteration index , error tolerance Step 2: Circulation: At the time instant, for , use Equation (28) to calculate Use Equation (30) to update Lagrange multipliers; Update Step 3: When or , end the cycle; Step 4: Repeat Parameter update: For , update |
3.3. Radar Selection Optimization
| Algorithm 2 Radar allocation method |
| Step 1: Solve the Equation (22) times to obtain the minimum dwell time matrix satisfying Step 2: Arrange the columns of matrix in ascending order, and assign the target corresponding to the smallest element in the first row to the corresponding radar combination. Step 3: Remove the column vector corresponding to the target assigned in step 2, and remove all row vectors containing the radar in the radar combination assigned in step 2. Step 4: Repeat steps 2 and 3 until all targets are assigned to get the optimal allocation of radar combination. |
4. Performance Verification
4.1. Simulation Settings
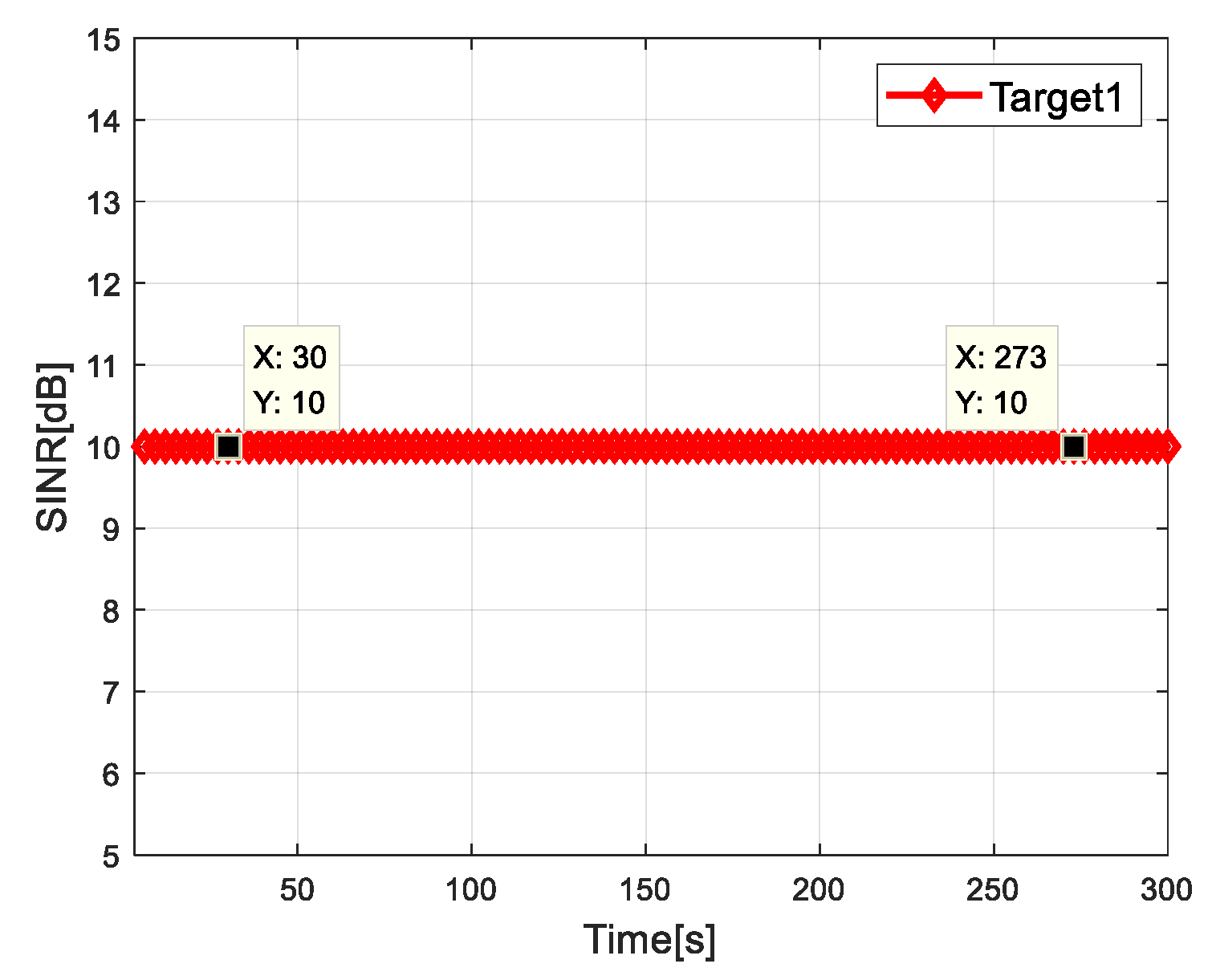
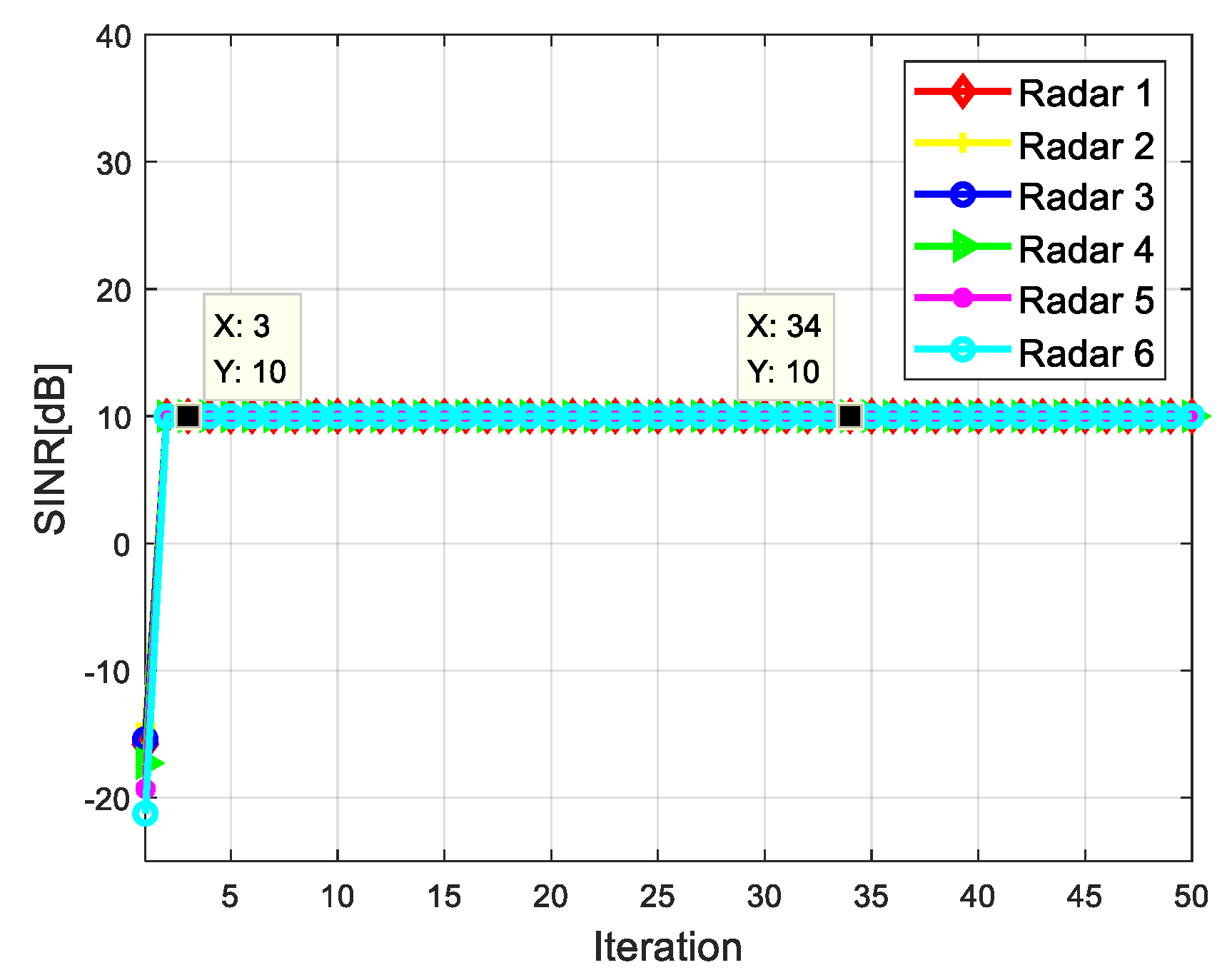
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zwaga, J.H.; Boers, Y.; Driessen, H. On tracking performance constrained MFR parameter control. In Proceedings of the Sixth International Conference of Information Fusion, Cairns, QLD, Australia, 8–11 July 2003; pp. 712–718. [Google Scholar]
- Wang, X.L.; Yi, W.; Xie, M.C. A joint beam and dwell time allocation strategy for multiple target tracking based on phase array radar system. In Proceedings of the 20th International Conference on Information Fusion, Xi’an, China, 10–13 July 2017; pp. 1–5. [Google Scholar]
- Kuo, T.W.; Chao, Y.S.; Kuo, C.F. Real-time dwell scheduling of component-oriented phased array radars. IEEE Trans. Comput. 2005, 54, 47–60. [Google Scholar]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech House: Boston, MA, USA, 2004. [Google Scholar]
- Ni, Q.; Zarakovitis, C.C. Nash bargaining game theoretic scheduling for joint channel and power allocation in cognitive radio systems. IEEE J. Sel. Areas Commun. 2012, 30, 70–81. [Google Scholar] [CrossRef]
- Zhou, S.H.; Liang, X.L.; Yu, Y.; Liu, H.W. Joint radarcommunications co-use waveform design using optimized phase perturbation. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1227–1240. [Google Scholar] [CrossRef]
- Wang, X.R.; Hassanien, A.; Amin, M.G. Dual-function MIMO radar communications system design via sparse array optimization. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1213–1226. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Masouros, C.; Li, A.; Ratnarajah, T.; Zhou, J.M. MIMO radar and cellular coexistence: A power-efficient approach enabled by interference exploitation. IEEE Trans. Signal Process. 2018, 66, 3681–3695. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.G.; Wang, F.; Salous, S.; Zhou, J.J. Distributed power allocation for spectral coexisting multistatic radar and communication systems based on Stackelberg game. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4265–4269. [Google Scholar]
- Gogineni, S.; Nehorai, A. Game theoretic design for polarimetric MIMO radar target detection. Signal Process. 2012, 92, 1281–1289. [Google Scholar] [CrossRef]
- Song, X.F.; Willett, P.; Zhou, S.L.; Luh, P.B. The MIMO radar and jammer games. IEEE Trans. Signal Process. 2012, 60, 687–699. [Google Scholar] [CrossRef]
- Piezzo, M.; Aubry, A.; Buzzi, S.; Maio, A.D.; Farina, A. Non-cooperative code design in radar networks: A game-theoretic approach. EURASIP J. Adv. Signal Process. 2013, 2013, 63. [Google Scholar] [CrossRef] [Green Version]
- Bacci, G.; Sanguinetti, L.; Greco, M.S.; Luise, M. A game-theoretic approach for energy-efficient detection in radar sensor networks. In Proceedings of the IEEE 7th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hoboken, NJ, USA, 17–20 June 2012; pp. 157–160. [Google Scholar]
- Deligiannis, A.; Rossetti, G.; Panoui, A.; Lambotharan, S.; Chambers, J.A. Power allocation game between a radar network and multiple jammers. In Proceedings of the IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–5. [Google Scholar]
- Deligiannis, A.; Panoui, A.; Lambotharan, S.; Chambers, J.A. Game-theoretic power allocation and the Nash equilibrium analysis for a multistatic MIMO radar network. IEEE Trans. Signal Process. 2017, 65, 6397–6408. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Chen, H.W.; Wei, X.Z.; Wang, H.Q.; Li, X. Power allocation for range-only localisation in distributed multiple-input multiple-output radar networks—A cooperative game approach. IET Radar Sonar Navig. 2014, 8, 708–718. [Google Scholar] [CrossRef]
- Chen, J.T.; Dai, W.H.; Shen, Y.; Lau, V.K.N.; Win, M.Z. Power management for cooperative localization: A game theoretical approach. IEEE Trans. Signal Process. 2016, 64, 6517–6532. [Google Scholar] [CrossRef]
- Chen, H.W.; Ta, S.Y.; Sun, B. Cooperative game approach to power allocation for target tracking in distributed MIMO radar sensor networks. IEEE Sens. J. 2015, 15, 5423–5432. [Google Scholar] [CrossRef]
- Zhang, Z.K.; Tian, Y.B. A novel resource scheduling method of netted radars based on Markov decision process during target tracking in clutter. EURASIP J. Adv. Signal Process. 2016, 2016, 16. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.G.; Zhou, J.J.; Wang, F. LPI based resource management for target tracking in distributed radar network. In Proceedings of the IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 822–826. [Google Scholar]
- Shi, C.G.; Wang, F.; Sellathurai, M.; Zhou, J.J. Low probability of intercept based multicarrier radar jamming power allocation for joint radar and wireless communications systems. IET Radar Sonar Navig. 2017, 11, 802–811. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.G.; Salous, S.; Wang, F.; Zhou, J.J. Power allocation for target detection in radar networks based on low probability of intercept: A cooperative game theoretical strategy. Radio Sci. 2017, 52, 1030–1045. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.G.; Wang, F.; Salous, S.; Zhou, J.J.; Hu, Z.T. Nash bargaining game-theoretic framework for power control in distributed multiple-radar architecture underlying wireless communication system. Entropy 2018, 20, 267. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.G.; Zhou, J.J.; Wang, F.; Chen, J. Mutual information–based LPI optimisation for radar network. Int. J. Electron. 2015, 102, 1114–1131. [Google Scholar] [CrossRef]
- Shi, C.G.; Wang, F.; Sellathurai, M.; Zhou, J.J. Non-cooperative game theoretic power allocation strategy for distributed multiple-radar architecture in a spectrum sharing environment. IEEE Access 2018, 6, 17787–17800. [Google Scholar] [CrossRef]
- Yang, C.G.; Li, J.D.; Tian, Z. Optimal power control for cognitive radio networks under coupled interference constraints: A cooperative game-theoretic perspective. IEEE Trans. Veh. Technol. 2010, 59, 1696–1706. [Google Scholar] [CrossRef] [Green Version]
- She, J.; Wang, F.; Zhou, J.J. A Novel Sensor Selection and Power Allocation Algorithm for Multiple-Target Tracking in an LPI Radar Network. Sensors 2016, 16, 2193. [Google Scholar] [CrossRef] [Green Version]
- Tichavsky, P.; Muravchik, C.H.; Nehorai, A. Posterior Cramér-Rao bounds for dscrete-time nonlinear filtering. IEEE Trans. Signal Process. 1998, 46, 1386–1396. [Google Scholar] [CrossRef] [Green Version]
- Glass, J.D.; Smith, L.D. MIMO radar resource allocation using posterior Cramér-Rao lower bounds. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–9. [Google Scholar]
- Yang, G.L.; Li, B.; Tian, X.Z.; Wang, X. Adaptive power control algorithm in cognitive radio based on game theory. IET Commun. 2015, 9, 1807–1811. [Google Scholar] [CrossRef] [Green Version]











| Minimum Dwell Time | Target No. | ||||
|---|---|---|---|---|---|
| 1 | 2 | ||||
| Radar No. | 1 | ||||
| 2 | |||||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Transmitted gain | Pulse repetition interval | ||
| Received gain | Wavelength | ||
| Transmitted side lobe gain | Correlation coefficient | ||
| Received side lobe gain Transmitted power | Background noise power Pulses number |
| Target 1 | Target 2 | Target 3 | All of the Targets | |
|---|---|---|---|---|
| Proposed Algorithm | 0.53 s | 0.35 s | 0.61 s | 1.49 s |
| ANCDTC | 2.27 s | 1.5 s | 2.61 s | 6.38 s |
| BCRLB-GA | 0.55 s | 0.38 s | 0.66 s | 1.59 s |
| FDTARA | 10 s | 10 s | 10 s | 30 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, C.; Wang, L.; Zhu, D. Dwell Time Allocation Algorithm for Multiple Target Tracking in LPI Radar Network Based on Cooperative Game. Sensors 2020, 20, 5944. https://doi.org/10.3390/s20205944
Xue C, Wang L, Zhu D. Dwell Time Allocation Algorithm for Multiple Target Tracking in LPI Radar Network Based on Cooperative Game. Sensors. 2020; 20(20):5944. https://doi.org/10.3390/s20205944
Chicago/Turabian StyleXue, Chenyan, Ling Wang, and Daiyin Zhu. 2020. "Dwell Time Allocation Algorithm for Multiple Target Tracking in LPI Radar Network Based on Cooperative Game" Sensors 20, no. 20: 5944. https://doi.org/10.3390/s20205944
APA StyleXue, C., Wang, L., & Zhu, D. (2020). Dwell Time Allocation Algorithm for Multiple Target Tracking in LPI Radar Network Based on Cooperative Game. Sensors, 20(20), 5944. https://doi.org/10.3390/s20205944





