Cross-Correlation Algorithm-Based Optimization of Aliasing Signals for Inductive Debris Sensors
Abstract
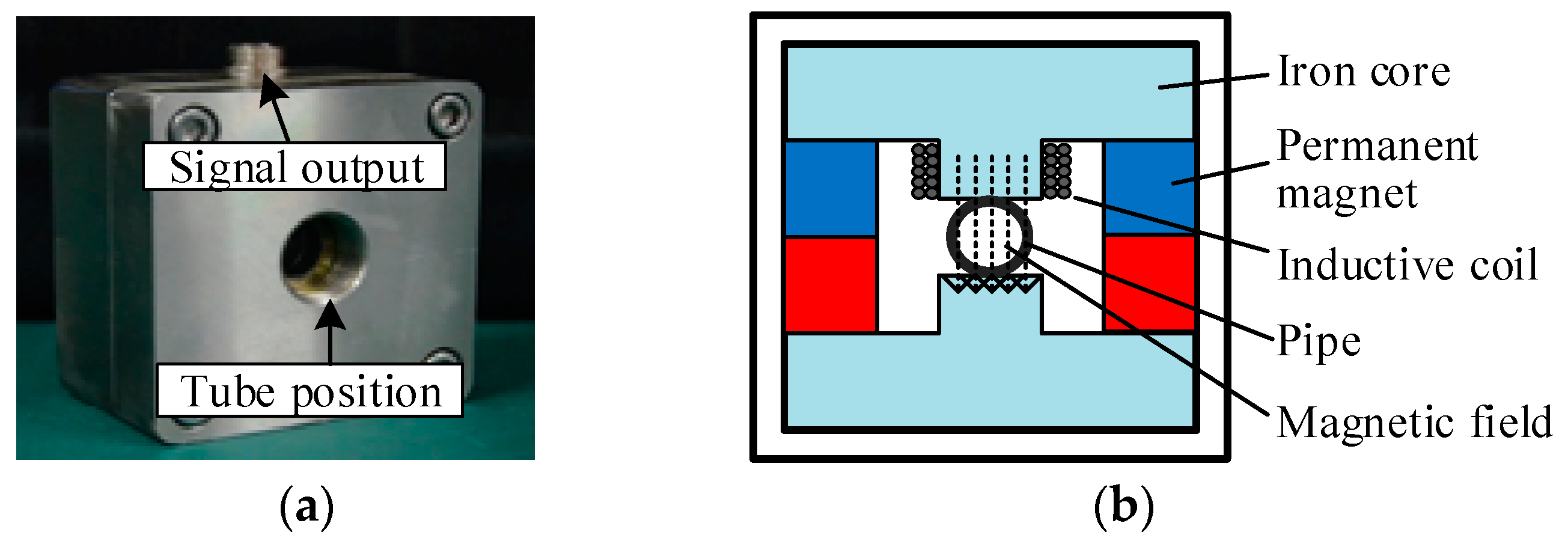
:1. Introduction
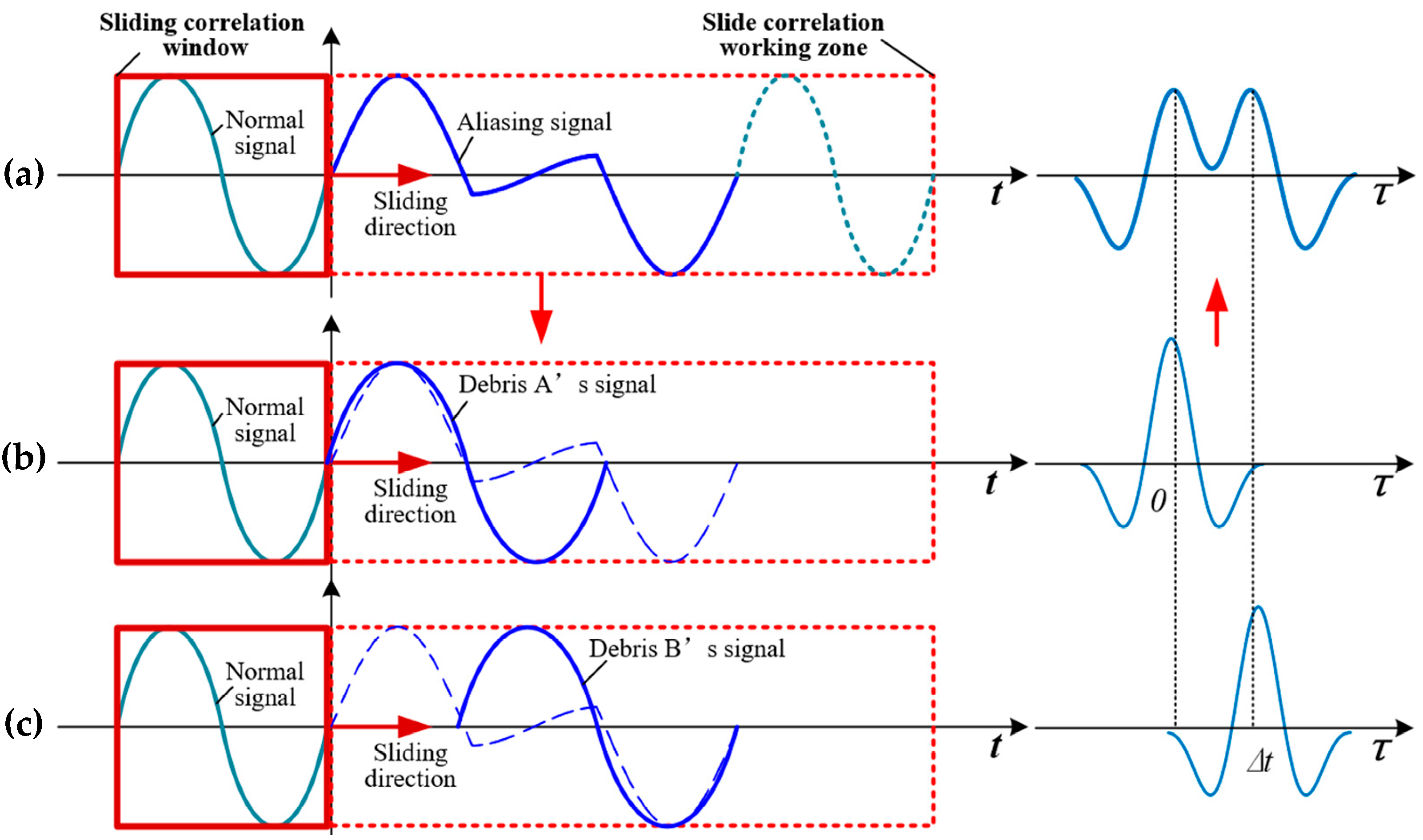
2. Model Analysis of Debris Aliasing Signal
2.1. Aliasing Signal Model of Debris Aliasing Behavior
2.2. Analysis of the Aliasing Signal Model
- When
- When
- When
- When
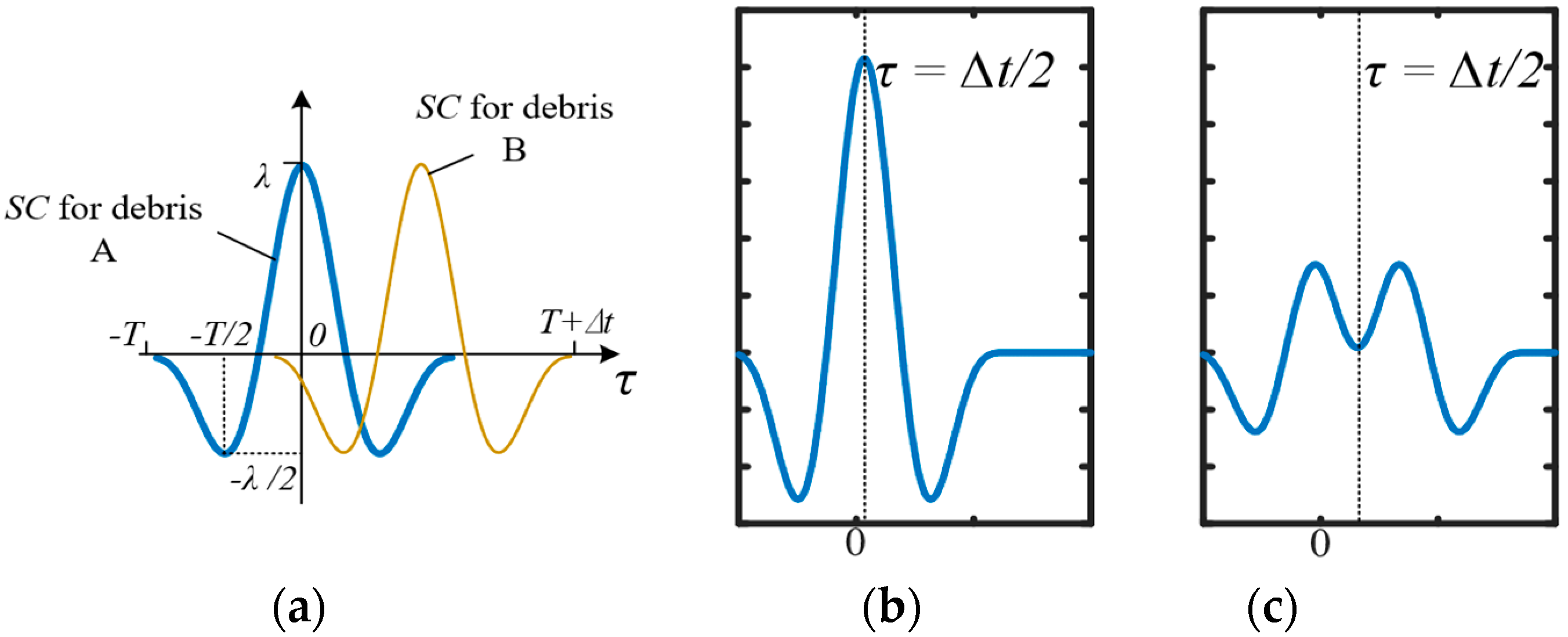
3. Cross-Correlation Algorithm-Based Optimization
3.1. Cross-Correlation Analysis of Aliasing Signal
- When
- When
- When
- When
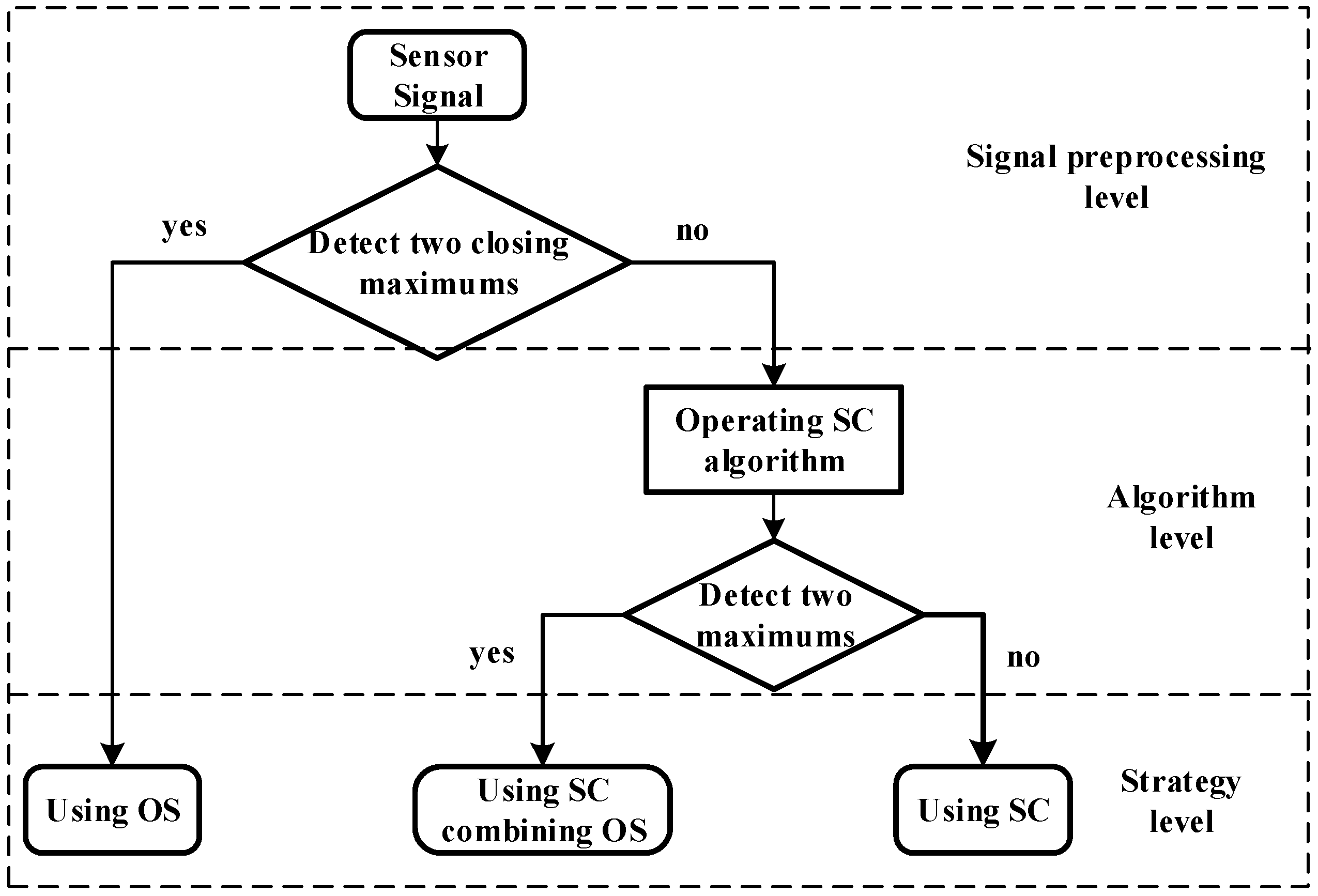
3.2. Optimization Strategy for Aliasing Signal Processing
4. Experiment Validation
4.1. Simulation Experiment
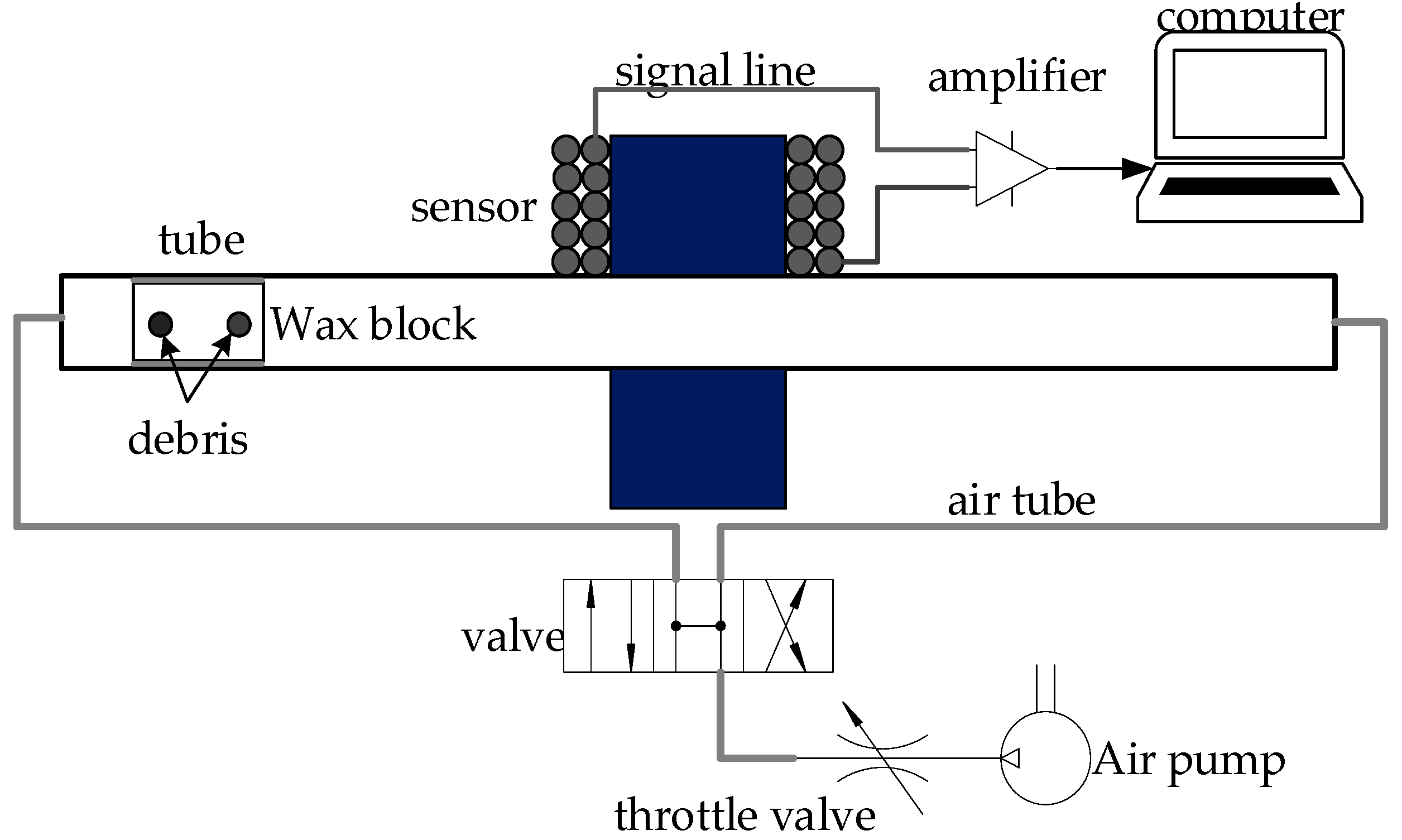
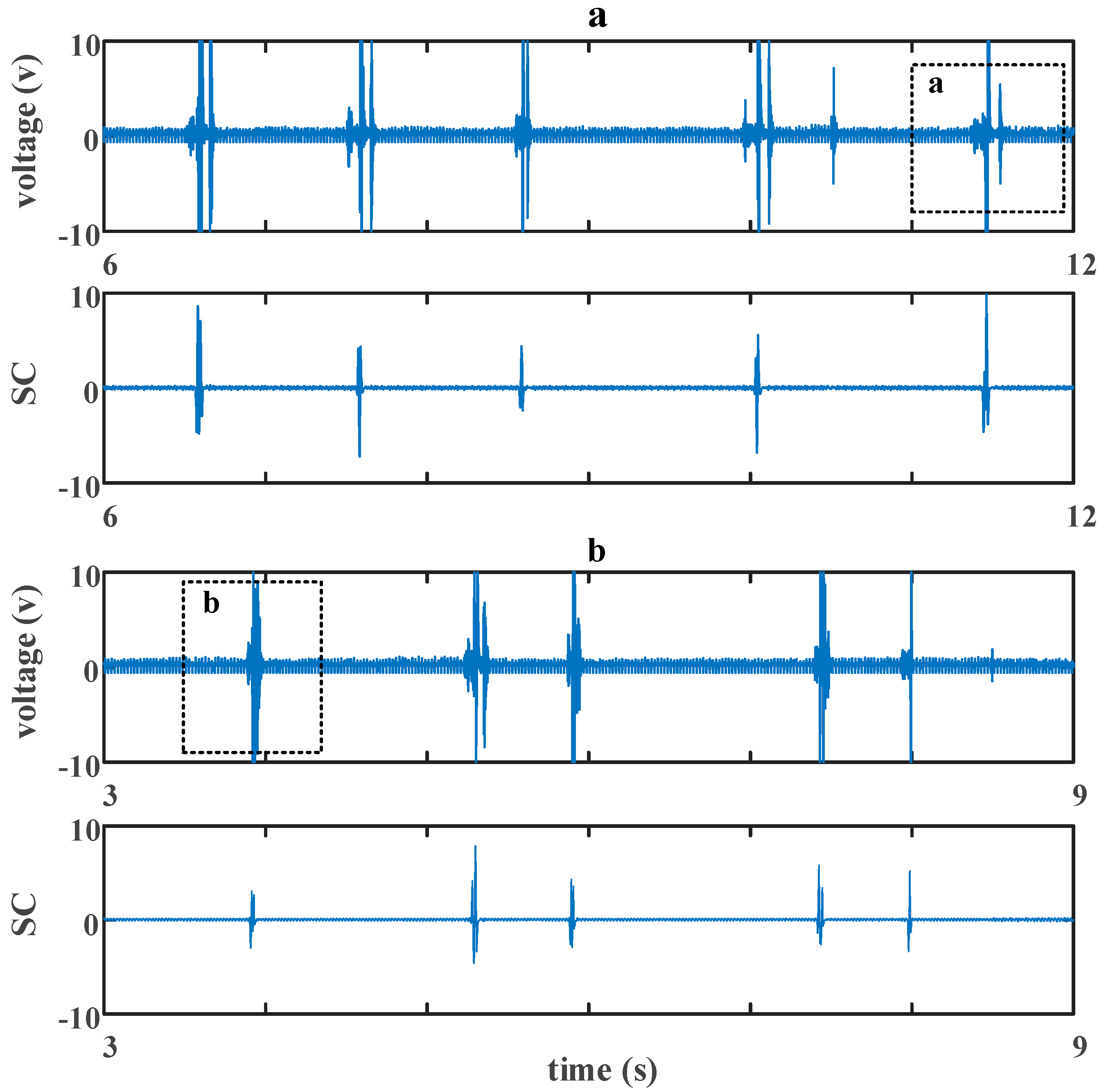
4.2. Wax Block Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Amiri, M.; Khonsari, M. On the Thermodynamics of Friction and Wear—A Review. Entropy 2010, 12, 1021–1049. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Peng, Y.; Wu, H.; Zhang, X.; Wang, J. Full-life dynamic identification of wear state based on on-line wear debris image features. Meas. Sci. Technol. 2014, 42, 404–414. [Google Scholar] [CrossRef]
- Wang, X.; Lin, S.; Wang, S.; He, Z.; Zhang, C. Remaining useful life prediction based on the Wiener process for an aviation axial piston pump. Chin. J. Aeronaut. 2016, 29, 779–788. [Google Scholar] [CrossRef] [Green Version]
- Dwyer-Joyce, R.; Williams, J.A.; Roylance, B.J. Wear debris and associated wear phenomena-fundamental research and practice. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2000, 214, 79–105. [Google Scholar]
- Seifert, W.W.; Westcott, V.C. A method for the study of wear particles in lubricating oil. Wear 1972, 21, 27–42. [Google Scholar] [CrossRef]
- Zhu, X.; Zhong, C.; Zhe, J. Lubricating oil conditioning sensors for online machine health monitoring—A review. Tribol. Int. 2017, 109, 473–484. [Google Scholar] [CrossRef] [Green Version]
- Edmonds, J.; Resner, M.S.; Shkarlet, K. Detection of precursor wear debris in lubrication systems. In Proceedings of the 2000 IEEE Aerospace Proceedings, Big Sky, MT, USA, 25–25 March 2000; Volume 76, pp. 73–77. [Google Scholar]
- Tucker, J.E.; Reintjes, J.; Galie, T.R.; Schultz, A.; Lu, C.; Tankersley, L.L.; Sebok, T.; Holloway, C.; Howard, P.L. Lasernet fines optical wear debris monitor: A Navy shipboard evaluation of CBM enabling technology. In Proceedings of the 54th Meeting of the Society for Machinery Failure Prevention Technology, Virginia Beach, VA, USA, 1–4 May 2000. [Google Scholar]
- Centers, P.W.; Price, F.D. Real time simultaneous in-line wear and lubricant condition monitoring. Wear 1998, 123, 303–312. [Google Scholar] [CrossRef]
- Hong, W.; Wang, S.; Tomovic, M.M.; Liu, H.; Shi, J.; Wang, X. A Novel Indicator for Mechanical Failure and Life Prediction Based on Debris Monitoring. IEEE Trans. Reliab. 2017, 66, 161–169. [Google Scholar] [CrossRef]
- Kumar, P.; Hirani, H.; Agrawal, A.K.; Gachot, C. Online condition monitoring of misaligned meshing gears using wear debris and oil quality sensors. Ind. Lubr. Tribol. 2018, 70, 645–655. [Google Scholar] [CrossRef]
- Gorritxategi, E.; García-Arribas, A.; Aranzabe, A. Innovative on-Line Oil Sensor Technologies for the Condition Monitoring of Wind Turbines. Key Eng. Mater. 2015, 644, 53–56. [Google Scholar] [CrossRef]
- Hong, W.; Wang, S.; Tomovic, M.M.; Han, L.; Shi, J. Radial inductive debris detection sensor and performance analysis. Meas. Sci. Technol. 2013, 24, 125103. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.L.; Kitaljevich, D. In-line oil debris monitor for aircraft engine condition assessment. In Proceedings of the 2000 IEEE Aerospace Proceedings, Big Sky, MT, USA, 25 March 2000; Volume 76, pp. 49–56. [Google Scholar]
- Kempster, R.W.; George, D.B. Detection and Discrimination between Ferromagnetic and Non-Ferromagnetic Conductive Particles in a Fluid. U.S. Patent 5,315,243, 24 May 1994. [Google Scholar]
- Chambers, K.W.; Arneson, M.C.; Waggoner, C.A. An on-line ferromagnetic wear debris sensor for machinery condition monitoring and failure detection. Wear 1988, 128, 325–337. [Google Scholar] [CrossRef]
- Hong, W.; Wang, S.; Tomovic, M.M.; Liu, H.; Wang, X. A new debris sensor based on dual excitation sources for online debris monitoring. Meas. Sci. Technol. 2015, 26, 095101. [Google Scholar] [CrossRef]
- Zhong, Z.; Wang, S.; Hong, W.; Tomovic, M. Aliasing signal separation of oil debris monitoring. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications, Hefei, China, 5–7 June 2016; pp. 1682–1687. [Google Scholar]
- Li, T.; Wang, S.; Zio, E.; Shi, J.; Hong, W. Aliasing signal separation of superimposed abrasive debris based on degenerate unmixing estimation technique. Sensors 2018, 18, 866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bozchalooi, I.S.; Liang, M. In-line identification of oil debris signals: An adaptive subband filtering approach. Meas. Sci. Technol. 2010, 21, 015104. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, S.; Hong, W.; Zhang, C.; Wang, X.; Haokuo, L.; Shaoping, W.; Wei, H.; Chao, Z.; Xingjian, W. Design and experimental test of an on-line particle detection sensor based on symmetrical magnetic field. In Proceedings of the 2015 International Conference on Fluid Power and Mechatronics (FPM), Harbin, China, 4–6 August 2015; pp. 241–245. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended Cross-Correlation Analysis: A New Method for Analyzing Two Non-stationary Time Series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [PubMed] [Green Version]






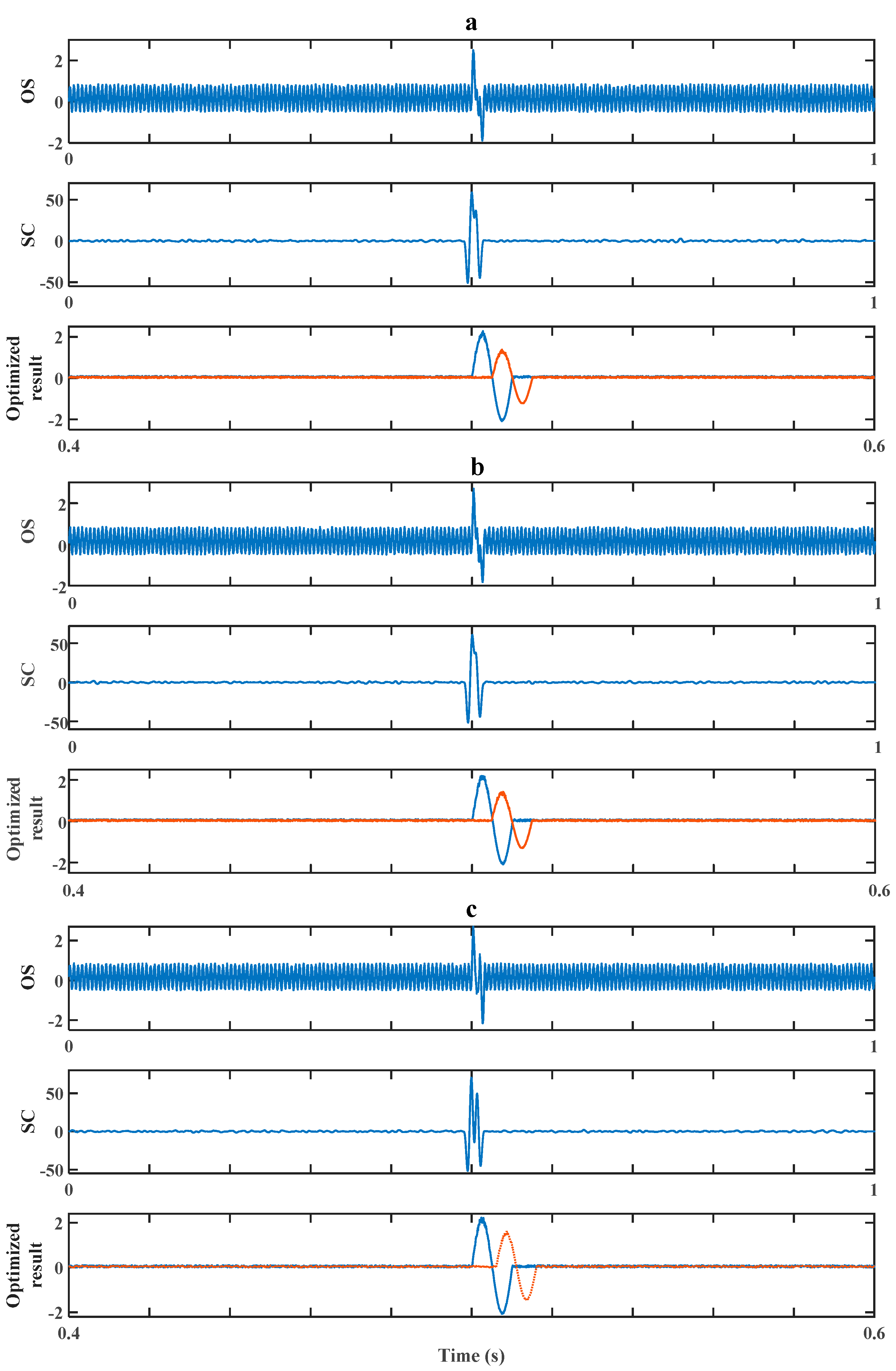


| Number of Detected Debris | RSO (Overall Size) | RSB (Debris B) | |
|---|---|---|---|
| 1 | ↓ | —— | |
| 2 | ↓ | ↓ | |
| 1 | 1/2 | 0 | |
| (T/2, 3T/4) | 2 | ↑ | ↑ |
| 2 | 1 | 1 |
| Number of Detected Debris | |||
|---|---|---|---|
| 1 | ↓ | —— | |
| 2 | ↑ | ↑ |
| Number of Detected Debris Particles | RS of Overall Size | RS of Debris B | Preferred | ||||
|---|---|---|---|---|---|---|---|
| OS | SC | ||||||
| I | 1 | 1 | > | - | - | SC | |
| II | 2 | 1 | < | >50% | - | OS | |
| III | 1 | 2 | < | - | >50% | SC and OS | |
| IV | 2 | 2 | < | 1 | <1 | OS | |
| Parameter | Value |
|---|---|
| Frequency of debris signal w | 100 Hz |
| Amplitude of inference | 0.5 |
| Amplifier of noise | 0.2 |
| Length of correlation T | 0.01 s |
| Sampling frequency | 10 kHz |
| Parameter | Value |
|---|---|
| Velocity of debris particle | 5 m/s |
| Size of particle | 200 μm |
| Amplifier magnification | 900 times |
| Space between two debris particles | 3 cm/6 cm |
| Sampling frequency | 10 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Sun, H.; Wang, S.; Huang, W. Cross-Correlation Algorithm-Based Optimization of Aliasing Signals for Inductive Debris Sensors. Sensors 2020, 20, 5949. https://doi.org/10.3390/s20205949
Wang X, Sun H, Wang S, Huang W. Cross-Correlation Algorithm-Based Optimization of Aliasing Signals for Inductive Debris Sensors. Sensors. 2020; 20(20):5949. https://doi.org/10.3390/s20205949
Chicago/Turabian StyleWang, Xingjian, Hanyu Sun, Shaoping Wang, and Wenhao Huang. 2020. "Cross-Correlation Algorithm-Based Optimization of Aliasing Signals for Inductive Debris Sensors" Sensors 20, no. 20: 5949. https://doi.org/10.3390/s20205949
APA StyleWang, X., Sun, H., Wang, S., & Huang, W. (2020). Cross-Correlation Algorithm-Based Optimization of Aliasing Signals for Inductive Debris Sensors. Sensors, 20(20), 5949. https://doi.org/10.3390/s20205949






