A Novel Alignment Method for SINS with Large Misalignment Angles Based on EKF2 and AFIS
Abstract
:1. Introduction
2. Nonlinear Error Equations of SINS with Large Misalignment Angles
2.1. Attitude Error Equation
2.2. Velocity Error Equation
3. Nonlinear Filtering Model and Second-Order EKF Algorithm
3.1. Filtering Model of SINS Nonlinear Alignment with Large Misalignment Angles
3.2. Simplified Second-Order EKF Algorithm
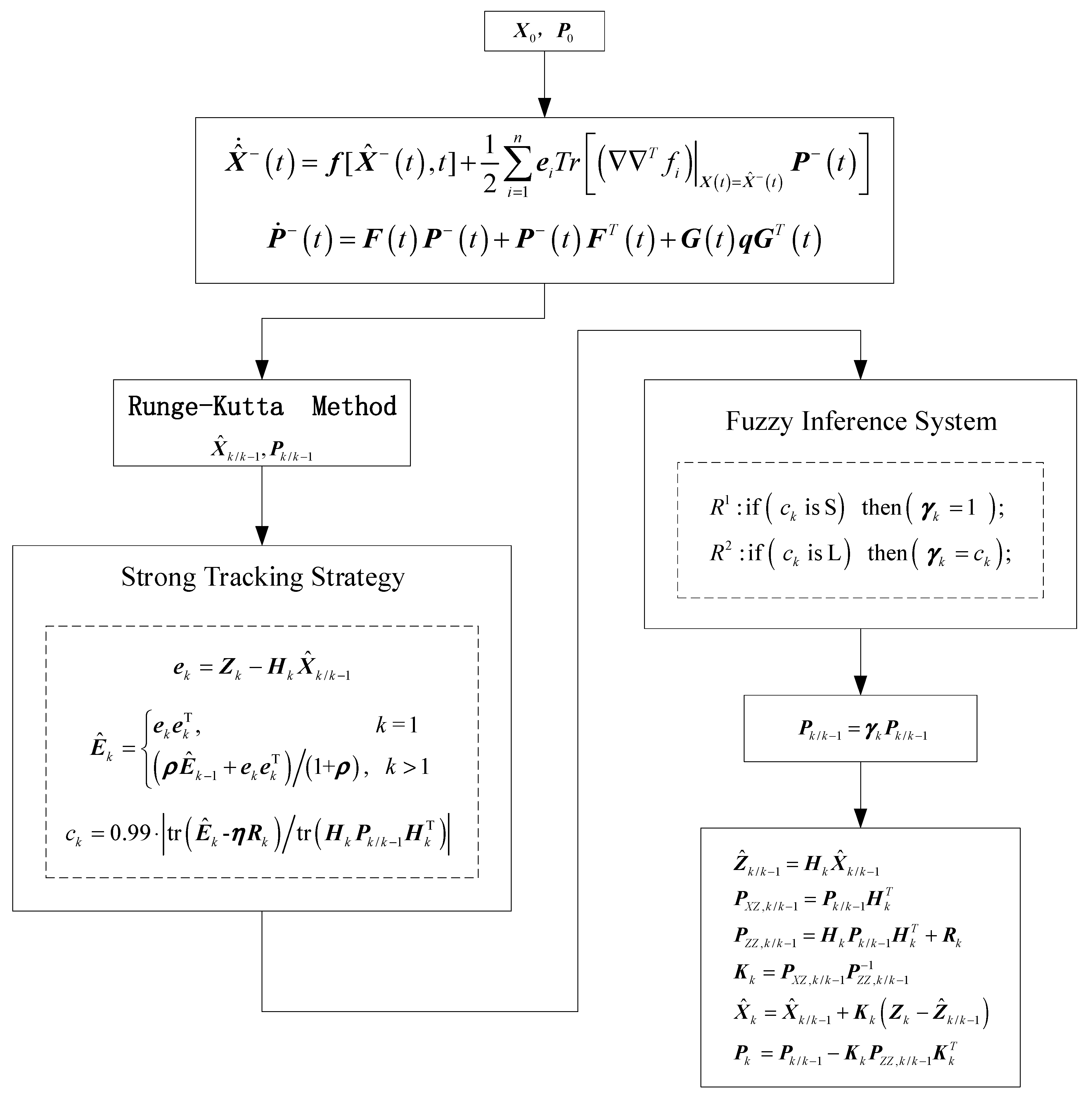
4. The Algorithms of Strong Tracking Strategy and Fuzzy Adaptive Parameter Adjustment
4.1. Strong Tracking Strategy
4.2. Fuzzy Adaptive Parameter Adjustment
5. Experiment Setup and Result Analysis
5.1. The Simulation of Fine Alignment on Stationary Base
5.1.1. Simulation Conditions
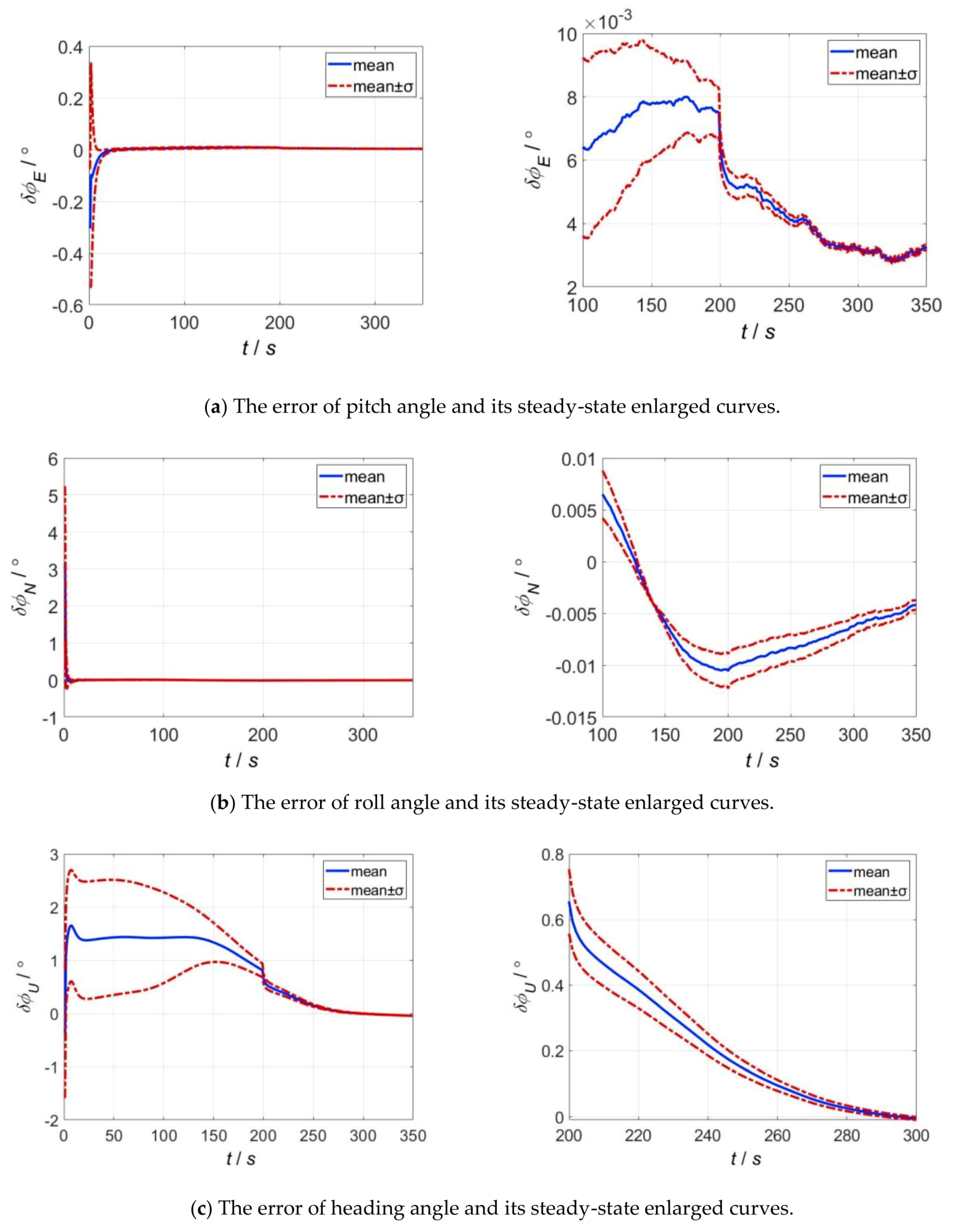
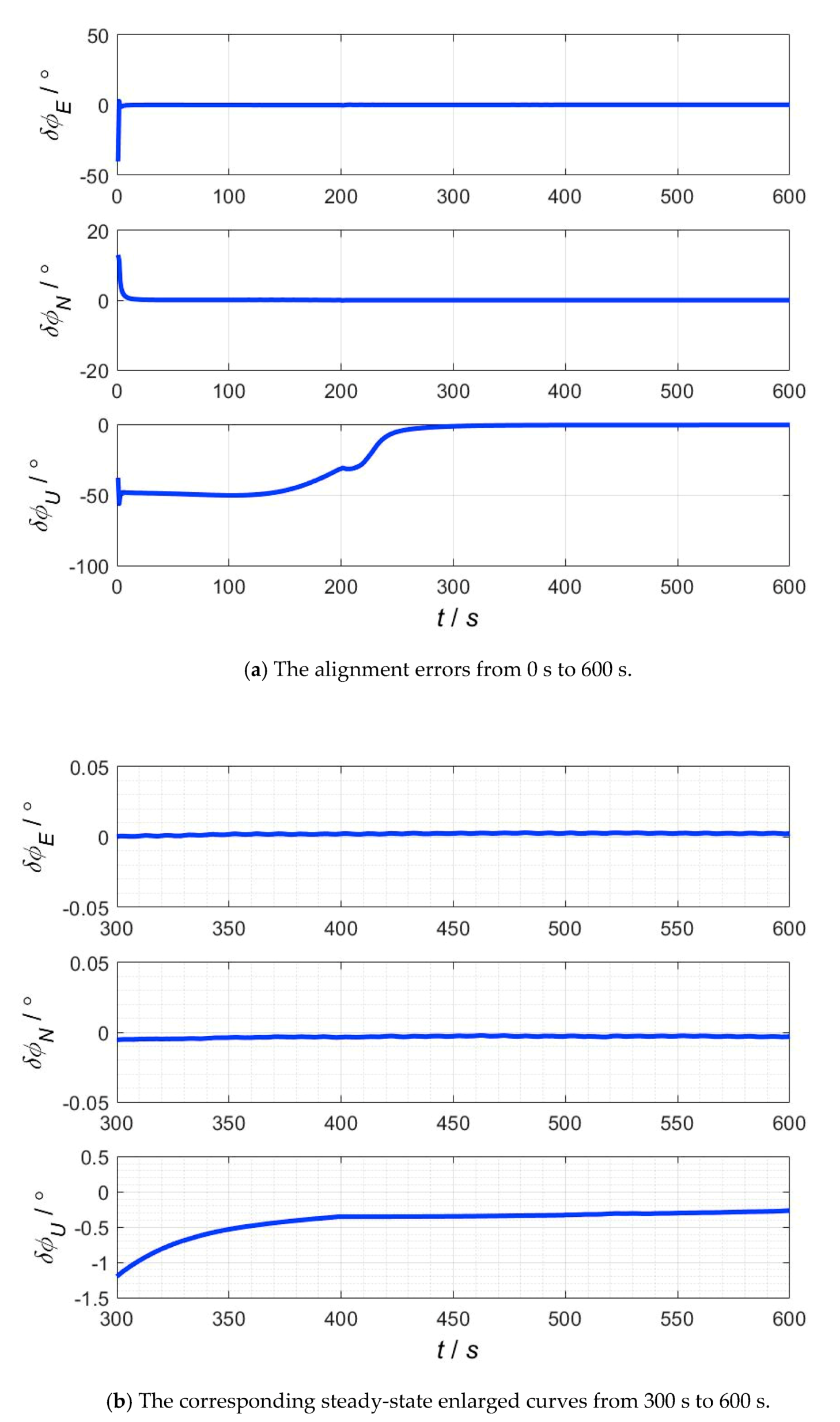
5.1.2. Simulation Results
5.2. The Simulation of Fine Alignment on Swaying Base
5.2.1. Simulation Conditions
5.2.2. Simulation Results
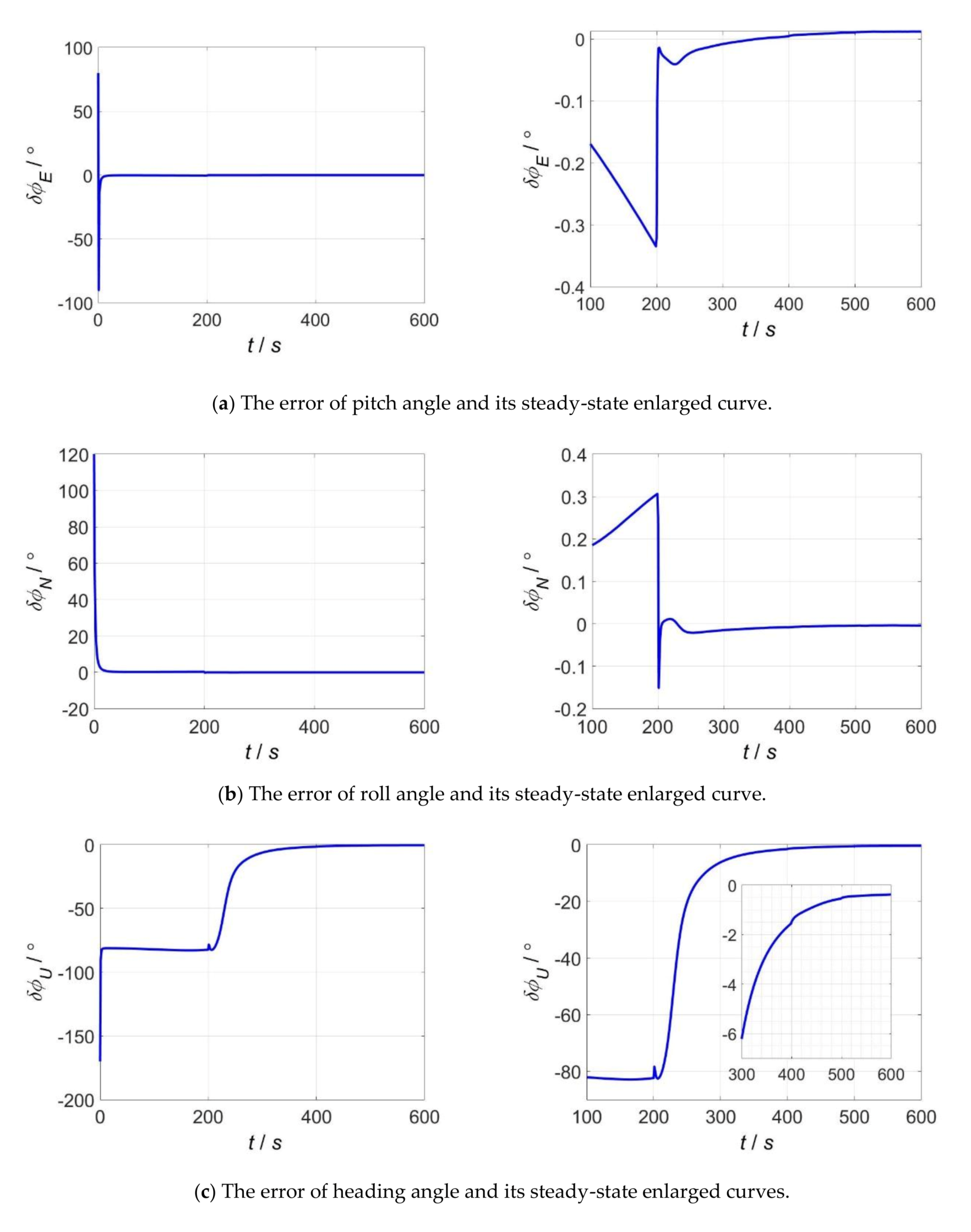
5.3. Experiment on Three-Axis Turntable
5.3.1. Experiment Conditions
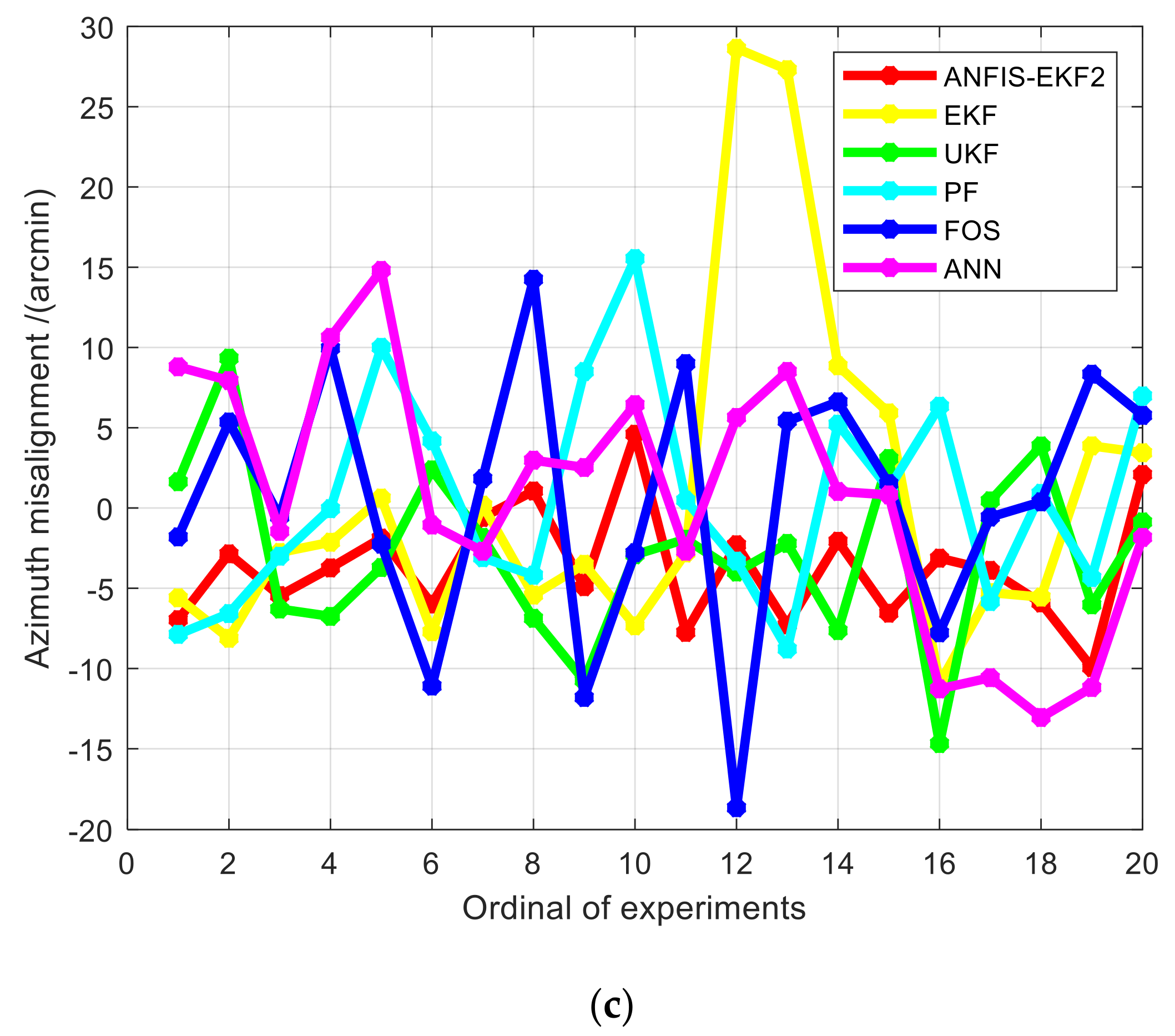
5.3.2. Experiment Results
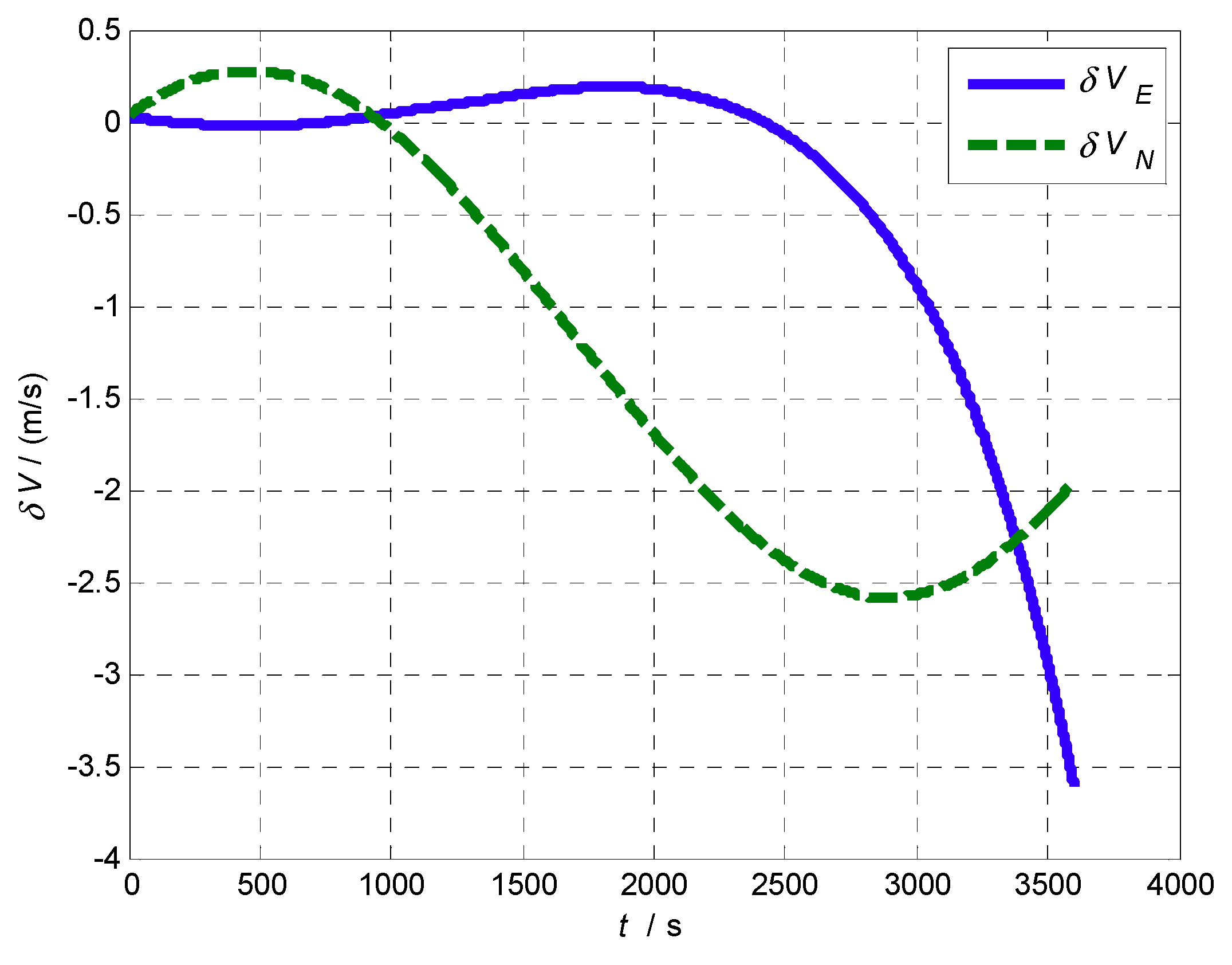
5.4. Navigation Experimental Test of SINS on Vehicle
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, S.; Wei, W.; Zhong, Y.; Feng, Z. Rapid alignment method based on local observability analysis for strapdown inertial navigation system. Acta Astronaut. 2014, 942, 790–798. [Google Scholar]
- Mei, C.; Qin, Y.; You, J. Nonlinear Measurement Based SINS Initial Alignment Algorithm Under Large Misalignment Angle. J. Astronaut. 2016, 37, 291–297. [Google Scholar]
- Zhao, L.; Guan, D.X.; Cheng, J.H.; Xu, X.M.; Fei, Z.H. Coarse Alignment of Marine Strapdown INS Based on the Trajectory Fitting of Gravity Movement in the Inertial Space. Sensors 2016, 16, 1714. [Google Scholar]
- Liu, X.; Xu, X.; Liu, Y.; Wang, L. A Method for SINS Alignment with Large Initial Misalignment Angles Based on Kalman Filter with Parameters Resetting. Math. Probl. Eng. 2014, 2014, 346291. [Google Scholar]
- Gao, W.; Xu, B.; Sun, H.; Yu, F. Application of Nonlinear Filtering for SINS Initial Alignment. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Luoyang, China, 25–28 June 2006; pp. 2259–2263. [Google Scholar]
- Cheng, J.; Wang, T.; Guan, D.; Li, M. Polar transfer alignment of shipborne SINS with a large misalignment angle. Meas. Sci. Technol. 2016, 27. [Google Scholar] [CrossRef] [Green Version]
- Shao, H.; Miao, L.; Gao, W.; Shen, J. Ensemble Particle Filter Based on KLD and Its Application to Initial Alignment of the SINS in Large Misalignment Angles. IEEE Trans. Ind. Electron. 2018, 65, 8946–8955. [Google Scholar]
- Salman, M.; Fang, J.C.; Xu, F. Nonlinear/linear combination filter for SINS alignment. In Proceedings of the 7th International Symposium on Instrumentation and Control Technology: Measurement Theory and Systems and Aeronautical Equipment, Beijing, China, 10–13 October 2008; Volume 7128. [Google Scholar]
- Yang, B.; Xu, X.; Zhang, T.; Sun, J.; Liu, X. Novel SINS Initial Alignment Method under Large Misalignment Angles and Uncertain Noise Based on Nonlinear Filter. Math. Probl. Eng. 2017, 2017, 5917917. [Google Scholar]
- Feng, J.; Yu, F.; Zhang, P.Y.; Zou, M.K. On initial alignment of large azimuth misalignment for SINS on the static base in Krein space. In Proceedings of the IEEE 10th World Congress on Intelligent Control and Automation (WCICA), Beijing, China, 6–8 July 2012; pp. 1964–1968. [Google Scholar]
- Zhao, L.; Nie, Q.; Gao, W. A Comparison of Nonlinear Filtering Approaches for In-motion Alignment of SINS. In Proceedings of the International Conference on Mechatronics and Automation (ICMA), Harbin, China, 5–8 August 2007; pp. 1310–1315. [Google Scholar]
- Xiong, Z.; Hao, Y.; Sun, F. SINS Rapid In-Motion Alignment Based on Nonlinear Filter. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; pp. 86–93. [Google Scholar]
- Cheng, K.; Huang, C.M.; Zhao, Y.Y. Study on SRUKF Applied in Initial Alignment with Large Misalignment Angle on Stationary Base of SINS. Adv. Mater. Res. 2011, 383, 5088–5093. [Google Scholar]
- Qian, H.; An, D.; Xia, Q. Application of SRUKF in SINS Initial Alignment for Large Misalignment Angles. Appl. Math. Model. 2010, 5, 303–308. [Google Scholar]
- Zhang, L.; Wu, W.; Wang, M.; Guo, Y. DVL-Aided SINS In-Motion Alignment Filter Based on a Novel Nonlinear Attitude Error Model. IEEE Access 2019, 7, 62457–62464. [Google Scholar]
- Yang, B.; Xu, X.S.; Zhang, T.; Liu, X.Y. Novel Nonlinear Filter for SINS Initial Alignment with Large Misalignment Angles. In Proceedings of the Integrated Communications Navigation and Surveillance Conference (ICNS), Herndon, VA, USA, 19–21 April 2016; pp. 3E2-1–3E2-10. [Google Scholar]
- Sun, W. Application of Sage-Husa adaptive filtering algorithm for high precision SINS initial alignment. In Proceedings of the 11th International Computer conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 19–21 December 2014; pp. 359–364. [Google Scholar]
- Li, H.; Wang, J.; Wang, S.; Liu, X. A method for SINS initial alignment of large misalignment angles based on simplified Sage-Husa filter with parameters resetting. In Proceedings of the Forum on Cooperative Positioning and Service (CPGPS), Harbin, China, 19–21 May 2017; pp. 278–282. [Google Scholar]
- Pei, F.; Zhu, L.; Zhao, J. Initial Self-Alignment for Marine Rotary SINS Using Novel Adaptive Kalman Filter. Math. Probl. Eng. 2015, 2015, 320536. [Google Scholar]
- Chu, H.; Sun, T.; Zhang, B.; Zhang, H.; Chen, Y. Rapid Transfer Alignment of MEMS SINS Based on Adaptive Incremental Kalman Filter. Sensors 2017, 17, 152. [Google Scholar]
- Su, W. Application of an Adaptive Nonlinear Filtering Algorithm Based on Large Azimut Misalignment Self Alignment of SINS. In Proceedings of the International Conference on Software Engineering and Information System (SEIS), Changsha, China, 12–13 December 2015; pp. 201–208. [Google Scholar]
- Su, W. An adaptive UKF filtering algorithm for self-alignment in the swaying base of SINS. In Proceedings of the 4th National Conference on Electrical, Electronics and Computer Engineering (NCEECE), Xi’an, China, 12–13 December 2015; pp. 1350–1356. [Google Scholar]
- Su, W. Application of adaptive Sage-Husa and AUKF filtering algorithm In Initial Alignment of SINS. In Proceedings of the 4th International Conference on Mechatronics, Materials, Chemistry and Computer Engineering (ICMMCCE), Xi’an, China, 12–13 December 2015; pp. 1933–1939. [Google Scholar]
- Zhang, Y.G.; Xu, G.; Liu, X. An Improved SINS Alignment Method Based on Adaptive Cubature Kalman Filter. Sensors 2019, 19, 5509. [Google Scholar]
- Chi, F.; Sun, F.; Yuan, S.; Xiao, Y. The Application of Adaptive Square Root Cubature Particle Filtering Algorithm in Initial Alignment of Large Azimuth Misalignment in SINS. J. Inf. Comput. Sci. 2013, 10, 5891–5901. [Google Scholar]
- Sun, J.; Xu, X.; Liu, Y.; Zhang, T.; Li, Y. Initial Alignment of Large Azimuth Misalignment Angles in SINS Based on Adaptive UPF. Sensors 2015, 15, 21807–21823. [Google Scholar]
- Yang, J.; Yuan, X.; Zhang, Y. A Fast Initial Alignment Method for SINS Used Adaptive Sample Size Unscented Particle Filter. In Proceedings of the International Conference on Chemical, Material and Food Engineering (CMFE), Kunming, China, 25–26 July 2015; pp. 660–663. [Google Scholar]
- Xu, H.; Pei, F.; Jiang, N. An In-Motion Initial Alignment Algorithm for SINS Using Adaptive Lie Group Filter. In Proceedings of the Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 4581–4586. [Google Scholar]
- Huang, D.; Zhang, X.; Liu, J. SINS initial alignment method using robust filtering for Towed Ocean Bottom Magnetometer. In Proceedings of the IEEE Oceans Conference, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–6. [Google Scholar]
- Wu, Z.; Wang, Y.; Zhu, X. Application of Nonlinear H∞ Filtering Algorithm for Initial Alignment of the Missile-borne SINS. AASRI Procedia 2014, 9, 99–106. [Google Scholar]
- Lyu, W.; Cheng, X.; Wang, J. An Improved Adaptive Compensation H∞ Filtering Method for the SINS’ Transfer Alignment under a Complex Dynamic Environment. Sensors 2019, 19, 401. [Google Scholar]
- Zha, F.; Guo, S.; Li, F. An improved nonlinear filter based on adaptive fading factor applied in alignment of SINS. Optik 2019, 184, 165–176. [Google Scholar]
- Guo, S.; Chang, L.; Li, Y.; Sun, Y. Robust fading cubature Kalman filter and its application in initial alignment of SINS. Optik 2019, 202, 163593. [Google Scholar]
- Zhang, L.; Yang, C.; Chen, Q.; Yan, F. Robust H-infinity CKF/KF hybrid filtering method for SINS alignment. IET Sci. Meas. Technol. 2016, 10, 916–925. [Google Scholar]
- Chi, F.; Gao, W. The application of robust adaptive cubature particle filter algorithm in initial alignment of SINS. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Harbin, China, 7–10 August 2016; pp. 1344–1349. [Google Scholar]
- Wang, D.Y.; Sun, P.; Peng, J.Y.; Xu, X.H. SINS Transfer Alignment Based on Robust SDRE Filter. Appl. Mech. Mater. 2014, 597, 557–561. [Google Scholar]
- Gu, D.; Qin, Y.; Zheng, J. Fuzzy adaptive Kalman filter for marine SINS initial alignment. In Proceedings of the 6th International Symposium on Test and Measurement (ISTM), Dalian, China, 1–4 June 2005; pp. 7473–7476. [Google Scholar]
- Yang, W.; Miao, L.; Guo, Z. Research of Fuzzy Inference based on Simplified UKF for large alignment errors in SINS alignment on a swaying base. In Proceedings of the IEEE International Conference on Advanced Computational Intelligence (ICACI), Nanjing, China, 8–20 October 2012; pp. 539–544. [Google Scholar]
- Li, J.; Song, N.; Yang, G.; Jiang, R. Fuzzy adaptive strong tracking scaled unscented Kalman filter for initial alignment of large misalignment angles. Rev. Sci. Instrum. 2016, 87, 75118. [Google Scholar]
- Wu, S.; Wang, B.; Zhou, Z.; Wang, H.; Song, L. The Application of the Fuzzy Strong Tracking UKF in the SINS Swing Base Initial Alignment. In Proceedings of the IEEE 6th International Conference on Intelligent Human- Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 26–27 August 2014; pp. 313–318. [Google Scholar]
- Sun, L.; Yi, W.; Yuan, D.; Guan, J. Application of Elman Neural Network Based on Genetic Algorithm in Initial Alignment of SINS for Guided Projectile. Math. Probl. Eng. 2019, 2019, 5810174. [Google Scholar]
- Wang, X.; Shen, L. Solution of transfer alignment problem of SINS on moving bases via neural networks. Eng. Computation. 2011, 28, 372–388. [Google Scholar]
- Li, T. The Initial Alignment of SINS Based on Neural Network. In Proceedings of the 6th International Symposium on Neural Networks (ISNN), Wuhan, China, 26–29 May 2009; pp. 1–6. [Google Scholar]
- Lin, X.; Li, T. Initial alignment of SINS based on N-Tupple neural network. In Proceedings of the 7th International Symposium on Test and Measurement (ISTM), Beijing, China, 5–8 August 2007; pp. 2280–2283. [Google Scholar]
- Xu, B.; Sun, F.; Yu, F.; Liu, F. A Fast and Optimal Method Based on Fuzzy Neural Networks for SINS Initial Alignment. In Proceedings of the First International Workshop on Knowledge Discovery and Data Mining (WKDD), Adelaide, Australia, 23–24 January 2008; pp. 601–606. [Google Scholar]
- Zhao, X.; Wang, L.; He, Z.; Zhang, B.; Zhao, H. Initial alignment of large misalignment angle in strapdown inertial navigation system based on Gaussian process regression. In Proceedings of the IEEE 26th Chinese Control and Decision Conference (CCDC), Changsha, China, 31 May–2 June 2014; pp. 3114–3118. [Google Scholar]
- Xiang, L.; Liu, Y.; Su, B.; Jiang, X. A novel nonlinear filter for initial alignment in strapdown inertial navigation system. In Proceedings of the IEEE 2nd International Symposium on Systems and Control in Aerospace and Astronautics (ISSCAA), Shenzhen, China, 10–12 December 2008; pp. 1–6. [Google Scholar]
- Abosekeen, A.; Iqbal, U.; Noureldin, A.; Korenberg, M.J. A Novel Multi-Level Integrated Navigation System for Challenging GNSS Environments. IEEE T. Intell. Transp. 2020, 1–15. [Google Scholar] [CrossRef]
- Deng, Z.L.; Mo, J.; Jia, B.Y.; Bian, X.M. A Fine Frequency Estimation Algorithm Based on Fast Orthogonal Search (FOS) for Base Station Positioning Receivers. Electronics 2018, 7, 376. [Google Scholar]
- Nematallah, H.; Korenberg, M.; Noureldin, A.; Atia, M.M. Enhancing Vision-Aided GNSS/INS Navigation Systems Using Nonlinear Modeling Techniques Based on Fast Orthogonal Search with Double-Filtering Mechanism. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2014), Tampa, FL, USA, 8–12 September 2014; pp. 627–634. [Google Scholar]
- Tamazin, M.; Noureldin, A.; Korenberg, M.J. Robust Modeling of Low-Cost MEMS Sensor Errors in Mobile Devices Using Fast Orthogonal Search. J. Sens. 2013, 2013, 101820. [Google Scholar]
- Zhou, D.H.; Frank, P.M. Strong tracking filtering of nonlinear time-varying stochastic systems with coloured noise: Application to parameter estimation and empirical robustness analysis. Int. J. Control 1996, 65, 295–307. [Google Scholar]
- Hu, G.G.; Gao, S.S.; Zhong, Y.M.; Gao, B.B.; Subic, A. Modified strong tracking unscented Kalman filter for nonlinear state estimation with process model uncertainty. Int. J. Adapt. Control 2015, 29, 1561–1577. [Google Scholar]
- Deng, Z.H.; Yin, L.J.; Huo, B.Y.; Xia, Y.Q. Adaptive robust unscented Kalman filter via fading factor and maximum correntropy criterion. Sensors 2018, 18, 2406. [Google Scholar]

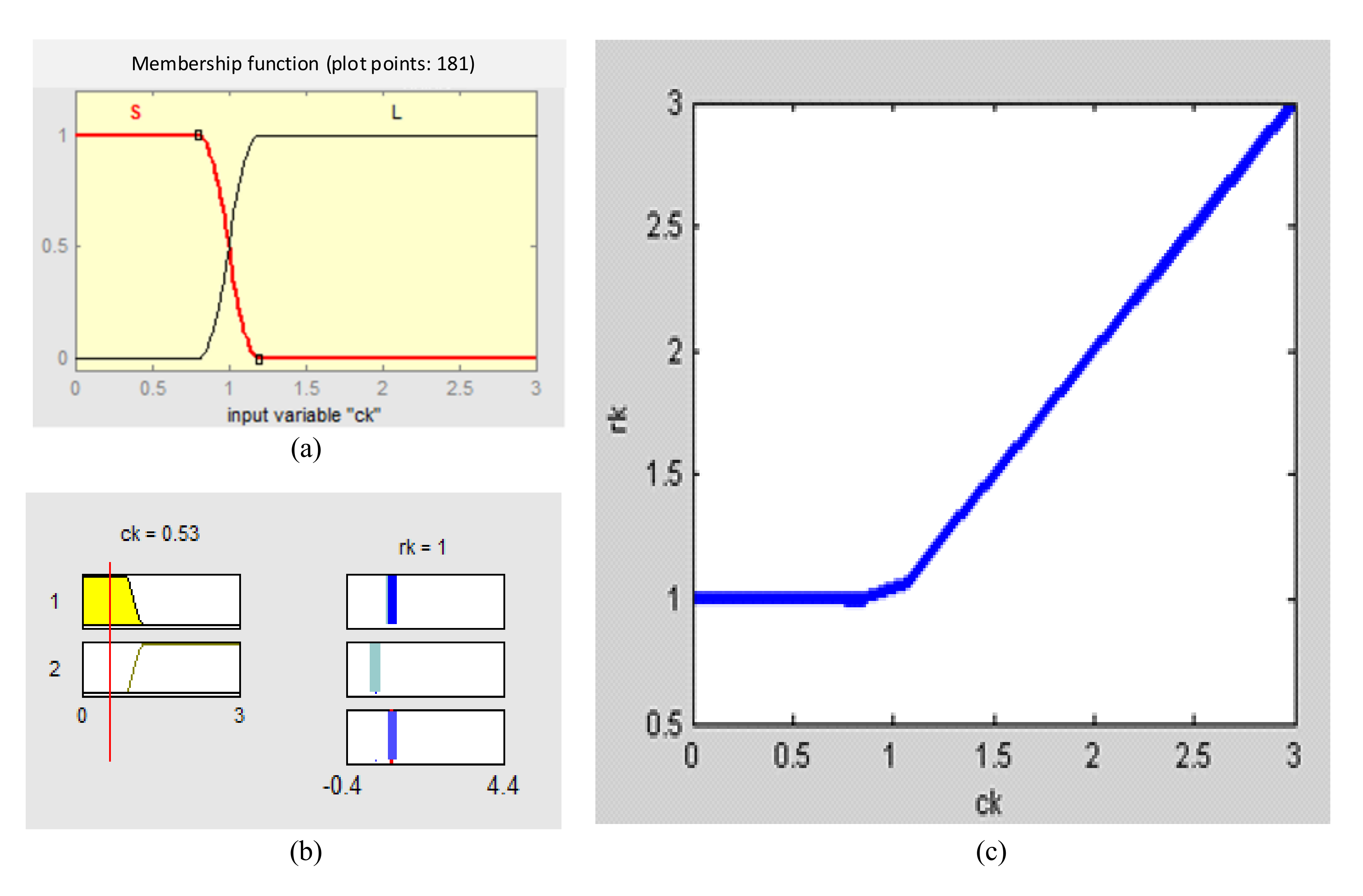





| Fuzzy Subsets | Domain | Membership Functions | Break Points |
|---|---|---|---|
| Small (S) | [0, 3] | zmf | [0.8, 1.2] |
| Large (L) | [0, 3] | smf | [0.8, 1.2] |
| Errors (°) | |||
|---|---|---|---|
| RMSE | 0.0032 | 0.0042 | 0.1271 |
| Limits | 0.0029 | −0.0029 | 0.0924 |
| Parameters | Value |
|---|---|
| Gyro measurement range | ±600°/s |
| Gyro bias stability | <0.01°/h |
| Gyro angle random walk | <0.001°/h1/2 |
| Accelerometer measurement range | ±20 g |
| Accelerometer bias stability | <50 µg |
| Accelerometer velocity random walk | <5 µg/h1/2 |
| Parameters | Value |
|---|---|
| Gyration accuracy | ±2″ |
| Rotation range | 0~360° |
| Angle accuracy | ±2″ |
| Angular repeatability | ±1″ |
| Angular rate range | 0.001~200°/s |
| Angular rate accuracy | 5 × 10−4°/s |
| Experiments | Initial Misalignment Angles | ||
|---|---|---|---|
| East | North | Azimuth | |
| Experiment 1 | |||
| Experiment 2 | |||
| Experiments | Method | Misalignment Angle Error RMSE (′) | ||
|---|---|---|---|---|
| East | North | Azimuth | ||
| Experiment 1 | AFIS-EKF2 | 0.2280 | 0.2520 | 4.5720 |
| EKF | 0.7079 | 0.9360 | 8.1605 | |
| UKF | 0.8164 | 0.9245 | 6.5188 | |
| PF | 0.8980 | 0.8782 | 5.8669 | |
| EKF-based FOS | 0.7787 | 1.0828 | 9.4473 | |
| EKF-based ANN | 0.9730 | 1.1793 | 8.5884 | |
| Experiment 2 | AFIS-EKF2 | 0.7302 | −0.2396 | −22.7640 |
| EKF | Failure | |||
| UKF | Failure | |||
| PF | Failure | |||
| EKF-based FOS | Failure | |||
| EKF-based ANN | Failure | |||
| t (s) | VE (m/s) | VN (m/s) | L (m) | λ (m) |
|---|---|---|---|---|
| 500 s | −0.018818 | 0.27268 | 101.89 | −1.3953 |
| 1000 s | 0.045686 | −0.044207 | 183.29 | 0.72195 |
| 1500 s | 0.14902 | −0.80396 | −16.265 | 59.255 |
| 2000 s | 0.17986 | −1.6915 | −644.07 | 167.41 |
| 2500 s | −0.065639 | −2.3809 | −1680.2 | 220.19 |
| 3000 s | −0.88205 | −2.5697 | −2946.9 | −24.945 |
| 3500 s | −2.9383 | −2.1155 | −4142.2 | −1083.3 |
| 3600 s | −3.6086 | −1.9593 | −4345.4 | −1474.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yan, G.; Qin, Y.; Fu, Q. A Novel Alignment Method for SINS with Large Misalignment Angles Based on EKF2 and AFIS. Sensors 2020, 20, 5975. https://doi.org/10.3390/s20215975
Zhao Y, Yan G, Qin Y, Fu Q. A Novel Alignment Method for SINS with Large Misalignment Angles Based on EKF2 and AFIS. Sensors. 2020; 20(21):5975. https://doi.org/10.3390/s20215975
Chicago/Turabian StyleZhao, Yanming, Gongmin Yan, Yongyuan Qin, and Qiangwen Fu. 2020. "A Novel Alignment Method for SINS with Large Misalignment Angles Based on EKF2 and AFIS" Sensors 20, no. 21: 5975. https://doi.org/10.3390/s20215975
APA StyleZhao, Y., Yan, G., Qin, Y., & Fu, Q. (2020). A Novel Alignment Method for SINS with Large Misalignment Angles Based on EKF2 and AFIS. Sensors, 20(21), 5975. https://doi.org/10.3390/s20215975








