The Degradation of Automotive Radar Sensor Signals Caused by Vehicle Vibrations and Other Nonlinear Movements
Abstract
:1. Introduction
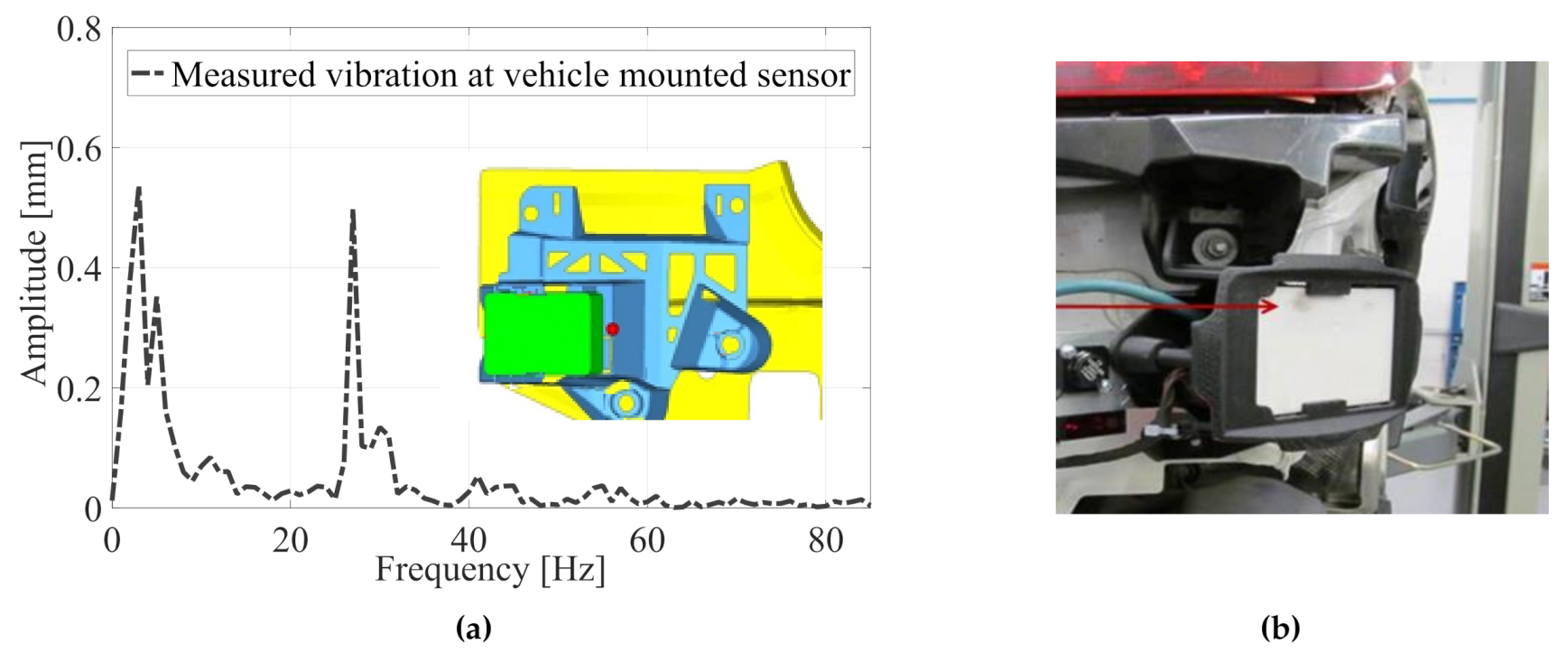
2. Vehicles Measurements
3. Theoretical Signal Deviations Due to Nonlinear Movements
3.1. Advanced Beat Signal Model
3.2. Signal Theories for Nonlinear Movements
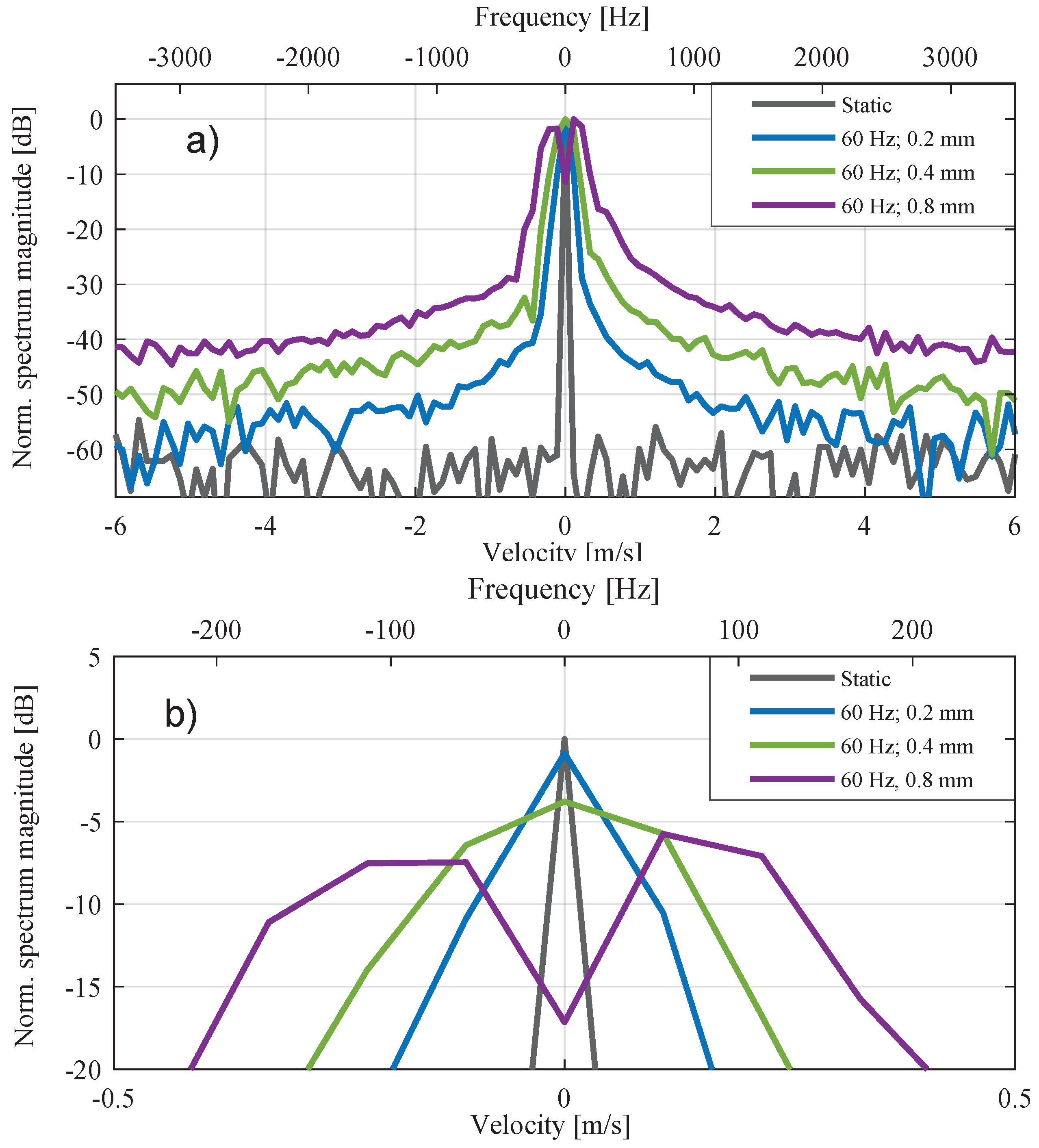
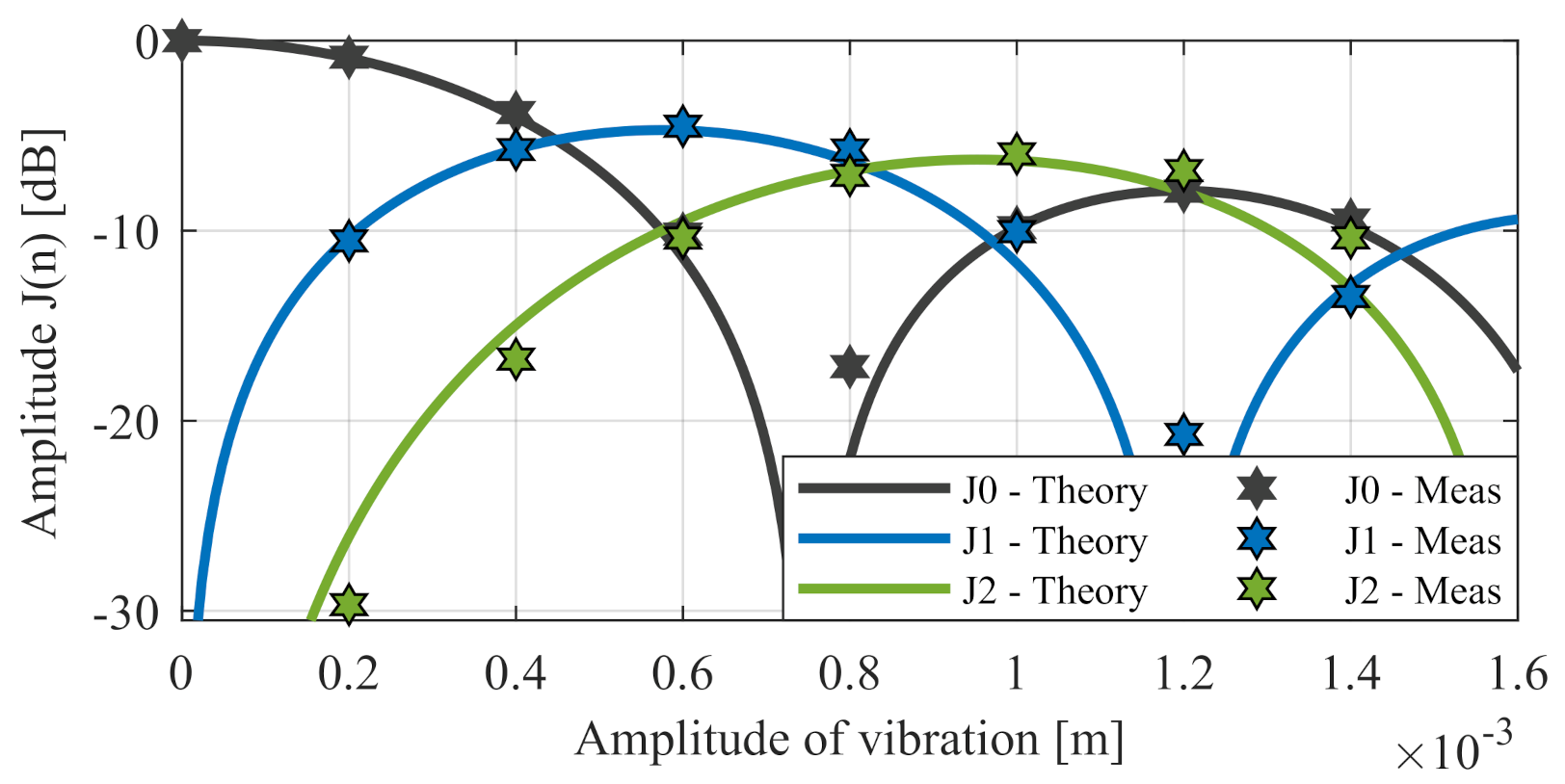
3.2.1. Sinusoidal Nonlinearity
Constant Acceleration
Complex Acceleration
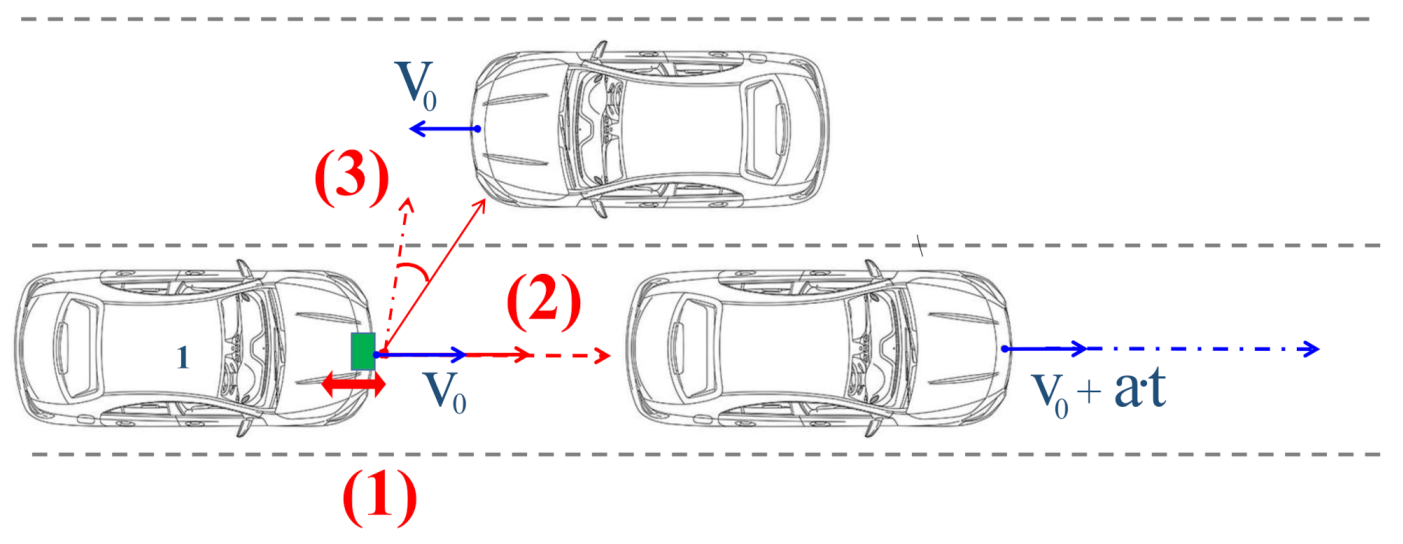
4. Effects on Real Road Users
5. From Signal Deviations to SNR degradation
5.1. General Contributions to SNR
5.2. Nonlinear Effects on Noise Level
6. Materials and Methods
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FMCW | Frequency modulated continuous wave |
| SNR | Signal-to-noise ratio |
| OS C-FAR | Ordered statistic constant false alarm rate |
References
- Winner, H.; Hakuli, S.; Wolf, G. Handbuch Fahrerassistenzsysteme, 2nd ed; Springer: Wiesbaden, Germany, 2012; Volume 4, pp. 123–177. [Google Scholar]
- Dickmann, J.; Appendrodt, N.; Klappstein, J.; Bloecher, H.; Muntzinger, M.; Sailer, A.; Hahn, M.; Brenk, C. Making Bertha See Even More: Radar Contribution. IEEE Access 2015, 3, 1233–1247. [Google Scholar] [CrossRef]
- Shapir, I.; Bilik, I.; Barkan, G. Doppler ambiguity resolving in TDMA automotive MIMO radar via digital multiple PRF. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 0175–0180. [Google Scholar]
- Jansen, F.G. Automotive Radar Doppler Division MIMO With Velocity Ambiguity Resolving Capabilities. In Proceedings of the 2019 16th European Radar Conference (EuRAD), Paris, France, 2–4 October 2019; pp. 245–248. [Google Scholar]
- Duggal, G.; Sundar Ram, S.; Mishra, K.V. Micro-Doppler and Micro-Range Detection via Doppler-resilient 802.11ad-Based Vehicle-to-Pedestrian Radar. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019. [Google Scholar]
- Sun, Y.; Fei, T.; Schliep, F.; Pohl, N. Gesture Classification with Handcrafted Micro-Doppler Features using a FMCW Radar. In Proceedings of the 2018 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Munich, Germany, 15–17 April 2018; pp. 1–4. [Google Scholar]
- Peng, Z.; Li, C.; Muñoz-Ferreras, J.; Gómez-García, R. An FMCW Radar Sensor for Human Gesture Recognition in the Presence of Multiple Targets. In Proceedings of the 2017 First IEEE MTT-S International Microwave Bio Conference (IMBIOC), Gothenburg, Sweden, 15–17 May 2017. [Google Scholar]
- Kellner, D.; Barjenbruch, M.; Klappstein, J.; Dickmann, J.; Dietmayer, K. Instantaneous ego-motion estimation using Doppler radar. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC), The Hague, The Netherlands, 6–9 October 2013; pp. 869–874. [Google Scholar]
- Liang, Y.; Zhang, Q.; Luo, Y.; Bai, Y.; Chen, Y. Micro-Doppler Features Analysis and Extraction of Vibrating Target in FMCW SAR Based on Slow Time Envelope Signatures. IEEE Geosci. Remote. Sens. Lett. 2015, 12, 2041–2045. [Google Scholar] [CrossRef]
- Lee, J.; Kim, D.; Jeong, S.; Ahn, G.; Kim, Y. Target classification scheme using phase characteristics for automotive FMCW radar. Electron. Lett. 2019, 52, 2061–2063. [Google Scholar] [CrossRef]
- Harter, M.; Hildebrandt, J. Vibrations in Automotive Radar Systems. In Proceedings of the 2016 IEEE Internaional conference on Microwave for Intellegent Mobility (ICMIM), San Diego, CA, USA, 19–20 May 2016. [Google Scholar]
- John, J.P.; Kirchgessner, J.; Ma, R.; Morgan, D.; To, I.; Trivedi, V.P. Si-based Technologies for mmWave Automotive Radar. In Proceedings of the 2016 IEEE Compound Semiconductor Integrated Circuit Symposium (CSICS), Austin, TX, USA, 23–26 October 2016. [Google Scholar]
- Stelzer, A.; Kolmhofer, E.; Scheiblhofer, S. Fast 77 GHz Chirps with Direct Digital Synthesisand Phase Locked Loop. In Proceedings of the Asia Pacific Microwave Conference Proceedings, Suzhou, China, 4–7 December 2005. [Google Scholar]
- Shi, T.; Gong, Y.; Buch, C.; Ravichandran, S.; Sundaam, V.; Cressler, J.D.; Tummala, R. Next Generation of Automotive Radar with Leading-edge Advances in SiGe Devices and Glass Panel Embedding (GPE). In Proceedings of the IEEE 68th Electronic Components and Technology Conference, San Diego, CA, USA, 29 May–1 June 2018. [Google Scholar]
- Taha, I.; Mirhassani, M.; Emadi, A. A Monotonically Linear DCO for 77 GHz Automotive Radars. In Proceedings of the 2018 IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS), Windsor, ON, Canada, 5–8 August 2018; pp. 77–80. [Google Scholar]
- Porranzl, M.; Wagner, C.; Jaeger, H.; Stelzer, A. An Active Quasi-Circulator for 77-GHz Automotive FMCW Radar Systems in SiGe Technology. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 313–315. [Google Scholar] [CrossRef]
- Ayhan, S.; Scherr, S.; Bhutani, A.; Fischbach, B.; Pauli, M.; Zwick, T. Impact of Frequency Ramp Nonlinearity, Phase Noise, and SNR on FMCW Radar Accuracy. IEEE Trans. Microw. Theory Tech. 2016, 64, 3290–3301. [Google Scholar] [CrossRef]
- Pichler, M.; Stelze, A.; Gulden, P.; Vossiek, M. Influence of Systematic Frequency-Sweep Nonlinearity on Object Distance Estimation in FMCW IF-SCW Radar Systems. In Proceedings of the 33rd European Microwave Conference, Munich, Germany, 4–6 November 2003. [Google Scholar]
- Piper, S.O. Homodyne FMCW radar range resolution effects with sinusoidal nonlinearities in the frequency sweep. In Proceedings of the Proceedings International Radar Conference, Alexandria, VA, USA, 8–11 May 1995; pp. 563–567. [Google Scholar]
- Cooper, K.B.; Durden, S.L.; Cochrane, C.J.; Monje, R.R.; Dengler, R.J.; Baldi, C. Using FMCW Doppler Radar to Detect Targets up to the Maximum Unambiguous Range. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 339–343. [Google Scholar] [CrossRef]
- Grosch, T. Correcting Nonlinear Modulation Error in Linear FMCW Radar Systems. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1577–1581. [Google Scholar]
- Ebelt, R.; Shmakov, D.; Vossiek, M. The effect of phase noise on ranging uncertainty in FMCW secondary radar-based local positioning systems. In Proceedings of the 9th European Radar Conference (Eu-RAD 2012), Amsterdam, The Netherlands, 31 October–2 November 2012; pp. 258–261. [Google Scholar]
- Thurn, K.; Ebelt, R.; Vossiek, M. Noise in homodyne FMCW Radar Systems and its effects on ranging precision. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013. [Google Scholar]
- Hau, F.; Baumgärtner, F.; Vossiek, M. Influence of Vibrations on the Signals of Automotive Integrated Radar Sensors. In Proceedings of the 2017 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Nagoya, Japan, 19–21 March 2017; pp. 159–162. [Google Scholar]
- Richards, M.A. Principles of Modern Radar; Scheer, J., Holm, W.A., Melvin, W.L., Eds.; SciTech Pub.: Raleigh, NC, USA, 2010. [Google Scholar]
- Banerjee, D. PLL Performance, Simulation and Design, 4th ed.; Dog Ear Publishing: Indianapolis, IN, USA, 2006. [Google Scholar]
- Klauder, J.R.; Price, A.C.; Darlington, S.; Albersheim, W.J. The theory and design of chirp radars. Bell Syst. Tech. J. 1960, 39, 745–808. [Google Scholar] [CrossRef]

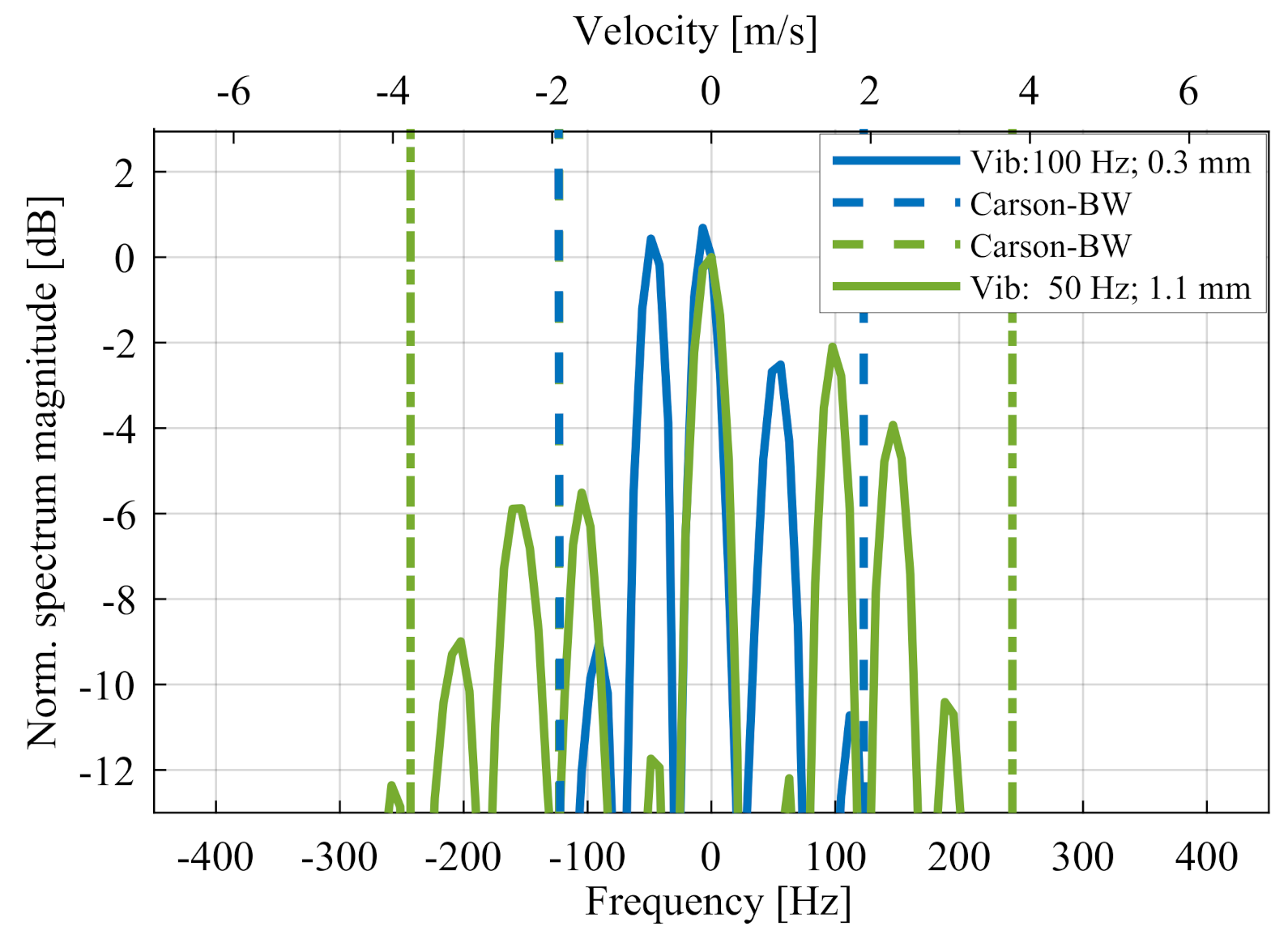
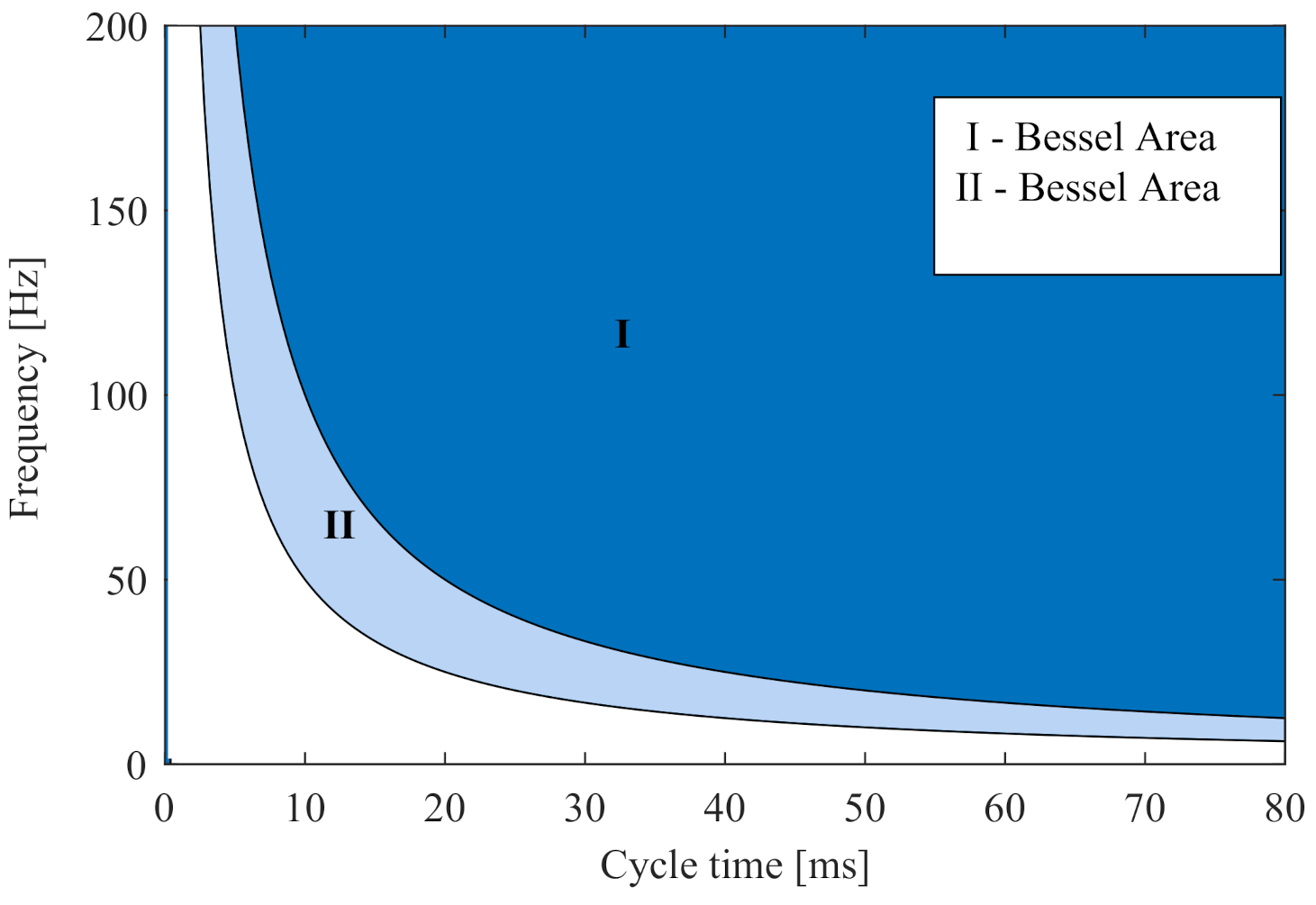


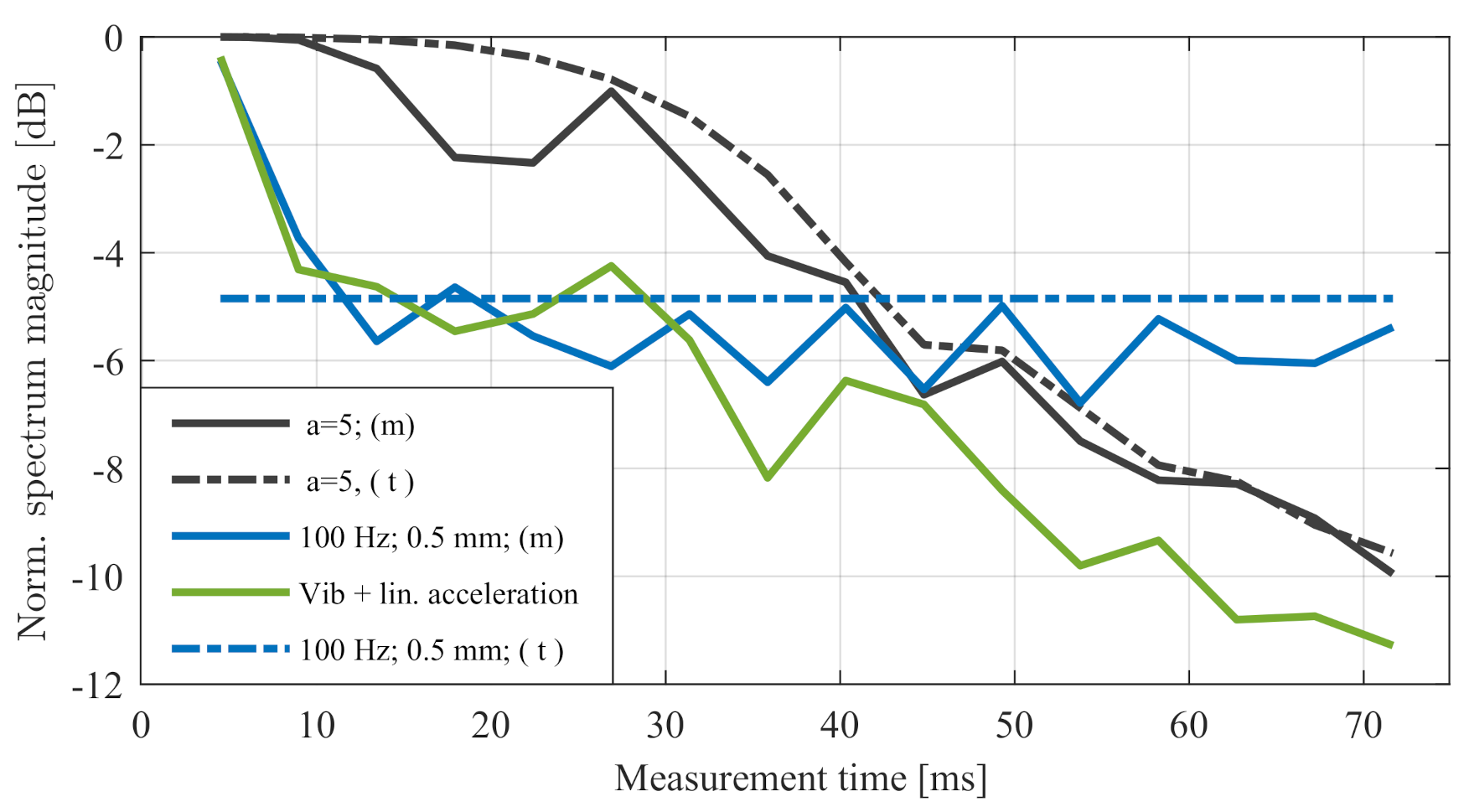

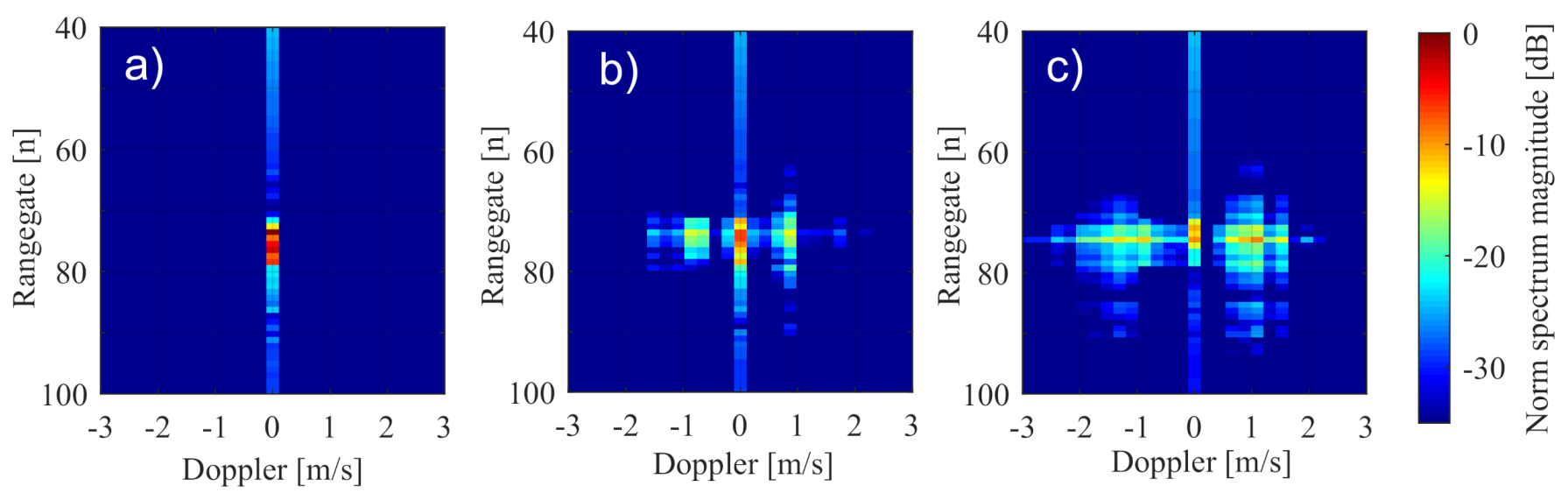

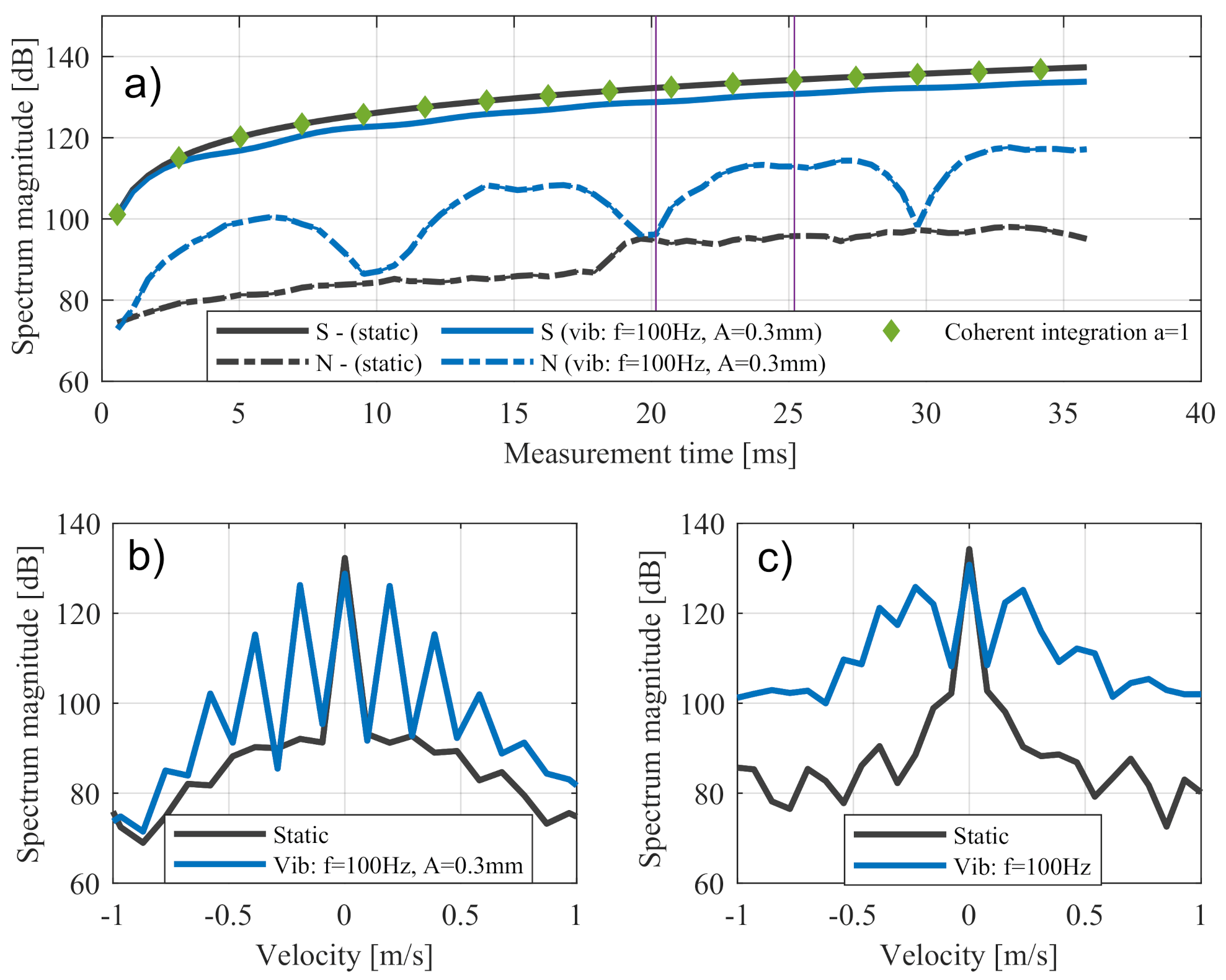
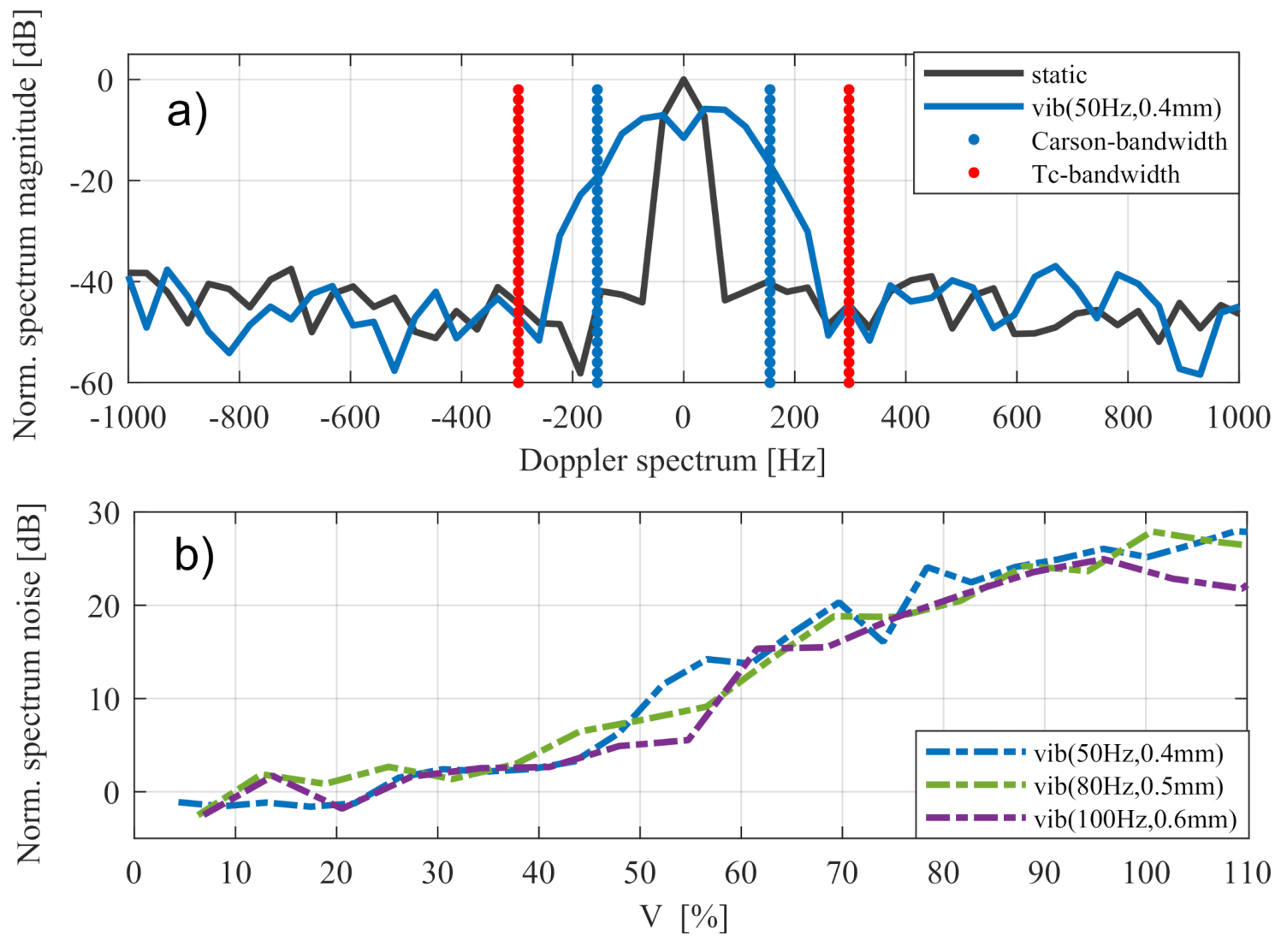

| Vibration Type | Frequency | Amplitude | Signal Degradation |
|---|---|---|---|
| weak vibration amplitudes | any | <0.2 mm | <2 dB |
| moderate vibration amplitudes | any | 0.2–0.5 mm | 2–5 dB |
| strong vibration amplitudes | any | >0.5 mm | >5 dB |
| Acceleration Type | Cycle Time | Acceleration | Signal Degradation |
|---|---|---|---|
| weak acceleration | 0–20 ms | <3 | <2 dB |
| moderate acceleration | 20–35 ms | 3–5 | 2–4 dB |
| strong acceleration | >20 ms | >5 | >4 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hau, F.; Baumgärtner, F.; Vossiek, M. The Degradation of Automotive Radar Sensor Signals Caused by Vehicle Vibrations and Other Nonlinear Movements. Sensors 2020, 20, 6195. https://doi.org/10.3390/s20216195
Hau F, Baumgärtner F, Vossiek M. The Degradation of Automotive Radar Sensor Signals Caused by Vehicle Vibrations and Other Nonlinear Movements. Sensors. 2020; 20(21):6195. https://doi.org/10.3390/s20216195
Chicago/Turabian StyleHau, Florian, Florian Baumgärtner, and Martin Vossiek. 2020. "The Degradation of Automotive Radar Sensor Signals Caused by Vehicle Vibrations and Other Nonlinear Movements" Sensors 20, no. 21: 6195. https://doi.org/10.3390/s20216195





