How Good Are RGB Cameras Retrieving Colors of Natural Scenes and Paintings?—A Study Based on Hyperspectral Imaging
Abstract
:1. Introduction
2. Materials and Methods
2.1. Paintings and Natural Scenes
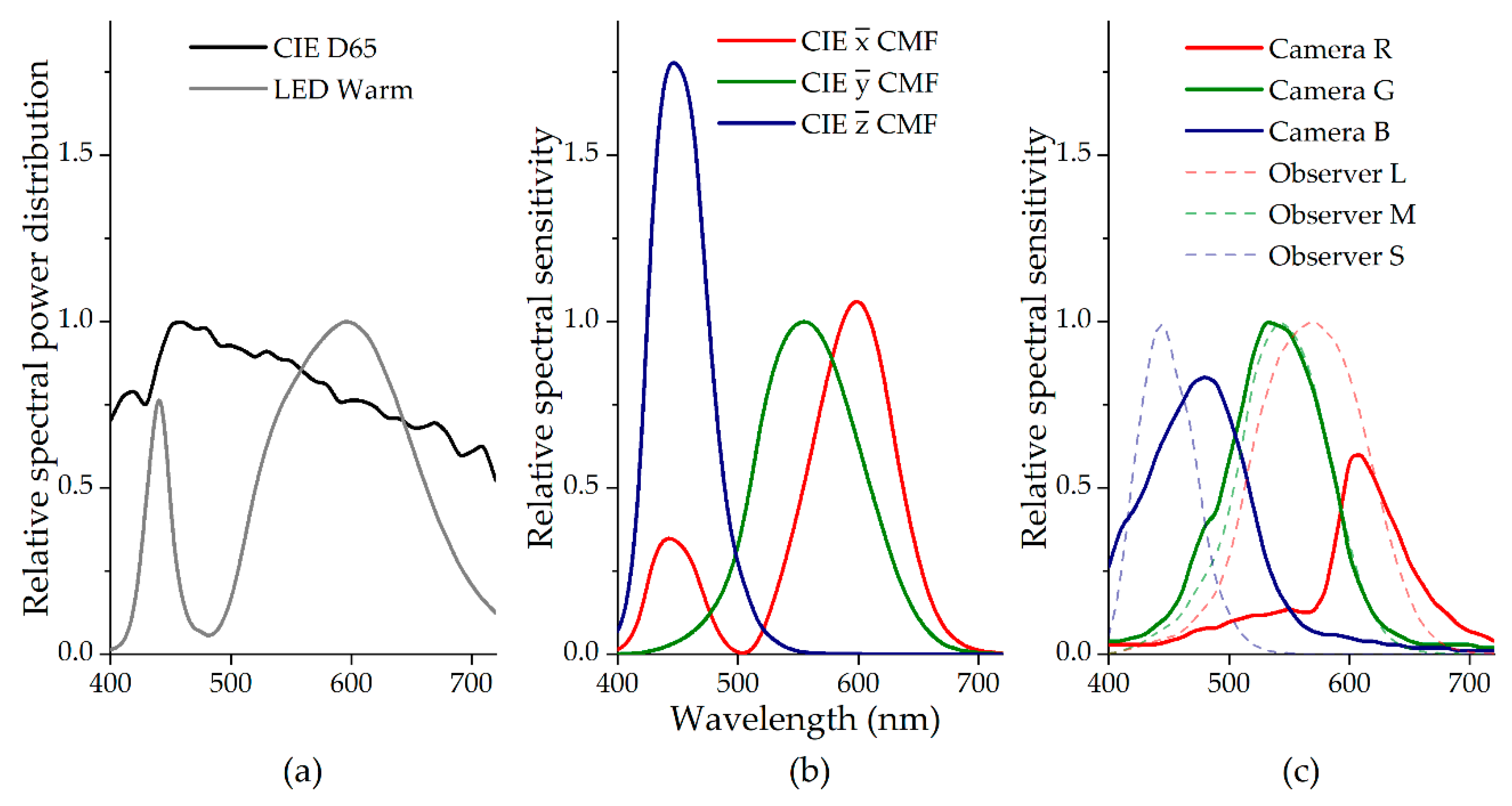
2.2. Camera and Standard Observer Spectral Sensitivity
2.3. Color Differences
2.4. Error Distribution
2.5. Number of Discernible Colors and Chromatic Volumes
3. Results
3.1. Colors and Gamuts
3.2. Color Differences
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CCT | Correlated color temperature |
| CCD | Charge-coupled device |
| CIE | Commission International de l′Éclairage |
| OBS | Data related to tristimulus values and device independent |
| RGB | Data related to a digital camera and device dependent |
| sRGB | standard Red Green Blue color space |
| STD | Standard deviation |
References
- Tkačik, G.; Garrigan, P.; Ratliff, C.; Milčinski, G.; Klein, J.M.; Seyfarth, L.H.; Sterling, P.; Brainard, D.H.; Balasubramanian, V. Natural Images from the Birthplace of the Human Eye. PLoS ONE 2011, 6, e20409. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, G.; Luo, M.R.; Rhodes, P.A. A study of digital camera colorimetric characterization based on polynomial modeling. Color. Res. Appl. 2001, 26, 76–84. [Google Scholar] [CrossRef]
- Foster, D.H.; Amano, K. Hyperspectral imaging in color vision research: Tutorial. J. Opt. Soc. Am. A 2019, 36, 606. [Google Scholar] [CrossRef] [PubMed]
- Pointer, M.R.; Attridge, G.G.; Jacobson, R.E. Practical camera characterization for colour measurement. Imaging Sci. J. 2001, 49, 63–80. [Google Scholar] [CrossRef]
- Brady, M.; Legge, G.E. Camera calibration for natural image studies and vision research. J. Opt. Soc. Am. A 2009, 26, 30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Millán, M.S.; Valencia, E.; Corbalán, M. 3CCD camera’s capability for measuring color differences: Experiment in the nearly neutral region. Appl. Opt. 2004, 43, 6523. [Google Scholar] [CrossRef] [PubMed]
- Penczek, J.; Boynton, P.A.; Splett, J.D. Color Error in the Digital Camera Image Capture Process. J. Digit. Imaging 2014, 27, 182–191. [Google Scholar] [CrossRef] [Green Version]
- Orava, J.; Jaaskelainen, T.; Parkkinen, J. Color errors of digital cameras. Color Res. Appl. 2004, 29, 217–221. [Google Scholar] [CrossRef]
- Prasad, D.K.; Wenhe, L. Metrics and statistics of frequency of occurrence of metamerism in consumer cameras for natural scenes. J. Opt. Soc. Am. A 2015, 32, 1390. [Google Scholar] [CrossRef]
- Mauer, C.; Wueller, D. Measuring the Spectral Response with a Set of Interference Filters. In Proceedings of the IS&T/SPIE Electronic Imaging, San Jose, CA, USA, 19–20 January 2009; p. 72500S. [Google Scholar] [CrossRef]
- Imai, F.H.; Berns, R.S.; Tzeng, D.-Y. A Comparative Analysis of Spectral Reflectance Estimated in Various Spaces Using a Trichromatic Camera System. J. imaging Sci. Technol. 2000, 44, 280–287. [Google Scholar]
- Garcia, J.E.; Girard, M.B.; Kasumovic, M.; Petersen, P.; Wilksch, P.A.; Dyer, A.G. Differentiating Biological Colours with Few and Many Sensors: Spectral Reconstruction with RGB and Hyperspectral Cameras. PLoS ONE 2015, 10, e0125817. [Google Scholar] [CrossRef] [PubMed]
- Charrière, R.; Hébert, M.; Trémeau, A.; Destouches, N. Color calibration of an RGB camera mounted in front of a microscope with strong color distortion. Appl. Opt. 2013, 52, 5262. [Google Scholar] [CrossRef] [PubMed]
- Pujol, J.; Martínez-Verdú, F.; Luque, M.J.; Capilla, P.; Vilaseca, M. Comparison between the Number of Discernible Colors in a Digital Camera and the Human Eye. In Proceedings of the Conference on Colour in Graphics, Imaging, and Vision, Aachen, Germany, 5–8 April 2004; Volume 2004, pp. 36–40. [Google Scholar]
- Pujol, J.; Martínez-Verdú, F.; Capilla, P. Estimation of the Device Gamut of a Digital Camera in Raw Performance Using Optimal Color-Stimuli. In Proceedings of the PICS 2003: The PICS Conference, An International Technical Conference on The Science and Systems of Digital Photography, Including the Fifth International Symposium on Multispectral Color Science, Rochester, NY, USA, 13 May 2003; pp. 530–535. [Google Scholar]
- Martínez-Verdú, F.; Luque, M.J.; Capilla, P.; Pujol, J. Concerning the calculation of the color gamut in a digital camera. Color Res. Appl. 2006, 31, 399–410. [Google Scholar] [CrossRef] [Green Version]
- Linhares, J.M.M.; Pinto, P.D.; Nascimento, S.M.C. The number of discernible colors in natural scenes. J. Opt. Soc. Am. A 2008, 25, 2918. [Google Scholar] [CrossRef]
- Webster, M.A.; Mollon, J.D. Adaptation and the color statistics of natural images. Vis. Res. 1997, 37, 3283–3298. [Google Scholar] [CrossRef] [Green Version]
- Carter, E.C.; Ohno, Y.; Pointer, M.R.; Robertson, A.R.; Sève, R.; Schanda, J.D.; Witt, K. Colorimetry, 3rd ed.; International Commission on Illumination (CIE): Vienna, Austria, 2004. [Google Scholar]
- Berns, R.S. Designing white-light LED lighting for the display of art: A feasibility study. Color. Res. Appl. 2011, 36, 324–334. [Google Scholar] [CrossRef]
- Garside, D.; Curran, K.; Korenberg, C.; MacDonald, L.; Teunissen, K.; Robson, S. How is museum lighting selected? An insight into current practice in UK museums. J. Inst. Conserv. 2017, 40, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Pelowski, M.; Graser, A.; Specker, E.; Forster, M.; von Hinüber, J.; Leder, H. Does Gallery Lighting Really Have an Impact on Appreciation of Art? An Ecologically Valid Study of Lighting Changes and the Assessment and Emotional Experience with Representational and Abstract Paintings. Front. Psychol. 2019, 10, 2148. [Google Scholar] [CrossRef]
- Martínez-Domingo, M.Á.; Melgosa, M.; Okajima, K.; Medina, V.J.; Collado-Montero, F.J. Spectral Image Processing for Museum Lighting Using CIE LED Illuminants. Sensors 2019, 19, 5400. [Google Scholar] [CrossRef] [Green Version]
- Fairchild, M.D. Color Appearance Models, 3rd ed.; The Wiley-IS&T Series in Imaging Science and Technology; John Wiley & Sons, Inc.: Chichester, West Sussex, UK, 2013; ISBN 978-1-118-65309-8. [Google Scholar]
- Hunt, R.W.G.; Li, C.; Luo, M.R. Chromatic adaptation transforms. Color. Res. Appl. 2005, 30, 69–71. [Google Scholar] [CrossRef]
- Fairchild, M.D. iCAM framework for image appearance, differences, and quality. J. Electron. Imaging 2004, 13, 126. [Google Scholar] [CrossRef] [Green Version]
- Kuang, J.; Johnson, G.M.; Fairchild, M.D. iCAM06: A refined image appearance model for HDR image rendering. J. Vis. Commun. Image Represent. 2007, 18, 406–414. [Google Scholar] [CrossRef]
- Safdar, M.; Cui, G.; Kim, Y.J.; Luo, M.R. Perceptually uniform color space for image signals including high dynamic range and wide gamut. Opt. Express 2017, 25, 15131. [Google Scholar] [CrossRef]
- Luo, M.R.; Cui, G.; Rigg, B. The development of the CIE 2000 colour-difference formula: CIEDE2000. Color Res. Appl. 2001, 26, 340–350. [Google Scholar] [CrossRef]
- Pinto, P.D.; Linhares, J.M.M.; Nascimento, S.M.C. Correlated color temperature preferred by observers for illumination of artistic paintings. J. Opt. Soc. Am. A 2008, 25, 623. [Google Scholar] [CrossRef] [Green Version]
- Nascimento, S.M.C.; Herdeiro, C.F.M.; Gomes, A.E.; Linhares, J.M.M.; Kondo, T.; Nakauchi, S. The Best CCT for Appreciation of Paintings under Daylight Illuminants is Different for Occidental and Oriental Viewers. LEUKOS 2020, 1–9. [Google Scholar] [CrossRef]
- Cucci, C.; Casini, A.; Picollo, M.; Stefani, L. Extending hyperspectral imaging from Vis to NIR spectral regions: A novel scanner for the in-depth analysis of polychrome surfaces. In Proceedings of the SPIE Optical Metrology, Munich, Germany, 13–16 May 2013; p. 879009. [Google Scholar] [CrossRef]
- Cucci, C.; Delaney, J.K.; Picollo, M. Reflectance Hyperspectral Imaging for Investigation of Works of Art: Old Master Paintings and Illuminated Manuscripts. Acc. Chem. Res. 2016, 49, 2070–2079. [Google Scholar] [CrossRef]
- Picollo, M.; Cucci, C.; Casini, A.; Stefani, L. Hyper-Spectral Imaging Technique in the Cultural Heritage Field: New Possible Scenarios. Sensors 2020, 20, 2843. [Google Scholar] [CrossRef]
- Stockman, A. Cone fundamentals and CIE standards. Curr. Opin. Behav. Sci. 2019, 30, 87–93. [Google Scholar] [CrossRef]
- Johnson, G.M.; Fairchild, M.D. A top down description of S-CIELAB and CIEDE2000. Color Res. Appl. 2003, 28, 425–435. [Google Scholar] [CrossRef]
- Zhao, B.; Luo, M.R. Hue linearity of color spaces for wide color gamut and high dynamic range media. J. Opt. Soc. Am. A 2020, 37, 865. [Google Scholar] [CrossRef]
- Fairchild, M.D.; Johnson, G.M. Meet iCAM: A Next-Generation Color Appearance Model. In Proceedings of the Color Imaging Conference, Scottsdale, AZ, USA, 12–15 November 2002; p. 7. [Google Scholar]
- Scott, D.W. Sturges’ rule. Wires Comp. Stat. 2009, 1, 303–306. [Google Scholar] [CrossRef]
- Pointer, M.R.; Attridge, G.G. The number of discernible colours. Color Res. Appl. 1998, 23, 52–54. [Google Scholar] [CrossRef]
- Montagner, C.; Linhares, J.M.M.; Vilarigues, M.; Melo, M.J.; Nascimento, S.M.C. Supporting history of art with colorimetry: The paintings of Amadeo de Souza-Cardoso. Color Res. Appl 2018, 43, 304–310. [Google Scholar] [CrossRef]
- Montagner, C.; Linhares, J.M.M.; Vilarigues, M.; Nascimento, S.M.C. Statistics of colors in paintings and natural scenes. J. Opt. Soc. Am. A 2016, 33, A170. [Google Scholar] [CrossRef]
- Huertas, R.; Melgosa, M.; Hita, E. Influence of random-dot textures on perception of suprathreshold color differences. J. Opt. Soc. Am. A 2006, 23, 2067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amano, K.; Linhares, J.M.M.; Nascimento, S.M.C. Color constancy of color reproductions in art paintings. J. Opt. Soc. Am. A 2018, 35, B324. [Google Scholar] [CrossRef] [Green Version]
- Aldaba, M.A.; Linhares, J.M.M.; Pinto, P.D.; Nascimento, S.M.C.; Amano, K.; Foster, D.H. Visual sensitivity to color errors in images of natural scenes. Vis. Neurosci 2006, 23, 555–559. [Google Scholar] [CrossRef]
- Seymour, J.C. Why do color transforms work? In Color Imaging: Device-Independent Color, Color Hardcopy, and Graphic Arts III; Beretta, G.B., Eschbach, R., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE): San Jose, CA, USA, 1997; pp. 156–164. [Google Scholar]
- Liu, H.; Huang, M.; Cui, G.; Luo, M.R.; Melgosa, M. Color-difference evaluation for digital images using a categorical judgment method. J. Opt. Soc. Am. A 2013, 30, 616. [Google Scholar] [CrossRef]
- Karaimer, H.C.; Brown, M.S. Improving Color Reproduction Accuracy on Cameras. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6440–6449. [Google Scholar]
- Lebourgeois, V.; Bégué, A.; Labbé, S.; Mallavan, B.; Prévot, L.; Roux, B. Can Commercial Digital Cameras Be Used as Multispectral Sensors? A Crop Monitoring Test. Sensors 2008, 8, 7300–7322. [Google Scholar] [CrossRef] [PubMed]
- Solli, M.; Andersson, M.; Lenz, R.; Kruse, B. Color Measurements with a Consumer Digital Camera Using Spectral Estimation Techniques. In Image Analysis; Kalviainen, H., Parkkinen, J., Kaarna, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg Germany, 2005; Volume 3540, pp. 105–114. ISBN 978-3-540-26320-3. [Google Scholar]
- Bainbridge, S.; Gardner, S. Comparison of Human and Camera Visual Acuity—Setting the Benchmark for Shallow Water Autonomous Imaging Platforms. JMSE 2016, 4, 17. [Google Scholar] [CrossRef]
- Wee, A.G.; Lindsey, D.T.; Kuo, S.; Johnston, W.M. Color accuracy of commercial digital cameras for use in dentistry. Dent. Mater. 2006, 22, 553–559. [Google Scholar] [CrossRef] [PubMed]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef] [Green Version]






| Paintings (×103) | Natural Scenes (×103) | ||||
|---|---|---|---|---|---|
| D65 | LED | D65 | LED | ||
| Volume | OBS | 160.9 | 162.0 | 439.2 | 441.5 |
| (± 126.4) | (± 126.3) | (± 284.5) | (± 284.8) | ||
| RGB | 25.0 | 22.9 | 69.6 | 61.0 | |
| (± 18.2) | (± 17.6) | (± 45.42) | (± 39.2) | ||
| NODC Volume | OBS | 43.4 | 43.4 | 92.2 | 94.4 |
| (± 32.5) | (± 32.4) | (± 48.2) | (± 49.5) | ||
| RGB | 10.6 | 9.5 | 25.7 | 22.8 | |
| (± 7.2) | (± 6.9) | (± 14.9) | (±12.9) | ||
| Area | OBS | 4.5 | 4.6 | 9.3 | 9.3 |
| (± 2.7) | (± 2.8) | (± 5.0) | (± 4.8) | ||
| RGB | 0.7 | 0.7 | 1.5 | 1.3 | |
| (± 0.4) | (± 0.4) | (± 0.9) | (± 0.7) | ||
| NODC Area | OBS | 2.8 | 2.8 | 5.1 | 5.2 |
| (± 1.7) | (± 1.7) | (± 2.4) | (± 2.4) | ||
| RGB | 0.6 | 0.5 | 1.1 | 1.0 | |
| (± 0.3) | (± 0.3) | (± 0.5) | (± 0.5) | ||
| NODC (%) | Color Volume (%) | ||||
|---|---|---|---|---|---|
| CIELAB | CIE(a*,b*) | CIELAB | CIE(a*,b*) | ||
| OBS vs. RGB | D65 | 26.3 | 20.9 | 15.7 | 16.2 |
| LED | 23.2 | 18.3 | 13.9 | 14.3 | |
| D65 vs. LED | OBS | 101.3 | 100.8 | 100.9 | 100.2 |
| RGB | 89.5 | 88.3 | 89.2 | 88.1 | |
| Paintings | Natural Scenes | |||
|---|---|---|---|---|
| D65 | LED | D65 | LED | |
| CIELAB | 5.1 (± 0.5) | 5.8 (± 0.5) | 4.7 (± 0.4) | 5.1 (± 0.4) |
| CIEDE2000 | 5.7 (± 0.2) | 6.2 (± 0.1) | 5.9 (± 0.1) | 6.1 (± 0.2) |
| Jzazbz (×10−3) | 34.5 (± 1.5) | 35.2 (± 1.3) | 74.0 (± 0.0) | 73.3 (± 0.6) |
| iCAM | 2.0 (± 0.1) | 1.8 (± 0.1) | 1.0 (± 0.2) | 0.9 (± 0.1) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Linhares, J.M.M.; Monteiro, J.A.R.; Bailão, A.; Cardeira, L.; Kondo, T.; Nakauchi, S.; Picollo, M.; Cucci, C.; Casini, A.; Stefani, L.; et al. How Good Are RGB Cameras Retrieving Colors of Natural Scenes and Paintings?—A Study Based on Hyperspectral Imaging. Sensors 2020, 20, 6242. https://doi.org/10.3390/s20216242
Linhares JMM, Monteiro JAR, Bailão A, Cardeira L, Kondo T, Nakauchi S, Picollo M, Cucci C, Casini A, Stefani L, et al. How Good Are RGB Cameras Retrieving Colors of Natural Scenes and Paintings?—A Study Based on Hyperspectral Imaging. Sensors. 2020; 20(21):6242. https://doi.org/10.3390/s20216242
Chicago/Turabian StyleLinhares, João M. M., José A. R. Monteiro, Ana Bailão, Liliana Cardeira, Taisei Kondo, Shigeki Nakauchi, Marcello Picollo, Costanza Cucci, Andrea Casini, Lorenzo Stefani, and et al. 2020. "How Good Are RGB Cameras Retrieving Colors of Natural Scenes and Paintings?—A Study Based on Hyperspectral Imaging" Sensors 20, no. 21: 6242. https://doi.org/10.3390/s20216242
APA StyleLinhares, J. M. M., Monteiro, J. A. R., Bailão, A., Cardeira, L., Kondo, T., Nakauchi, S., Picollo, M., Cucci, C., Casini, A., Stefani, L., & Nascimento, S. M. C. (2020). How Good Are RGB Cameras Retrieving Colors of Natural Scenes and Paintings?—A Study Based on Hyperspectral Imaging. Sensors, 20(21), 6242. https://doi.org/10.3390/s20216242







