Digital Cultural Heritage Preservation in Art Painting: A Surface Roughness Approach to the Brush Strokes
Abstract
:1. Introduction
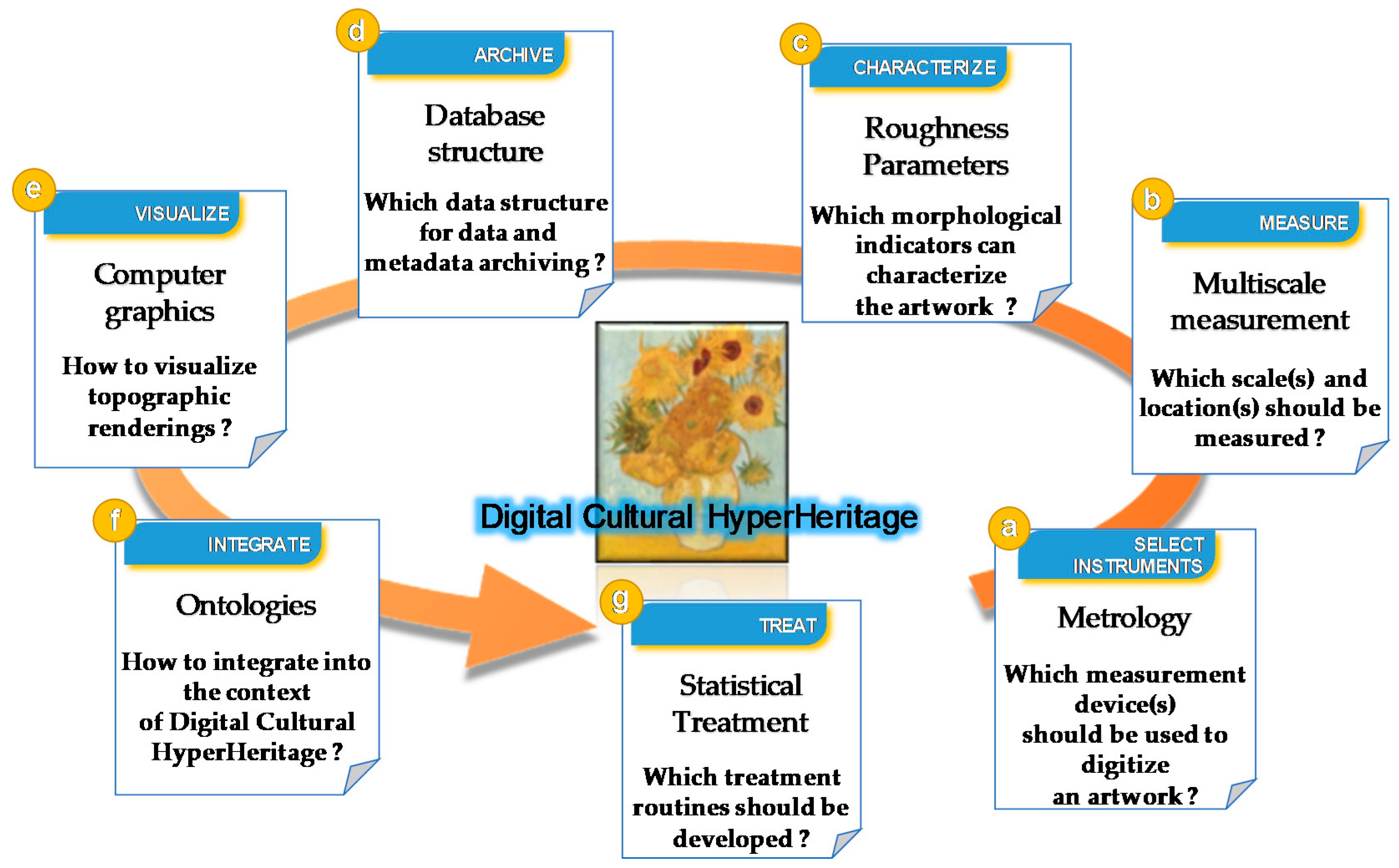
1.1. The Digital Surface HyperHeritage: An HyperHeritage Concept
1.2. The Implementation of the Digital Surface HyperHeritage Approach
- (a)
- Define the optimal methodology of automated measurements suited to the topography of the investigated surfaces (apparatus selection and protocol) allowing a set of repetitive, reliable, and robust measurements to be performed and quantified by a quality indicator.
- (b)
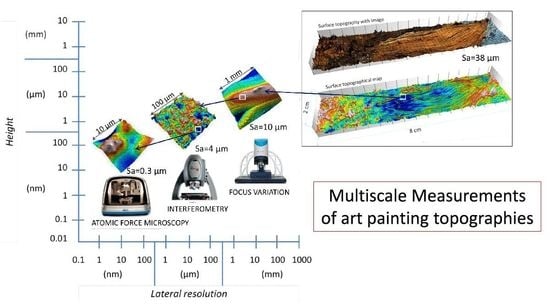
- Deployment of a multi-scale measurement strategy to capture all of the features and particularities of the masterpiece. Indeed, the whole measurement of the masterpiece is technically impossible, at the moment, with a lateral resolution of the order of 1 μm. A three-dimensional multi-resolution and multi-technique approach must then be built.
- (c)
- Create multi-scale topographic processing procedures in order to define a set of morphological descriptors.
- (d)
- Define a topographic database structure to access the information, regardless of the device used to carry out the measurements and the sets of descriptors.
- (e)
- Define, by simulation, the 3D graphic rendering of the surface texture to offer a realistic panel of visual renderings of the surfaces.
- (f)
- Reference the partners (institute, museum, associative world, private collector, etc.) and classify them to build a strategy of elaboration of the most representative database of the diversity of the surface heritage.
- -
- Paints: source (manufacturer/supplier, year, paint product name, identifier, bottle label), paint type, structure, chemical composition, formula, properties, pigment;
- -
- Additives: thickeners, stabilizers, preservatives, surfactants, coalescing solvents and defoamers;
- -
- Paint degradation: types of degradation (cracking, peeling, fading, discoloration, mold growth), causes (humidity, light, temperature, water, technique), and associated physical/chemical processes/reactions;
- -
- Paint analysis methods: macroscopic, microscopic, SEM, TEM, FTIR, infrared, Raman, X-ray diffraction, X-ray spectroscopy (EDS), X-ray fluorescence (XRF), chromatography, synchrotron;
- -
- Paint observation: preservation treatments, cleaning, protective coatings, environmental conditions.
- (g)
- Implement the set of informatic routines that characterize the relationship between artwork morphology and the parameters described in an information system (concepts and semantic links of ontology relating to painting artworks [88]).
1.3. A Digital Surface HyperHeritage Example
- A multi-instrument analysis was undertaken on paintings, made by a panel of ten selected painters reproducing Vincent Van Gogh’s sunflowers;
- These paintings serve as supports for topographic investigations. Different measuring devices are used (focus variation, interferometry, atomic force microscopy);
- Surface topographies are investigated and characterized (list of descriptors).
2. Materials and Methods
2.1. Art Painting Protocol: “Sunflowers” in Reference to Vincent Van Gogh
2.1.1. Context
2.1.2. Selection of Painters and Painting Instruction
- -
- the presence of different types of objects for reproduction (sky, petals, sunflower head, grass);
- -
- the shape of the flower allows several identical objects from different angles (petals) to be viewed;
- -
- painter repeatability: each painter is able to reproduce objects, accurately maintaining their forms, sizes, directions, and positions.
2.1.3. Canvas and Paintings
- -
- 1 printed picture of a sunflower with dimensions 20 × 20 cm;
- -
- 1 pre-coated linen canvas with dimensions 20 × 20 cm;
- -
- 1 set of oil paints “Pebeo XL” (20 colors);
- -
- 1 round brush “Gerstaecker” with synthetic white fibers, size 10;
- -
- 1 bottle of turpentine “Lefranc Bourgeois”;
- -
- 1 list of instructions and tutorial video.
2.2. Multi-Instrumental Strategy
Selection of Metrology Devices
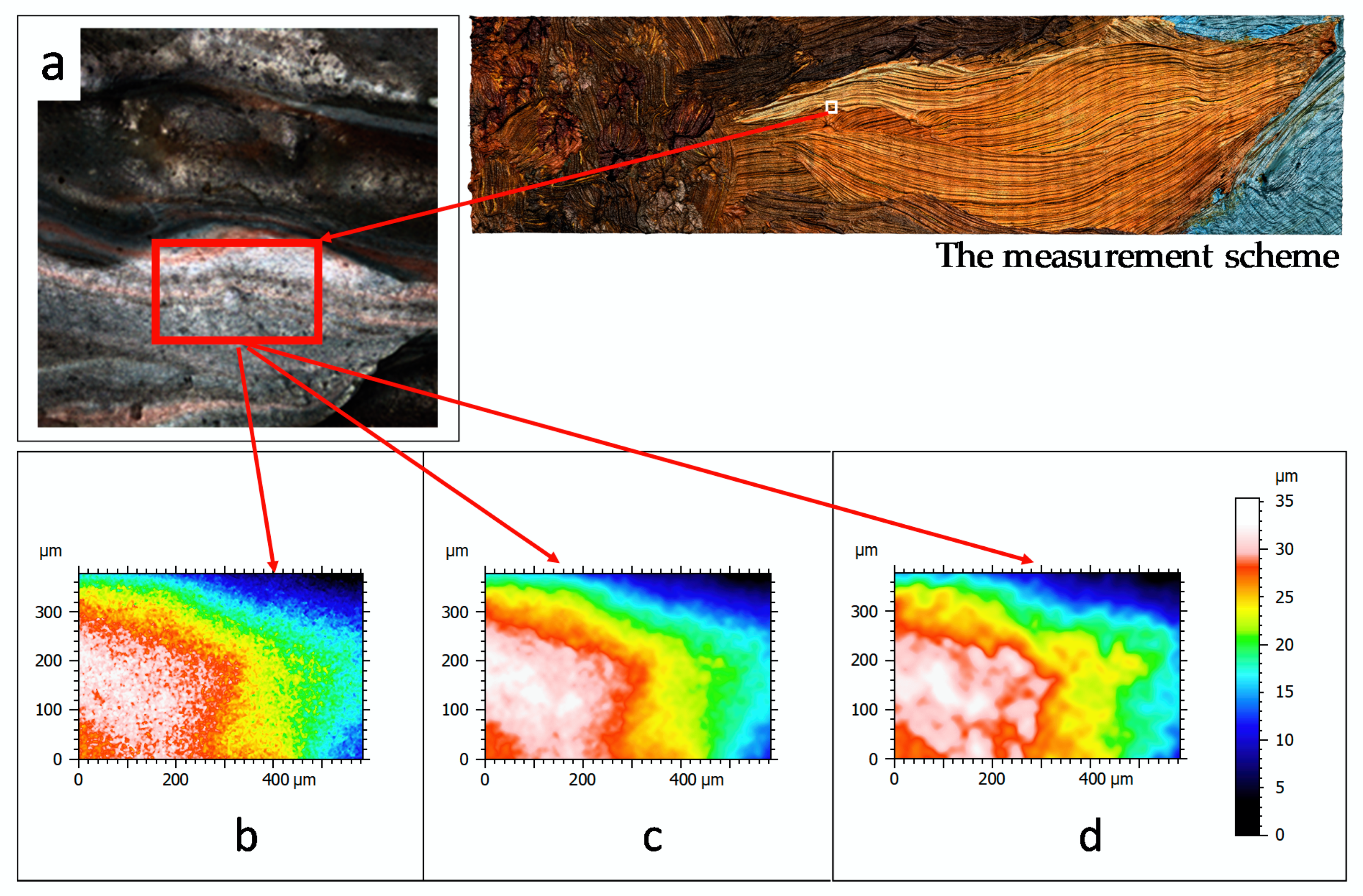
2.3. Measurement Strategy
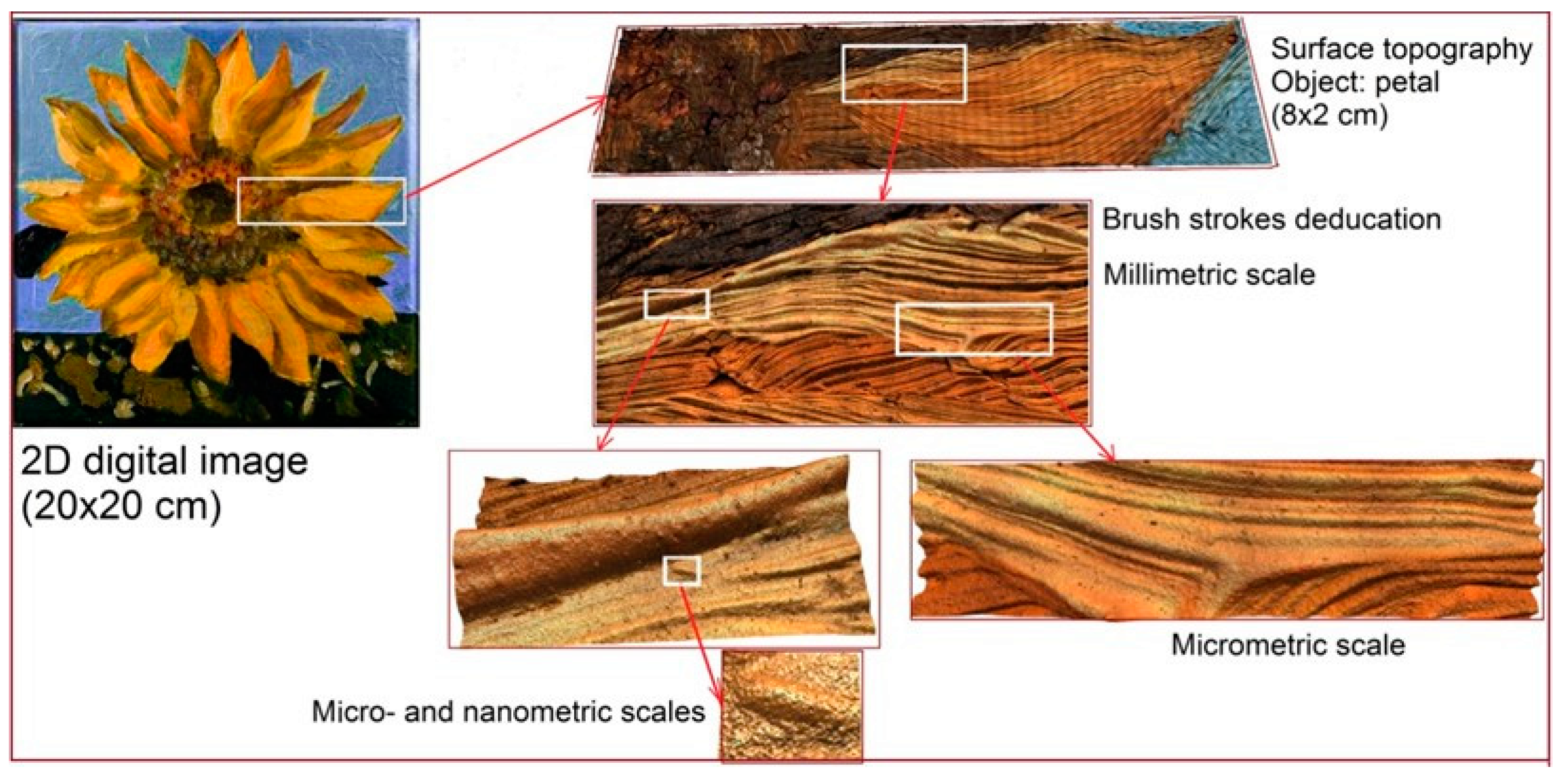
- -
- A surface including a region of the petal with angle of 0° compared to the lateral axis. The dimensions of the measurement region were defined to fully contain a flower petal (see Figure 7, zone 1) with dimensions of 50 × 25 mm (depending on the petal).
- -
- A surface with dimensions of 10 × 10 mm (see Figure 7, zone 2)
- -
- A surface with dimensions of 1 × 1 mm (see Figure 7, zone 3).
3. Results and Discussion
3.1. Multi-Scale Topographic Map
- -
- -
- -
- -
- -
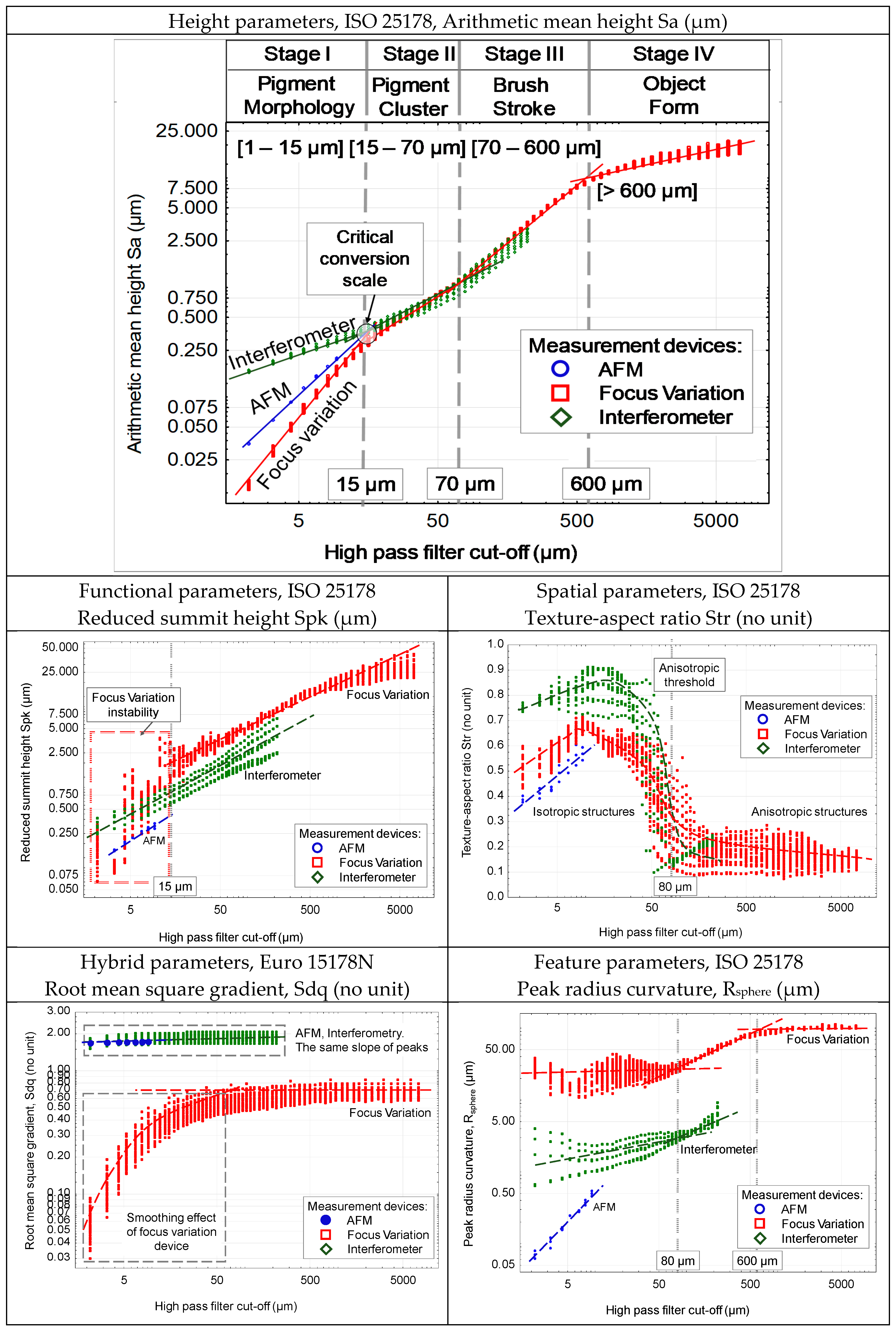
3.2. Multi-Scale Analyses
3.2.1. Multi-Scale Decomposition
3.2.2. Multi-Scale Topographical Graph
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A



References
- Zreik, K.; Bouhai, N. Post-digital design: The Hyperheritage project. In Proceedings of the SHoCK—Sharing of Computable Knowledge; Fioravanti, A., Cursi, S., Elahmar, S., Gargaro, S., Eds.; eCAADe 35: Rome, Italy, 2017; pp. 49–54. [Google Scholar]
- Leach, R.K.; Giusca, C.L.; Rubert, P. A single set of material measures for the calibration of areal surface topography measuring instruments: The NPL areal bento box. In Proceedings of the Metrology and Properties of Engineering Surfaces, Taipei, Taiwan, 17–21 June 2013; pp. 406–413. [Google Scholar]
- Ekberg, P.; Su, R.; Leach, R. High-precision lateral distortion measurement and correction in coherence scanning interferometry using an arbitrary surface. Opt. Express 2017, 25, 18703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ohlsson, R.; Wihlborg, A.; Westberg, H. The accuracy of fast 3D topography measurements. Int. J. Mach. Tools Manuf. 2001, 41, 1899–1907. [Google Scholar] [CrossRef]
- Li, Z.; Brand, U.; Ahbe, T. Towards quantitative modelling of surface deformation of polymer micro-structures under tactile scanning measurement. Meas. Sci. Technol. 2014, 25, 044010. [Google Scholar] [CrossRef]
- Garabedian, C.; Vayron, R.; Bricout, N.; Deltombe, R.; Anselme, K.; Bigerelle, M. In vivo damage study of different textured breast implants. Biotribology 2020, 23, 100133. [Google Scholar] [CrossRef]
- Brand, U.; Beckert, E.; Beutler, A.; Dai, G.; Stelzer, C.; Hertwig, A.; Klapetek, P.; Koglin, J.; Thelen, R.; Tutsch, R. Comparison of optical and tactile layer thickness measurements of polymers and metals on silicon or SiO2. Meas. Sci. Technol. 2011, 22, 094021. [Google Scholar] [CrossRef]
- Helmli, F. Focus Variation instruments. In Optical Measurement of Surface Topography; Leach, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 131–166. [Google Scholar]
- ISO 25178-6. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 6: Classification of Methods for Measuring Surface Texture; International Organization for Standardization: Geneva, Switzerland, 2010. [Google Scholar]
- ISO 25178-6. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 601: Nominal Characteristics of Contact (Stylus) Instruments; International Organization for Standardization: Geneva, Switzerland, 2010. [Google Scholar]
- ISO 25178-6. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 602: Nominal Characteristics of Non-Contact (Confocal Chromatic Probe) Instruments; International Organization for Standardization: Geneva, Switzerland, 2010. [Google Scholar]
- ISO 25178-6. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 603: Nominal Characteristics of Non-Contact (Phase Shifting Interferometric Microscopy) Instruments; International Organization for Standardization: Geneva, Switzerland, 2010. [Google Scholar]
- ISO 25178-6. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 604: Nominal Characteristics of Non-Contact (Coherence Scanning Interferometry) Instruments; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- ISO 25178-6. Geometrical Product Specifications (GPS)—Surface Texture: Area —Part 605: Nominal Characteristics of Non-Contact (Point Autofocus) Instruments; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- ISO 25178-6. Geometrical Product Specifications (GPS)—Surface Texture: Area—Part 606: Nominal Characteristics of Non-Contact (Variable Focus) Instruments; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Tsai, M.-J.; Hung, C.-C. Development of a high-precision surface metrology system using structured light projection. Measurement 2005, 38, 236–247. [Google Scholar] [CrossRef]
- Costa, M.F.M. Optical triangulation-based Microtopographic inspection of surfaces. Sensors 2012, 12, 4399–4420. [Google Scholar] [CrossRef] [Green Version]
- Jouini, N.; Gautier, A.; Revel, P.; Mazeran, P.E.; Bigerelle, M. Multi-scale analysis of high precision surfaces by stylus profiler, scanning white-light interferometry and atomic force microscopy. Int. J. Surf. Sci. Eng. 2009, 3, 310. [Google Scholar] [CrossRef] [Green Version]
- Garabédian, C.; Delille, R.; Deltombe, R.; Anselme, K.; Atlan, M.; Bigerelle, M. A multi-topographical-instrument analysis: The breast implant texture measurement. Surf. Topogr. Metrol. Prop. 2017, 5, 025004. [Google Scholar] [CrossRef]
- Elkhuizen, W.S.; Callewaert, T.W.J.; Leonhardt, E.; Vandivere, A.; Song, Y.; Pont, S.C.; Geraedts, J.M.P.; Dik, J. Comparison of three 3D scanning techniques for paintings, as applied to Vermeer’s ‘Girl with a Pearl Earring’ . Herit. Sci. 2019, 7, 89. [Google Scholar] [CrossRef]
- Van Loon, A.; Vandivere, A.; Delaney, J.K.; Dooley, K.A.; De Meyer, S.; Vanmeert, F.; Gonzalez, V.; Janssens, K.; Leonhardt, E.; Haswell, R.; et al. Beauty is skin deep: The skin tones of Vermeer’s girl with a pearl earring. Herit. Sci. 2019, 7, 102. [Google Scholar] [CrossRef]
- Callewaert, T.; Dik, J.; Kalkman, J. Segmentation of thin corrugated layers in high-resolution OCT images. Opt. Express 2017, 25, 32816–32828. [Google Scholar] [CrossRef]
- Van Hengstum, M.J.W.; Essers, T.T.W.; Elkhuizen, W.S.; Dodou, D.; Song, Y.; Geraedts, J.M.P.; Dik, J. Development of a high resolution topography and color scanner to capture crack patterns of paintings. In Proceedings of the EUROGRAPHICS Workshop on Graphics and Cultural Heritage, Vienna, Austria, 12–15 November 2018; pp. 11–20. [Google Scholar]
- Crina Anca Sandu, I.; de Sá, M.H.; Pereira, M.C. Ancient ‘gilded’ art objects from European cultural heritage: A review on different scales of characterization. Surf. Interface Anal. 2011, 43, 1134–1151. [Google Scholar] [CrossRef]
- Lawrence, J.; Sosso, G.C.; Đorđević, L.; Pinfold, H.; Bonifazi, D.; Costantini, G. Combining high-resolution scanning tunnelling microscopy and first-principles simulations to identify halogen bonding. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef]
- Ahmad, A.; Nikolov, N.; Angelov, T.; Ivanov, T.; Reum, A.; Atanasov, I.; Guliyev, E.; Ishchuk, V.; Kaestner, M.; Krivoshapkina, Y.; et al. Large area fast-AFM scanning with active “Quattro” cantilever arrays. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2016, 34, 06KM03. [Google Scholar] [CrossRef]
- Kampasakali, E.; Ormsby, B.; Cosentino, A.; Miliani, C.; Learner, T. A preliminary evaluation of the surfaces of acrylic emulsion paint films and the effects of wet-cleaning treatment by Atomic Force Microscopy (AFM). Stud. Conserv. 2011, 56, 216–230. [Google Scholar] [CrossRef]
- Callewaert, T.; Guo, J.; Harteveld, G.; Vandivere, A.; Eisemann, E.; Dik, J.; Kalkman, J. Multi-scale optical coherence tomography imaging and visualization of Vermeer’s Girl with a Pearl Earring. Opt. Express 2020, 28, 26239–26256. [Google Scholar] [CrossRef]
- Brown, C.A.; Hansen, H.N.; Jiang, X.J.; Blateyron, F.; Berglund, J.; Senin, N.; Bartkowiak, T.; Dixon, B.; Le Goïc, G.; Quinsat, Y.; et al. Multiscale analyses and characterizations of surface topographies. CIRP Ann. 2018, 67, 839–862. [Google Scholar] [CrossRef]
- Le Goïc, G.; Bigerelle, M.; Samper, S.; Favrelière, H.; Pillet, M. Multiscale roughness analysis of engineering surfaces: A comparison of methods for the investigation of functional correlations. Mech. Syst. Signal Process. 2016, 66–67, 437–457. [Google Scholar] [CrossRef]
- ISO 25178. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- ISO 25178. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 3: Specification Operators; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- ISO/CD 16610 Part 61. Geometrical Product Specifications (GPS)—Linear areal Filters: Gaussian Filters; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- ISO/CD 16610 Part 71. Geometrical Product Specifications (GPS)—Robust Areal Filters: Gaussian Regression Filters; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- ISO/TS 16610 Part 32. Geometrical Product Specifications (GPS)—Robust Profile Filters: Spline Filters; International Organization for Standardization: Geneva, Switzerland, 2009. [Google Scholar]
- ISO/TS 16610 Part 22. Geometrical Product Specifications (GPS)—Linear Profile Filters: Spline Filters; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- ISO/DIS 16610 Part 41. Geometrical Product Specifications (GPS)—Morphological Profile Filters: Disk and Horizontal Line-Segment Filters; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- ISO/DIS 16610 Part 49. Geometrical Product Specifications (GPS)—Morphological Profile Filters: Disk and Horizontal Line-Scale Space Techniques; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- ISO/TS 16610 Part 29. Geometrical Product Specifications (GPS)—Linear Profile Filters: Spline Wavelets; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- ISO/TS 16610 Part 28. Geometrical Product Specifications (GPS)—Linear Profile Filters: End Effects; International Organization for Standardization: Geneva, Switzerland, 2012. [Google Scholar]
- Deltombe, R.; Kubiak, K.J.; Bigerelle, M. How to select the most relevant 3D roughness parameters of a surface: Relevance of 3D roughness parameters. Scanning 2014, 36, 150–160. [Google Scholar] [CrossRef] [Green Version]
- Elkhuizen, W.S.; Lenseigne, B.A.J.; Baar, T.; Verhofstad, W.; Tempelman, E.; Geraedts, J.M.P.; Dik, J. Reproducing oil paint gloss in print for the purpose of creating reproductions of Old Masters. In Proceedings of the Measuring, Modeling, and Reproducing Material Appearance 2015, San Francisco, CA, USA, 9–10 February 2015; Ortiz Segovia, M.V., Urban, P., Imai, F.H., Eds.; International Society for Optics and Photonics: San Francisco, CA, USA, 2015; Volume 9398, p. 93980W. [Google Scholar]
- Taylor, R. Fractal expressionism—Where art meets science. In Art and Complexity; Elsevier: Amsterdam, The Netherlands, 2003; pp. 117–144. [Google Scholar]
- Van Laerhoven, T.; Van Reeth, F. Brush up your painting skills: Realistic brush design for interactive painting applications. Vis. Comput. 2007, 23, 763–771. [Google Scholar] [CrossRef]
- Lemesle, J.; Robache, F.; Le Goic, G.; Mansouri, A.; Brown, C.A.; Bigerelle, M. Surface reflectance: An optical method for multiscale curvature characterization of wear on ceramic–metal composites. Materials 2020, 13, 1024. [Google Scholar] [CrossRef] [Green Version]
- Guibert, R.; Hanafi, S.; Deltombe, R.; Bigerelle, M.; Brown, C.A. Comparison of three multiscale methods for topographic analyses. Surf. Topogr. Metrol. Prop. 2020, 8, 024002. [Google Scholar] [CrossRef]
- Bigerelle, M.; Iost, A. A numerical method to calculate the Abbott parameters: A wear application. Tribol. Int. 2007, 40, 1319–1334. [Google Scholar] [CrossRef] [Green Version]
- Schinckus, C. From canvas to flatness: A ready-made perspective. J. Arts Humanit. 2020, 9, 78–86. [Google Scholar]
- Schinckus, C. Delimitation of flatness in paintings. Art Percept. 2018, 6, 67–75. [Google Scholar] [CrossRef]
- Carbon, C.-C.; Hesslinger, V.M. On the nature of the background behind Mona Lisa. Leonardo 2015, 48, 183–184. [Google Scholar] [CrossRef]
- Scott, P.J. Feature parameters. Wear 2009, 266, 548–551. [Google Scholar] [CrossRef]
- Wolf, G.W. Surfaces—Topography and topology. Surf. Topogr. Metrol. Prop. 2020, 8, 014003. [Google Scholar] [CrossRef] [Green Version]
- Pal, N.R.; Pal, S.K. A review on image segmentation techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
- Shen, X.; Hertzmann, A.; Jia, J.; Paris, S.; Price, B.; Shechtman, E.; Sachs, I. Automatic portrait segmentation for image stylization. Comput. Graph. Forum 2016, 35, 93–102. [Google Scholar] [CrossRef]
- Hegde, S.; Gatzidis, C.; Tian, F. Painterly rendering techniques: A state-of-the-art review of current approaches. Comput. Animat. Virtual Worlds 2013, 24, 43–64. [Google Scholar] [CrossRef]
- Romero-Zaliz, R.; Reinoso-Gordo, J.F. An updated review on watershed algorithms. In Soft Computing for Sustainability Science; Cruz Corona, C., Ed.; Springer International Publishing: Cham, Switzerland, 2018; Volume 358, pp. 235–258. [Google Scholar]
- Bigerelle, M.; Marteau, J.; Paulin, C. Brightness versus roughness: A multiscale approach. Surf. Topogr. Metrol. Prop. 2015, 3, 015004. [Google Scholar] [CrossRef]
- Blateyron, F. The areal feature parameters. In Characterisation of Areal Surface Texture; Leach, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 45–65. [Google Scholar]
- Belaud, V.; Valette, S.; Stremsdoerfer, G.; Bigerelle, M.; Benayoun, S. Wettability versus roughness: Multi-scales approach. Tribol. Int. 2015, 82, 343–349. [Google Scholar] [CrossRef]
- Leach, R.K.; Giusca, C.L.; Haitjema, H.; Evans, C.; Jiang, X. Calibration and verification of areal surface texture measuring instruments. CIRP Ann. 2015, 64, 797–813. [Google Scholar] [CrossRef]
- Seewig, J.; Eifler, M.; Schneider, F.; Aurich, J.C. Design and verification of geometric roughness standards by reverse engineering. In Proceedings of the 3rd CIRP Conference on Surface Integrity, Charlotte, NC, USA, 8–10 June 2016; Volume 45, pp. 259–262. [Google Scholar]
- Todhunter, L. Surface Topography Analysis Software Validation. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2020. [Google Scholar]
- Todhunter, L.; Leach, R.; Lawes, S.; Harris, P.; Blateyron, F. Mathematical approach to the validation of functional surface texture parameter software. Surf. Topogr. Metrol. Prop. 2019, 7, 015020. [Google Scholar] [CrossRef]
- Leach, R.K. Traceable measurement of surface texture at the National Physical Laboratory using NanoSurf IV. Meas. Sci. Technol. 2000, 11, 1162–1172. [Google Scholar] [CrossRef]
- Orburger, T.V.; Yen, J.H.; Bachrach, B.; Renegar, T.B.; Filliben, J.J.; Ma, L.; Rhee, H.G.; Zheng, A.; Song, J.F.; Riley, M.; et al. Surface Topography Analysis for a Feasibility Assessment of a National Ballistics Imaging Database; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007; p. NIST IR 7362. [Google Scholar]
- Bui, S.H.; Vorburger, T.V. Surface metrology algorithm testing system. Precis. Eng. 2007, 31, 218–225. [Google Scholar] [CrossRef]
- Qi, Q.; Scott, P.J.; Jiang, X.; Lu, W. Design and implementation of an integrated surface texture information system for design, manufacture and measurement. Comput.-Aided Des. 2014, 57, 41–53. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Lu, W.; Qi, Q.; Liu, X.; Huang, M.; Scott, P.J.; Jiang, X. Towards a tolerance representation model for generating tolerance specification schemes and corresponding tolerance zones. Int. J. Adv. Manuf. Technol. 2018, 97, 1801–1821. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Qi, Q.; Lu, W.; Liu, X.; Scott, P.J.; Jiang, X. A review of representation models of tolerance information. Int. J. Adv. Manuf. Technol. 2018, 95, 2193–2206. [Google Scholar] [CrossRef] [Green Version]
- Berglund, J.; Söderberg, R.; Wärmefjord, K.; Leach, R.; Morse, E. Functional tolerancing of surface texture—A review of existing methods. Procedia CIRP 2020, 92, 230–235. [Google Scholar] [CrossRef]
- Qi, Q.; Scott, P.J.; Jiang, X.; Lu, W. A hierarchical category model for geometrical product specifications (GPS). Procedia CIRP 2016, 43, 214–219. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Chen, J.; Fieguth, P.; Zhao, G.; Chellappa, R.; Pietikäinen, M. From BoW to CNN: Two decades of texture representation for texture classification. Int. J. Comput. Vis. 2019, 127, 74–109. [Google Scholar] [CrossRef] [Green Version]
- Vakis, A.I.; Yastrebov, V.A.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Seeler, F.; Hager, C.; Tiedje, O.; Schneider, M. Simulations and experimental investigation of paint film leveling. J. Coat. Technol. Res. 2017, 14, 767–781. [Google Scholar] [CrossRef]
- Eumelen, G.J.A.M.; Bosco, E.; Suiker, A.S.J.; van Loon, A.; Iedema, P.D. A computational model for chemo-mechanical degradation of historical oil paintings due to metal soap formation. J. Mech. Phys. Solids 2019, 132, 103683. [Google Scholar] [CrossRef]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech House: Norwood, MA, USA, 1987; pp. 1–512. [Google Scholar]
- Montes, R.; Ureña, C. An Overview of BRDF Models; University of Granada: Granada, Spain, 2012; p. 26. [Google Scholar]
- Tominaga, S.; Tanaka, N. Spectral image acquisition, analysis, and rendering for art paintings. J. Electron. Imaging 2008, 17, 043022. [Google Scholar] [CrossRef]
- Chen, Y. Model Evaluation and Measurement Optimization for the Reproduction of Artist Paint Surfaces through Computer Graphics Renderings. Ph.D. Thesis, Rochester Institute of Technology, Rochester, NY, USA, 2008. [Google Scholar]
- Tsang, L.; Kong, J.A.; Ding, K.-H.; Ao, C.O. Scattering of Electromagnetic Waves, Numerical Simulations; John Wiley&Sons: New York, NY, USA, 2001; pp. 1–736. [Google Scholar]
- Ashikmin, M.; Premože, S.; Shirley, P. A microfacet-based BRDF generator. In Proceedings of the 27th annual Conference on Computer Graphics and Interactive Techniques—SIGGRAPH ’00, Anaheim, CA, USA, 21–25 July 2000; pp. 65–74. [Google Scholar]
- Dana, K.J.; Van Ginneken, B.; Nayar, S.K.; Koenderink, J.J. Reflectance and texture of real-world surfaces. ACM Trans. Graph. 1999, 18, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Elkhuizen, W.S.; Essers, T.T.W.; Lenseigne, B.; Weijkamp, C.; Song, Y.; Pont, S.C.; Geraedts, J.M.-P.; Dik, J. Reproduction of gloss, color and relief of paintings using 3D scanning and 3D printing. In Proceedings of the EUROGRAPHICS Workshop on Graphics and Cultural Heritage, Graz, Austria, 27–29 September 2017; pp. 183–187. [Google Scholar]
- Doerr, M. Ontologies for cultural heritage. In Handbook on Ontologies; Staab, S., Studer, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 463–486. [Google Scholar]
- ISO 21127:2014. Information and Documentation—A Reference Ontology for the Interchange of Cultural Heritage Information; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- CIDOC Conceptual Reference Model, Version 5.02. Available online: http://www.cidoc-crm.org/Version/version-5.0.2 (accessed on 17 October 2020).
- Hunter, J.; Odat, S. Building a semantic knowledge-base for painting conservators. In Proceedings of the 2011 IEEE Seventh International Conference on eScience, Stockholm, Sweden, 5–8 December 2011; IEEE: Stockholm, Sweden, 2011; pp. 173–180. [Google Scholar]
- Lagoze, C. The oreChem project: Integrating chemistry, scholarship with the semantic web. In Proceedings of the WebSci’09: Society On-Line, Athens, Greece, 18–20 March 2009; pp. 406–413. [Google Scholar]
- Maillot, N.E.; Thonnat, M. Ontology based complex object recognition. Image Vis. Comput. 2008, 26, 102–113. [Google Scholar] [CrossRef] [Green Version]
- Gowsikhaa, D.; Abirami, S.; Baskaran, R. Construction of image ontology using low-level features for image retrieval. In Proceedings of the 2012 International Conference on Computer Communication and Informatics, Coimbatore, India, 10–12 January 2012; pp. 1–7. [Google Scholar]
- Jiang, S.-Q.; Du, J.; Huang, Q.-M.; Huang, T.-J.; Gao, W. Visual ontology construction for digitized art image retrieval. J. Comput. Sci. Technol. 2005, 20, 855–860. [Google Scholar] [CrossRef]
- Najjar, D.; Bigerelle, M.; Iost, A. The computer-based bootstrap method as a tool to select a relevant surface roughness parameter. Wear 2003, 254, 450–460. [Google Scholar] [CrossRef]
- Bigerelle, M.; Najjar, D.; Iost, A. Relevance of roughness parameters for describing and modelling machined surfaces. J. Mater. Sci. 2003, 38, 2525–2536. [Google Scholar] [CrossRef]
- Hennebelle, F.; Najjar, D.; Bigerelle, M.; Iost, A. Influence of the morphological texture on the low wear damage of paint coated sheets. Prog. Org. Coat. 2006, 56, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Rudermann, Y.; Iost, A.; Bigerelle, M. Scratch tests to contribute designing performance maps of multilayer polymeric coatings. Tribol. Int. 2011, 44, 585–591. [Google Scholar] [CrossRef] [Green Version]
- Bigerelle, M.; Anselme, K. Bootstrap analysis of the relation between initial adhesive events and long-term cellular functions of human osteoblasts cultured on biocompatible metallic substrates. Acta Biomater. 2005, 1, 499–510. [Google Scholar] [CrossRef] [PubMed]
- Hubert, C.; Marteau, J.; Deltombe, R.; Chen, Y.M.; Bigerelle, M. Roughness characterization of the galling of metals. Surf. Topogr. Metrol. Prop. 2014, 2, 034002. [Google Scholar] [CrossRef]
- Xia, Y.; Bigerelle, M.; Marteau, J.; Mazeran, P.-E.; Bouvier, S.; Iost, A. Effect of surface roughness in the determination of the mechanical properties of material using nanoindentation test: Effect of surface roughness. Scanning J. Scanning Microsc. 2014, 36, 134–149. [Google Scholar] [CrossRef] [Green Version]
- Bigerelle, M.; Hagege, B.; El Mansori, M. Mechanical modelling of micro-scale abrasion in superfinish belt grinding. Tribol. Int. 2008, 41, 992–1001. [Google Scholar] [CrossRef]
- Bigerelle, M.; Van Gorp, A.; Iost, A. Multiscale roughness analysis in injection-molding process. Polym. Eng. Sci. 2008, 48, 1725–1736. [Google Scholar] [CrossRef] [Green Version]
- Marteau, J.; Bigerelle, M.; Mazeran, P.-E.; Bouvier, S. Relation between roughness and processing conditions of AISI 316L stainless steel treated by ultrasonic shot peening. Tribol. Int. 2015, 82, 319–329. [Google Scholar] [CrossRef]
- Bigerelle, M.; Mathia, T.; Iost, A.; Correvits, T.; Anselme, K. An expert system to characterize the surface morphological properties according to their functionalities. J. Phys. Conf. Ser. 2011, 311, 012010. [Google Scholar] [CrossRef]
- Bigerelle, M.; Najjar, D.; Mathia, T.; Iost, A.; Coorevits, T.; Anselme, K. An expert system to characterise the surfaces morphological properties according to their tribological functionalities: The relevance of a pair of roughness parameters. ENERGY Health 2013, 59, 190–202. [Google Scholar] [CrossRef] [Green Version]
- Bigerelle, M.; Marteau, J.; Blateyron, F. Assessing the discriminating power of roughness parameters using a roughness databank. Surf. Topogr. Metrol. Prop. 2017, 5, 025002. [Google Scholar] [CrossRef]
- Cacciari, I.; Nieri, P.; Siano, S. 3D digital microscopy for characterizing Punchworks on medieval panel paintings. J. Comput. Cult. Herit. 2014, 7, 1–15. [Google Scholar] [CrossRef]
- Van den Berg, K.J.; Daudin, M.; Joosten, I.; Wei, B. A comparison of light microscopy techniques with scanning electron microscopy for imaging the surface of cleaning of paintings. In Proceedings of the 9th International Conference on NDT of Art, Jerusalem, Israel, 25–30 May 2008; pp. 25–30. [Google Scholar]
- Newton, L.; Senin, N.; Gomez, C.; Danzl, R.; Helmli, F.; Blunt, L.; Leach, R. Areal topography measurement of metal additive surfaces using focus variation microscopy. Addit. Manuf. 2019, 25, 365–389. [Google Scholar] [CrossRef]
- Bigerelle, M.; Mathia, T.; Bouvier, S. The multi-scale roughness analyses and modeling of abrasion with the grit size effect on ground surfaces. Wear 2012, 286–287, 124–135. [Google Scholar] [CrossRef]
- Guillemot, G.; Bigerelle, M.; Khawaja, Z. 3D parameter to quantify the anisotropy measurement of periodic structures on rough surfaces: A Parameter to Quantify Anisotropy. Scanning 2014, 36, 127–133. [Google Scholar] [CrossRef]
- Schlick, C. An inexpensive BRDF model for physically-based rendering. Comput. Graph. Forum 1994, 13, 233–246. [Google Scholar] [CrossRef]
- Hubert, C.; Kubiak, K.J.; Bigerelle, M.; Dubois, A.; Dubar, L. Identification of lubrication regime on textured surfaces by multi-scale decomposition. Tribol. Int. 2015, 82, 375–386. [Google Scholar] [CrossRef] [Green Version]









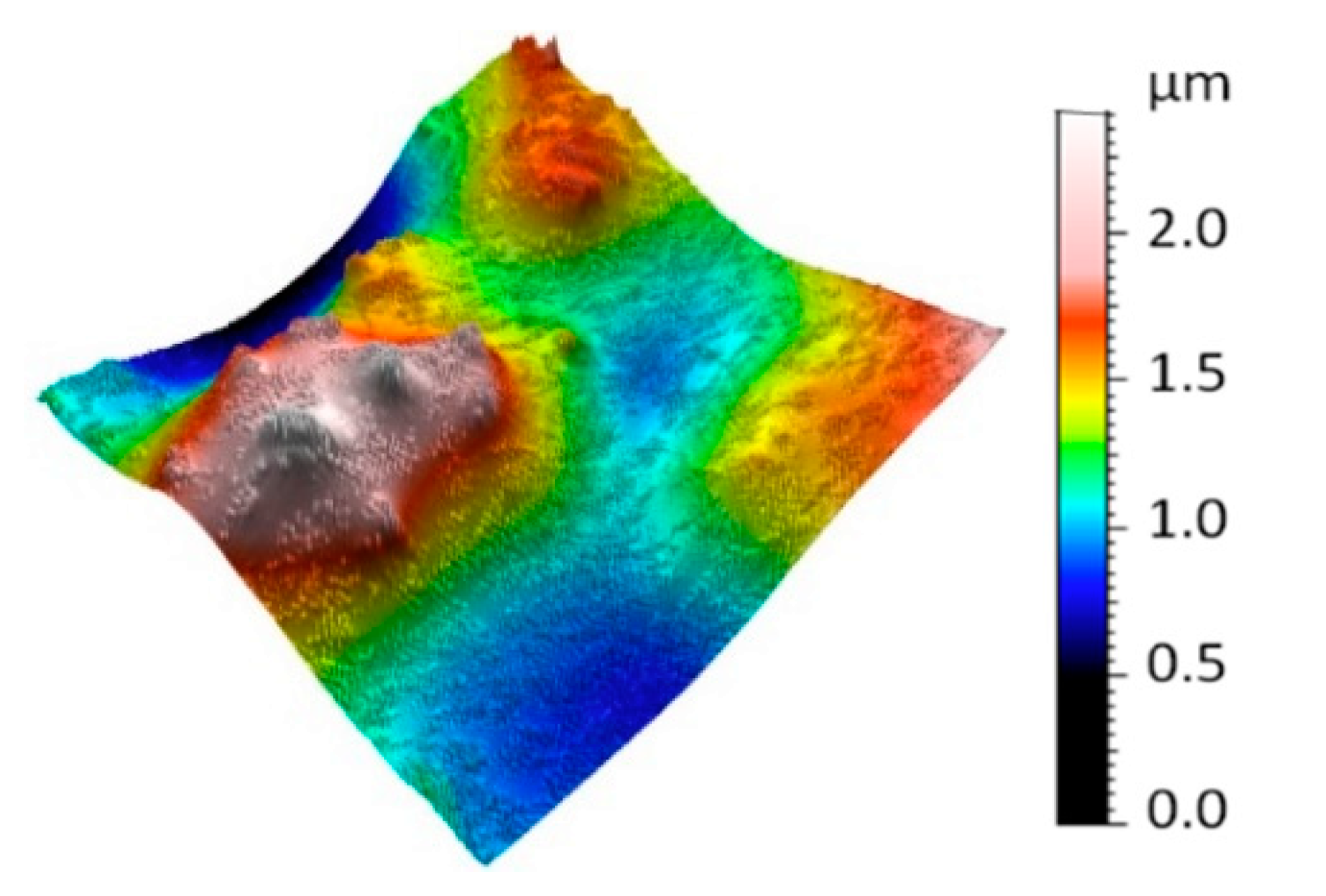
| Technique | Specification | Vertical Resolution | Lateral Resolution | Field of View | Phenomenon to Study |
|---|---|---|---|---|---|
| Focus variation Magnification: 10× | Allows topographic maps to be obtained combined with color images of surfaces up to 10 cm by 10 cm with high resolution | 100 nm | 1.76 µm | 1.62 × 1.62 mm | Geometry of canvas, brushstrokes, painter’s modus operandi. |
| Interferometry Magnification 50× | Allows acquisition of topography with micrometer and sub-micrometer accuracy, less influenced by color, which allows certain mistakes during the measurement process to be avoided | 10 nm (using motorized extended scan) | 0.52 µm (with Sparrow criteria) | 0.14 × 0.11 mm | Traces of brush hair, small-sized damages, bubbles, pigment clusters |
| Atomic Force Microscopy (peak force tapping mode) | Allows topographies with sub-micrometer and nanometer accuracy to be acquired | 0.2 nm | 0.5 nm | 10 μm | Paint pigments |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mironova, A.; Robache, F.; Deltombe, R.; Guibert, R.; Nys, L.; Bigerelle, M. Digital Cultural Heritage Preservation in Art Painting: A Surface Roughness Approach to the Brush Strokes. Sensors 2020, 20, 6269. https://doi.org/10.3390/s20216269
Mironova A, Robache F, Deltombe R, Guibert R, Nys L, Bigerelle M. Digital Cultural Heritage Preservation in Art Painting: A Surface Roughness Approach to the Brush Strokes. Sensors. 2020; 20(21):6269. https://doi.org/10.3390/s20216269
Chicago/Turabian StyleMironova, Anna, Frederic Robache, Raphael Deltombe, Robin Guibert, Ludovic Nys, and Maxence Bigerelle. 2020. "Digital Cultural Heritage Preservation in Art Painting: A Surface Roughness Approach to the Brush Strokes" Sensors 20, no. 21: 6269. https://doi.org/10.3390/s20216269
APA StyleMironova, A., Robache, F., Deltombe, R., Guibert, R., Nys, L., & Bigerelle, M. (2020). Digital Cultural Heritage Preservation in Art Painting: A Surface Roughness Approach to the Brush Strokes. Sensors, 20(21), 6269. https://doi.org/10.3390/s20216269