Cooperative Localization and Time Synchronization Based on M-VMP Method
Abstract
:1. Introduction
2. System Model
3. M-VMP Joint Estimation Algorithm
3.1. Probability Model
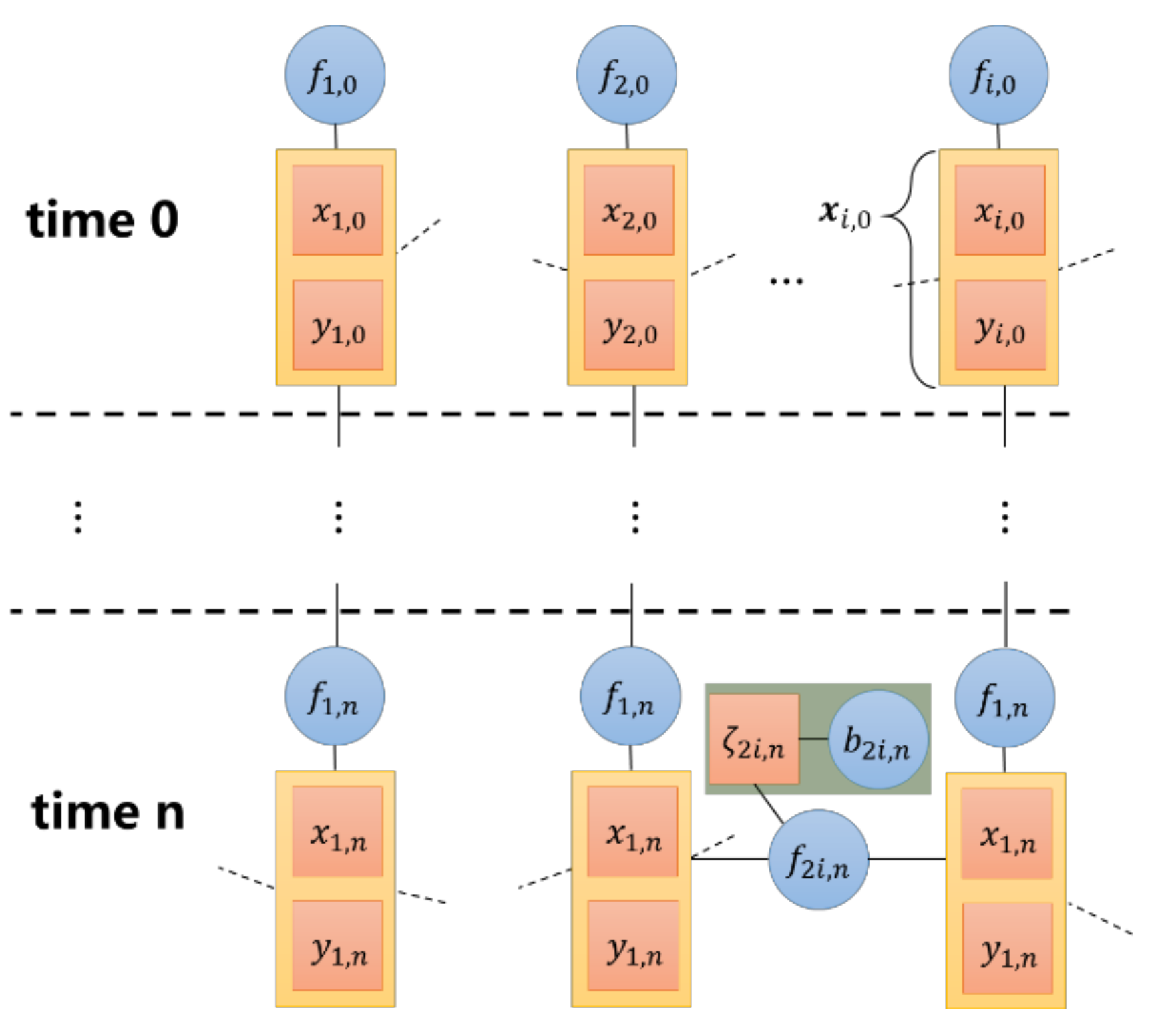
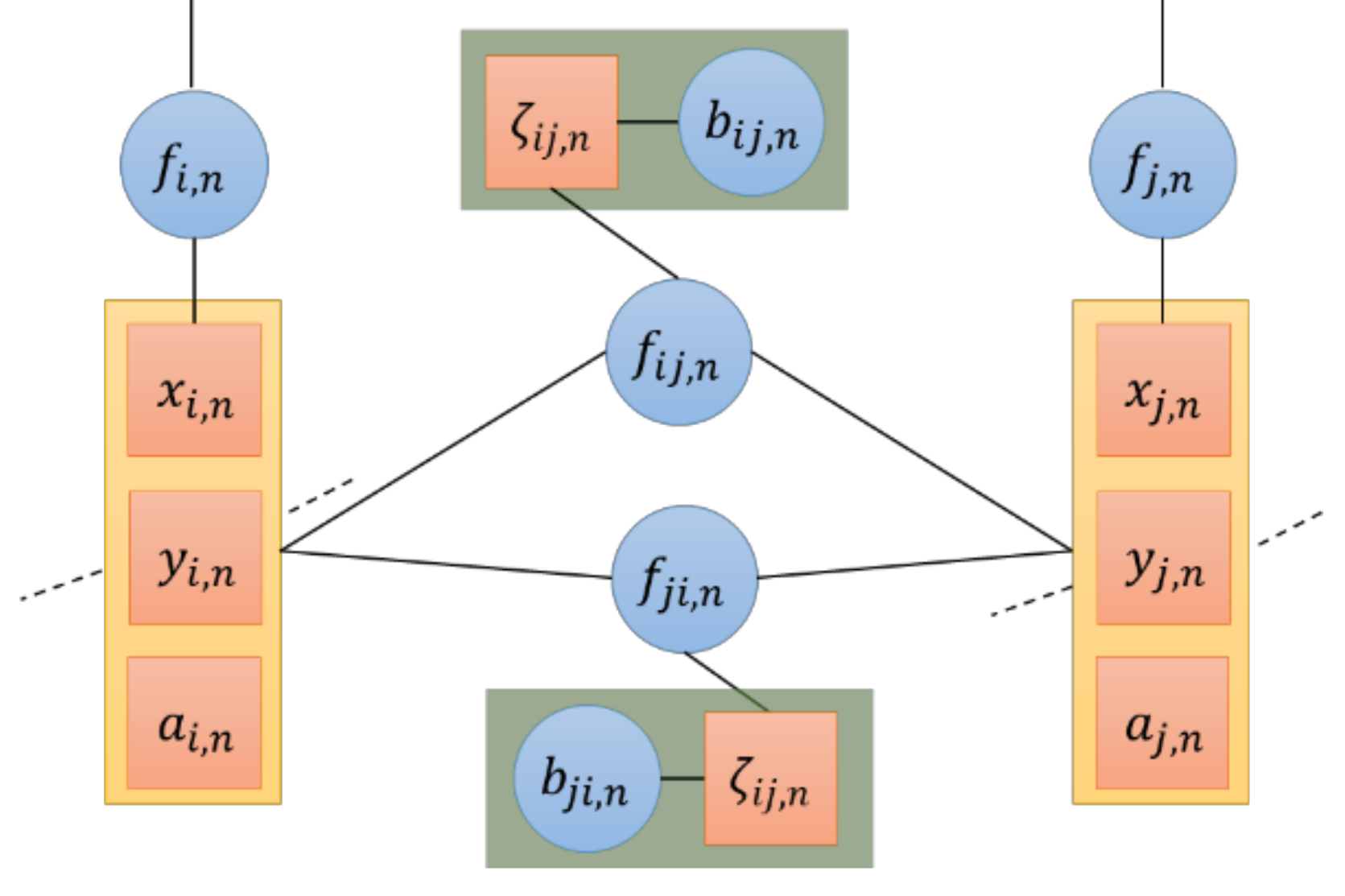
3.2. Factor Graph Model
3.3. VMP-Based Localization Algorithm
3.4. M-VMP-Based Joint Estimation Algorithm
- a.
- Second-order Taylor series expansion for nonlinear term is expanded at by a second-order Taylor to get:where and are the first and second steps of at .
- b.
- Second-order Taylor series expansion for nonlinear term : is expanded at and by a second-order Taylor to get:where and are the first-order partial derivatives of with respect to and at , and , is the Hessian matrix of at and .
| Algorithm 1: M-VMP joint estimation algorithm |
| Initialization: |
| Initialize node location distribution |
| Location estimation: |
| for n = 1 to N (time index) do |
| Nodes |
| 1) Compute covariance of belief according to (32) |
| 2) Compute mean of belief according to (33) |
| 3) Broadcast means and variances of belief , and receive the mean |
| and covariance matrix of location variables of neighbor nodes |
| 4) Estimate location information of node according to MMSE principle |
| 5) Update location information and form messages |
| end parallel |
| end for |
4. Simulation Analysis and Test Results
4.1. CRLB Lower Bound of
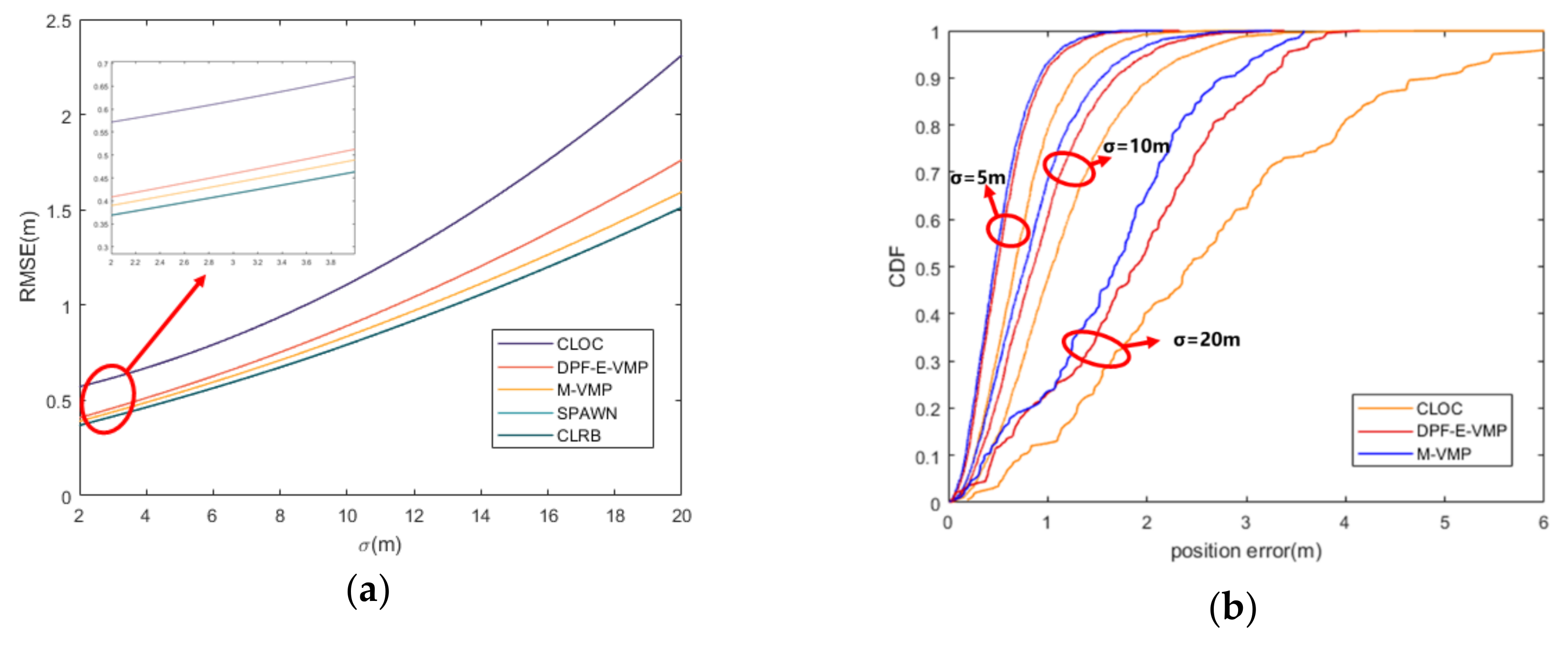
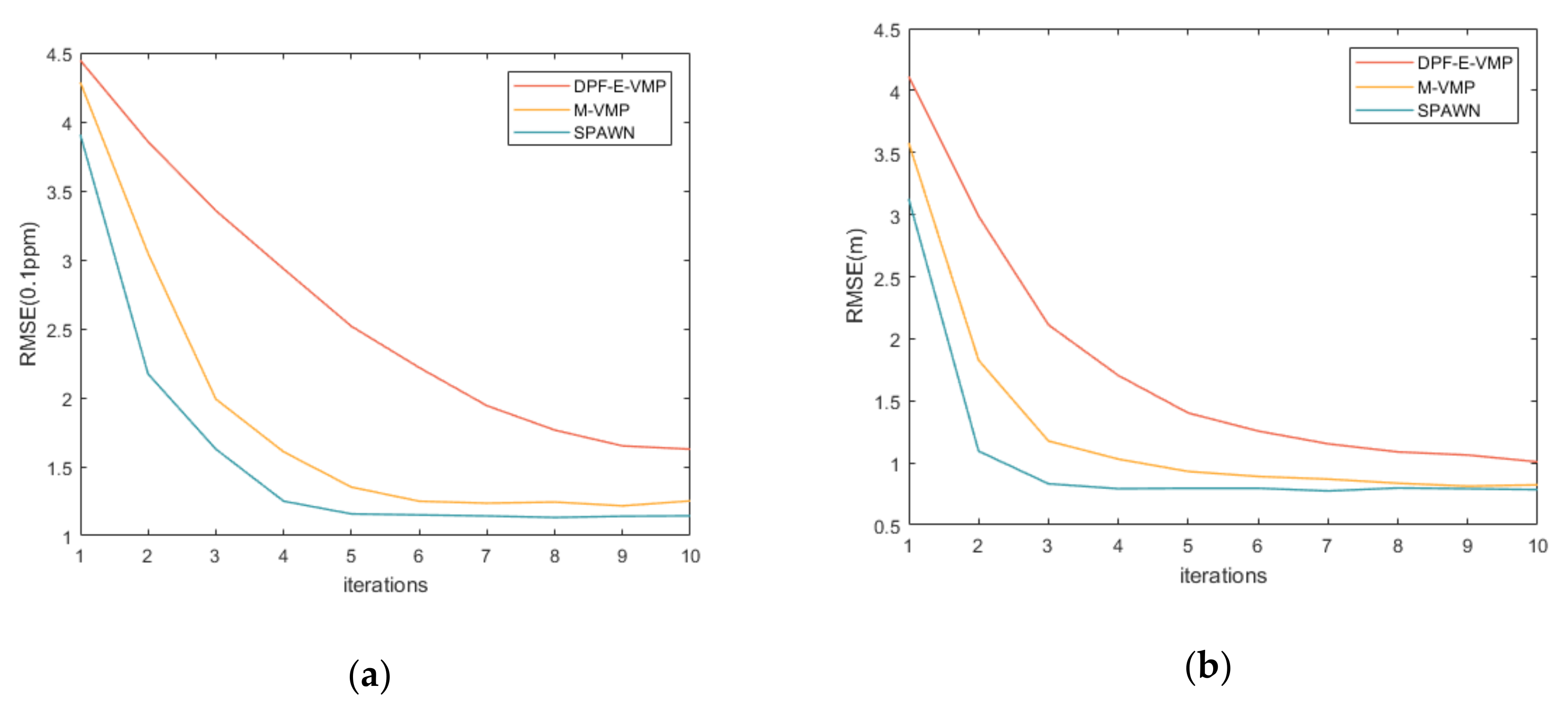
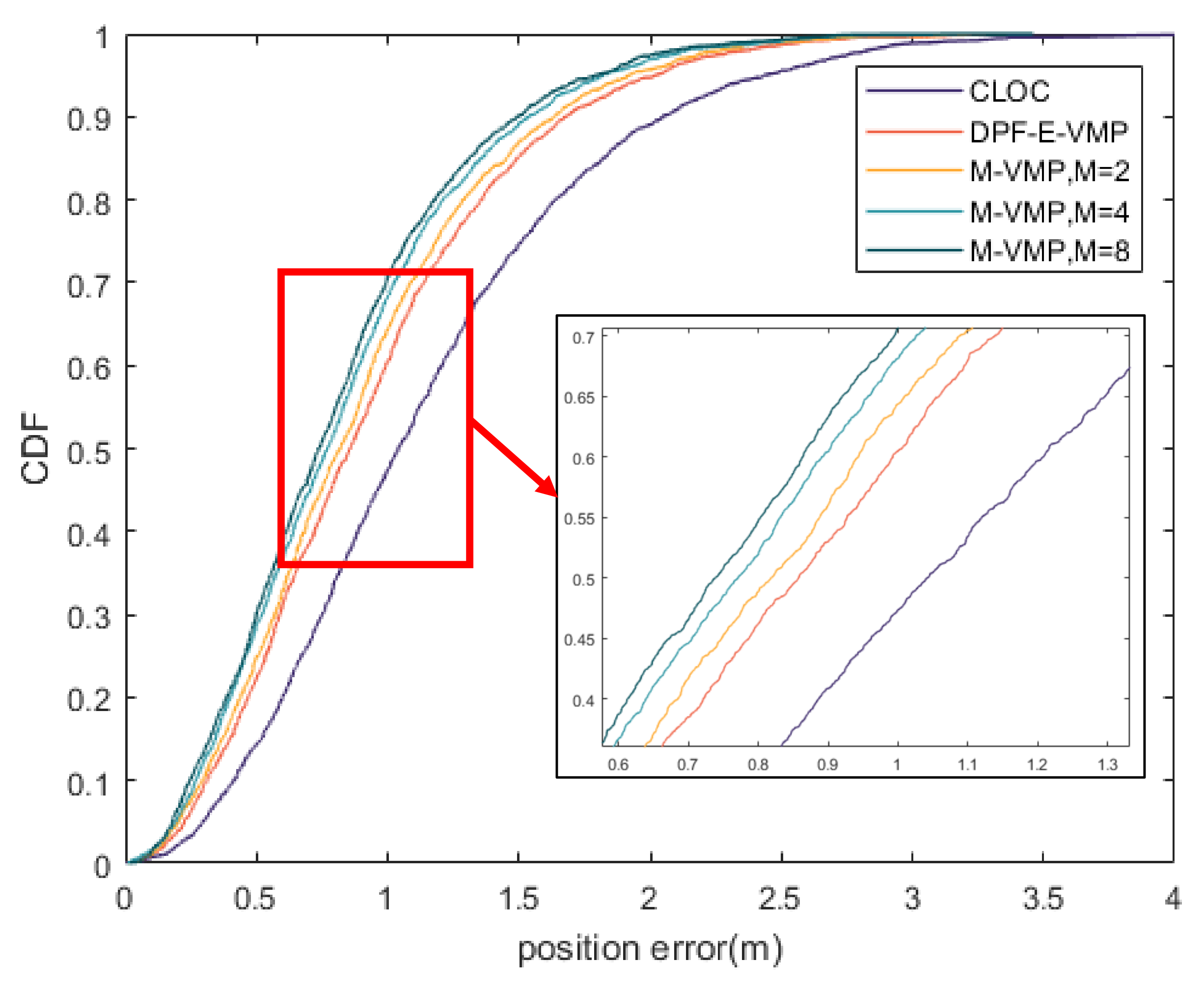
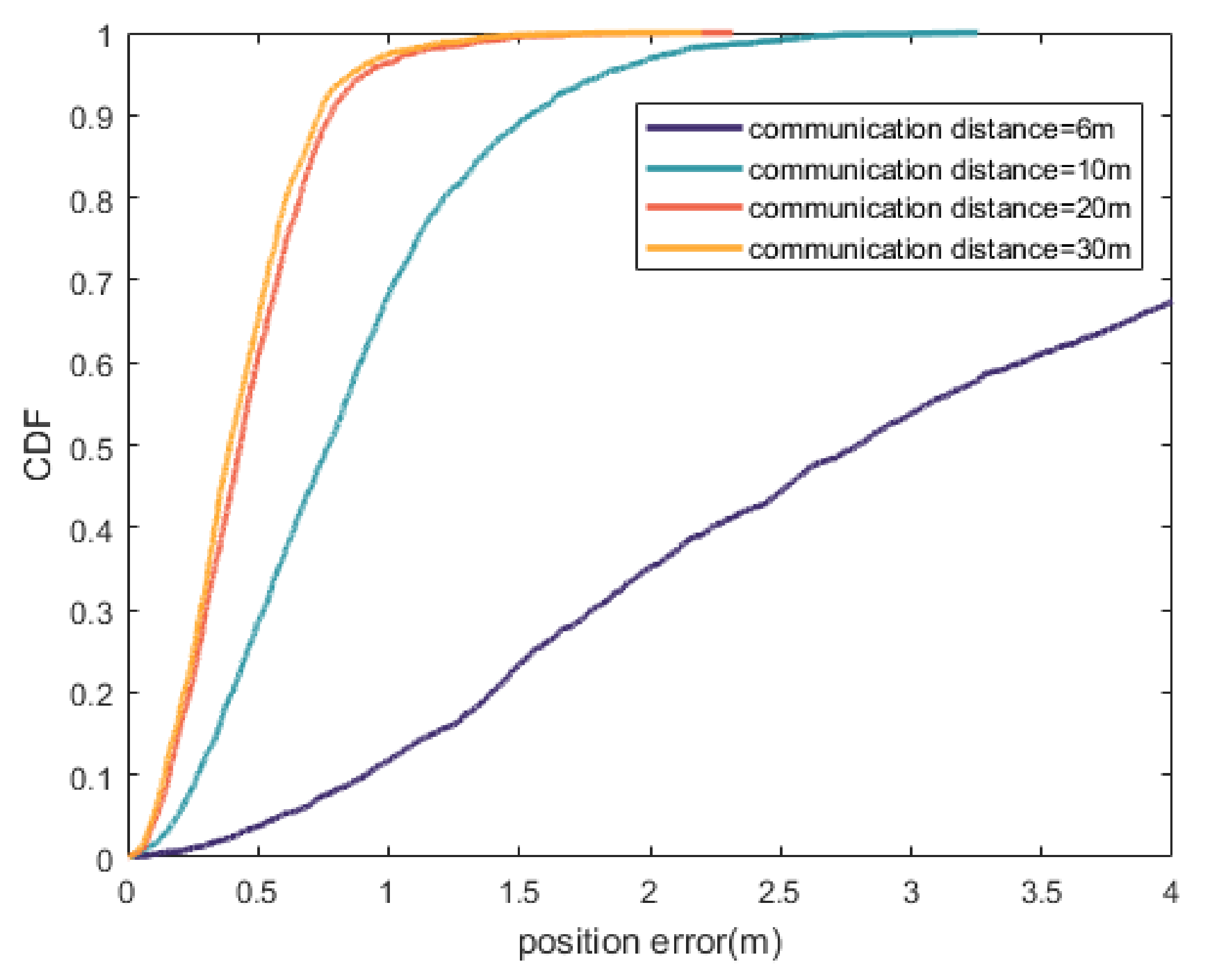
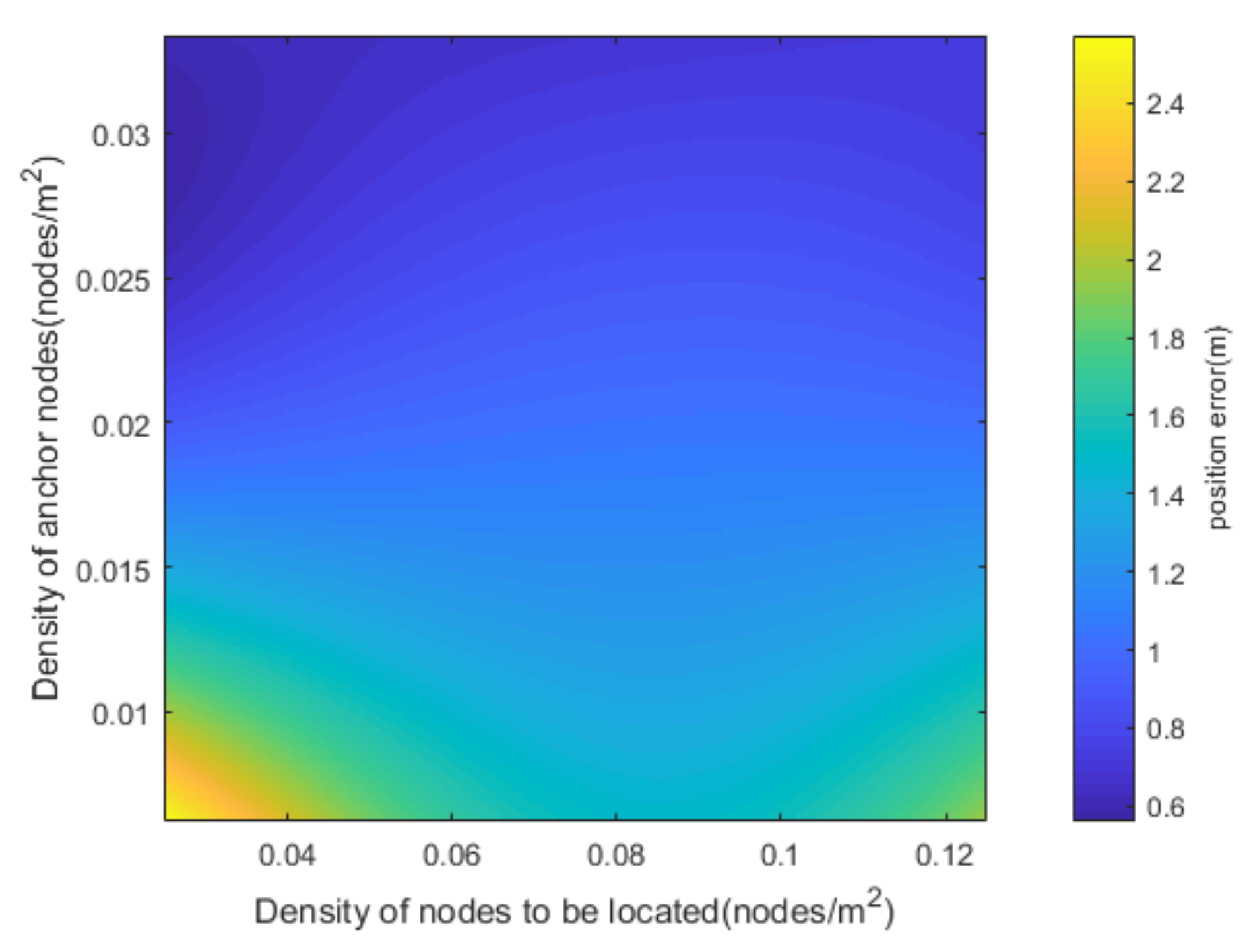
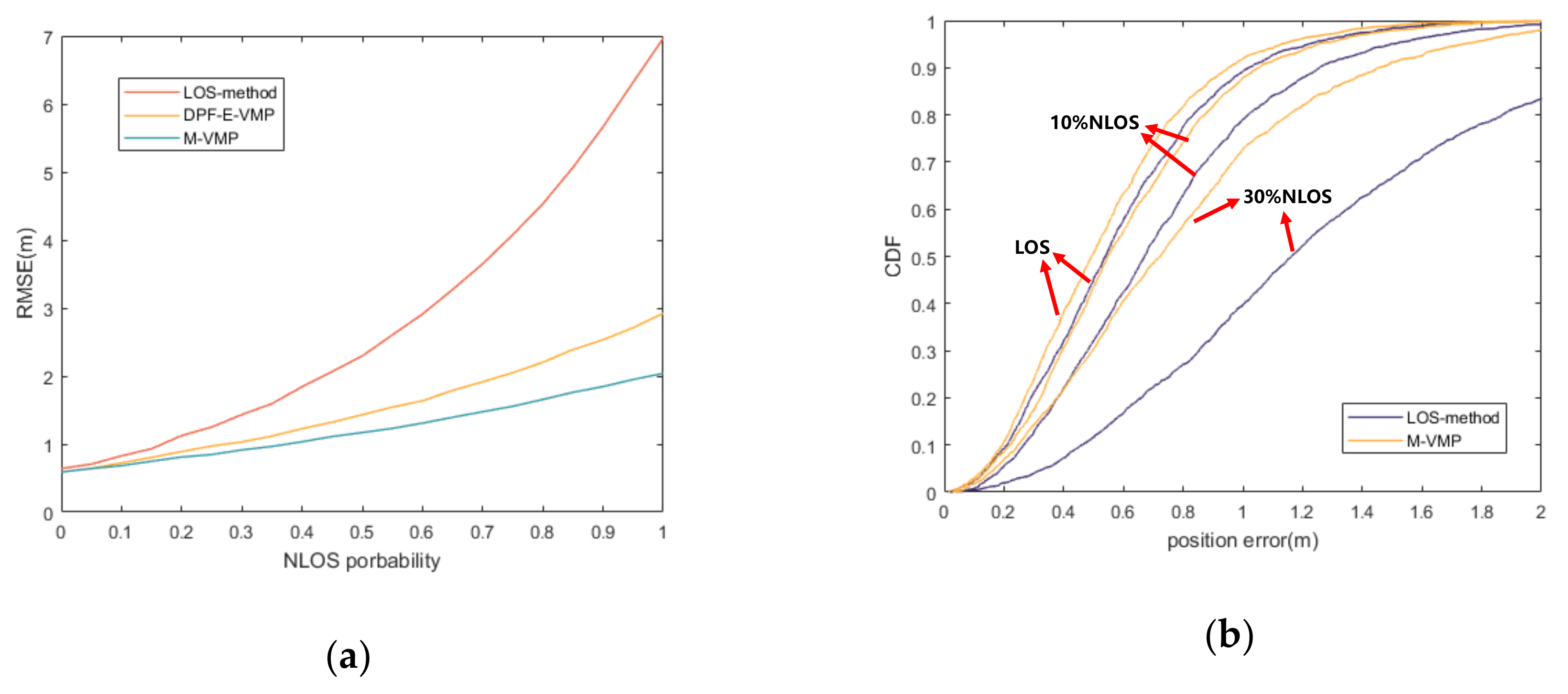
4.2. Simulation Scenario and Result Analysis
4.3. Computational Complexity and Communication Overhead Analysis
4.4. Future Research Directions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Amin, R.; Biswas, G. A secure light weight scheme for user authentication and key agreement in multi-gateway based wireless sensor networks. Ad Hoc Netw. 2016, 36, 58–80. [Google Scholar] [CrossRef]
- Yassin, A.; Nasser, Y.; Awad, M.; Al-Dubai, A.; Liu, R.; Yuen, C.; Raulefs, R.; Aboutanios, E. Recent advances in indoor localization: A survey on theoretical approaches and applications. IEEE Commun. Surv. Tutor. 2016, 19, 1327–1346. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Xu, H.; Duong, T.Q.; Jiang, J.; Hara, T. Localization algorithms of wireless sensor networks: A survey. Telecommun. Syst. 2013, 52, 2419–2436. [Google Scholar] [CrossRef]
- Han, G.; Jiang, J.; Zhang, C.; Duong, T.Q.; Guizani, M.; Karagiannidis, G.K. A survey on mobile anchor node assisted localization in wireless sensor networks. IEEE Commun. Surv. Tutor. 2016, 18, 2220–2243. [Google Scholar] [CrossRef]
- Wymeersch, H.; Lien, J.; Win, M.Z. Cooperative localization in wireless networks. Proc. IEEE 2009, 97, 427–450. [Google Scholar] [CrossRef]
- Shang, Y.; Rumi, W.; Zhang, Y.; Fromherz, M. Localization from connectivity in sensor networks. IEEE Trans. Parallel Distrib. Syst. 2004, 15, 961–974. [Google Scholar] [CrossRef] [Green Version]
- Sert, S.A.; Bagci, H.; Yazici, A. MOFCA: Multi-objective fuzzy clustering algorithm for wireless sensor networks. Appl. Soft Comput. 2015, 30, 151–165. [Google Scholar] [CrossRef]
- Ghari, P.M.; Shahbazian, R.; Ghorashi, S.A. Wireless sensor network localization in harsh environments using SDP relaxation. IEEE Commun. Lett. 2015, 20, 137–140. [Google Scholar] [CrossRef]
- Doherty, L.; El Ghaoui, L. Convex position estimation in wireless sensor networks. In Proceedings of the IEEE INFOCOM 2001. Conference on Computer Communications. Twentieth Annual Joint Conference of the IEEE Computer and Communications Society, Anchorage, AK, USA, 22–26 April 2001. [Google Scholar]
- Niculescu, D.; Nath, B. Ad hoc positioning system (APS). In Proceedings of the GLOBECOM′01. IEEE Global Telecommunications Conference, San Antonio, TX, USA, 25–29 November 2001. [Google Scholar]
- Shi, W.; Jia, C.; Liang, H. An Improved DV-Hop Localization Algorithm for Wireless Sensor Networks. Chin. J. Sens. Actuators 2011, 24, 83–87. [Google Scholar]
- He, T.; Huang, C.; Blum, B.M.; Stankovic, J.A.; Abdelzaher, T. Range-free localization schemes for large scale sensor networks. In Proceedings of the 9th Annual International Conference on Mobile Computing and Networking, San Diego, CA, USA, 16–18 September 2003. [Google Scholar]
- Liu, Z.; Fang, Z.; Ren, N.; Zhao, Y. A new range-free localization algorithm based on Annulus Intersection and Grid Scan in wireless sensor networks. J. Inf. Comput. Sci. 2012, 9, 831–841. [Google Scholar]
- Das, K.; Wymeersch, H. Censoring for Bayesian cooperative positioning in dense wireless networks. IEEE J. Sel. Areas Commun. 2012, 30, 1835–1842. [Google Scholar] [CrossRef] [Green Version]
- Pedersen, C.; Pedersen, T.; Fleury, B.H. A variational message passing algorithm for sensor self-localization in wireless networks. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 31 July–5 August 2011. [Google Scholar]
- Wang, Z.; Jin, X.; Wang, X.; Xu, J.; Bai, Y. Hard decision-based cooperative localization for wireless sensor networks. Sensors 2019, 19, 4665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hehdly, K.; Laaraiedh, M.; Abdelkefi, F.; Siala, M. Cooperative localization and tracking in wireless sensor networks. Int. J. Commun. Syst. 2019, 32, e3842. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Cui, J.; Wang, Z.; Ding, Y.; Xia, Y. Distributed Joint Cooperative Self-Localization and Target Tracking Algorithm for Mobile Networks. Sensors 2019, 19, 3829. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cakmak, B.; Urup, D.N.; Meyer, F.; Pedersen, T.; Fleury, B.H.; Hlawatsch, F. Cooperative localization for mobile networks: A distributed belief propagation–mean field message passing algorithm. IEEE Signal Process. Lett. 2016, 23, 828–832. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Tian, S. Vertical Positioning Technologies and its Application of Pseudolites Augmentation. In Proceedings of the 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008. [Google Scholar]
- Peral-Rosado, J.A.D.; Bavaro, M.; Lopez-Salcedo, J.A.; Seco-Granados, G.; Chawdhry, P.; Fortuny-Guasch, J.; Crosta, P.; Zanier, F.; Crisci, M. Floor Detection with indoor vertical positioning in LTE femtocell networks. In Proceedings of the Globecom Workshops, San Diego, CA, USA, 6–10 December 2010. [Google Scholar]
- Gezici, S.; Sahinoglu, Z. UWB Geolocation Techniques for IEEE 802.15.4a Personal Area Networks. Available online: https://merl.com/publications/docs/TR2004-110.pdf (accessed on 5 November 2020).
- Nguyen, T.V.; Jeong, Y.; Shin, H.; Win, M.Z. Least Square Cooperative Localization. IEEE Trans. Veh. Technol. 2015, 64, 1318–1330. [Google Scholar] [CrossRef]
- Alsindi, N.A.; Pahlavan, K.; Alavi, B.; Li, X. A novel cooperative localization algorithm for indoor sensor networks. In Proceedings of the IEEE International Symposium on Personal, Helsinki, Finland, 11–14 November 2006. [Google Scholar]
- Zheng, J.; Wu, Y.-C. Joint time synchronization and localization of an unknown node in wireless sensor networks. IEEE Trans. Signal Process. 2009, 58, 1309–1320. [Google Scholar] [CrossRef] [Green Version]
- Wymeersch, H.; Ferner, U.; Win, M. Cooperative Bayesian Self-Tracking for Wireless Networks. IEEE Commun. Lett. 2008, 12, 505–507. [Google Scholar] [CrossRef]
- Sottile, F.; Wymeersch, H.; Caceres, M.A.; Spirito, M.A. Hybrid GNSS-terrestrial cooperative positioning based on particle filter. In Proceedings of the Global Telecommunications Conference, Kathmandu, Nepal, 5–9 December 2011. [Google Scholar]
- Yuan, W.; Wu, N.; Etzlinger, B.; Wang, H.; Kuang, J.-M. Cooperative Joint Localization and Clock Synchronization Based on Gaussian Message Passing in Asynchronous Wireless Networks. IEEE Trans. Veh. Technol. 2016, 65, 1. [Google Scholar] [CrossRef] [Green Version]

| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| Set of neighbor anchor nodes of node at time | Set of neighbor nodes to be located of node at time | ||
| Position vector of node at time | Measurement value of local clock of note at time | ||
| Real time value at time | Slope of local clock of node at time | ||
| Relative slope of local clock offset between nodes | Set of neighbor nodes of node at time | ||
| Range measurement between node , at time | Measurement noise of | ||
| Variance of | NLOS error of | ||
| Set of all communicable node pairs at time | Set of all node pairs with NLOS error at time | ||
| Position vector of all nodes at time | Clock offset of all nodes at time | ||
| Average velocity of node from time to time | Measurement noise of | ||
| Variance of | Vector to be estimated of note at time | ||
| Estimation result of node at time | Range measurement in all node pairs at time | ||
| NLOS error in all node pairs at time | Vector sets of from time 1 to time | ||
| Message send from to | Belief of variable | ||
| Confluent Hypergeometric Function of the First Type | Mean of belief | ||
| Covariance of belief | Weight of the -th Gaussian distribution | ||
| Fisher Information Matrix (FIM) of | Cramer-Rao Lower Bound of |
| Method | Computational Complexity | Run-Time | Communication Overhead |
|---|---|---|---|
| M-VMP (proposed method) | 84.449 ms | ||
| CLOC | 288.500 ms | ||
| SPAWN | 5469.089 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Z.; Tang, S.; Jia, B.; Wang, H.; Deng, X.; Zheng, X. Cooperative Localization and Time Synchronization Based on M-VMP Method. Sensors 2020, 20, 6315. https://doi.org/10.3390/s20216315
Deng Z, Tang S, Jia B, Wang H, Deng X, Zheng X. Cooperative Localization and Time Synchronization Based on M-VMP Method. Sensors. 2020; 20(21):6315. https://doi.org/10.3390/s20216315
Chicago/Turabian StyleDeng, Zhongliang, Shihao Tang, Buyun Jia, Hanhua Wang, Xiwen Deng, and Xinyu Zheng. 2020. "Cooperative Localization and Time Synchronization Based on M-VMP Method" Sensors 20, no. 21: 6315. https://doi.org/10.3390/s20216315
APA StyleDeng, Z., Tang, S., Jia, B., Wang, H., Deng, X., & Zheng, X. (2020). Cooperative Localization and Time Synchronization Based on M-VMP Method. Sensors, 20(21), 6315. https://doi.org/10.3390/s20216315





