Synchronization Theory-Based Analysis of Coupled Vibrations of Dual-Tube Coriolis Mass Flowmeters
Abstract
:1. Introduction
2. Nonlinearity Analysis of Single-Beam Forced Vibration Model
3. Analysis of Coupled Vibrations of the Dual-Tube Model
4. Numerical Solutions
5. Nonlinearity Suppression Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zheng, D.; Wang, S.; Fan, S. Nonlinear vibration characteristics of Coriolis mass flowmeter. Chin. J. Aeronaut. 2009, 22, 198–205. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Zheng, D.; Fan, S. Experimental study and implementation of a novel digital closed-loop control system for coriolis mass flowmeter. IEEE Sens. J. 2013, 13, 3032–3038. [Google Scholar] [CrossRef]
- Wang, T.; Baker, R. Coriolis flowmeters: A review of developments over the past 20 years, and an assessment of the state of the art and likely future directions. Flow Meas. Instrum. 2014, 40, 99–123. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Zheng, D.; Fan, S.; Gong, J. Research and implementation of amplitude ratio calculating system for coriolis mass flowmeter. In Proceedings of the 2012 8th IEEE International Symposium on Instrumentation and Control Technology (ISICT) Proceedings, London, UK, 11–13 July 2012; pp. 147–152. [Google Scholar]
- Cheesewright, R.; Clark, C.; Bisset, D. Understanding the experimental response of Coriolis massflow meters to flow pulsations. Flow Meas. Instrum. 1999, 10, 207–215. [Google Scholar] [CrossRef]
- Cheesewright, R.; Clark, C. The effect of flow pulsations on Coriolis mass flow meters. J. Fluids Struct. 1998, 12, 1025–1039. [Google Scholar] [CrossRef]
- Belhadj, A.; Cheesewright, R.; Clark, C. The simulation of Coriolis meter response to pulsating flow using a general purpose FE code. J. Fluids Struct. 2000, 14, 613–634. [Google Scholar] [CrossRef]
- Kutin, J.; Bajsić, I. An analytical estimation of the Coriolis meter’s characteristics based on modal superposition. Flow Meas. Instrum. 2002, 12, 345–351. [Google Scholar] [CrossRef]
- Wang, T.; Baker, R.C. Manufacturing variation of the measuring tube in a Coriolis flowmeter. IEE Proc. Sci. Meas. Technol. 2003, 151, 201–204. [Google Scholar] [CrossRef]
- Bobovnik, G.; Mole, N.; Kutin, J.; Štok, B.; Bajsić, I. Coupled finite-volume/finite-element modelling of the straight-tube Coriolis flowmeter. J. Fluids Struct. 2005, 20, 785–800. [Google Scholar] [CrossRef]
- Bobovnik, G.; Kutin, J.; Mole, N.; Štok, B.; Bajsić, I. Numerical analysis of installation effects in Coriolis flowmeters: Single and twin tube configurations. Flow Meas. Instrum. 2015, 44, 71–78. [Google Scholar] [CrossRef]
- Enz, S. Effect of asymmetric actuator and detector position on Coriolis flowmeter and measured phase shift. Flow Meas. Instrum. 2010, 21, 497–503. [Google Scholar] [CrossRef]
- Svete, A.; Kutin, J.; Bobovnik, G.; Bajsić, I. Theoretical and experimental investigations of flow pulsation effects in Coriolis mass flowmeters. J. Sound Vib. 2015, 352, 30–45. [Google Scholar] [CrossRef]
- Thomsen, J.J.; Fuglede, N. Perturbation-based prediction of vibration phase shift along fluid-conveying pipes due to Coriolis forces, nonuniformity, and nonlinearity. Nonlinear Dyn. 2020, 99, 173–199. [Google Scholar] [CrossRef]
- Cairone, F.; Gagliano, S.; Carbone, D.C.; Recca, G.; Bucolo, M. Micro-optofluidic switch realized by 3D printing technology. Microfluid. Nanofluidics 2016, 20, 61. [Google Scholar] [CrossRef]
- Gagliano, S.; Stella, G.; Bucolo, M. Real-Time Detection of Slug Velocity in Microchannels. Micromachines 2020, 11, 241. [Google Scholar] [CrossRef] [Green Version]
- Sapuppo, F.; Schembri, F.; Fortuna, L.; Bucolo, M. Microfluidic circuits and systems. IEEE Circuits Syst. Mag. 2009, 9, 6–19. [Google Scholar] [CrossRef]
- Keita, N.M. Contribution to the understanding of the zero shift effects in Coriolis mass flowmeters. Flow Meas. Instrum. 1989, 1, 39–43. [Google Scholar] [CrossRef]
- Thomsen, J.J.; Dahl, J. Phase shift effects for fluid conveying pipes on non-ideal supports. J. Sound Vib. 2010, 329, 3065–3081. [Google Scholar] [CrossRef]
- Thomsen, J.J.; Dahl, J.; Fuglede, N.; Enz, S. Predicting phase shift of elastic waves in pipes due to fluid flow and imperfections. In Proceedings of the 16th International Congress on Sound and Vibration, Krakow, Poland, 5–9 July 2009; pp. 1–8. [Google Scholar]
- Sun, Y.; Zhang, T.; Zheng, D. New analysis scheme of flow-acoustic coupling for gas ultrasonic flowmeter with vortex near the transducer. Sensors 2018, 18, 1151. [Google Scholar]
- Chen, S. Dynamic stability of tube conveying fluid. J. Eng. Mech. 1971, 97, 1469–1485. [Google Scholar]
- Enz, S.; Thomsen, J.J. Predicting phase shift effects for vibrating fluid-conveying pipes due to Coriolis forces and fluid pulsations. J. Sound Vib. 2011, 330, 5096–5113. [Google Scholar] [CrossRef]
- Kabaciński, M.; Pospolita, J. Effect of Distortion in Velocity Profile on Flow Measurements Using Averaging Flow Sensors. Sensors 2020, 20, 2839. [Google Scholar] [CrossRef]
- Hemp, J.; Kutin, J. Theory of errors in Coriolis flowmeter readings due to compressibility of the fluid being metered. Flow Meas. Instrum. 2006, 17, 359–369. [Google Scholar] [CrossRef]
- Torres, F.; Uranga, A.; Riverola, M.; Sobreviela, G.; Barniol, N. Enhancement of frequency stability using synchronization of a cantilever array for mems-based sensors. Sensors 2016, 16, 1690. [Google Scholar] [CrossRef]
- Blekhman, I.I.; Fradkov, A.L.; Tomchina, O.P.; Bogdanov, D.E. Self-synchronization and controlled synchronization: General definition and example design. Math. Comput. Simul. 2002, 58, 367–384. [Google Scholar] [CrossRef]
- Xin, X.; Muraoka, Y.; Hara, S. Analysis of synchronization of n metronomes on a cart via describing function method: New results beyond two metronomes. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 6604–6609. [Google Scholar]
- Nour, M.A.; Hussain, M.M. A Review of the Real-Time Monitoring of Fluid-Properties in Tubular Architectures for Industrial Applications. Sensors 2020, 20, 3907. [Google Scholar] [CrossRef]
- Krysko, A.V.; Awrejcewicz, J.; Saltykova, O.A.; Vetsel, S.S.; Krysko, V.A. Nonlinear dynamics and contact interactions of the structures composed of beam-beam and beam-closed cylindrical shell members. Chaos Solitons Fractals 2016, 91, 622–638. [Google Scholar] [CrossRef]
- Chen, L.; Xu, D.; Du, J.; Zhong, C. Flexural vibration analysis of nonuniform double-beam system with general boundary and coupling conditions. Shock Vib. 2018, 2018, 8. [Google Scholar] [CrossRef] [Green Version]


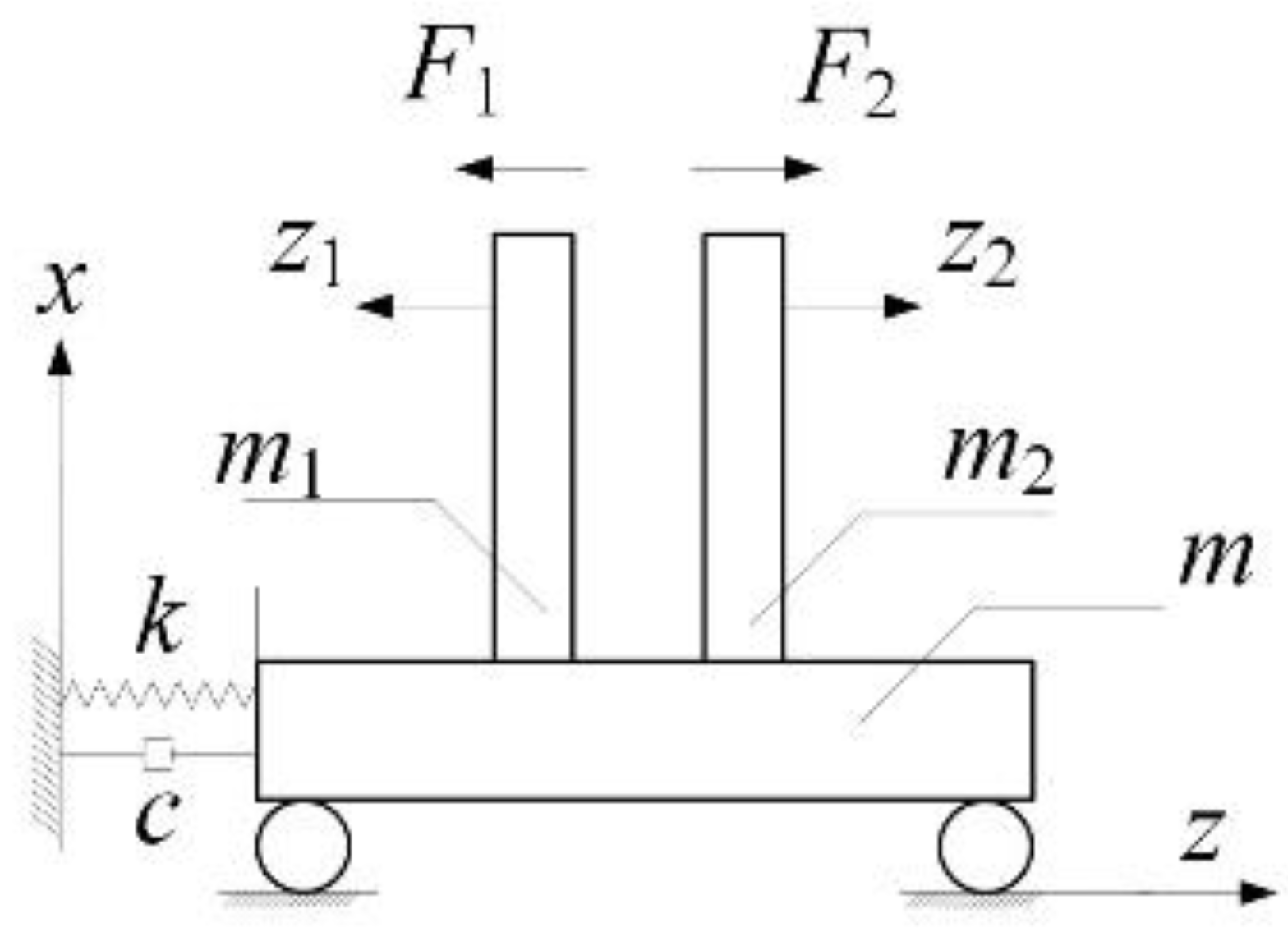

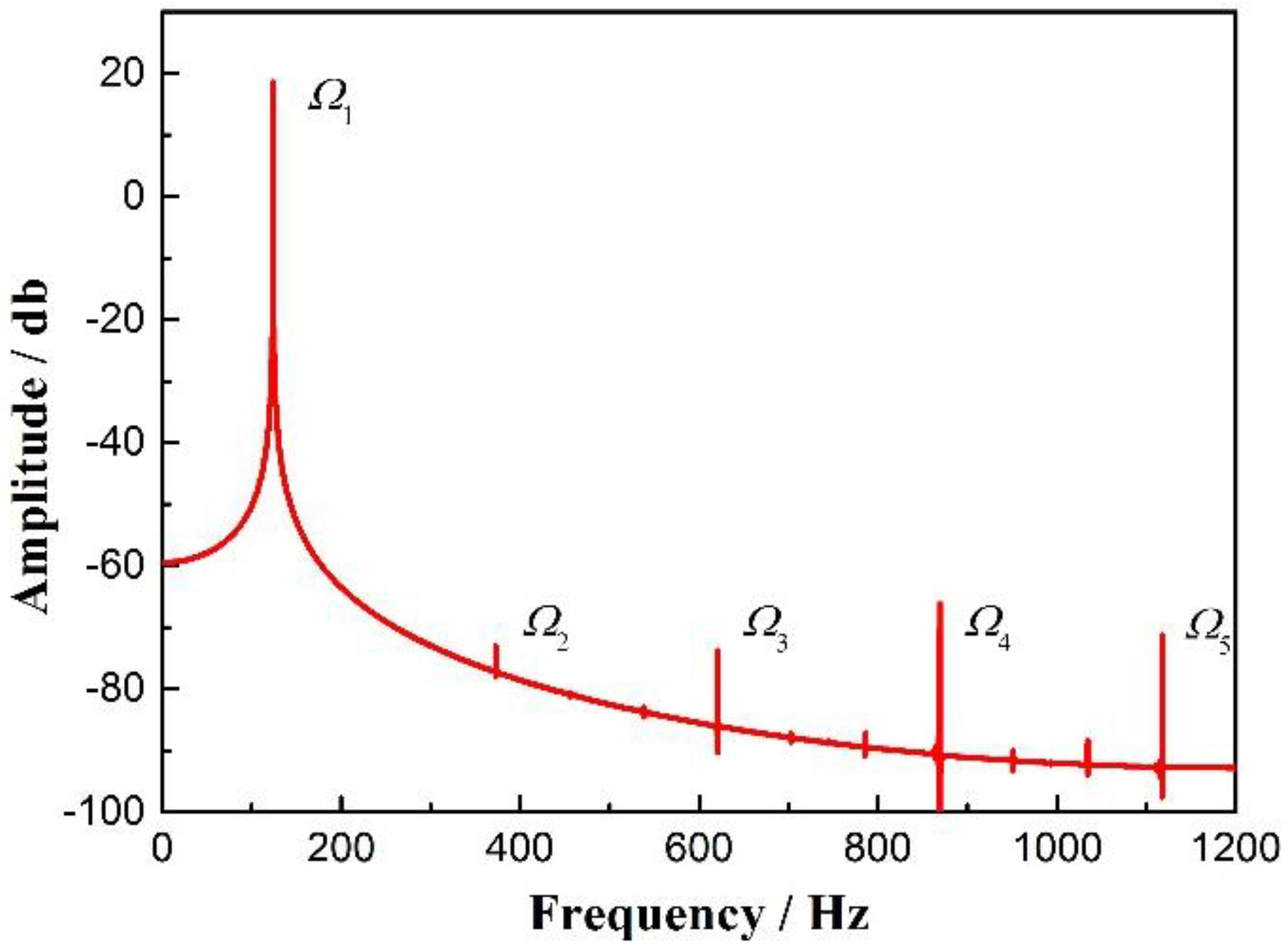


| Parameter | Value |
|---|---|
| Mass of a single beam | 0.7010 kg |
| Length of a single beam | 0.232 m |
| Diameter of a single beam | 0.5 cm |
| Density | 7890 kg/ |
| Mass of the base | 3 kg |
| Elastic modulus | 200 GPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.-X.; Hu, C.; Zheng, D.-Z.; Fan, S.-C. Synchronization Theory-Based Analysis of Coupled Vibrations of Dual-Tube Coriolis Mass Flowmeters. Sensors 2020, 20, 6340. https://doi.org/10.3390/s20216340
Li Z-X, Hu C, Zheng D-Z, Fan S-C. Synchronization Theory-Based Analysis of Coupled Vibrations of Dual-Tube Coriolis Mass Flowmeters. Sensors. 2020; 20(21):6340. https://doi.org/10.3390/s20216340
Chicago/Turabian StyleLi, Zhong-Xiang, Chun Hu, De-Zhi Zheng, and Shang-Chun Fan. 2020. "Synchronization Theory-Based Analysis of Coupled Vibrations of Dual-Tube Coriolis Mass Flowmeters" Sensors 20, no. 21: 6340. https://doi.org/10.3390/s20216340
APA StyleLi, Z.-X., Hu, C., Zheng, D.-Z., & Fan, S.-C. (2020). Synchronization Theory-Based Analysis of Coupled Vibrations of Dual-Tube Coriolis Mass Flowmeters. Sensors, 20(21), 6340. https://doi.org/10.3390/s20216340







