Intelligent Steam Power Plant Boiler Waterwall Tube Leakage Detection via Machine Learning-Based Optimal Sensor Selection
Abstract
:1. Introduction
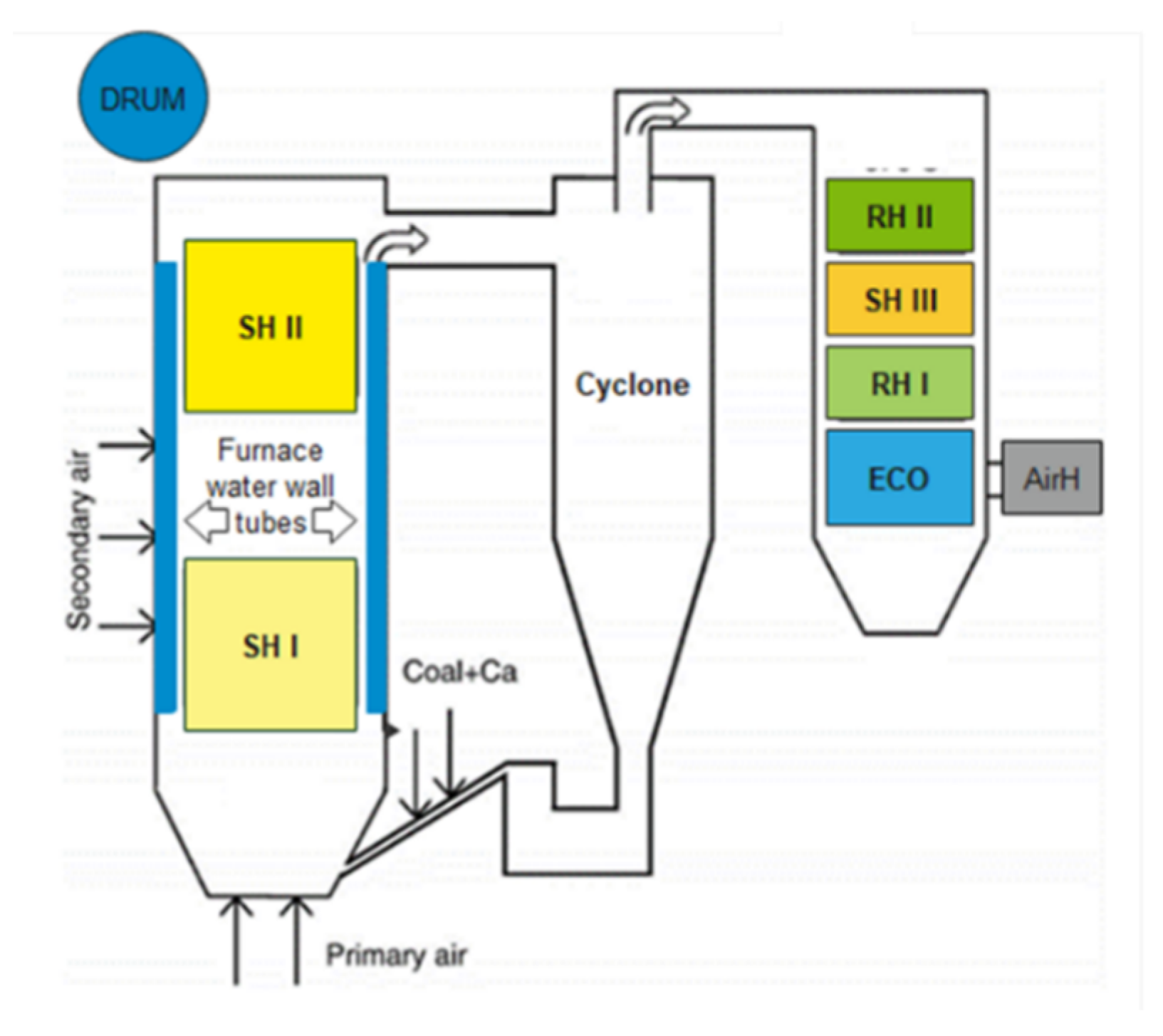
2. Significance of the Boiler Waterwall Tube in an SPP
2.1. Equipment in a Coal-Fired Power Plant
- Boiler: A boiler is the primary piece of equipment in an SPP. It transfers energy to water until it becomes a heated steam, which is then utilized to run the steam turbine. The boiler consists of three main subsystems, i.e., a feedwater system, steam system, and fuel/air draft system. Each subsystem comprises numerous additional components that make them suitable for application in advanced power plants.
- Turbine: The turbine uses high-temperature, pressurized steam to transform heat energy into mechanical energy in order to run the electric generator. The associated subsystems are the turbine gear/barring gear, gland sealing system, and turbine oil system.
- Condenser: High-temperature steam travels to the condenser from the turbine exhaust outlet. The condenser condenses the steam via heat transfer with cooling water from another source. It includes the steam ejectors, cooling water system, condensate pumps, and heat exchangers as associated subsystems.
- Electrical generator: The function of an electrical generator is to convert mechanical energy into electrical energy. It includes an exciter and transformer as subsystems.
- Monitoring alarm system: The alarm system is used to check the health status of the equipment mentioned above. It rings alarms in case of any abnormality.
2.2. Waterwall Tube Failure Analysis
3. Proposed Methodology
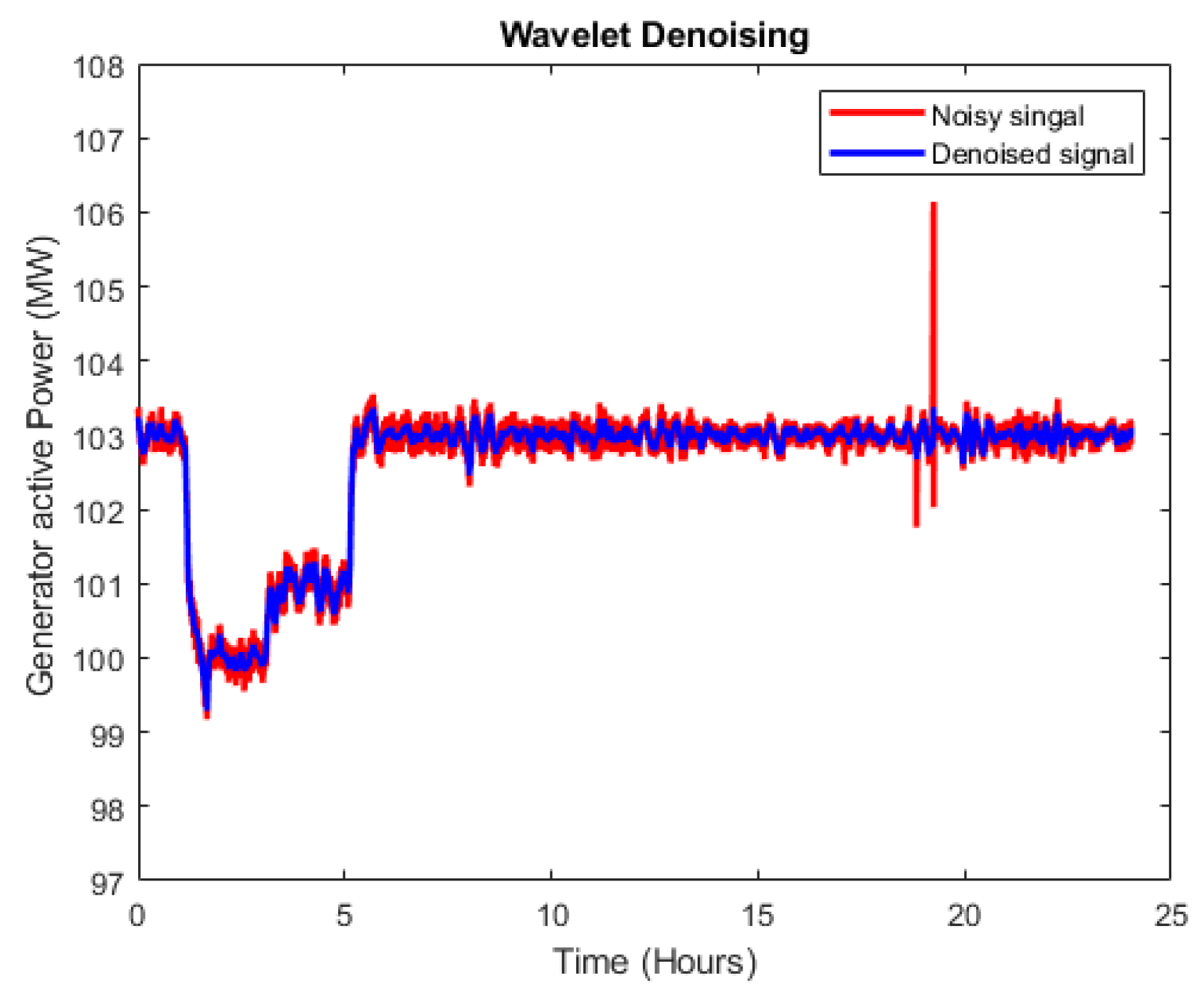
3.1. Data Preprocessing
3.2. Optimal Sensor Selection
3.3. Machine Learning Algorithms
3.3.1. SVM Classifier
- Linear kernel
- Polynomial kernel
- Radial basis function
- Hyperbolic tangential kernelwhere .
3.3.2. k-NN Classifier
3.3.3. NB Classifier
3.3.4. LDA Classifier
4. Real-World Power Plant Scenario—Computational Results
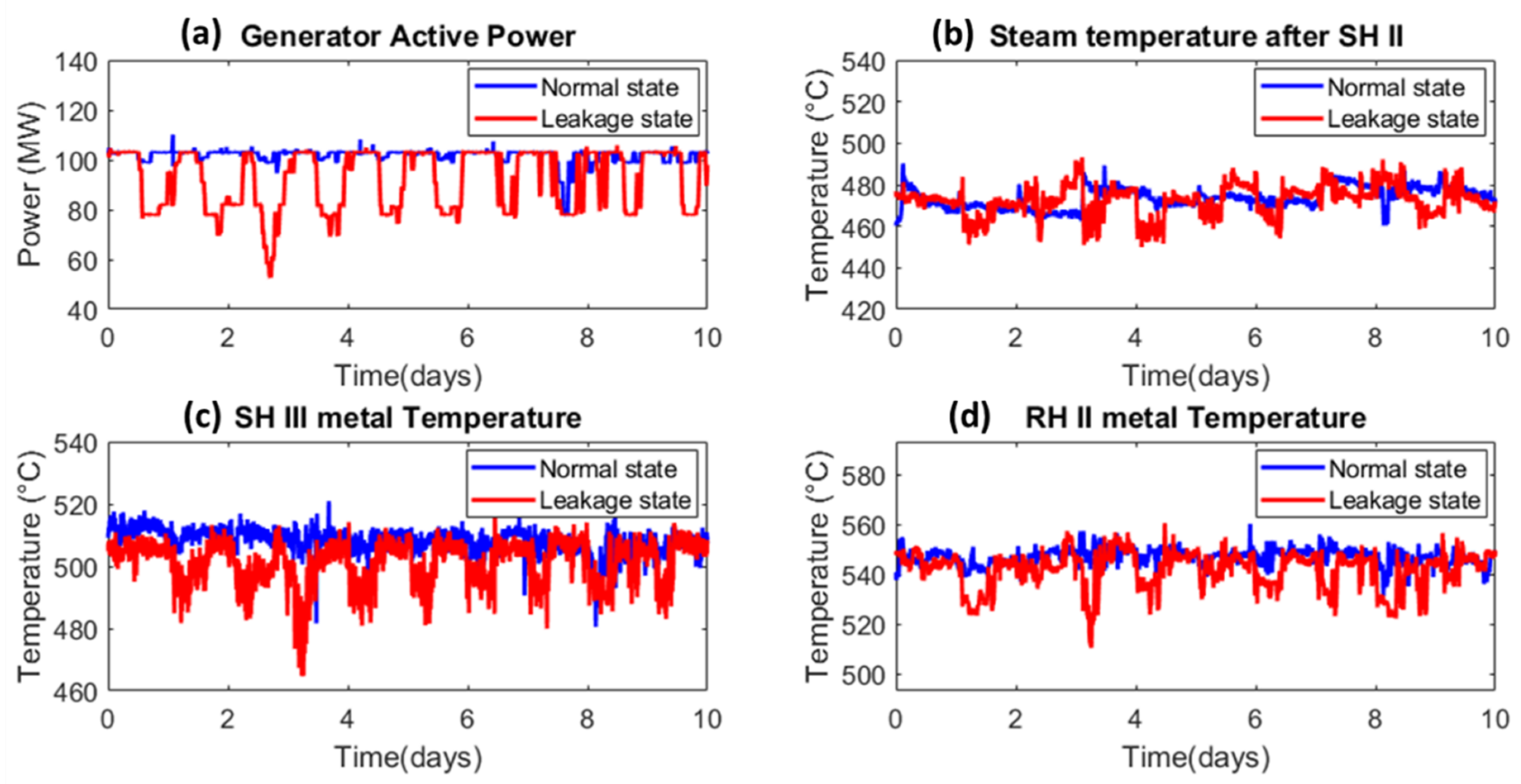
4.1. Acquisition of Leak-Sensitive Sensor Data and Data Preprocessing
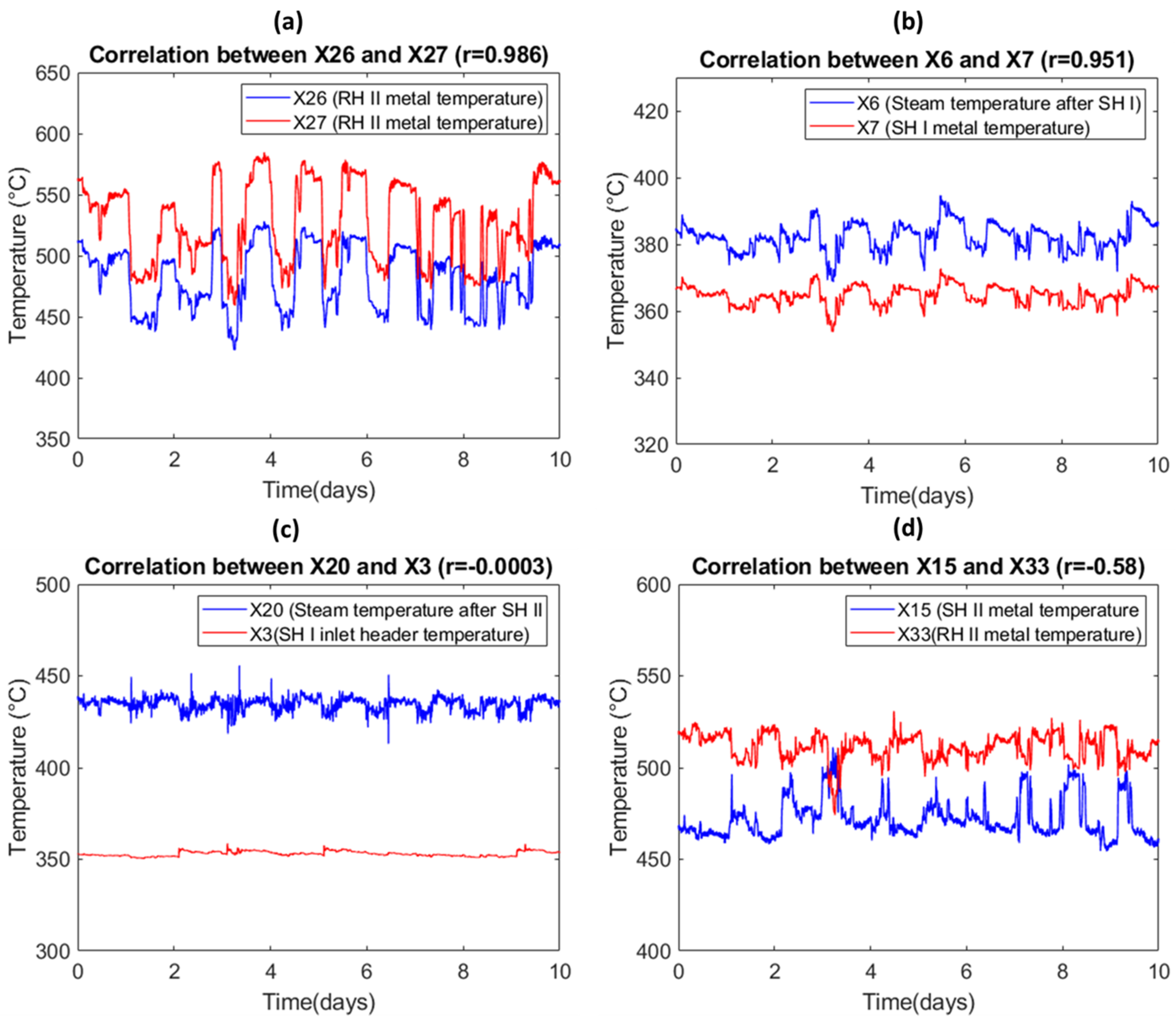
4.2. Optimal Sensor Selection via Correlation Analysis
4.3. Characteristics of the Dataset
4.4. Time Domain Statistical Feature Extraction
4.5. Machine Learning Classifiers and Performance Evaluation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaushik, S.C.; Reddy, V.S.; Tyagi, S.K. Energy and exergy analyses of thermal power plants: A review. Renew. Sustain. Energy Rev. 2011, 15, 1857–1872. [Google Scholar] [CrossRef]
- An, L.; Wang, P.; Sarti, A.; Antonacci, F.; Shi, J. Hyperbolic boiler tube leak location based on quaternary acoustic array. Appl. Therm. Eng. 2011, 31, 3428–3436. [Google Scholar] [CrossRef]
- Xue, S.; Guo, R.; Hu, F.; Ding, K.; Liu, L.; Zheng, L.; Yang, T. Analysis of the causes of leakages and preventive strategies of boiler water-wall tubes in a thermal power plant. Eng. Fail. Anal. 2020, 110, 104381. [Google Scholar] [CrossRef]
- Widarsson, B.; Dotzauer, E. Bayesian network-based early-warning for leakage in recovery boilers. Appl. Therm. Eng. 2008, 28, 754–760. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.M.; Mahmood, J. Stress Assisted Corrosion of Waterwall Tubes in Recovery Boiler Tubes: Failure Analysis. J. Fail. Anal. Prev. 2007, 7, 361–370. [Google Scholar] [CrossRef]
- Liu, S.W.; Wang, W.Z.; Liu, C.J. Failure analysis of the boiler water-wall tube. Case Stud. Eng. Fail. Anal. 2017, 9, 35–39. [Google Scholar] [CrossRef]
- Che, C.; Qian, G.; Yang, X.; Liu, X. Fatigue Damage of Waterwall Tubes in a 1000 MW USC Boiler. In Proceedings of the 7th International Conference on Fracture Fatigue and Wear; Abdel Wahab, M., Ed.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2019; pp. 314–324. ISBN 9789811304101. [Google Scholar]
- Sun, X.; Chen, T.; Marquez, H.J. Boiler Leak Detection Using a System Identification Technique. Ind. Eng. Chem. Res. 2002, 41, 5447–5454. [Google Scholar] [CrossRef]
- Afgan, N.; Coelho, P.J.; Carvalho, M.G. Boiler tube leakage detection expert system. Appl. Therm. Eng. 1998, 18, 317–326. [Google Scholar] [CrossRef]
- Sun, X.; Marquez, H.J.; Chen, T.; Riaz, M. An improved PCA method with application to boiler leak detection. Isa Trans. 2005, 44, 379–397. [Google Scholar] [CrossRef]
- Yang, P.; Liu, S.S. Fault diagnosis for boilers in thermal power plant by data mining. In Proceedings of the ICARCV 2004 8th Control, Automation, Robotics and Vision Conference, Kunming, China, 6–9 December 2004; IEEE: Kunming, China, 2004; Volume 3, pp. 2176–2180. [Google Scholar]
- Prasad, G.; Swidenbank, E.; Hogg, B.W. A novel performance monitoring strategy for economical thermal power plant operation. Ieee Trans. Energy Convers. 1999, 14, 802–809. [Google Scholar] [CrossRef]
- Kim, D.; Yang, B.; Lee, S. 3D boiler tube leak detection technique using acoustic emission signals for power plant structure health monitoring. In Proceedings of the 2011 Prognostics and System Health Managment Confernece, Shenzhen, China, 24–25 May 2011; IEEE: Shenzhen, China, 2011; pp. 1–7. [Google Scholar]
- Korbicz, J.; Kościelny, J.M. (Eds.) Modeling, Diagnostics and Process Control; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-642-16652-5. [Google Scholar]
- Zhang, S.; Shen, G.; An, L.; Gao, X. Power station boiler furnace water-cooling wall tube leak locating method based on acoustic theory. Appl. Therm. Eng. 2015, 77, 12–19. [Google Scholar] [CrossRef]
- Korbicz, J.; Kowalczuk, Z.; Kościelny, J.M.; Cholewa, W. (Eds.) Fault Diagnosis; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-642-62199-4. [Google Scholar]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- Swiercz, M.; Mroczkowska, H. Multiway PCA for Early Leak Detection in a Pipeline System of a Steam Boiler—Selected Case Studies. Sensors 2020, 20, 1561. [Google Scholar] [CrossRef] [Green Version]
- Rostek, K.; Morytko, Ł.; Jankowska, A. Early detection and prediction of leaks in fluidized-bed boilers using artificial neural networks. Energy 2015, 89, 914–923. [Google Scholar] [CrossRef]
- Yu, J.; Yoo, J.; Jang, J.; Park, J.H.; Kim, S. A novel plugged tube detection and identification approach for final super heater in thermal power plant using principal component analysis. Energy 2017, 126, 404–418. [Google Scholar] [CrossRef]
- Soft Sensors for Monitoring and Control of Industrial Processes; Advances in Industrial Control; Springer: London, UK, 2007; ISBN 978-1-84628-479-3.
- Lin, T.-H.; Wu, S.-C. Sensor fault detection, isolation and reconstruction in nuclear power plants. Ann. Nucl. Energy 2019, 126, 398–409. [Google Scholar] [CrossRef]
- Jing, C.; Hou, J. SVM and PCA based fault classification approaches for complicated industrial process. Neurocomputing 2015, 167, 636–642. [Google Scholar] [CrossRef]
- Li, W.; Peng, M.; Wang, Q. Fault identification in PCA method during sensor condition monitoring in a nuclear power plant. Ann. Nucl. Energy 2018, 121, 135–145. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Kim, Y.H.; Kim, J.; Kim, J.M. Leakage Detection of a Boiler Tube Using a Genetic Algorithm-like Method and Support Vector Machines. In Proceedings of the Tenth International Conference on Soft Computing and Pattern Recognition (SoCPaR 2018); Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Tariq, R.; Hussain, Y.; Sheikh, N.A.; Afaq, K.; Ali, H.M. Regression-Based Empirical Modeling of Thermal Conductivity of CuO-Water Nanofluid using Data-Driven Techniques. Int. J. 2020, 41, 43. [Google Scholar] [CrossRef]
- Sugumaran, V.; Muralidharan, V.; Ramachandran, K.I. Feature selection using Decision Tree and classification through Proximal Support Vector Machine for fault diagnostics of roller bearing. Mech. Syst. Signal Process. 2007, 21, 930–942. [Google Scholar] [CrossRef]
- Chen, K.-Y.; Chen, L.-S.; Chen, M.-C.; Lee, C.-L. Using SVM based method for equipment fault detection in a thermal power plant. Comput. Ind. 2011, 62, 42–50. [Google Scholar] [CrossRef]
- El Hefni, B.; Bouskela, D. Modeling and Simulation of Thermal Power Plants. In Modeling and Simulation of Thermal Power Plants with ThermoSysPro; Springer International Publishing: Cham, Switzerland, 2019; pp. 99–152. ISBN 978-3-030-05104-4. [Google Scholar]
- Basu, S.; Debnath, A.K. Power Plant Instrumentation and Control Handbook: A Guide to Thermal Power Plants; Academic Press: Cambridge, MA, USA, 2015; ISBN 978-0-12-800940-6. [Google Scholar]
- Huang, Z.; Deng, L.; Che, D. Development and technical progress in large-scale circulating fluidized bed boiler in China. Front. Energy 2020. [Google Scholar] [CrossRef]
- Nurbanasari, M. Abdurrachim Investigation of Leakage on Water Wall Tube in a 660 MW Supercritical Boiler. J. Fail. Anal. Preven. 2014, 14, 657–661. [Google Scholar] [CrossRef]
- Ahmad, J.; Purbolaksono, J.; Beng, L.C.; Rashid, A.Z.; Khinani, A.; Ali, A.A. Failure investigation on rear water wall tube of boiler. Eng. Fail. Anal. 2009, 16, 2325–2332. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, Z.Y.; Kong, W.; Meng, K. A Composite Anomaly Detection System for Data-Driven Power Plant Condition Monitoring. IEEE Trans. Ind. Inf. 2020, 16, 4390–4402. [Google Scholar] [CrossRef]
- Sohaib, M.; Kim, J.-M. Data Driven Leakage Detection and Classification of a Boiler Tube. Appl. Sci. 2019, 9, 2450. [Google Scholar] [CrossRef] [Green Version]
- Sohaib, M.; Islam, M.; Kim, J.; Jeon, D.-C.; Kim, J.-M. Leakage Detection of a Spherical Water Storage Tank in a Chemical Industry Using Acoustic Emissions. Appl. Sci. 2019, 9, 196. [Google Scholar] [CrossRef] [Green Version]
- Shaheryar, A.; Yin, X.-C.; Hao, H.-W.; Ali, H.; Iqbal, K. A Denoising Based Autoassociative Model for Robust Sensor Monitoring in Nuclear Power Plants. Sci. Technol. Nucl. Install. 2016, 2016, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Zhang, H.; Niu, Y.; Zeng, D.; Liu, J.; Kong, X.; Lee, K.Y. Modeling of an ultra-supercritical boiler-turbine system with stacked denoising auto-encoder and long short-term memory network. Inf. Sci. 2020, 525, 134–152. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Xiong, J.; Xiao, M.; Sun, G.; He, J. Fault Diagnosis of a Rolling Bearing Using Wavelet Packet Denoising and Random Forests. Ieee Sens. J. 2017, 17, 5581–5588. [Google Scholar] [CrossRef]
- Abbasion, S.; Rafsanjani, A.; Farshidianfar, A.; Irani, N. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mech. Syst. Signal Process. 2007, 21, 2933–2945. [Google Scholar] [CrossRef]
- Yoshizawa, T.; Hirobayashi, S.; Misawa, T. Noise reduction for periodic signals using high-resolution frequency analysis. Eurasip J. Audio Speech Music Process. 2011, 2011, 5. [Google Scholar] [CrossRef] [Green Version]
- Curling, L.l.R.; Gagnon, J.O.; Païdoussis, M.P. Noise removal from power spectral densities of multicomponent signals by the coherence method. Mech. Syst. Signal Process. 1992, 6, 17–27. [Google Scholar] [CrossRef]
- Srivastava, M.; Anderson, C.L.; Freed, J.H. A New Wavelet Denoising Method for Selecting Decomposition Levels and Noise Thresholds. IEEE Access 2016, 4, 3862–3877. [Google Scholar] [CrossRef] [PubMed]
- Poggi, J.; Oppenheim, G.; Oppenheim, G.; Misiti, M. Yves Misiti Wavelet Toolbox User’s Guide; The Mathworks, Inc.: Natick, MA, USA, 2002; p. 153. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer Topics in Signal Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–4. ISBN 978-3-642-00295-3. [Google Scholar]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.G.; Botti, S.; Marques, M.A.L. Recent advances and applications of machine learning in solid-state materials science. npj Comput Mater 2019, 5, 83. [Google Scholar] [CrossRef]
- Guenther, N.; Schonlau, M. Support Vector Machines. Stata J. 2016, 16, 917–937. [Google Scholar] [CrossRef] [Green Version]
- Jack, L.B.; Nandi, A.K. FAULT DETECTION USING SUPPORT VECTOR MACHINES AND ARTIFICIAL NEURAL NETWORKS, AUGMENTED BY GENETIC ALGORITHMS. Mech. Syst. Signal Process. 2002, 16, 373–390. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, C.; Zhou, Z. Study on refined control and prediction model of district heating station based on support vector machine. Energy 2019, 189, 116193. [Google Scholar] [CrossRef]
- Vernekar, K.; Kumar, H.; Gangadharan, K.V. Engine gearbox fault diagnosis using empirical mode decomposition method and Naïve Bayes algorithm. Sādhanā 2017, 42, 1143–1153. [Google Scholar] [CrossRef] [Green Version]
- Zhang, N.; Wu, L.; Yang, J.; Guan, Y. Naive Bayes Bearing Fault Diagnosis Based on Enhanced Independence of Data. Sensors 2018, 18, 463. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Hu, G.; Spanos, C.J. A data-driven strategy for detection and diagnosis of building chiller faults using linear discriminant analysis. Energy Build. 2016, 128, 519–529. [Google Scholar] [CrossRef]
- Gaja, H.; Liou, F. Defect classification of laser metal deposition using logistic regression and artificial neural networks for pattern recognition. Int. J. Adv. Manuf. Technol. 2018, 94, 315–326. [Google Scholar] [CrossRef]
- Mokeev, A.V.; Mokeev, V.V. Pattern recognition by means of linear discriminant analysis and the principal components analysis. Pattern Recognit. Image Anal. 2015, 25, 685–691. [Google Scholar] [CrossRef]





| ID | Description | Notation | ID | Description | Notation |
|---|---|---|---|---|---|
| P1CHA01GH001XQ01 | Gen. Active Power | X1 | P1HAH72CT003XQ01 | Steam Temperature After SH II | X20 |
| P1HAH55CT001XQ01 | SH I Inlet Header Temperature | X2 | P1HAH77CT001XQ01 | SH III Metal Temperature | X21 |
| P1HAH55CT002XQ01 | SH I Inlet Header Temperature | X3 | P1HAH77CT002XQ01 | SH III Metal Temperature | X22 |
| P1HAH55CT003XQ01 | SH I Inlet Header Temperature | X4 | P1HAH77CT003XQ01 | SH III Metal Temperature | X23 |
| P1HAH62CT001XQ01 | Steam Temperature After SH I | X5 | P1HAH77CT004XQ01 | SH III Metal Temperature | X24 |
| P1HAH62CT002XQ01 | Steam Temperature After SHI | X6 | P1HAH77CT005XQ01 | SH III Metal Temperature | X25 |
| P1HAH57CT001XQ01 | SH I Metal Temperature | X7 | P1HAJ15CT001XQ01 | RH I Metal Temperature | X26 |
| P1HAH57CT002XQ01 | SH I Metal Temperature | X8 | P1HAJ15CT002XQ01 | RH I Metal Temperature | X27 |
| P1HAH57CT003XQ01 | SH I Metal Temperature | X9 | P1HAJ15C003XQ01 | RH I Metal Temperature | X28 |
| P1HAH57CT004XQ01 | SH I Metal Temperature | X10 | P1HAJ15CT004XQ01 | RH I Metal Temperature | X29 |
| P1HAH57CT005XQ01 | SH I Metal Temperature | X11 | P1HAJ15CT005XQ01 | RH I Metal Temperature | X30 |
| P1HAH57CT006XQ01 | SH I Metal Temperature | X12 | P1HAJ15CT006XQ01 | RH I Metal Temperature | X31 |
| P1HAH67CT001XQ01 | SH II Metal Temperature | X13 | P1HAJ20CT001XQ01 | RH I Outlet Steam Temperature | X32 |
| P1HAH67CT002XQ01 | SH II Metal Temperature | X14 | P1HAJ35CT001XQ01 | RH II Metal Temperature | X33 |
| P1HAH67CT003XQ01 | SH II Metal Temperature | X15 | P1HAJ35CT002XQ01 | RH II Metal Temperature | X34 |
| P1HAH67CT004XQ01 | SH II Metal Temperature | X16 | P1HAJ35CT003XQ01 | RH II Metal Temperature | X35 |
| P1HAH67CT005XQ01 | SH II Metal Temperature | X17 | P1HAJ35CT004XQ01 | RH II Metal Temperature | X36 |
| P1HAH72CT001XQ01 | Steam Temperature After SH II | X18 | P1HAJ35CT005XQ01 | RH II Metal Temperature | X37 |
| P1HAH72CT002XQ01 | Steam Temperature After SH II | X19 | P1HAJ35CT006XQ01 | RH II Metal Temperature | X38 |
| Input Attributes | Highly Correlated Attributes | Correlation Coefficient (R) |
|---|---|---|
| X6 (Steam Temperature After SHI) | X7 (SHI Metal temperature) | 0.951 |
| X6 | X8 (SHI Metal temperature) | 0.987 |
| X6 | X9 (SHI Metal temperature) | 0.977 |
| X6 | X10 (SHI Metal temperature) | 0.989 |
| X6 | X11 (SHI Metal temperature) | 0.989 |
| X6 | X12 (SHI Metal temperature) | 0.965 |
| X26 (RH I Metal Temperature) | X27 (RH I Metal Temperature) | 0.986 |
| X26 | X28(RH I Metal Temperature) | 0.986 |
| X26 | X29(RH I Metal Temperature) | 0.979 |
| X26 | X30(RH I Metal Temperature) | 0.982 |
| X26 | X31(RH I Metal Temperature) | 0.975 |
| X26 | X32 (RH I Outlet Steam Temperature) | 0.982 |
| # | Sensor ID | Sensor Description | Sensor Notation |
|---|---|---|---|
| 1 | P1CHA01GH001XQ01 | Gen. active power | X1 |
| 2 | P1HAH55CT002XQ01 | SH I Inlet Header Temperature | X3 |
| 3 | P1HAH55CT003XQ01 | SH I Inlet Header Temperature | X4 |
| 4 | P1HAH62CT001XQ01 | Steam Temperature After SH I | X5 |
| 5 | P1HAH67CT001XQ01 | SH II Metal Temperature | X13 |
| 6 | P1HAH67CT002XQ01 | SH II Metal Temperature | X14 |
| 7 | P1HAH67CT003XQ01 | SH II Metal Temperature | X15 |
| 8 | P1HAH67CT004XQ01 | SH II Metal Temperature | X16 |
| 9 | P1HAH72CT003XQ01 | Steam Temperature After SH II | X20 |
| 10 | P1HAH77CT001XQ01 | SH III Metal Temperature | X21 |
| 11 | P1HAH77CT002XQ01 | SH III Metal Temperature | X22 |
| 12 | P1HAH77CT003XQ01 | SH III Metal Temperature | X23 |
| 13 | P1HAH77CT004XQ01 | SH III Metal Temperature | X24 |
| 14 | P1HAH77CT005XQ01 | SH III Metal Temperature | X25 |
| 15 | P1HAJ15CT001XQ01 | RH I Metal Temperature | X26 |
| 16 | P1HAJ35CT001XQ01 | RH II Metal Temperature | X33 |
| 17 | P1HAJ35CT002XQ01 | RH II Metal Temperature | X34 |
| 18 | P1HAJ35CT003XQ01 | RH II Metal Temperature | X35 |
| 19 | P1HAJ35CT004XQ01 | RH II Metal Temperature | X36 |
| 20 | P1HAJ35CT005XQ01 | RH II Metal Temperature | X37 |
| 21 | P1HAJ35CT006XQ01 | RH II Metal Temperature | X38 |
| Data Type | Input Sensors | No of Records | Train Set | Test Set | Target |
|---|---|---|---|---|---|
| Raw dataset | 38 | 1,728,000 | 80% | 20% | • Normal |
| Optimal dataset | 21 | • Leakage |
| Features | Mathematical Expression |
|---|---|
| Root mean square | RMS = |
| Variance (V) | V = |
| Skewness (S) | |
| Kurtosis |
| Machine Learning Classification | Raw Data | Optimal Sensors Data | ||
|---|---|---|---|---|
| Algorithms | Training Accuracy (%) | Testing Accuracy (%) | Training Accuracy (%) | Testing Accuracy (%) |
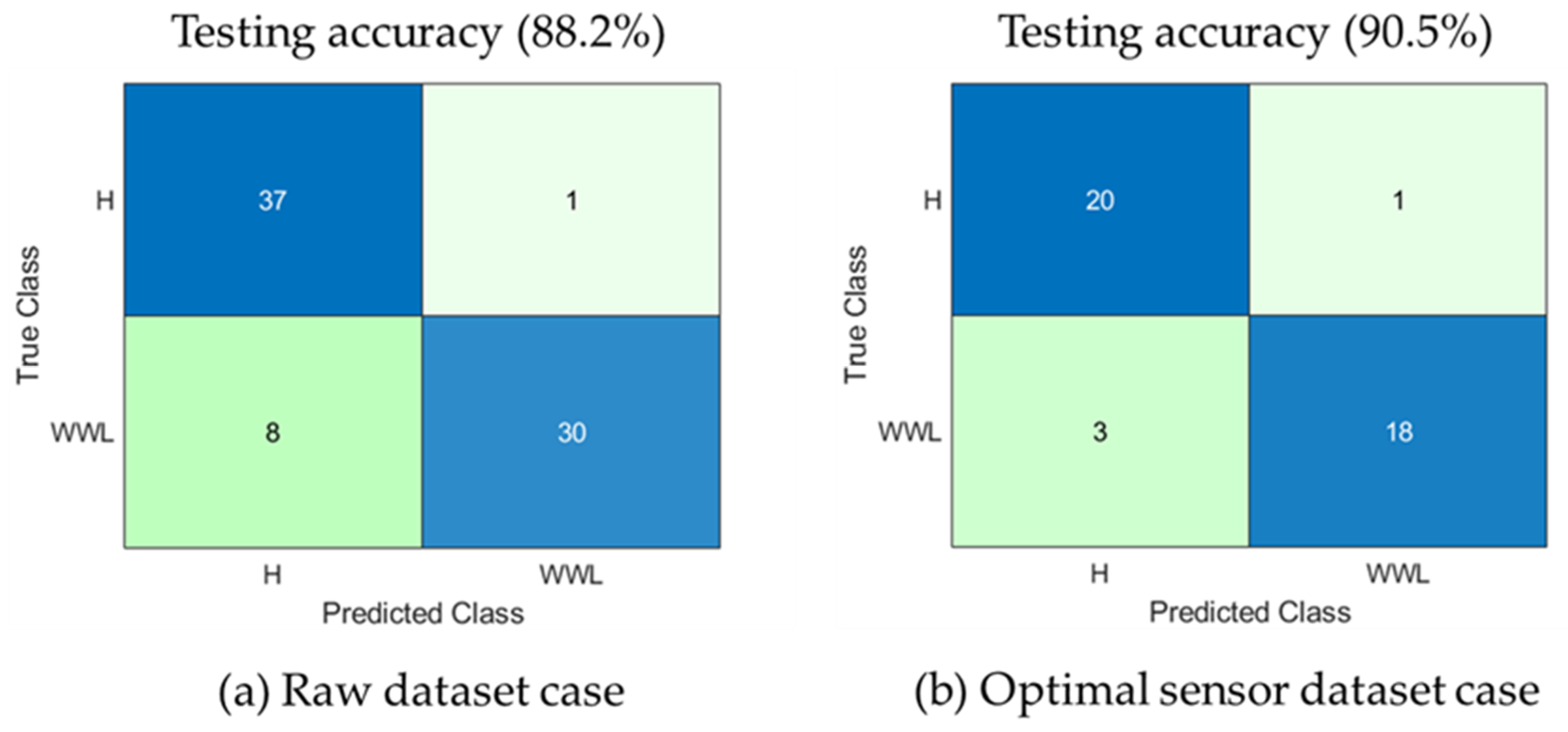
| SVM | 90.8 | 88.2 | 92.9 | 90.5 |
| k-NN | 88.2 | 85.5 | 92.9 | 88.1 |
| NB | 86.8 | 84.2 | 88.1 | 85.7 |
| LDA | 89.5 | 86.8 | 90.5 | 88.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalid, S.; Lim, W.; Kim, H.S.; Oh, Y.T.; Youn, B.D.; Kim, H.-S.; Bae, Y.-C. Intelligent Steam Power Plant Boiler Waterwall Tube Leakage Detection via Machine Learning-Based Optimal Sensor Selection. Sensors 2020, 20, 6356. https://doi.org/10.3390/s20216356
Khalid S, Lim W, Kim HS, Oh YT, Youn BD, Kim H-S, Bae Y-C. Intelligent Steam Power Plant Boiler Waterwall Tube Leakage Detection via Machine Learning-Based Optimal Sensor Selection. Sensors. 2020; 20(21):6356. https://doi.org/10.3390/s20216356
Chicago/Turabian StyleKhalid, Salman, Woocheol Lim, Heung Soo Kim, Yeong Tak Oh, Byeng D. Youn, Hee-Soo Kim, and Yong-Chae Bae. 2020. "Intelligent Steam Power Plant Boiler Waterwall Tube Leakage Detection via Machine Learning-Based Optimal Sensor Selection" Sensors 20, no. 21: 6356. https://doi.org/10.3390/s20216356
APA StyleKhalid, S., Lim, W., Kim, H. S., Oh, Y. T., Youn, B. D., Kim, H.-S., & Bae, Y.-C. (2020). Intelligent Steam Power Plant Boiler Waterwall Tube Leakage Detection via Machine Learning-Based Optimal Sensor Selection. Sensors, 20(21), 6356. https://doi.org/10.3390/s20216356






