A Novel Framework Using Deep Auto-Encoders Based Linear Model for Data Classification
Abstract
:1. Introduction
2. Literature Review
3. Material and Methods
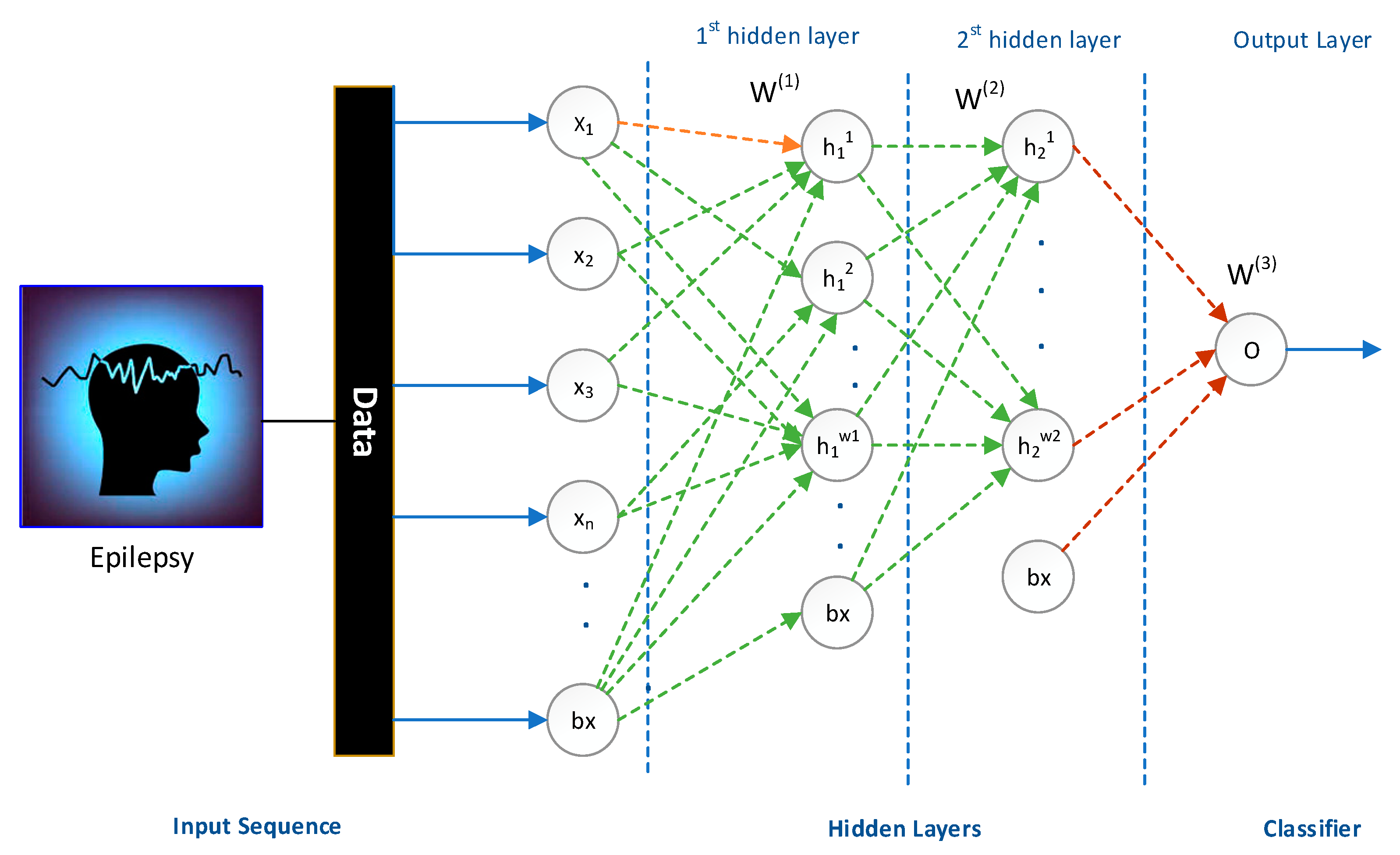
3.1. Stacked Sparse Auto-Encoder
3.2. The Particle Swarm Optimization (PSO) Algorithm
| Algorithm 1. Pseudo Code of PSO Algorithm. |
| For each particle Set particles in a random manner End Do Estimate the Local best “pBest” for each particle If the “pBest” is enhanced Update “pBest” value End Global Best (gBest) is updated as the best of “pBests” For each particle Estimate the velocity of particles via Equations (5) and (6) Update the positions of the particles End End |
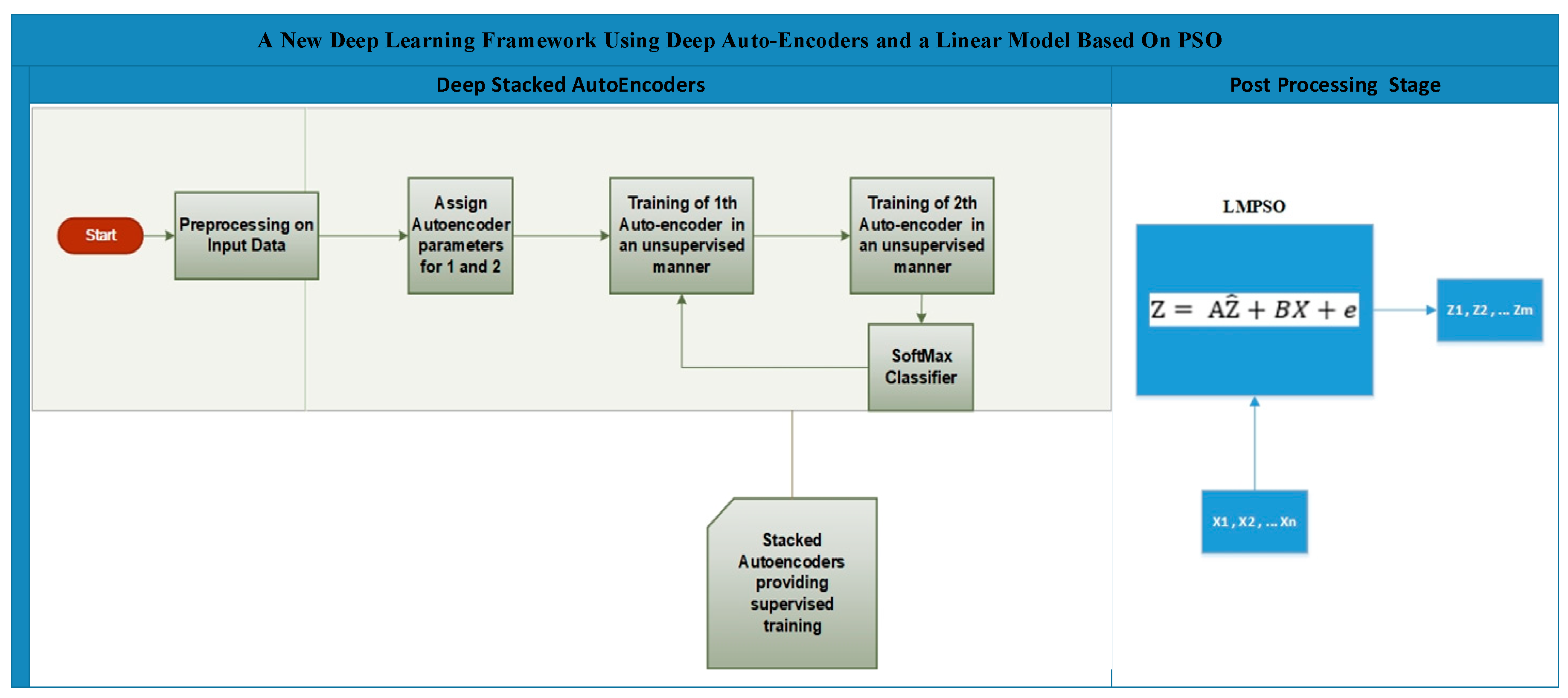
3.3. A New Deep Learning Framework Using Deep Auto-Encoders and a Linear Model Based on PSO
4. Experimental Results
4.1. Epileptic Seizure
4.2. SPECTF Classification
4.3. Diagnosis of Cardiac Arrhythmia
4.4. Statistical Significance Analysis of Algorithms in the Proposed Method
4.5. Performance Evaluation of the Framework Using Benchmark Datasets
4.5.1. Epileptic Seizure Dataset
4.5.2. SPECTF Dataset
4.5.3. Cardiac Arrhythmia Dataset
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Xu, M.; Fralick, D.; Zheng, J.Z.; Wang, B.; Tu, X.M.; Feng, C. The Differences and Similarities between Two-Sample t-test and Paired t-test. Shanghai Arch. Psychiatry 2017, 29, 184–188. [Google Scholar] [PubMed]
- Sze, V.; Chen, Y.-H.; Yang, T.-J.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef] [Green Version]
- Luckow, A.; Cook, M.; Ashcraft, N.; Weill, E.; Djerekarov, E.; Vorster, B. Deep learning in the automotive industry: Applications and tools. In Proceedings of the 2016 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 3759–3768. [Google Scholar] [CrossRef] [Green Version]
- Memisevic, R. Deep learning: Architectures, algorithms, applications. In Proceedings of the 2015 IEEE Hot Chips 27 Symposium (HCS), Cupertino, CA, USA, 22–25 August 2015; pp. 1–127. [Google Scholar]
- Chu, L.W. Alzheimer’s disease: Early diagnosis and treatment. Hong Kong Med. J. 2012, 18, 228–237. [Google Scholar] [PubMed]
- Pushkar, B.; Paul, M. Early Diagnosis of Alzheimer’s Disease: A Multi—Class Deep Learning Framework with Modified k- sparse Autoencoder Classification. In Proceedings of the 2016 International Conference on Image and Vision Computing New Zealand (IVCNZ), Palmerston North, New Zealand, 21–22 November 2016. [Google Scholar]
- Tong, H.; Liu, B.; Wang, S. Software defect prediction using stacked denoising autoencoders and two-stage ensemble learning. Inf. Softw. Technol. 2018, 96, 94–111. [Google Scholar] [CrossRef]
- Kuo, J.Y.; Pan, C.W.; Lei, B. Using stacked denoising autoencoder for the student droupout predication. In Proceedings of the 2017 IEEE International Symposium on Multimedia (ISM), Taichung, Taiwan, 11–13 December 2017; pp. 483–488. [Google Scholar]
- Xiong, Y.; Zuo, R. Recognition of geochemical anomalies using a deep autoencoder network. Comput. Geosci. 2016, 86, 75–82. [Google Scholar] [CrossRef]
- Salaken, S.M.; Khosravi, A.; Khatami, A.; Nahavandi, S.; Hosen, M.A. Lung cancer classification using deep learned features on low population dataset. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–5. [Google Scholar]
- Khatab, Z.E.; Hajihoseini, A.; Ghorashi, S.A. A Fingerprint Method for Indoor Localization Using Autoencoder Based Deep Extreme Learning Machine. IEEE Sens. Lett. 2017, 2, 1–4. [Google Scholar] [CrossRef]
- Khan, U.M.; Kabir, Z.; Hassan, S.A.; Ahmed, S.H. A Deep Learning Framework Using Passive Wi-Fi Sensing for Respiration Monitoring. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Tang, X.-S.; Hao, K.; Wei, H.; Ding, Y. Using line segments to train multi-stream stacked autoencoders for image classification. Pattern Recognit. Lett. 2017, 94, 55–61. [Google Scholar] [CrossRef]
- Yin, C.; Zhu, Y.; Fei, J.; He, X. A Deep Learning Approach for Intrusion Detection Using Recurrent Neural Networks. IEEE Access 2017, 5, 21954–21961. [Google Scholar] [CrossRef]
- Yu, Z.; Tan, E.-L.; Ni, D.; Qin, J.; Chen, S.; Li, S.; Lei, B.; Wang, T. A Deep Convolutional Neural Network-Based Framework for Automatic Fetal Facial Standard Plane Recognition. IEEE J. Biomed. Health Inform. 2017, 22, 874–885. [Google Scholar] [CrossRef]
- Srinivas, M.; Bharath, R.; Rajalakshmi, P.; Mohan, C.K. Multi-level classification: A generic classification method for medical datasets. In Proceedings of the 2015 17th International Conference on E-health Networking, Application & Services (HealthCom), Boston, MA, USA, 14–17 October 2015; pp. 262–267. [Google Scholar] [CrossRef]
- Subasi, A.; Erçelebi, E. Classification of EEG signals using neural network and logistic regression. Comput. Methods Programs Biomed. 2005, 78, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Subasi, A. EEG signal classification using wavelet feature extraction and a mixture of expert model. Expert Syst. Appl. 2007, 32, 1084–1093. [Google Scholar] [CrossRef]
- Kannathal, N.; Choo, M.L.; Acharya, U.R.; Sadasivan, P. Entropies for detection of epilepsy in EEG. Comput. Methods Programs Biomed. 2005, 80, 187–194. [Google Scholar] [CrossRef]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Automatic Seizure Detection Based on Time-Frequency Analysis and Artificial Neural Networks. Comput. Intell. Neurosci. 2007, 2007, 80510. [Google Scholar] [CrossRef] [PubMed]
- Polat, K.; Güneş, S. Classification of epileptiform EEG using a hybrid system based on decision tree classifier and fast Fourier transform. Appl. Math. Comput. 2007, 187, 1017–1026. [Google Scholar] [CrossRef]
- Acharya, U.R.; Sree, S.V.; Alvin, A.P.C.; Suri, J.S. Use of principal component analysis for automatic classification of epileptic EEG activities in wavelet framework. Expert Syst. Appl. 2012, 39, 9072–9078. [Google Scholar] [CrossRef]
- Acharya, U.R.; Sree, S.V.; Ang, P.C.A.; Yanti, R.; Suri, J.S. Application of non-linear and wavelet based features for the automated identification of epileptic EEG signals. Int. J. Neural Syst. 2012, 22, 1250002. [Google Scholar] [CrossRef] [PubMed]
- Peker, M.; Şen, B.; Delen, D. A Novel Method for Automated Diagnosis of Epilepsy Using Complex-Valued Classifiers. IEEE J. Biomed. Heal. Inform. 2015, 20, 108–118. [Google Scholar] [CrossRef]
- Karim, A.M.; Güzel, M.S.; Tolun, M.R.; Kaya, H.; Çelebi, F.V. A New Generalized Deep Learning Framework Combining Sparse Autoencoder and Taguchi Method for Novel Data Classification and Processing. Math. Probl. Eng. 2018, 2018, 3145947. [Google Scholar] [CrossRef]
- Karim, A.M.; Serdar, G.M.; Tolun, M.R.; Kaya, H.; Çelebi, F.V. A new framework using deep auto-encoder and energy spectral density for medical waveform data classification and processing. Biocybern. Biomed. Eng. 2019, 39, 148–159. [Google Scholar] [CrossRef]
- Niazi, K.A.K.; Khan, S.A.; Shaukat, A.; Akhtar, M. Identifying best feature subset for cardiac arrhythmia classification. In Proceedings of the 2015 Science and Information Conference (SAI), London, UK, 28–30 July 2015; pp. 494–499. [Google Scholar]
- Mustaqeem, A.; Anwar, S.M.; Majid, M.; Khan, A.R. Wrapper method for feature selection to classify cardiac arrhythmia. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Seogwipo, Korea, 11–15 July 2017; pp. 3656–3659. [Google Scholar] [CrossRef]
- Zuo, W.; Lu, W.; Wang, K.; Zhang, H. Diagnosis of cardiac arrhythmia using kernel difference weighted KNN classifier. Comput. Cardiol. 2008, 35, 253–256. [Google Scholar] [CrossRef] [Green Version]
- Jadhav, S.M.; Nalbalwar, S.L.; Ghatol, A.A. ECG arrhythmia classification using modular neural network model. In Proceedings of the IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysi, 30 November–2 December 2010; pp. 62–66. [Google Scholar]
- Persada, A.G.; Setiawan, N.A.; Nugroho, H. Comparative study of attribute reduction on arrhythmia classification dataset. In Proceedings of the International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 7–8 October 2013; pp. 68–72. [Google Scholar] [CrossRef]
- Jadhav, S.M.; Nalbalwar, S.L.; Ghatol, A. Artificial Neural Network based cardiac arrhythmia classification using ECG signal data. In Proceedings of the International Conference on Electronics and Information Engineering, Kyoto, Japan, 1–3 August 2010; Volume 1, pp. V1–V228. [Google Scholar] [CrossRef]
- Jadhav, S.M.; Nalbalwar, S.L.; Ghatol, A.A. Artificial Neural Network Based Cardiac Arrhythmia Disease Diagnosis. In Proceedings of the International Conference on Process. Automation, Control. and Computing, Coimbatore, India, 20–22 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Kohli, N.; Verma, N.K.; Roy, A. SVM based methods for arrhythmia classification in ECG. In Proceedings of the International Conference on Computer and Communication Technology (ICCCT), Allahabad, India, 17–19 September 2010; pp. 486–490. [Google Scholar] [CrossRef]
- Özçift, A. Random forests ensemble classifier trained with data resampling strategy to improve cardiac arrhythmia diagnosis. Comput. Biol. Med. 2011, 41, 265–271. [Google Scholar] [CrossRef]
- Srinivasan, V.; Eswaran, C.; Sriraam, A.N. Artificial Neural Network Based Epileptic Detection Using Time-Domain and Frequency-Domain Features. J. Med. Syst. 2005, 29, 647–660. [Google Scholar] [CrossRef]
- Wei, J.; Yu, H.; Wang, J. The research of Bayesian method from small sample of high-dimensional dataset in poison identification. In Proceedings of the IEEE 4th International Conference on Software Engineering and Service Science, Beijing, China, 23–25 May 2013; pp. 705–709. [Google Scholar]
- Cha, M.; Kim, J.S.; Baek, J.-G. Density weighted support vector data description. Expert Syst. Appl. 2014, 41, 3343–3350. [Google Scholar] [CrossRef]
- Liu, B.; Xiao, Y.; Cao, L.; Hao, Z.; Deng, F. SVDD-based outlier detection on uncertain data. Knowl. Inf. Syst. 2013, 34, 597–618. [Google Scholar] [CrossRef]
- Cui, L.-l.; Zhu, H.-c.; Zhang, L.-k.; Luan, R.-p. Improved kNearest Neighbors Transductive Confidence Machine for Pattern Recognition. IEEE Int. Conf. Comput. Des. Appl. 2010, 3, 172–176. [Google Scholar]
- Tian, D.; Zeng, X.-J.; Keane, J. Core-generating approximate minimum entropy discretization for rough set feature selection in pattern classification. Int. J. Approx. Reason. 2011, 52, 863–880. [Google Scholar] [CrossRef]
- Zeng, N.; Zhang, H.; Song, B.; Liu, W.; Li, Y.; Dobaie, A.M. Facial expression recognition via learning deep sparse autoencoders. Neurocomputing 2018, 273, 643–649. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks (ICNN’95), Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Harman, R. A Very Brief Introduction to Particle Swarm Optimization; Technical Report; Department of Applied Mathematics and Statistics: Bratislava, Slovakia, 1995; pp. 1–4. [Google Scholar]
- Kaveh, A.; Nasrollahi, A. A new probabilistic particle swarm optimization algorithm for size optimization of spatial truss structures. Int. J. Civ. Eng. 2014, 12, 1–13. [Google Scholar]
- Ding, W.; Lin, C.-T.; Cao, Z. Deep Neuro-Cognitive Co-Evolution for Fuzzy Attribute Reduction by Quantum Leaping PSO With Nearest-Neighbor Memeplexes. IEEE Trans. Cybern. 2018, 49, 2744–2757. [Google Scholar] [CrossRef] [PubMed]
- Serdar, G.M.; Kara, M.; Beyazkılıç, M.S. An adaptive framework for mobile robot navigation. Adapt. Behav. 2017, 25, 30–39. [Google Scholar] [CrossRef]
- Rizvi, S.Z.; Abbasi, F.; Velni, J.M. Model Reduction in Linear Parameter-Varying Models using Autoencoder Neural Networks. In Proceedings of the Annual American Control Conference (ACC), Milwaukee, WI, USA, 27 June 2018; pp. 6415–6420. [Google Scholar]
- Siswantoro, J.; Prabuwono, A.S.; Abdullah, A.; Idrus, B. A linear model based on Kalman filter for improving neural network classification performance. Expert Syst. Appl. 2016, 49, 112–122. [Google Scholar] [CrossRef]
- Noy, D.; Menezes, R. Parameter estimation of the Linear Phase Correction model by hierarchical linear models. J. Math. Psychol. 2018, 84, 1–12. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef] [Green Version]
- Dua, D.; Karra, T. Machine Learning Repository; School of Information and Computer Sciences, University of California: Irvine, CA, USA, 2017; Available online: http://archive.ics.uci.edu/ml (accessed on 12 July 2019).
- Xu, G.; Fang, W. Shape retrieval using deep autoencoder learning representation. In Proceedings of the 13th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 16–18 December 2016; pp. 227–230. [Google Scholar] [CrossRef]
- Kim, T.K. T test as a parametric statistic. Korean J. Anesthesiol. 2015, 68, 540–546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, R.; Chen, T.; Hardt, M.; Beymer, D.; Brannon, K.; Syeda-Mahmood, T. Multiple Kernel Completion and its application to cardiac disease discrimination. In Proceedings of the IEEE 10th International Symposium on Biomedical Imaging, San Francisco, CA, USA, 7 April 2013; pp. 764–767. [Google Scholar]








| Parameter | First Auto-Encoder | Second Auto-Encoder |
|---|---|---|
| Hidden Layer Size (HLS) | 2007 | 112 |
| Max Epoch Number (MEN) | 420 | 110 |
| L2 Regularization Parameter | 0.004 | 0.002 |
| Sparsity Regularization (SR) | 4 | 2 |
| Sparsity Proportion (SP) | 0.14 | 0.12 |
| PSO Parameter | Value |
|---|---|
| Number of particles | 50 |
| Maximum iteration | 30 |
| Cognitive parameter | 2 |
| Social parameter | 2 |
| Min inertia weight | 0.9 |
| Max inertia weight | 0.2 |
| Parameter | DSAEs without Post-Processing | DSAEs Using PSO |
|---|---|---|
| Recall | 0.9348 | 1.0000 |
| TNR | 0.7222 | 1.0000 |
| Precision | 0.7414 | 1.0000 |
| NPV | 0.9286 | 1.0000 |
| ACC | 0.8200 | 1.0000 |
| F1-s | 0.8269 | 1.0000 |
| MCC | 0.6634 | 1.0000 |
| Parameter | Auto-Encoder 1 | Auto-Encoder 2 |
|---|---|---|
| Hidden Layer Size (HLS) | 40 | 35 |
| Max Epoch Number (MEN) | 110 | 60 |
| L2 Regularization Parameter | 0.003 | 0.001 |
| Sparsity Regularization (SR) | 2 | 1 |
| Sparsity Proportion (SP) | 0.1 | 0.1 |
| PSO Parameter | Value |
|---|---|
| Number of particles | 40 |
| Maximum iteration | 40 |
| Cognitive parameter | 2 |
| Social parameter | 2 |
| Min inertia weight | 0.9 |
| Max inertia weight | 0.2 |
| Parameter. | DSAEs without Post-Processing | DSAEs Using PSO |
|---|---|---|
| Recall | 0.9554 | 1.0000 |
| TNR | 0.3333 | 0.8750 |
| Precision | 0.8824 | 0.9884 |
| NPV | 0.5882 | 1.0000 |
| ACC | 0.8556 | 0.9893 |
| F1-s | 0.9174 | 0.9942 |
| MCC | 0.3686 | 0.9300 |
| Parameter | First Auto-Encoder | Second Auto-Encoder |
|---|---|---|
| Hidden Layer Size (HS) | 250 | 200 |
| Max Epoch Number (MEN) | 130 | 109 |
| L2 Weight Regularization | 0.003 | 0.001 |
| Sparsity Regularization (SR) | 3 | 1 |
| Sparsity Proportion (SP) | 0.12 | 0.1 |
| PSO Parameter | Value |
|---|---|
| Number of particles | 60 |
| Maximum iteration | 45 |
| Cognitive parameter | 2 |
| Social parameter | 2 |
| Min inertia weight | 0.9 |
| Max inertia weight | 0.2 |
| Parameter | DSAEs without Post-Processing | DSAEs Using PSO |
|---|---|---|
| Recall | 0.7843 | 0.9959 |
| TNR | 0.8667 | 0.9904 |
| Precision | 0.8000 | 0.9918 |
| NPV | 0.8553 | 0.9952 |
| ACC | 0.8333 | 0.9934 |
| F1-s | 0.7921 | 0.9939 |
| MCC | 0.6531 | 0.9866 |
| Reference | Method | Accuracy |
|---|---|---|
| [36] | Time–frequency domain feature-RNN | 99.6% |
| [17] | WT + ANN | 92.0% |
| [18] | Discrete WT-mixture of expert model | 94.5% |
| [19] | Entropy measures-ANFIS | 92.22% |
| [20] | Time–frequency analysis—ANN | 100% |
| [21] | Fast Fourier transform-DT | 98.72% |
| [22] | WPD-PCA-GMM | 99.00% |
| [23] | Entropies + HOS + Higuchi FD + Hurst exponent + FC | 99.70% |
| [24] | DTCWT + CVANN-3 | 100% |
| [25] | Deep auto-encoder using Taguchi method | 100% |
| [26] | Deep Auto-Encoder + Energy Spectral Density | 100% |
| Proposed Framework | Deep auto-encoder and linear model based PSO | 100% |
| Reference | Method | Accuracy |
|---|---|---|
| [38] | SVDD | 82.7% |
| [39] | SVDD-based outlier detection | 90% |
| [37] | K2 | 94.03% |
| SDBNS | 95.59% | |
| ECFBN | 95.76% | |
| [55] | mc-MKC | 79.9% |
| mc-SVM | 79.1% | |
| [40] | TCM-IKN N | 90% |
| [41] | C-GAME + Johnson + c4.5 | 84.4% |
| RMEP + Johnson + c4.5 | 81.7% | |
| [16] | Sparsity-based dictionary learning + SVM | 97.8% |
| [26] | Deep Auto-Encoder + Energy Spectral Density | 96.79% |
| Proposed Framework | Deep auto-encoder and linear model based PSO | 98.93% |
| Reference | Method | Accuracy | |
|---|---|---|---|
| Feature Extraction Technique | Classifier | ||
| [27] | Enhanced F-score and sequential forward search | k-NN SVM | 74% 69% |
| [28] | Wrapper method | MLP k-NN SVM | 78.26% 76.6% 74.4% |
| [29] | PCA | Kernel difference weighted k-NN | 70.66% |
| [30] | - | MLP+ Static backpropagation algorithm | 86.67% |
| [31] | Best First and CsfSubsetEval | RBF | 81% |
| [32] | - | Modular neural network model | 82.22% |
| [33] | - | ANN models + Static backpropagation algorithm + momentum learning rule | 86.67% |
| [34] | One-against-all | SVM | 73.40% |
| [35] | - | Resampling strategy based random forest (RF) ensemble classifier | 90% |
| [26] | Energy Spectral Density + Deep Auto-Encoders | Softmax | 99.1% |
| Proposed Framework | Deep auto-encoder and linear model based PSO | Softmax | 99.27% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karim, A.M.; Kaya, H.; Güzel, M.S.; Tolun, M.R.; Çelebi, F.V.; Mishra, A. A Novel Framework Using Deep Auto-Encoders Based Linear Model for Data Classification. Sensors 2020, 20, 6378. https://doi.org/10.3390/s20216378
Karim AM, Kaya H, Güzel MS, Tolun MR, Çelebi FV, Mishra A. A Novel Framework Using Deep Auto-Encoders Based Linear Model for Data Classification. Sensors. 2020; 20(21):6378. https://doi.org/10.3390/s20216378
Chicago/Turabian StyleKarim, Ahmad M., Hilal Kaya, Mehmet Serdar Güzel, Mehmet R. Tolun, Fatih V. Çelebi, and Alok Mishra. 2020. "A Novel Framework Using Deep Auto-Encoders Based Linear Model for Data Classification" Sensors 20, no. 21: 6378. https://doi.org/10.3390/s20216378
APA StyleKarim, A. M., Kaya, H., Güzel, M. S., Tolun, M. R., Çelebi, F. V., & Mishra, A. (2020). A Novel Framework Using Deep Auto-Encoders Based Linear Model for Data Classification. Sensors, 20(21), 6378. https://doi.org/10.3390/s20216378






