A New Method of Secure Authentication Based on Electromagnetic Signatures of Chipless RFID Tags and Machine Learning Approaches
Abstract
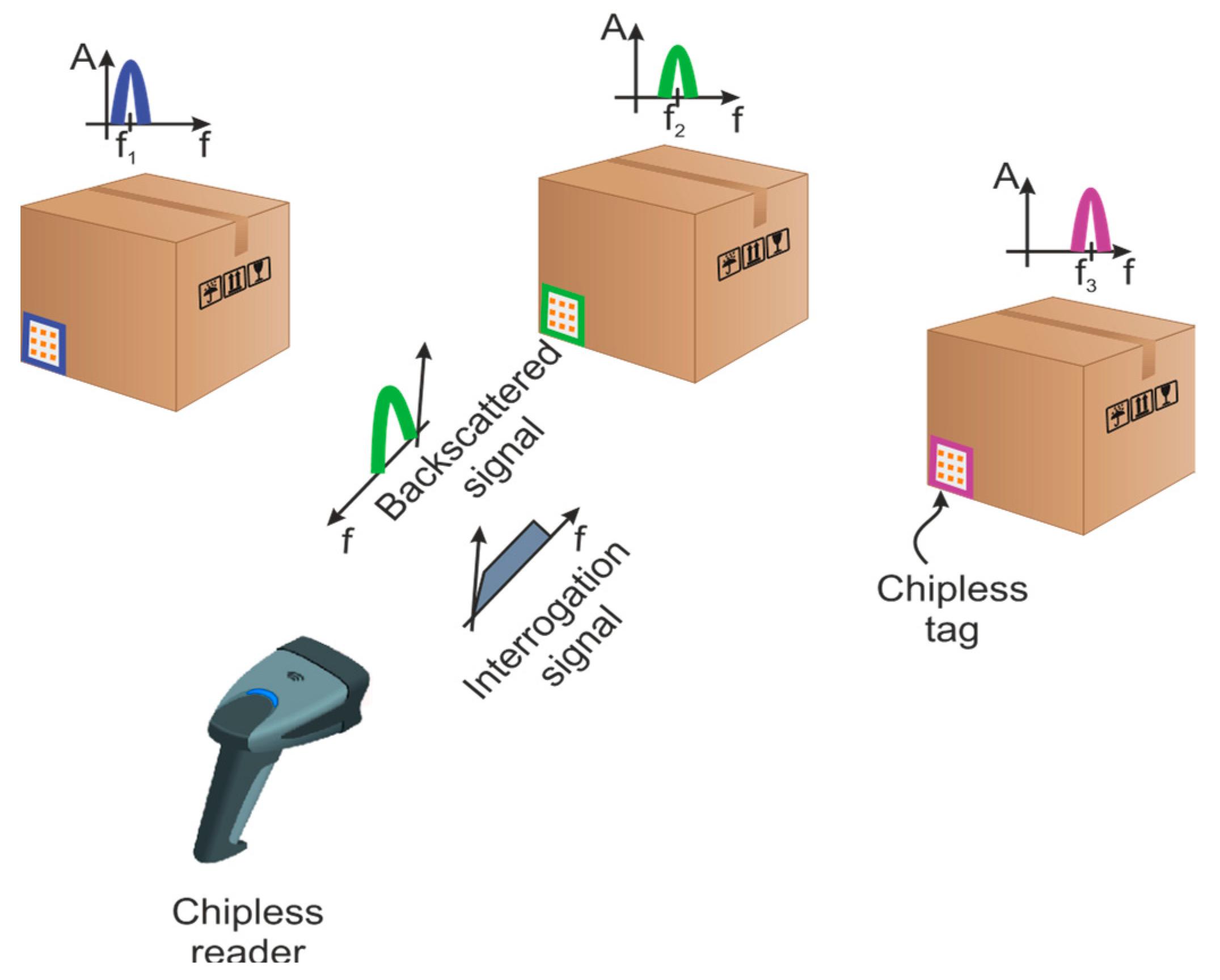
:1. Introduction
- We propose chipless RFID tags operating in V-band, which are more sensitive to geometrical inhomogeneities than other bands at lower frequencies. In order to harness the fabrication randomness, EM signatures are employed to characterize each tag.
- We evaluate the capacity of a neural model to identify and authenticate the EM signatures of the tags in a supply chain scenario and we obtained a high recognition rate.
2. Materials and Methods
2.1. Proof of Concept to V-Band Applications
2.2. Chipless RFID Tags
2.3. Neural Network
2.3.1. Data Preprocessing
2.3.2. Neural Network Optimization
3. Results and Analysis
3.1. Neural Model Evaluation
3.2. K-Fold Cross Validation
3.3. Performance Comparison
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

Appendix B
- SGD is a simple and robust algorithm where the gradient of the cost function with respect to the weights, , is computed, and a fraction, , of that gradient is subtracted off of the weights:
Algorithm A1: SGD Algorithm - Adaptive Subgradient Descent (AdaGrad) divides of every step by the norm of all previous gradients. The method stabilizes the model’s representation of common features and allows it to learn the rare ones.
Algorithm A2: Adagrad Algorithm - RMSprop replaces the sum in with a decaying mean parameterized by . It solves the halting training of AdaGrad.
Algorithm A3: RMSprop Algorithm - Adam method combines classical momentum with RMSprop to improve the advantages of both algorithms. Bias correction terms and are initialized to 0.
Algorithm A4: Adam Algorithm
References
- Jechlitschek, C. A Survey Paper on Radio Frequency Identification (RFID) Trends. 2010. Available online: https://www.researchgate.net/publication/228573858_A_survey_paper_on_Radio_Frequency_Identification_RFID_trends (accessed on 8 November 2020).
- Al-Ali, A.R.; Aloul, F.A.; Aji, N.R.; Al-Zarouni, A.A.; Fakhro, N.H. Mobile RFID Tracking System. In Proceedings of the 2008 3rd International Conference on Information and Communication Technologies: From Theory to Applications, Damascus, Syria, 7–11 April 2008. [Google Scholar]
- Al-Zewairi, M.; Alqatawna, J.; Al-Kadi, O. Privacy and security for RFID Access Control Systems: RFID Access Control Systems without back-end database. In Proceedings of the 2011 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Amman, Jordan, 6–8 December 2011. [Google Scholar]
- Sabbaghi, A.; Vaidyanathan, G. Effectiveness and Efficiency of RFID technology in Supply Chain Management: Strategic values and Challenges. J. Theor. Appl. Electron. Commer. Res. 2008, 3, 71–81. [Google Scholar] [CrossRef] [Green Version]
- Power, G. Anti-Counterfeit Technologies for the Protection of Medicines; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Li, L. Technology designed to combat fakes in the global supply chain. Bus. Horiz. 2013, 56, 167–177. [Google Scholar] [CrossRef]
- Periaswamy, S.C.G.; Thompson, D.R.; Di, J. Fingerprinting RFID Tags. IEEE Trans. Dependable Secur. Comput. 2010, 8, 938–943. [Google Scholar] [CrossRef]
- Bertoncini, C.; Rudd, K.; Nousain, B.; Hinders, M. Wavelet Fingerprinting of Radio-Frequency Identification (RFID) Tags. IEEE Trans. Ind. Electron. 2011, 59, 4843–4850. [Google Scholar] [CrossRef]
- Kheir, M.; Kreft, H.; Hölken, I.; Knöchel, R. On the physical robustness of RF on-chip nanostructured security. J. Inf. Secur. Appl. 2014, 19, 301–307. [Google Scholar] [CrossRef]
- Yang, L.; Peng, P.; Dang, F.; Wang, C.; Li, X.Y.; Liu, Y. Anti-counterfeiting via federated RFID tags’ fingerprints and geometric relationships. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), Kowloon, Hong Kong, 26 April–1 May 2015. [Google Scholar]
- Romero, H.P.; Remley, K.A.; Williams, D.F.; Wang, C.M. Electromagnetic Measurements for Counterfeit Detection of Radio Frequency Identification Cards. IEEE Trans. Microw. Theory Tech. 2009, 57, 1383–1387. [Google Scholar] [CrossRef]
- Danev, B.; Heydt-Benjamin, T.S.; Capkun, S. Physical-layer Identification of RFID Devices. In Proceedings of the 8th Conference USENIX Security Symposia, Montreal, QC, Canada, 10–14 August 2009. [Google Scholar]
- Danev, B.; Capkun, S.; Masti, R.J.; Benjamin, T.S. Towards Practical Identification of HF RFID Devices; ACM Transactions on Information and System Security (TISSEC): New York, NY, USA, 2012; Volume 15, p. 7. [Google Scholar]
- Romero, H.P.; Remley, K.A.; Williams, D.F.; Wang, C.M.; Brown, T.X. Identifying RF Identification Cards from Measurements of Resonance and Carrier Harmonics. IEEE Trans. Microw. Theory Tech. 2010, 58, 1758–1765. [Google Scholar] [CrossRef]
- Zhang, G.; Xia, L.; Jia, S.; Ji, Y. Identification of Cloned HF RFID Proximity Cards Based on RF Fingerprinting. In Proceedings of the IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23–26 August 2016. [Google Scholar]
- Perret, E. Radio Frequency Identification and Sensors: From RFID to Chipless RFID; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Rance, O.; Siragusa, R.; Lemaître-Auger, P.; Perret, E. Toward RCS Magnitude Level Coding for Chipless RFID. IEEE Trans. Microw. Theory Tech. 2016, 64, 2315–2325. [Google Scholar] [CrossRef]
- Vena, A.; Perret, E.; Tedjini, S. RFID chipless tag based on multiple phase shifters. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011. [Google Scholar]
- Vena, A.; Perret, E.; Tedjni, S. A Depolarizing Chipless RFID Tag for Robust Detection and Its FCC Compliant UWB Reading System. IEEE Trans. Microw. Theory Tech. 2013, 61, 2982–2994. [Google Scholar] [CrossRef]
- De Amorim, R.; Fontgalland, G.; Rodrigues, R.A.A. Low cost folded chipless tag for millimeter-wave applications. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018. [Google Scholar]
- Ramos, A.; Lazaro, A.; Girbau, D.; Villarino, R. Time-Domain Measurement of Time-Coded UWB Chipless RFID Tags. Prog. Electromagn. Res. 2011, 116, 313–331. [Google Scholar] [CrossRef] [Green Version]
- Nair, R.S.; Perret, E. Folded Multilayer C-Sections with Large Group Delay Swing for Passive Chipless RFID Applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 4298–4311. [Google Scholar] [CrossRef]
- Jalaly, I.; Robertson, I.D. Capacitively-tuned split microstrip resonators for RFID barcodes. In Proceedings of the European Microwave Conference, Paris, France, 4–6 October 2005. [Google Scholar]
- Ali, Z.; Barbot, N.; Siragusa, R.; Hely, D.; Bernier, M.; Garet, F.; Perret, E. Chipless RFID Tag Discrimination and the Performance of Resemblance Metrics to be used for it. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium—IMS, Philadelphia, PA, USA, 10–15 June 2018; pp. 363–366. [Google Scholar]
- II, W.C.S.; Temple, M.A.; Mendenhall, M.J.; Mills, R.F. Radio Frequency Fingerprinting Commercial Communication Devices to Enhance Electronic Security. Int. J. Electron. Secur. Digit. Forensics 2008, 1, 301. [Google Scholar] [CrossRef]
- Gerdes, R.M.; Daniels, T.E.; Mina, M.; Russell, S. Device Identification via Analog Signal Fingerprinting: A Matched Filter Approach. In Proceedings of the NDSS, San Diego, CA, USA, 2–3 February 2006. [Google Scholar]
- Zia, T.; Ghafoor, M.; Tariq, S.A.; Taj, I.A. Robust fingerprint classification with Bayesian convolutional networks. IET Image Process. 2019, 13, 1280–1288. [Google Scholar] [CrossRef]
- Yang, K.; Botero, U.; Shen, H.; Woodard, D.; Forte, D.; Tehranipoor, M. UCR: An Unclonable Environmentally Sensitive Chipless RFID Tag for Protecting Supply Chain. ACM Trans. Des. Autom. Electr. Syst. 2018, 23, 1–24. [Google Scholar] [CrossRef]
- Tharwat, A.; Gaber, T.; Ibrahim, A.; Hassanien, A. Linear discriminant analysis: A detailed tutorial. AI Commun. 2017, 30, 169–190. [Google Scholar] [CrossRef] [Green Version]
- Silva, D.F.; Batista, G. Speeding up all-pairwise dynamic time warping matrix calculation. In Proceedings of the 2016 SIAM International Conference on Data Mining, Miami, FL, USA, 5–7 May 2016; SIAM: Philadelphia, PA, USA, 2016; pp. 837–845. [Google Scholar]
- Akansu, A.; Serdijn, W.; Selesnick, I. Emerging applications of wavelets: A review. Phys. Commun. 2010, 3, 1–18. [Google Scholar] [CrossRef]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Dursun, D.; Ramesh, S. Artificial Neural Networks in Decision Support Systems. In Handbook on Decision Support Systems 1; Springer: Berlin/Heidelberg, Germany, 2008; pp. 557–580. [Google Scholar] [CrossRef]
- Ali, Z.; Perret, E.; Barbot, N.; Siragusa, R.; Hély, D.; Bernier, M.; Garet, F. Detection of Natural Randomness by Chipless RFID Approach and Its Application to Authentication. IEEE Trans. Microw. Theory Tech. 2019, 67, 3867–3881. [Google Scholar] [CrossRef]
- Reed, R.D.; Marks, R.J. Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ketkar, N. Introduction to Keras. In Deep Learning with Python; Manning Publications Country: New York, NY, USA, 2017; pp. 95–109. [Google Scholar]
- Le Guennec, A.; Malinowski, S.; Tavenard, R. Data Augmentation for Time Series Classification using Convolutional Neural Networks. In Proceedings of the ECML/PKDD Workshop on Advanced Analytics and Learning on Temporal Data, Riva Del Garda, Italy, 19–23 September 2016. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 1137–1143. [Google Scholar]












| Frequency | |||
|---|---|---|---|
| X-band | 0.9966 | 0.9971 | 0.9875 |
| V-band | 0.6059 | 0.6031 | 0.5750 |
| Model 1 | Loss | Accuracy (%) |
|---|---|---|
| Model 1 | 0.0208994 | 100% |
| Model 2 | 0.0371103 | 100% |
| Model 3 | 0.0369607 | 100% |
| Classification Technique | Recognition Rate |
|---|---|
| Euclidean Distance | 92.12% |
| Normalized Correlation | 91.97% |
| Lorentzian Distance | 91.33% |
| Manhattan Distance | 96.06% |
| ML with LDA | 98.44% |
| Dynamic Time Warping | 100% |
| Wavelet Transform Manhattan Distance | 100% |
| Our approach | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nastasiu, D.; Scripcaru, R.; Digulescu, A.; Ioana, C.; De Amorim, R., Jr.; Barbot, N.; Siragusa, R.; Perret, E.; Popescu, F. A New Method of Secure Authentication Based on Electromagnetic Signatures of Chipless RFID Tags and Machine Learning Approaches. Sensors 2020, 20, 6385. https://doi.org/10.3390/s20216385
Nastasiu D, Scripcaru R, Digulescu A, Ioana C, De Amorim R Jr., Barbot N, Siragusa R, Perret E, Popescu F. A New Method of Secure Authentication Based on Electromagnetic Signatures of Chipless RFID Tags and Machine Learning Approaches. Sensors. 2020; 20(21):6385. https://doi.org/10.3390/s20216385
Chicago/Turabian StyleNastasiu, Dragoș, Răzvan Scripcaru, Angela Digulescu, Cornel Ioana, Raymundo De Amorim, Jr., Nicolas Barbot, Romain Siragusa, Etienne Perret, and Florin Popescu. 2020. "A New Method of Secure Authentication Based on Electromagnetic Signatures of Chipless RFID Tags and Machine Learning Approaches" Sensors 20, no. 21: 6385. https://doi.org/10.3390/s20216385
APA StyleNastasiu, D., Scripcaru, R., Digulescu, A., Ioana, C., De Amorim, R., Jr., Barbot, N., Siragusa, R., Perret, E., & Popescu, F. (2020). A New Method of Secure Authentication Based on Electromagnetic Signatures of Chipless RFID Tags and Machine Learning Approaches. Sensors, 20(21), 6385. https://doi.org/10.3390/s20216385







