A Comprehensive Dependability Model for QoM-Aware Industrial WSN When Performing Visual Area Coverage in Occluded Scenarios
Abstract
:1. Introduction
- Integrate different methodologies proposed in previous works, defining a comprehensive unified mathematical model to assess the dependability of wireless visual sensor networks, specially considering the particularities of sensors-based industrial applications;
- Create a consistent reference for quality assessment in critical applications, associating the most relevant failure causes in visual monitoring, which has not been considered before by the literature;
- Discuss how the parameters of the proposed mathematical model can be achieved in practical applications, potentially supporting more effective dependability evaluations;
- Demonstrate a practical use of the proposed methodology considering realistic parameters, which can be easily replicated when evaluating other applications in industrial scenarios.
2. Related Works
2.1. Occlusion and QoM when Considering Area Coverage
2.2. Dependability Assessment
3. Definitions and Basic Concepts
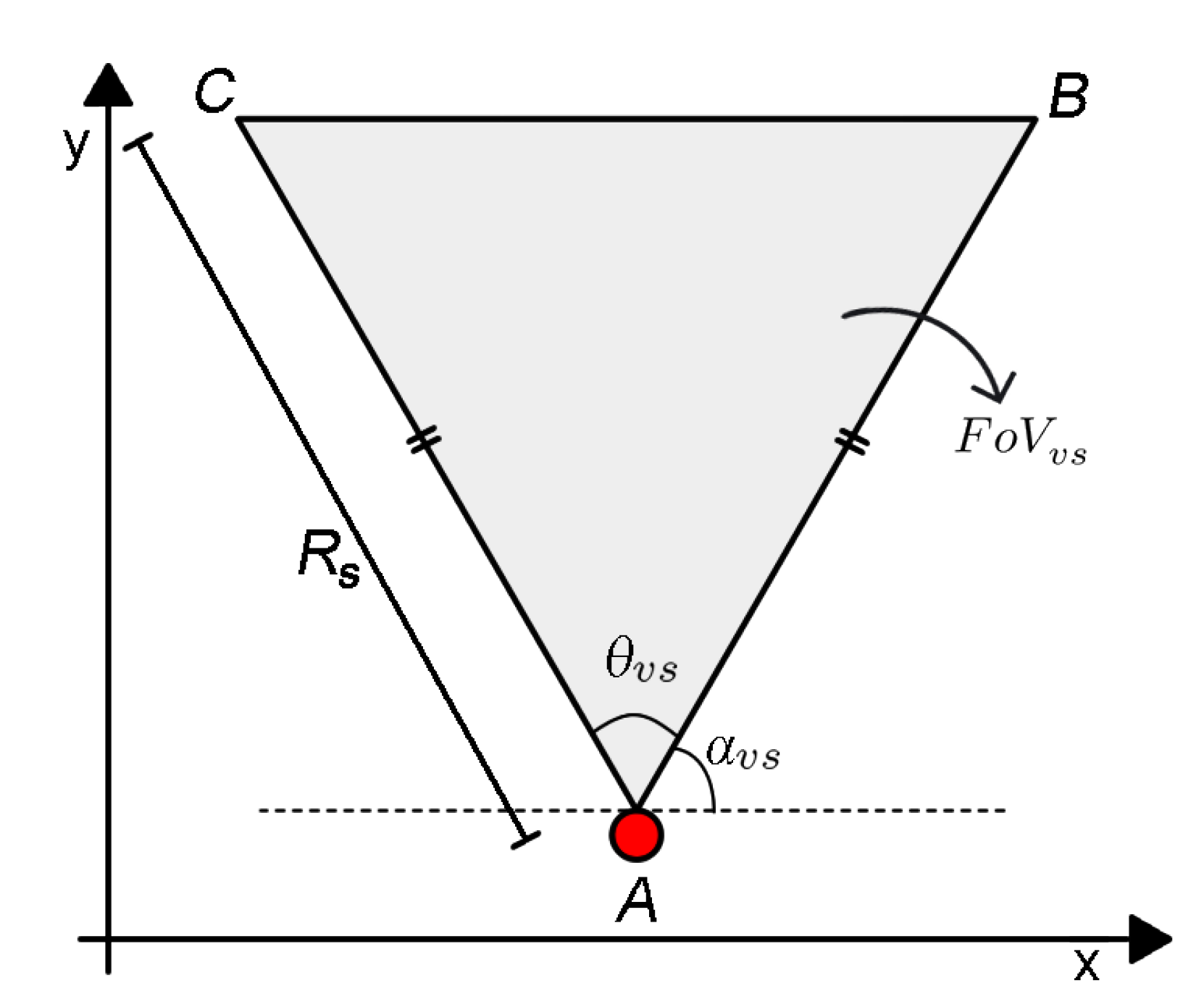
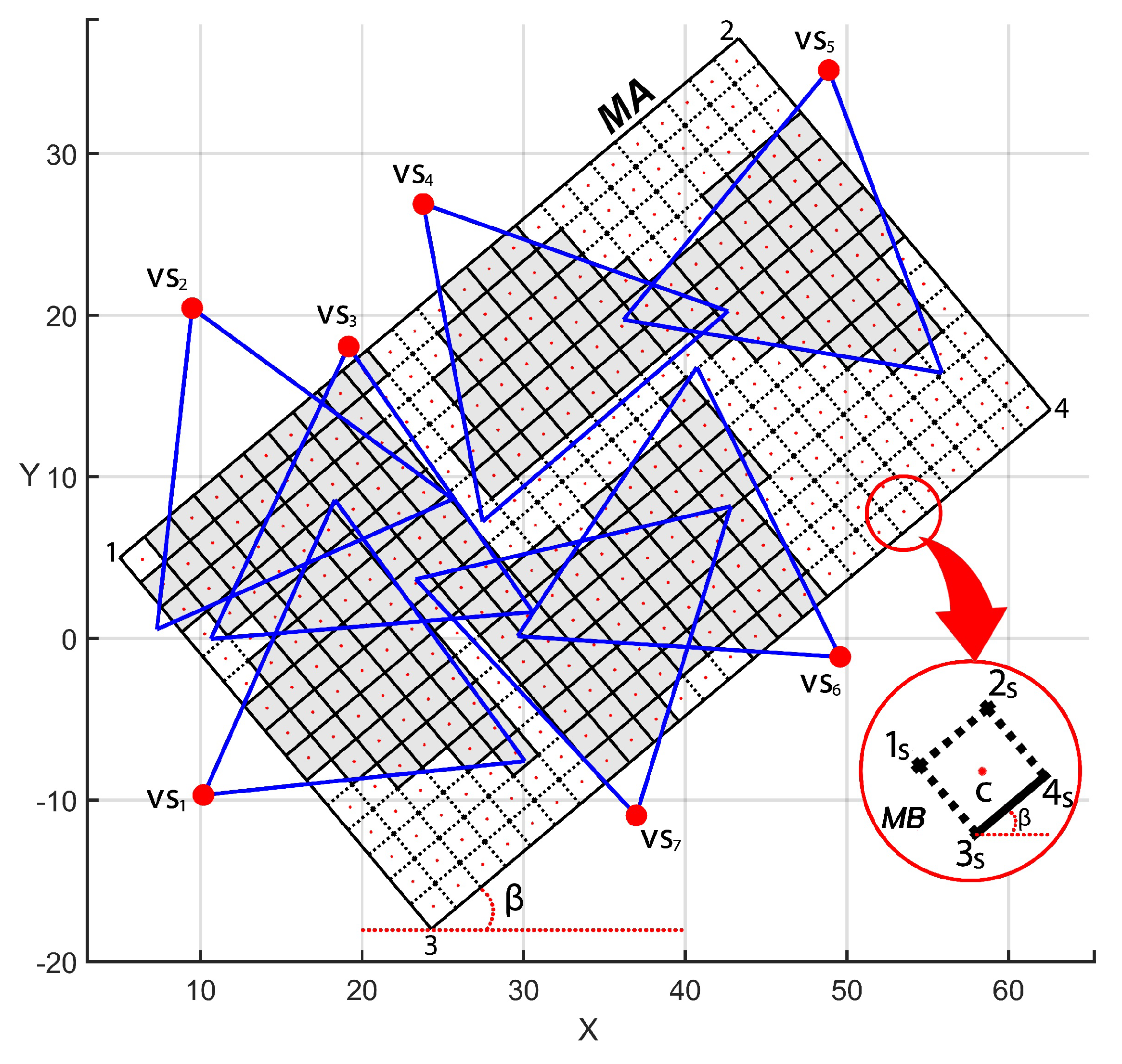
3.1. Area Coverage
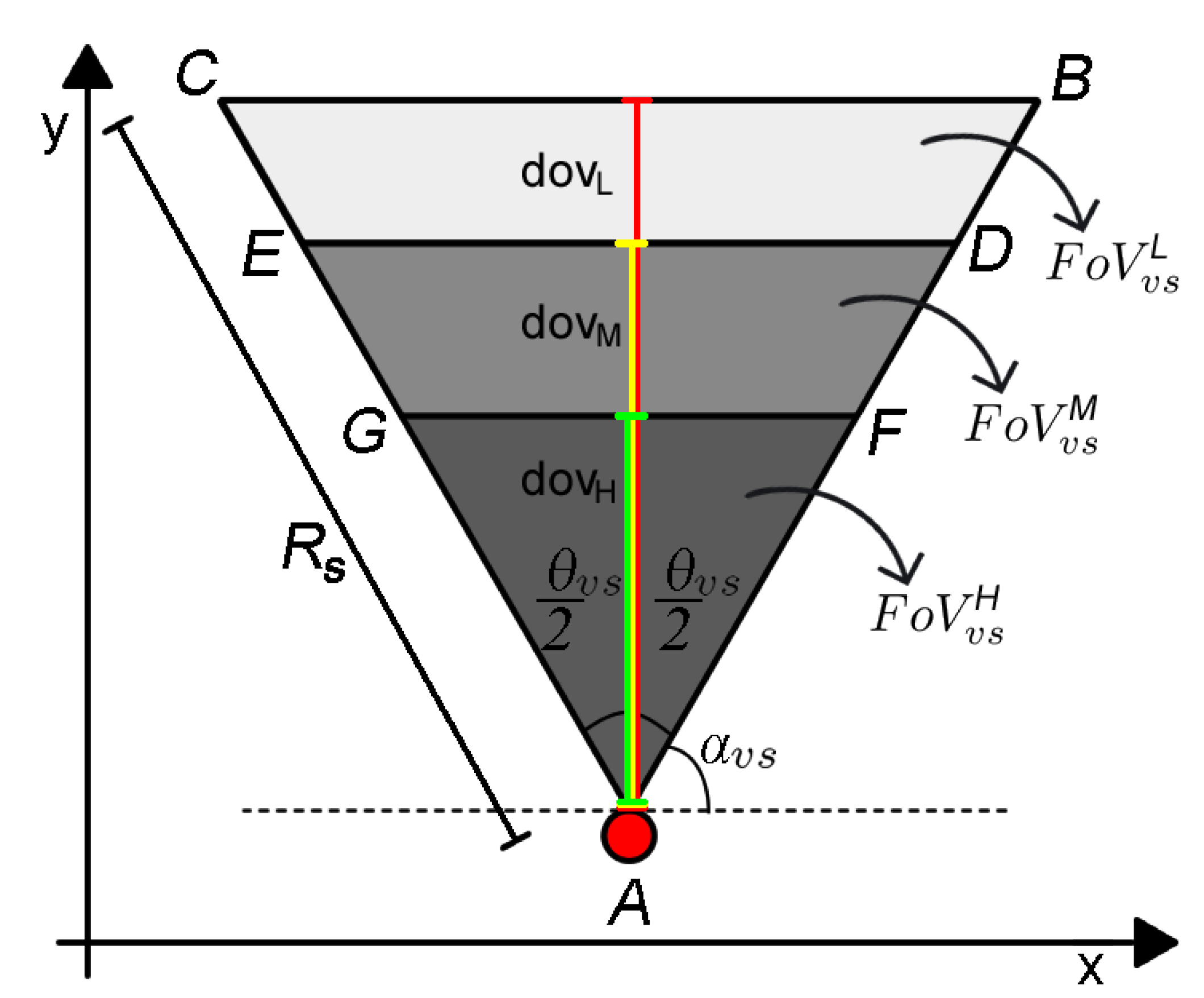
3.2. Quality of Monitoring
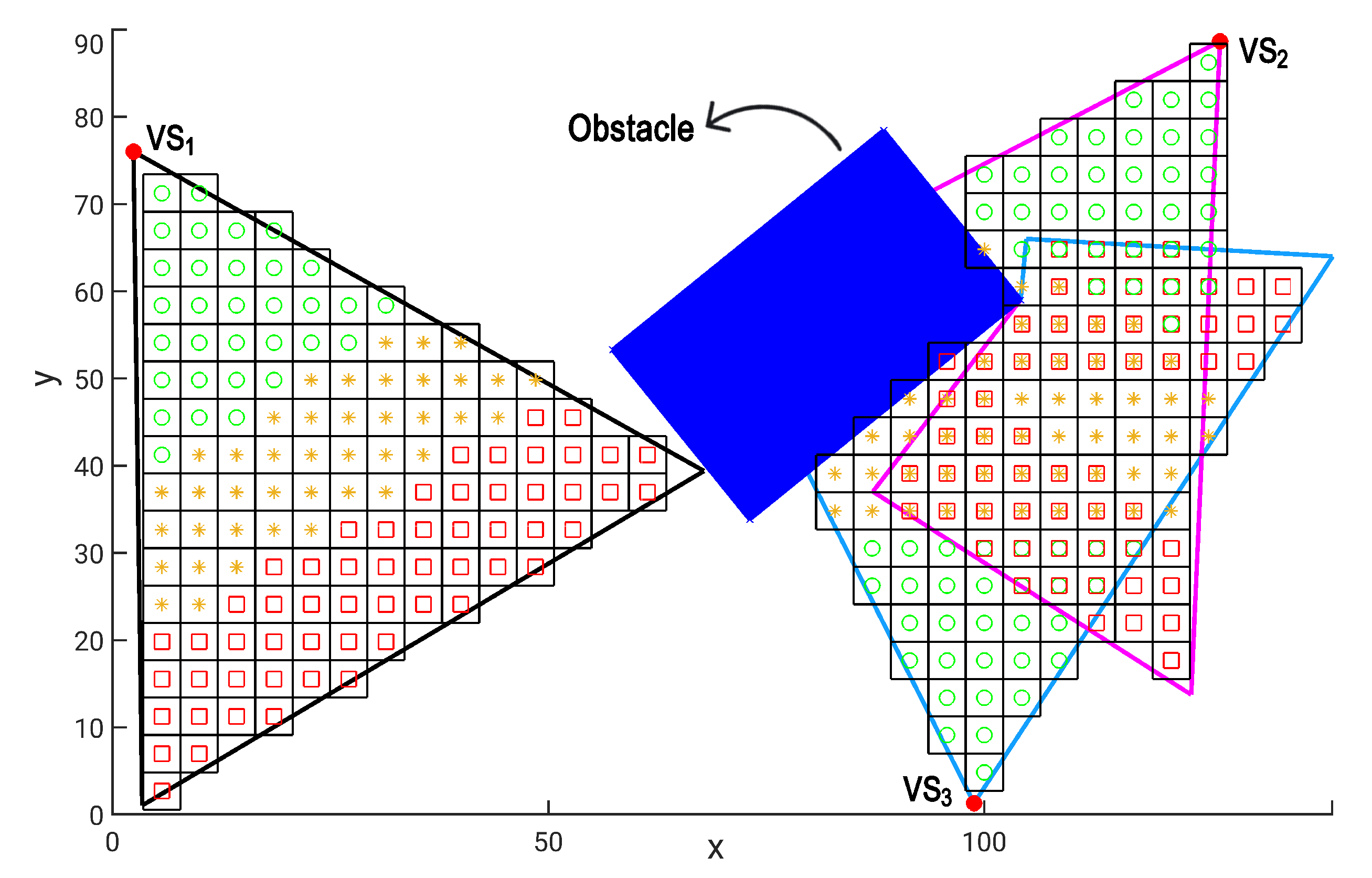
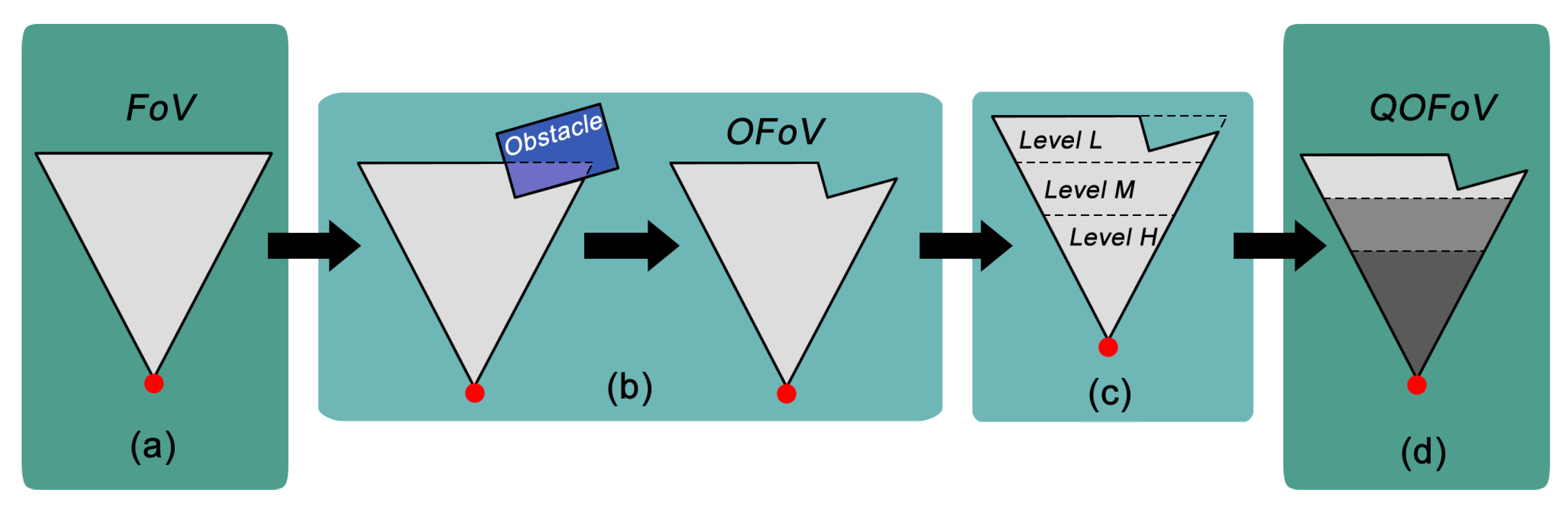
3.3. Occlusion
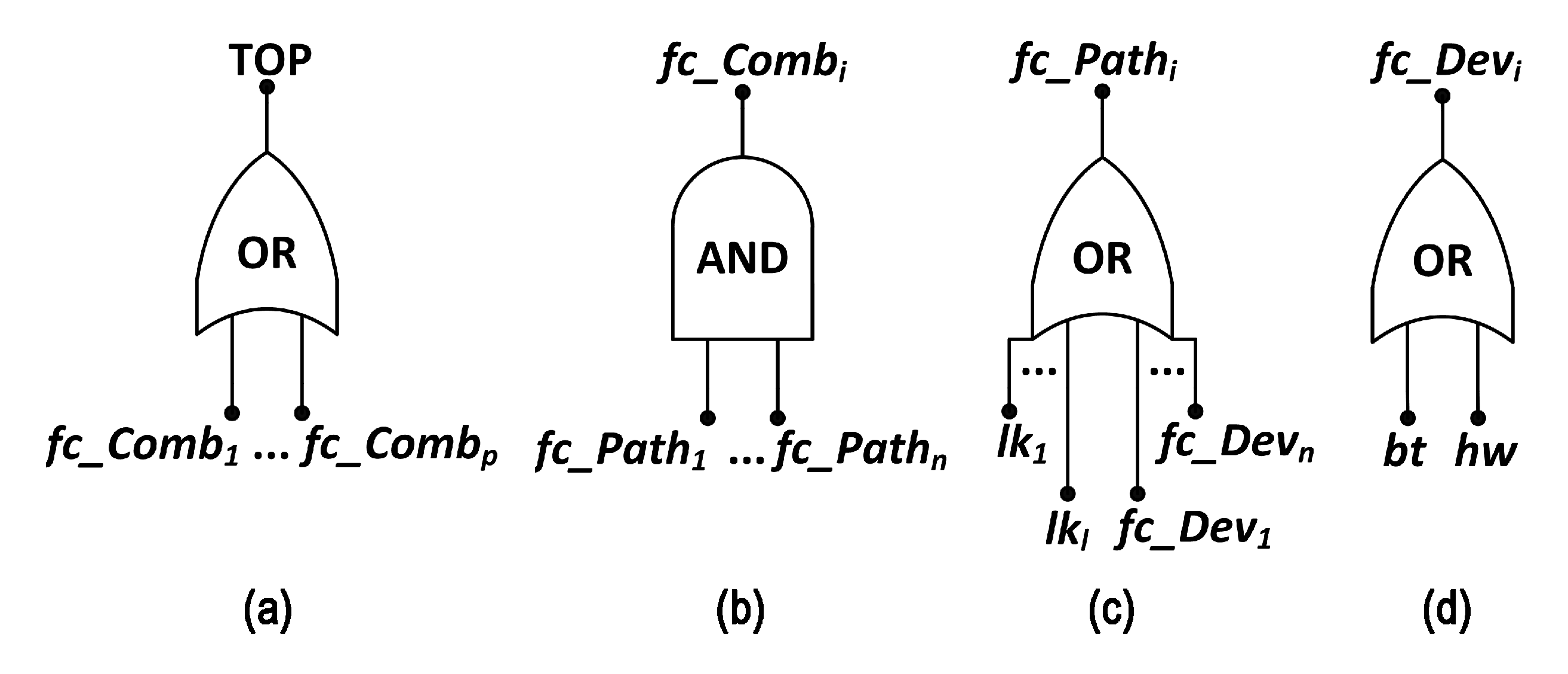
4. Proposed Methodology
| Algorithm 1: NFC. |
 |
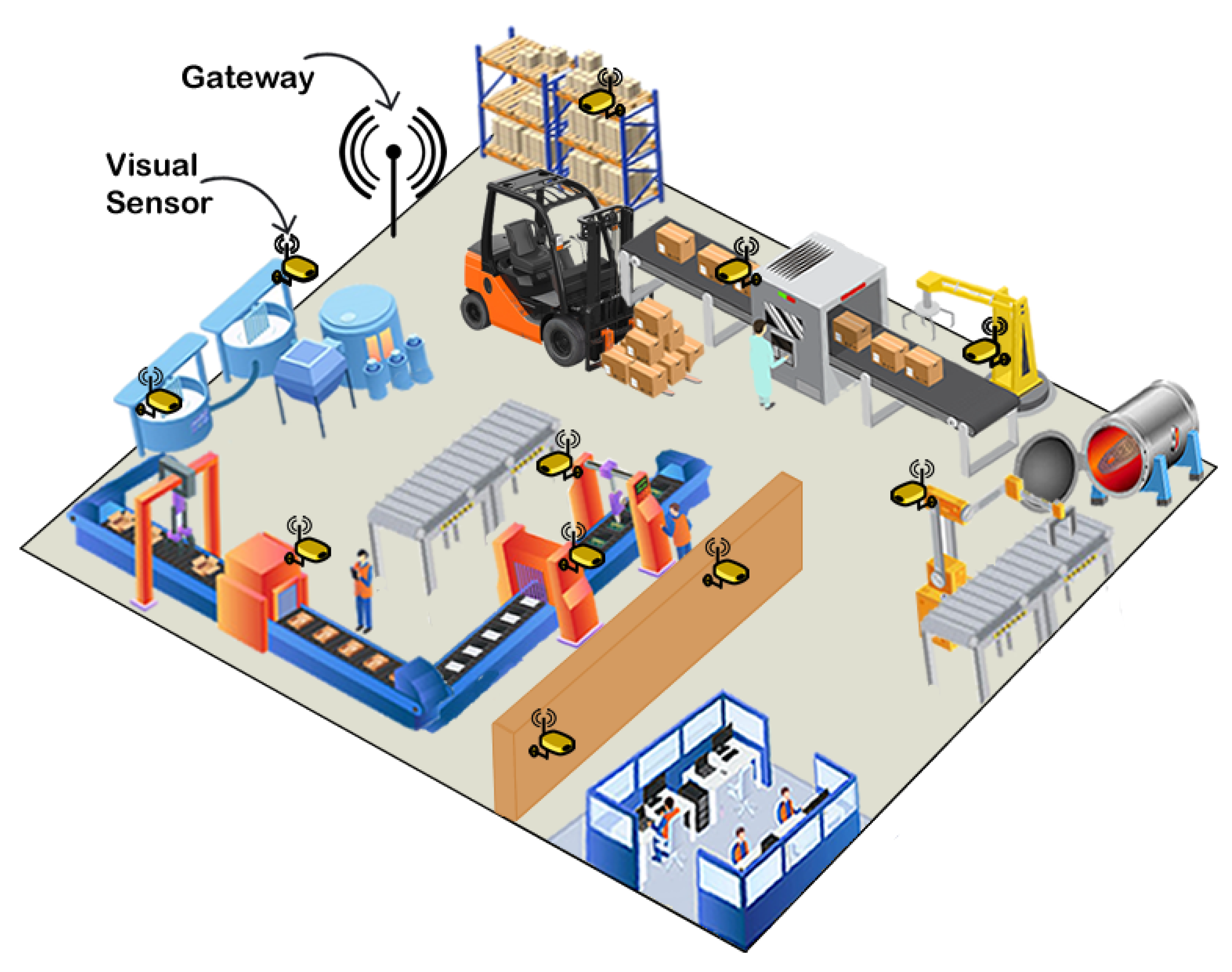
5. Practical Dependability Assessment
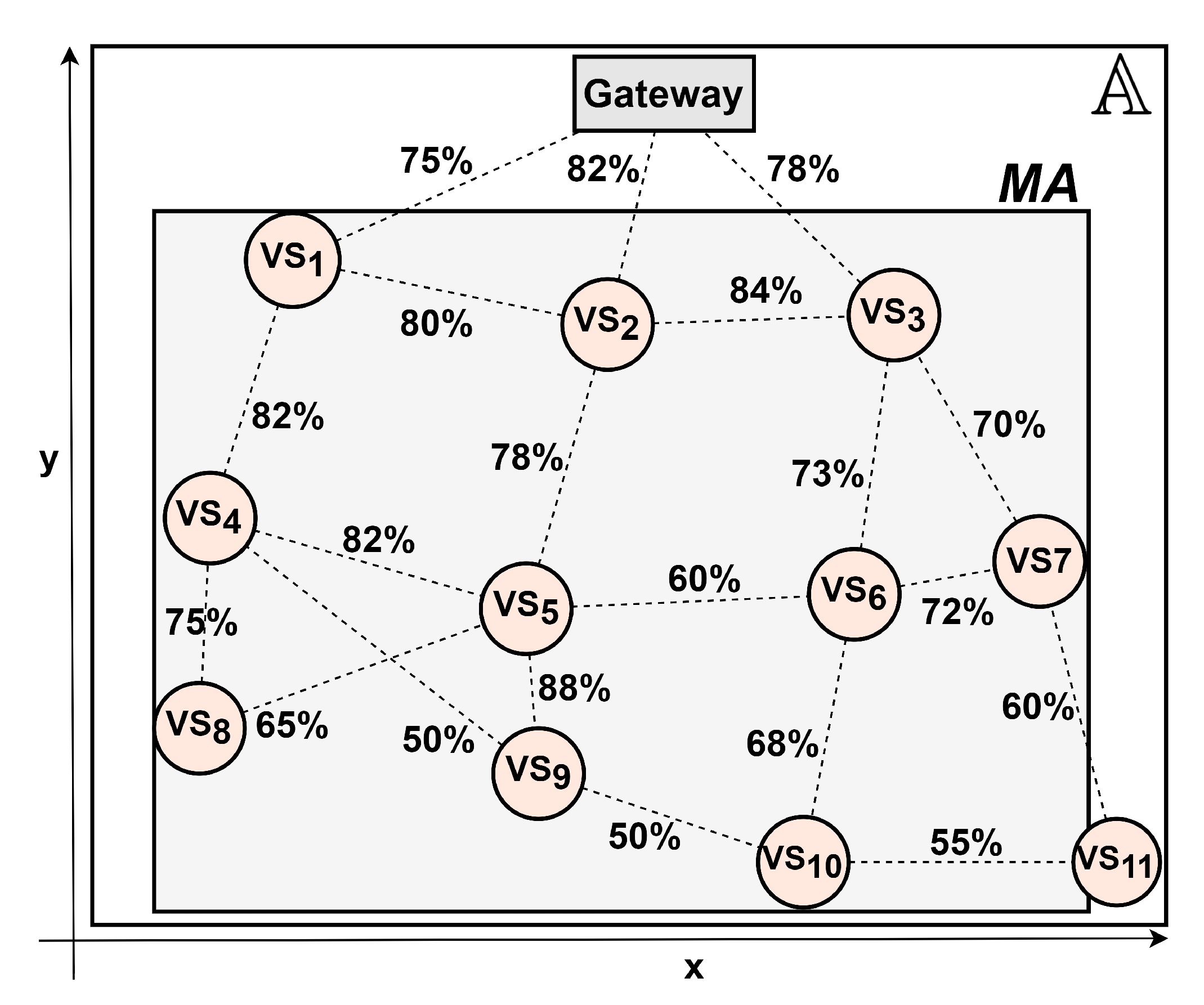
5.1. Experimental Parameter Settings
5.2. Dependability Evaluation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qin, F.; Zhang, Q.; Zhang, W.; Yang, Y.; Ding, J.; Dai, X. Link Quality Estimation in Industrial Temporal Fading Channel With Augmented Kalman Filter. IEEE Trans. Ind. Inform. 2019, 15, 1936–1946. [Google Scholar] [CrossRef]
- Lucas-Estan, M.C.; Coll-Perales, B.; Gozalvez, J. Redundancy and Diversity in Wireless Networks to Support Mobile Industrial Applications in Industry 4.0. IEEE Trans. Ind. Inform. 2020, 17, 311–320. [Google Scholar] [CrossRef]
- Raposo, D.; Rodrigues, A.; Sinche, S.; Sá Silva, J.; Boavida, F. Industrial IoT Monitoring: Technologies and Architecture Proposal. Sensors 2018, 18, 3568. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costa, D.G.; Silva, I.; Guedes, L.A.; Portugal, P.; Vasques, F. Selecting redundant nodes when addressing availability in wireless visual sensor networks. In Proceedings of the 2014 12th IEEE International Conference on Industrial Informatics (INDIN), Porto Alegre, Brazil, 27–30 July 2014; pp. 130–135. [Google Scholar] [CrossRef]
- Jesus, T.C.; Costa, D.G.; Portugal, P.; Vasques, F. FoV-Based Quality Assessment and Optimization for Area Coverage in Wireless Visual Sensor Networks. IEEE Access 2020, 8, 109568–109580. [Google Scholar] [CrossRef]
- Tao, J.; Zhai, T.; Wu, H.; Xu, Y.; Dong, Y. A quality-enhancing coverage scheme for camera sensor networks. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 8458–8463. [Google Scholar] [CrossRef]
- Shi, H.; Sun, G.; Wang, Y.; Hwang, K. Adaptive Image-Based Visual Servoing with Temporary Loss of the Visual Signal. IEEE Trans. Ind. Inform. 2019, 15, 1956–1965. [Google Scholar] [CrossRef]
- Ahlen, A.; Akerberg, J.; Eriksson, M.; Isaksson, A.J.; Iwaki, T.; Johansson, K.H.; Knorn, S.; Lindh, T.; Sandberg, H. Toward Wireless Control in Industrial Process Automation: A Case Study at a Paper Mill. IEEE Control Syst. Mag. 2019, 39, 36–57. [Google Scholar]
- Wang, Q.; Wang, P. A Finite-State Markov Model for Reliability Evaluation of Industrial Wireless Network. In Proceedings of the 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, China, 23–25 September 2010; pp. 1–4. [Google Scholar]
- Jesus, T.C.; Portugal, P.; Vasques, F.; Costa, D.G. Automated Methodology for Dependability Evaluation of Wireless Visual Sensor Networks. Sensors 2018, 18, 2629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jesus, T.C.; Costa, D.G.; Portugal, P.; Vasques, F.; Aguiar, A. Modelling Coverage Failures Caused by Mobile Obstacles for the Selection of Faultless Visual Nodes in Wireless Sensor Networks. IEEE Access 2020, 8, 41537–41550. [Google Scholar] [CrossRef]
- He, S.; Shin, D.H.; Zhang, J.; Chen, J.; Sun, Y. Full-View Area Coverage in Camera Sensor Networks: Dimension Reduction and Near-Optimal Solutions. IEEE Trans. Veh. Technol. 2016, 65, 7448–7461. [Google Scholar] [CrossRef]
- Hsiao, Y.P.; Shih, K.P.; Chen, Y.D. On Full-View Area Coverage by Rotatable Cameras in Wireless Camera Sensor Networks. In Proceedings of the 2017 IEEE 31st International Conference on Advanced Information Networking and Applications (AINA), Taipei, Taiwan, 27–29 March 2017; pp. 260–265. [Google Scholar] [CrossRef]
- Konda, K.R.; Conci, N.; Natale, F.D. Global Coverage Maximization in PTZ-Camera Networks Based on Visual Quality Assessment. IEEE Sens. J. 2016, 16, 6317–6332. [Google Scholar] [CrossRef]
- Shriwastav, S.; Song, Z. Coordinated Coverage and Fault Tolerance Using Fixed-Wing Unmanned Aerial Vehicles. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 1231–1240. [Google Scholar] [CrossRef]
- Scott, K.; Dai, R.; Kumar, M. Occlusion-Aware Coverage for Efficient Visual Sensing in Unmanned Aerial Vehicle Networks. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Costa, D.G.; Vasques, F.; Portugal, P. Enhancing the availability of wireless visual sensor networks: Selecting redundant nodes in networks with occlusion. Appl. Math. Model. 2017, 42, 223–243. [Google Scholar] [CrossRef]
- Andrade, E.; Nogueira, B. Dependability evaluation of a disaster recovery solution for IoT infrastructures. J. Supercomput. 2020, 76, 1828–1849. [Google Scholar] [CrossRef]
- Silva, I.; Guedes, L.A.; Portugal, P.; Vasques, F. Reliability and Availability Evaluation of Wireless Sensor Networks for Industrial Applications. Sensors 2012, 12, 806–838. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costa, D.G.; Silva, I.; Guedes, L.A.; Portugal, P.; Vasques, F. Availability assessment of wireless visual sensor networks for target coverage. In Proceedings of the 2014 IEEE Emerging Technology and Factory Automation (ETFA), Barcelona, Spain, 16–19 September 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Costa, D.G.; Rangel, E.; Peixoto, J.P.J.; Jesus, T.C. An Availability Metric and Optimization Algorithms for Simultaneous Coverage of Targets and Areas by Wireless Visual Sensor Networks. In Proceedings of the 2019 IEEE 17th International Conference on Industrial Informatics (INDIN), Helsinki, Finland, 22–25 July 2019; pp. 617–622. [Google Scholar]
- Jesus, T.C.; Costa, D.G.; Portugal, P. On the Computing of Area Coverage by Visual Sensor Networks: Assessing Performance of Approximate and Precise Algorithms. In Proceedings of the 2018 IEEE 16th International Conference on Industrial Informatics (INDIN), Porto, Portugal, 18–20 July 2018; pp. 193–198. [Google Scholar] [CrossRef]
- Frühwirth, T.; Krammer, L.; Kastner, W. Dependability demands and state of the art in the internet of things. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies Factory Automation (ETFA), Luxembourg, 8–11 September 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Martins, M.; Portugal, P.; Vasques, F. A framework to support dependability evaluation of WSNs from AADL models. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies Factory Automation (ETFA), Luxembourg, 8–11 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Dar, K.S.; Taherkordi, A.; Eliassen, F. Enhancing Dependability of Cloud-Based IoT Services through Virtualization. In Proceedings of the 2016 IEEE 1st International Conference on Internet-of-Things Design and Implementation (IoTDI), Berlin, Germany, 4–8 April 2016; pp. 106–116. [Google Scholar] [CrossRef]
- Jesus, T.C.; Costa, D.G.; Portugal, P. Wireless Visual Sensor Networks Redeployment Based on Dependability Optimization. In Proceedings of the 2019 IEEE 17th International Conference on Industrial Informatics (INDIN), Helsinki, Finland, 22–25 July 2019; pp. 1111–1116. [Google Scholar]
- Trivedi, K.S.; Sahner, R. SHARPE at the Age of Twenty Two. SIGMETRICS Perform. Eval. Rev. 2009, 36, 52–57. [Google Scholar] [CrossRef]
- Ye, Y.; Guangrui, F.; Shiqi, O. An Algorithm for Judging Points Inside or Outside a Polygon. In Proceedings of the 2013 7th International Conference on Image and Graphics, Qingdao, China, 26–28 July 2013; pp. 690–693. [Google Scholar] [CrossRef]
- Kularathne, D.; Jayarathne, L. Point in Polygon Determination Algorithm for 2-D Vector Graphics Applications. In Proceedings of the 2018 National Information Technology Conference (NITC), Colombo, Sri Lanka, 2–4 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, J. Comparative Examination on Architecture and Protocol of Industrial Wireless Sensor Network Standards. IEEE Commun. Surv. Tutor. 2016, 18, 2197–2219. [Google Scholar] [CrossRef]
- Raptis, T.P.; Passarella, A.; Conti, M. Performance Analysis of Latency-Aware Data Management in Industrial IoT Networks. Sensors 2018, 18, 2611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Endress+Hauser. WirelessHART Adapter SWA70; Technical Information: (TI00026S/04/EN/21.16 71339584); 2016; Available online: https://portal.endress.com/wa001/dla/5000557/8065/000/11/TI00026SEN_2116_PV2.40.xx.pdf (accessed on 10 June 2020).
- Texas Instruments. CC2420 Reliability Report; SWRK007 Report (Rev. 1.2); 2005; Available online: http://www.ti.com/lit/rr/swrk007/swrk007.pdf (accessed on 10 June 2020).
- FLIR® Integrated Imaging Solutions Inc. FLIR BLACKFLY®S BFS-U3-13Y3 Reliability. 2017. Available online: http://softwareservices.flir.com/BFS-U3-13Y3/latest/Quality/MTBF.htm (accessed on 10 June 2020).
- Zonouz, A.E.; Xing, L.; Vokkarane, V.M.; Sun, Y.L. A time-dependent link failure model for wireless sensor networks. In Proceedings of the 2014 Reliability and Maintainability Symposium, Colorado Springs, CO, USA, 27–30 January 2014; pp. 1–7. [Google Scholar]
- Purba, J.H.; Lu, J.; Zhang, G.; Ruan, D. An Area Defuzzification Technique to Assess Nuclear Event Reliability Data from Failure Possibilities. Int. J. Comput. Intell. Appl. 2012, 11, 1250022. [Google Scholar] [CrossRef]
- Egeland, G.; Engelstad, P.E. The availability and reliability of wireless multi-hop networks with stochastic link failures. IEEE J. Sel. Areas Commun. 2009, 27, 1132–1146. [Google Scholar] [CrossRef]
- Gomez, C.; Cuevas, A.; Paradells, J. AHR: A Two-State Adaptive Mechanism for Link Connectivity Maintenance in AODV. In Proceedings of the 2nd International Workshop on Multi-Hop Ad Hoc Networks: From Theory to Reality, REALMAN ’06, Florence, Italy, 26 May 2006; pp. 98–100. [Google Scholar] [CrossRef]
- Miyazaki, M.; Fujiwara, R.; Mizugaki, K.; Kokubo, M. Adaptive channel diversity method based on ISA100.11a standard for wireless industrial monitoring. In Proceedings of the 2012 IEEE Radio and Wireless Symposium, Santa Clara, CA, USA, 15–18 January 2012; pp. 131–134. [Google Scholar]
- Muller, I.; Netto, J.C.; Pereira, C.E. WirelessHART field devices. IEEE Instrum. Meas. Mag. 2011, 14, 20–25. [Google Scholar] [CrossRef]


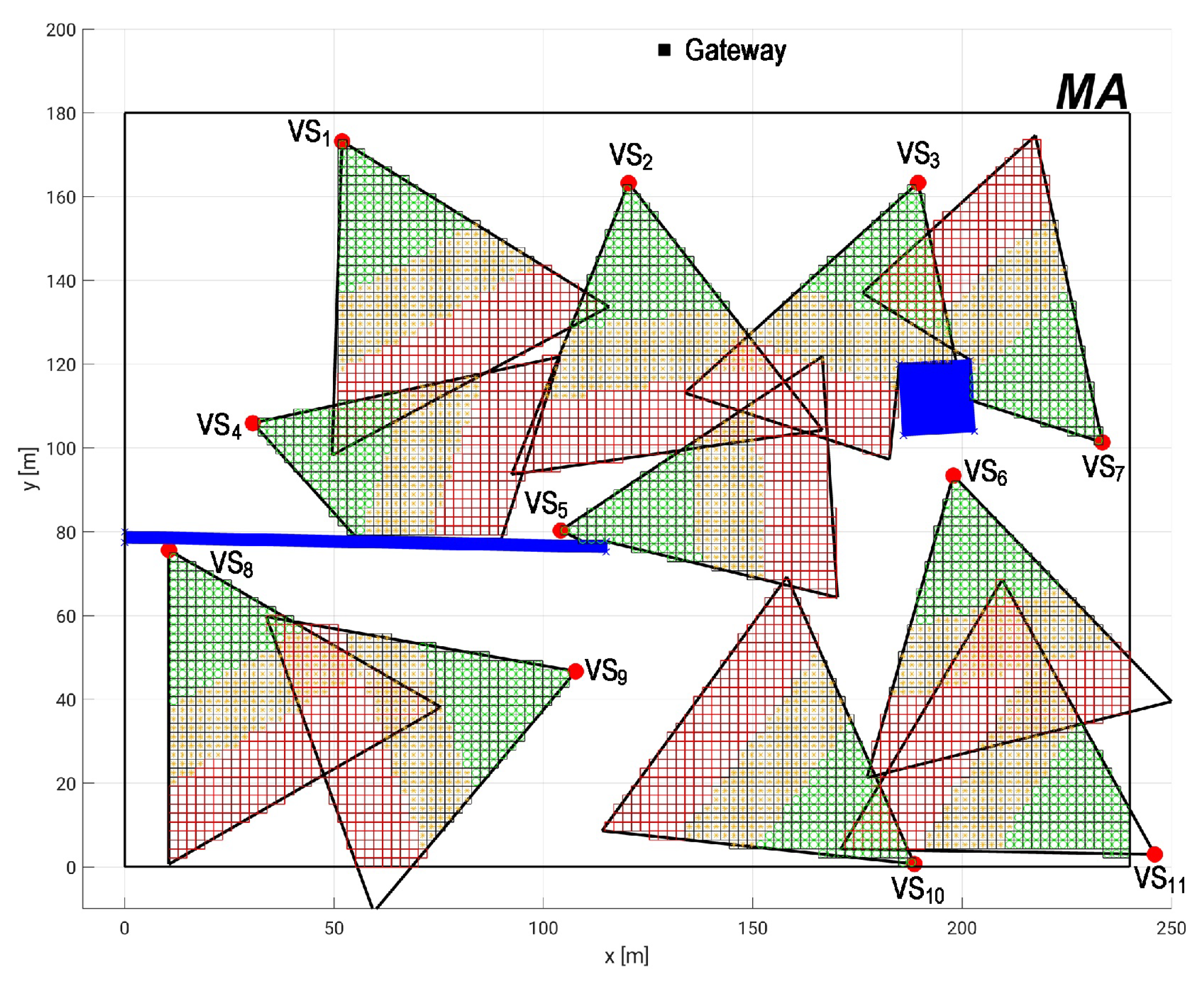
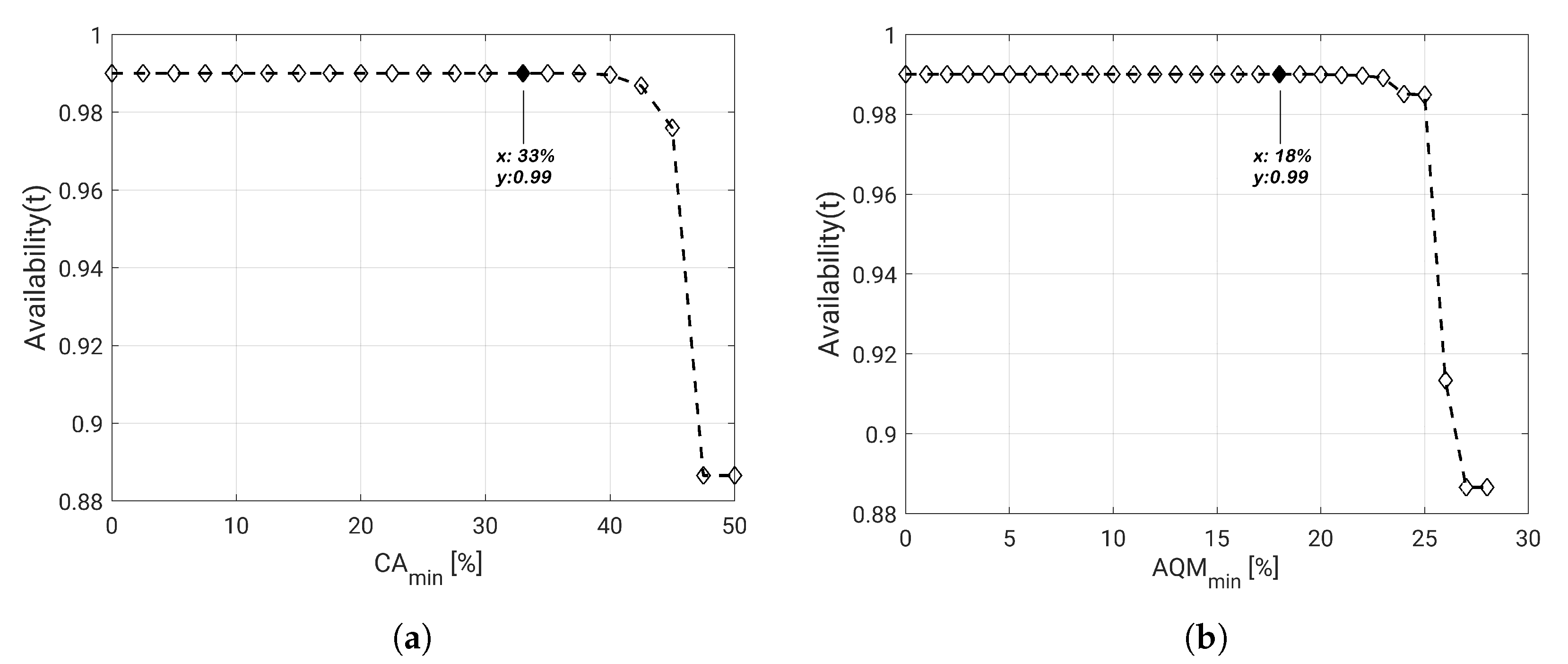
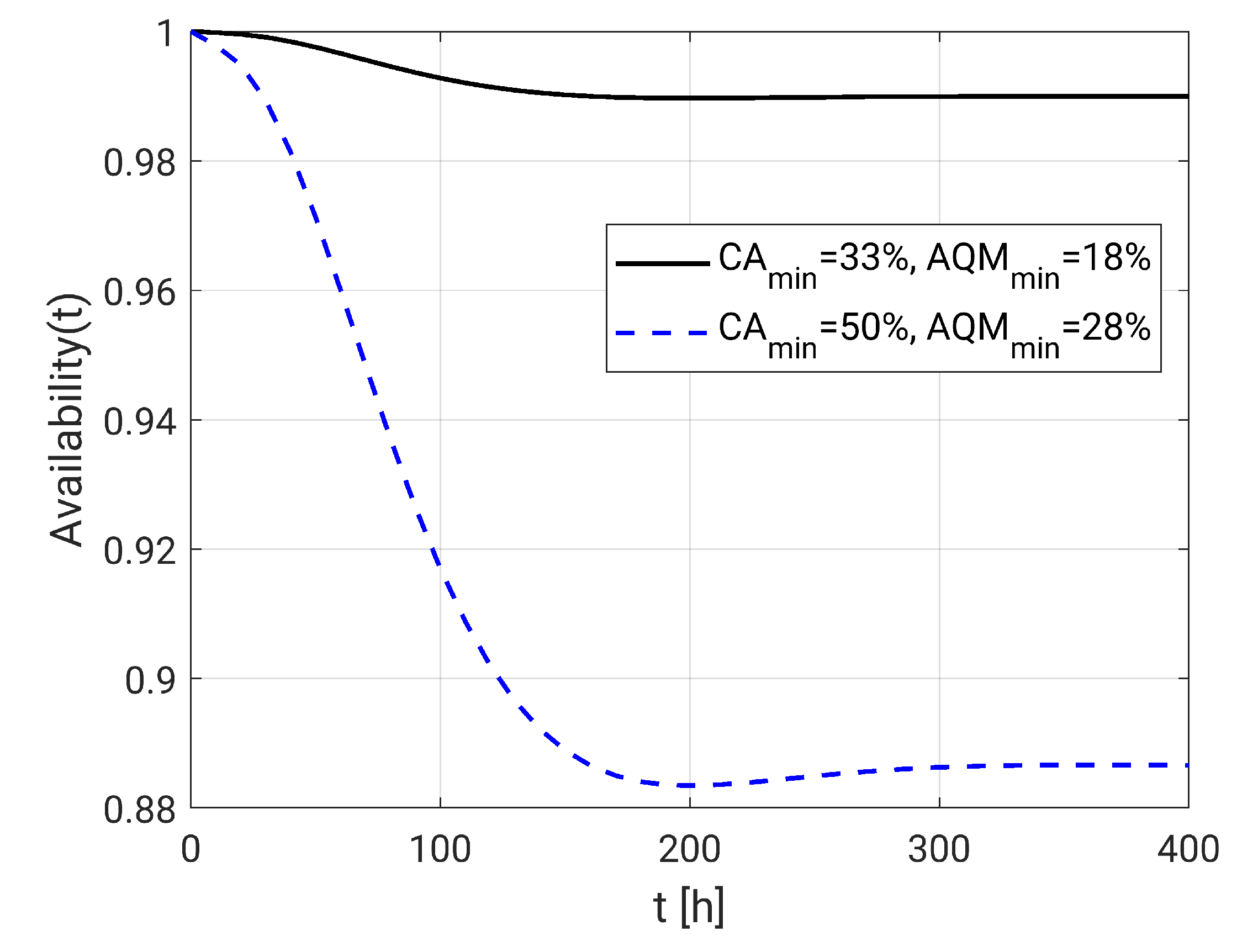

| Work | QoM | Occlusion | WSN Evaluation | VCF | Brief Description |
|---|---|---|---|---|---|
| He et al. [12] and Hsiao et al. [13] | X | – | – | – | Area coverage analysis aiming at full-view coverage, considering QoM by the facing angle of points of interest. |
| Konda et al. [14] | X | – | – | – | Automatic deployment of WVSN to maximize coverage and visual quality in indoor environments, considering perspective distortion of the acquired images. |
| Shriwastav and Song [15] | X | – | – | – | UAV network for area coverage. Network parameters are carefully handled during redeployment to keep the coverage quality constant. |
| Tao et al. [6] | X | X | – | – | QoM-enhancing coverage scheme in a full area coverage scenario, considering the different area importance and the weighted quality of captured image. |
| Jesus et al. [5] | X | X | – | – | Proposal of metrics to QoM assement and optimization in WVSN for area coverage. The QoM model is realistic and flexible to guide (re)deployment. |
| Scott et al. [16] | X | X | – | – | Occlusion-aware area coverage with aerial sensing quality, providing satisfactory spatial resolution subject to the energy constraints of UAVs. |
| Costa et al. [17] | – | X | – | X | Selection of redundant visual nodes for enhanced resistance to visual failures, considering occlusion caused by obstacles modeled by lines. |
| Jesus et al. [11] | – | X | – | X | Selection of faultless visual nodes based on the amount of monitored area, considering occlusion caused by mobile obstacles modeled by rectangles. |
| Andrade and Nogueira [18] | – | – | X | – | Petri net-based approach for modeling and analysis of dependability on IoT networks for disaster recovery. |
| Silva et al. [19] | – | – | X | – | Integrative methodology for dependability evaluation of industrial WSN, based on fault tree analysis, considering hardware and communication failures. |
| Costa et al. [20] | – | – | X | X | Integrative methodology for dependability evaluation of WVSN, based on fault tree analysis, considering hardware, communication and visual failures. |
| Jesus et al. [10] | – | – | X | X | Automated integrative methodology for dependability evaluation of WVSN, based on fault tree analysis, considering hardware, communication and visual failures. |
| Proposed approach | X | X | X | X | Automated integrative methodology for dependability evaluation of WVSN, based on fault tree analysis, considering hardware, communication and visual failures, related to occlusion and QoM. |
| PRR | Failure Probability | Fuzzy Function Parameters () | |
|---|---|---|---|
| 0–50% | Down link | (0, 0, 0, 0) | ∞ |
| 50–60% | Very High | (0.94, 0.95, 1, 1) | |
| 60–70% | High | (0.865, 0.875, 0.925, 0.935) | |
| 70–80% | Reasonably High | (0.77, 0.80, 0.85, 0.86) | |
| 80–90% | Moderate | (0.715, 0.725, 0.775, 0.785) | |
| 90–95% | Reasonably Low | (0.64, 0.65, 0.70, 0.71) | |
| 95–98% | Low | (0.565, 0.575, 0.625, 0.635) | |
| 98–100% | Very Low | (0.5, 0.5, 0.55, 0.56) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jesus, T.C.; Portugal, P.; Costa, D.G.; Vasques, F. A Comprehensive Dependability Model for QoM-Aware Industrial WSN When Performing Visual Area Coverage in Occluded Scenarios. Sensors 2020, 20, 6542. https://doi.org/10.3390/s20226542
Jesus TC, Portugal P, Costa DG, Vasques F. A Comprehensive Dependability Model for QoM-Aware Industrial WSN When Performing Visual Area Coverage in Occluded Scenarios. Sensors. 2020; 20(22):6542. https://doi.org/10.3390/s20226542
Chicago/Turabian StyleJesus, Thiago C., Paulo Portugal, Daniel G. Costa, and Francisco Vasques. 2020. "A Comprehensive Dependability Model for QoM-Aware Industrial WSN When Performing Visual Area Coverage in Occluded Scenarios" Sensors 20, no. 22: 6542. https://doi.org/10.3390/s20226542
APA StyleJesus, T. C., Portugal, P., Costa, D. G., & Vasques, F. (2020). A Comprehensive Dependability Model for QoM-Aware Industrial WSN When Performing Visual Area Coverage in Occluded Scenarios. Sensors, 20(22), 6542. https://doi.org/10.3390/s20226542








