Voltage-Mode Multifunction Biquad Filter and Its Application as Fully-Uncoupled Quadrature Oscillator Based on Current-Feedback Operational Amplifiers
Abstract
:1. Introduction
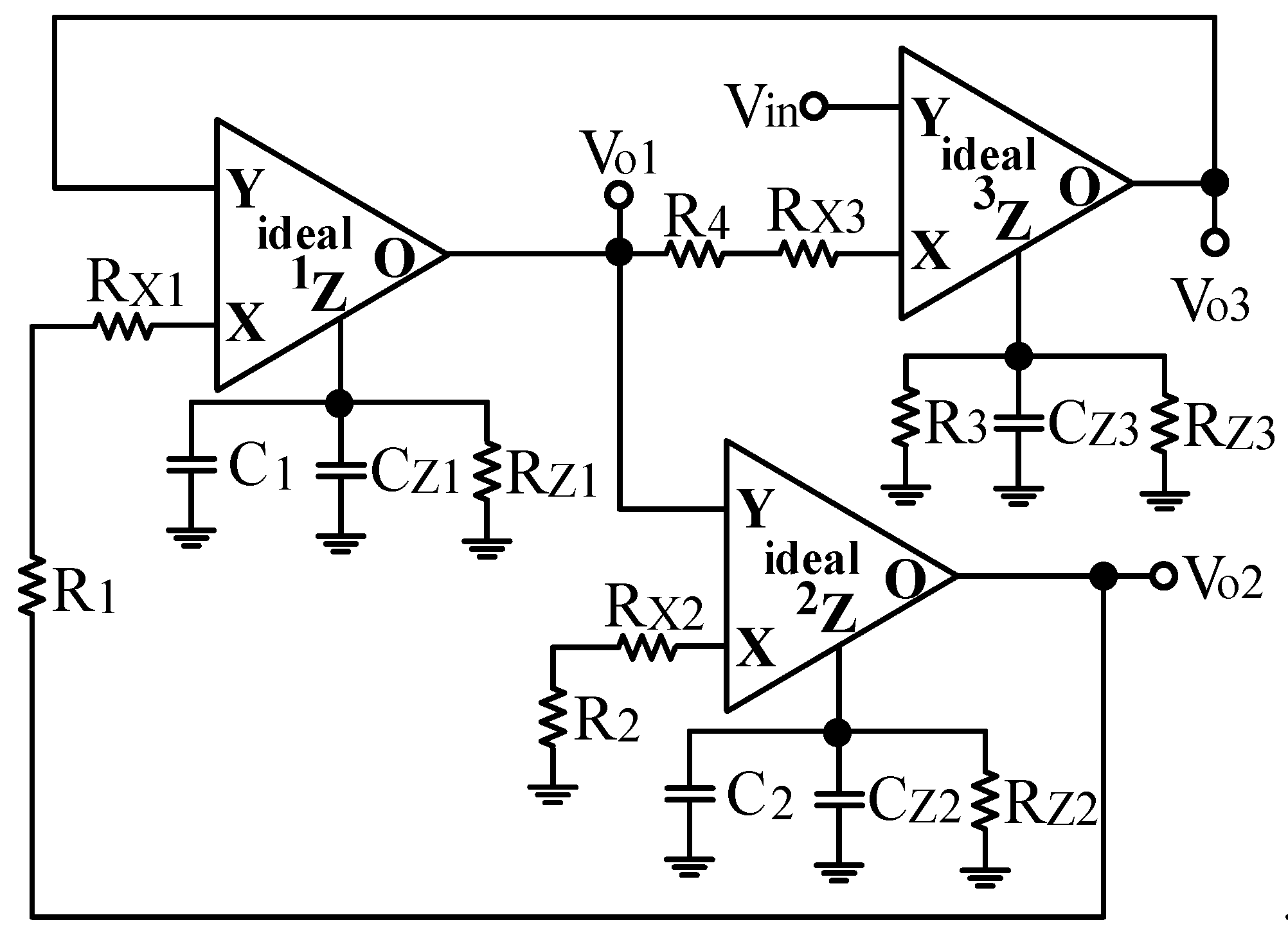
2. Proposed VM CFOA-Based Circuits
2.1. Proposed VM CFOA-Based Multifunction Biquad Filter
2.2. Proposed Fully-Uncoupled VM QO
3. Simulation and Experimental Results
3.1. Test Setup
3.2. Effective Frequency Ranges of AD844AN-Based Circuit
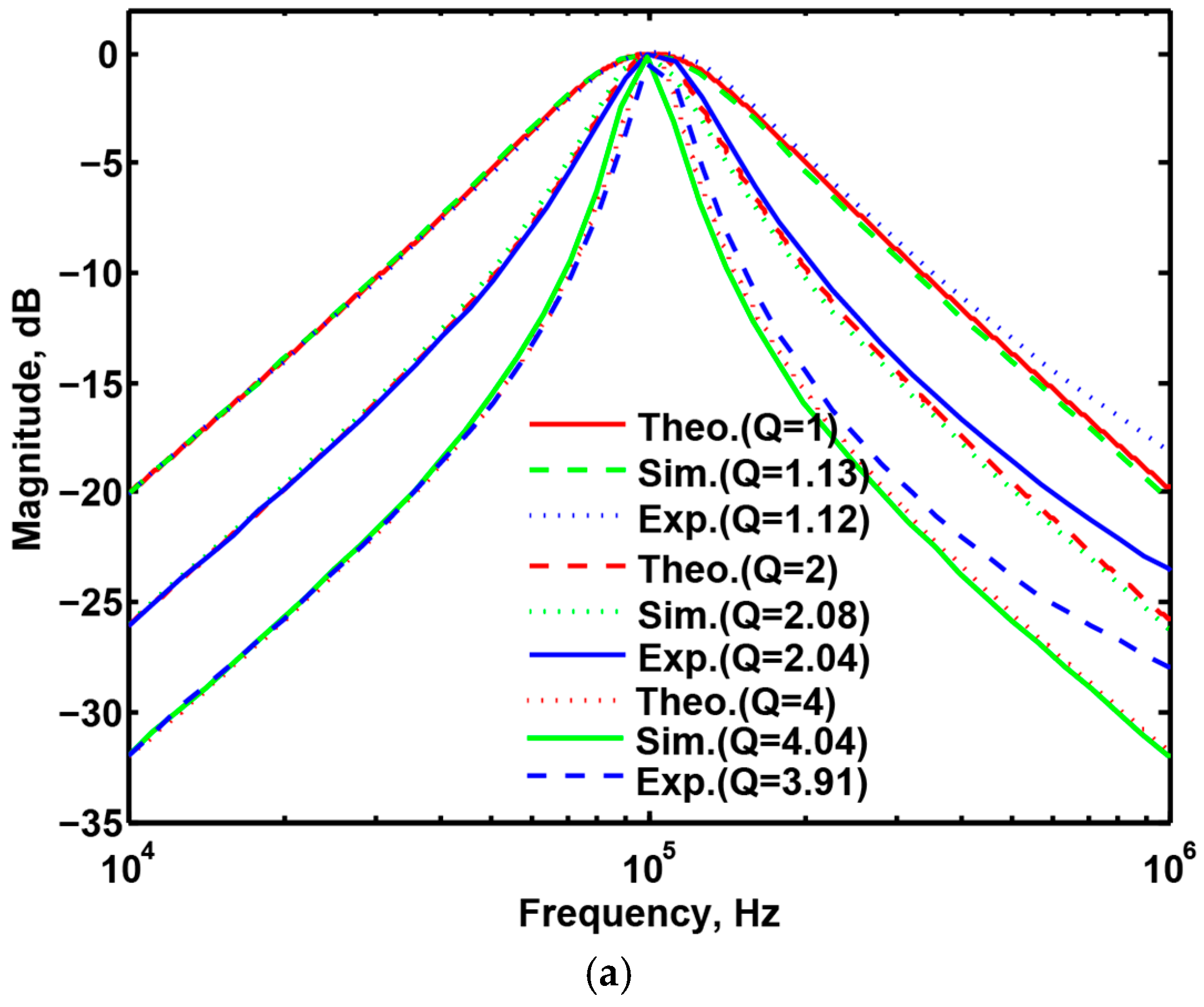
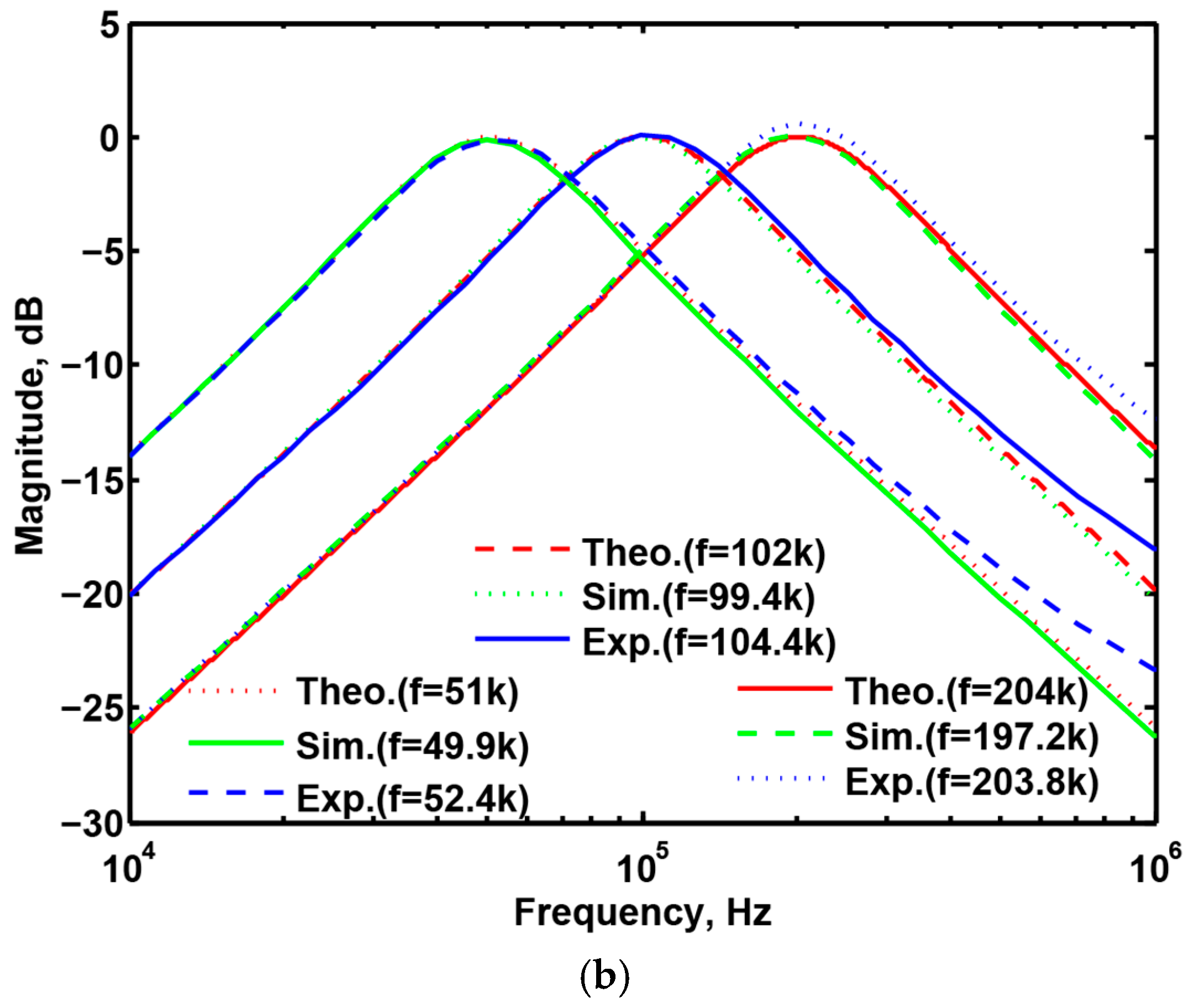
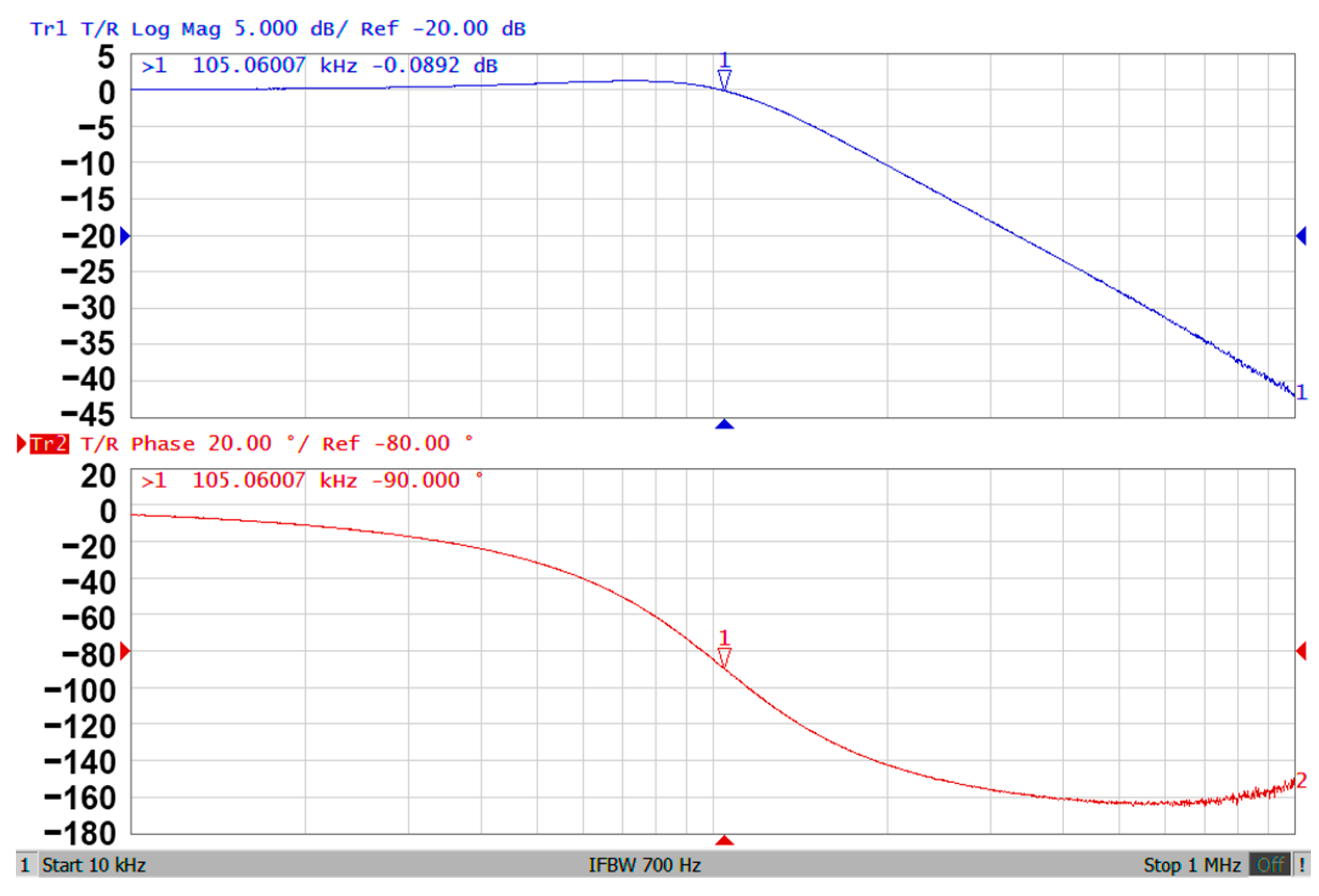
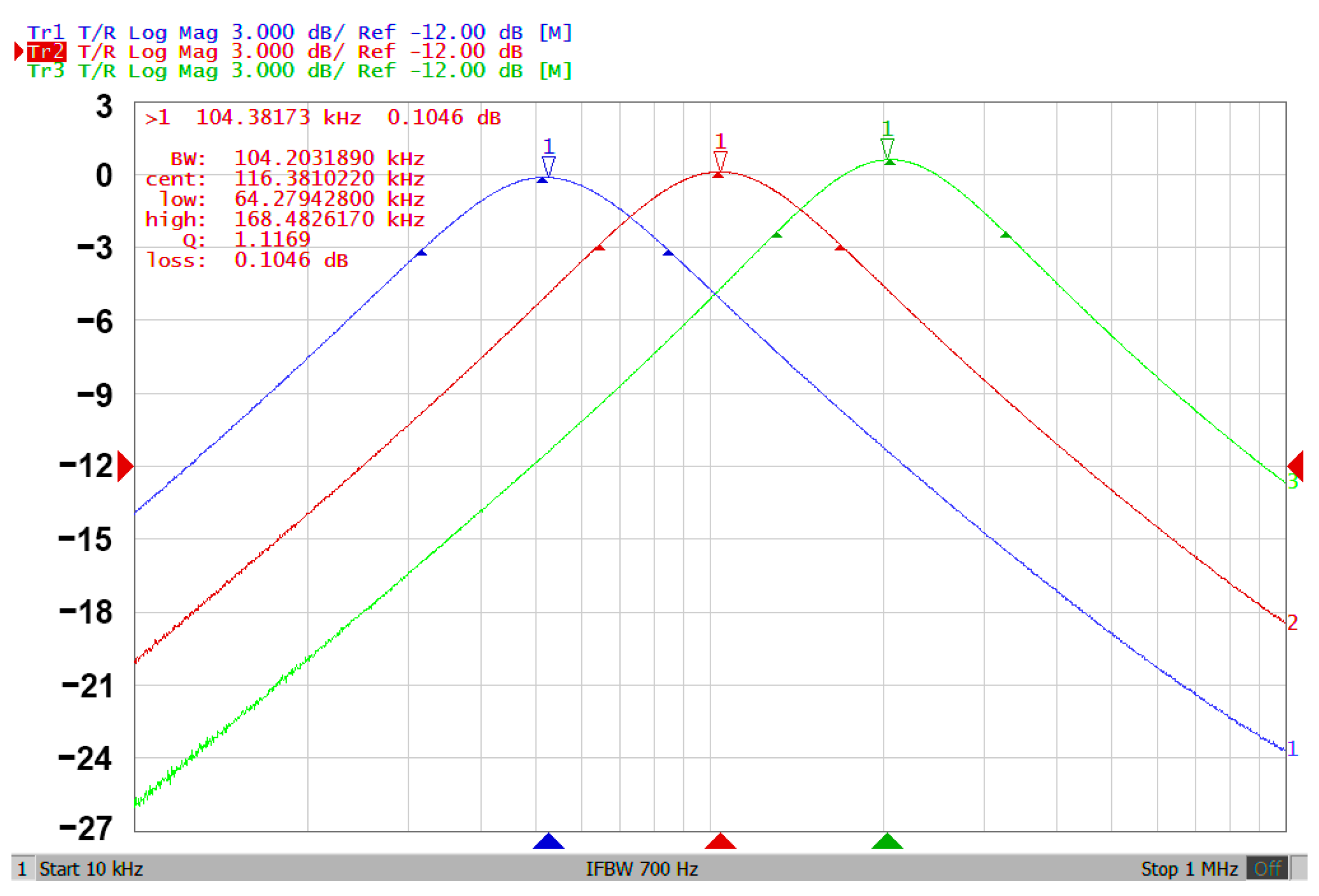
3.3. Proposed CFOA-Based VM Multifunction Biquad Filter
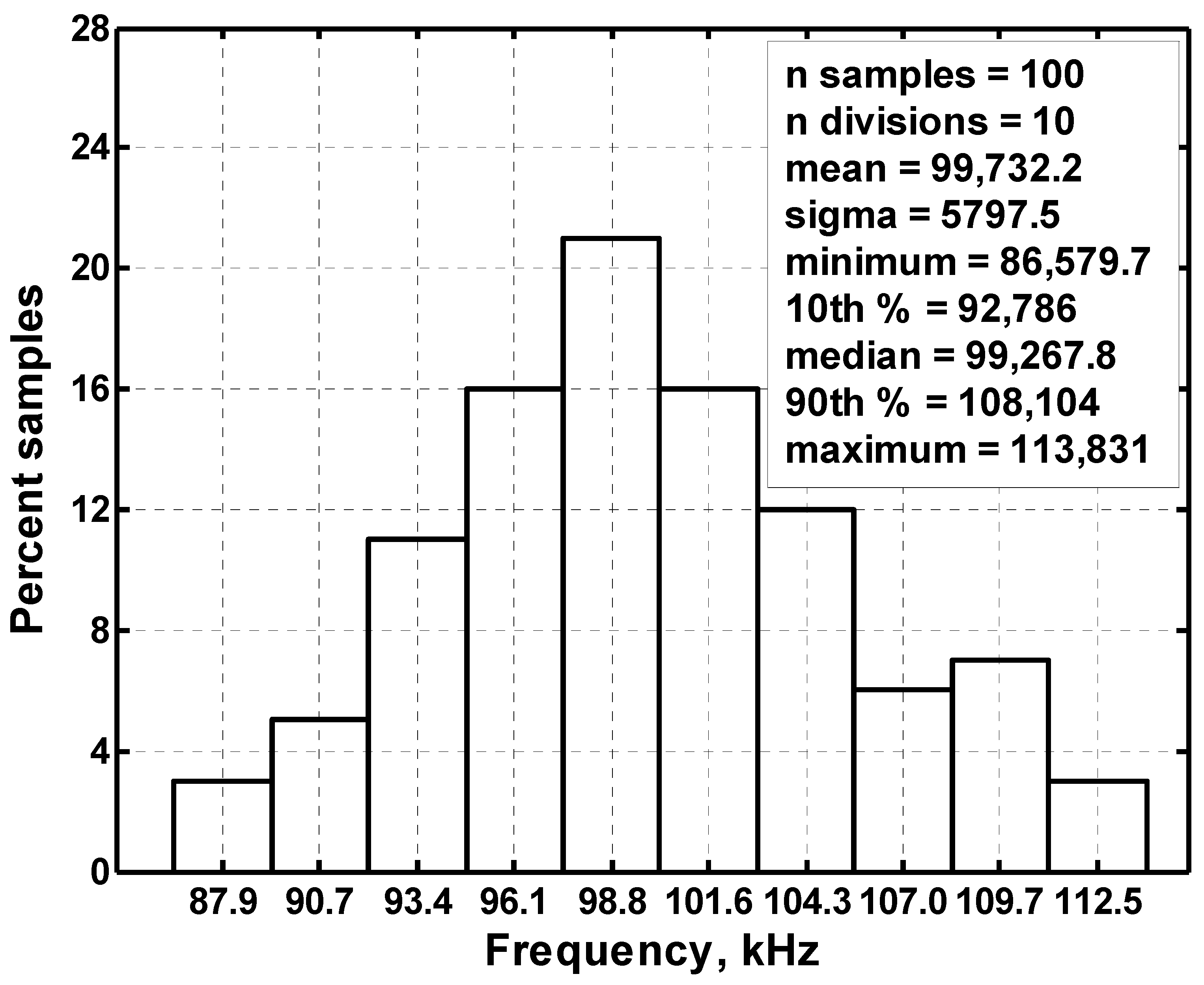
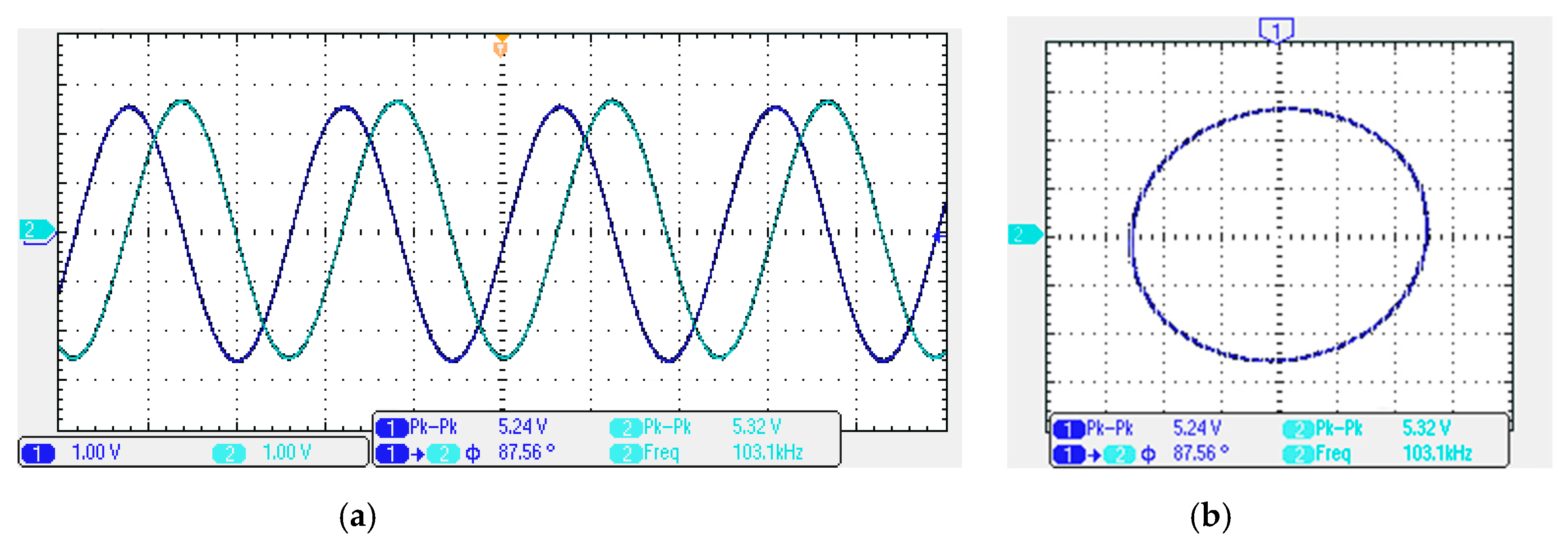
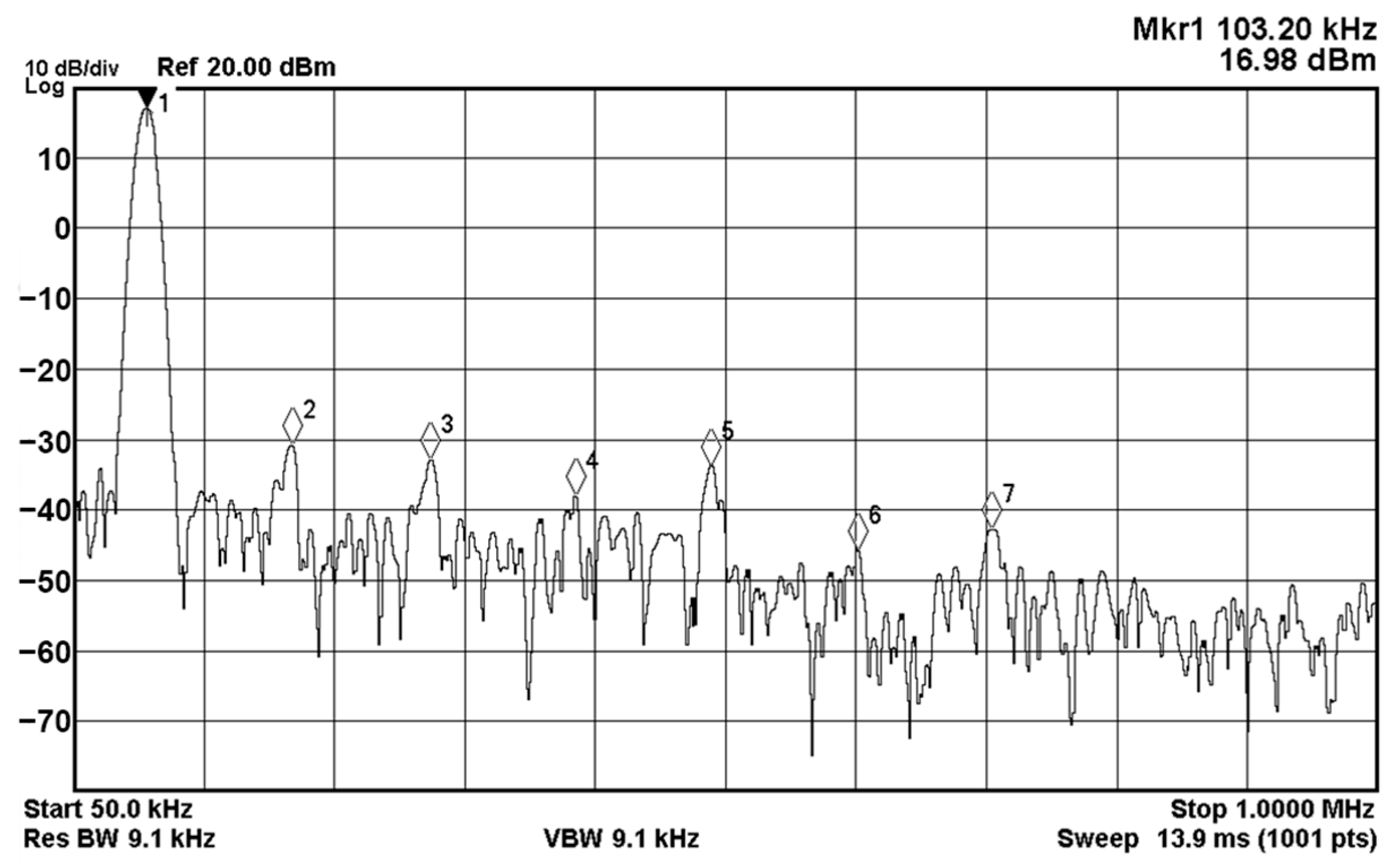
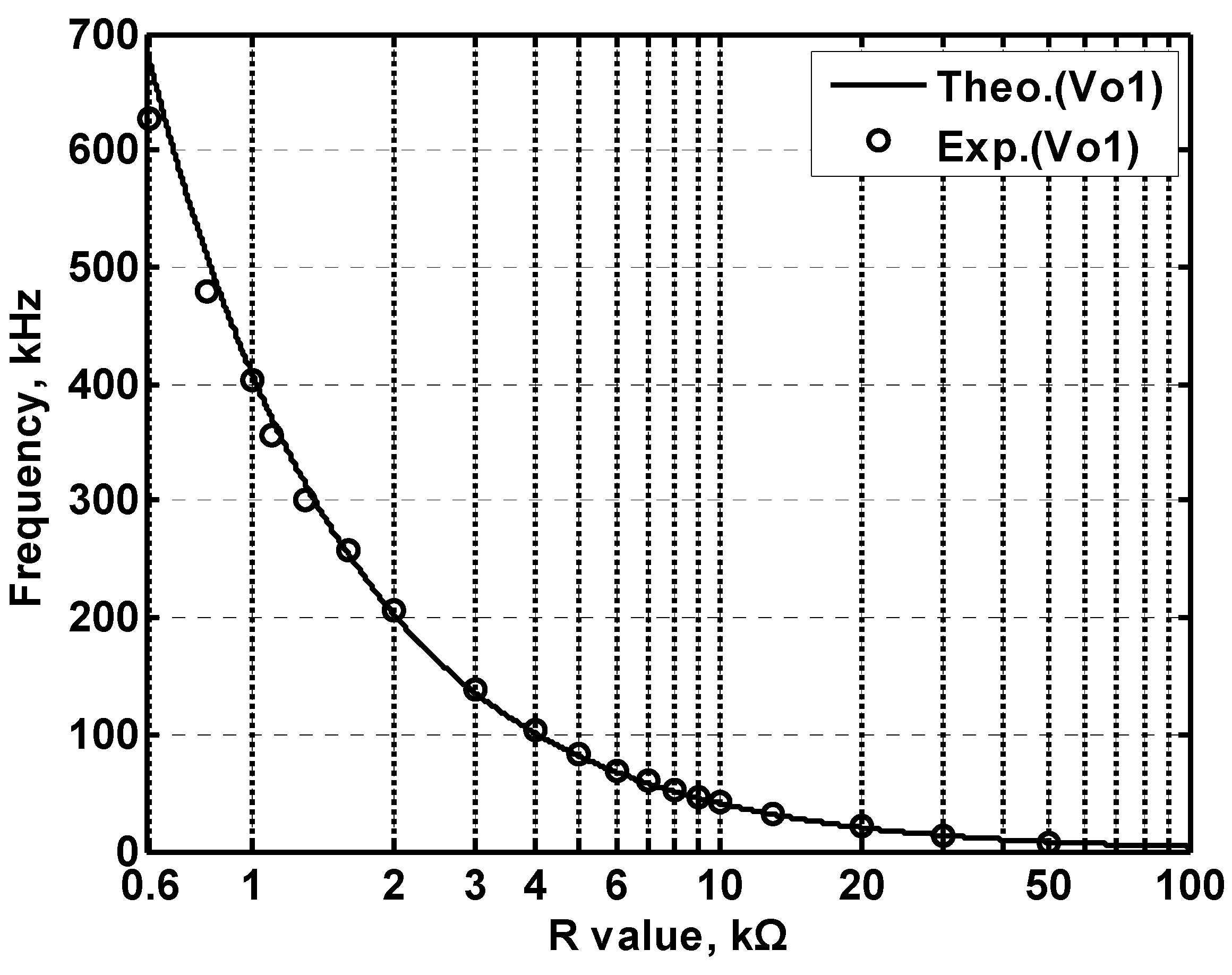
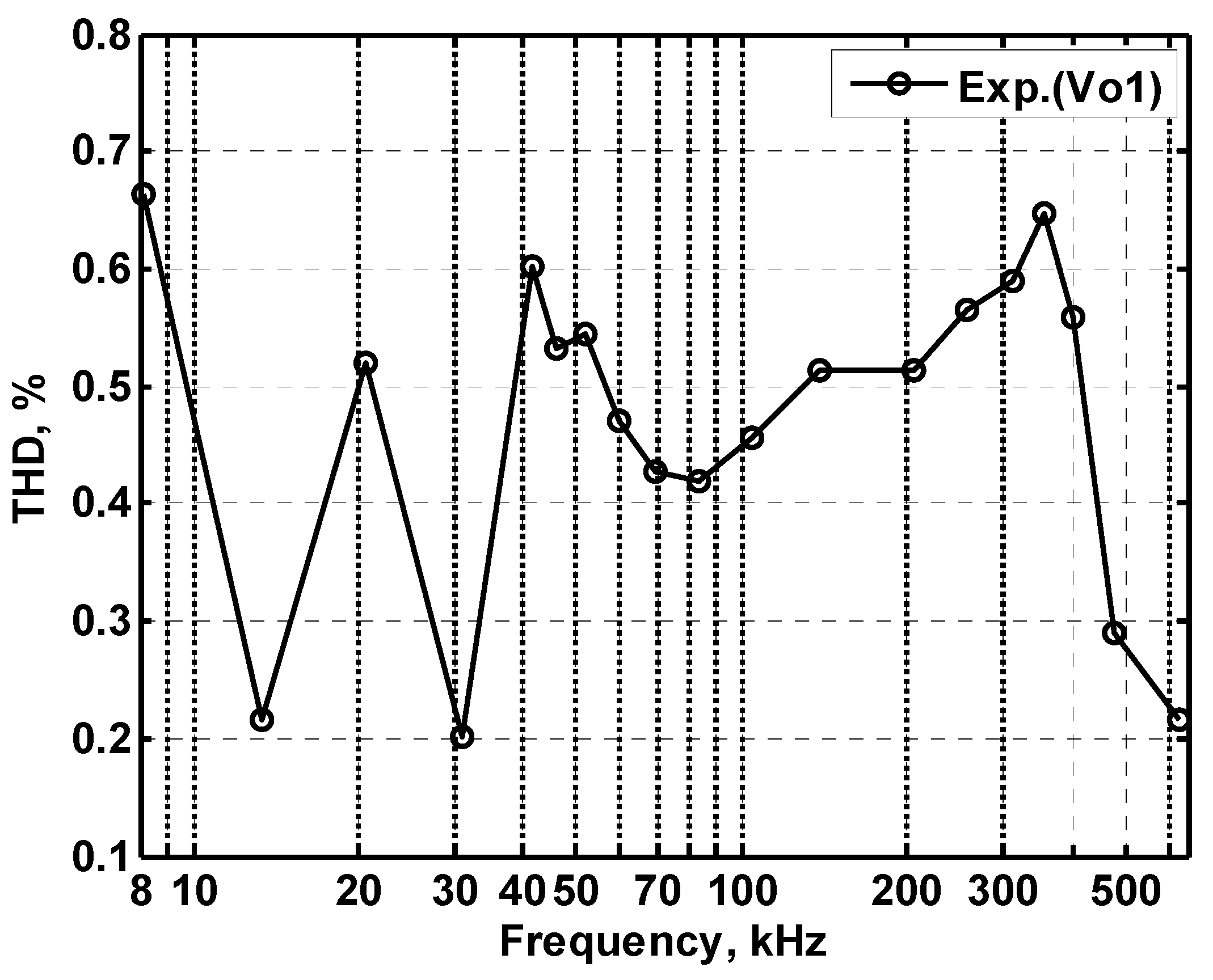
3.4. Proposed CFOA-Based VM QO Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tran, H.D.; Wang, H.Y.; Lin, M.C.; Nguyen, Q.M. Synthesis of cascadable DDCC-based universal filter using NAM. Appl. Sci. 2015, 5, 320–343. [Google Scholar] [CrossRef]
- Herencsar, N.; Koton, J.; Hanak, P. Universal voltage conveyor and its novel dual-output fully-cascadable VM APF application. Appl. Sci. 2017, 7, 307. [Google Scholar] [CrossRef]
- Safari, L.; Barile, G.; Ferri, G.; Stornelli, V. A new low-voltage low-power dual-mode VCII-based SIMO universal filter. Electronics 2019, 8, 765. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.F.; Chen, H.P.; Ku, Y.; Lin, Y.C. Versatile tunable voltage-mode biquadratic filter and its application in quadrature oscillator. Sensors 2019, 19, 2349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, H.Y.; Tran, H.D.; Nguyen, Q.M.; Yin, L.T.; Liu, C.Y. Derivation of oscillators from biquadratic band pass filters using circuit transformations. Appl. Sci. 2014, 4, 482–492. [Google Scholar] [CrossRef]
- Sotner, R.; Jerabek, J.; Langhammer, L.; Dvorak, J. Design and analysis of CCII-Based oscillator with amplitude stabilization employing optocouplers for linear voltage control of the output frequency. Electronics 2018, 7, 157. [Google Scholar] [CrossRef] [Green Version]
- Ullah, F.; Liu, Y.; Li, Z.; Wang, X.; Sarfraz, M.M.; Zhang, H. A bandwidth-enhanced differential LC-voltage controlled oscillator (LC-VCO) and superharmonic coupled quadrature VCO for K-band applications. Electronics 2018, 7, 127. [Google Scholar] [CrossRef] [Green Version]
- Márquez, A.; Pérez-Bailón, J.; Calvo, B.; Medrano, N.; Martínez, P.A. A CMOS self-contained quadrature signal generator for SoC impedance spectroscopy. Sensors 2018, 18, 1382. [Google Scholar] [CrossRef] [Green Version]
- Jaikla, W.; Adhan, S.; Suwanjan, P.; Kumngern, M. Current/voltage controlled quadrature sinusoidal oscillators for phase sensitive detection using commercially available IC. Sensors 2020, 20, 1319. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.F.; Chen, H.P.; Ku, Y.; Lee, C.L. Versatile voltage-mode biquadratic filter and quadrature oscillator using four OTAs and two grounded capacitors. Electronics 2020, 9, 1493. [Google Scholar] [CrossRef]
- Ibrahim, M.A.; Minaei, S.; Kuntman, H. A 22.5 MHz current-mode KHN biquad using differential voltage current conveyor and grounded passive element. AEU Int. J. Electron. Commun. 2005, 59, 311–318. [Google Scholar] [CrossRef]
- Liu, S.I.; Wu, D.S. New current-feedback amplifier-based universal biquadratic filter. IEEE Trans. Instrum. Meas. 1995, 44, 915–917. [Google Scholar]
- Horng, J.W. New configuration for realizing universal voltage-mode filter using two current-feedback amplifiers. IEEE Trans. Instrum. Meas. 2000, 49, 1043–1045. [Google Scholar] [CrossRef]
- Tangsrirat, W.; Surakampontorn, W. Single-resistance-controlled quadrature oscillator and universal biquad filter using CFOAs. AEU Int. J. Electron. Commun. 2009, 63, 1080–1086. [Google Scholar] [CrossRef]
- Shah, N.A.; Iqbal, S.Z.; Rather, M.F. Versatile voltage-mode CFA-based universal filter. AEU Int. J. Electron. Commun. 2005, 59, 192–194. [Google Scholar] [CrossRef]
- Shan, N.A.; Rather, M.F.; Iqbal, S.Z. CFA-based three input and two outputs voltage-mode universal filer. Indian J. Pure Appl. Phy. 2005, 43, 636–639. [Google Scholar]
- Singh, V.K.; Singh, A.K.; Bhaskar, D.R.; Senani, R. New universal biquads employing CFOAs. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 1299–1303. [Google Scholar] [CrossRef]
- Horng, J.W. Voltage-mode universal biquad with five inputs and two outputs using two current feedback amplifiers. Indian J. Eng. Mater. Sci. 2013, 20, 87–91. [Google Scholar]
- Chang, C.M.; Hwang, C.S.; Tu, S.H. Voltage-mode notch, lowpass and bandpass filter using current-feedback amplifiers. Electron. Lett. 1994, 30, 2022–2023. [Google Scholar] [CrossRef]
- Shah, N.A.; Malik, M.A. Multifunction filter using current feedback amplifiers. Frequenz 2005, 59, 264–267. [Google Scholar] [CrossRef]
- Nikoloudis, S.; Psychalinos, C. Multiple input single output universal biquad filter with current feedback operational amplifiers. Circuits Syst. Signal Process. 2010, 29, 1167–1180. [Google Scholar] [CrossRef]
- Topaloglu, S.; Sagbas, M.; Anday, F. Three-input single-output second-order filters using current-feedback amplifiers. AEU Int. J. Electron. Commun. 2012, 66, 683–686. [Google Scholar] [CrossRef]
- Singh, A.K.; Senani, R. CFOA-based state-variable biquad and its high-frequency compensation. IEICE Electron. Express 2005, 2, 232–238. [Google Scholar] [CrossRef] [Green Version]
- Horng, J.W.; Lee, M.H. High input impedance voltage-mode lowpass, bandpass and highpass filter using current-feedback amplifiers. Electron. Lett. 1997, 33, 947–948. [Google Scholar] [CrossRef]
- Shan, N.A.; Malik, M.A. High input impedance voltage-mode lowpass, bandpass, highpass and notch filter using current feedback amplifiers. Indian J. Eng. Mater. Sci. 2005, 12, 278–280. [Google Scholar]
- Shan, N.A.; Malik, M.A. New high input impedance voltage-mode lowpass, bandpass and highpass filter using current feedback amplifiers. J. Circuits Syst. Comp. 2005, 14, 1037–1043. [Google Scholar]
- Wang, S.F.; Chen, H.P.; Ku, Y.; Chen, P.Y. A CFOA-based voltage-mode multifunction biquadratic filter and a quadrature oscillator using the CFOA-based biquadratic filter. Appl. Sci. 2019, 9, 2304. [Google Scholar] [CrossRef] [Green Version]
- Soliman, A.M. Applications of the current feedback operational amplifiers. Analog Integr. Circuits Process. 1996, 11, 265–302. [Google Scholar] [CrossRef]
- AD844: 60 MHz, 2000 V/μs, Monolithic Op Amp with Quad Low Noise Data Sheet (Rev. G). May 2017. Available online: www.linear.com (accessed on 29 April 2019).
- Bhaskar, D.R.; Gupta, S.S.; Senani, R. New CFOA-based sinusoidal oscillators retaining independent control of oscillation frequency even under the influence of parasitic impedances. Analog Integr. Circuits Process. 2012, 73, 427–437. [Google Scholar] [CrossRef]
- Senani, R.; Singh, V.K. Novel single-resistance-controlled-oscillator configuration using current-feedback-amplifiers. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1996, 43, 698–700. [Google Scholar] [CrossRef]
- Bhaskar, D.R.; Senani, R. New CFOA-based single-element-controlled sinusoidal oscillators. IEEE Trans. Instrum. Meas. 2006, 55, 2014–2021. [Google Scholar] [CrossRef]
- Andreani, P.; Wang, X. On the phase-noise and phase-error performances of multiphase LC CMOS VCOs. IEEE J. Solid-State Circuit 2004, 39, 1883–1893. [Google Scholar] [CrossRef] [Green Version]
- Razavi, B. A study of phase noise in CMOS oscillators. IEEE J. Solid State Circuits 1996, 31, 331–343. [Google Scholar] [CrossRef] [Green Version]















| Parameter | (i) | (ii) | (iii) | (iv) | (v) | (vi) | (vii) | Simul./Meas. | Supply (V) | Technology |
|---|---|---|---|---|---|---|---|---|---|---|
| Ref. [12] | yes | no | no | no | yes | no | no | Meas. | N/A | AD844 ICs |
| Ref. [13] | yes | no | no | no | yes | no | no | Meas. | N/A | AD844 ICs |
| Ref. [14] | yes | no | no | no | yes | no | no | Simul. | ±12 | AD844 model |
| Ref. [15] | yes | no | yes | no | yes | no | no | Simul. | N/A | AD844 model |
| Ref. [16] | yes | no | no | no | yes | no | no | Simul. | N/A | AD844 model |
| Ref. [17] | no | yes | yes | no | yes | no | no | Both | ±12 | AD844 ICs |
| Ref. [18] | yes | no | no | no | yes | no | no | Meas. | N/A | AD844 ICs |
| Ref. [19] | yes | yes | yes | no | yes | no | no | Meas. | N/A | AD844 ICs |
| Ref. [20] | yes | no | no | no | no | no | no | Simul. | N/A | AD844 model |
| Ref. [21] | no | yes | no | yes | yes | no | no | Meas. | ±5 | AD844 ICs |
| Ref. [22] | yes | yes | no | yes | yes | no | no | Simul. | ±5 | AD844 model |
| Ref. [23] | no | yes | yes | yes | yes | no | no | Simul. | N/A | AD844 model |
| Ref. [24] | yes | no | yes | yes | no | no | no | Simul. | N/A | AD844 model |
| Ref. [25] | no | yes | yes | yes | yes | no | no | Both | N/A | AD844 ICs |
| Ref. [26] | yes | yes | yes | yes | no | no | no | Simul. | ±12 | AD844 model |
| Ref. [27] | yes | yes | yes | yes | yes | no | no | Both | ±6 | AD844 ICs |
| Proposed | yes | yes | yes | yes | yes | yes | yes | Both | ±6 | AD844 ICs |
| Parameter | Ref. [27] | Proposed |
|---|---|---|
| Number of active and passive components of the biquad filter | 3 CFOAs, 3 R, 2 C | 3 CFOAs, 4 R, 2 C |
| Number of active and passive components of the quadrature oscillator | 3 CFOAs, 4 R, 2 C | 3 CFOAs, 4 R, 2 C |
| Center frequency of the biquad filter (kHz) | 39.79 | 102 |
| Independent tuning of the filter control factor parameters ωo and Q | no | yes |
| Fully-uncoupled tuning of the oscillator parameters CO and FO | no | yes |
| Constant amplitude ratio of quadrature waveforms | no | yes |
| Measured the oscillation frequency range (kHz) | N/A | 8.16~628 |
| Measured the total harmonic distortion of the quadrature oscillator (%) | N/A | <0.7 |
| Measured the power dissipation (mW) | 180 | 168 |
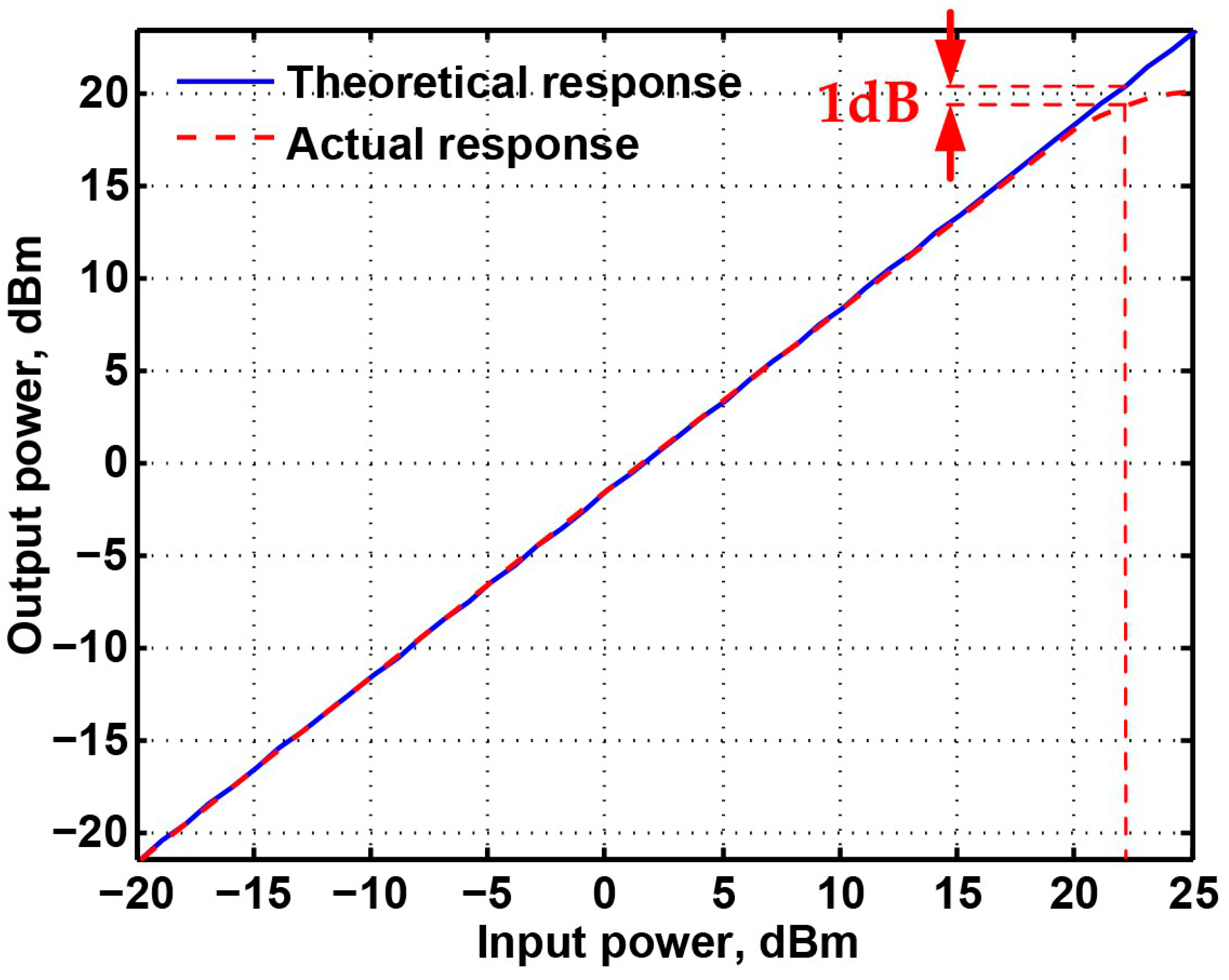
| Measured the input one-dB power gain compression point (dBm) | 12 | 22 |
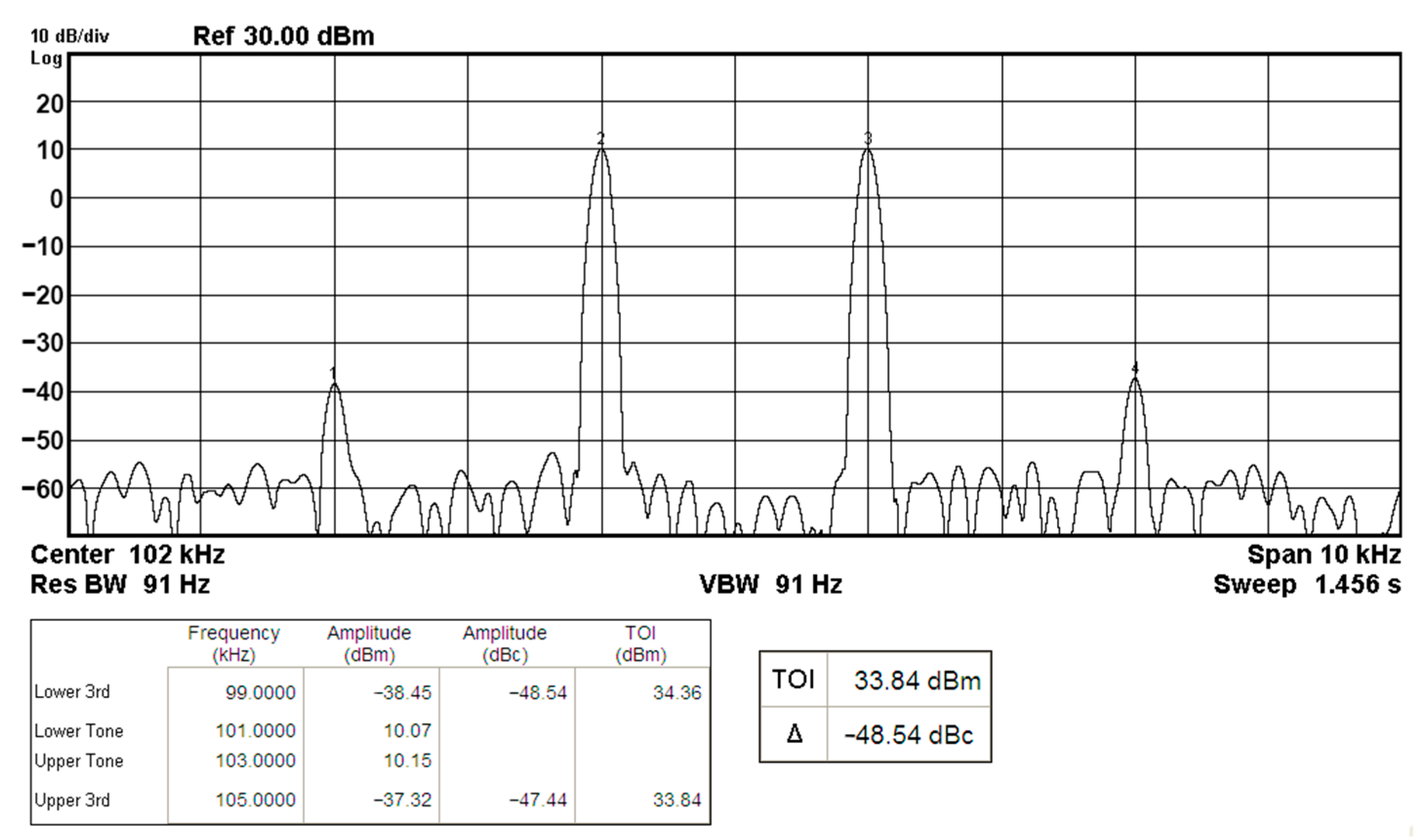
| Measured the third-order intermodulation distortion point (dBm) | 21.59 | 33.84 |
| Supply (V) | Band-Pass Filter (Vo1) | Low-Pass Filter (Vo2) | Band-Reject Filter (Vo3) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Power (dBm) | PD (mW) | P1dB (dBm) | Power (dBm) | PD (mW) | P1dB (dBm) | Power(dBm) | PD (mW) | P1dB (dBm) | ||||
| Input | Output | Input | Output | Input | Output | |||||||
| ±6 | −20 | −21.56 | 264 | 22 | −20 | −21.38 | 264 | 21 | −20 | −21.19 | 264 | 22 |
| −10 | −11.53 | 264 | −10 | −11.32 | 264 | −10 | −11.15 | 264 | ||||
| 0 | −1.49 | 264 | 0 | −1.26 | 264 | 0 | −1.1 | 264 | ||||
| 10 | 8.46 | 300 | 10 | 8.67 | 300 | 10 | 9 | 300 | ||||
| 20 | 18.16 | 396 | 20 | 18.15 | 396 | 20 | 18.72 | 408 | ||||
| 21 | 18.91 | 408 | 21 | 18.79 | 408 | 21 | 19.42 | 432 | ||||
| 22 | 19.46 | 420 | 22 | 19.25 | 408 | 22 | 19.82 | 444 | ||||
| 23 | 19.8 | 432 | 23 | 19.47 | 420 | 23 | 20.11 | 456 | ||||
| 24 | 20.02 | 432 | 24 | 19.58 | 420 | 24 | 20.33 | 456 | ||||
| 25 | 20.24 | 444 | 25 | 19.65 | 420 | 25 | 20.52 | 456 | ||||
| ±9 | −20 | −21.6 | 396 | 26.8 | −20 | −21.3 | 396 | 26.1 | −20 | −21.23 | 396 | 26.3 |
| −10 | −11.56 | 396 | −10 | −11.26 | 396 | −10 | −11.19 | 396 | ||||
| 0 | −1.5 | 396 | 0 | −1.22 | 396 | 0 | −1.12 | 396 | ||||
| 10 | 8.44 | 450 | 10 | 8.68 | 450 | 10 | 8.97 | 450 | ||||
| 20 | 18.35 | 666 | 20 | 18.4 | 666 | 20 | 19.02 | 684 | ||||
| 24 | 22.26 | 846 | 24 | 22.2 | 846 | 24 | 22.92 | 864 | ||||
| 25 | 23.18 | 900 | 25 | 23.09 | 900 | 25 | 23.76 | 918 | ||||
| 26 | 23.92 | 936 | 26 | 23.77 | 936 | 26 | 24.23 | 972 | ||||
| 26.8 | 24.2 | 972 | 26.1 | 23.8 | 936 | 26.3 | 24.3 | 972 | ||||
| 27 | 24.28 | 990 | 27 | 24.11 | 972 | 27 | 24.51 | 990 | ||||
| ±12 | −20 | −21.54 | 528 | 28.5 | −20 | −21.26 | 528 | 27.7 | −20 | −21.15 | 528 | 27.5 |
| −10 | −11.5 | 528 | −10 | −11.23 | 528 | −10 | −11.11 | 528 | ||||
| 0 | −1.46 | 528 | 0 | −1.22 | 528 | 0 | −1.06 | 528 | ||||
| 10 | 8.49 | 600 | 10 | 8.7 | 600 | 10 | 9.04 | 600 | ||||
| 20 | 18.35 | 888 | 20 | 18.46 | 888 | 20 | 19.04 | 912 | ||||
| 25 | 23.3 | 1224 | 25 | 23.2 | 1224 | 25 | 24.08 | 1272 | ||||
| 26 | 24.26 | 1320 | 26 | 24.03 | 1320 | 26 | 24.92 | 1368 | ||||
| 27 | 25.12 | 1416 | 27 | 25.1 | 1416 | 27 | 25.35 | 1440 | ||||
| 28 | 25.8 | 1608 | 27.7 | 25.58 | 1536 | 27.5 | 25.5 | 1464 | ||||
| 28.5 | 26 | 1680 | 28 | 25.7 | 1584 | 28 | 25.72 | 1512 | ||||
| ±15 | −20 | −21.48 | 660 | 28.8 | −20 | −21.17 | 660 | 28 | −20 | −21.8 | 630 | 27.5 |
| −10 | −11.36 | 660 | −10 | −11.14 | 660 | −10 | −11.04 | 630 | ||||
| 0 | −1.41 | 690 | 0 | −1.1 | 690 | 0 | −0.99 | 660 | ||||
| 10 | 8.53 | 750 | 10 | 8.82 | 750 | 10 | 9.1 | 750 | ||||
| 20 | 18.43 | 1110 | 20 | 18.57 | 1110 | 20 | 19.11 | 1110 | ||||
| 25 | 23.35 | 1560 | 25 | 23.34 | 1560 | 25 | 23.98 | 1590 | ||||
| 26 | 24.33 | 1680 | 26 | 24.36 | 1680 | 26 | 24.63 | 1710 | ||||
| 27 | 25.15 | 1920 | 27 | 25.16 | 1830 | 27 | 25.4 | 1800 | ||||
| 28 | 25.9 | 2010 | 28 | 25.8 | 2010 | 27.5 | 25.7 | 1830 | ||||
| 28.8 | 26.4 | 2160 | 28.2 | 25.9 | 2040 | 28 | 25.8 | 1890 | ||||
| Quadrature Output Voltage Vo1 | Quadrature Output Voltage Vo2 | ||||
|---|---|---|---|---|---|
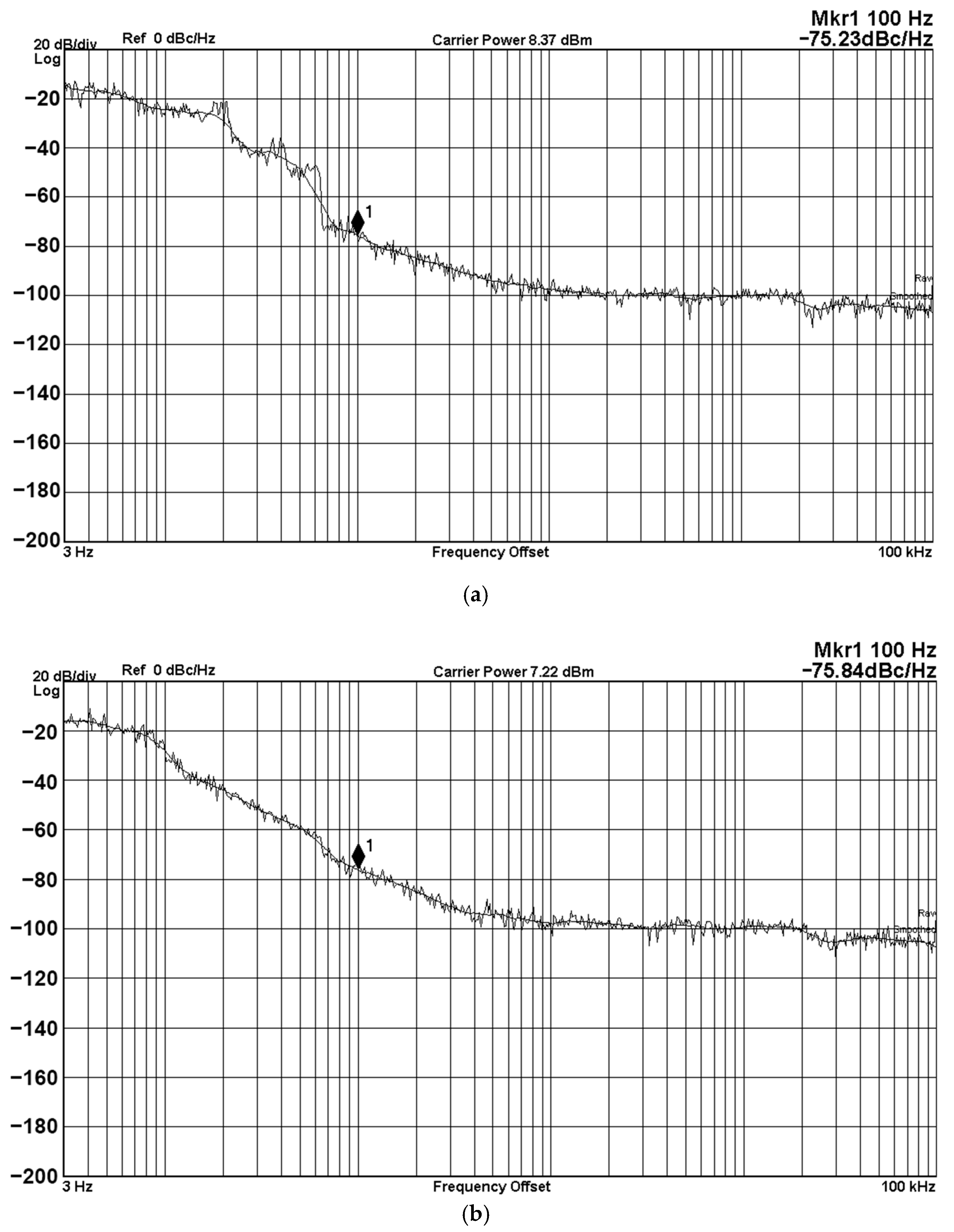
| fo (kHz) | Phase Noise (dBc/Hz) | FoM (dBc/Hz) | fo (kHz) | Phase Noise (dBc/Hz) | FoM (dBc/Hz) |
| 8.1 | 85.23 | 98.5 | 8.1 | 87.6 | 101.2 |
| 13.3 | 83.36 | 103.9 | 13.3 | 84.35 | 102.2 |
| 20.7 | 84.27 | 105.7 | 20.7 | 80.59 | 102.3 |
| 30.9 | 84.98 | 110.0 | 30.9 | 84.61 | 109.8 |
| 41.6 | 83.56 | 111.2 | 41.6 | 81.87 | 109.7 |
| 46.1 | 84.09 | 112.4 | 46.1 | 84.39 | 113.1 |
| 52.1 | 82.84 | 112.4 | 52.1 | 82.66 | 112.4 |
| 59.6 | 81.95 | 112.7 | 59.6 | 83.29 | 114.2 |
| 69.3 | 80.74 | 112.8 | 69.3 | 81.76 | 114.0 |
| 83.4 | 92.25 | 126.5 | 83.4 | 82.21 | 116.0 |
| 104.1 | 75.23 | 110.8 | 104.1 | 74.24 | 110.0 |
| 138 | 68.28 | 120.8 | 138 | 65.43 | 103.6 |
| 205.8 | 62.26 | 118.4 | 205.8 | 76.57 | 118.2 |
| 256.7 | 47.09 | 90.3 | 256.7 | 76.48 | 120.1 |
| 300.5 | 75.29 | 119.9 | 300.5 | 71.3 | 116.3 |
| 356.9 | 73.92 | 119.9 | 356.9 | 53.93 | 100.4 |
| 402.7 | 73.54 | 120.7 | 402.7 | 72.43 | 119.9 |
| VDC | Output Voltage Vo1 | Output Voltage Vo2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Phase Noise (dBc/Hz) | Δf (Hz) | PDC (mW) | fo (kHz) | FoM (dBc/Hz) | Phase Noise (dBc/Hz) | Δf (Hz) | PDC (mW) | fo (kHz) | FoM (dBc/Hz) | |
| ±4.5 | 71.41 | 100 | 216 | 102 | 108.4 | 73.46 | 100 | 225 | 102 | 110.2 |
| ±6 | 72.26 | 100 | 300 | 102 | 107.8 | 74.24 | 100 | 300 | 102 | 109.8 |
| ±9 | 72.67 | 100 | 432 | 102 | 106.7 | 76.91 | 100 | 450 | 102 | 110.7 |
| ±12 | 71.9 | 100 | 576 | 102 | 104.6 | 71.6 | 100 | 624 | 102 | 103.9 |
| ±15 | 69.88 | 100 | 720 | 102 | 101.7 | 76.28 | 100 | 780 | 102 | 107.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.-F.; Chen, H.-P.; Ku, Y.; Zhong, M.-X. Voltage-Mode Multifunction Biquad Filter and Its Application as Fully-Uncoupled Quadrature Oscillator Based on Current-Feedback Operational Amplifiers. Sensors 2020, 20, 6681. https://doi.org/10.3390/s20226681
Wang S-F, Chen H-P, Ku Y, Zhong M-X. Voltage-Mode Multifunction Biquad Filter and Its Application as Fully-Uncoupled Quadrature Oscillator Based on Current-Feedback Operational Amplifiers. Sensors. 2020; 20(22):6681. https://doi.org/10.3390/s20226681
Chicago/Turabian StyleWang, San-Fu, Hua-Pin Chen, Yitsen Ku, and Ming-Xiu Zhong. 2020. "Voltage-Mode Multifunction Biquad Filter and Its Application as Fully-Uncoupled Quadrature Oscillator Based on Current-Feedback Operational Amplifiers" Sensors 20, no. 22: 6681. https://doi.org/10.3390/s20226681
APA StyleWang, S.-F., Chen, H.-P., Ku, Y., & Zhong, M.-X. (2020). Voltage-Mode Multifunction Biquad Filter and Its Application as Fully-Uncoupled Quadrature Oscillator Based on Current-Feedback Operational Amplifiers. Sensors, 20(22), 6681. https://doi.org/10.3390/s20226681







