Copper Content Inversion of Copper Ore Based on Reflectance Spectra and the VTELM Algorithm
Abstract
:1. Introduction
2. Data Acquisition and Processing
3. Introduction to Neural Network
3.1. Extreme Learning Machine (ELM)
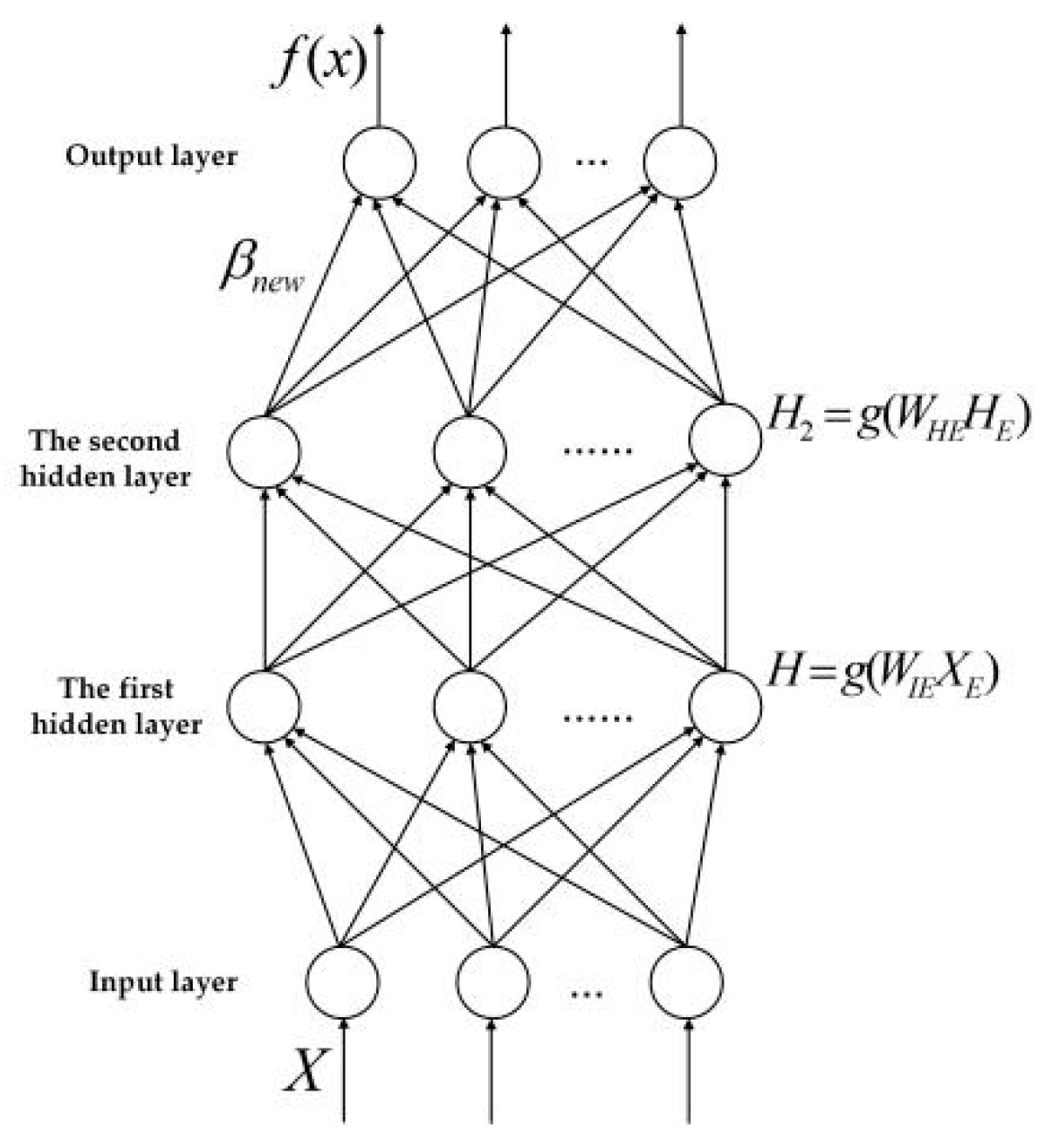
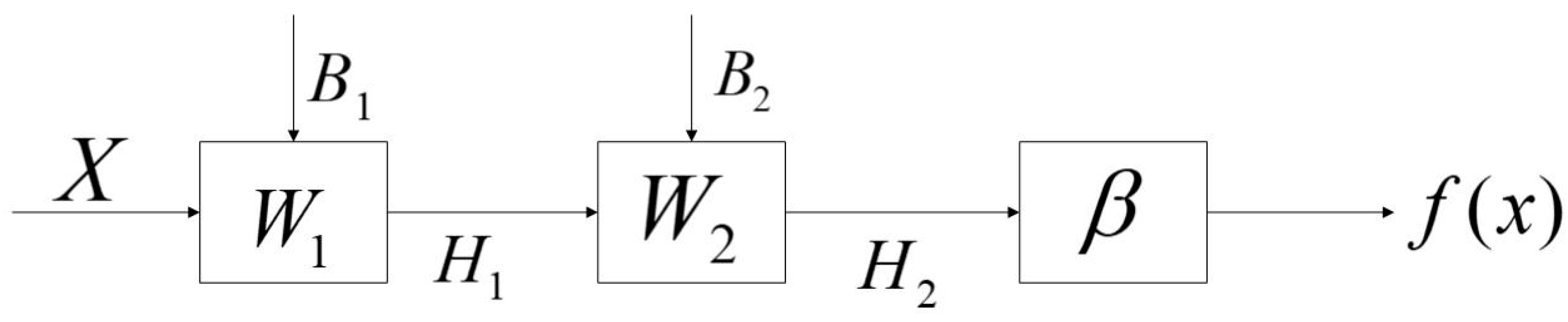
3.2. Two Hidden Layer Extreme Learning Machine (TELM)
3.3. Two Hidden Layer Extreme Learning Machine Algorithm with Variable Hidden Layer Nodes (VTELM)
4. Experimental Results and Discussion
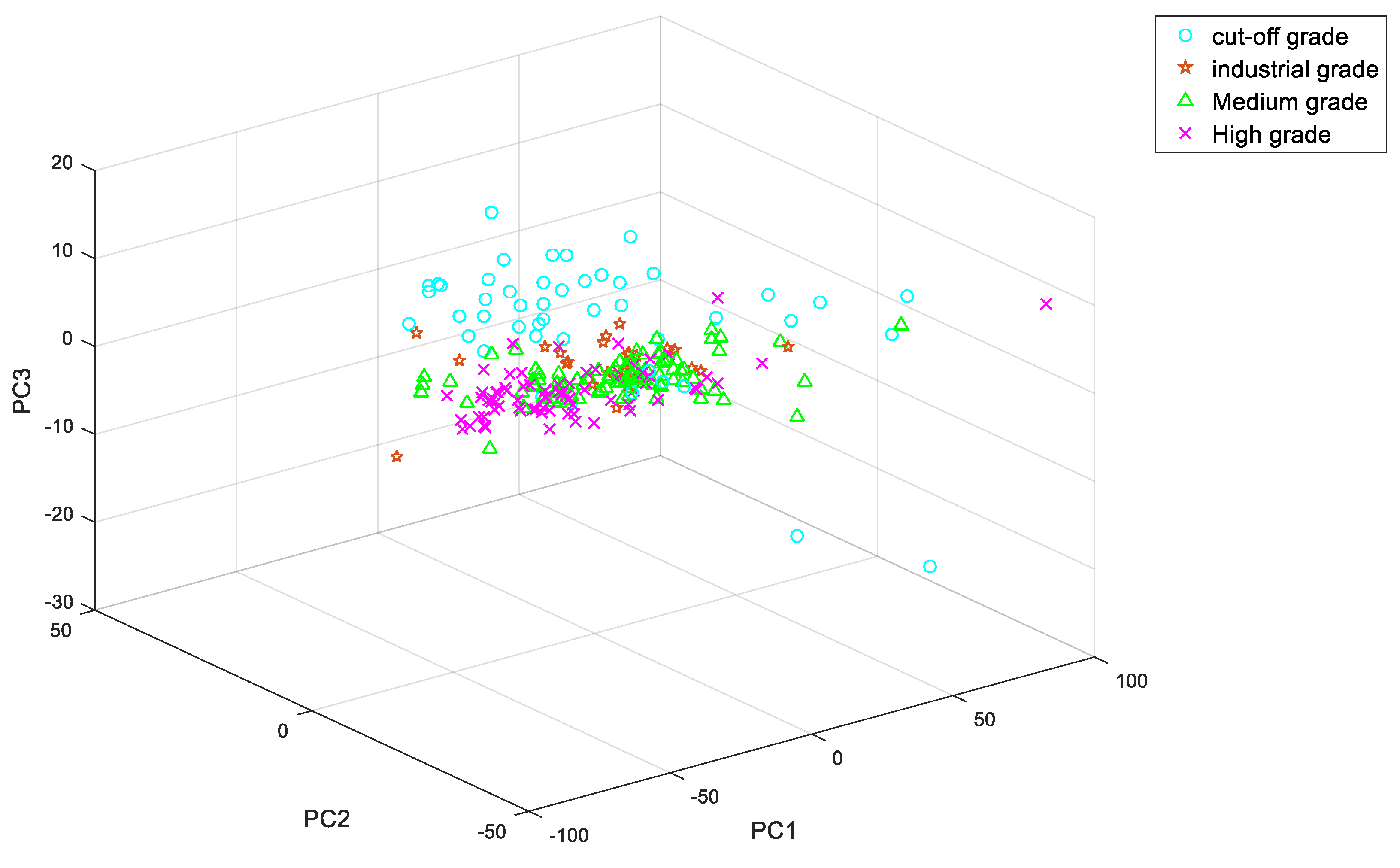
4.1. Processing of Copper Ore Spectral Data
4.2. Neural Network Comparison
4.3. Comparison of Copper Content Detection Models of Different Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Radivojevic, M.; Rehren, T.; Pernicka, E.; Sljivar, D.; Brauns, M.; Boric, D. On the origins of extractive metallurgy: New evidence from Europe. J. Archaeol. 2010, 37, 2775–2787. [Google Scholar] [CrossRef]
- Jiang, S.Q. Distribution of copper resources in the world. World Nonferr. Met. 2018, 2, 1–3. [Google Scholar]
- Zhou, C.Y.; Qu, W. Rapid Determination of Copper and Iron in Ore Leaching Solution by Iodometry. In Proceedings of the 3rd International Conference on Chemical Engineering and Advanced Materials (CEAM 2013), Guangzhou, China, 6–7 July 2013. [Google Scholar]
- Gao, W. Determination of Copper, Lead, Zinc, Cobalt and Nickel in Ore by Flame Atomic Absorption Spectrophotometry. World Nonferr. Met. 2019, 04, 171–172. [Google Scholar]
- Shi, C.Y.; Xie, S.A.; Jia, J.P. The Study of a New Method to Determine Copper Ion by Square-Wave Voltammetry-Extraction Iodometry at the Liquid/Liquid Interfaces. J. Autom. Methods Manag. Chem. 2008, 2008, 453429. [Google Scholar] [CrossRef] [Green Version]
- Song, U. Improvement of soil properties and plant responses by compost generated from biomass of phytoremediation plant. Environ. Eng. Res. 2020, 5, 638–644. [Google Scholar] [CrossRef] [Green Version]
- Luo, F.; Hu, X.F.; Oh, K.; Yan, L.J.; Lu, X.Z.; Zhang, W.J.; Yonekura, T.; Yonemochi, S.; Isobe, Y. Using profitable chrysanthemums for phytoremediation of Cd- and Zn-contaminated soils in the suburb of Shanghai. J. Soils Sediments 2020, 20, 4011–4022. [Google Scholar] [CrossRef]
- Saleem, M.H.; Rehman, M.; Kamran, M.; Afzal, J.; Noushahi, H.A.; Liu, L.J. Investigating the potential of different jute varieties for phytoremediation of copper-contaminated soil. Environ. Sci. Pollut. Res. 2020, 27, 30367–30377. [Google Scholar] [CrossRef]
- Muro-Gonzalez, D.A.; Mussali-Galante, P.; Valencia-Cuevas, L.; Flores-Trujillo, K.; Tovar-Sanchez, E. Morphological, physiological, and genotoxic effects of heavy metal bioaccumulation inProsopis laevigatareveal its potential for phytoremediation. Environ. Sci. Pollut. Res. 2020, 32, 40187–40204. [Google Scholar] [CrossRef]
- Chauhan, P.; Mathur, J. Phytoremediation efficiency of Helianthus annuus L. for reclamation of heavy metals-contaminated industrial soil. Environ. Sci. Pollut. Res. 2020, 27, 29954–29966. [Google Scholar]
- Mao, Y.C.; Xiao, D.; Cheng, J.P.; Jiang, J.H.; Le, B.T.; Liu, S.J. Research in magnesite grade classification based on near infrared spectroscopy and ELM algorithm. Spectrosc. Spectr. Anal. 2017, 37, 89–94. [Google Scholar]
- Wang, N.; Zhang, L. Beer Freshness Detection Method Based on Spectral Analysis Technology. Spectrosc. Spectr. Anal. 2020, 7, 2273–2277. [Google Scholar]
- Mortet, V.; Gregora, I.; Taylor, A.; Lambert, N.; Ashcheulov, P.; Gedeonova, Z.; Hubik, P. New perspectives for heavily boron-doped diamond Raman spectrum analysis. Carbon 2020, 168, 319–327. [Google Scholar] [CrossRef]
- Yang, R.Y.; Qiao, T.Z.; Pang, Y.S.; Yang, Y.; Zhang, H.T.; Yan, G.W. Infrared Spectrum Analysis Method for Detection and Early Warning of Longitudinal Tear of Mine Conveyor Belt. Measurement 2020, 165, 107856. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, C.M.; Le, B.T. Detection method of TFe content of iron ore based on visible-infrared spectroscopy and IPSO-TELM neural network. Infrared Phys. Technol. 2019, 97, 341–348. [Google Scholar] [CrossRef]
- Le, B.T.; Mao, Y.C.; He, D.K. Coal analysis based on visible-infrared spectroscopy and a deep neural network. Infrared Phys. Technol. 2018, 93, 34–40. [Google Scholar] [CrossRef]
- Percival, J.B.; Bosman, S.A.; Potter, E.G.; Peter, J.M.; Laudadio, A.B.; Abraham, A.C.; Shiley, D.A.; Sherry, C. Customized Spectral Libraries for Effective Mineral Exploration: Mining National MIneral Collections. Clays Clay Miner. 2018, 66, 297–314. [Google Scholar] [CrossRef]
- Zhou, M.; Zou, B.; TU, Y.L.; Xia, J.P. Hyperspectral Modeling of Pb Content in Mining Area Based on Spectral Feature Band Extracted from Near Standard Soil Samples. Spectrosc. Spectr. Anal. 2020, 7, 2182–2187. [Google Scholar]
- Zhao, Y.L.; Zheng, W.X.; Xiao, W.; Zhang, S.; Lv, X.J.; Zhang, J.Y. Rapid monitoring of reclaimed farmland effects in coal mining subsidence area using a multi-spectralUAV platform. Environ. Monit. Assess. 2020, 7, 474. [Google Scholar] [CrossRef]
- Shin, J.H.; Yu, J.; Wang, L.; Kim, J.; Koh, S.M.; Kim, S.O. Spectral Responses of Heavy Metal Contaminated Soils in the Vicinity of a Hydrothermal Ore Deposit: A Case Study of Boksu Mine, South Korea. IEEE Trans. Geosci. Remote Sens. 2019, 6, 4092–4106. [Google Scholar] [CrossRef]
- Zhang, S.W.; Shen, Q.; Nie, C.J.; Huang, Y.F.; Wang, J.H.; Hu, Q.Q.; Ding, X.J.; Zhou, Y.; Chen, Y.P. Hyperspectral inversion of heavy metal content in reclaimed soil from a mining wasteland based on different spectral transformation and modeling methods. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 211, 393–400. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Parida, A.K.; Maity, K.; Ghadei, S.B. Optimization of hot turning parameters using principal component analysis method. Mater. Today Proc. 2020, 22, 2081–2087. [Google Scholar] [CrossRef]
- Machidon, A.L.; Del Frate, F.; Picchiani, M.; Machidon, O.M.; Ogrutan, P.L. Ogrutan, Geometrical Approximated Principal Component Analysis for Hyperspectral Image Analysis. Remote Sens. 2020, 12, 1698. [Google Scholar] [CrossRef]
- Sell, S.L.; Widen, S.G.; Prough, D.S.; Hellmich, H.L. Principal component analysis of blood microRNA datasets facilitates diagnosis of diverse diseases. PLoS ONE 2020, 15, e0234185. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhao, T.L.; Ju, W.W.; Shi, S.Q. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Xiong, Z.; Cui, Y.X.; Liu, Z.H.; Zhao, Y.; Hu, M.; Hu, J.J. Evaluating explorative prediction power of machine learning algorithms for materials discovery using k-fold forward cross-validation. Comput. Mater. Sci. 2020, 171, 109203. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, B.R.; Zou, X.X.; Li, Y.J.; Shi, S.Q. Machine learning assisted materials design and discovery for rechargeable batteries. Energy Storage Mater. 2020, 31, 434–450. [Google Scholar] [CrossRef]
- Kilic, A.; Odabaşı, Ç.; Yildirim, R.; Erogluss, D. Assessment of critical materials and cell design factors for high performance lithium-sulfur batteries using machine learning. Chem. Eng. J. 2020, 390, 124117. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE international joint conference on neural networks, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Zong, W.; Huang, G.B. Face recognition based on Extreme learning machine. Neurocomputing 2011, 74, 2541–2551. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2011, 42, 513–529. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.Y.; Yu, Y.L.; Gu, J.S.; Liu, H.P. An efficient method for traffic sign recognition based on Extreme learning machine. IEEE Trans. Cybern. 2016, 47, 920–933. [Google Scholar] [CrossRef] [PubMed]
- Kang, F.; Liu, J.; Li, J.J.; Li, S.J. Concrete dam deformation prediction model for health monitoring based on extreme learning machin. Struct. Control Health Monit. 2017, 24, e1997. [Google Scholar] [CrossRef]
- Liang, N.Y.; Huang, G.B. A Fast and accurate online sequential learning algorithm for feedforward networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef] [PubMed]
- Lan, Y.; Soh, Y.C.; Huang, G.B. Ensemble of online sequential Extreme learning machine. Neurocomputing 2009, 72, 3391–3395. [Google Scholar] [CrossRef]
- Qu, B.Y.; Lang, B.G. Two-hidden-layer Extreme learning machine for regression and classification. Neurocomputing 2016, 175, 826–834. [Google Scholar] [CrossRef]
- Feng, T. Imputing Missing Data in Large-Scale Multivariate Biomedical Wearable Recordings Using Bidirectional Recurrent Neural Networks with Temporal Activation Regularization. In Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 2529–2534. [Google Scholar]
- Girosi, F.; Jones, M.; Poggio, T. Regularization theory and neural networks architectures. Neural Comput. 1995, 7, 219–269. [Google Scholar] [CrossRef]
- Wang, R.B.; Xu, H.Y.; Feng, Y. Research on Method of Determining Hidden Layer Nodes in BP Neural Network. Comput. Technol. Dev. 2018, 28, 31–35. [Google Scholar]
- Wang, J.; Xue, F. Self-adaptive Nonlinear Approximation Algorithm of RBF Neural Network. Mod. Electron. Tech. 2011, 34, 141–143. [Google Scholar]






| Spectrometer Parameters | Parameter Value |
|---|---|
| Spectral Range | 350–2500 nm |
| Internal Memory | 500 Scans |
| Channels | 1024 |
| Spectral Resolution (FWHM) | ≤3.5 nm, 350–1000 nm ≤9.5 nm, 1000–1850 nm ≤6.5 nm, 1850–2500 nm |
| Bandwidth (nominal) | ≤1.5 nm, 350–1000 nm ≤3.6 nm, 1000–1850 nm ≤2.5 nm, 1850–2500 nm |
| Minimum Integration | 1 millisecond |
| Model Type | Time Consumption (s) | R2 | RMSE |
|---|---|---|---|
| BP | 0.202432 | 0.62688 | 0.15404 |
| ELM | 0.025085 | 0.62834 | 0.13653 |
| RBF | 0.062342 | 0.13653 | 1.6936 |
| Model Type | R2 | RMSE | S | Number of Hidden Layer Nodes |
|---|---|---|---|---|
| ELM | 0.74822 | 0.12112 | 0.020792 | 11 |
| TELM | 0.83589 | 0.075211 | 0.135268 | 48 |
| VTELM | 0.88309 | 0.055629 | 0.027361 | 46/137 |
| Test Method | Detection Accuracy (%) | Time Consumed (h) | Cost Detection (yuan) |
|---|---|---|---|
| Instrument testing | 73 | 3 | About 400 |
| Chemical method | 99 | 70 | About 21,000 |
| VTELM | 98.4 | 3 | About 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Y.; Xie, H.; Mao, Y.; Ren, T.; Xiao, D. Copper Content Inversion of Copper Ore Based on Reflectance Spectra and the VTELM Algorithm. Sensors 2020, 20, 6780. https://doi.org/10.3390/s20236780
Fu Y, Xie H, Mao Y, Ren T, Xiao D. Copper Content Inversion of Copper Ore Based on Reflectance Spectra and the VTELM Algorithm. Sensors. 2020; 20(23):6780. https://doi.org/10.3390/s20236780
Chicago/Turabian StyleFu, Yanhua, Hongfei Xie, Yachun Mao, Tao Ren, and Dong Xiao. 2020. "Copper Content Inversion of Copper Ore Based on Reflectance Spectra and the VTELM Algorithm" Sensors 20, no. 23: 6780. https://doi.org/10.3390/s20236780
APA StyleFu, Y., Xie, H., Mao, Y., Ren, T., & Xiao, D. (2020). Copper Content Inversion of Copper Ore Based on Reflectance Spectra and the VTELM Algorithm. Sensors, 20(23), 6780. https://doi.org/10.3390/s20236780





