Impact of Different Metals on the Performance of Slab Tamm Plasmon Resonators
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mirror Materials
2.2. Simulation Domain and Optimization
2.2.1. Initialization of Modified Quarter Wave Stack
2.2.2. Genetic Algorithm Optimization
3. Results
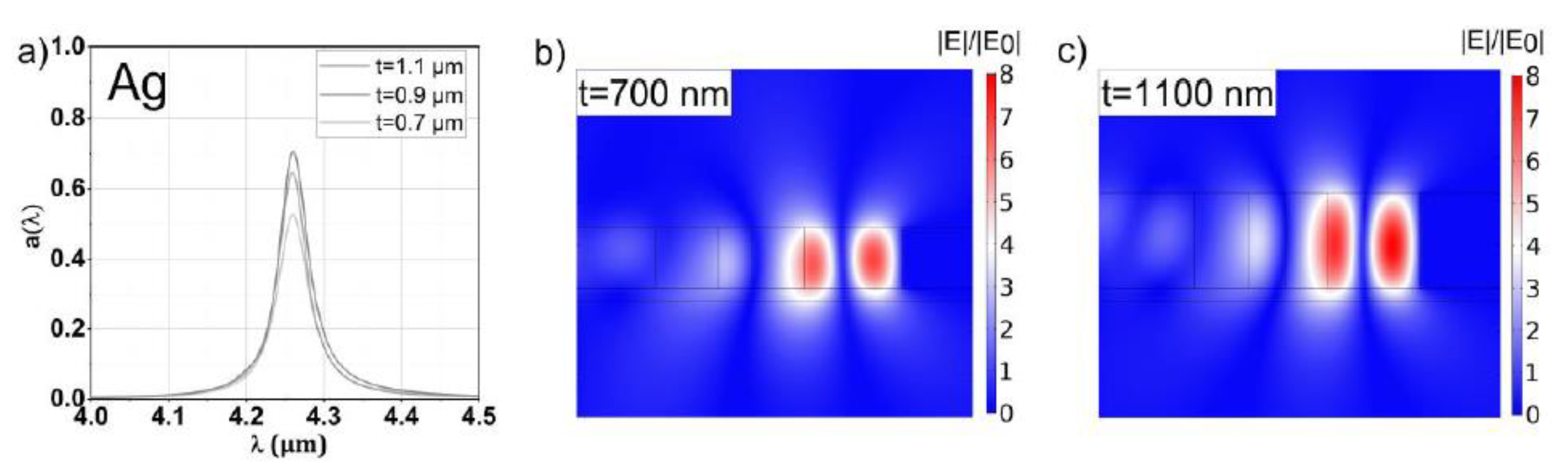
3.1. Silver
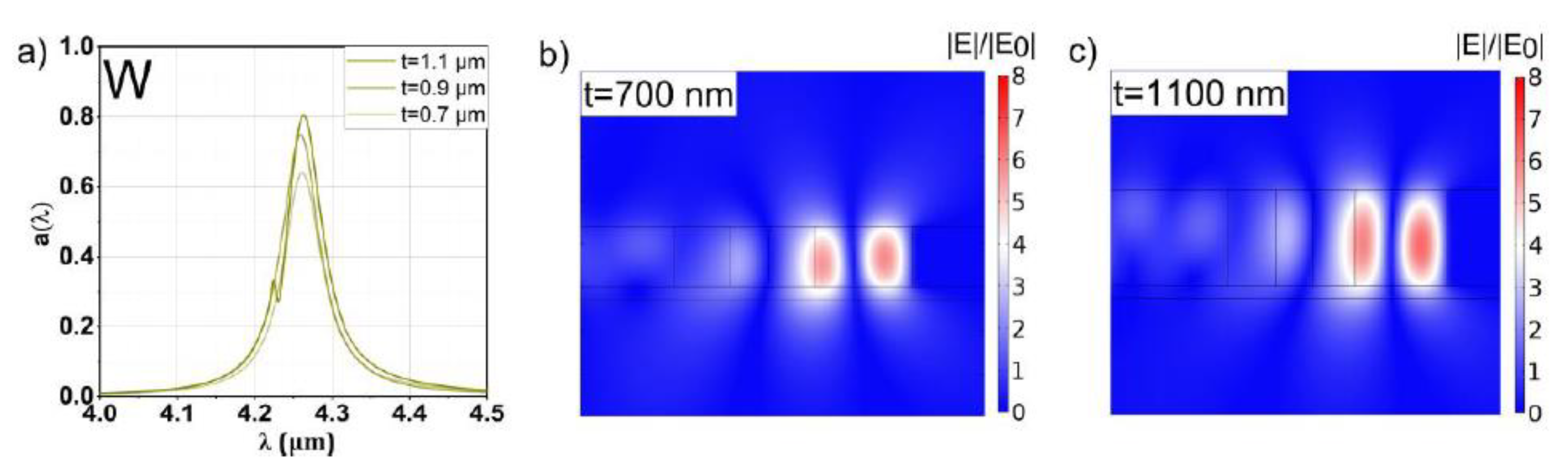
3.2. Tungsten
3.3. Molybdenum
3.4. Heavily Doped Silicon
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiao, M.; Zhang, Z.Q.; Chan, C.T. Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems. Phys. Rev. X 2014, 4, 021017. [Google Scholar] [CrossRef] [Green Version]
- Abasahl, B.; Jannesari, R.; Jakoby, B. Narrow-Band Thermal Photonic Crystal Emitter for Mid-Infrared Applications. Multidiscip. Digit. Publ. Inst. Proc. 2018, 2, 752. [Google Scholar] [CrossRef] [Green Version]
- Celanovic, I.; Perreault, D.; Kassakian, J. Resonant-cavity enhanced thermal emission. Phys. Rev. B 2005, 72, 2–7. [Google Scholar] [CrossRef]
- Yang, Z.-Y.; Ishii, S.; Yokoyama, T.; Dao, T.D.; Sun, M.-G.; Nagao, T.; Chen, K.-P. Tamm plasmon selective thermal emitters. Opt. Lett. 2016, 41, 4453–4456. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.-Y.; Ishii, S.; Yokoyama, T.; Dao, T.D.; Sun, M.-G.; Pankin, P.S.; Timofeev, I.V.; Nagao, T.; Chen, K.-P. Narrowband Wavelength Selective Thermal Emitters by Confined Tamm Plasmon Polaritons. ACS Photon. 2017, 4, 2212–2219. [Google Scholar] [CrossRef] [Green Version]
- Wen, Y.; Liang, Z.; Lin, Y.-S.; Chen, C.-H. Active modulation of polarization-sensitive infrared metamaterial. Opt. Commun. 2020, 463, 125489. [Google Scholar] [CrossRef]
- Xu, R.; Lin, Y.-S. Tunable Infrared Metamaterial Emitter for Gas Sensing Application. Nanomaterials 2020, 10, 1442. [Google Scholar] [CrossRef]
- Spott, A.; Peters, J.; Davenport, M.L.; Stanton, E.J.; Merritt, C.D.; Bewley, W.W.; Vurgaftman, I.; Kim, C.S.; Meyer, J.R.; Kirch, J. Quantum cascade laser on silicon. Optica 2016, 3, 545–551. [Google Scholar] [CrossRef] [Green Version]
- Razeghi, M. High-performance InP-based mid-IR quantum cascade lasers. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 941–951. [Google Scholar] [CrossRef]
- Symonds, C.; Lheureux, G.; Hugonin, J.P.; Greffet, J.J.; Laverdant, J.; Brucoli, G.; Lemaitre, A.; Senellart, P.; Bellessa, J. Confined tamm plasmon lasers. Nano Lett. 2013, 13, 3179–3184. [Google Scholar] [CrossRef]
- Auguié, B.; Bruchhausen, A.; Fainstein, A. Critical coupling to Tamm plasmons. J. Opt. 2015, 17, 293–295. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Clark, J.K.; Ho, Y.-L.; Vilquin, B.; Daiguji, H.; Delaunay, J.-J. Narrowband Thermal Emission Realized through the Coupling of Cavity and Tamm Plasmon Resonances. ACS Photon. 2018, 5, 2446–2452. [Google Scholar] [CrossRef]
- Pühringer, G.; Jakoby, B. Highly Selective CMOS-Compatible Mid-Infrared Thermal Emitter/Detector Slab Design Using Optical Tamm-States. Materials 2019, 12, 929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Granier, C.H.; Afzal, F.O.; Min, C.; Dowling, J.P.; Veronis, G. Optimized aperiodic highly directional narrowband infrared emitters. J. Opt. Soc. Am. B 2014, 31, 1316–1321. [Google Scholar] [CrossRef]
- Ranacher, C.; Consani, C.; Vollert, N.; Tortschanoff, A.; Bergmeister, M.; Grille, T.; Jakoby, B. Characterization of Evanescent Field Gas Sensor Structures Based on Silicon Photonics. IEEE Photon. J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Consani, C.; Ranacher, C.; Tortschanoff, A.; Grille, T.; Irsigler, P.; Jakoby, B. Mid-infrared photonic gas sensing using a silicon waveguide and an integrated emitter. Sens. Actuators B Chem. 2018, 274, 60–65. [Google Scholar] [CrossRef]
- Kaliteevski, M.A.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef] [Green Version]
- Lheureux, G.; Azzini, S.; Symonds, C.; Senellart, P.; Lemaître, A.; Sauvan, C.; Hugonin, J.P.; Greffet, J.J.; Bellessa, J. Polarization-Controlled Confined Tamm Plasmon Lasers. ACS Photonics 2015, 2, 842–848. [Google Scholar] [CrossRef]
- Greffet, J.-J.; Nieto-Vesperinas, M. Field theory for generalized bidirectional reflectivity: Derivation of Helmholtz’s reciprocity principle and Kirchhoff’s law. J. Opt. Soc. Am. A 1998, 15, 2735. [Google Scholar] [CrossRef]
- Hsieh, W.T.; Wu, P.C.; Khurgin, J.B.; Tsai, D.P.; Liu, N.; Sun, G. Comparative Analysis of Metals and Alternative Infrared Plasmonic Materials. ACS Photonics 2018, 5, 2541–2548. [Google Scholar] [CrossRef] [Green Version]
- Franzen, D.; Videll, C. Tunable multiresonance using complementary circular metamaterial: Publisher’s note. Opt. Lett. 2020, 45, 5339. [Google Scholar] [CrossRef]
- Luo, J.; Lin, Y.-S. High-efficiency of infrared absorption by using composited metamaterial nanotubes. Appl. Phys. Lett. 2019, 114, 051601. [Google Scholar] [CrossRef]
- Laroche, M.; Arnold, C.; Marquier, F.; Carminati, R.; Greffet, J.-J.; Collin, S.; Bardou, N.; Pelouard, J.-L. Highly directional radiation generated by a tungsten thermal source. Opt. Lett. 2005, 30, 2623–2625. [Google Scholar] [CrossRef] [PubMed]
- Joannopoulos, J.J.D.; Johnson, S.; Winn, J.N.J.; Meade, R.R.D. Photonic Crystals: Molding the Flow of Light; Princeton and Oxford; Princeston University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Srinivasan, K.; Painter, O. Momentum space design of high-Q photonic crystal optical cavities. Opt. Express 2002, 10, 670–684. [Google Scholar] [CrossRef] [Green Version]
- Kita, D.M.; Michon, J.; Johnson, S.G.; Hu, J. Are slot and sub-wavelength grating waveguides better than strip waveguides for sensing? Optica 2018, 5, 1046–1054. [Google Scholar] [CrossRef] [Green Version]
- Robinson, J.T.; Preston, K.; Painter, O.; Lipson, M. First-principle derivation of gain in high-index-contrast waveguides. Opt. Express 2008, 16, 16659–16669. [Google Scholar] [CrossRef]
- Ranacher, C.; Consani, C.; Maier, F.J.; Hedenig, U.; Jannesari, R.; Lavchiev, V.; Tortschanoff, A.; Grille, T.; Jakoby, B. Spectroscopic Gas Sensing Using a Silicon Slab Waveguide. Procedia Eng. 2016, 168, 1265–1269. [Google Scholar] [CrossRef]
- Kischkat, J.; Peters, S.; Gruska, B.; Semtsiv, M.; Chashnikova, M.; Klinkmüller, M.; Fedosenko, O.; Machulik, S.; Aleksandrova, A.; Monastyrskyi, G.; et al. Mid-infrared optical properties of thin films of aluminum oxide, titanium dioxide, silicon dioxide, aluminum nitride, and silicon nitride. Appl. Opt. 2012, 51, 6789–6798. [Google Scholar] [CrossRef]
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef]
- Li, H.H. Refracitve Index of Silicon and Germanium and Its Wavelength and Temperature Derivatives. J. Phys. Chem. Ref. Data 1980, 9, 561–658. [Google Scholar] [CrossRef]
- Vandenabeele, P.; Maex, K. Influence of temperature and backside roughness on the emissivity of Si wafers during rapid thermal processing. J. Appl. Phys. 1992, 72, 5867–5875. [Google Scholar] [CrossRef]
- Basu, S.; Lee, B.J.; Zhang, Z.M. Infrared Radiative Properties of Heavily Doped Silicon at Room Temperature. J. Heat Transf. 2009, 132, 023301. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, J.R.W.; Newquist, L.A.; Querry, M.R. Optical properties of Al, Fe, Ti, Ta, W, and Mo at submillimeter wavelengths. Appl. Opt. 1988, 27, 1203–1209. [Google Scholar] [CrossRef] [PubMed]
- Ordal, M.A.; Long, L.L.; Bell, R.J.; Bell, S.E.; Alexander, R.W.; Ward, C.A. Optical properties of the metals Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl. Opt. 1983, 22, 1099–1119. [Google Scholar] [CrossRef] [PubMed]
- Soref, R.; Peale, R.E.; Buchwald, W. Longwave plasmonics on doped silicon and silicides. Opt. Express 2008, 16, 6507–6514. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Malagari, S.D.; Hamilton, T.; Wasserman, D. Review of mid-infrared plasmonic materials. J. Nanophotonics 2015, 9, 093791. [Google Scholar] [CrossRef] [Green Version]
- West, P.; Ishii, S.; Naik, G.; Emani, N.; Shalaev, V.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef] [Green Version]
- Puhringer, G.; Jakoby, B. Modeling of a CMOS-Compatible Slab Tamm Plasmon Absorber using N-Type Silicon. In Proceedings of the 2019 IEEE Sensors Applications Symposium (SAS), Montreal, QC, Canada, 27–30 October 2019. [Google Scholar]
- Shahzad, M.; Medhi, G.; Peale, R.E.; Buchwald, W.R.; Cleary, J.W.; Soref, R.; Boreman, G.D.; Edwards, O. Infrared surface plasmons on heavily doped silicon. J. Appl. Phys. 2011, 110, 123105. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Debernardi, A.; Berencén, Y.; Heller, R.; Xu, C.; Yuan, Y.; Xie, Y.; Böttger, R.; Rebohle, L.; Skorupa, W.; et al. Breaking the Doping Limit in Silicon by Deep Impurities. Phys. Rev. Appl. 2019, 11, 054039. [Google Scholar] [CrossRef] [Green Version]
- Khurgin, J.B. How to deal with the loss in plasmonics and metamaterials. Nat. Nanotechnol. 2015, 10, 2–6. [Google Scholar] [CrossRef]
- Krishnakumar, K. Micro-Genetic Algorithms for Stationary and Non-Stationary Function Optimization. SPIE-Intl. Soc. Opt. Eng. 1990, 289–296. [Google Scholar] [CrossRef]
- Minissale, M.; Zeweldi, G.T.; Bisson, R.; Gallais, L. The effect of surface temperature on optical properties of molybdenum mirrors in the visible and near-infrared domains. Nucl. Fusion 2018, 58, 096012. [Google Scholar] [CrossRef] [Green Version]
- Reflectivity of Molybdenum Laser Mirrors—Laser Beam Products—Precision Optics. Available online: https://www.lbp.co.uk/pdfs/Reflectivity of Molybdenumlasermirrors.pdf (accessed on 31 August 2020).
- Ujihara, K. Reflectivity of metals at high temperatures. J. Appl. Phys. 1972, 43, 2376–2383. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, G.; Wang, K.; Long, H.; Lu, P. Multiple optical Tamm states at a metal–dielectric mirror interface. Opt. Lett. 2010, 35, 4112–4114. [Google Scholar] [CrossRef] [PubMed]
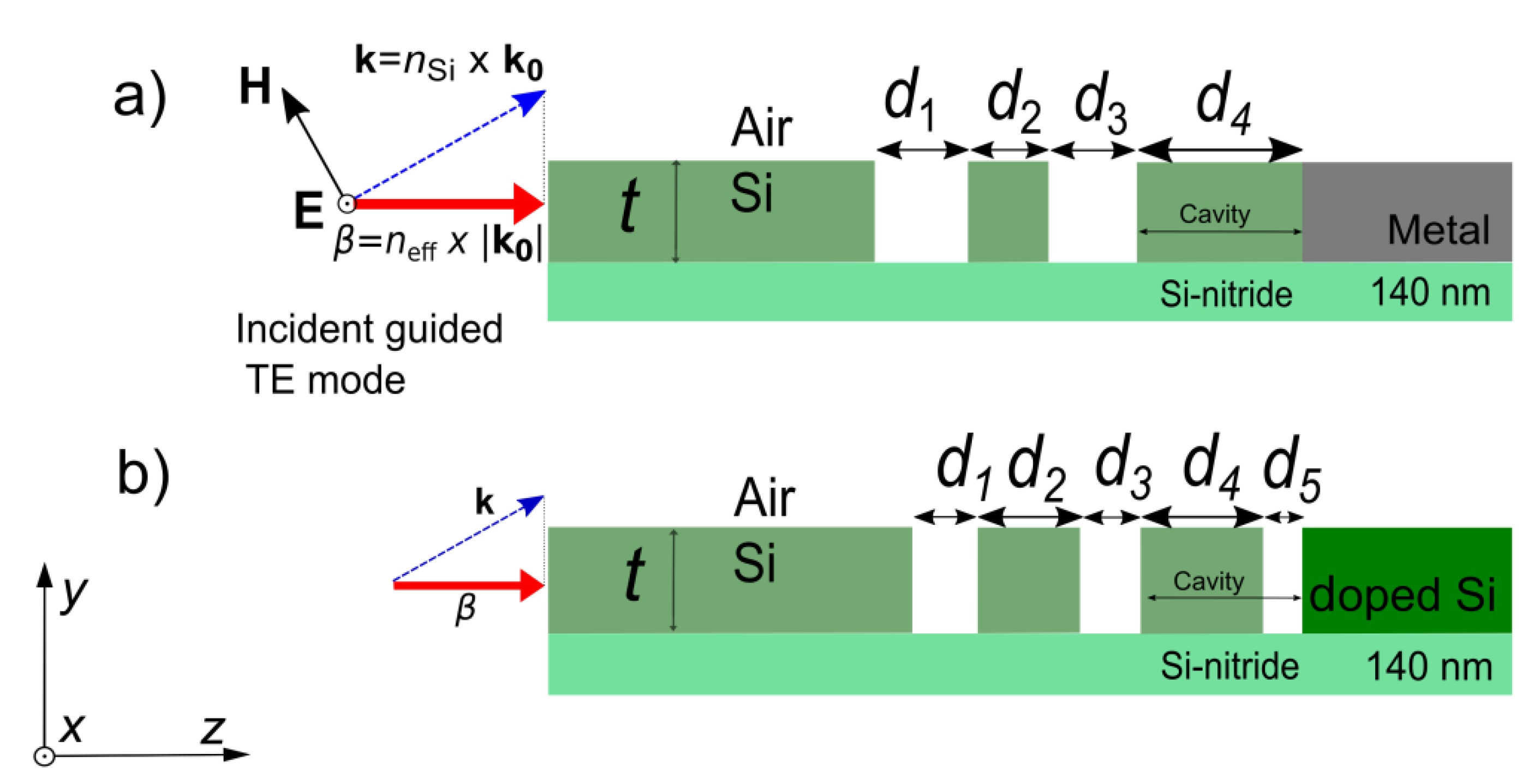




| d1 | d2 | d3 | d4 | |
|---|---|---|---|---|
| conventional QWS | ||||
| modified QWS |
| Mirror Material | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ag | 0.7 | 0.73 | 0.40 | 0.62 | 1.14 | - | 52.7% | 1.7% | 82.6 |
| Ag | 0.9 | 0.68 | 0.45 | 0.52 | 1.09 | - | 64.7% | 4.7% | 88.8 |
| Ag | 1.1 | 0.63 | 0.41 | 0.49 | 1.07 | - | 70.6% | 5.1% | 82.6 |
| W | 0.7 | 0.66 | 0.41 | 0.55 | 1.135 | - | 64.3% | 1.7% | 62.2 |
| W | 0.9 | 0.64 | 0.50 | 0.45 | 1.08 | - | 75.0% | 2.4% | 66.5 |
| W | 1.1 | 0.56 | 0.42 | 0.49 | 1.06 | - | 79.5% | 4.3% | 66.4 |
| Mo | 0.7 | 0.74 | 0.48 | 0.50 | 1.14 | - | 57.1% | 2.8% | 76.1 |
| Mo | 0.9 | 0.63 | 0.43 | 0.49 | 1.10 | - | 69.7% | 4.2% | 71.0 |
| Mo | 1.1 | 0.63 | 0.365 | 0.50 | 1.07 | - | 74.3% | 6.2% | 76.6 |
| doped Si | 0.7 | 0.27 | 0.59 | 0.39 | 0.95 | 0.25 | 65.5% | 1.8% | 21.5 |
| doped Si | 0.9 | 0.31 | 0.51 | 0.35 | 0.92 | 0.24 | 74.5% | 11.1% | 23.5 |
| doped Si | 1.1 | 0.30 | 0.49 | 0.39 | 0.89 | 0.23 | 81.5% | 6.6% | 23.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pühringer, G.; Consani, C.; Jakoby, B. Impact of Different Metals on the Performance of Slab Tamm Plasmon Resonators. Sensors 2020, 20, 6804. https://doi.org/10.3390/s20236804
Pühringer G, Consani C, Jakoby B. Impact of Different Metals on the Performance of Slab Tamm Plasmon Resonators. Sensors. 2020; 20(23):6804. https://doi.org/10.3390/s20236804
Chicago/Turabian StylePühringer, Gerald, Cristina Consani, and Bernhard Jakoby. 2020. "Impact of Different Metals on the Performance of Slab Tamm Plasmon Resonators" Sensors 20, no. 23: 6804. https://doi.org/10.3390/s20236804
APA StylePühringer, G., Consani, C., & Jakoby, B. (2020). Impact of Different Metals on the Performance of Slab Tamm Plasmon Resonators. Sensors, 20(23), 6804. https://doi.org/10.3390/s20236804




