Comparison of Signal-Analysis Techniques for Seismic Detection System for High-Speed Train Data: Effect of Bridge Structures
Abstract
:1. Introduction
2. Train Acceleration Data and Seismic-Response Data
2.1. Train Acceleration Data
2.2. Seismic-Response Data
2.2.1. Earthquake Data
2.2.2. Bridge Seismic-Response Analysis
3. Data Analysis
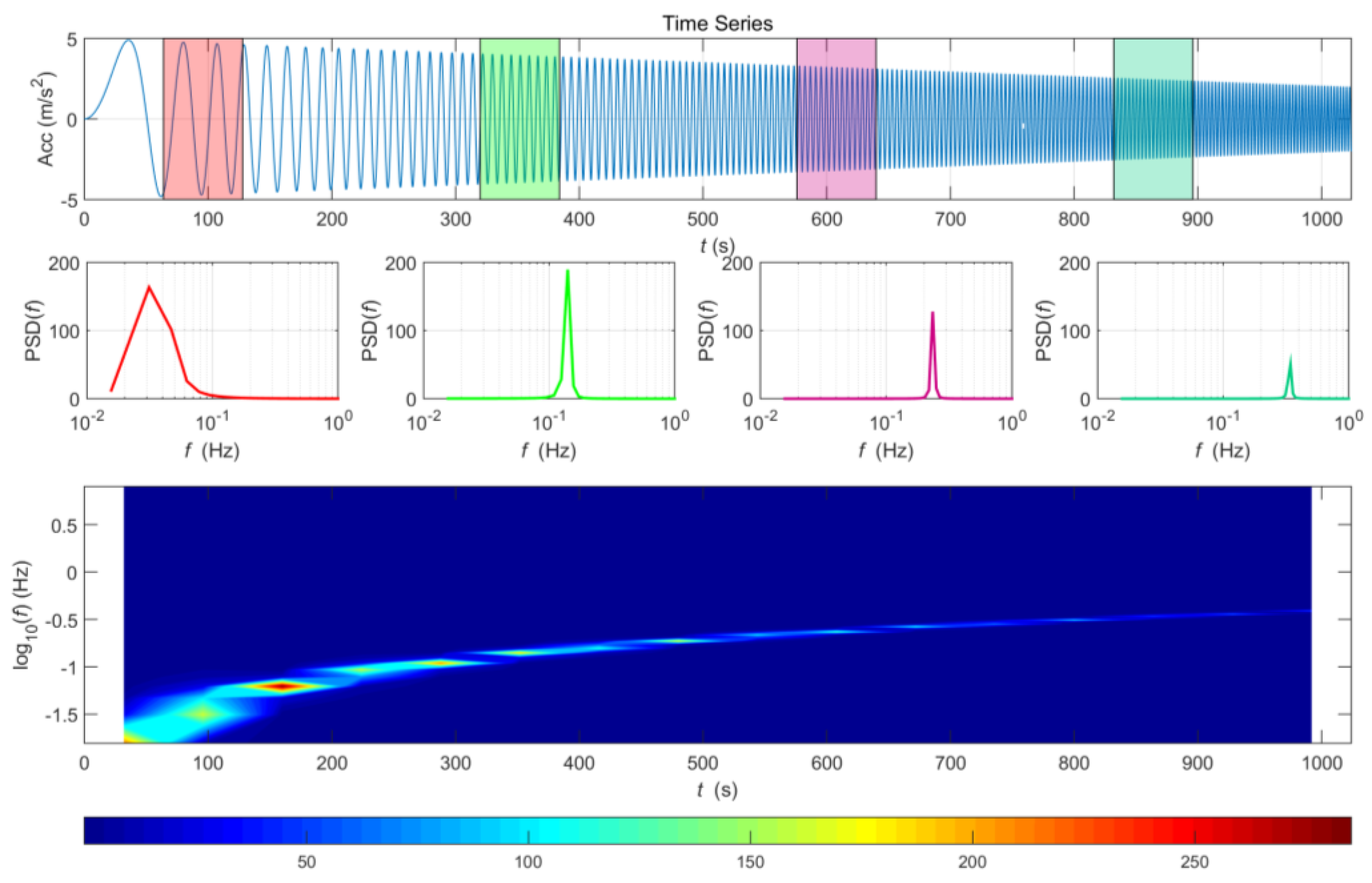
3.1. Data-Analysis Methods
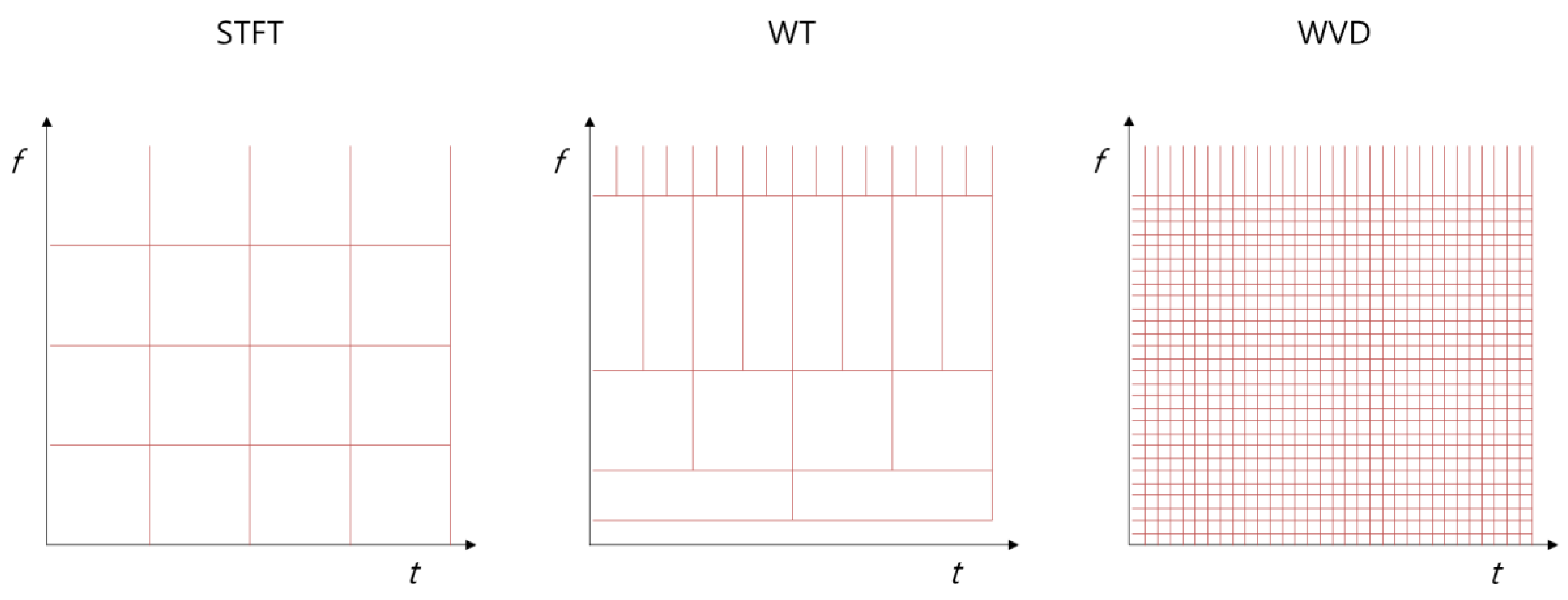
3.1.1. STFT
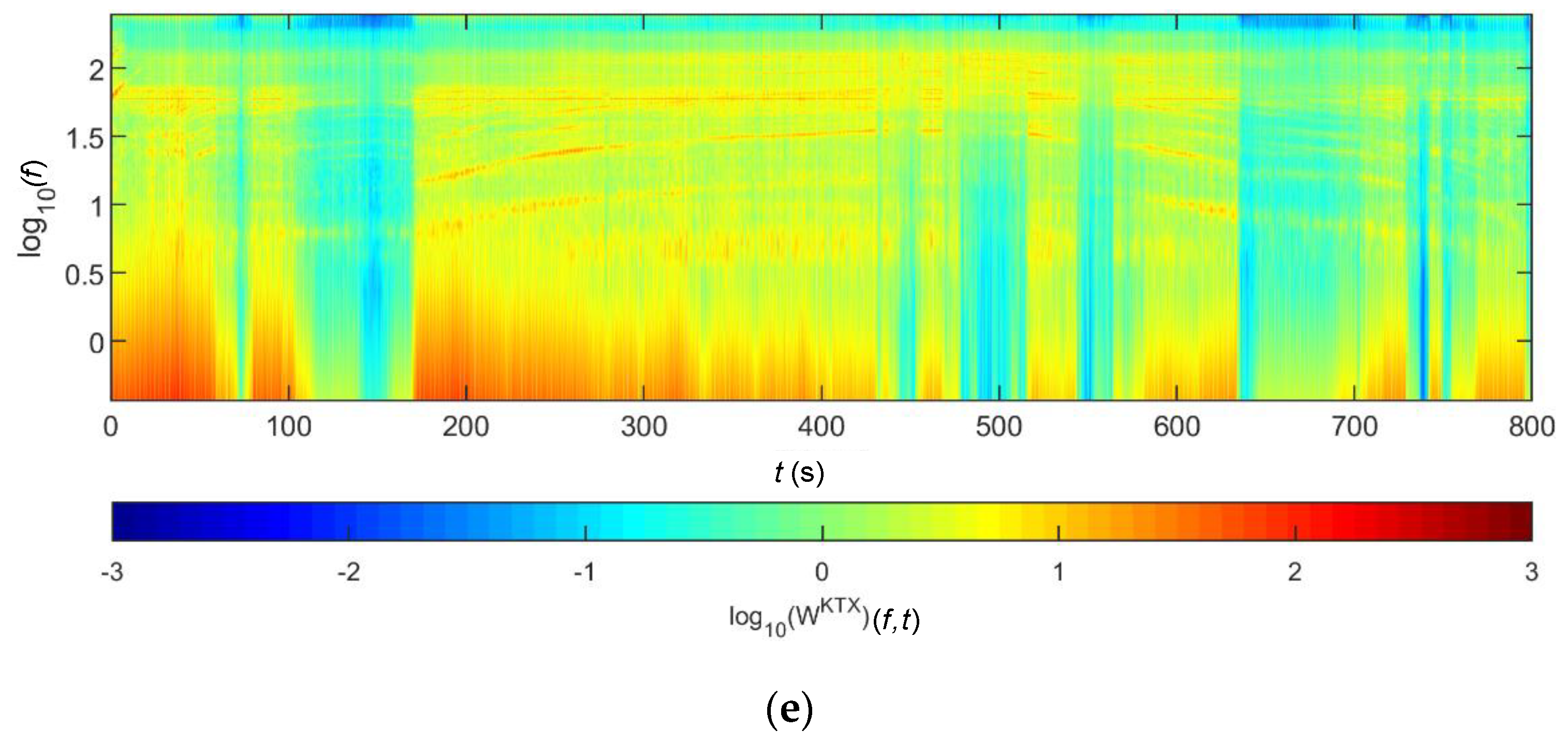
3.1.2. WT
3.1.3. WVD
3.2. Data Characteristics
3.2.1. Seismic Response of Bridges
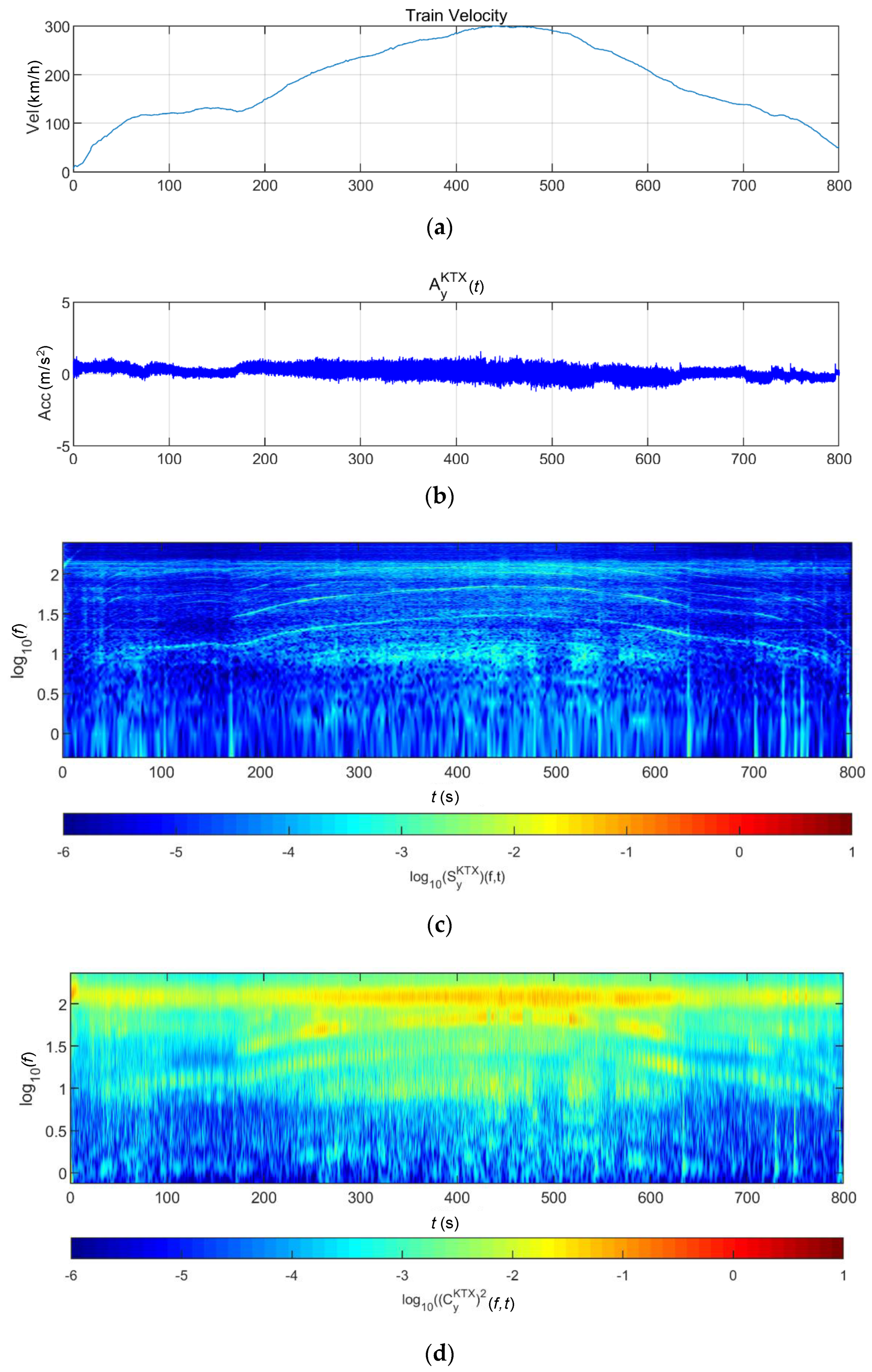
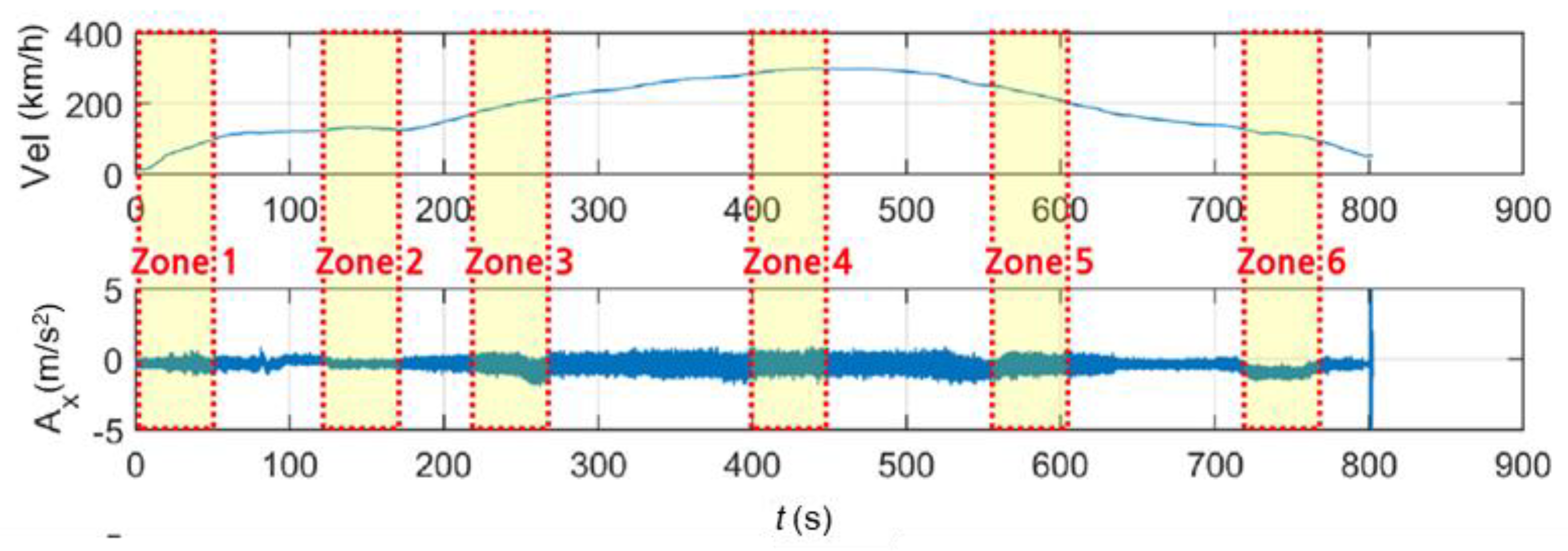
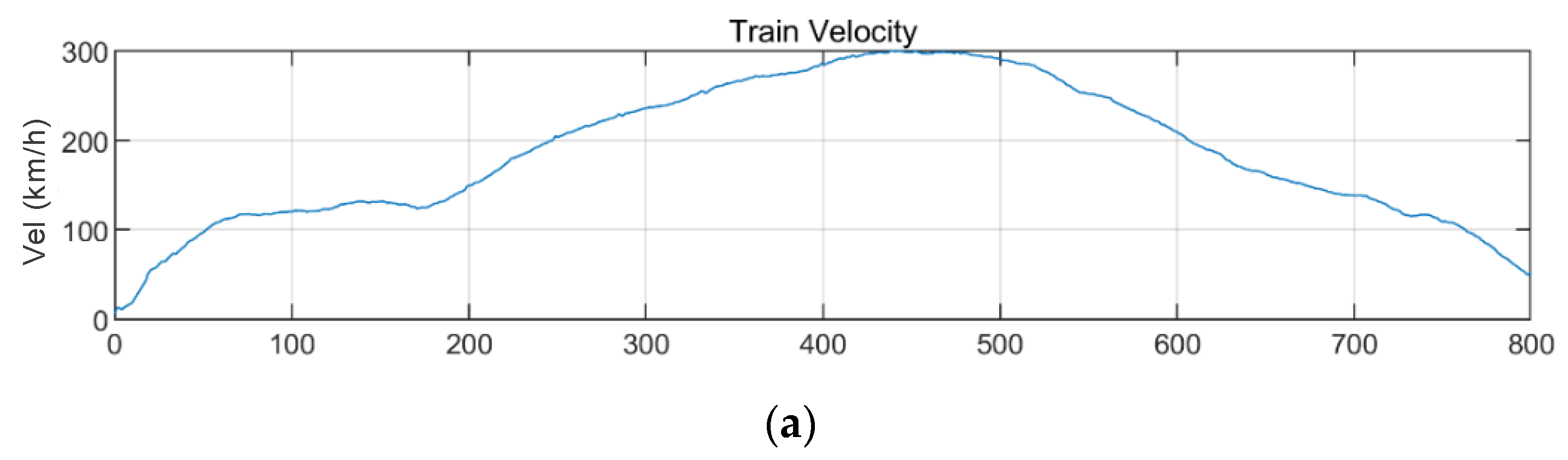
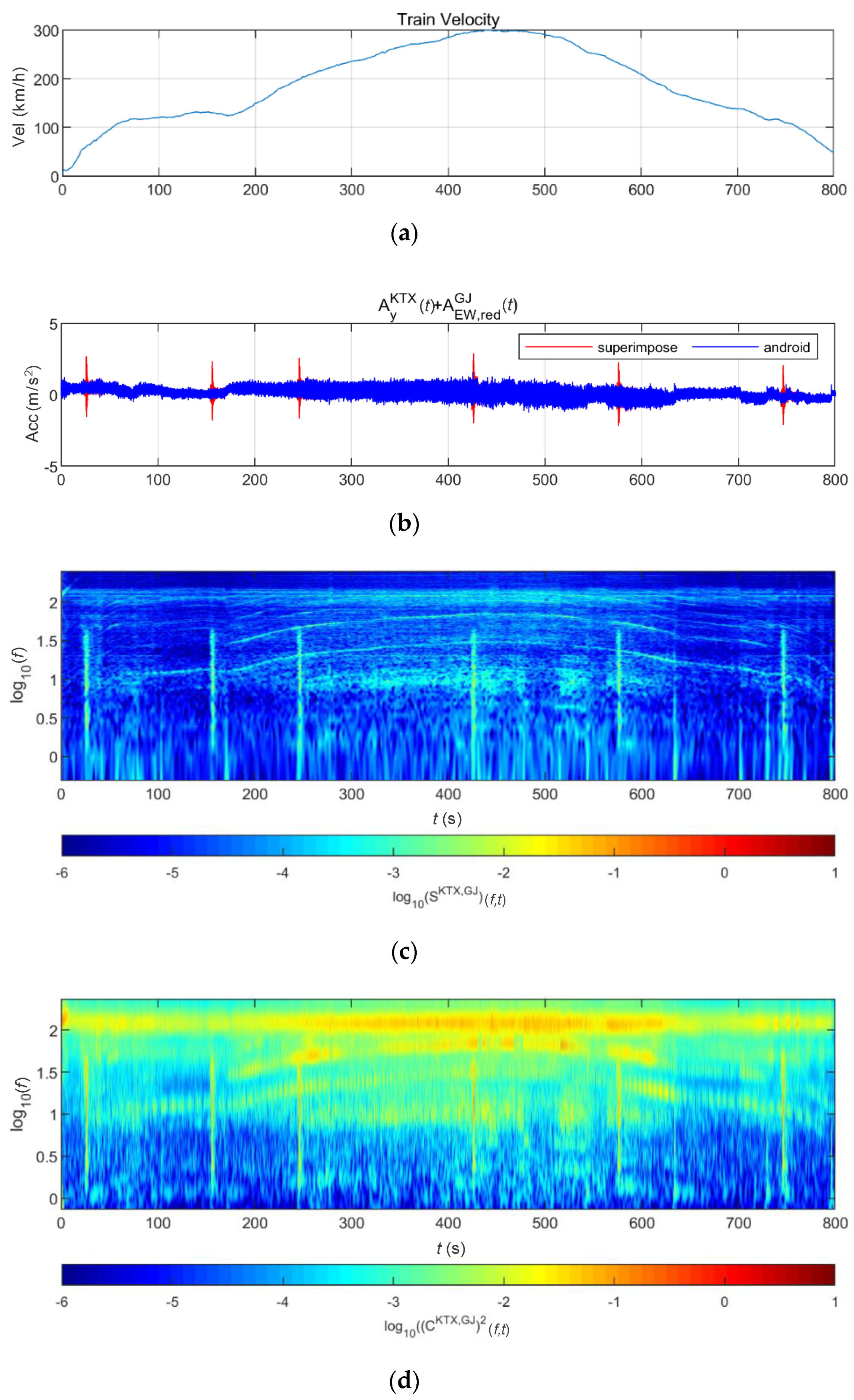
3.2.2. Train Data
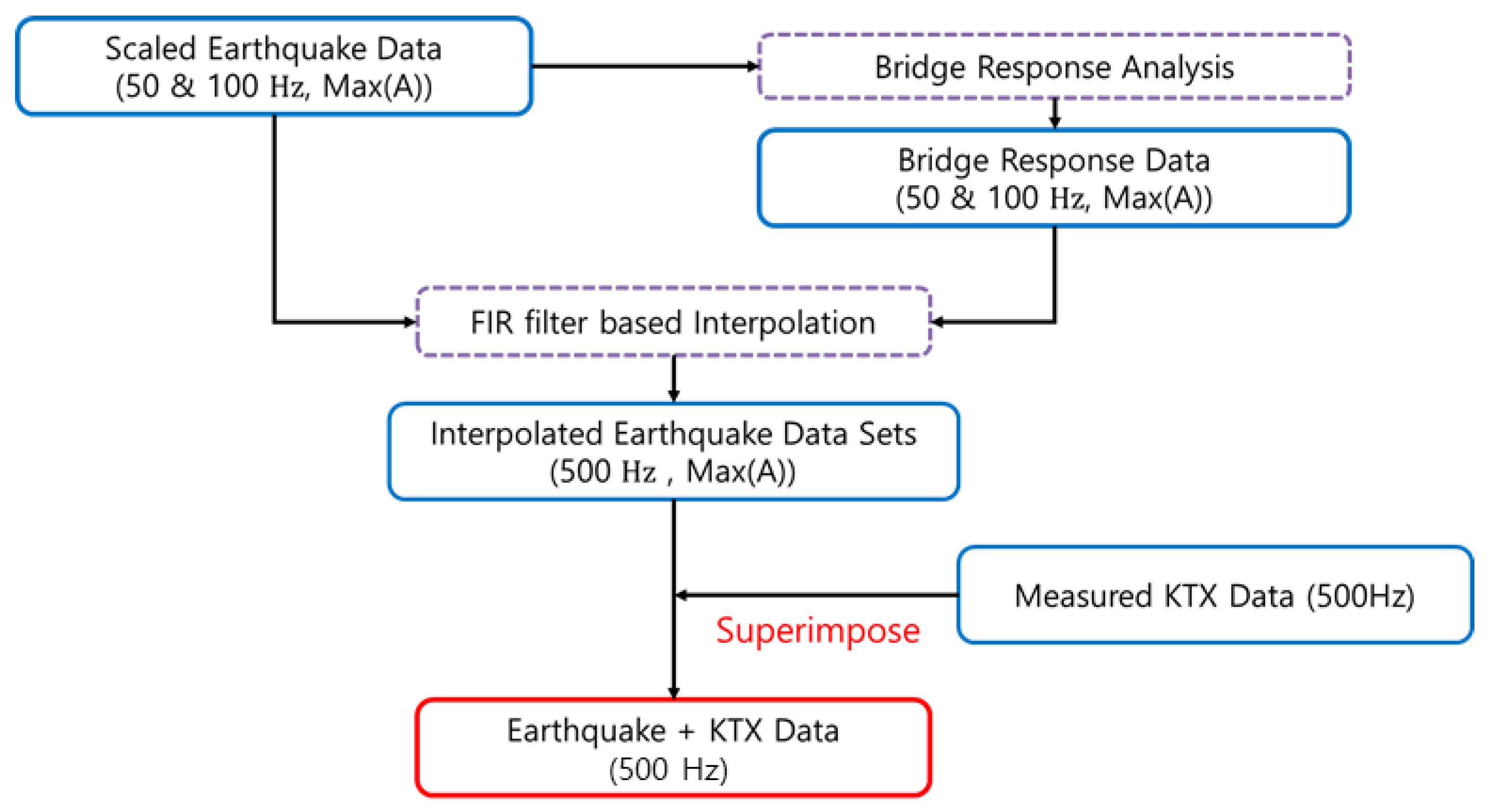
3.3. Data Synthesis
4. Results and Discussion
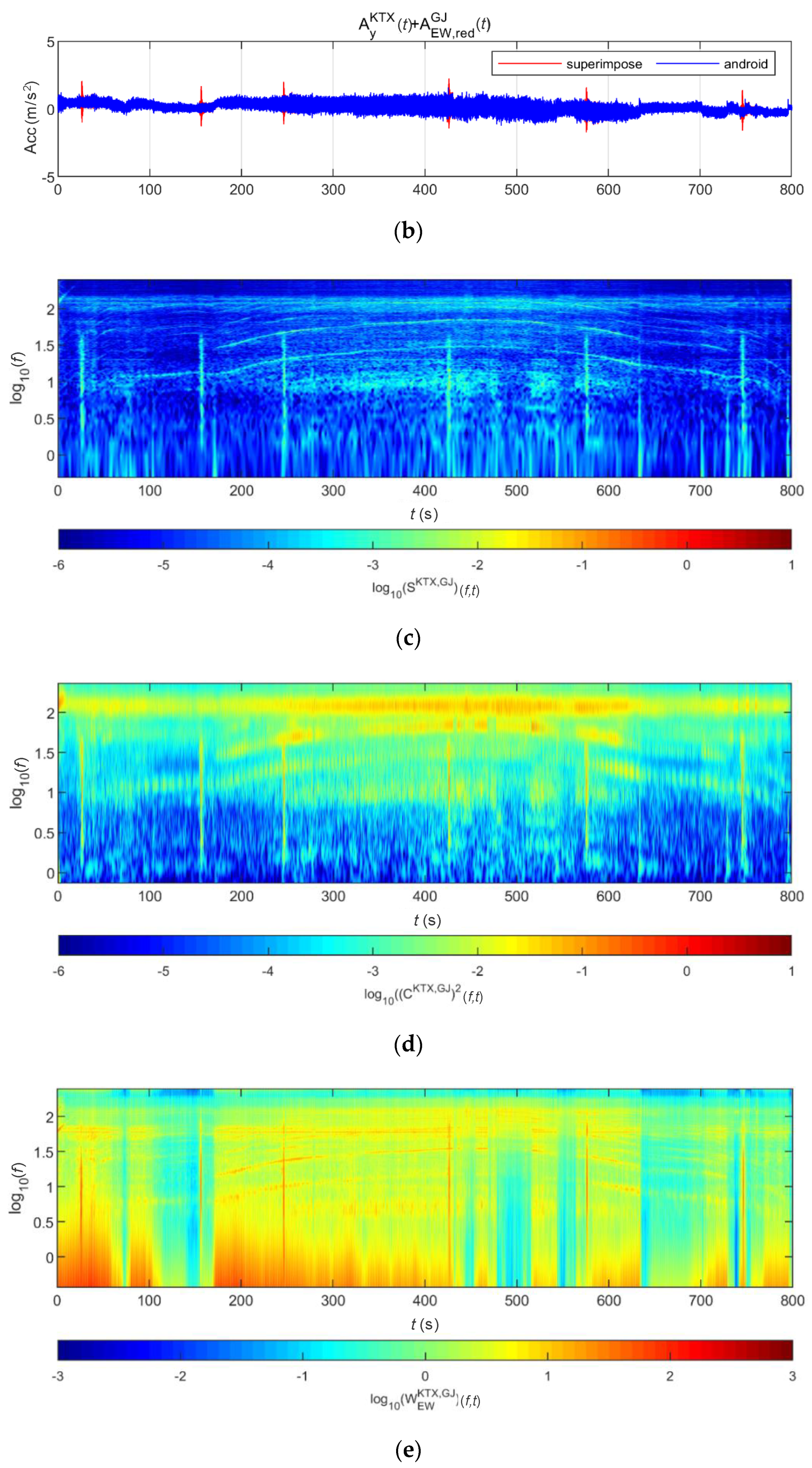
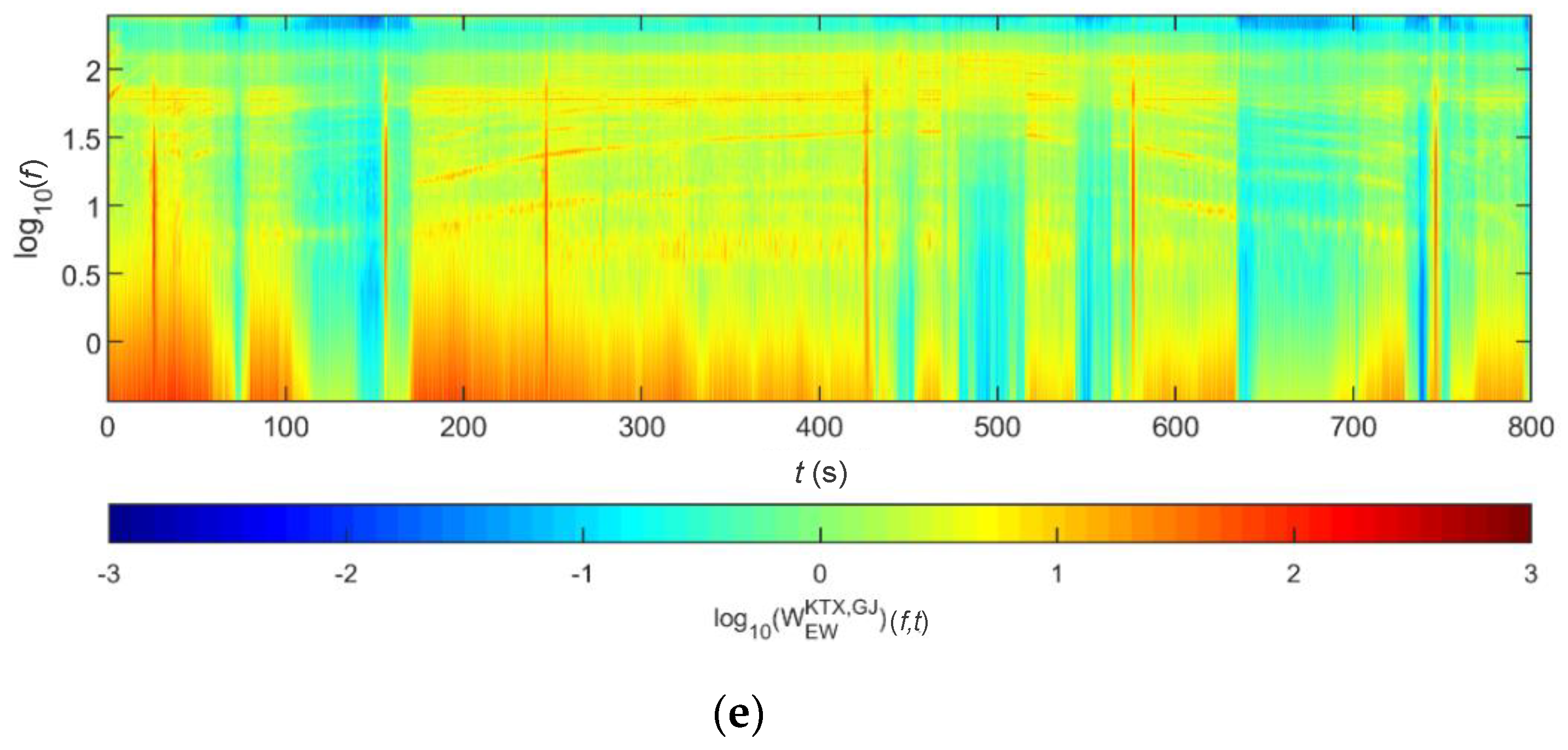
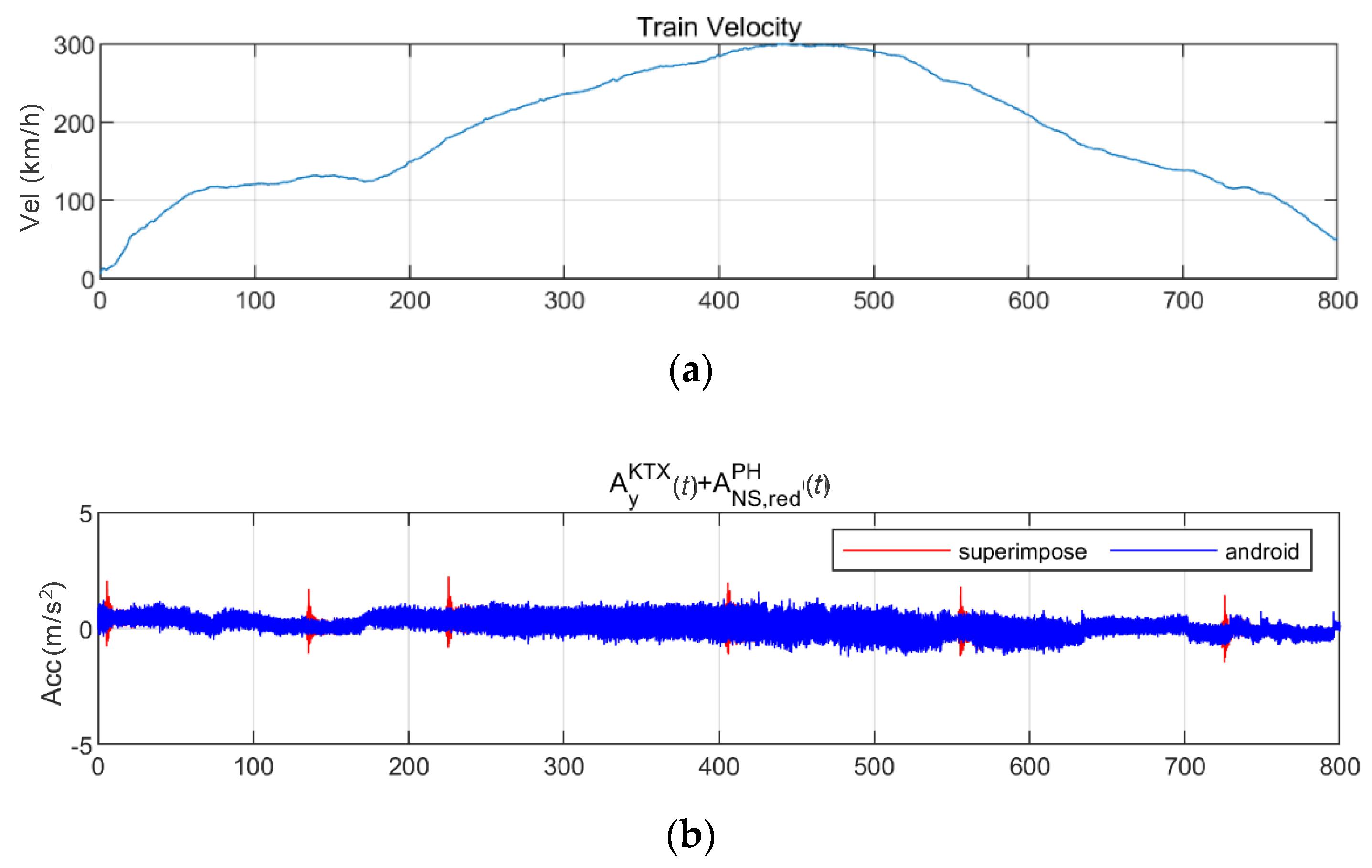
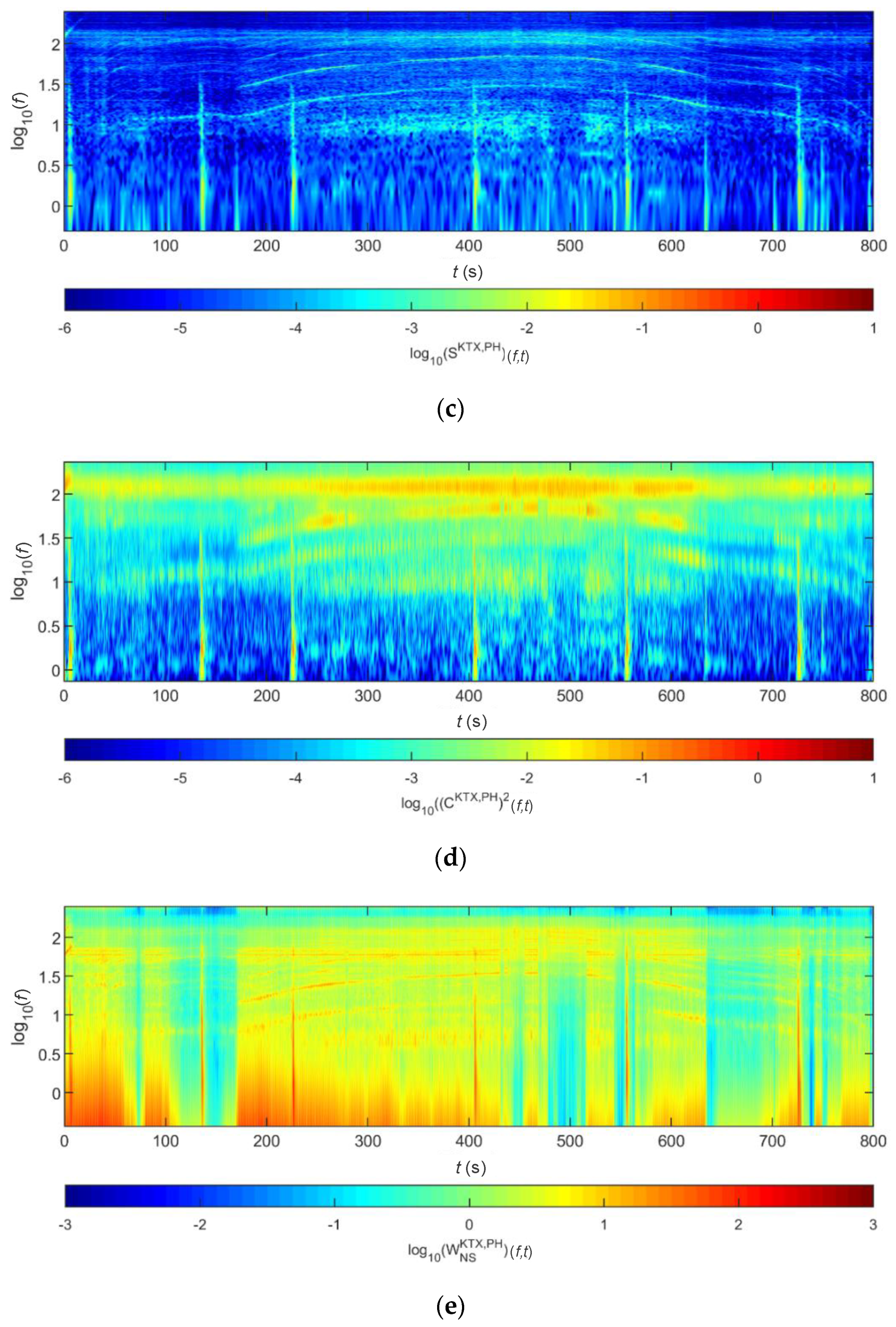
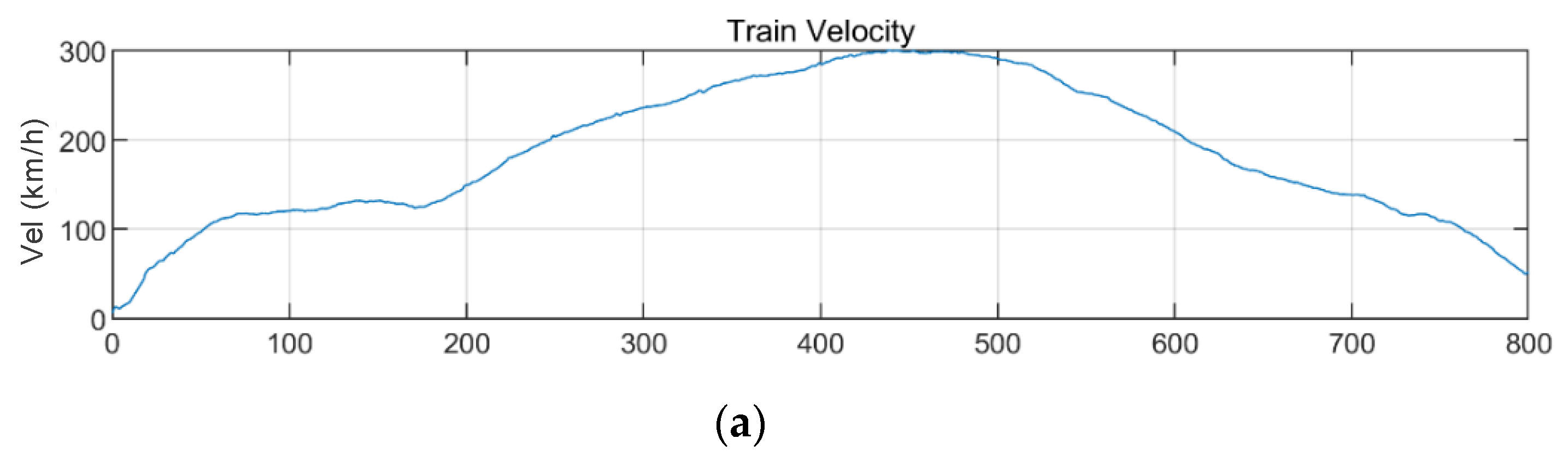
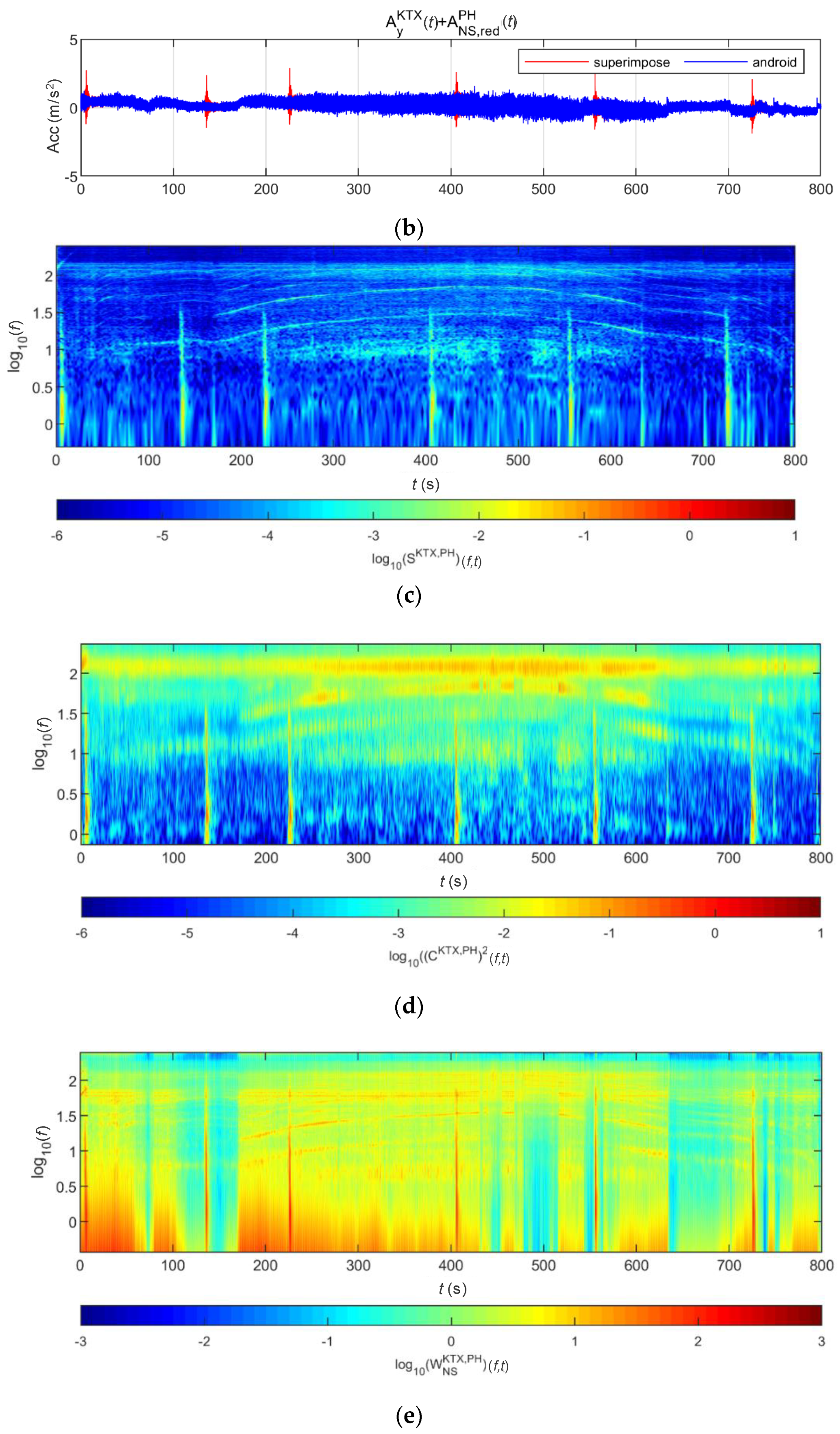
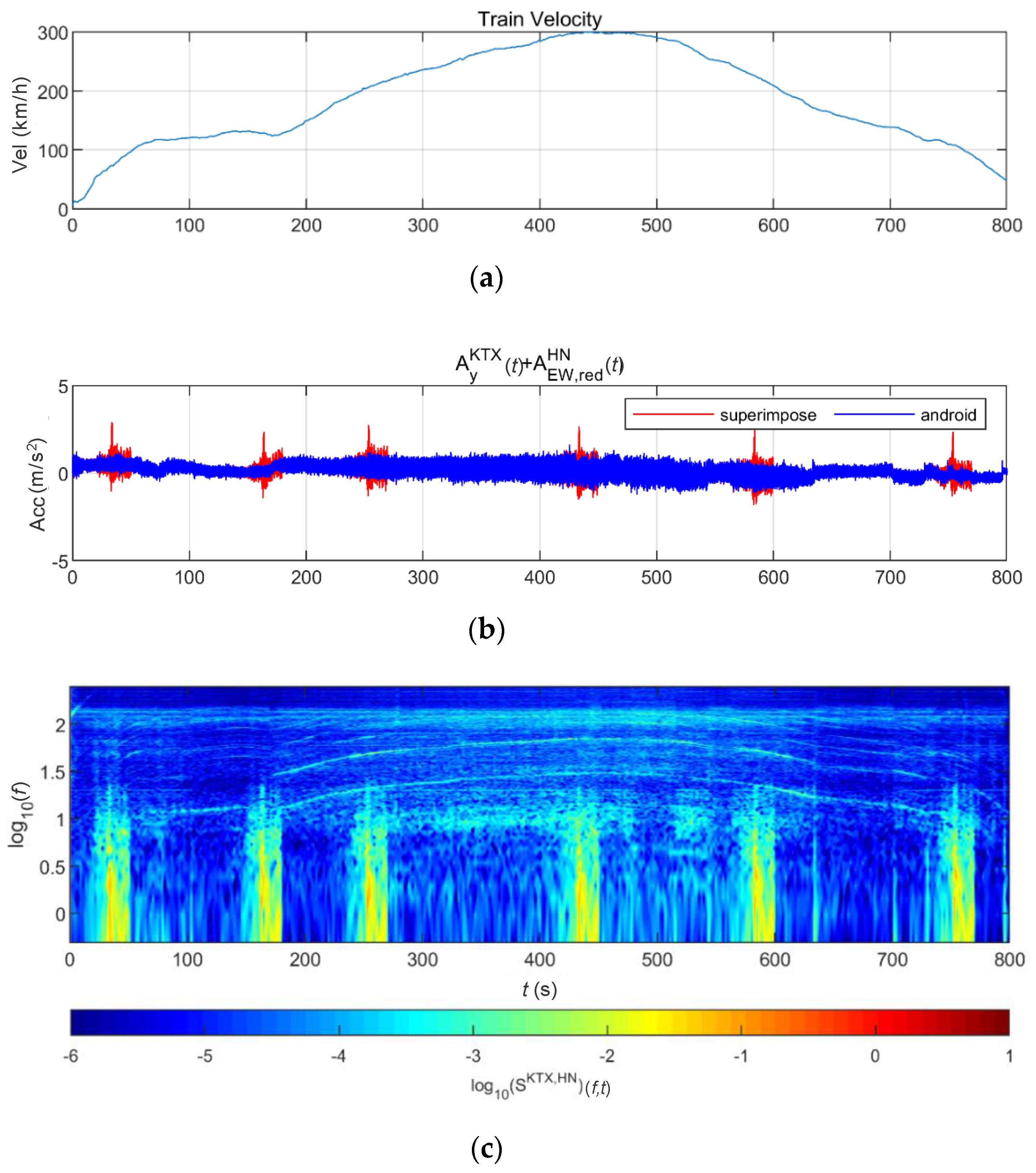
4.1. Train-Measured Seismic Data
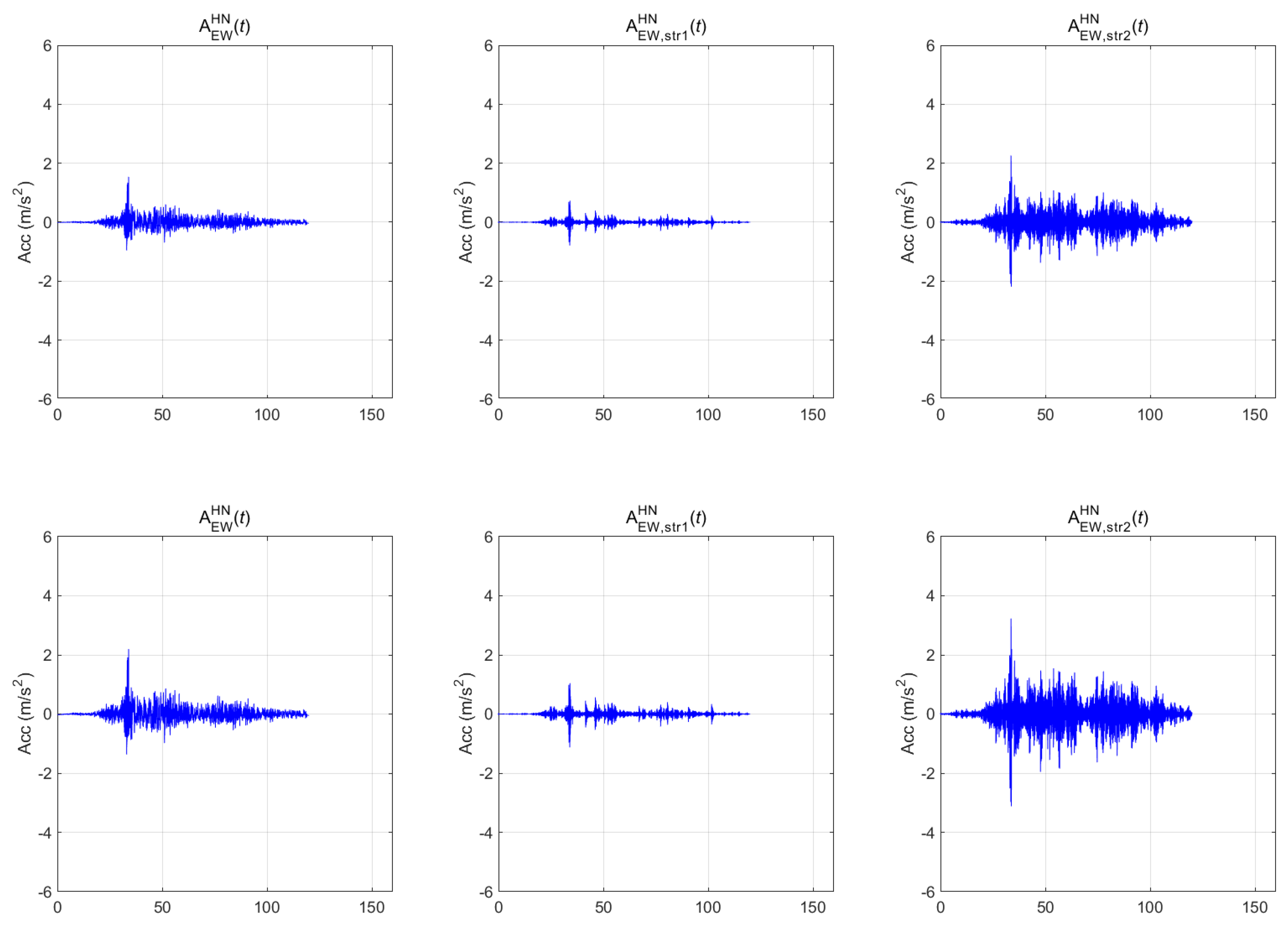
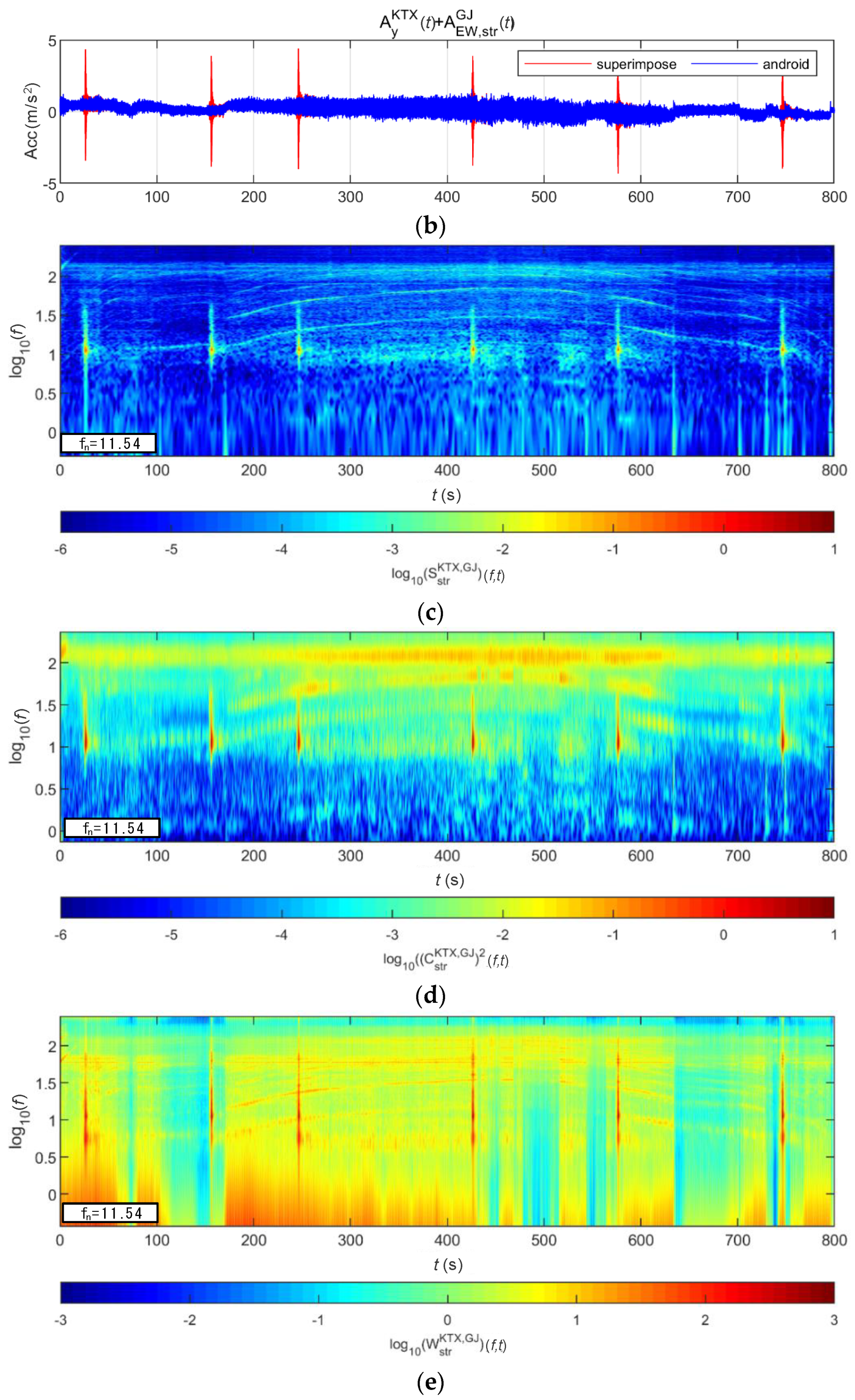
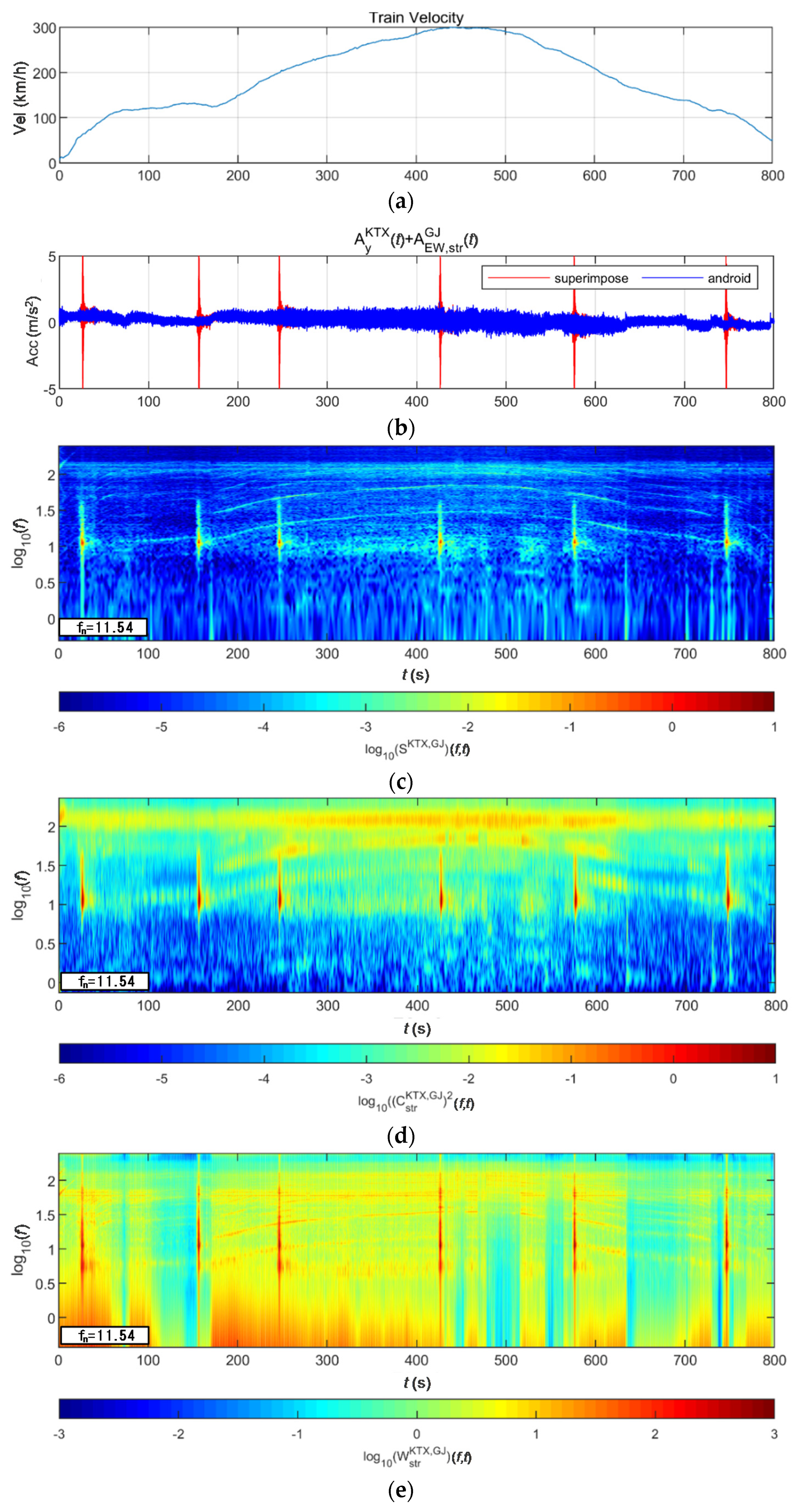
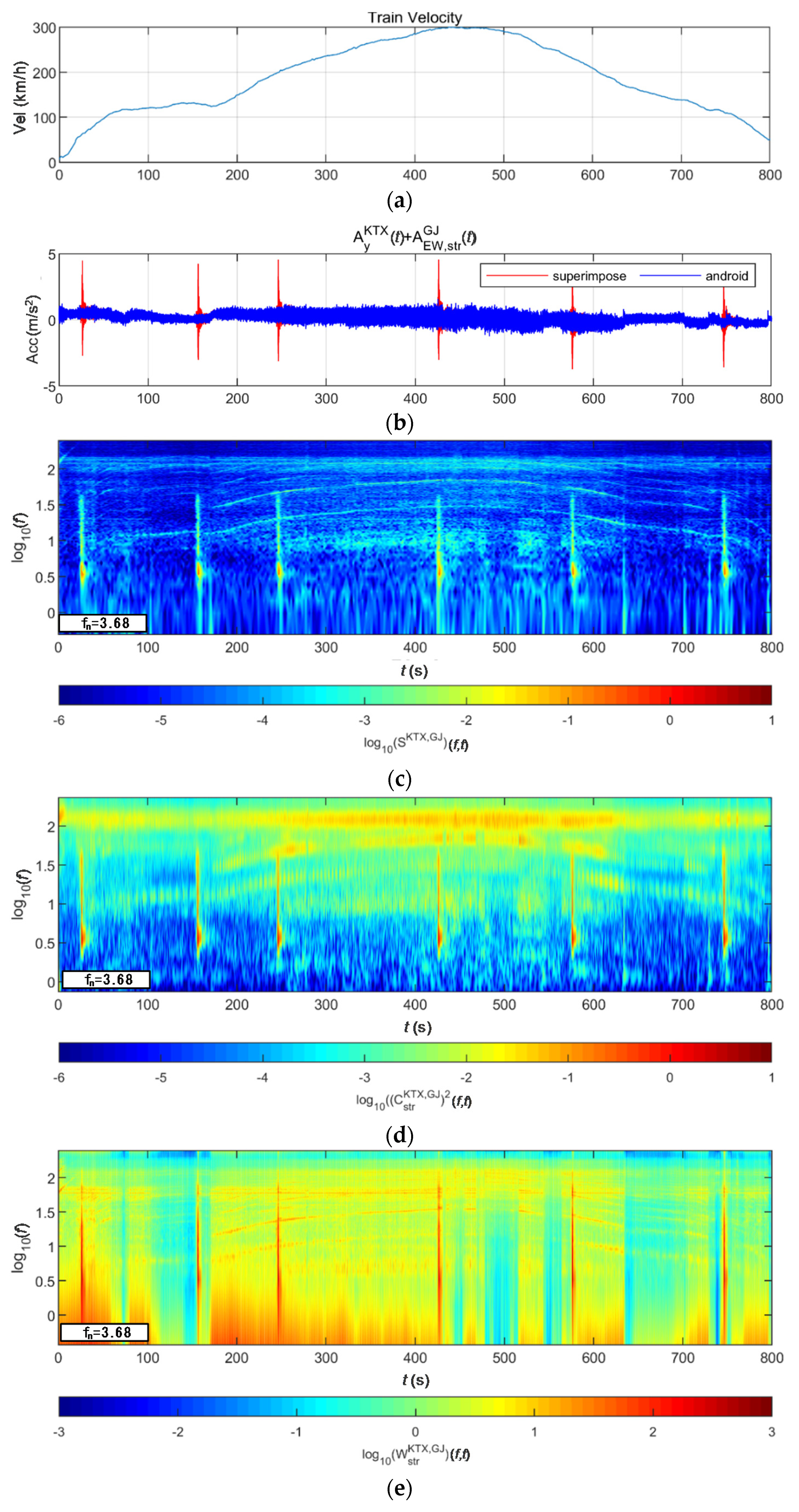
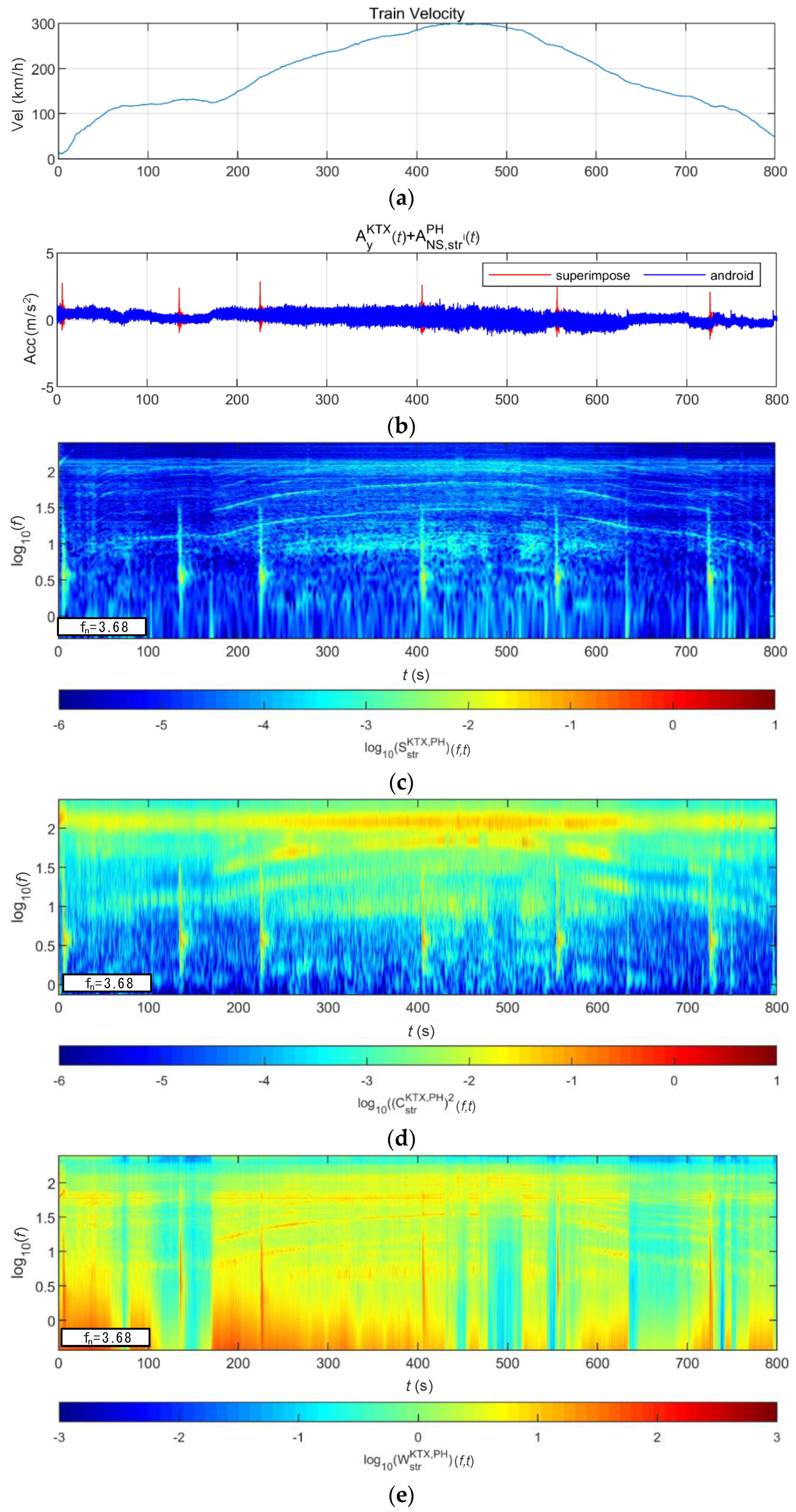
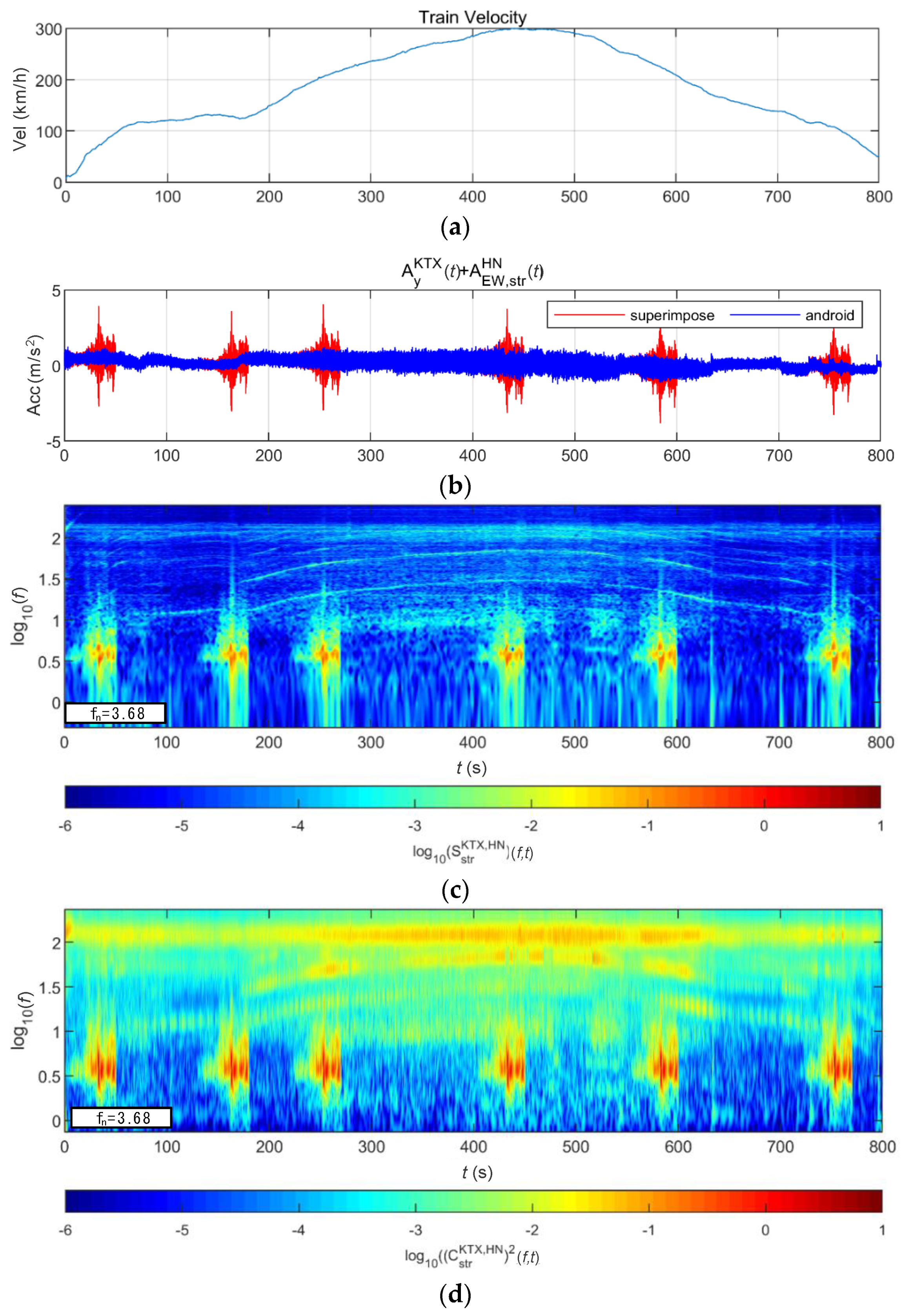
4.2. Train-Measured Bridge-Response Data
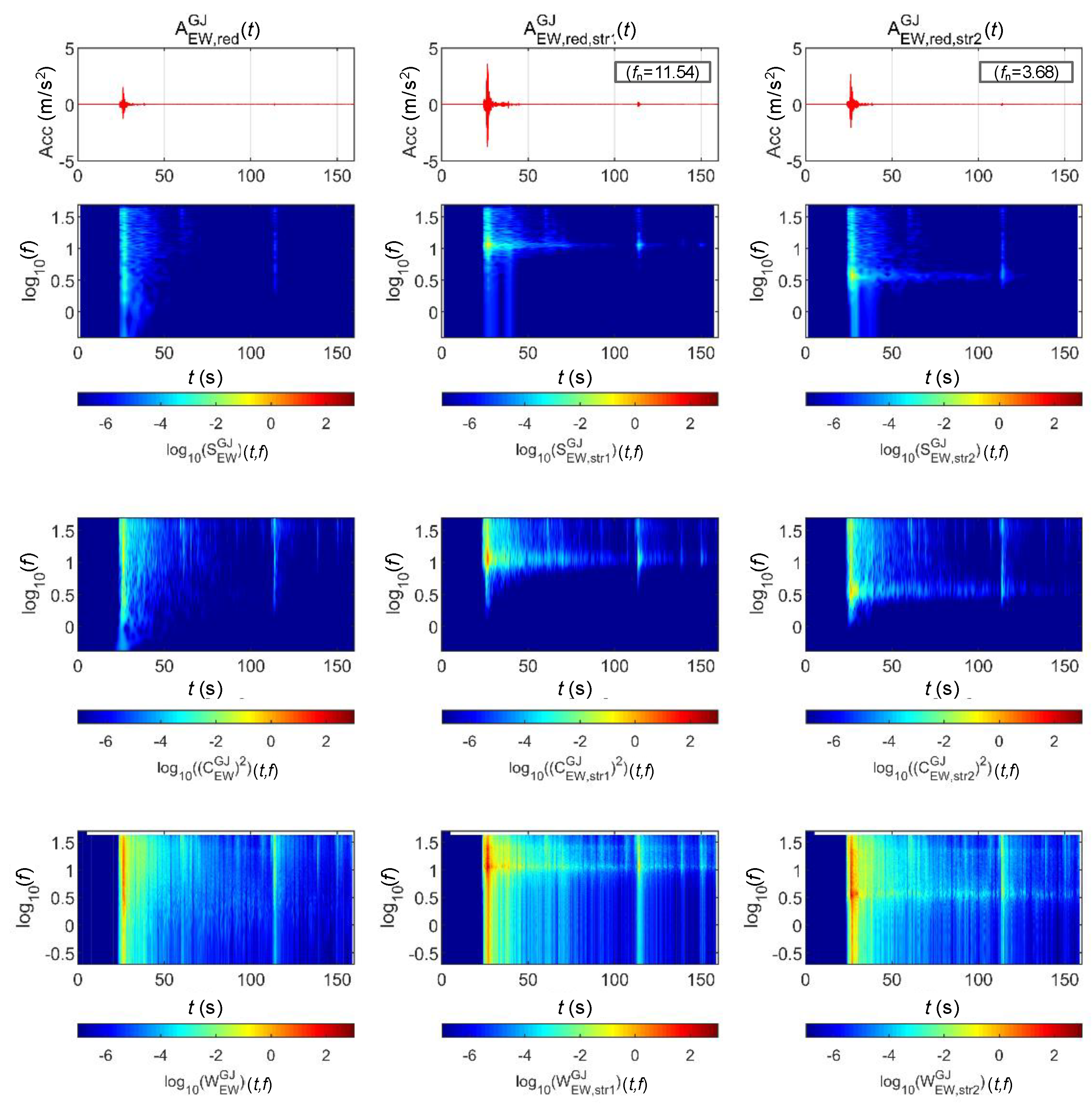
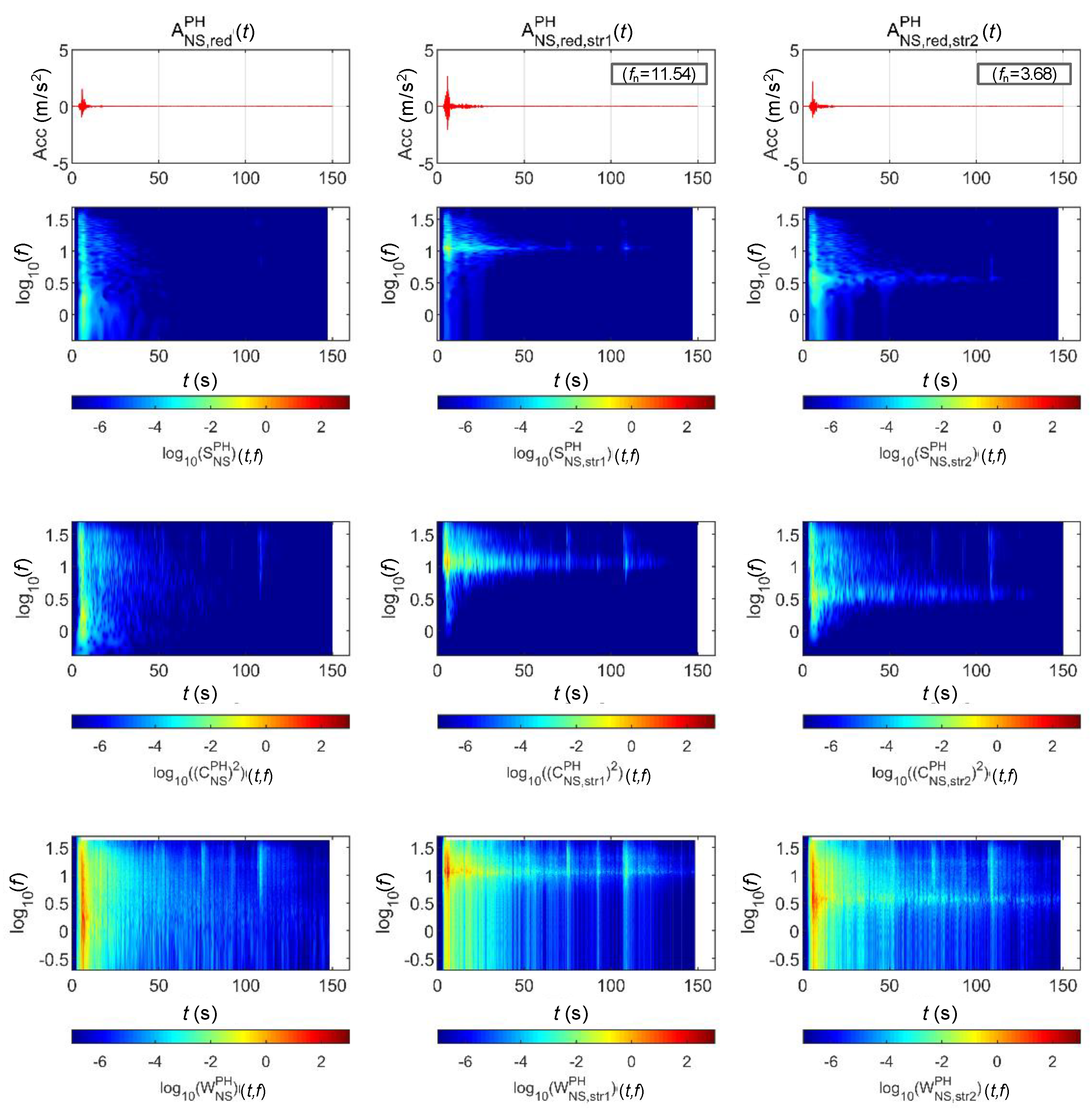
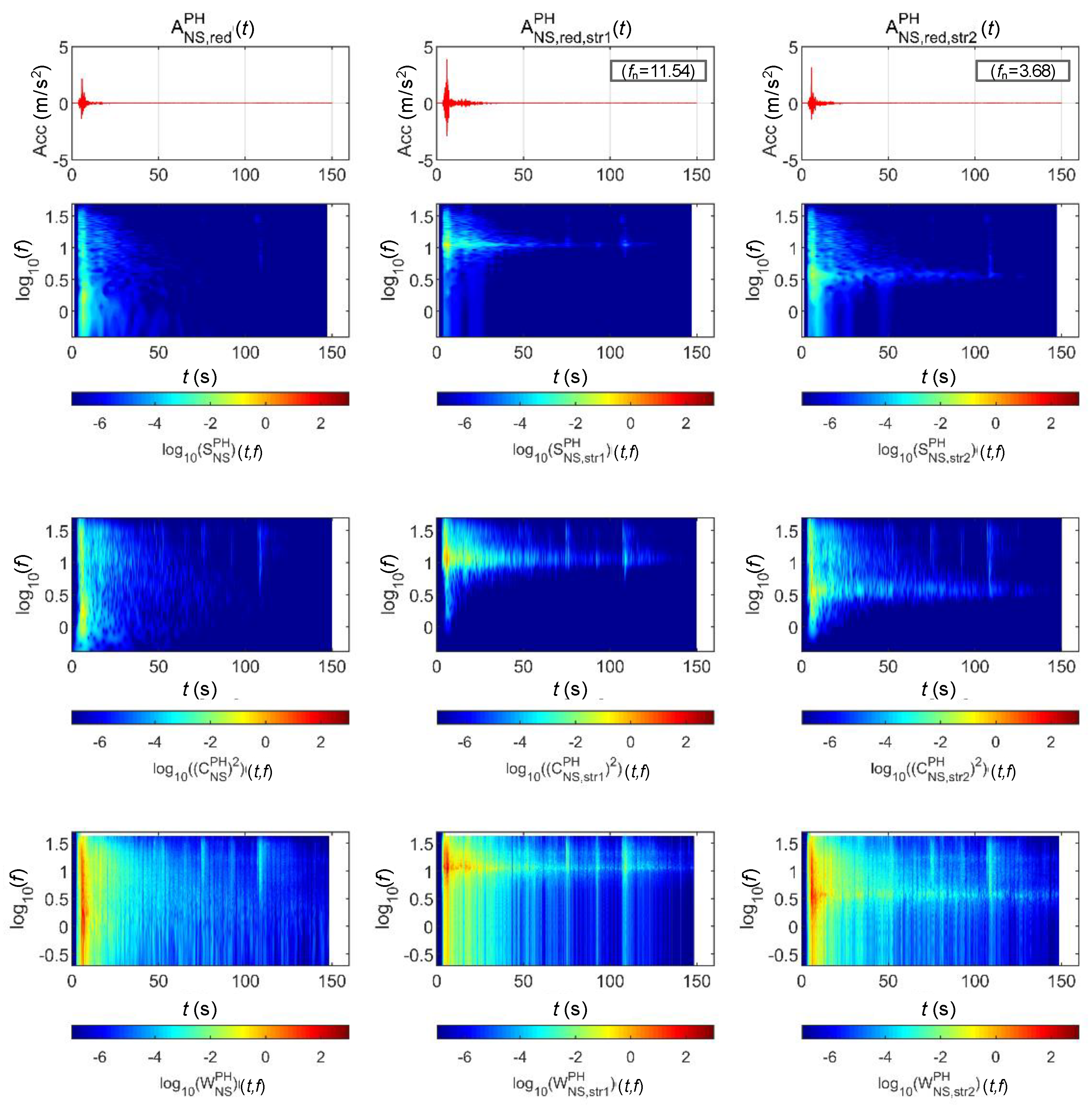
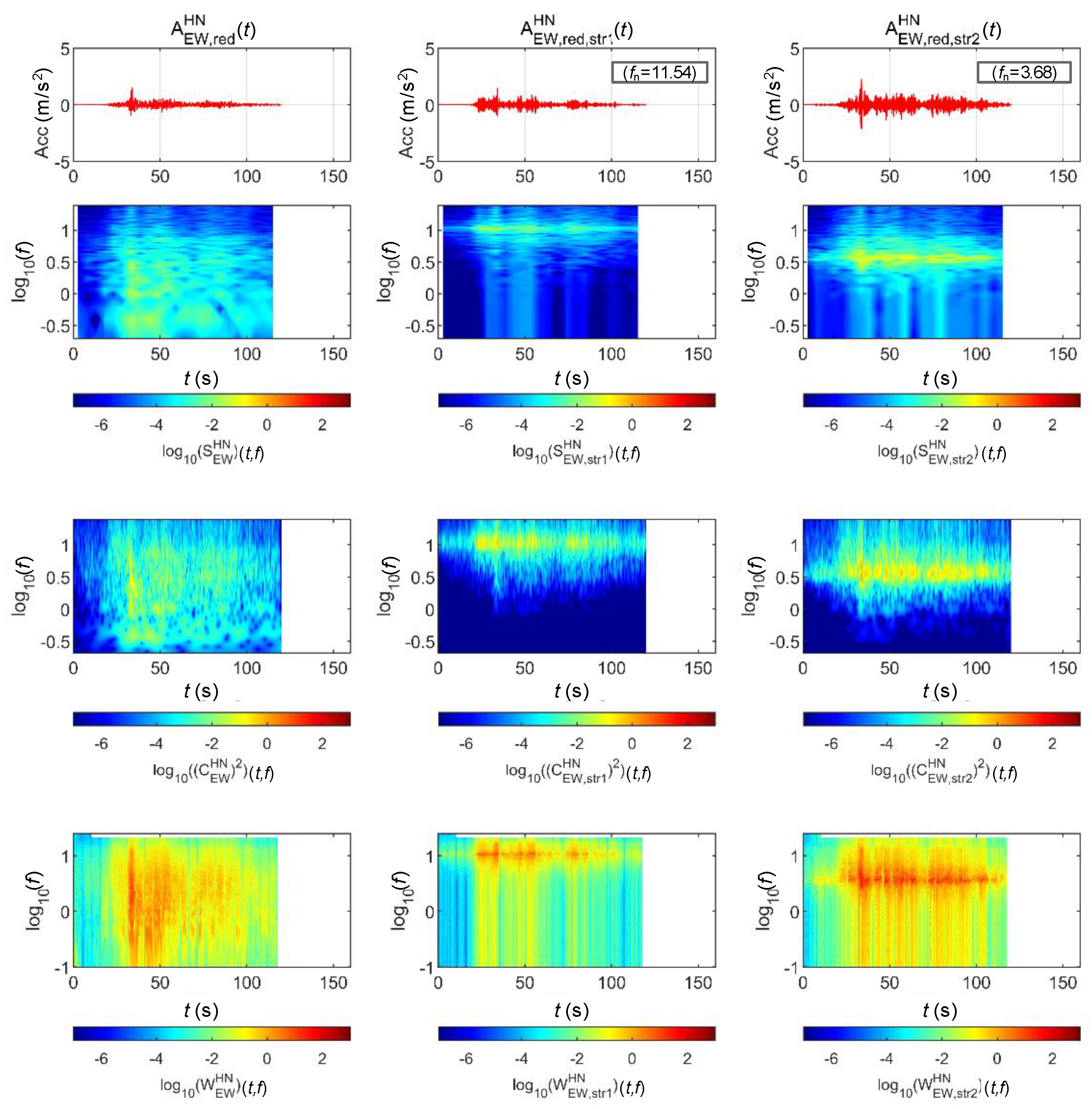
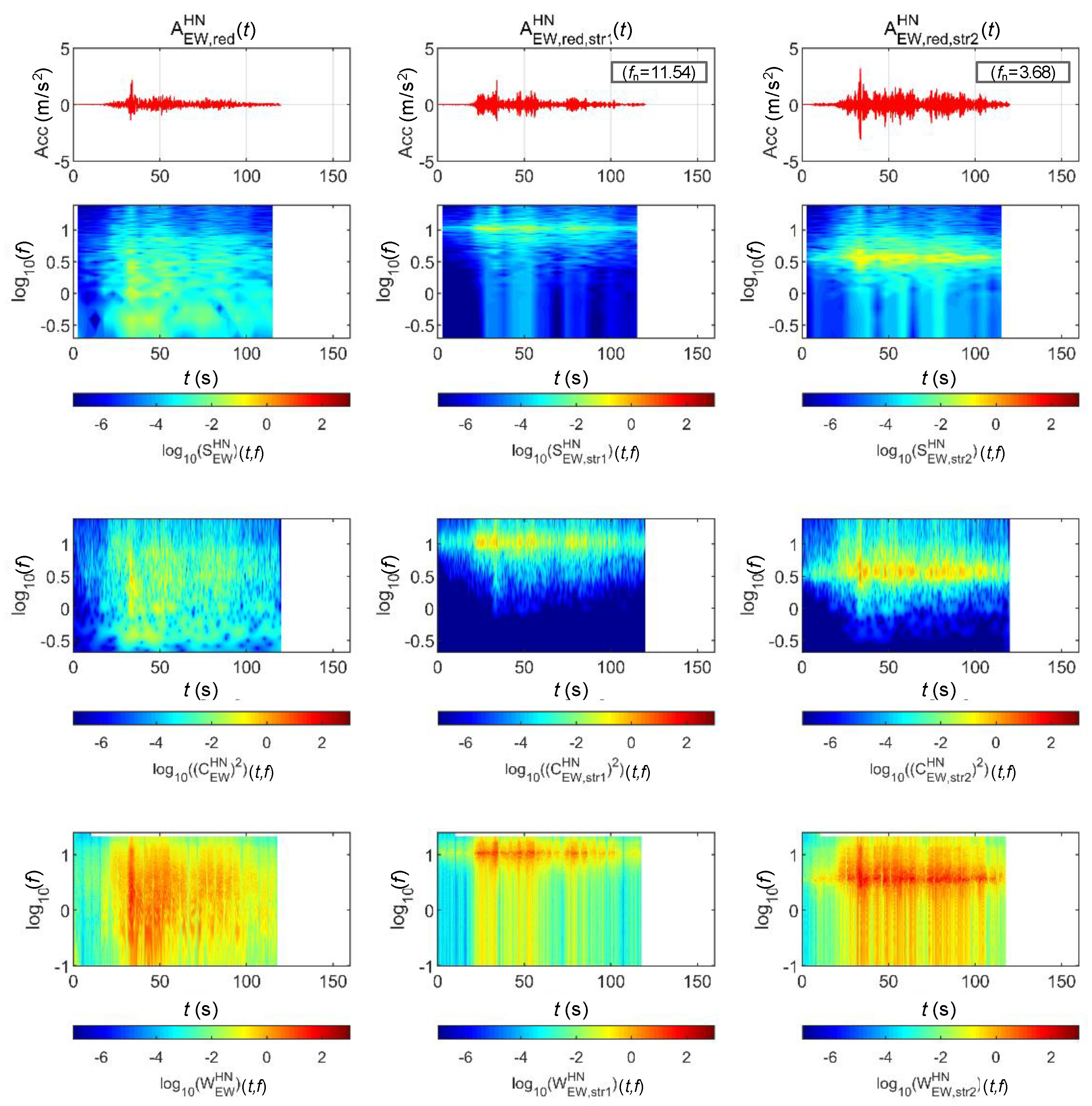
4.2.1. BR2 Bridge
4.2.2. BR3 Bridge
4.3. Computational Time
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Korea Meteorological Administration. Annual Report 2016: Korea Meteorological Administration; Korea Meteorological Administration: Seoul, Korea, 2016. Available online: http://www.kma.go.kr/download_01/yearbook_2016.pdf (accessed on 26 November 2020).
- Korea Meteorological Administration. Annual Report 2017: Korea Meteorological Administration; Korea Meteorological Administration: Seoul, Korea, 2017. Available online: http://www.kma.go.kr/download_01/yearbook_2017.pdf (accessed on 26 November 2020).
- Sheen, D.H.; Park, J.H.; Chi, H.C.; Hwang, E.H.; Lim, I.S.; Seong, Y.J.; Pak, J. The first stage of an earthquake early warning system in South Korea. Seismol. Res. Lett. 2017, 88, 1491–1498. [Google Scholar] [CrossRef]
- Nakamura, Y. UrEDAS, urgent earthquake detection and alarm system, now and future. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004; p. 209. [Google Scholar]
- Ashiya, K. Development of a New Early Earthquake Detection and Alarm System. Available online: https://www.rtri.or.jp/publish/qr/2002/v43_2/news1.html (accessed on 26 June 2020).
- Cochran, E.S.; Lawrence, J.F.; Christensen, C.; Jakka, R.S. The quake-catcher network: Citizen science expanding seismic horizons. Seismol. Res. Lett. 2009, 80, 26–30. [Google Scholar] [CrossRef]
- Cochran, E.S. To catch a quake. Nat. Commun. 2018, 9, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Neighbors, C.; Cochran, E.S.; Ryan, K.J.; Kaiser, A.E. Solving for source parameters using nested array data: A case study from the Canterbury, New Zealand earthquake sequence. Pure Appl. Geophys. 2017, 174, 875–893. [Google Scholar] [CrossRef]
- Kohler, M.D.; Guy, R.; Bunn, J.; Massari, A.; Clayton, R.; Heaton, T.; Chandy, K.M.; Ebrahimian, H.; Dorn, C. Community seismic network and localized earthquake situational awareness. In Proceedings of the 11th U.S. National Conference on Earthquake Engineering (11NCEE), Los Angeles, CA, USA, 25–29 June 2018; pp. 1–9. Available online: https://authors.library.caltech.edu/87838/1/Kohler_etal_11ncee_1675.pdf (accessed on 26 November 2020).
- Massari, A.; Kohler, M.; Clayton, R.; Guy, R.; Heaton, T.; Bunn, J.; Chandy, K.M.; Demetri, D. Dense building instrumentation application for city-wide structural health monitoring and resilience. In Proceedings of the 16th World Conference on Earthquake Engineering (16WCEE), Santiago, Chile, 9–13 January 2017; p. 3735. Available online: https://authors.library.caltech.edu/73802/2/Massari_etal_Paper%20N%C2%B0_3735.pdf (accessed on 26 November 2020).
- Clayton, R.W.; Heaton, T.; Kohler, M.; Chandy, M.; Guy, R.; Bunn, J. Community seismic network: A dense array to sense earthquake strong motions. Seismol. Res. Lett. 2015, 86, 1354–1363. [Google Scholar] [CrossRef] [Green Version]
- Faulkner, M.; Clayton, R.; Heaton, T.; Chandy, K.M.; Kohler, M.; Bunn, J.; Guy, R.; Liu, A.; Olson, M.; Cheng, M.H.; et al. Community sense and response systems: Your phone as quake detector. Commun. ACM 2014, 57, 66–75. [Google Scholar] [CrossRef]
- Kohler, M.D.; Heaton, T.H.; Cheng, M.H.; Singh, P. Structural health monitoring through dense instrumentation by community participants: The community seismic network and quake-catcher network. In Proceedings of the 10th U.S. National Conference on Earthquake Engineering (10NCEE), Anchorage, Alaska, 21–25 July 2014; Available online: https://authors.library.caltech.edu/64356/1/Kohler_10NCEE_2014.pdf (accessed on 26 November 2020).
- Kohler, M.D.; Heaton, T.H.; Cheng, M.H. The community seismic network and quake-catcher network: Enabling structural health monitoring through instrumentation by community participants. In Proceedings of the SPIE Smart Structures/Non-destructive Evaluation Conference, San Diego, CA, USA, 10–14 March 2013; p. 86923X. Available online: https://authors.library.caltech.edu/41435/1/Kohler_2013p86923.pdf (accessed on 26 November 2020).
- Clayton, R.; Heaton, T.; Chandy, M.; Krause, A.; Kohler, M.; Bunn, J.; Guy, R.; Olson, M.; Faulkner, M.; Cheng, M.H.; et al. Community seismic network. Ann. Geophys. 2011, 54, 6. [Google Scholar]
- Kong, Q.; Allen, R.M.; Schreier, L. MyShake: Initial observations from a global smartphone seismic network. Geophys. Res. Lett. 2016, 106, 9588–9594. [Google Scholar] [CrossRef]
- Kong, Q.; Allen, R.M.; Schreier, L.; Kwon, Y.-W. MyShake: A smartphone seismic network for earthquake early warning and beyond. Sci. Adv. 2016, 2, e1501055. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.M.; Kong, Q.; Martin-Short, R. The MyShake platform: A global vision for earthquake early warning. Pure Appl. Geophys. 2020, 177, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Moon, J.S.; Yoo, M. Development of a seismic detection technology for high-speed trains using signal analysis techniques. Sensors 2020, 20, 3708. [Google Scholar] [CrossRef] [PubMed]
- Midorikawa, S.; Miura, H. Re-digitization of Strong Motion Accelerogram at Hachinohe Harbor during the 1968 Tokachi-oki, Japan Earthquake. J. Jpn. Assoc. Earthq. Eng. 2011, 10, 12–21. [Google Scholar] [CrossRef] [Green Version]
- The Ministry of Land, Infrastructure and Transport, Korean Design Standard, KDS 17 10 00 2018. Available online: http://www.kcsc.re.kr (accessed on 26 November 2020).
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]
- Griffin, D.; Lim, J. Signal estimation from modified short-time Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 236–243. [Google Scholar] [CrossRef]
- Zhong, J.; Huang, Y. Time-frequency representation based on an adaptive short-time Fourier transform. IEEE Trans. Signal Process. 2010, 58, 5118–5128. [Google Scholar] [CrossRef]
- Wongsaroj, W.; Hamdani, A.; Thong-Un, N.; Takahashi, H.; Kikura, H. Extended short-time fourier transform for ultrasonic velocity profiler on two-phase bubbly flow using a single resonant frequency. Appl. Sci. 2019, 9, 50. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.; Ko, D.K.; Lim, S.C.; Kim, H.S. Structural vibration-based classification and prediction of delamination in smart composite laminates using deep learning neural network. Compos. Part B Eng. 2019, 161, 586–594. [Google Scholar] [CrossRef]
- Pan, X.; Cheng, Z.; Zheng, Z.; Zhang, Y. Sparse Bayesian learning beamforming combined with short-time Fourier transform for fault detection of wind turbine blades. J. Acoust. Soc. Am. 2019, 145, 1802. [Google Scholar] [CrossRef]
- Lei, J.; Liu, C.; Jiang, D. Fault diagnosis of wind turbine based on Long Short-term memory networks. Renew. Energy 2019, 133, 422–432. [Google Scholar] [CrossRef]
- Sinha, S.; Routh, P.S.; Anno, P.D.; Castagna, J.P. Spectral decomposition of seismic data with continuous-wavelet transform. Geophysics 2005, 70, 19–25. [Google Scholar] [CrossRef]
- Liu, W.; Cao, S.; Chen, Y. Seismic time-frequency analysis via empirical wavelet transform. IEEE Geosci. Remote Sens. Lett. 2015, 13, 28–32. [Google Scholar] [CrossRef]
- Anvari, R.; Siahsar, M.A.N.; Gholtashi, S.; Kahoo, A.R.; Mohammadi, M. Seismic random noise attenuation using synchrosqueezed wavelet transform and low-rank signal matrix approximation. IEEE Trans. on Geosci. Remote Sens. 2017, 55, 6574–6581. [Google Scholar] [CrossRef]
- Ukil, A.; Živanović, R. Abrupt change detection in power system fault analysis using adaptive whitening filter and wavelet transform. Electr. Power Syst. Res. 2006, 76, 815–823. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.Q.; Yan, Y. A wavelet-based approach to abrupt fault detection and diagnosis of sensors. IEEE Trans. Instrum. Meas. 2001, 50, 1389–1396. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, H.; Zeng, J.; Ma, L.; Guan, L. Short-term dynamic radar quantitative precipitation estimation based on wavelet transform and support vector machine. J. Meteorol. Res. 2020, 4, 413–426. [Google Scholar] [CrossRef]
- Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Huerta-Lopez, C.I.; Shin, Y.; Powers, E.J.; Roesset, J.M. Time-Frequency Analysis of Earthquake records. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; Available online: https://www.iitk.ac.in/nicee/wcee/article/1724.pdf (accessed on 26 November 2020).
- Kalra, M.; Kumar, S.; Das, B. Moving ground target detection with seismic signal using smooth pseudo Wigner–Ville distribution. IEEE Trans. Instrum. Meas. 2020, 69, 3896–3906. [Google Scholar] [CrossRef]
- Wu, X.; Liu, T. Spectral decomposition of seismic data with reassigned smoothed pseudo Wigner–Ville distribution. J. Appl. Geophys. 2009, 68, 386–393. [Google Scholar] [CrossRef]
- Shekar, B.; Nanda, D. Seismic spectral decomposition with smoothed pseudo Wigner-Ville distribution. In Proceedings of the 80th EAGE Conference and Exhibition 2018, European Association of Geoscientists & Engineers, Copenhagen, Denmark, 10 June–15 July 2018; pp. 1–5. [Google Scholar]
- Staszewski, W.J.; Worden, K.; Tomlinson, G.R. Time-frequency analysis in gearbox fault detection using the Wigner–Ville distribution and pattern recognition. Mech. Syst. Signal Process. 1997, 11, 673–692. [Google Scholar] [CrossRef]
- Shin, Y.S.; Jeon, J.J. Pseudo Wigner-Ville time-frequency distribution and its application to machinery condition monitoring. Shock Vib. 1993, 1, 65–76. [Google Scholar] [CrossRef]
- Pukhova, V.M.; Kustov, T.V.; Ferrini, G. Time-frequency analysis of non-stationary signals. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow, Russia, 29 January–1 February 2018; pp. 1141–1145. [Google Scholar]
- Tang, B.; Liu, W.; Song, T. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution. Renew. Energy 2010, 35, 2862–2866. [Google Scholar] [CrossRef]
- Chi, P.J.; Russell, C.T. Use of the Wigner-Ville distribution in interpreting and identifying ULF waves in triaxial magnetic records. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Wang, C.; Liu, W. Nonstationary vibration signal analysis using wavelet-based time-frequency filter and Wigner–Ville distribution. ASME J. Vib. Acoust. 2016, 138, 051009. [Google Scholar] [CrossRef]
- Taebi, A.; Mansy, H.A. Analysis of seismocardiographic signals using polynomial chirplet transform and smoothed pseudo Wigner-Ville distribution. In Proceedings of the 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 2 December 2017; pp. 1–6. [Google Scholar]
- Bouchikhi, E.H.; Choqueuse, V.; Benbouzid, M.E.H.; Charpentier, J.F.; Barakat, G. A comparative study of time-frequency representations for fault detection in wind turbine. In Proceedings of the 37th Annual Conference of the IEEE Industrial Electronics Society (IECON 2011), Melbourne, VIC, Australia, 7–10 November 2011; pp. 3584–3589. [Google Scholar]
- Fedotenkova, M. Extraction de Composants Multivariés des Signaux Cérébraux Obtenus Pendant L’anesthésie Générale. Ph.D Thesis, Université de Lorraine, Nancy and Metz, Grand Est, France, December 2016. [Google Scholar]
- Auger, F.; Flandrin, P.; Gonçalvès, P.; Lemoine, O. Time-Frequency Toolbox For Use with MATLAB; CNRS: Paris, France, 1995. [Google Scholar]
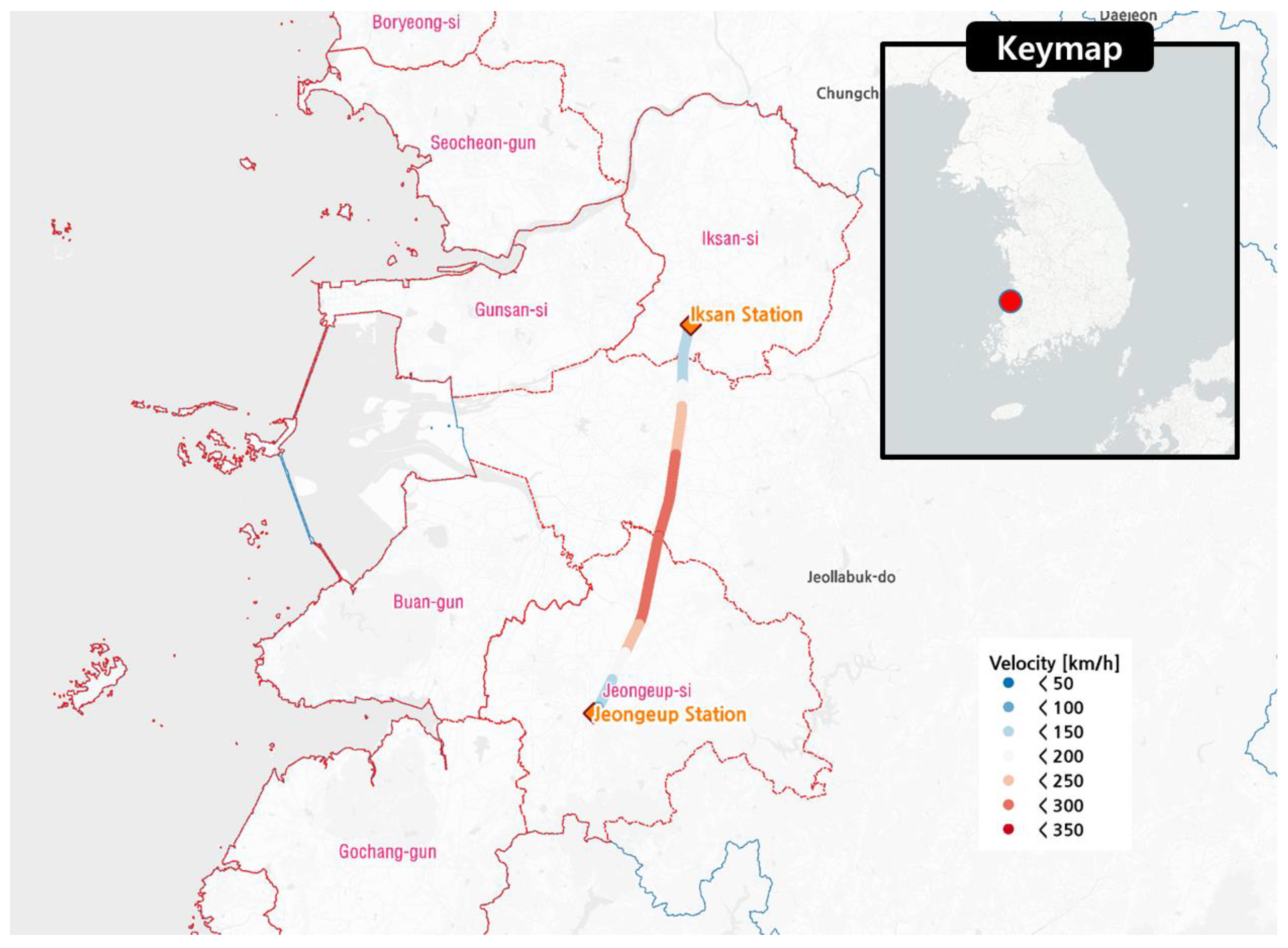
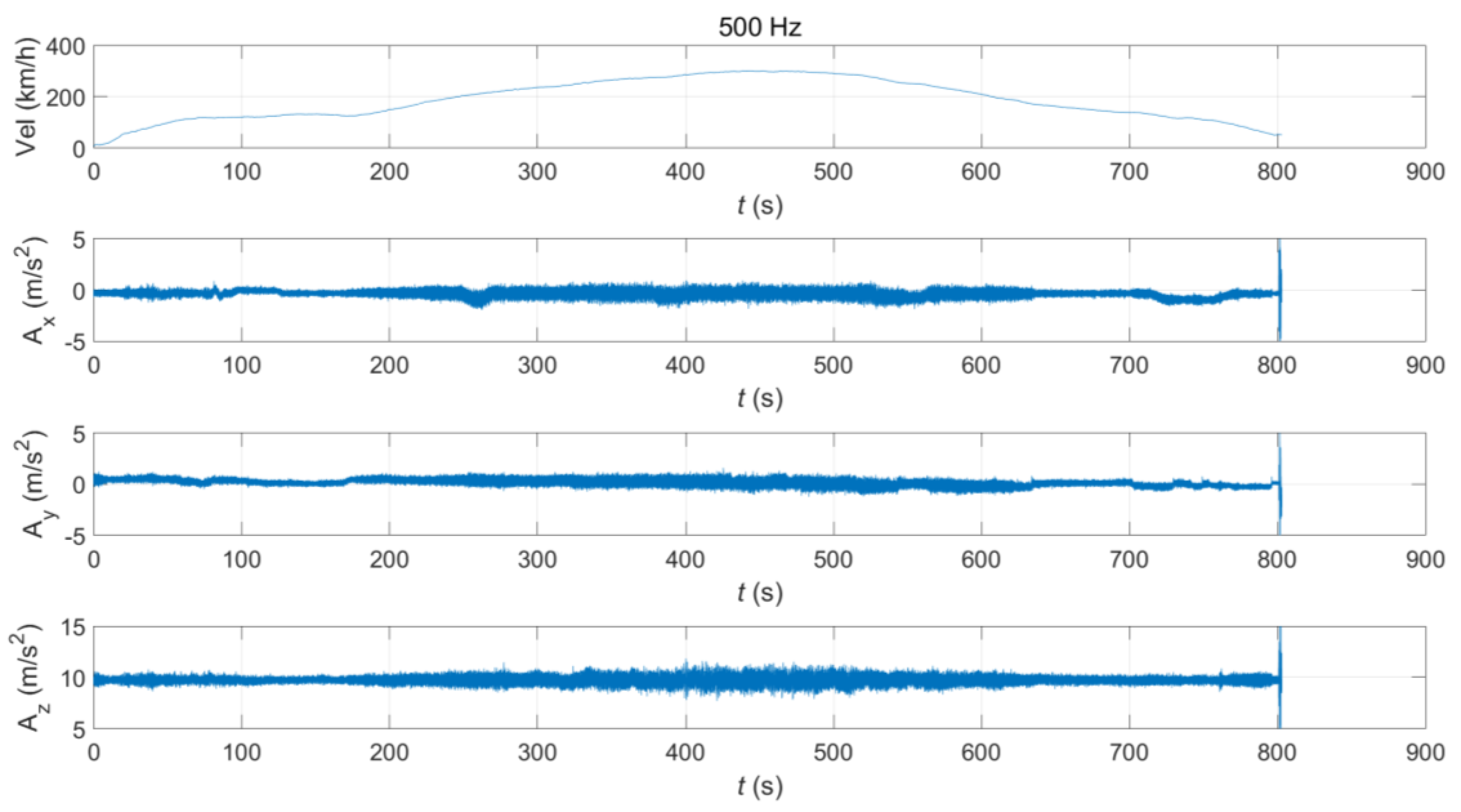
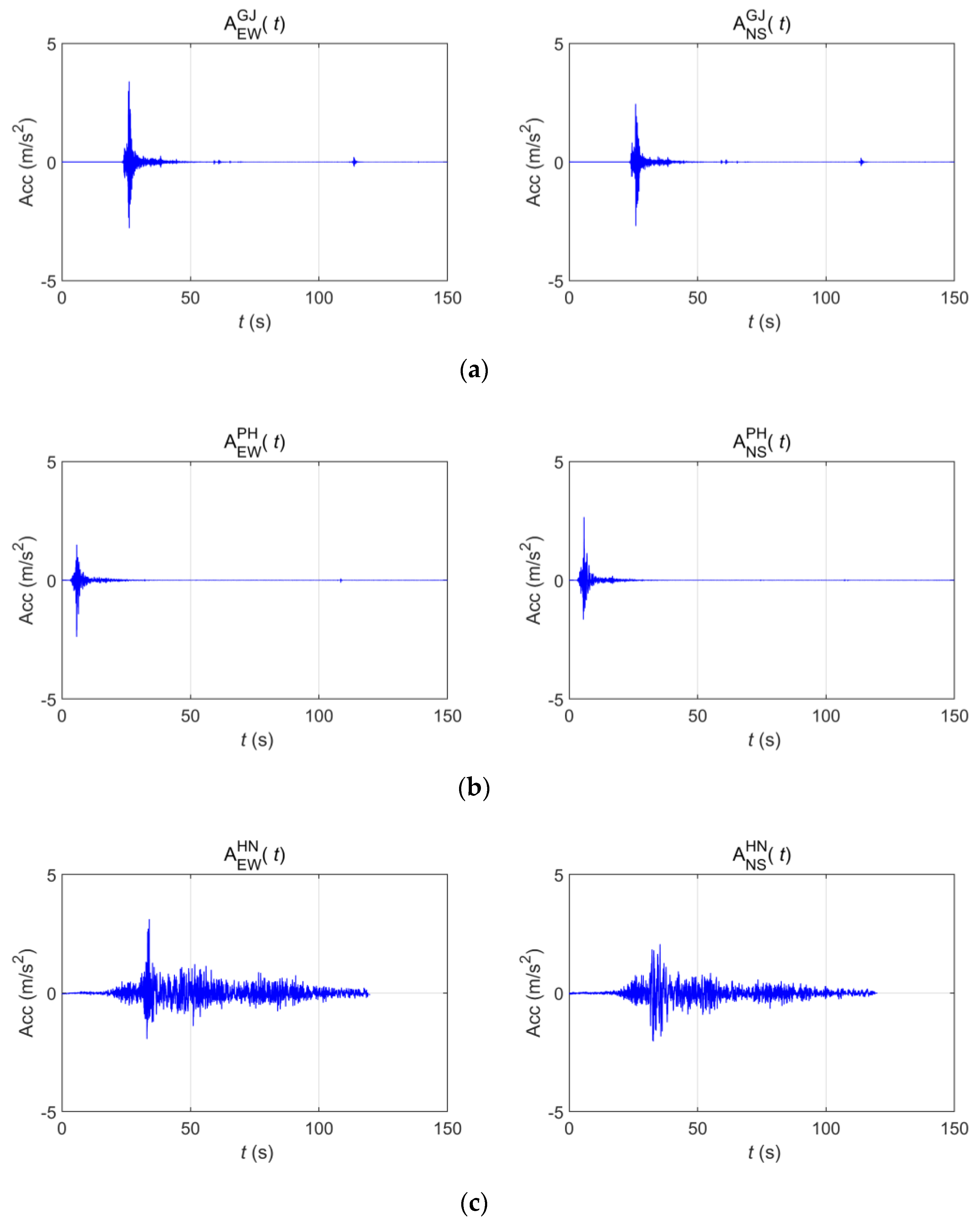
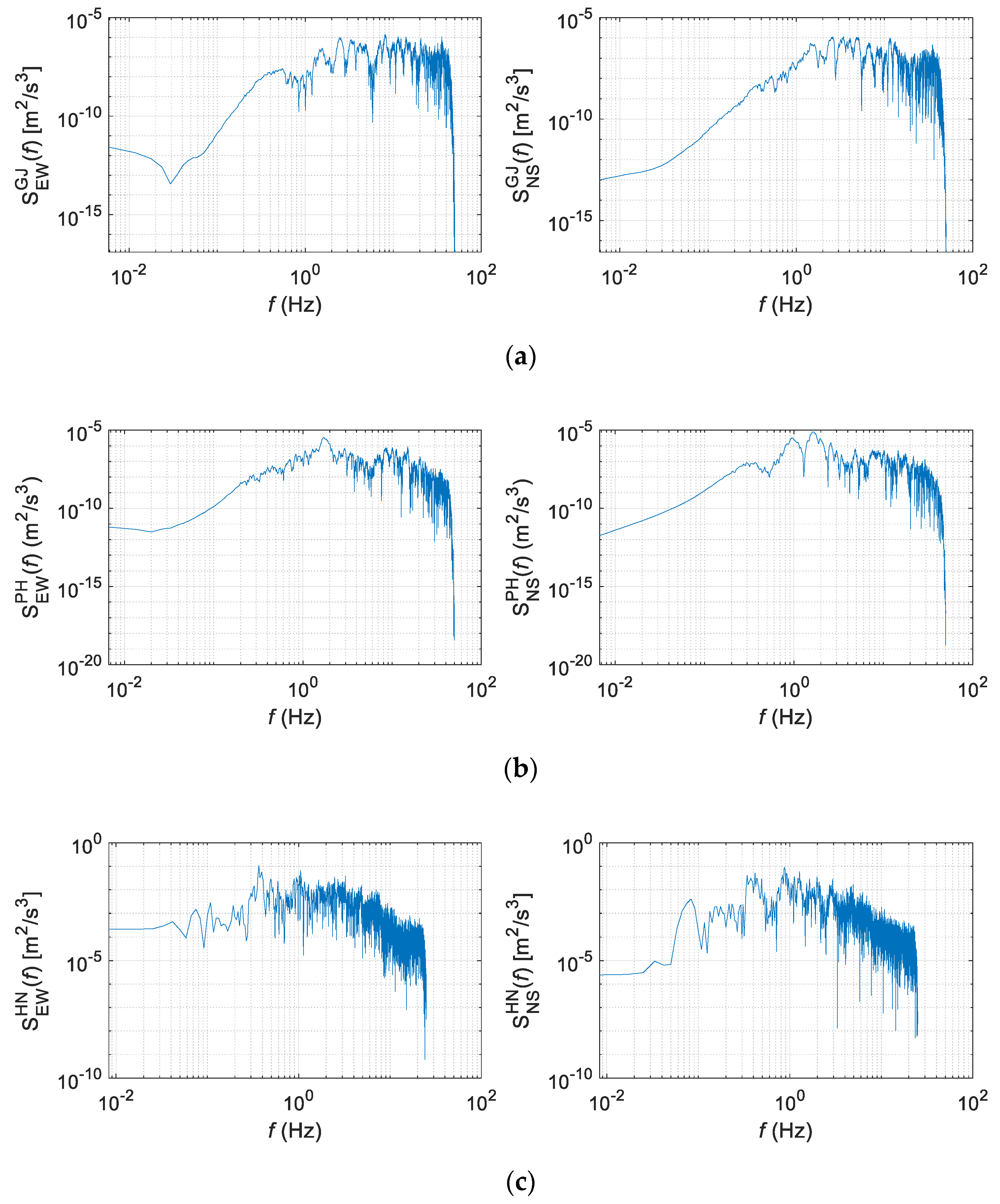





















| Index | Location | Year | Magnitude (MW) | Sampling Rate (Hz) | Peak Acceleration (g) |
|---|---|---|---|---|---|
| GJ | Gyeongju | 2016 | 5.8 | 100 | 0.346 (East–West) |
| PH | Pohang | 2017 | 5.4 | 100 | 0.271 (North–South) |
| HN | Hachinohe | 1994 | 7.7 | 50 | 0.317 (East–West) |
| Bridge | Index | Meff (t) | Leff (mm) | Keff (kN/mm) | ζ (%) | fn (Hz) |
|---|---|---|---|---|---|---|
| BR2 | STR 1 | 689.08 | 10,000 | 3621.5 | 5 | 11.54 |
| BR3 | STR 2 | 846.16 | 20,000 | 452.69 | 5 | 3.68 |
| Method | STFT | WT | WVD |
|---|---|---|---|
| Time (s) | 0.055 | 4.15 | 12.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, M.; Moon, J.S. Comparison of Signal-Analysis Techniques for Seismic Detection System for High-Speed Train Data: Effect of Bridge Structures. Sensors 2020, 20, 6805. https://doi.org/10.3390/s20236805
Yoo M, Moon JS. Comparison of Signal-Analysis Techniques for Seismic Detection System for High-Speed Train Data: Effect of Bridge Structures. Sensors. 2020; 20(23):6805. https://doi.org/10.3390/s20236805
Chicago/Turabian StyleYoo, Mintaek, and Jae Sang Moon. 2020. "Comparison of Signal-Analysis Techniques for Seismic Detection System for High-Speed Train Data: Effect of Bridge Structures" Sensors 20, no. 23: 6805. https://doi.org/10.3390/s20236805
APA StyleYoo, M., & Moon, J. S. (2020). Comparison of Signal-Analysis Techniques for Seismic Detection System for High-Speed Train Data: Effect of Bridge Structures. Sensors, 20(23), 6805. https://doi.org/10.3390/s20236805





