LPCF: Robust Correlation Tracking via Locality Preserving Tracking Validation
Abstract
:1. Introduction
- We extend the translation estimation component with a generic scale estimation approach, which has shown to obtain excellent performance for addressing visual tracking scale variation.
- We resample the feature in different sizes. Furthermore, PCA is introduced to reduce the computational cost of the translation estimation approach and to antagonize minor disturbance. This PCA method increases the real-time performance of the translation estimation approach without sacrificing its robustness.
- We derive a linearithmic complexity solution of locality-preserving tracking validation and adjust it for the practical tracking process.
- Extensive experiments on challenging large datasets OTB-2015, TrackingNet, and LASOT are performed. The results demonstrate that the presented decontamination method is effective and it increases the baseline remarkably in the AUC score on all three datasets. What’s more, the experimental results also show that the complete tracker performs approvingly against other decontamination trackers and state-of-the-art methods.
2. Materials and Methods
2.1. Revisist of Kernelized Correlation Filter
2.2. Proposed Approaches
2.2.1. Dimensionality Reduction Strategy
2.2.2. Decontamination
| Algorithm 1 Proposed tracking algorithm |
|
3. Results and Discussion
3.1. Implemental Details
3.2. Baseline Experiments
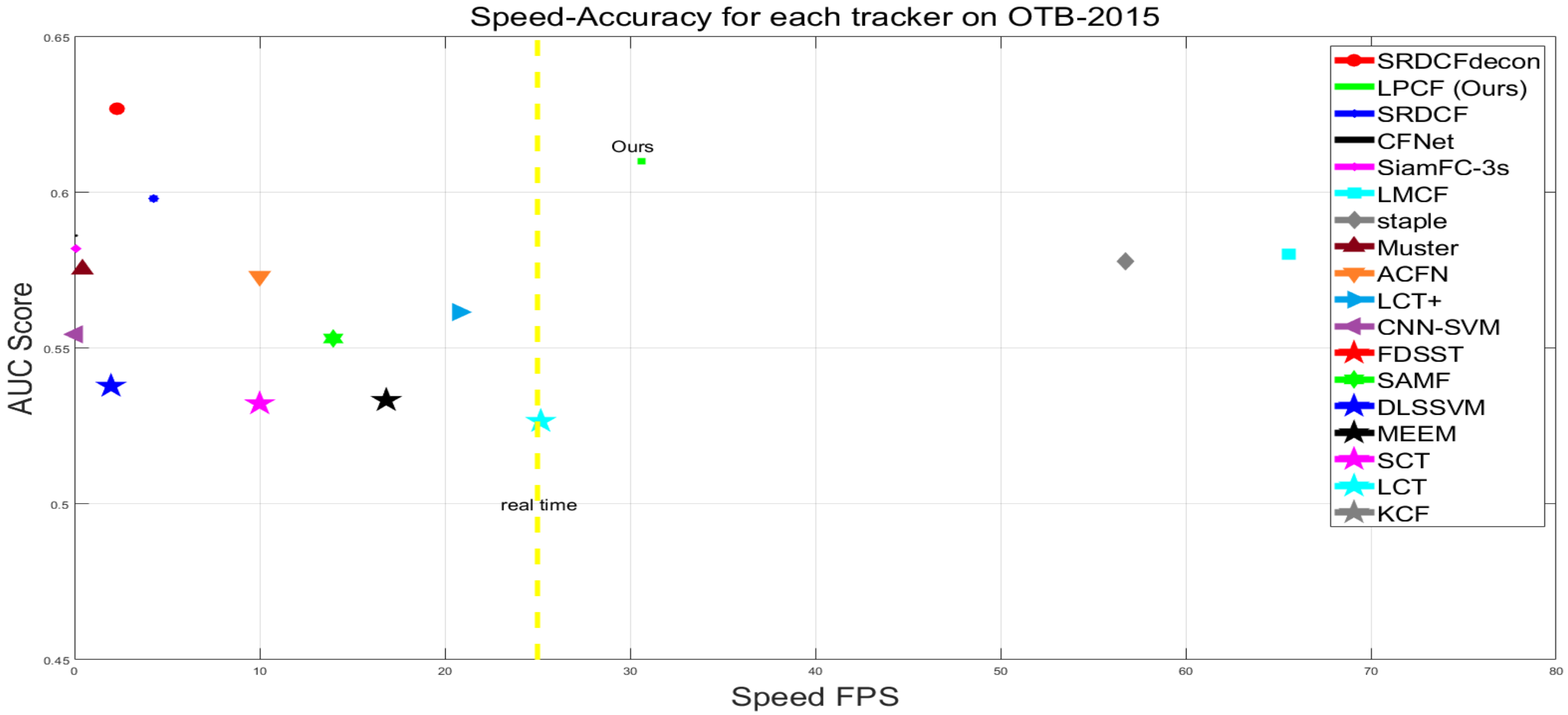
3.3. Comparison with Other Decontamination Trackers
3.3.1. Comparison with State-of-the-Art Trackers
3.3.2. Qualitative Evaluation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual object tracking using adaptive correlation filters. In Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 2544–2550. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. Exploiting the circulant structure of tracking-by-detection with kernels. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7 October 2012; pp. 702–715. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-Speed Tracking with Kernelized Correlation Filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 3, 583–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Danelljan, M.; Häger, G.; Khan, F.; Felsberg, M. Accurate scale estimation for robust visual tracking. In Proceedings of the British Machine Vision Conference, Nottingham, UK, 1–5 September 2014; BMVA Press: Nottingham, UK, 2014. [Google Scholar]
- Danelljan, M.; Hager, G.; Shahbaz Khan, F.; Felsberg, M. Learning spatially regularized correlation filters for visual tracking. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4310–4318. [Google Scholar]
- Bertinetto, L.; Valmadre, J.; Henriques, J.F.; Vedaldi, A.; Torr, P.H.S. Fully-Convolutional Siamese Networks for Object Tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8 October 2016. [Google Scholar]
- Danelljan, M.; Bhat, G.; Shahbaz Khan, F.; Felsberg, M. Eco: Efficient convolution operators for tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6638–6646. [Google Scholar]
- Valmadre, J.; Bertinetto, L.; Henriques, J.F.; Vedaldi, A.; Torr, P.H.S. End-to-end representation learning for Correlation Filter based tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Danelljan, M.; Bhat, G.; Khan, F.S.; Felsberg, M. Atom: Accurate tracking by overlap maximization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4660–4669. [Google Scholar]
- Bhat, G.; Danelljan, M.; Gool, L.V.; Timofte, R. Learning discriminative model prediction for tracking. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6182–6191. [Google Scholar]
- Xu, T.; Feng, Z.H.; Wu, X.J.; Kittler, J. Joint group feature selection and discriminative filter learning for robust visual object tracking. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 7950–7960. [Google Scholar]
- Guo, Q.; Feng, W.; Zhou, C.; Huang, R.; Wan, L.; Wang, S. Learning dynamic siamese network for visual object tracking. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1763–1771. [Google Scholar]
- Tu, F.; Ge, S.S.; Tang, Y.; Hang, C.C. Robust visual tracking via collaborative motion and appearance model. IEEE Trans. Ind. Inform. 2017, 13, 2251–2259. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, M.; Sun, F.; Zhang, J. Spatial neighborhood-constrained linear coding for visual object tracking. IEEE Trans. Ind. Inform. 2013, 10, 469–480. [Google Scholar] [CrossRef]
- Bai, T.; Li, Y. Robust visual tracking using flexible structured sparse representation. IEEE Trans. Ind. Inform. 2013, 10, 538–547. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; He, B.; Bai, T. GM-PHD-based multi-target visual tracking using entropy distribution and game theory. IEEE Trans. Ind. Inform. 2013, 10, 1064–1076. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M.H. Object Tracking Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1834–1848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muller, M.; Bibi, A.; Giancola, S.; Alsubaihi, S.; Ghanem, B. TrackingNet: A Large-Scale Dataset and Benchmark for Object Tracking in the Wild. In Proceedings of the The European Conference on Computer Vision (ECCV), Munich, Germany, 8 September 2018. [Google Scholar]
- Fan, H.; Bai, H.; Lin, L.; Yang, F.; Chu, P.; Deng, G.; Yu, S.; Huang, M.; Liu, J.; Xu, Y.; et al. LaSOT: A High-quality Large-scale Single Object Tracking Benchmark. Int. J. Comput. Vis. 2020, 1–23. [Google Scholar] [CrossRef]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Discriminative scale space tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1561–1575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bertinetto, L.; Valmadre, J.; Golodetz, S.; Miksik, O.; Torr, P.H.S. Staple: Complementary Learners for Real-Time Tracking. In Proceedings of the Computer Vision & Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Adaptive Decontamination of the Training Set: A Unified Formulation for Discriminative Visual Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Kalal, Z.; Matas, J.; Mikolajczyk, K. P-N learning: Bootstrapping binary classifiers by structural constraints. In Proceedings of the Computer Vision & Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Zhong, W.; Lu, H.; Yang, M.H. Robust object tracking via sparse collaborative appearance model. IEEE Trans. Image Process. 2014, 23, 2356–2368. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking-learning-detection. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1409. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Supancic, J.S.; Ramanan, D. Self-Paced Learning for Long-Term Tracking. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Zhang, J.; Ma, S.; Sclaroff, S. MEEM: Robust tracking via multiple experts using entropy minimization. In Proceedings of the European Conference on Computer Vision, Zürich, Switzerland, 6–12 September 2014; pp. 188–203. [Google Scholar]
- Ma, C.; Yang, X.; Zhang, C.; Yang, M.H. Long-term correlation tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5388–5396. [Google Scholar]
- Wang, M.; Liu, Y.; Huang, Z. Large margin object tracking with circulant feature maps. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4021–4029. [Google Scholar]
- Zhibin, H.; Chen, Z.; Wang, C.; Mei, X.; Prokhorov, D.; Tao, D. MUlti-Store Tracker (MUSTer): A Cognitive Psychology Inspired Approach to Object Tracking. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Ma, J.; Zhao, J.; Jiang, J.; Zhou, H.; Guo, X. Locality preserving matching. Int. J. Comput. Vis. 2019, 127, 512–531. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J. A Scale Adaptive Kernel Correlation Filter Tracker with Feature Integration. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Ma, C.; Huang, J.B.; Yang, X.; Yang, M.H. Adaptive correlation filters with long-term and short-term memory for object tracking. Int. J. Comput. Vis. 2018, 126, 771–796. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; You, T.; Kwak, S.; Han, B. Online Tracking by Learning Discriminative Saliency Map with Convolutional Neural Network. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Ning, J.; Yang, J.; Jiang, S.; Zhang, L.; Yang, M.H. Object Tracking via Dual Linear Structured SVM and Explicit Feature Map. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Choi, J.; Jin Chang, H.; Jeong, J.; Demiris, Y.; Young Choi, J. Visual tracking using attention-modulated disintegration and integration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4321–4330. [Google Scholar]
- Choi, J.; Chang, H.J.; Yun, S.; Fischer, T.; Choi, J.Y. Attentional Correlation Filter Network for Adaptive Visual Tracking. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Huang, L.; Zhao, X.; Huang, K. Globaltrack: A simple and strong baseline for long-term tracking. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11037–11044. [Google Scholar]
- Zhu, Z.; Wang, Q.; Li, B.; Wu, W.; Yan, J.; Hu, W. Distractor-aware siamese networks for visual object tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 101–117. [Google Scholar]
- Li, B.; Wu, W.; Wang, Q.; Zhang, F.; Xing, J.; Yan, J. Siamrpn++: Evolution of siamese visual tracking with very deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4282–4291. [Google Scholar]
- Wang, Q.; Zhang, L.; Bertinetto, L.; Hu, W.; Torr, P.H. Fast online object tracking and segmentation: A unifying approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1328–1338. [Google Scholar]
- Fan, H.; Ling, H. Siamese cascaded region proposal networks for real-time visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7952–7961. [Google Scholar]
- Yan, B.; Zhao, H.; Wang, D.; Lu, H.; Yang, X. ‘Skimming-Perusal’Tracking: A Framework for Real-Time and Robust Long-term Tracking. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 22 April 2019; pp. 2385–2393. [Google Scholar]
- Nam, H.; Han, B. Learning multi-domain convolutional neural networks for visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4293–4302. [Google Scholar]
- Song, Y.; Ma, C.; Wu, X.; Gong, L.; Bao, L.; Zuo, W.; Shen, C.; Lau, R.W.; Yang, M.H. Vital: Visual tracking via adversarial learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8990–8999. [Google Scholar]
- Zhang, Z.; Peng, H. Deeper and wider siamese networks for real-time visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4591–4600. [Google Scholar]
- Li, F.; Tian, C.; Zuo, W.; Zhang, L.; Yang, M.H. Learning spatial-temporal regularized correlation filters for visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4904–4913. [Google Scholar]
- Dai, K.; Wang, D.; Lu, H.; Sun, C.; Li, J. Visual tracking via adaptive spatially-regularized correlation filters. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4670–4679. [Google Scholar]
- Zhang, Y.; Wang, L.; Qi, J.; Wang, D.; Feng, M.; Lu, H. Structured siamese network for real-time visual tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 351–366. [Google Scholar]
- Kiani Galoogahi, H.; Fagg, A.; Lucey, S. Learning background-aware correlation filters for visual tracking. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1135–1143. [Google Scholar]
- Choi, J.; Jin Chang, H.; Fischer, T.; Yun, S.; Lee, K.; Jeong, J.; Demiris, Y.; Young Choi, J. Context-aware deep feature compression for high-speed visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 479–488. [Google Scholar]
- Ma, C.; Huang, J.B.; Yang, X.; Yang, M.H. Hierarchical convolutional features for visual tracking. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3074–3082. [Google Scholar]
- Fan, H.; Ling, H. Parallel tracking and verifying: A framework for real-time and high accuracy visual tracking. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5486–5494. [Google Scholar]
- Lukezic, A.; Vojir, T.; Cehovin Zajc, L.; Matas, J.; Kristan, M. Discriminative correlation filter with channel and spatial reliability. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6309–6318. [Google Scholar]
- Mueller, M.; Smith, N.; Ghanem, B. Context-aware correlation filter tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1396–1404. [Google Scholar]
- Hare, S.; Golodetz, S.; Saffari, A.; Vineet, V.; Cheng, M.M.; Hicks, S.L.; Torr, P.H. Struck: Structured output tracking with kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2096–2109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jia, X.; Lu, H.; Yang, M.H. Visual tracking via adaptive structural local sparse appearance model. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1822–1829. [Google Scholar]
- Danelljan, M.; Khan, F.S.; Felsberg, M.; Weijer, J.V.D. Adaptive Color Attributes for Real-Time Visual Tracking. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Columbus, OH, USA, 23–28 June 2014. [Google Scholar]
- Zhang, K.; Zhang, L.; Yang, M.H. Real-Time Compressive Tracking. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Bao, C.; Wu, Y.; Ling, H.; Ji, H. Real time robust l1 tracker using accelerated proximal gradient approach. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1830–1837. [Google Scholar]
- Babenko, B.; Yang, M.H.; Belongie, S. Visual tracking with online multiple instance learning. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 983–990. [Google Scholar]
- Zhang, K.; Zhang, L.; Liu, Q.; Zhang, D.; Yang, M.H. Fast visual tracking via dense spatio-temporal context learning. In Proceedings of the European Conference on Computer Vision, Zürich, Switzerland, 6–12 September 2014; pp. 127–141. [Google Scholar]
- Ross, D.A.; Lim, J.; Lin, R.S.; Yang, M.H. Incremental learning for robust visual tracking. Int. J. Comput. Vis. 2008, 77, 125–141. [Google Scholar] [CrossRef]







| Name | KCF [3] | FDSST [20] | KCF+FDSST | RKCF+FDSST | PKCF+FDSST | LPCF (Ours) |
|---|---|---|---|---|---|---|
| OP (%) | 54.6 | 67.2 | 60.5 | 63.5 | 70.2 | 75.3 |
| DP (pixel) | 68.8 | 72.5 | 66.9 | 71.2 | 75.3 | 78.9 |
| Speed (FPS) | 154.6 | 52.7 | 53.7 | 44.5 | 59.4 | 30.3 |
| Name | KCF | FDSST | KCF+FDSST | RKCF+FDSST | PKCF+FDSST | LPCF (Ours) |
|---|---|---|---|---|---|---|
| Precision (%) | 42.14 | 42.64 | 40.09 | 41.32 | 42.14 | 46.25 |
| Norm. Precision (%) | 55.13 | 54.57 | 52.67 | 53.66 | 56.13 | 58.80 |
| Success | 45.24 | 49.69 | 47.69 | 48.45 | 50.67 | 52.44 |
| Name | LPCF (Ours) | Dsiam | MDNet | SiamRPN++ | HCFT | ATOM | SiamMask | VITAL | ECO |
|---|---|---|---|---|---|---|---|---|---|
| Speed (FPS) | 30 | 18 | <1 | 21 | 10 | 30 | 22 | <1 | 7 |
| AUC (%) | 24.9 | 33.3 | 39.7 | 49.5 | 25.0 | 49.9 | 46.7 | 39.0 | 32.4 |
| Name | LPCF (Ours) | CFNet | MDNet | ECO | DaSiamRPN | SiamRPN++ |
|---|---|---|---|---|---|---|
| Precision (%) | 46.3 | 53.3 | 56.5 | 49.2 | 59.1 | 69.4 |
| Norm. Precision (%) | 58.8 | 65.4 | 70.5 | 61.8 | 73.3 | 80.0 |
| Success | 52.4 | 57.8 | 60.6 | 55.4 | 63.8 | 73.3 |
| Name | SV | OCC | BC | LR | OPR | DEF | IPR | OV | L |
|---|---|---|---|---|---|---|---|---|---|
| Box | √ | √ | √ | √ | - | √ | √ | √ | 1161 |
| Car1 | √ | - | √ | √ | - | - | - | - | 1020 |
| ClifBar | √ | √ | √ | - | - | - | √ | √ | 472 |
| Couple | √ | √ | - | √ | √ | - | - | - | 140 |
| Freeman4 | √ | √ | - | - | √ | - | √ | - | 283 |
| Jogging_2 | - | √ | - | - | √ | √ | - | - | 307 |
| Lemming | √ | √ | - | - | √ | - | - | √ | 1136 |
| Panda | √ | √ | - | √ | √ | √ | √ | √ | 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Zhang, W.; Shi, Y.; Wang, Z.; Li, F.; Huang, Q. LPCF: Robust Correlation Tracking via Locality Preserving Tracking Validation. Sensors 2020, 20, 6853. https://doi.org/10.3390/s20236853
Zhou Y, Zhang W, Shi Y, Wang Z, Li F, Huang Q. LPCF: Robust Correlation Tracking via Locality Preserving Tracking Validation. Sensors. 2020; 20(23):6853. https://doi.org/10.3390/s20236853
Chicago/Turabian StyleZhou, Yixuan, Weimin Zhang, Yongliang Shi, Ziyu Wang, Fangxing Li, and Qiang Huang. 2020. "LPCF: Robust Correlation Tracking via Locality Preserving Tracking Validation" Sensors 20, no. 23: 6853. https://doi.org/10.3390/s20236853
APA StyleZhou, Y., Zhang, W., Shi, Y., Wang, Z., Li, F., & Huang, Q. (2020). LPCF: Robust Correlation Tracking via Locality Preserving Tracking Validation. Sensors, 20(23), 6853. https://doi.org/10.3390/s20236853







