Output-Only Damage Detection in Plate-Like Structures Based on Proportional Strain Flexibility Matrix
Abstract
1. Introduction
2. Definition of PSFM and Damage Index
2.1. Definition of PSFM
2.2. Definition of the Uniform Load Strain Field
2.3. ULSF Difference-Based Damage Index
3. The Improved Method for Constructing PSFM
4. Results and Discussions
4.1. Case 1: The Simulation Model Constructed in FEM
- (1)
- Analysis of the influence of mass matrix:
- (2)
- The simplified construction method of PSFM:
- (3)
- Effect of measurement noise:
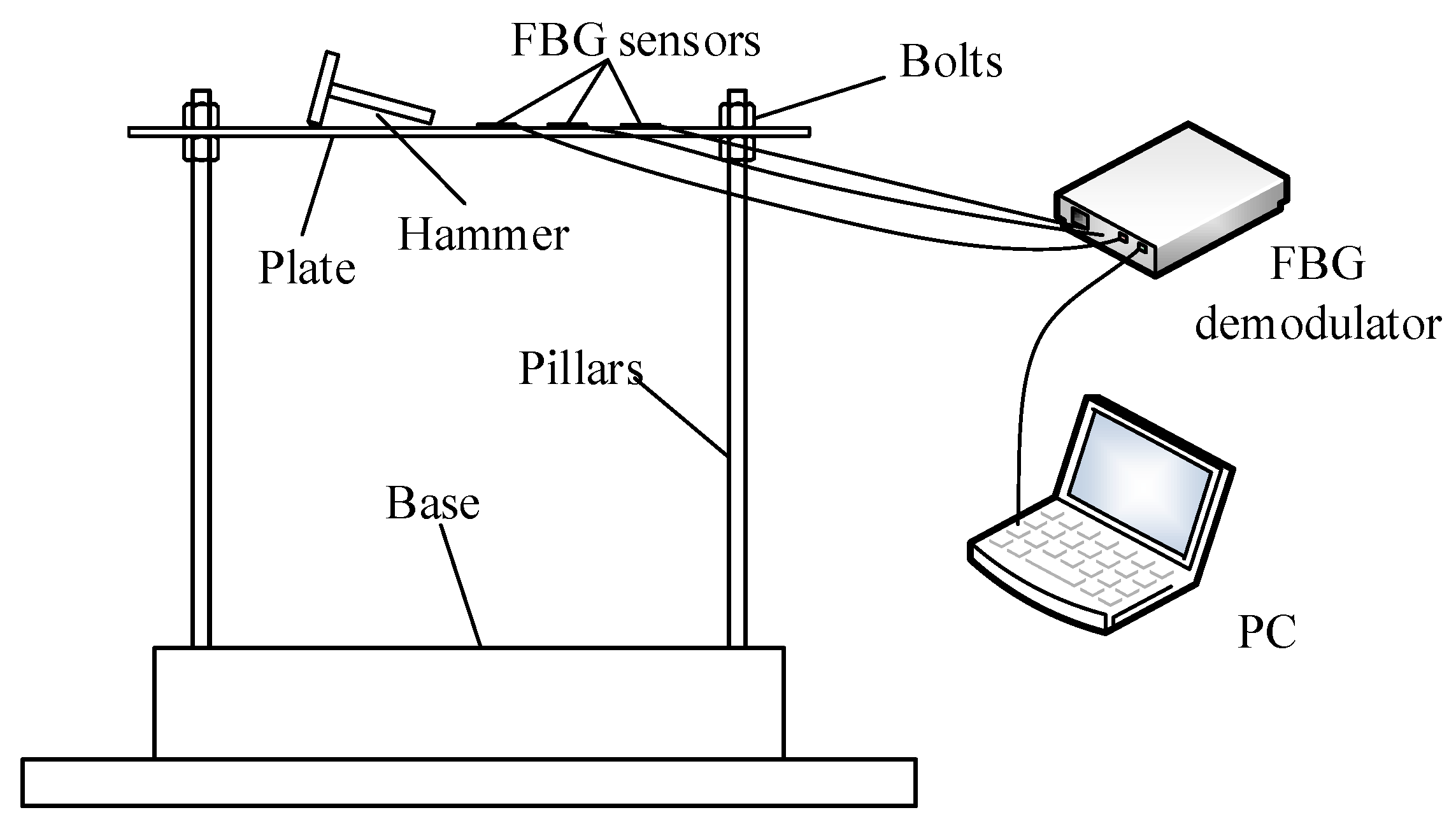
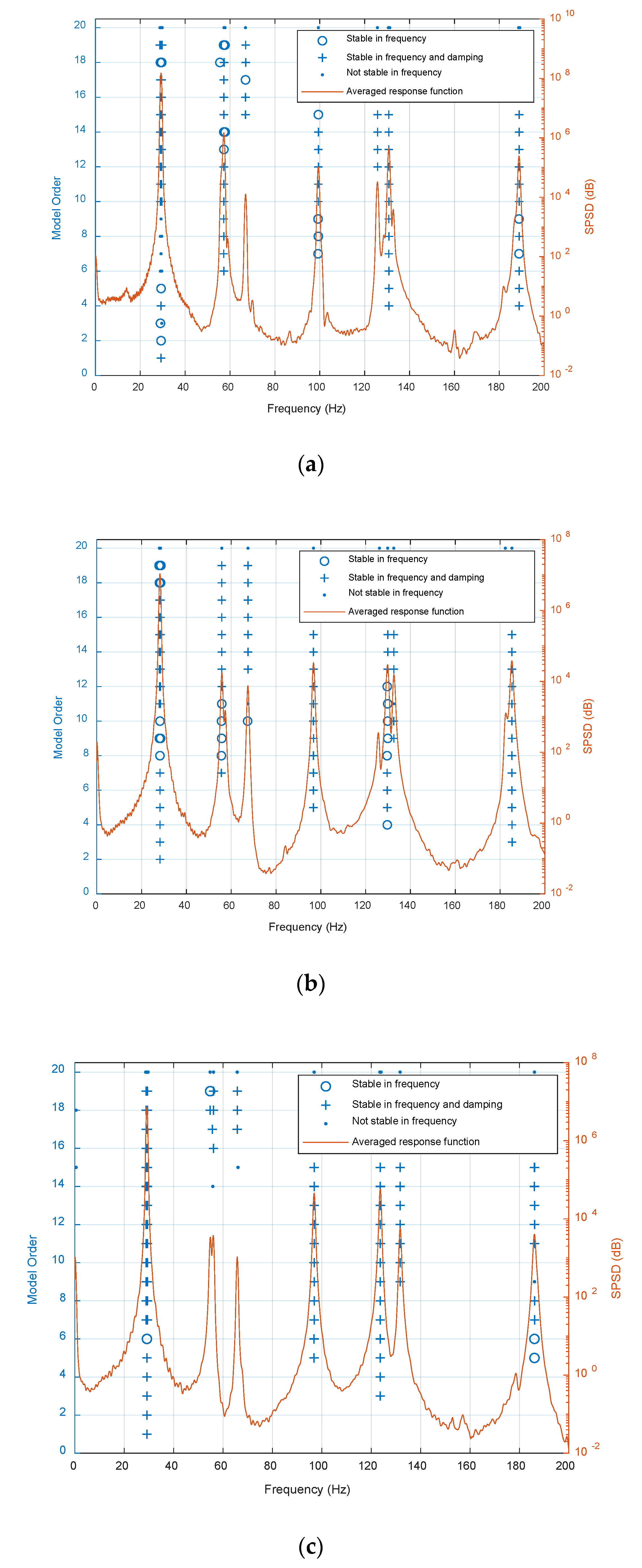
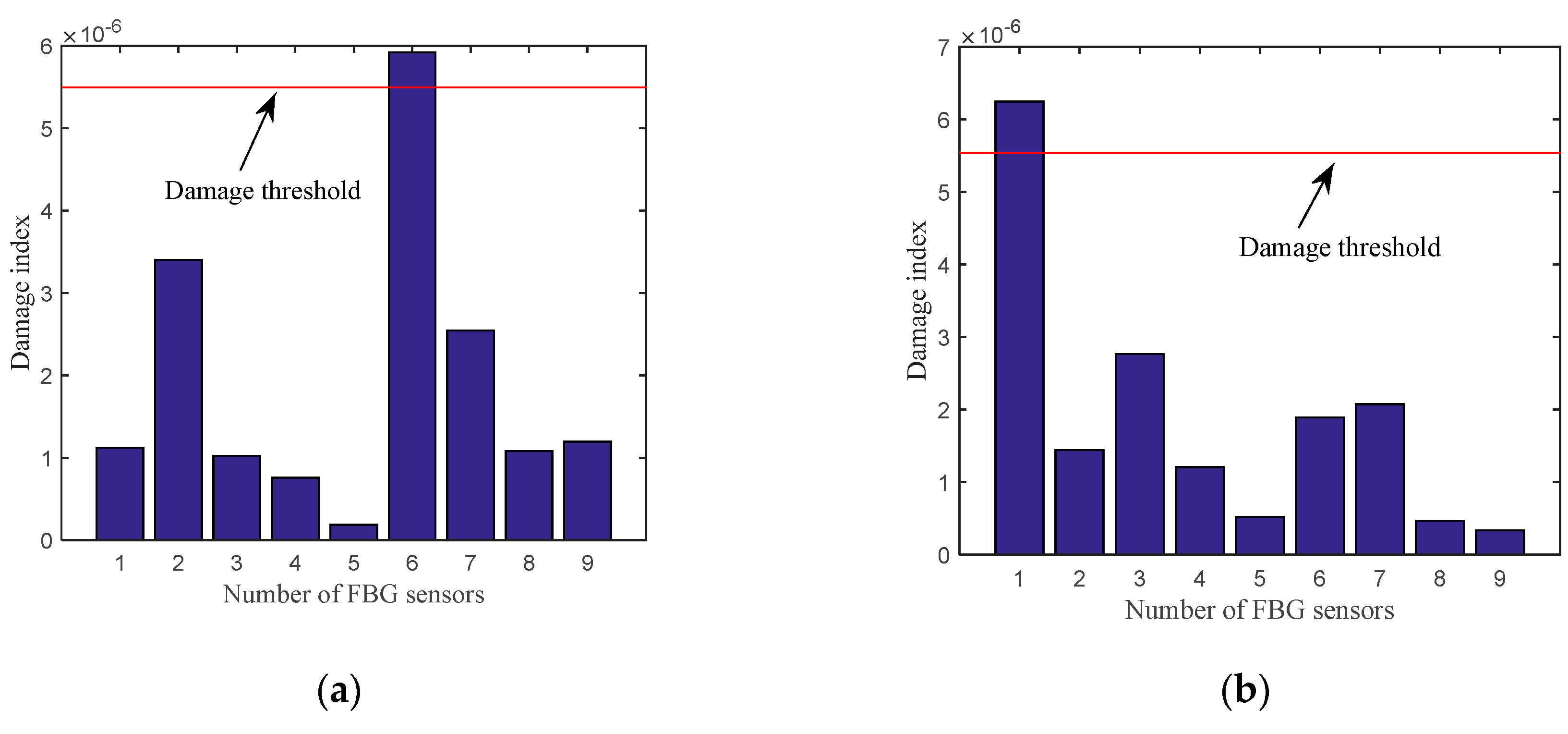
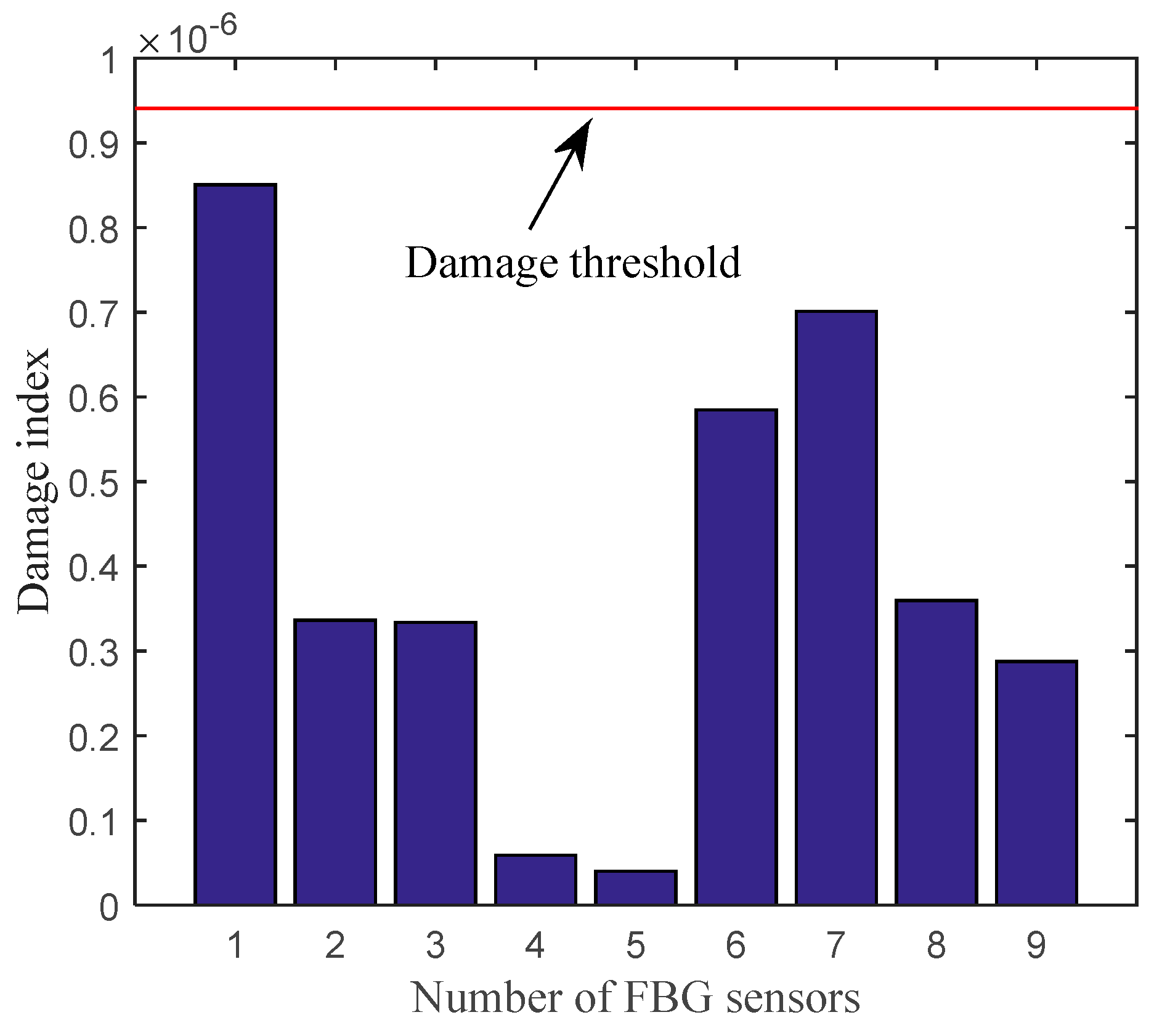
4.2. Case 2: Experimental Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A


References
- Goyal, D.; Pabla, B.S. The vibration monitoring methods and signal processing techniques for structural health monitoring: A review. Arch. Comput. Method Eng. 2015, 23, 585–594. [Google Scholar] [CrossRef]
- Das, S.; Saha, P.; Patro, S.K. Vibration-based damage detection techniques used for health monitoring of structures: A review. J. Civ. Struct. Health Monit. 2016, 6, 477–507. [Google Scholar] [CrossRef]
- Wu, D.; Law, S.S. Anisotropic damage model for an inclined crack in thick plate and sensitivity study for its detection. Int. J. Solids Struct. 2004, 41, 4321–4336. [Google Scholar] [CrossRef]
- Shadan, F.; Khoshnoudian, F.; Esfandiari, A. A frequency response-based structural damage identification using model updating method. Struct. Control Health Monit. 2016, 23, 286–302. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Astroza, R.; Conte, J.P.; de Callafon, R.A. Nonlinear finite element model updating for damage identification of civil structures using batch Bayesian estimation. Mech. Syst. Signal. Process. 2017, 84, 194–222. [Google Scholar] [CrossRef]
- Su, W.C.; Huang, C.S.; Hung, S.L.; Chen, L.J.; Lin, W.J. Locating damaged storeys in a shear building based on its sub-structural natural frequencies. Eng. Struct. 2012, 39, 126–138. [Google Scholar] [CrossRef]
- Salawu, O.S. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Shi, B.; Qiao, P. A new surface fractal dimension for displacement mode shape-based damage identification of plate-type structures. Mech. Syst. Signal. Process. 2018, 103, 139–161. [Google Scholar] [CrossRef]
- Xu, Y.F.; Zhu, W.D. Non-model-based damage identification of plates using curvature mode shapes. In Dynamics of Civil Structures; Springer: Berlin/Heidelberg, Germany, 2016; Volume 2, pp. 65–86. [Google Scholar]
- Wang, Z.; Liu, M.; Zhu, Z.; Qu, Y.; Wei, Q.; Zhou, Z.; Tan, Y.; Yu, Z.; Yang, F. Clamp looseness detection using modal strain estimated from FBG based operational modal analysis. Measurement 2019, 137, 82–97. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, M.; Qu, Y.; Wei, Q.; Zhou, Z.; Tan, Y.; Hong, L.; Song, H. The detection of the pipe crack utilizing the operational modal strain identified from fiber bragg grating. Sensors 2019, 19, 2556. [Google Scholar] [CrossRef] [PubMed]
- Navabian, N.; Bozorgnasab, M.; Taghipour, R.; Yazdanpanah, O. Damage identification in plate-like structure using mode shape derivatives. Arch. Appl. Mech. 2015, 86, 819–830. [Google Scholar] [CrossRef]
- Rehman, A.U.; Worden, K.; Rongong, J.A. On crack detection in tuned and mistuned repeating structures using the modal assurance criterion. Strain 2016, 52, 175–185. [Google Scholar] [CrossRef]
- Meo, M.; Zumpano, G. Damage assessment on plate-like structures using a global-local optimization approach. Optim. Eng. 2007, 9, 161–177. [Google Scholar] [CrossRef]
- Seyedpoor, S.M. A two stage method for structural damage detection using a modal strain energy based index and particle swarm optimization. Int. J. Non-Linear Mech. 2012, 47, 1–8. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Nobahari, M.; Shabakhty, N. Enhanced optimization-based structural damage detection method using modal strain energy and modal frequencies. Eng. Comput. 2017, 34, 637–647. [Google Scholar] [CrossRef]
- Aloisio, A.; Di Battista, L.; Alaggio, R.; Fragiacomo, M. Sensitivity analysis of subspace-based damage indicators under changes in ambient excitation covariance, severity and location of damage. Eng. Struct. 2020, 208, 110235. [Google Scholar] [CrossRef]
- Basseville, M.; Mevel, L.; Vecchio, A.; Peeters, B.; Van der Auweraer, H. Output-only subspace-based damage detection-application to a reticular structure. Struct. Health Monit. 2003, 2, 161–168. [Google Scholar] [CrossRef]
- Zhao, J.; Dewolf, J.T. Sensitivity study for vibrational parameters used in damage detection. J. Struct. Eng. 1999, 125, 410–416. [Google Scholar] [CrossRef]
- Hong, W.; Zhang, W.; Gang, G.; Zhishen, W. Comprehensive comparison of macro-strain mode and displacement mode based on different sensing technologies. Mech. Syst. Signal. Process. 2015, 50, 563–579. [Google Scholar] [CrossRef]
- Zonta, D.; Lanaro, A.; Zanon, P. A strain-flexibility-based approach to damage location. Key Eng. Mater. 2003, 245, 87–94. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, Q.; Cheng, Y.; Wu, Z. Strain flexibility identification of bridges from long-gauge strain measurements. Mech. Syst. Signal. Process. 2015, 62, 272–283. [Google Scholar] [CrossRef]
- Adewuyi, A.P.; Wu, Z.S. Modal macro-strain flexibility methods for damage localization in flexural structures using long-gage FBG sensors. Struct. Control Health Monit. 2011, 18, 341–360. [Google Scholar] [CrossRef]
- Zhang, Z.; Aktan, A.E. Application of modal flexibility and its derivatives in structural identification. J. Res. Nondestruct. Eval. 1998, 10, 43–61. [Google Scholar] [CrossRef]
- Loutas, T.H.; Bourikas, A. Strain sensors optimal placement for vibration-based structural health monitoring. The effect of damage on the initially optimal configuration. J. Sound Vib. 2017, 410, 217–230. [Google Scholar] [CrossRef]
- Liu, J.K.; Wei, Z.T.; Lu, Z.R.; Ou, Y.J. Structural damage identification using gravitational search algorithm. Struct. Eng. Mech. 2016, 60, 729–747. [Google Scholar] [CrossRef]
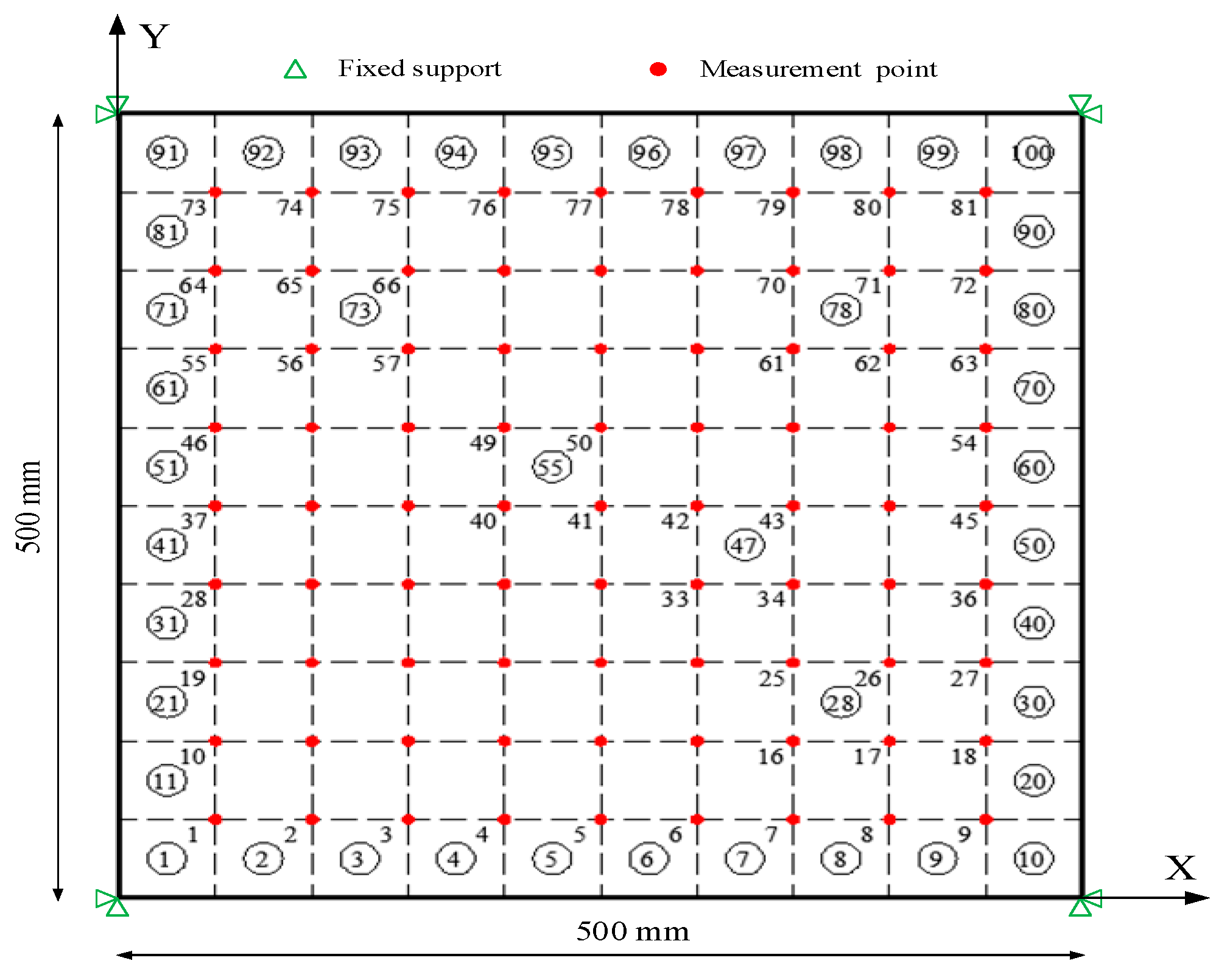
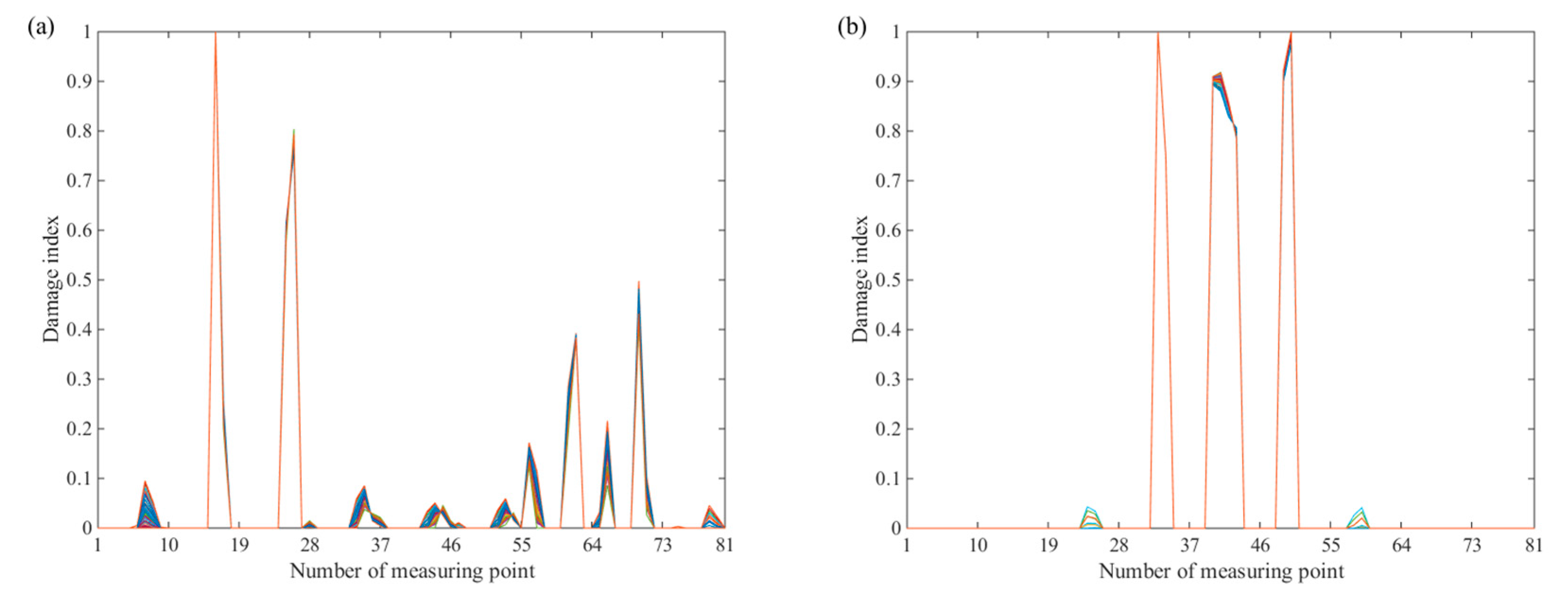
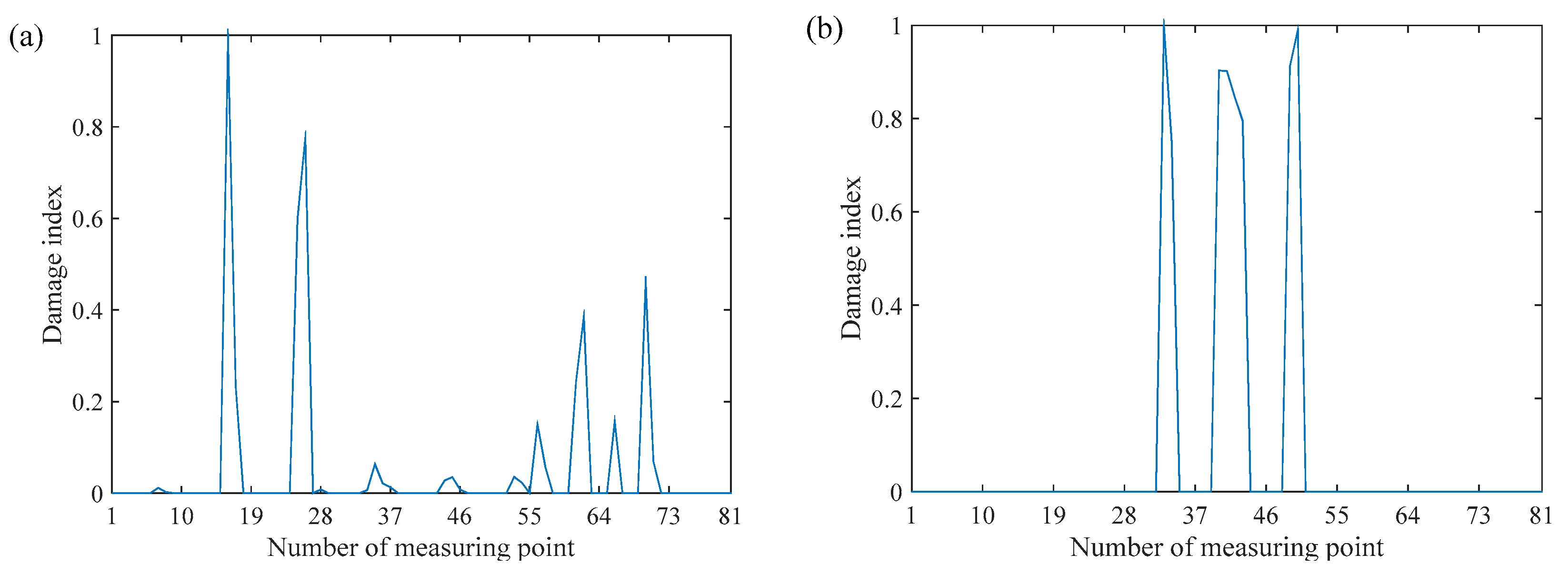
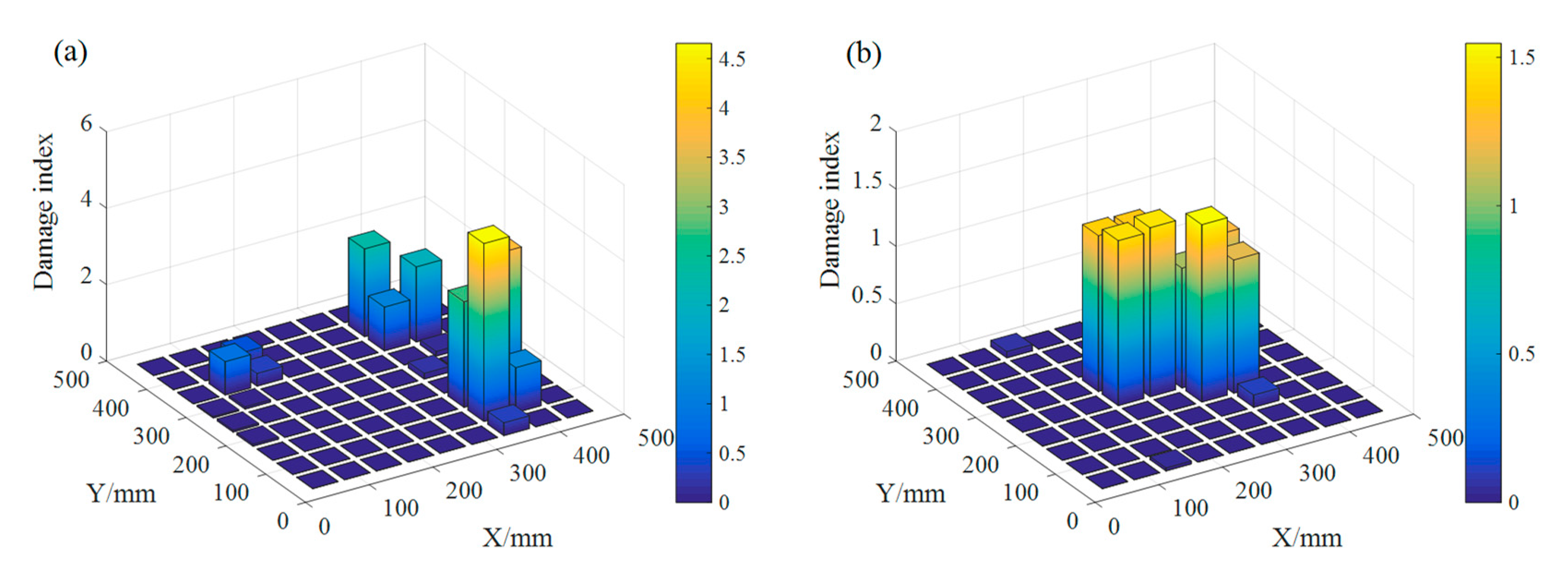



| Case | Element N. | Damage Extent |
|---|---|---|
| 1 | 64 | 15% |
| 73 | 20% | |
| 28 | 30% | |
| 18 | 40% | |
| 2 | 36 | 25% |
| 38 | 20% | |
| 47 | 25% |
| Parameters | Center (x, y) (mm) | Length (mm) | Width (mm) | State |
|---|---|---|---|---|
| Plate A | — | — | — | Intact |
| Plate B | (325, 250) | 50 | 0.3 | Damaged |
| Plate C | (225, 25) | 50 | 0.3 | Damaged |
| Modes | Plates | Natural Frequencies (Hz) | Modal Strain | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | 9# | |||
| 1st | A | 29.25 | −11.4 | −15.9 | −13.4 | 2.16 | 2.37 | −12.5 | −9.26 | 6.91 | −11.7 |
| B | 28.38 | −4.06 | −6.22 | −6.14 | 0.83 | 0.60 | −7.00 | −2.81 | 3.10 | −4.42 | |
| C | 29.13 | 3.18 | 2.52 | 1.95 | −0.39 | −0.75 | 2.58 | 2.14 | −1.01 | 1.93 | |
| 2nd | A | 57.25 | 1.16 | 1.35 | 0.16 | −0.18 | −0.04 | 0.16 | −1.25 | 0.88 | −1.69 |
| B | 57.13 | 6.40 | 5.61 | 2.40 | −0.69 | −0.01 | 0.08 | −3.37 | 3.83 | −8.22 | |
| C | 54.88 | 5.49 | 4.51 | 1.99 | −0.60 | 0.11 | 0.50 | −2.39 | 2.40 | −5.03 | |
| 3rd | A | 67.0 | −1.12 | −1.26 | −1.08 | 0.05 | −0.23 | −1.15 | −1.01 | 0.50 | −1.70 |
| B | 67.13 | 3.24 | 3.03 | 3.01 | −0.05 | 0.46 | 2.66 | 2.30 | −1.31 | 5.02 | |
| C | 65.88 | 0.64 | 0.55 | 0.59 | 0.04 | 0.14 | 0.52 | 0.58 | −0.32 | 1.26 | |
| 4th | A | 99.38 | 1.15 | −0.16 | −2.18 | 0.19 | 0.10 | −2.33 | 0.01 | −0.58 | 1.09 |
| B | 97.13 | −0.66 | 0.31 | 1.46 | −0.06 | −0.06 | 1.97 | −0.20 | 0.58 | −1.34 | |
| C | 96.88 | −0.53 | 0.30 | 0.6 | −0.16 | −0.04 | 1.16 | −0.02 | 0.09 | −0.13 | |
| 5th | A | 125.8 | 1.52 | −1.84 | 0.94 | −0.14 | 0.26 | −0.69 | −0.43 | −0.43 | −0.12 |
| B | 125.6 | −2.54 | 2.48 | −1.72 | 0.17 | −0.32 | 1.11 | 0.58 | 0.61 | 0.31 | |
| C | 123.6 | 3.21 | −3.41 | 2.17 | −0.15 | 0.37 | −1.07 | −0.64 | −0.55 | −0.90 | |
| 6th | A | 130.8 | −0.64 | 2.56 | −2.18 | 0.56 | −0.88 | 2.44 | −2.21 | −0.46 | −0.71 |
| B | 129.4 | 0.37 | −1.59 | 1.73 | −0.32 | 0.52 | −1.88 | 0.96 | 0.16 | 0.48 | |
| C | 130.3 | 0.08 | −1.14 | 0.83 | −0.17 | 0.26 | −0.73 | 0.23 | −0.07 | 0.69 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, K.; Liu, M.; Lv, J.; Wang, J.; Li, Z.; Song, H. Output-Only Damage Detection in Plate-Like Structures Based on Proportional Strain Flexibility Matrix. Sensors 2020, 20, 6862. https://doi.org/10.3390/s20236862
Yun K, Liu M, Lv J, Wang J, Li Z, Song H. Output-Only Damage Detection in Plate-Like Structures Based on Proportional Strain Flexibility Matrix. Sensors. 2020; 20(23):6862. https://doi.org/10.3390/s20236862
Chicago/Turabian StyleYun, Kang, Mingyao Liu, Jiangtao Lv, Jingliang Wang, Zhao Li, and Han Song. 2020. "Output-Only Damage Detection in Plate-Like Structures Based on Proportional Strain Flexibility Matrix" Sensors 20, no. 23: 6862. https://doi.org/10.3390/s20236862
APA StyleYun, K., Liu, M., Lv, J., Wang, J., Li, Z., & Song, H. (2020). Output-Only Damage Detection in Plate-Like Structures Based on Proportional Strain Flexibility Matrix. Sensors, 20(23), 6862. https://doi.org/10.3390/s20236862





