Observer-Based Event-Triggered Predictive Control for Networked Control Systems under DoS Attacks
Abstract
1. Introduction
- (1)
- Our method is very different to that in the works of networked PCs [32,33,34] which have used time-triggered communication schemes. This paper adopts event-triggered predictive communication schemes to design a controller. Whether the observer’s state measurement information is sent depends on the error between the current observer state and the observer state of the most recently sent information. The event-triggered generator on the controller side greatly reduces the size of the sent predictive control sequences, greatly reduces the occupation of bandwidth resources and can also meet the needs of control performance [35].
- (2)
- Compared with the existing predictive control compensation scheme for DoS attacks [7], another advantage of the OB-ETPC scheme adopted in this paper is the combination of the advantages of PC and ET [27,36,37,38,39,40,41,42]. With the combination of a model and static observer, it can cope with the problem that state information cannot be obtained directly and can also actively compensate for data packet dropout due to DoS attacks and greatly improve the stability of NCSs under DoS attacks.
- (3)
- Compared with the latest DoS attack compensation scheme, the method in [27] only considers DoS attacks from the controller to the actuator side. In real-life scenarios, the attack from the sensor to controller side is often through a network link. In this paper, the novel OB-ETPC solves the problem of DoS attacks on both the sensor-to-controller and controller-to-actuator sides, which is more in line with real-life scenarios.
- (4)
- The OB-ETPC is established to actively compensate for DoS attacks in NCSs. The observer gain matrix L and controller gain matrix K are co-designed based on the Lyapunov function method, and related criteria for event-triggered matrices are proposed based on linear matrix inequalities (LMIs).
2. Problem Descriptions and Preliminaries
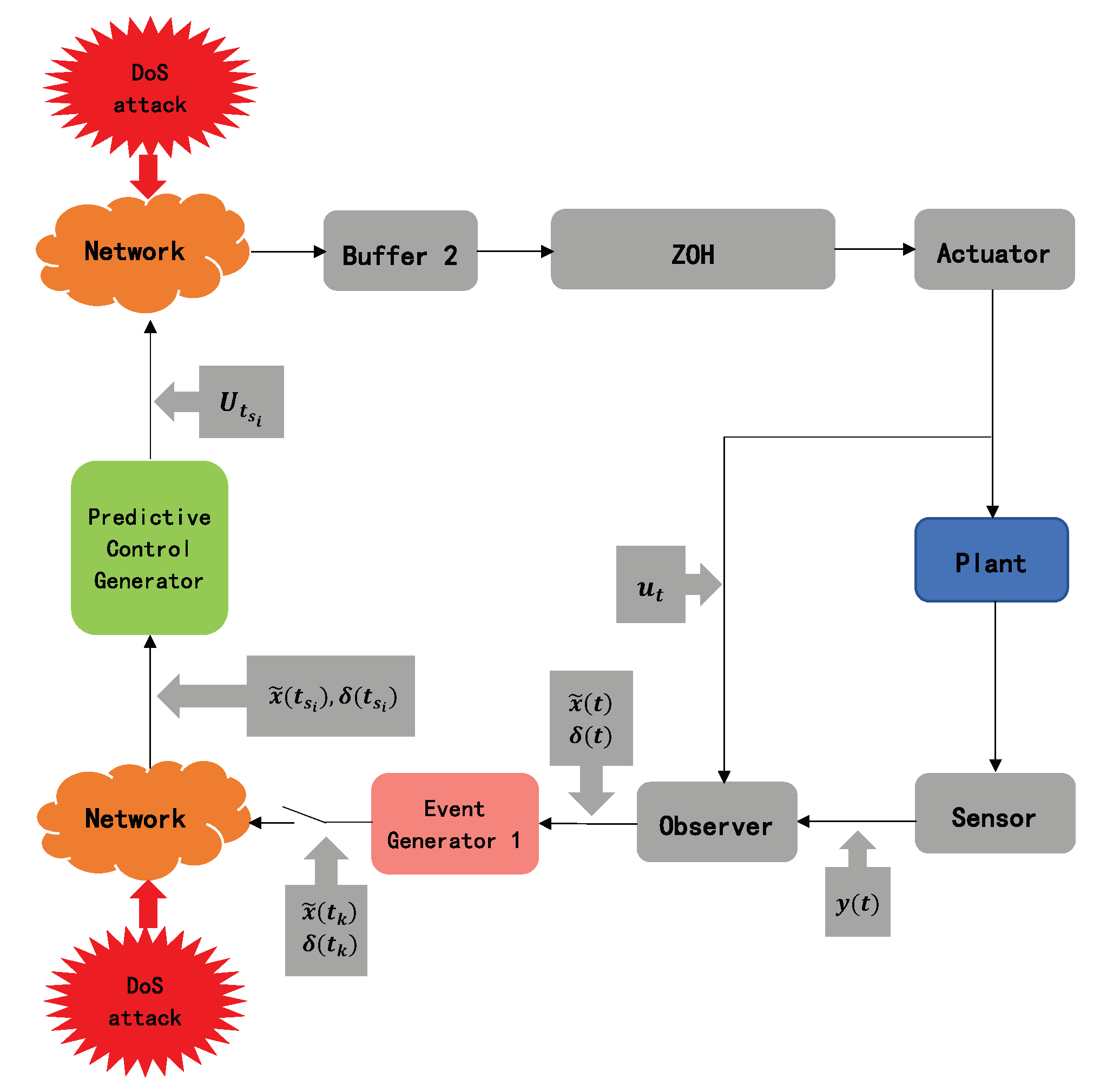
Description of Each Component
- (1)
- Sensor: The high-sensitivity sensor sends the output signal from plant to the observer [45].
- (2)
- Observer: In reality, most systems cannot directly obtain the system’s state vector . Using to analyze the problem is restrictive and inaccurate. Therefore, in order to estimate plant state information, the observer is introduced into the NCSs. The full-dimension state observer iswhere is the state vector of the observer, is the output vector of the observer and L is the gain matrix of the observer. We define as the observer state error. Then,and the observer error system can be described by
- (3)
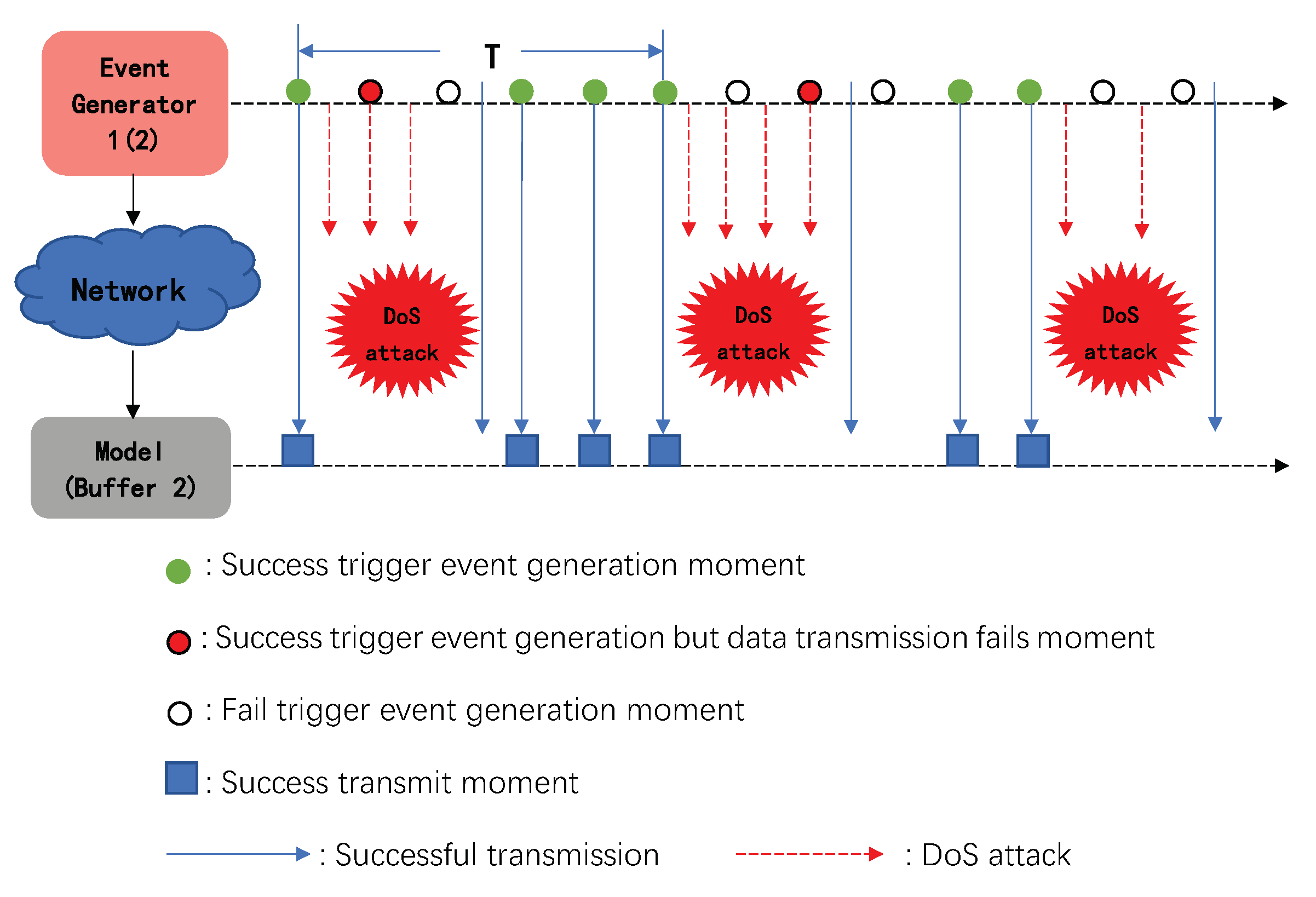
- Event Generator 1: Due to the limitation of network bandwidth resources, in order to reduce the transmission of data packets, prevent network congestion and improve the utilization of network bandwidth resources and the performance of NCSs, Event Generator 1 is designed on the sensor side to determine whether data packets need to be transmitted to the controller side [46].In this paper, we first introduce the event-triggered scheme in Event Generator 1 and assume that the time to trigger the Event Generator 1 is ; then, the observer state information which is transmitted at this time is . The next trigger moment iswhere is a given scalar, M is a given positive integer, and is a positive definite weight matrix. According to the above condition (5), the next trigger time is determined by the current observer state and the observer state at the latest trigger time, and . Therefore, for and , if , the state data packets at need not be transmitted.In other words, the embedded trigger condition of the Event Generator 1 isWhen the trigger condition (7) is satisfied, the observer’s state information and state error are transmitted through the network and released to the controller.Remark 1.Remark 2.The data packet which is transmitted from the observer to the controller includes and .Remark 3.M is the upper limit of the trigger time interval given by us to prevent long-term non-triggering from affecting the stability of the system.
- (4)
- Predictive control generator: Combined with the model-based event-triggered predictive control (MB-ETPC) system, the plant’s predictive model is introduced on the control side. The predictive model is used to actively compensate a DoS attack and generate corresponding predictive control sequences. Then, Event Generator 2 is introduced at the control side, which is used to reduce the sending size of the predictive control sequences and further reduce the occupation of bandwidth resources. The predictive control sequences that trigger Event Generator 2 are packaged into a single data packet and sent to the actuator side through the network.
- (5)
- Buffer: The buffers are used to store the incoming data packets.
- (6)
- Zero-order holder (ZOH): The ZOH is used to choose a suitable control signal with a hold event interval of . is the moment that the predictive control generator successfully receives the data.
- (7)
- Actuator: The function of the actuator is to receive the control signal from the ZOH and control the plant.In order to facilitate the analysis, we make the following assumptions regarding the above OB-ETPC system:Assumption 1.System (1) performs isochronous sampling. The sampling time is h, and all data packets are time-stamped.Assumption 2.The sensor is time-driven, and the predictive controller and actuator are event-driven.Assumption 3.This paper does not consider the time delay of the system and the delay of the transmission process.Assumption 4.Assume that (A, B) is completely controllable and (A, C) is completely observable.Assumption 5.and are successfully sent at the initial moment from the observer to the controller.
3. OB-ETPC of NCSs under DoS Attacks and Stability Analysis
3.1. DoS Attack Description
3.2. OB-ETPC of NCSs under DoS Attacks
3.3. The Closed-Loop System
3.4. Stability Analysis
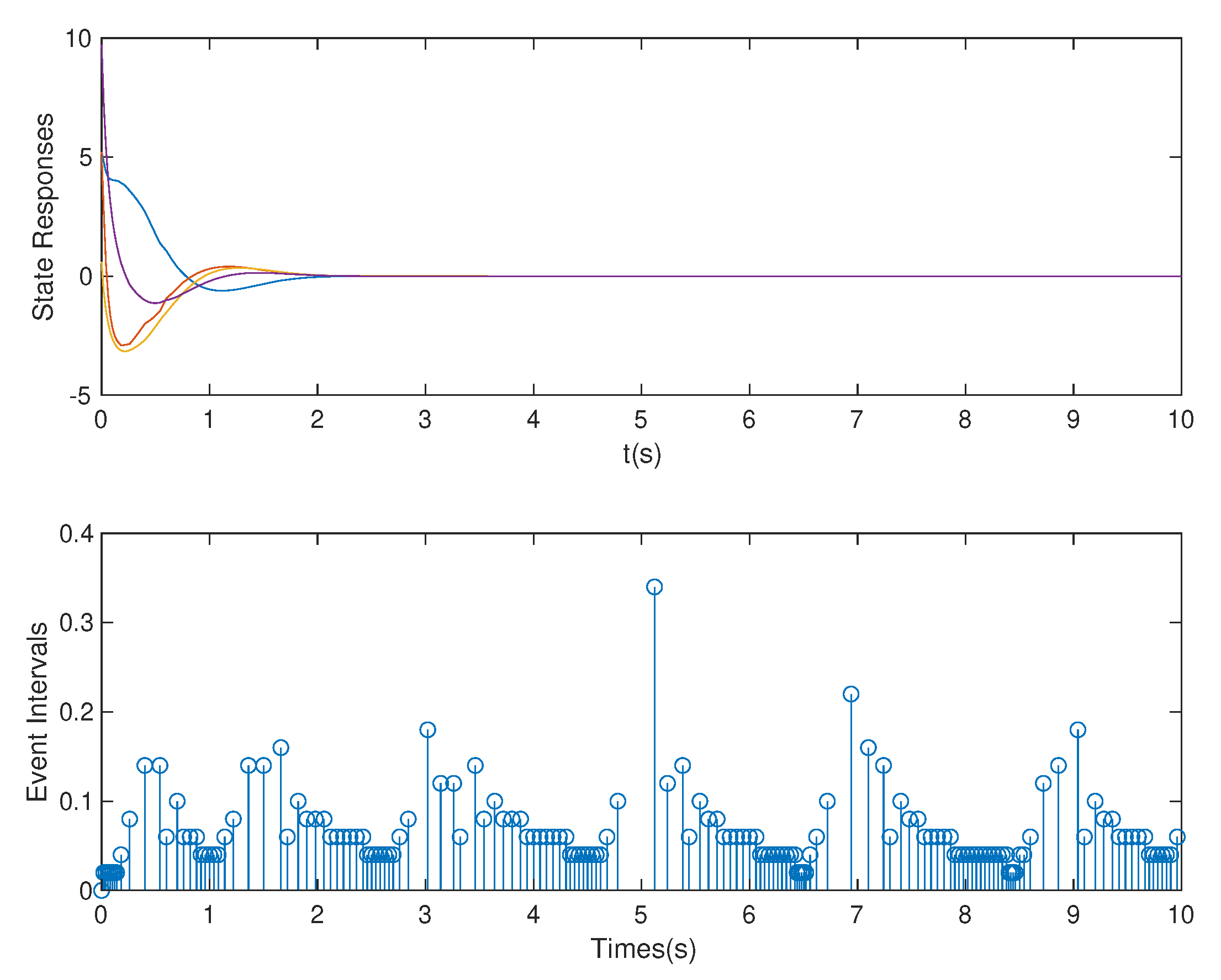
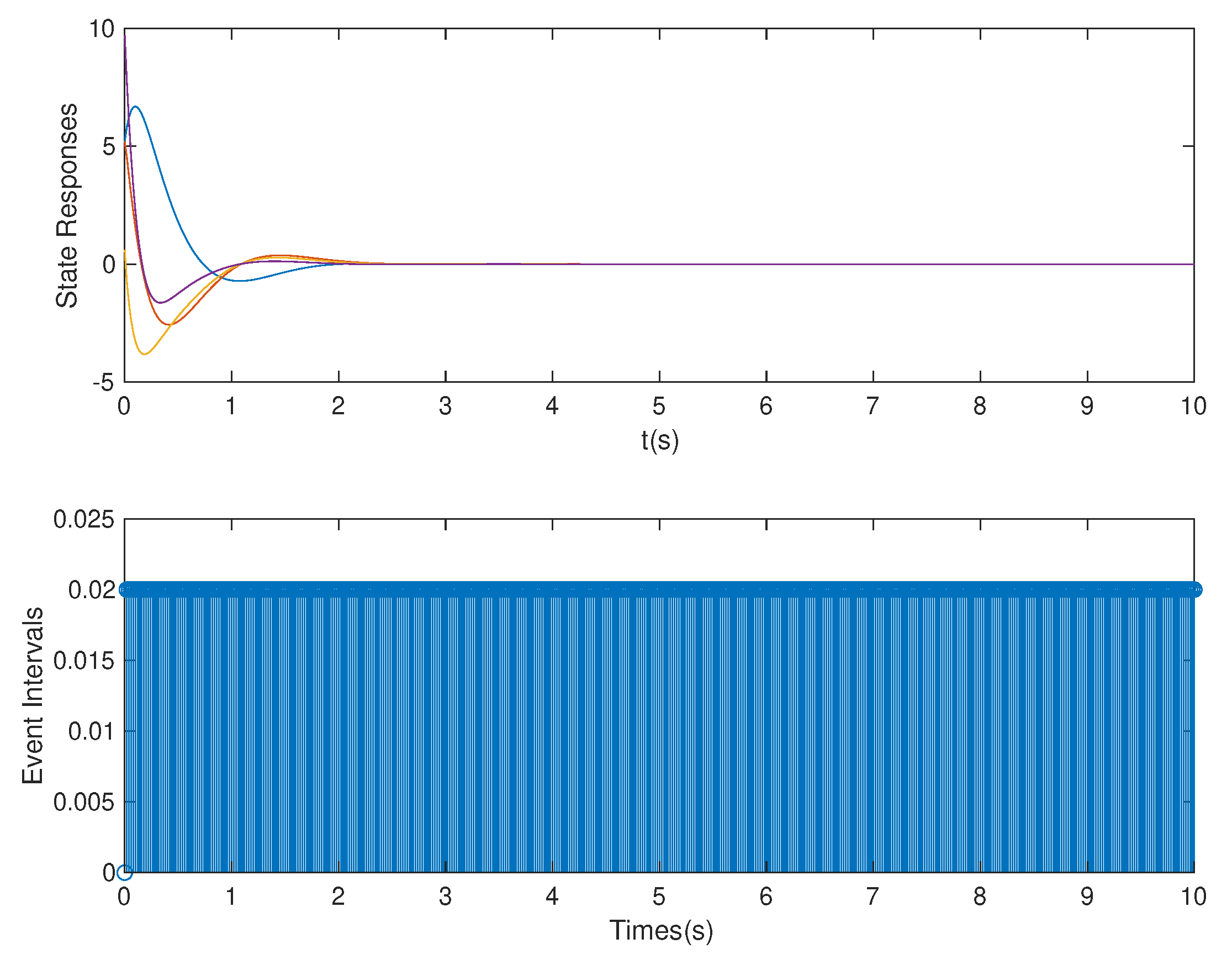
4. Simulation Example
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Demestichas, P.; Georgakopoulos, A.; Karvounas, D.; Tsagkaris, K.; Stavroulaki, V.; Lu, J.; Xiong, C.; Yao, J. 5G on the horizon: Key challenges for the radio-access network. IEEE Veh. Technol. Mag 2013, 8, 47–53. [Google Scholar] [CrossRef]
- Foukas, X.; Patounas, G.; Elmokashfi, A.; Marina, M.K. Network slicing in 5G: Survey and challenges. IEEE Commun. Mag 2017, 55, 94–100. [Google Scholar] [CrossRef]
- Park, B.; Nah, J.; Choi, J.Y.; Yoon, I.J.; Park, P. Robust wireless sensor and actuator networks for networked control systems. Sensors 2019, 19, 1535. [Google Scholar] [CrossRef] [PubMed]
- Galeano-Brajones, J.; Carmona-Murillo, J.; Valenzuela-Valdés, J.F.; Luna-Valero, F. Detection and mitigation of dos and ddos attacks in iot-based stateful sdn: An experimental approach. Sensors 2020, 20, 816. [Google Scholar] [CrossRef]
- Singh, A.K.; Singh, R.; Pal, B.C. Stability analysis of networked control in smart grids. IEEE Trans. Smart Grid 2014, 6, 381–390. [Google Scholar] [CrossRef]
- Aristidou, P.; Valverde, G.; Van Cutsem, T. Contribution of distribution network control to voltage stability: A case study. IEEE Trans. Smart Grid 2015, 8, 106–116. [Google Scholar] [CrossRef]
- Liu, J.; Suo, W.; Zha, L.; Tian, E.; Xie, X. Security distributed state estimation for nonlinear networked systems against dos attacks. Int. J. Robust Nonlinear Control 2020, 30, 1156–1180. [Google Scholar] [CrossRef]
- Yousef, K.M.A.; Almajali, A.; Ghalyon, S.A.; Dweik, W.; Mohd, B.J. Analyzing cyber-physical threats on robotic platforms. Sensors 2018, 18, 1643. [Google Scholar] [CrossRef]
- Yang, T.C. Networked control system: A brief survey. IEEE Proc. Control Theory Appl. 2006, 153, 403–412. [Google Scholar] [CrossRef]
- Gupta, R.A.; Chow, M.Y. Networked control system: Overview and research trends. IEEE Trans. Ind. Electron. 2009, 57, 2527–2535. [Google Scholar] [CrossRef]
- Xia, F.; Ma, L.; Peng, C.; Sun, Y.; Dong, J. Cross-layer adaptive feedback scheduling of wireless control systems. Sensors 2008, 8, 4265–4281. [Google Scholar] [CrossRef] [PubMed]
- Montestruque, L.A.; Antsaklis, P.J. On the model-based control of networked systems. Automatica 2003, 39, 1837–1843. [Google Scholar] [CrossRef]
- Peng, C.; Sun, H.; Yang, M.; Wang, Y.L. A survey on security communication and control for smart grids under malicious cyber attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1554–1569. [Google Scholar] [CrossRef]
- Antunes, D.; Hespanha, J.P.; Silvestre, C. Stochastic hybrid systems with renewal transitions: Moment analysis with application to networked control systems with delays. SIAM J. Control Optim. 2013, 51, 1481–1499. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Ge, X.; Ding, D.; Ding, L.; Yue, D.; Peng, C. Networked control systems: A survey of trends and techniques. IEEE/CAA J. Autom. Sin.. 2020, 7, 1–17. [Google Scholar] [CrossRef]
- Garcia, E.; Cao, Y.; Casbeer, D.W. Periodic event-triggered synchronization of linear multi-agent systems with communication delays. IEEE Trans. Autom. Control 2017, 62, 366–371. [Google Scholar] [CrossRef]
- Ge, X.; Yang, F.; Han, Q.L. Distributed networked control systems: A brief overview. Inf. Sci. 2017, 380, 117–131. [Google Scholar] [CrossRef]
- Ding, L.; Han, Q.L.; Ge, X.; Zhang, X.M. An overview of recent advances in event-triggered consensus of multiagent systems. IEEE Trans. Cybern. 2018, 48, 1110–1123. [Google Scholar] [CrossRef]
- Shisheh, H.F.; Mart, S. On triggering control of single-input linear systems under pulse-width modulated dos signals. SIAM J. Control Optim. 2016, 54, 3084–3105. [Google Scholar] [CrossRef]
- De, C.; Persis, C.; Tesi, P. Input-to-state stabilizing control under denial-of-service. IEEE Trans. Autom. Control 2015, 60, 2930–2944. [Google Scholar]
- Feng, S.; Tesi, P. Resilient control under denial-of-service: Robust design. Automatica 2017, 79, 42–51. [Google Scholar] [CrossRef]
- De, C.; Persis, C.; Tesi, P. Networked control of nonlinear systems under denial-of-service. Syst. Control Lett. 2016, 96, 124–131. [Google Scholar]
- Feng, S.; Tesi, P.; De Persis, C. Towards stabilization of distributed systems under denial-of-service. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 5360–5365. [Google Scholar]
- Cetinkaya, A.; Ishii, H.; Hayakawa, T. Networked control under random and malicious packet losses. IEEE Trans. Autom. Control 2017, 62, 2434–2449. [Google Scholar] [CrossRef]
- Zhao, Y.; He, X.; Zhou, D. Optimal joint control and triggering strategies against denial of service attacks: A zero-sum game. IET Control Theory Appl. 2017, 11, 2352–2360. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Ge, X.; Ding, L. Resilient control design based on a sampled-data model for a class of networked control systems under denial-of-service attacks. IEEE Trans. Cybern. 2020, 50, 3616–3626. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Yue, D.; Han, Q.L.; Xie, X.; Chen, X.; Dou, C. Observer-based event-triggered control for networked linear systems subject to denial-of-service attacks. IEEE Trans. Cybern. 2020, 50, 1952–1964. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.L. Consensus of multiagent systems subject to partially accessible and overlapping markovian network topologies. IEEE Trans. Cybern. 2017, 47, 1807–1819. [Google Scholar] [CrossRef]
- Wang, X.; Lemmon, M.D. Event-triggering in distributed networked control systems. IEEE Trans. Autom. Control 2010, 56, 586–601. [Google Scholar] [CrossRef]
- You, X.; Hua, C.; Guan, X. Event-triggered leader-following consensus for nonlinear multiagent systems subject to actuator saturation using dynamic output feedback method. IEEE Trans. Autom. Control 2018, 63, 4391–4396. [Google Scholar] [CrossRef]
- You, X.; Hua, C.; Guan, X. Self-triggered leader-following consensus for high-order nonlinear multiagent systems via dynamic output feedback control. IEEE Trans. Cybern. 2018, 49, 2002–2010. [Google Scholar] [CrossRef]
- Onat, A.; Naskali, T.; Parlakay, E.; Mutluer, O. Control over imperfect networks: Model-based predictive networked control systems. IEEE Trans. Ind. Electron. 2011, 58, 905–913. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Networked min–max model predictive control of constrained nonlinear systems with delays and packet dropouts. Int. J. Control 2013, 86, 610–624. [Google Scholar] [CrossRef]
- Pang, Z.H.; Liu, G.P.; Zhou, D. Design and performance analysis of incremental networked predictive control systems. IEEE Trans. Cybern. 2015, 46, 1400–1410. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Cheng, Z.; Yue, D.; Dou, C.; Xue, Y. Bandwidth allocation-based switched dynamic triggering control against dos attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef]
- Yin, X.X.; Yue, D.; Hu, S. Model-based event-triggered predictive control for networked systems with communication delays compensation. Int. J. Robust Nonlinear Control 2015, 25, 3572–3595. [Google Scholar] [CrossRef]
- Amullen, E.M.; Shetty, S.; Keel, L.H. Model-based resilient control for a multi-agent system against denial of service attacks. In Proceedings of the 2016 World Automation Congress (WAC), Rio Grande, Puerto Rico, 31 July–4 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Zhang, J.; Chai, S.; Zhang, B. Model-based event-triggered dynamic output predictive control of networked uncertain systems with random delay. Int. J. Syst. Sci. 2020, 51, 20–34. [Google Scholar] [CrossRef]
- Li, Y.X.; Yang, G.H. Model-based adaptive event-triggered control of strict-feedback nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1033–1045. [Google Scholar] [CrossRef]
- Sun, Y.C.; Yang, G.H. Robust event-triggered model predictive control for cyber-physical systems under denial-of-service attacks. Int. J. Robust Nonlinear Control 2019, 29, 4797–4811. [Google Scholar] [CrossRef]
- Yin, X.X.; Yue, D.; Hu, S. Observer-based control for networked systems with event-triggering predictive scheme. In Proceedings of the IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 4774–4780. [Google Scholar]
- Peng, C.; Sun, H. Switching-like event-triggered control for networked control systems under malicious denial of service attacks. IEEE Trans. Autom. Control 2020. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, Y.; Shi, P. Design and stability analysis of networked predictive control systems. IEEE Trans. Control Syst. Technol. 2012, 21, 1495–1501. [Google Scholar] [CrossRef]
- Liu, J.; Yang, M.; Tian, E.; Cao, J.; Fei, S. Event-based security control for state-dependent uncertain systems under hybrid-attacks and its application to electronic circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 4817–4828. [Google Scholar] [CrossRef]
- Mohammed, A.A.S.; Moussa, W.A.; Lou, E. High sensitivity mems strain sensor: Design and simulation. Sensors 2008, 8, 642–2661. [Google Scholar] [CrossRef] [PubMed]
- Tian, E.; Wang, Z.; Zou, L.; Yue, D. Probabilistic-constrained filtering for a class of nonlinear systems with improved static event-triggered communication. Int. J. Robust Nonlinear Control 2019, 29, 1484–1498. [Google Scholar] [CrossRef]
- Cao, R.; Wu, J.; Long, C.; Li, S. Stability analysis for networked control systems under denial-of-service attacks. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 7476–7481. [Google Scholar]
- Sun, H.; Peng, C.; Zhang, W.; Yang, T.; Wang, Z. Security-based resilient event-triggered control of networked control systems under denial of service attacks. J. Frankl. Inst. 2019, 356, 277–295. [Google Scholar] [CrossRef]
- Hu, S.; Yue, D.; Xie, X.; Chen, X.; Yin, X. Resilient event-triggered controller synthesis of networked control systems under periodic dos jamming attacks. IEEE Trans. Cybern. 2018, 49, 4271–4281. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Ye, D. Observer-based output feedback h∞ control for cyber–physical systems under randomly occurring packet dropout and periodic dos attacks. ISA Trans. 2019, 95, 58–67. [Google Scholar] [CrossRef]
- Kersting, W.H. Radial distribution test feeders. IEEE Trans. Power Syst. 1991, 6, 975–985. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, K.; Shi, Y. Resilient model predictive control of cyber–physical systems under dos attacks. IEEE Trans. Ind. Inform. 2020, 16, 4920–4927. [Google Scholar] [CrossRef]
- Liu, G.P.; Xia, Y.; Chen, J.; Rees, D.; Hu, W. Networked predictive control of systems with random network delays in both forward and feedback channels. IEEE Trans. Ind. Electron. 2007, 54, 1282–1297. [Google Scholar] [CrossRef]
- Liu, G.P. Predictive controller design of networked systems with communication delays and data loss. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 481–485. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, Z.; Gao, Z. A novel fault detection with minimizing the noise-signal ratio using reinforcement learning. Sensors 2018, 18, 3087. [Google Scholar] [CrossRef] [PubMed]






| Notations | Definitions |
|---|---|
| The state vector. | |
| The control vector. | |
| The device output vector. | |
| The state vector of the observer. | |
| The output vector of the observer. | |
| The state vector of the predictive control generator. | |
| The observer state error. | |
| The time to trigger the Event Generator 1. | |
| The moment at which the predictive control generator that successfully receives the data. | |
| A, B and C | The appropriate dimension matrices of the system. |
| L | The gain matrix of the observer. |
| K | The feedback gain matrix. |
| A given scalar. | |
| M | A given positive integer. |
| A positive definite weight matrix. | |
| T | The period of DoS attacks. |
| The number of the DoS attack cycle. | |
| A real number which satisfies . | |
| p | A real number which satisfies . |
| M | A given positive integer. |
| P and Q | The symmetrical positive definite matrices. |
| Different Methods | OB-ETPC | OB-ETPC | TTPC | TTPC | ETC | ETC |
|---|---|---|---|---|---|---|
| Cases | Case 1 and Case 2 | Case 1 and Case 3 | Case 1 | Case 1 | Case2 | Case 3 |
| Methods | This paper | This paper | [52,53,54] | [52,53,54] | [27,48,49] | [27,48,49] |
| Sampled numbers | 500 | 500 | 500 | 500 | 500 | 500 |
| Released numbers | 154 | 154 | 500 | 500 | 143 | 117 |
| Average trigger time | 0.0649 s | 0.0649 s | 0.02 s | 0.02 s | 0.0699 s | 0.0855 s |
| Data numbers | 114 | 54 | 380 | 130 | 100 | 40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Yin, X.; Fu, Y.; Gao, Z. Observer-Based Event-Triggered Predictive Control for Networked Control Systems under DoS Attacks. Sensors 2020, 20, 6866. https://doi.org/10.3390/s20236866
Lu W, Yin X, Fu Y, Gao Z. Observer-Based Event-Triggered Predictive Control for Networked Control Systems under DoS Attacks. Sensors. 2020; 20(23):6866. https://doi.org/10.3390/s20236866
Chicago/Turabian StyleLu, Weifan, Xiuxia Yin, Yichuan Fu, and Zhiwei Gao. 2020. "Observer-Based Event-Triggered Predictive Control for Networked Control Systems under DoS Attacks" Sensors 20, no. 23: 6866. https://doi.org/10.3390/s20236866
APA StyleLu, W., Yin, X., Fu, Y., & Gao, Z. (2020). Observer-Based Event-Triggered Predictive Control for Networked Control Systems under DoS Attacks. Sensors, 20(23), 6866. https://doi.org/10.3390/s20236866







