Seismological Processing of Six Degree-of-Freedom Ground-Motion Data
Abstract
1. Introduction
“Instruments ought to be devised [...] to ends [...], such as the measurement of horizontal concussions, of vertical elevation, and of heaving or angular motion of the surface. It is no part of my present object to consider the probable movements of the soil in earthquakes. I limit myself to the description of a single instrument intended to measure lateral shocks, such as are experienced by objects placed upon a table which is abruptly shoved forwards.”James David Forbes (1844) [1].
2. Theoretical Foundations
Rotational Ground Motion at the Free Surface
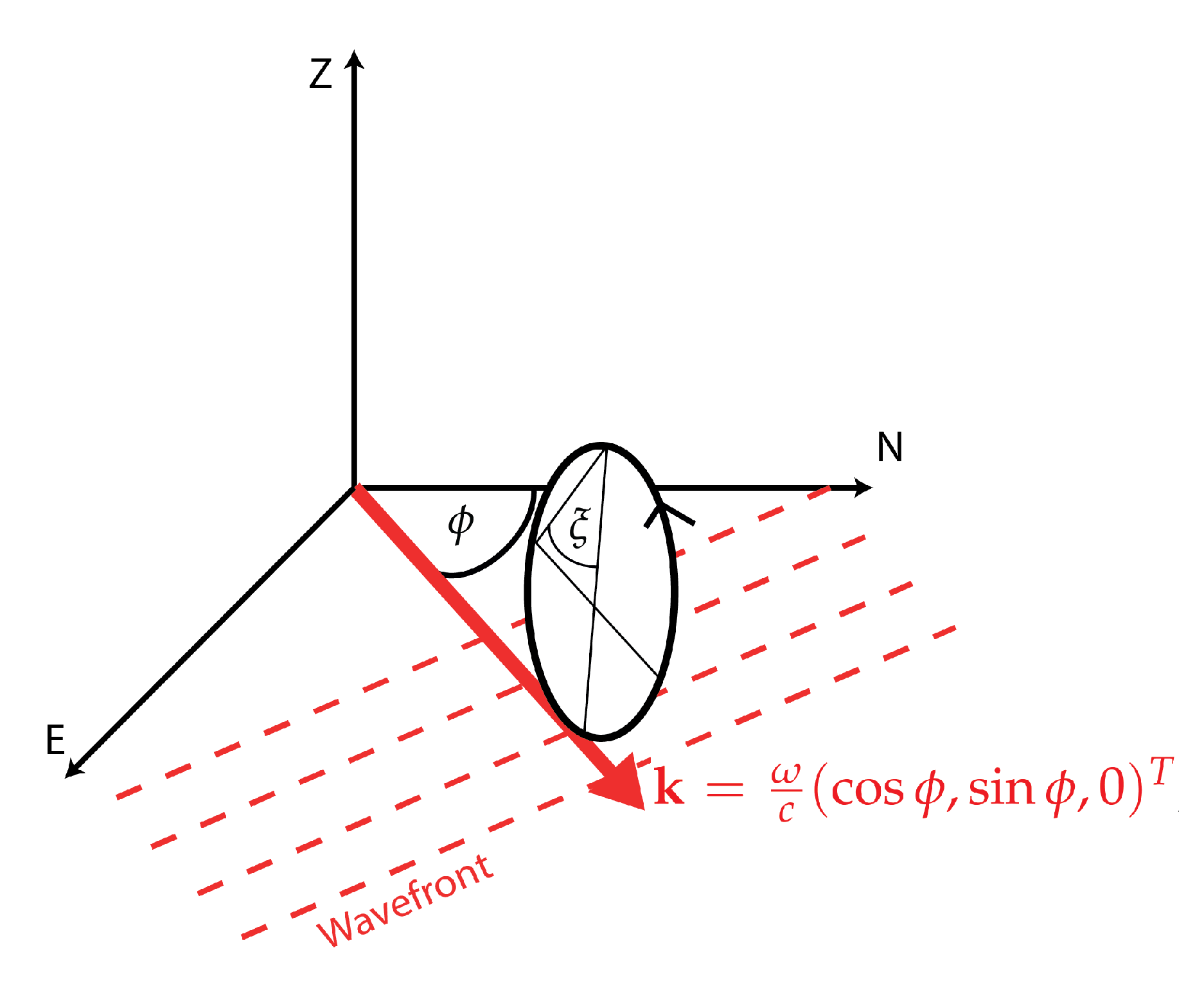
3. Processing of 6DOF Ground-Motion Measurements
3.1. Array-Like Capabilites of Single-Station 6DOF Measurements
3.1.1. Single-Station 6DOF Wave Parameter Estimation
3.1.2. Single-Station 6DOF Wave Mode Filtering
3.1.3. Example: Tutorial on 6DOF Processing Using the 2018 Gulf of Alaska Earthquake
3.2. Sparse Wavefield Sampling
“I do not see that land equipment and exploration can expect a bright future if oil continues to hover around its current price. However, this is only if land seismic carries on in the way it has been doing. If we make some overdue technological changes and adhere better to the science, the future is bright and potentially very profitable.”Bob Heath (2018) [71].
3.3. Rotational Data as a New Observable to Constrain Inverse Problems
3.4. Tilt Corrections of Translational Data
3.5. Earthquake Engineering
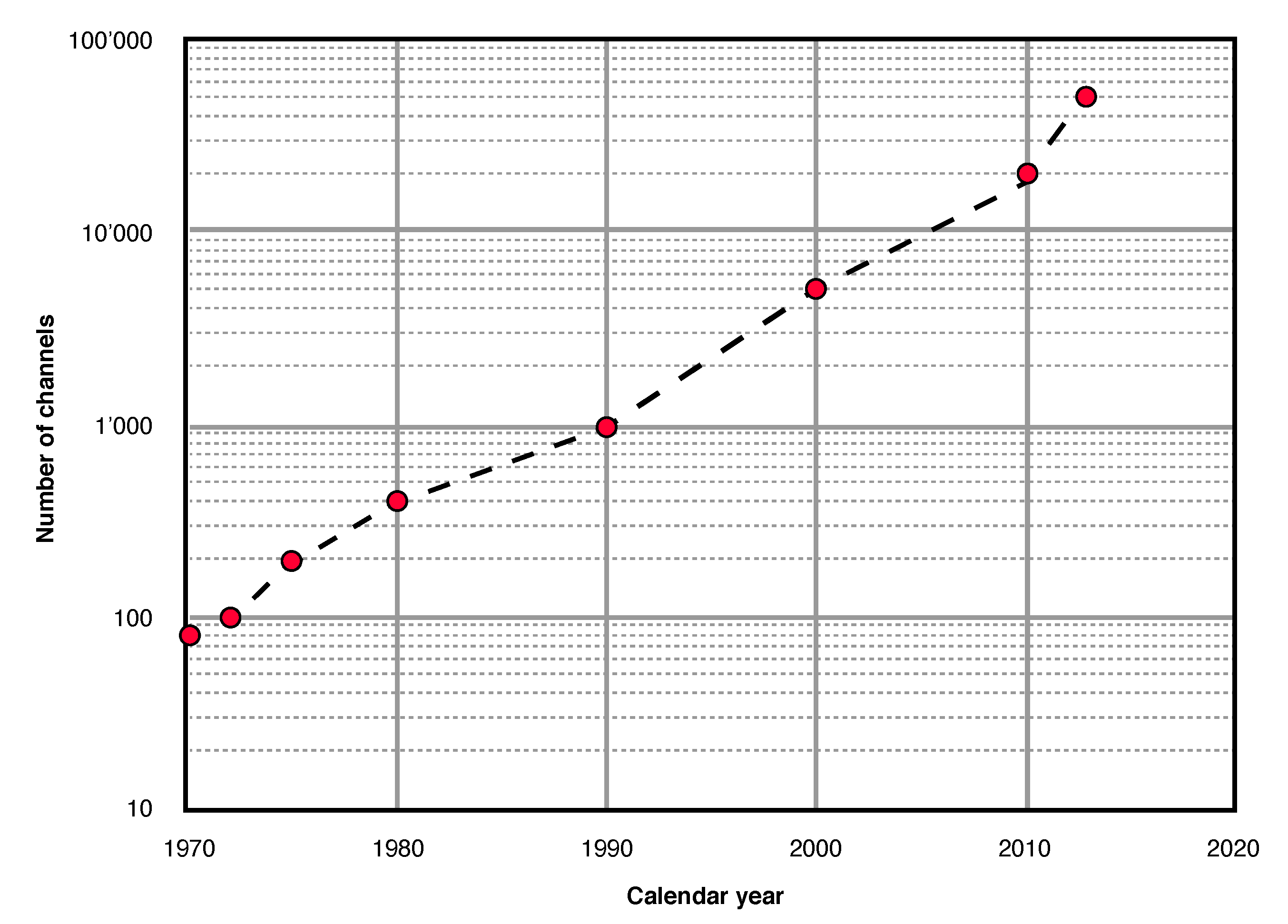
4. How to Measure Rotational Motions
4.1. Direct Observations
4.2. Array-Derived Rotational Motions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Milne-Home, D. Report of a committee for obtaining instruments and registers to record shocks of earthquakes in Scotland and Ireland. In Reports of the British Association for the Advancement of Science; British Association for the Advancement of Science: London, UK, 1842; pp. 46–49. [Google Scholar]
- Wood, R.M. Robert Mallet and John Milne—Earthquakes incorporated in Victorian Britain. Earthq. Eng. Struct. Dyn. 1988, 17, 107–142. [Google Scholar] [CrossRef]
- Forbes, J. On the theory and construction of a seismometer, or instrument for measuring earthquake shocks, and other concussions. Trans. R. Soc. Edinb. 1844, 15, 219–228. [Google Scholar] [CrossRef]
- Nigbor, R.L. Six-degree-of-freedom ground-motion measurement. Bull. Seismol. Soc. Am. 1994, 84, 1665–1669. [Google Scholar]
- Takeo, M. Ground rotational motions recorded in near-source region of earthquakes. Geophys. Res. Lett. 1998, 25, 789–792. [Google Scholar] [CrossRef]
- McLeod, D.P.; Stedman, G.E.; Webb, T.H.; Schreiber, U. Comparison of standard and ring laser rotational seismograms. Bull. Seismol. Soc. Am. 1998, 88, 1495–1503. [Google Scholar]
- Pancha, A.; Webb, T.H.; Stedman, G.E.; McLeod, D.P.; Schreiber, U. Ring laser detection of rotations from teleseismic waves. Geophys. Res. Lett. 2000, 27, 3553–3556. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Velikoseltsev, A.; Igel, H.; Cochard, A.; Flaws, A.; Drewitz, W.; Müller, F. The GEOsensor: A new instrument for seismology. In Geo-Technologien Science Report No. 3: “Observation of the System Earth from Space”, Status Seminar, Bavarian State Mapping Agency (BLVA), Munich, Germany, 12–13 June 2003, Programme & Abstracts; Bavarian State Mapping Agency (BLVA): Los Angeles, CA, USA, 2003. [Google Scholar]
- Igel, H.; Schreiber, U.; Flaws, A.; Schuberth, B.; Velikoseltsev, A.; Cochard, A. Rotational motions induced by the M8.1 Tokachi-oki earthquake, September 25, 2003. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Stedman, G.E.; Igel, H.; Flaws, A. Ring Laser Gyroscopes as Rotation Sensors for Seismic Wave Studies. In Earthquake Source Asymmetry, Structural Media and Rotation Effects; Springer: Berlin/Heidelberg, 2006; pp. 377–390. [Google Scholar] [CrossRef]
- Schreiber, K.U.; Hautmann, J.N.; Velikoseltsev, A.; Wassermann, J.; Igel, H.; Otero, J.; Vernon, F.; Wells, J.P.R. Ring Laser Measurements of Ground Rotations for Seismology. Bull. Seismol. Soc. Am. 2009, 99, 1190–1198. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Guattari, F.; Frenois, A.; Bigueur, A.; Gaillot, A.; de Toldi, E.; Ponceau, D.; Schreiber, U.; Igel, H. BlueSeis3A: Full Characterization of a 3C Broadband Rotational Seismometer. Seismol. Res. Lett. 2018. [Google Scholar] [CrossRef]
- Brokešová, J.; Málek, J. New portable sensor system for rotational seismic motion measurements. Rev. Sci. Instrum. 2010, 81, 084501. [Google Scholar] [CrossRef]
- Salvermoser, J.; Hadziioannou, C.; Hable, S.; Krischer, L.; Chow, B.; Ramos, C.; Wassermann, J.; Schreiber, U.; Gebauer, A.; Igel, H. An Event Database for Rotational Seismology. Seismol. Res. Lett. 2017, 88, 935–941. [Google Scholar] [CrossRef]
- Cochard, A.; Igel, H.; Schuberth, B.; Suryanto, W.; Velikoseltsev, A.; Schreiber, U.; Wassermann, J.; Scherbaum, F.; Vollmer, D. Rotational motions in seismology: Theory, observation, simulation. In Earthquake Source Asymmetry, Structural Media and Rotation Effects; Springer: Berlin/Heidelberg, Germany, 2006; pp. 391–411. [Google Scholar] [CrossRef]
- Lee, W.H.K.; Igel, H.; Trifunac, M.D. Recent Advances in Rotational Seismology. Seismol. Res. Lett. 2009, 80, 479–490. [Google Scholar] [CrossRef]
- Lee, W.H.K.; Çelebi, M.; Todorovska, M.I.; Igel, H. Introduction to the special issue on rotational seismology and engineering applications. Bull. Seismol. Soc. Am. 2009, 99, 945–957. [Google Scholar] [CrossRef]
- Lee, W.H.K. A glossary for rotational seismology. Bull. Seismol. Soc. Am. 2009, 99, 1082–1090. [Google Scholar] [CrossRef]
- Igel, H.; Bernauer, M.; Wassermann, J.; Schreiber, K.U. Rotational Seismology: Theory, Instrumentation, Observations, Applications. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Li, Z.; van der Baan, M. Tutorial on rotational seismology and its applications in exploration geophysics. Geophysics 2017, 82, W17–W30. [Google Scholar] [CrossRef]
- Schmelzbach, C.; Donner, S.; Igel, H.; Sollberger, D.; Taufiqurrahman, T.; Bernauer, F.; Häusler, M.; Van Renterghem, C.; Wassermann, J.; Robertsson, J. Advances in 6-C seismology: Applications of combined translational and rotational motion measurements in global and exploration seismology. Geophysics 2018, 83, WC53–WC69. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology; University Science Books: Mill Valley, CA, USA, 2002; p. 700. [Google Scholar]
- Wassermann, J.; Bernauer, F.; Shiro, B.; Johanson, I.; Guattari, F.; Igel, H. Six-Axis Ground Motion Measurements of Caldera Collapse at Kilauea Volcano, Hawaii—More Data, More Puzzles? Geophys. Res. Lett. 2020. [Google Scholar] [CrossRef]
- Pham, N.D.; Igel, H.; de la Puente, J.; Käser, M.; Schoenberg, M.A. Rotational motions in homogeneous anisotropic elastic media. Geophysics 2010, 75, D47–D56. [Google Scholar] [CrossRef][Green Version]
- Sollberger, D.; Greenhalgh, S.A.; Schmelzbach, C.; Van Renterghem, C.; Robertsson, J.O.A. 6-C polarization analysis using point measurements of translational and rotational ground-motion: Theory and applications. Geophys. J. Int. 2018, 213, 77–97. [Google Scholar] [CrossRef]
- Rost, S.; Thomas, C. Array seismology: Methods and applications. Rev. Geophys. 2002, 40, 2-1–2-27. [Google Scholar] [CrossRef]
- Aldridge, D.F.; Abbot, R.E. Investigating the Point Seismic Array Concept with Seismic Rotation Measurements; Technical Report; Sandia National Lab.: Albuquerque, NM, USA, 2009. [Google Scholar]
- Lindner, F.; Wassermann, J.; Schmidt-Aursch, M.C.; Schreiber, K.U.; Igel, H. Seafloor Ground Rotation Observations: Potential for Improving Signal-to-Noise Ratio on Horizontal OBS Components. Seismol. Res. Lett. 2017, 88, 32–38. [Google Scholar] [CrossRef]
- Sollberger, D.; Schmelzbach, C.; Robertsson, J.O.A.; Greenhalgh, S.A.; Nakamura, Y.; Khan, A. The shallow elastic structure of the lunar crust: New insights from seismic wavefield gradient analysis. Geophys. Res. Lett. 2016, 43, 10,078–10,087. [Google Scholar] [CrossRef]
- Schlüter, W. Schwingungsart und Weg der Erdbebenwellen. Beiträge zur Geophysik 1903, 5, 314–359. [Google Scholar]
- Igel, H.; Cochard, A.; Wassermann, J.; Flaws, A.; Schreiber, U.; Velikoseltsev, A.; Pham Dinh, N. Broad-band observations of earthquake-induced rotational ground motions. Geophys. J. Int. 2007, 168, 182–196. [Google Scholar] [CrossRef]
- Ferreira, A.M.; Igel, H. Rotational motions of seismic surface waves in a laterally heterogeneous earth. Bull. Seismol. Soc. Am. 2009, 99, 1429–1436. [Google Scholar] [CrossRef]
- Simonelli, A.; Igel, H.; Wassermann, J.; Belfi, J.; Di Virgilio, A.; Beverini, N.; De Luca, G.; Saccorotti, G. Rotational motions from the 2016, Central Italy seismic sequence, as observed by an underground ring laser gyroscope. Geophys. J. Int. 2018, 214, 705–715. [Google Scholar] [CrossRef]
- Hadziioannou, C.; Gaebler, P.; Schreiber, U.; Wassermann, J.; Igel, H. Examining ambient noise using colocated measurements of rotational and translational motion. J. Seismol. 2012, 16, 787–796. [Google Scholar] [CrossRef]
- Kurrle, D.; Igel, H.; Ferreira, A.M.; Wassermann, J.; Schreiber, U. Can we estimate local Love wave dispersion properties from collocated amplitude measurements of translations and rotations? Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Wassermann, J.; Wietek, A.; Hadziioannou, C.; Igel, H. Toward a single-station approach for microzonation: Using vertical component rotation rate to estimate Love wave dispersion curves and direction finding. Bull. Seismol. Soc. Am. 2016, 106, 1316–1330. [Google Scholar] [CrossRef]
- Edme, P.; Yuan, S. Local dispersion curve estimation from seismic ambient noise using spatial gradients. Interpretation 2016, 4, SJ17–SJ27. [Google Scholar] [CrossRef]
- Ringler, A.T.; Anthony, R.E.; Holland, A.A.; Wilson, D.C.; Lin, C.J. Observations of rotational motions from local earthquakes using two temporary portable sensors in waynoka, oklahoma. Bull. Seismol. Soc. Am. 2018, 108, 3562–3575. [Google Scholar] [CrossRef]
- Ross, M.P.; Venkateswara, K.; Hagedorn, C.A.; Gundlach, J.H.; Kissel, J.S.; Warner, J.; Radkins, H.; Shaffer, T.J.; Coughlin, M.W.; Bodin, P. Low-frequency tilt seismology with a precision ground-rotation sensor. Seismol. Res. Lett. 2018, 89, 67–76. [Google Scholar] [CrossRef]
- Yoshida, K.; Uebayashi, H. Love-Wave Phase-Velocity Estimation from Array-Based Rotational Motion Microtremor. Bull. Seismol. Soc. Am. 2020. [Google Scholar] [CrossRef]
- Keil, S.; Wassermann, J.; Igel, H. Single-station seismic microzonation using 6C measurements. J. Seismol. 2020, 1–12. [Google Scholar] [CrossRef]
- Maranò, S.; Fäh, D. Processing of translational and rotational motions of surface waves: Performance analysis and applications to single sensor and to array measurements. Geophys. J. Int. 2013, 196, 317–339. [Google Scholar] [CrossRef]
- Langston, C.A. Spatial Gradient Analysis for Linear Seismic Arrays. Bull. Seismol. Soc. Am. 2007, 97, 265–280. [Google Scholar] [CrossRef]
- Langston, C.A. Wave gradiometry in two dimensions. Bull. Seismol. Soc. Am. 2007, 97, 401–416. [Google Scholar] [CrossRef]
- Liang, C.; Langston, C.A. Wave gradiometry for USArray: Rayleigh waves. J. Geophys. Res. 2009, 114, B02308. [Google Scholar] [CrossRef]
- Liu, Y.; Holt, W.E. Wave gradiometry and its link with Helmholtz equation solutions applied to USArray in the eastern U.S. J. Geophys. Res. B Solid Earth 2015, 120, 5717–5746. [Google Scholar] [CrossRef]
- Curtis, A.; Robertsson, J.O.A. Volumetric wavefield recording and wave equation inversion for near-surface material properties. Geophysics 2002, 68, 760. [Google Scholar] [CrossRef]
- De Ridder, S.A.L.; Biondi, B.L. Near-surface Scholte wave velocities at Ekofisk from short noise recordings by seismic noise gradiometry. Geophys. Res. Lett. 2015, 42, 7031–7038. [Google Scholar] [CrossRef]
- De Ridder, S.; Curtis, A. Seismic Gradiometry using Ambient Seismic Noise in an Anisotropic Earth. Geophys. J. Int. 2017, 209, 1168–1179. [Google Scholar] [CrossRef][Green Version]
- Yilmaz, Ö. Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data. EarthArxiv 2001. [Google Scholar] [CrossRef]
- Greenhalgh, S.A.; Mason, I.M.; Lucas, E.; Pant, D.; Eames, R.T. Controlled Direction Reception Filtering of P- and S-Waves In Tau-P Space. Geophys. J. Int. 1990, 100, 221–234. [Google Scholar] [CrossRef]
- Donno, D.; Nehorai, A.; Spagnolini, U. Seismic velocity and polarization estimation for wavefield separation. IEEE Trans. Signal Process. 2008, 56, 4794–4809. [Google Scholar] [CrossRef]
- Robertsson, J.O.A.; Muyzert, E. Wavefield separation using a volume distribution of three component recordings. Geophys. Res. Lett. 1999, 26, 2821–2824. [Google Scholar] [CrossRef]
- Robertsson, J.O.A.; Curtis, A. Wavefield separation using densely deployed three-component single-sensor groups in land surface-seismic recordings. Geophysics 2002, 67, 1624–1633. [Google Scholar] [CrossRef]
- Van Renterghem, C.; Schmelzbach, C.; Sollberger, D.; Robertsson, J.O. Spatial wavefield gradient-based seismic wavefield separation. Geophys. J. Int. 2018, 212, 1588–1599. [Google Scholar] [CrossRef]
- Woelz, S.; Rabbel, W.; Mueller, C. Shear waves in near surface 3D media-SH-wavefield separation, refraction time migration and tomography. J. Appl. Geophys. 2009, 68, 104–116. [Google Scholar] [CrossRef]
- Tanimoto, T.; Hadziioannou, C.; Igel, H.; Wassermann, J.; Schreiber, U.; Gebauer, A. Estimate of Rayleigh-to-Love wave ratio in the secondary microseism by colocated ring laser and seismograph. Geophys. Res. Lett. 2015, 42, 2650–2655. [Google Scholar] [CrossRef]
- Chow, B.; Wassermann, J.; Schuberth, B.S.; Hadziioannou, C.; Donner, S.; Igel, H. Love wave amplitude decay from rotational ground motions. Geophys. J. Int. 2019, 218, 1336–1347. [Google Scholar] [CrossRef]
- Yuan, S.; Simonelli, A.; Lin, C.J.; Bernauer, F.; Donner, S.; Braun, T.; Wassermann, J.; Igel, H. Six Degree-of-Freedom Broadband Ground- Motion Observations with Portable Sensors: Validation, Local Earthquakes, and Signal Processing. Bull. Seismol. Soc. Am. 2020, 110, 953–969. [Google Scholar] [CrossRef]
- Gessele, K.; Yuan, S.; Gabriel, A.A.; May, D.; Igel, H. Earthquake rupture tracking with six degree-of-freedom ground motion observations: A synthetic proof of concept. EarthArxiv 2020. [Google Scholar] [CrossRef]
- Barak, O.; Herkenhoff, F.; Dash, R.; Jaiswal, P.; Giles, J.; de Ridder, S.; Brune, R.; Ronen, S. Six-component seismic land data acquired with geophones and rotation sensors: Wave-mode selectivity by application of multicomponent polarization filtering. Lead. Edge 2014, 33, 1224–1232. [Google Scholar] [CrossRef]
- Barak, O.; Jaiswal, P.; Ridder, S.D.; Giles, J.; Brune, R.; Ronen, S. Six-component seismic land data acquired with geophones and rotation sensors: Wave-mode separation using 6C SVD. In SEG Technical Program Expanded Abstracts; SEG: Tulsa, OK, USA, 2014; pp. 1863–1867. [Google Scholar] [CrossRef]
- Edme, P.; Muyzert, E. Rotational Data Measurement. In Proceedings of the 75th EAGE Conference & Exhibition, London, UK, 10–13 June 2013; p. Tu0407. [Google Scholar] [CrossRef]
- Edme, P.; Daly, M.; Muyzert, E.; Kragh, E. Side Scattered Noise Attenuation Using Rotation Data. In Proceedings of the 75th EAGE Conference & Exhibition, London, UK, 10–13 June 2013; p. THP1106. [Google Scholar] [CrossRef]
- Sollberger, D.; Schmelzbach, C.; Van Renterghem, C.; Robertsson, J.; Greenhalgh, S. Automated, six-component, single-station ground-roll identification and suppression by combined processing of translational and rotational ground motion. In SEG Technical Program Expanded Abstracts 2017; SEG: Tulsa, OK, USA, 2017; pp. 5064–5068. [Google Scholar] [CrossRef]
- Hand, E. Lord of the rings. Science 2017, 356, 236–238. [Google Scholar] [CrossRef] [PubMed]
- Gebauer, A.; Tercjak, M.; Schreiber, K.U.; Igel, H.; Kodet, J.; Hugentobler, U.; Wassermann, J.; Bernauer, F.; Lin, C.J.; Donner, S.; et al. Reconstruction of the Instantaneous Earth Rotation Vector with Sub-Arcsecond Resolution Using a Large Scale Ring Laser Array. Phys. Rev. Lett. 2020, 125, 033605. [Google Scholar] [CrossRef] [PubMed]
- Sollberger, D.; Igel, H.; Schmelzbach, C.; Bernauer, F.; Yuan, S.; Wassermann, J.; Gebauer, A.; Schreiber, U.; Robertsson, J. Towards Field Data Applications of Six-Component Polarization Analysis; EGU General Assembly: Lund, Sweden, 2020; p. 16191. [Google Scholar]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Samson, J.C.; Olson, J.V. Some comments on the descriptions of the polarization states of waves. Geophys. J. R. Astron. Soc. 1980, 61, 115–129. [Google Scholar] [CrossRef]
- Heath, B. The future of land exploration: Brute force and ignorance, or adherence to the science? First Break 2018, 36, 85–89. [Google Scholar]
- Lansley, M. Shifting paradigms in land data acquisition. First Break 2013, 31, 73–77. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Papoulis, A. Generalized Sampling Expansion. IEEE Trans. Circuits Syst. 1977, 24, 652–654. [Google Scholar] [CrossRef]
- Muyzert, E.; Kashubin, A.; Kragh, E.; Edme, P. Land Seismic Data Acquisition Using Rotation Sensors. In Proceedings of the 74th EAGE Conference & Exhibition, Copenhagen, Denmark, 4–7 June 2012. [Google Scholar] [CrossRef]
- Robertsson, J.O.A.; Moore, I.; Vassallo, M.; Ozdemir, K.; van Manen, D.J.; Ozbek, A. On the use of multicomponent streamer recordings for reconstruction of pressure wavefields in the crossline direction. Geophysics 2008, 73, A45–A49. [Google Scholar] [CrossRef]
- Vassallo, M.; Ozbek, A.; Ozdemir, K.; Eggenberger, K. Crossline wavefield reconstruction from multicomponent streamer data: Part 1—Multichannel interpolation by matching pursuit (MIMAP) using pressure and its crossline gradient. Geophysics 2010, 75, WB53–WB67. [Google Scholar] [CrossRef]
- Muyzert, E.; Allouche, N.; Edme, P.; Goujon, N. A five component land seismic sensor for measuring lateral gradients of the wavefield. Geophys. Prospect. 2019, 67, 97–113. [Google Scholar] [CrossRef]
- Singh, S.; Capdeville, Y.; Igel, H. Correcting wavefield gradients for the effects of local small-scale heterogeneities. Geophys. J. Int. 2020, 220, 996–1011. [Google Scholar] [CrossRef]
- Fichtner, A.; Igel, H. Sensitivity densities for rotational ground-motion measurements. Bull. Seismol. Soc. Am. 2009, 99, 1302–1314. [Google Scholar] [CrossRef]
- Bernauer, M.; Fichtner, A.; Igel, H. Inferring earth structure from combined measurements of rotational and translational ground motions. Geophysics 2009, 74, 41–47. [Google Scholar] [CrossRef]
- Bernauer, M.; Fichtner, A.; Igel, H. Measurements of translation, rotation and strain: New approaches to seismic processing and inversion. J. Seismol. 2012, 16, 669–681. [Google Scholar] [CrossRef]
- Bernauer, M.; Fichtner, A.; Igel, H. Reducing nonuniqueness in finite source inversion using rotational ground motions. J. Geophys. Res. Solid Earth 2014, 119, 4860–4875. [Google Scholar] [CrossRef]
- Reinwald, M.; Bernauer, M.; Igel, H.; Donner, S. Improved finite-source inversion through joint measurements of rotational and translational ground motions: A numerical study. Solid Earth 2016, 7, 1467–1477. [Google Scholar] [CrossRef]
- Donner, S.; Bernauer, M.; Igel, H. Inversion for seismic moment tensors combining translational and rotational ground motions. Geophys. J. Int. 2016, 207, 562–570. [Google Scholar] [CrossRef][Green Version]
- Igel, H.; Nader, M.F.; Kurrle, D.; Ferreira, A.M.G.; Wassermann, J.; Schreiber, K.U. Observations of Earth’s toroidal free oscillations with a rotation sensor: The 2011 magnitude 9.0 Tohoku-Oki earthquake. Geophys. Res. Lett. 2011, 38, L21303. [Google Scholar] [CrossRef]
- Nader, M.F.; Igel, H.; Ferreira, A.M.G.; Kurrle, D.; Wassermann, J.; Schreiber, K.U. Toroidal free oscillations of the Earth observed by a ring laser system: A comparative study. J. Seismol. 2012, 16, 745–755. [Google Scholar] [CrossRef]
- Nader, M.F.; Igel, H. Normal mode coupling observations with a rotation sensor. Geophys. J. Int. 2015, 201, 1482–1490. [Google Scholar] [CrossRef]
- Li, Z.; van der Baan, M. Elastic passive source localization using rotational motions. Geophys. J. Int. 2017, 211, 1206–1222. [Google Scholar] [CrossRef]
- Paitz, P.; Sager, K.; Fichtner, A. Rotation and strain ambient noise interferometry. Geophys. J. Int 2019, 216, 1938–1952. [Google Scholar] [CrossRef]
- Graizer, V.M. Inertial Seismometry Methods. Phys. Solid Earth 1991, 27, 51–61. [Google Scholar]
- Trifunac, M.D.; Todorovska, M.I. A note on the useable dynamic range of accelerographs recording translation. Soil Dyn. Earthq. Eng. 2001, 21, 275–286. [Google Scholar] [CrossRef]
- Graizer, V.M. Effect of tilt on strong motion data processing. Soil Dyn. Earthq. Eng. 2005, 25, 197–204. [Google Scholar] [CrossRef]
- Pillet, R.; Virieux, J. The effects of seismic rotations on inertial sensors. Geophys. J. Int. 2007, 171, 1314–1323. [Google Scholar] [CrossRef]
- Lin, C.J.; Huang, H.P.; Liu, C.C.; Chiu, H.C. Application of Rotational Sensors to Correcting Rotation-Induced Effects on Accelerometers. Bull. Seismol. Soc. Am. 2010, 100, 585–597. [Google Scholar] [CrossRef]
- Venkateswara, K.; Hagedorn, C.A.; Gundlach, J.H.; Kissel, J.; Warner, J.; Radkins, H.; Shaffer, T.; Lantz, B.; Mittleman, R.; Matichard, F.; et al. Subtracting tilt from a horizontal seismometer using a ground-rotation sensor. Bull. Seismol. Soc. Am. 2017, 107, 709–717. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Igel, H. Dynamic Tilt Correction Using Direct Rotational Motion Measurements. Seismol. Res. Lett. 2020. [Google Scholar] [CrossRef]
- Van Driel, M.; Wassermann, J.; Pelties, C.; Schiemenz, A.; Igel, H. Tilt effects on moment tensor inversion in the near field of active volcanoes. Geophys. J. Int. 2015, 202, 1711–1721. [Google Scholar] [CrossRef][Green Version]
- Ferrari, G. Note on the Historical Rotation Seismographs. In Earthquake Source Asymmetry, Structural Media and Rotation Effects; Springer: Berlin/Heidelberg, Germany, 2006; pp. 367–376. [Google Scholar] [CrossRef]
- Sarconi, M. Istoria de’ Fenomeni del Tremoto Avvenuto Nelle CALABRIE, e Nel Valdemone Nell’Anno 1783; Technical Report, Reale Accademia Delle Scienze, e Delle Belle Lettere di Napoli; CAMPO: Austin, TX, USA, 1784. [Google Scholar]
- Oldham, R.D. Report on the great earthquake of 12 June 1897. Mem. Geol. Surv. India 1899, 29, 379. [Google Scholar]
- Galitzin, F. Vorlesnungen über Seismometrie; BG Teubner: Leipzig, Germany; Berlin, Germany, 1914. [Google Scholar]
- Basu, D.; Whittaker, A.S.; Constantinou, M.C. Characterizing rotational components of earthquake ground motion using a surface distribution method and response of sample structures. Eng. Struct. 2015, 99, 685–707. [Google Scholar] [CrossRef]
- Nathan, N.D.; Mackenzie, J.R. Rotational Components of Earthquake Motion. Can. J. Civ. Eng. 1975, 2, 430–436. [Google Scholar] [CrossRef]
- Trifunac, M.D. A note on rotational components of earthquake motions on ground surface for incident body waves. Int. J. Soil Dyn. Earthq. Eng. 1982, 1, 11–19. [Google Scholar] [CrossRef]
- Abdel-Ghaffar, A.M.; Rubin, L.I. Torsional Earthquake Response of Suspension Bridges. J. Eng. Mech. 1984, 110, 1467–1484. [Google Scholar] [CrossRef]
- Castellani, A.; Boffi, G. On the rotational components of seismic motion. Earthq. Eng. Struct. Dyn. 1989, 18, 785–797. [Google Scholar] [CrossRef]
- Bońkowski, P.A.; Zembaty, Z.; Minch, M.Y. Time history response analysis of a slender tower under translational-rocking seismic excitations. Eng. Struct. 2018, 155, 387–393. [Google Scholar] [CrossRef]
- Bońkowski, P.A.; Zembaty, Z.; Minch, M.Y. Engineering analysis of strong ground rocking and its effect on tall structures. Soil Dyn. Earthq. Eng. 2019, 116, 358–370. [Google Scholar] [CrossRef]
- Bońkowski, P.A.; Bobra, P.; Zembaty, Z.; Jędraszak, B. Application of Rotation Rate Sensors in Modal and Vibration Analyses of Reinforced Concrete Beams. Sensors 2020, 20, 4711. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.S. Ground rotational motions of the 1999 Chi-Chi, Taiwan earthquake as inferred from dense array observations. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Stupazzini, M.; De La Puente, J.; Smerzini, C.; Käser, M.; Igel, H.; Castellani, A. Study of rotational ground motion in the near-field region. Bull. Seismol. Soc. Am. 2009, 99, 1271–1286. [Google Scholar] [CrossRef]
- Zembaty, Z.; Kokot, S.; Bobra, P. Application of rotation rate sensors in an experiment of stiffness ‘reconstruction’. Smart Mater. Struct. 2013, 22, 077001. [Google Scholar] [CrossRef]
- Schreiber, U.; Velikoseltsev, A.; Stedman, G.E.; Hurst, R.B.; Klügel, T. Large Ring Laser Gyros as High Resolution Sensors for Applications in Geoscience. In Proceedings of the 11th International Conference on Integrated Navigation Systems, Saint Petersburg, Russia, 24–26 May 2004; pp. 326–331. [Google Scholar]
- Stedman, G.E.; Li, Z.; Bilger, H.R. Sideband analysis and seismic detection in a large ring laser. Appl. Opt. 1995, 34, 5375–5385. [Google Scholar] [CrossRef]
- Lefevre, H.C. The Fiber-Optic Gyroscope; Artech House: Boston, MA, USA, 2014. [Google Scholar]
- Huang, H.; Agafonov, V.; Yu, H. Molecular electric transducers as motion sensors: A review. Sensors 2013, 13, 4581–4597. [Google Scholar] [CrossRef]
- Egorov, E.V.; Egorov, I.V.; Agafonov, V.M. Self-Noise of the MET angular motion seismic sensors. J. Sens. 2015, 2015. [Google Scholar] [CrossRef]
- Wasserman, J.; Lehndorfer, S.; Igel, H.; Schreiber, U. Performance test of a commercial rotational motions sensor. Bull. Seismol. Soc. Am. 2009, 99, 1449–1456. [Google Scholar] [CrossRef]
- Nigbor, R.L.; Evans, J.R.; Hutt, C.R. Laboratory and field testing of commercial rotational seismometers. Bull. Seismol. Soc. Am. 2009, 99, 1215–1227. [Google Scholar] [CrossRef]
- Bernauer, F.; Wassermann, J.; Igel, H. Rotational sensors–A comparison of different sensor types. J. Seismol. 2012, 16, 595–602. [Google Scholar] [CrossRef]
- Pierson, B.; Laughlin, D.; Brune, R. Advances in rotational seismic measurements. In SEG Technical Program Expanded Abstracts; SEG: Tulsa, OK, USA, 2016; pp. 2263–2267. [Google Scholar] [CrossRef]
- Jaroszewicz, L.R.; Krajewski, Z.; Solarz, L.; Teisseyer, R. Application of the fibre-optic Sagnac interferometer in the investigation of seismic rotational waves. Meas. Sci. Technol. 2006, 17, 1186–1193. [Google Scholar] [CrossRef]
- Velikoseltsev, A.; Schreiber, K.U.; Yankovsky, A.; Wells, J.P.R.; Boronachin, A.; Tkachenko, A. On the application of fiber optic gyroscopes for detection of seismic rotations. J. Seismol. 2012, 16, 623–637. [Google Scholar] [CrossRef]
- Jaroszewicz, L.R.; Krajewski, Z.; Teisseyre, K.P. Usefulness of AFORS-autonomous fibre-optic rotational seismograph for investigation of rotational phenomena. J. Seismol. 2012, 16, 573–586. [Google Scholar] [CrossRef]
- Kurzych, A.; Sakowicz, B.; Kowalski, J.K.; Jaroszewicz, L.R.; Marć, P.; Krajewski, Z. Fibre-Optic Sagnac Interferometer in a FOG Minimum Configuration as Instrumental Challenge for Rotational Seismology. J. Light. Technol. 2018, 36, 879–884. [Google Scholar] [CrossRef]
- Jaroszewicz, L.R. Innovative Fibre-Optic Rotational Seismograph. Proceedings 2019, 15, 45. [Google Scholar] [CrossRef]
- D’Alessandro, A.; D’Anna, G. Retrieval of Ocean Bottom and Downhole Seismic sensors orientation using integrated MEMS gyroscope and direct rotation measurements. Adv. Geosci. 2014, 40, 11–17. [Google Scholar] [CrossRef]
- Liu, H.; Pike, W.T. A micromachined angular-acceleration sensor for geophysical applications. Appl. Phys. Lett. 2016, 109, 173506. [Google Scholar] [CrossRef]
- Brokešová, J.; Málek, J. Six-degree-of-freedom near-source seismic motions II: Examples of real seismogram analysis and S-wave velocity retrieval. J. Seismol. 2015, 19, 511–539. [Google Scholar] [CrossRef]
- Barak, O.; Key, K.; Constable, S.; Ronen, S. Recording active-seismic ground rotations using induction-coil magnetometers. Geophysics 2018, 83, P19–P42. [Google Scholar] [CrossRef]
- Basu, D.; Whittaker, A.S.; Asce, M.; Constantinou, M.C. Estimating Rotational Components of Ground Motion Using Data Recorded at a Single Station. J. Eng. Mech. 2012, 138, 1141–1156. [Google Scholar] [CrossRef]
- Spudich, P.; Steck, L.K.; Hellweg, M.; Fletcher, J.B.; Baker, L.M. Transient stresses at Parkfield, California, produced by the 7.4 Landers earthquake of 28 June 1992: Observations from the UPSAR dense seismograph array. J. Geophys. Res. 1995, 100, 675–690. [Google Scholar] [CrossRef]
- Langston, C.A. Wave gradiometry in the time domain. Bull. Seismol. Soc. Am. 2007, 97, 926–933. [Google Scholar] [CrossRef]
- Spudich, P.; Fletcher, J.B. Software for inference of dynamic ground strains and rotations and their errors from short baseline array observations of ground motions. Bull. Seismol. Soc. Am. 2009, 99, 1480–1482. [Google Scholar] [CrossRef]
- Suryanto, W.; Igel, H.; Wassermann, J.; Cochard, A.; Schuberth, B.; Vollmer, D.; Scherbaum, F.; Schreiber, U.; Velikoseltsev, A. First comparison of array-derived rotational ground motions with direct ring laser measurements. Bull. Seismol. Soc. Am. 2006, 96, 2059–2071. [Google Scholar] [CrossRef]
- Muijs, R.; Holliger, K.; Robertsson, J.O.A. Perturbation analysis of an explicit wavefield separation scheme for P- and S-waves. Geophysics 2002, 67, 1972–1982. [Google Scholar] [CrossRef]
- Poppeliers, C.; Evans, E.V. The Effects of Measurement Uncertainties in Seismic-Wave Gradiometry. Bull. Seismol. Soc. Am. 2015, 105, 3143–3155. [Google Scholar] [CrossRef]
- Schmelzbach, C.; Sollberger, D.; Van Renterghem, C.; Häuseler, M.; Robertsson, J.O.A.; Greenhalgh, S. Seismic spatial wavefield gradient and rotational rate measurements as new observables in land seismic exploration. In EGU General Assembly Geophysical Research Abstracts; EGU: Munich, Germany, 2016. [Google Scholar]
- Allouche, N.; Muyzert, E.; Edme, P. On the Accuracy of Seismic Wavefield Spatial Gradients. In Proceedings of the 23rd European Meeting of Environmental and Engineering Geophysics, Malmo, Sweden, 3–7 September 2017. [Google Scholar] [CrossRef]
- Sollberger, D.; Schmelzbach, C.; Manukyan, E.; Greenhalgh, S.A.; Van Renterghem, C.; Robertsson, J.O.A. Accounting for receiver perturbations in seismic wavefield gradiometry. Geophys. J. Int. 2019, 218, 1748–1760. [Google Scholar] [CrossRef]
- Van Driel, M.; Wassermann, J.; Nader, M.F.; Schuberth, B.S.A.; Igel, H. Strain rotation coupling and its implications on the measurement of rotational ground motions. J. Seismol. 2012, 16, 657–668. [Google Scholar] [CrossRef][Green Version]
- Garcia, R.F.; Mimoun, D.; Shariati, S.; Guattari, F.; Bonnefois, J.J.; Wassermann, J.; Bernauer, F.; Igel, H.; de Raucourt, S.; Lognonné, P.; et al. Innovative ground motion sensors for planets and asteroids: PIONEERS H2020-SPACE European project. In Proceedings of the 13th International Academy of Astronautics (IAA) Meeting on Low-Cost Planetary Missions, Toulouse, France, 3–5 June 2019. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sollberger, D.; Igel, H.; Schmelzbach, C.; Edme, P.; van Manen, D.-J.; Bernauer, F.; Yuan, S.; Wassermann, J.; Schreiber, U.; Robertsson, J.O.A. Seismological Processing of Six Degree-of-Freedom Ground-Motion Data. Sensors 2020, 20, 6904. https://doi.org/10.3390/s20236904
Sollberger D, Igel H, Schmelzbach C, Edme P, van Manen D-J, Bernauer F, Yuan S, Wassermann J, Schreiber U, Robertsson JOA. Seismological Processing of Six Degree-of-Freedom Ground-Motion Data. Sensors. 2020; 20(23):6904. https://doi.org/10.3390/s20236904
Chicago/Turabian StyleSollberger, David, Heiner Igel, Cedric Schmelzbach, Pascal Edme, Dirk-Jan van Manen, Felix Bernauer, Shihao Yuan, Joachim Wassermann, Ulrich Schreiber, and Johan O. A. Robertsson. 2020. "Seismological Processing of Six Degree-of-Freedom Ground-Motion Data" Sensors 20, no. 23: 6904. https://doi.org/10.3390/s20236904
APA StyleSollberger, D., Igel, H., Schmelzbach, C., Edme, P., van Manen, D.-J., Bernauer, F., Yuan, S., Wassermann, J., Schreiber, U., & Robertsson, J. O. A. (2020). Seismological Processing of Six Degree-of-Freedom Ground-Motion Data. Sensors, 20(23), 6904. https://doi.org/10.3390/s20236904




