Hierarchical Optimization of 3D Point Cloud Registration
Abstract
:1. Introduction
2. Related Work
2.1. Point Cloud Filtering
2.2. Coarse Registration
2.3. Fine Registration
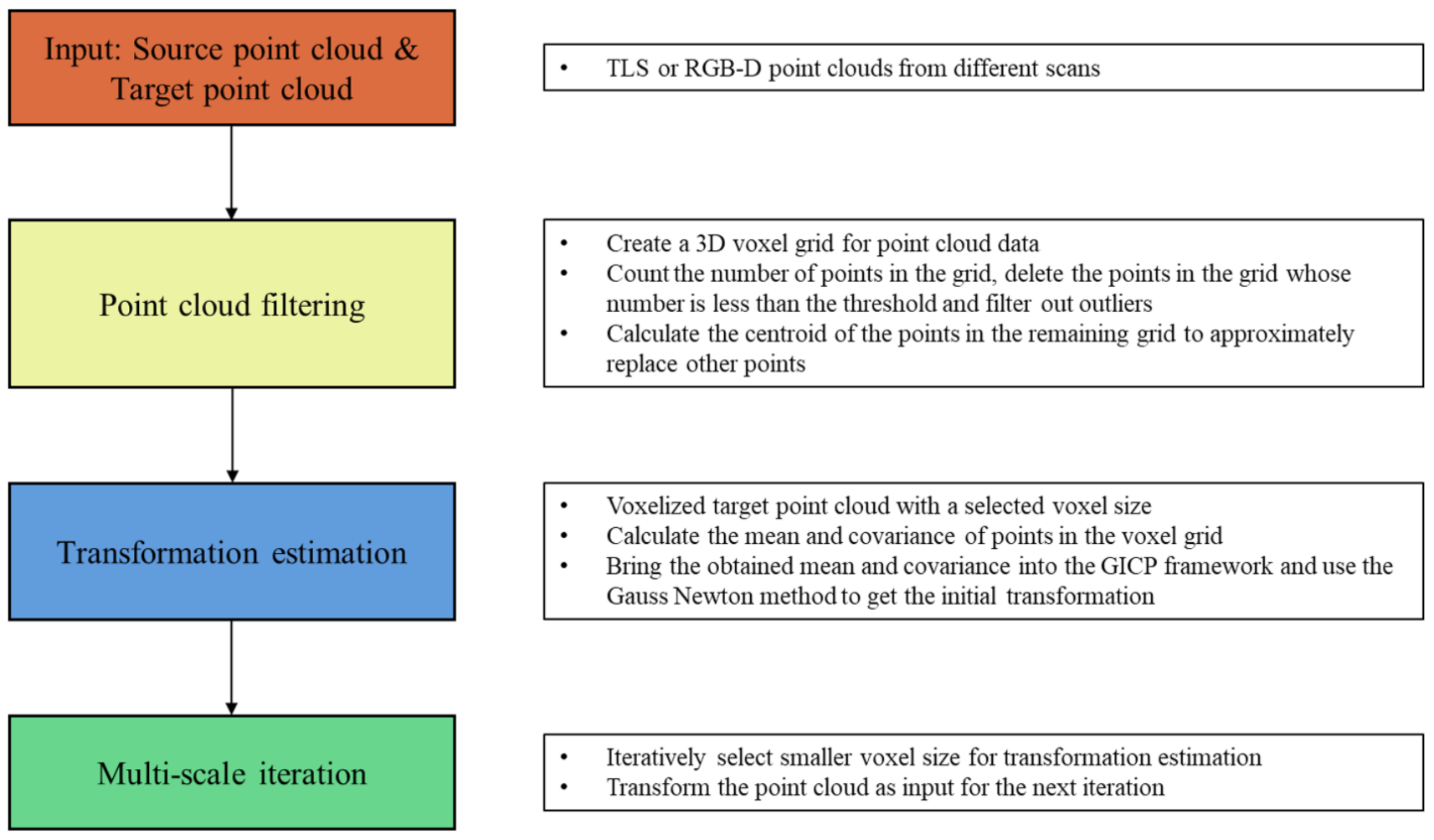
3. Methodology
3.1. Problem Formulation
3.2. Pointcloud Filtering
3.3. Mvgicp: Point Cloud Registration
| Algorithm 1: MVGICP |
 |
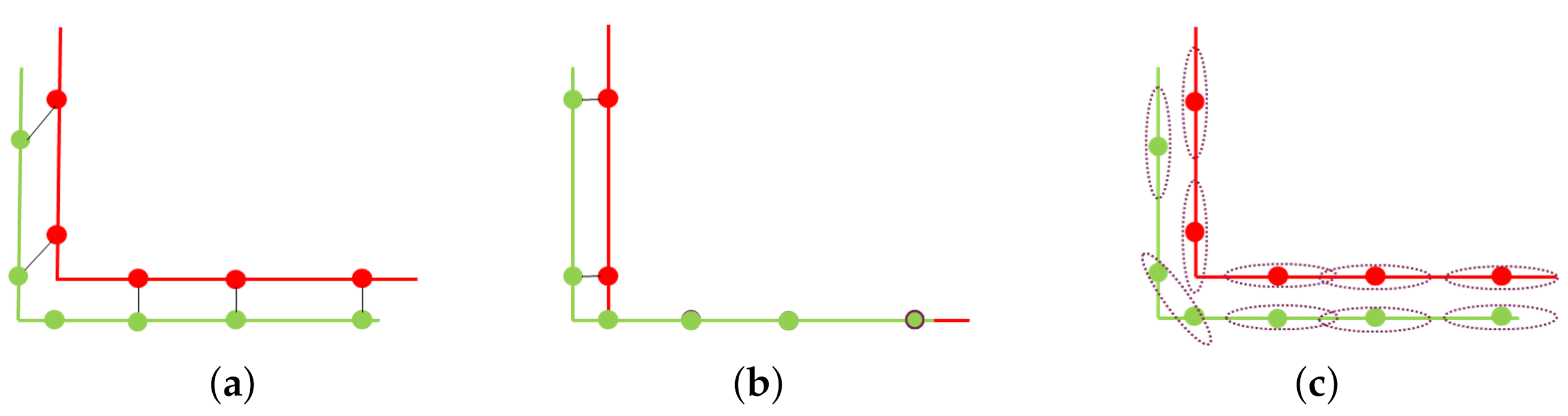
3.3.1. Basic Concept of Gicp
3.3.2. Mvgicp’S Optimization of Local Minimum
3.3.3. Mvgicp’S Fine Registration
4. Experiment and Analysis
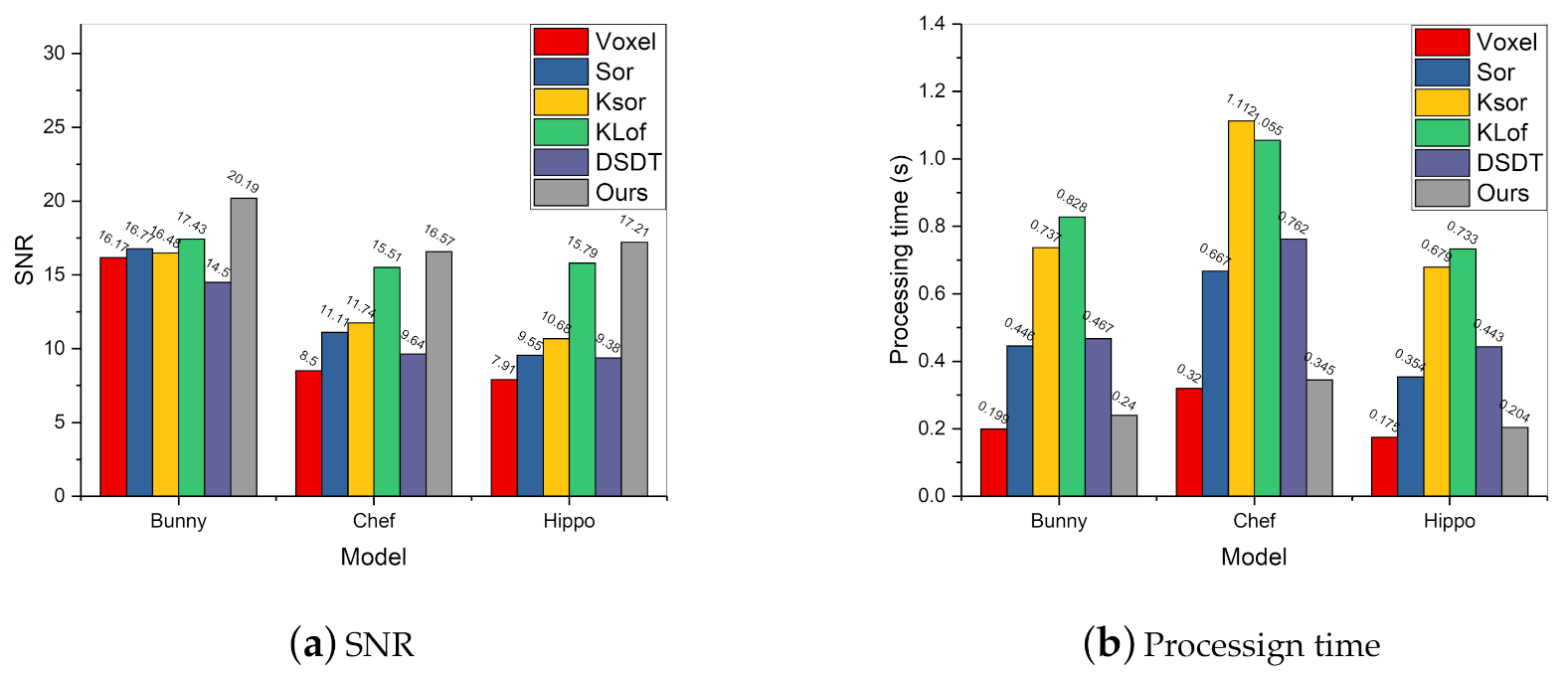
4.1. Outlier Filtering Result
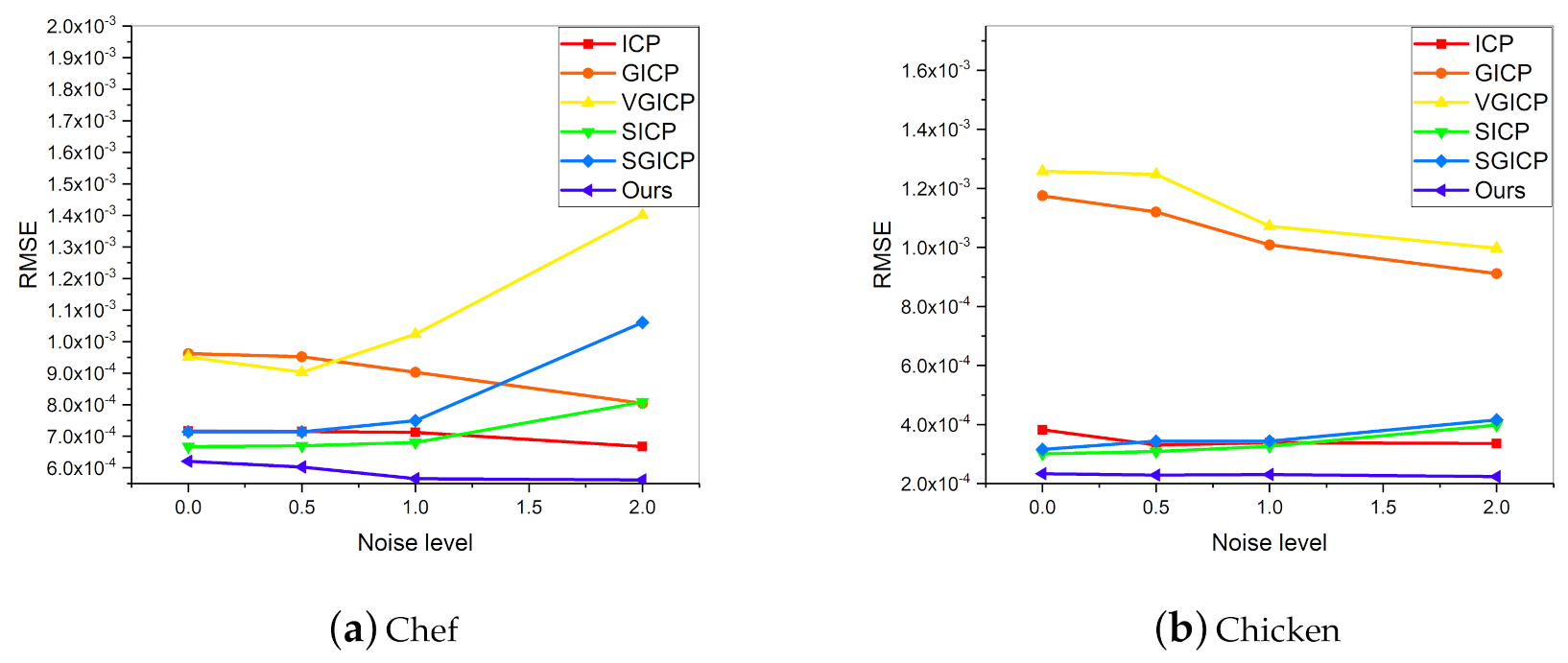
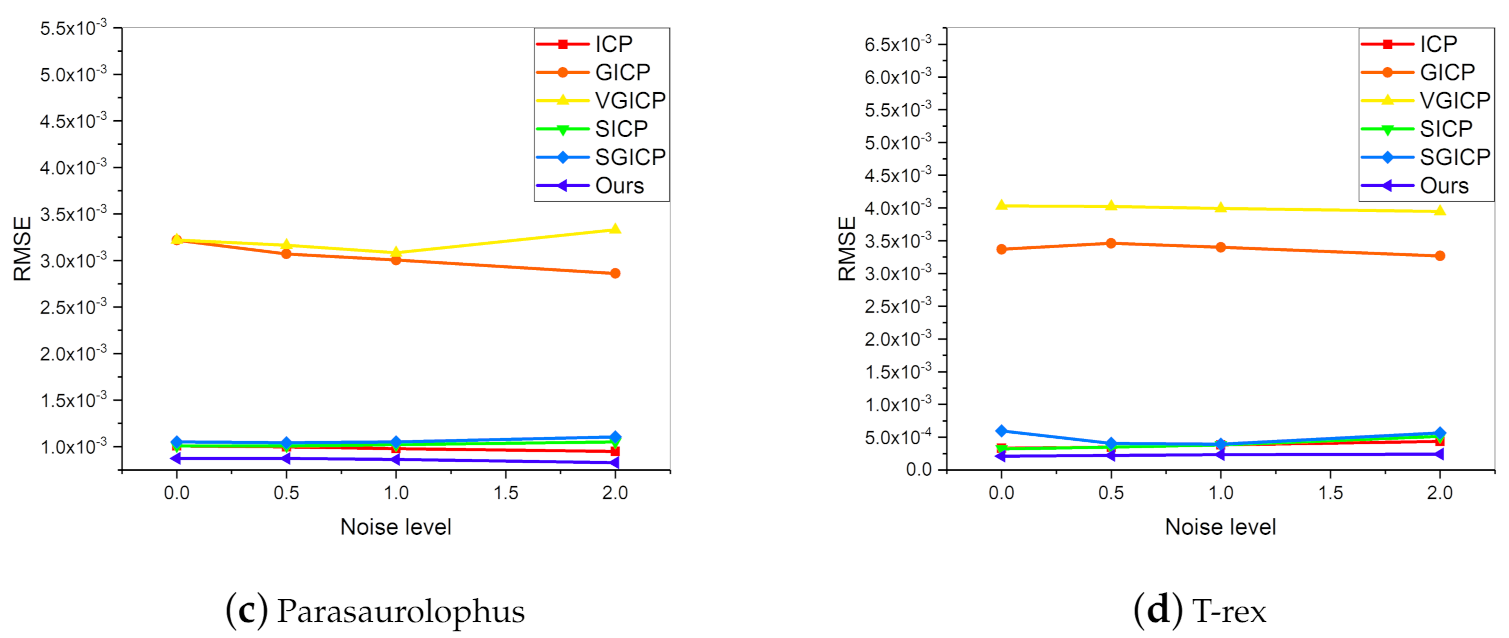
4.2. Synthetic Data Registration
4.3. Multi-View Registration
4.3.1. Multi-View Synthetic Data Registration
4.3.2. Multi-View Real Data Registration
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wolff, K.; Kim, C.; Zimmer, H.; Schroers, C.; Botsch, M.; Sorkine-Hornung, O.; Sorkine-Hornung, A. Point cloud noise and outlier removal for image-based 3D reconstruction. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 118–127. [Google Scholar]
- Drost, B.; Ulrich, M.; Navab, N.; Ilic, S. Model globally, match locally: Efficient and robust 3D object recognition. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 998–1005. [Google Scholar]
- Sobreira, H.; Costa, C.M.; Sousa, I.; Rocha, L.; Lima, J.; Farias, P.; Costa, P.; Moreira, A.P. Map-matching algorithms for robot self-localization: A comparison between perfect match, iterative closest point and normal distributions transform. J. Intell. Robot. Syst. 2019, 93, 533–546. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Sensor Fusion IV: Control Paradigms and Data Structures; International Society for Optics and Photonics: Boston, CA, USA, 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3D is here: Point Cloud Library (PCL). In Proceedings of the IEEE International Conference on Robotics Automation, Shanghai, China, 9–13 May 2011. [Google Scholar]
- Rusu, R.B.; Marton, Z.C.; Blodow, N.; Dolha, M.; Beetz, M. Towards 3D point cloud based object maps for household environments. Rob. Autom. Syst. 2008, 56, 927–941. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, K.; Huang, G.; Wu, P. Outliers detection method based on dynamic standard deviation threshold using neighborhood density constraints for three dimensional point cloud. J. Comput. Aided Des. Comput. Graph. 2018, 30, 1034–1045. [Google Scholar] [CrossRef]
- Ramaswamy, S.; Rastogi, R.; Shim, K. Efficient algorithms for mining outliers from large data sets. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Houston, TX, USA, 16–18 May 2000; pp. 427–438. [Google Scholar]
- Pirotti, F.; Ravanelli, R.; Fissore, F.; Masiero, A. Implementation and assessment of two density-based outlier detection methods over large spatial point clouds. Open Geospat. Data Softw. Stand. 2018, 3, 1–12. [Google Scholar] [CrossRef]
- Guo, Y.; Sohel, F.; Bennamoun, M.; Wan, J.; Lu, M. An accurate and robust range image registration algorithm for 3D object modeling. IEEE Trans. Multimedia 2014, 16, 1377–1390. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Cao, Z. Multi-attribute statistics histograms for accurate and robust pairwise registration of range images. Neurocomputing 2017, 251, 54–67. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Y.; Wang, H.; Chen, M.; Wang, X.; Yan, G. Efficient registration of terrestrial LiDAR scans using a coarse-to-fine strategy for forestry applications. Agric. For. Meteorol. 2016, 225, 8–23. [Google Scholar] [CrossRef]
- Yuan, C.; Yu, X.; Luo, Z. 3D point cloud matching based on principal component analysis and iterative closest point algorithm. In Proceedings of the 2016 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 11–12 July 2016; pp. 404–408. [Google Scholar]
- Huang, R.; Xu, Y.; Hoegner, L.; Stilla, U. Temporal comparison of construction sites using photogrammetric point cloud sequences and robust phase correlation. Autom. Constr. 2020, 117, 103247. [Google Scholar] [CrossRef]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-points congruent sets for robust pairwise surface registration. In ACM SIGGRAPH 2008 Papers; ACM: San Antonio, TX, USA, 2008; pp. 1–10. [Google Scholar]
- Theiler, P.W.; Wegner, J.D.; Schindler, K. Markerless point cloud registration with keypoint-based 4-points congruent sets. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 1, 283–288. [Google Scholar] [CrossRef] [Green Version]
- Mellado, N.; Aiger, D.; Mitra, N.J. Super 4pcs fast global pointcloud registration via smart indexing. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2014; Volume 33, pp. 205–215. [Google Scholar]
- Xu, Y.; Boerner, R.; Yao, W.; Hoegner, L.; Stilla, U. Pairwise coarse registration of point clouds in urban scenes using voxel-based 4-planes congruent sets. ISPRS J. Photogramm. Remote Sens. 2019, 151, 106–123. [Google Scholar] [CrossRef]
- Frome, A.; Huber, D.; Kolluri, R.; Bülow, T.; Malik, J. Recognizing objects in range data using regional point descriptors. In Proceedings of the European Conference on Computer Vision, Prague, Czech, 11–14 May 2004; pp. 224–237. [Google Scholar]
- Petrelli, A.; Di Stefano, L. On the repeatability of the local reference frame for partial shape matching. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2244–2251. [Google Scholar]
- Tombari, F.; Salti, S.; Di Stefano, L. Unique signatures of histograms for local surface description. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 356–369. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Flint, A.; Dick, A.; Van Den Hengel, A. Thrift: Local 3d structure recognition. In Proceedings of the 9th Biennial Conference of the Australian Pattern Recognition Society on Digital Image Computing Techniques and Applications (DICTA 2007), Glenelg, Australia, 3–5 December 2007; pp. 182–188. [Google Scholar]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. 3D object recognition in cluttered scenes with local surface features: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2270–2287. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Cao, Z.; Zhang, Q. A fast and robust local descriptor for 3D point cloud registration. Inf. Sci. 2016, 346, 163–179. [Google Scholar] [CrossRef]
- Chen, S.; Nan, L.; Xia, R.; Zhao, J.; Wonka, P. PLADE: A Plane-Based Descriptor for Point Cloud Registration With Small Overlap. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2530–2540. [Google Scholar] [CrossRef]
- Wang, J.; Lindenbergh, R.; Menenti, M. SigVox–A 3D feature matching algorithm for automatic street object recognition in mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 128, 111–129. [Google Scholar] [CrossRef]
- Chetverikov, D.; Svirko, D.; Stepanov, D.; Krsek, P. The trimmed iterative closest point algorithm. In Object Recognition Supported by User Interaction for Service Robots; IEEE: New York, NY, USA, 2002; Volume 3, pp. 545–548. [Google Scholar]
- Yang, J.; Li, H.; Jia, Y. Go-icp: Solving 3d registration efficiently and globally optimally. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1457–1464. [Google Scholar]
- Biber, P.; Straßer, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; pp. 2743–2748. [Google Scholar]
- Chen, Y.; Medioni, G. Object modeling by registration of multiple range images. Image Vision Comput. 2002, 10, 145–155. [Google Scholar] [CrossRef]
- Khoshelham, K. Closed-form solutions for estimating a rigid motion from plane correspondences extracted from point clouds. ISPRS J. Photogramm. Remote Sens. 2016, 114, 78–91. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-icp. In Robotics: Science and Systems; DBLP: Seattle, WA, USA, 2009; Volume 2, p. 435. [Google Scholar]
- Bouaziz, S.; Tagliasacchi, A.; Pauly, M. Sparse Iterative Closest Point; Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2013; Volume 32, pp. 113–123. [Google Scholar]
- Koide, K.; Yokozuka, M.; Oishi, S.; Banno, A. Voxelized GICP for Fast and Accurate 3D Point Cloud Registration; Technical Report; EasyChair: Manchester, UK, 2020. [Google Scholar]
- Korn, M.; Holzkothen, M.; Pauli, J. Color supported generalized-ICP. In Proceedings of the 2014 International Conference on Computer Vision Theory and Applications (VISAPP), Lisbon, Portugal, 5–8 January 2014; pp. 592–599. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. Pointnetlk: Robust & efficient point cloud registration using pointnet. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7163–7172. [Google Scholar]
- Wang, Y.; Solomon, J.M. Deep closest point: Learning representations for point cloud registration. In Proceedings of the IEEE International Conference on Computer Vision, Long Beach, CA, USA, 15–20 June 2019; pp. 3523–3532. [Google Scholar]
- Mian, A.S.; Bennamoun, M.; Owens, R. Three-dimensional model-based object recognition and segmentation in cluttered scenes. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1584–1601. [Google Scholar] [CrossRef] [PubMed] [Green Version]



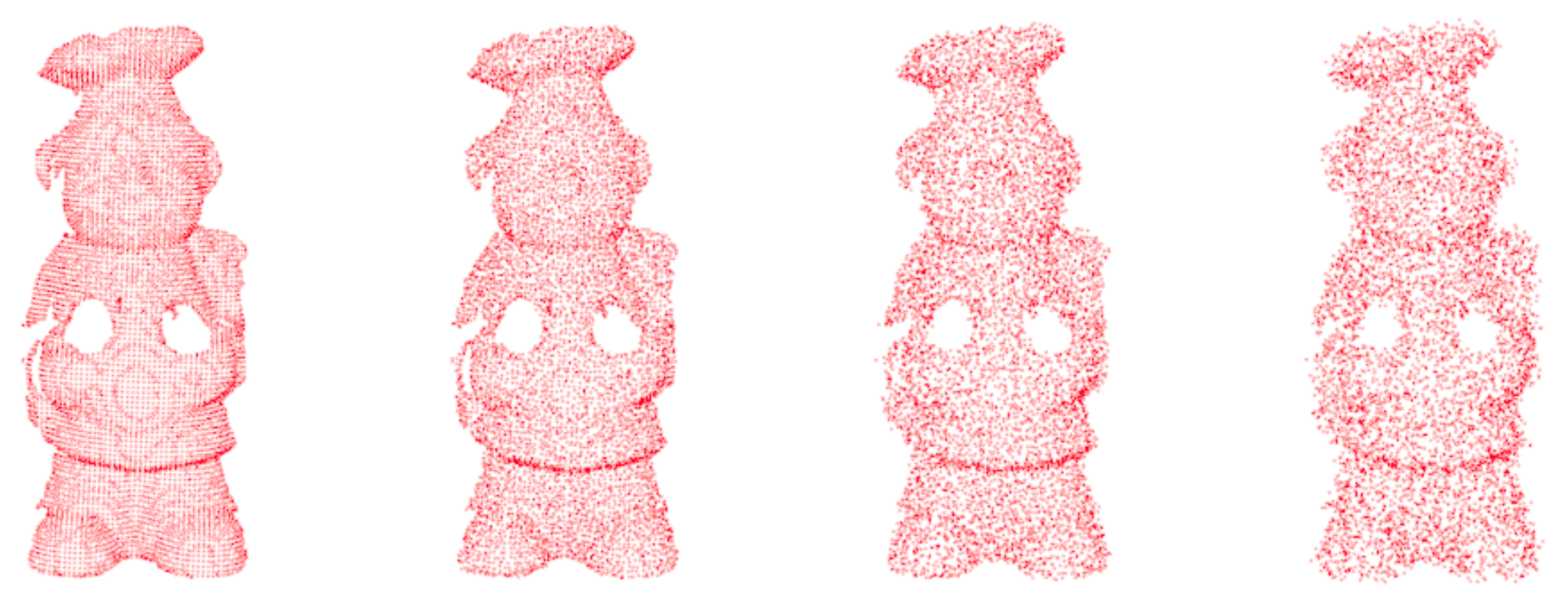





| Groundtruth | Voxel | Sor | KSor | KLof | DSDT | Ours | |
|---|---|---|---|---|---|---|---|
| Bunny | |||||||
| Chef | |||||||
| Hippo |
| Groundtruth | Voxel | Sor | KSor | KLof | DSDT | Ours | |
|---|---|---|---|---|---|---|---|
| Bunny | |||||||
| Chef | |||||||
| Hippo |
| ICP | GICP | VGICP | SICP | SGICP | Ours | |
|---|---|---|---|---|---|---|
| Chef | 12.22 | 10.98 | 8.64 | 14.33 | 11.20 | 2.39 |
| Chicken | 15.74 | 10.95 | 10.27 | 14.66 | 15.69 | 2.77 |
| Parasaurolophus | 13.81 | 9.84 | 8.51 | 14.39 | 17.71 | 2.28 |
| T-rex | 10.53 | 10.88 | 7.61 | 11.74 | 17.54 | 2.00 |
| Model | Chicken | T-Rex | ||
|---|---|---|---|---|
| Method | MVGICP | ICP | MVGICP | ICP |
| Error | 0.1952 | 0.238 | 0.0563 | 0.0712 |
| Error | 0.1491 | 0.250312 | 0.0707 | 0.0871 |
| Method | Filtered-MVGICP | MVGICP |
|---|---|---|
| Error | 0.9267 | 9.278 |
| Error | 0.0085 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhang, Y.; Lei, L.; Xie, H.; Li, Y.; Sun, S. Hierarchical Optimization of 3D Point Cloud Registration. Sensors 2020, 20, 6999. https://doi.org/10.3390/s20236999
Liu H, Zhang Y, Lei L, Xie H, Li Y, Sun S. Hierarchical Optimization of 3D Point Cloud Registration. Sensors. 2020; 20(23):6999. https://doi.org/10.3390/s20236999
Chicago/Turabian StyleLiu, Huikai, Yue Zhang, Linjian Lei, Hui Xie, Yan Li, and Shengli Sun. 2020. "Hierarchical Optimization of 3D Point Cloud Registration" Sensors 20, no. 23: 6999. https://doi.org/10.3390/s20236999
APA StyleLiu, H., Zhang, Y., Lei, L., Xie, H., Li, Y., & Sun, S. (2020). Hierarchical Optimization of 3D Point Cloud Registration. Sensors, 20(23), 6999. https://doi.org/10.3390/s20236999




