Hydraulic Conductivity of Saturated Soil Medium through Time-Domain Reflectometry
Abstract
:1. Introduction
2. Background Theory
2.1. Dielectric Constant
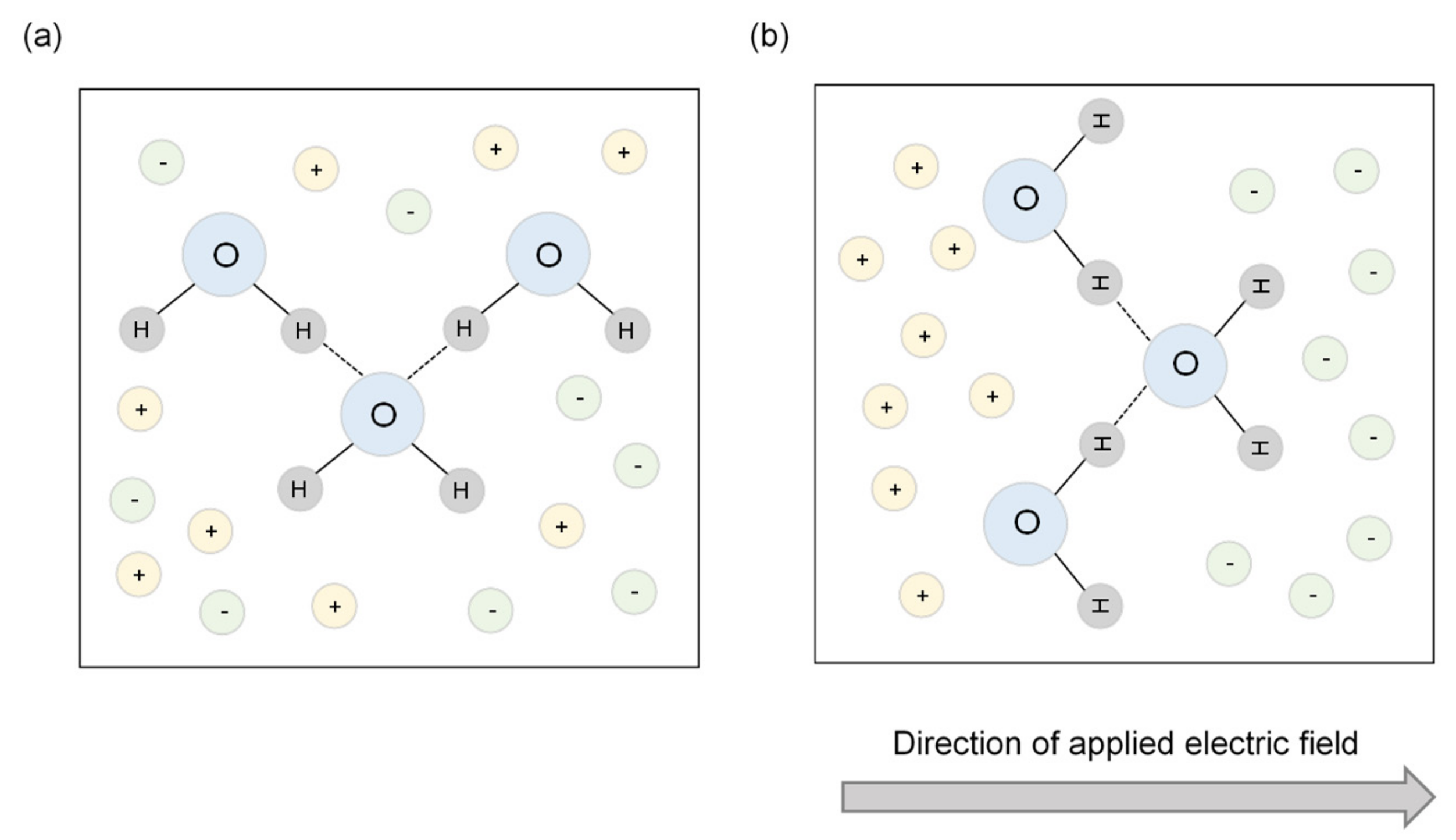
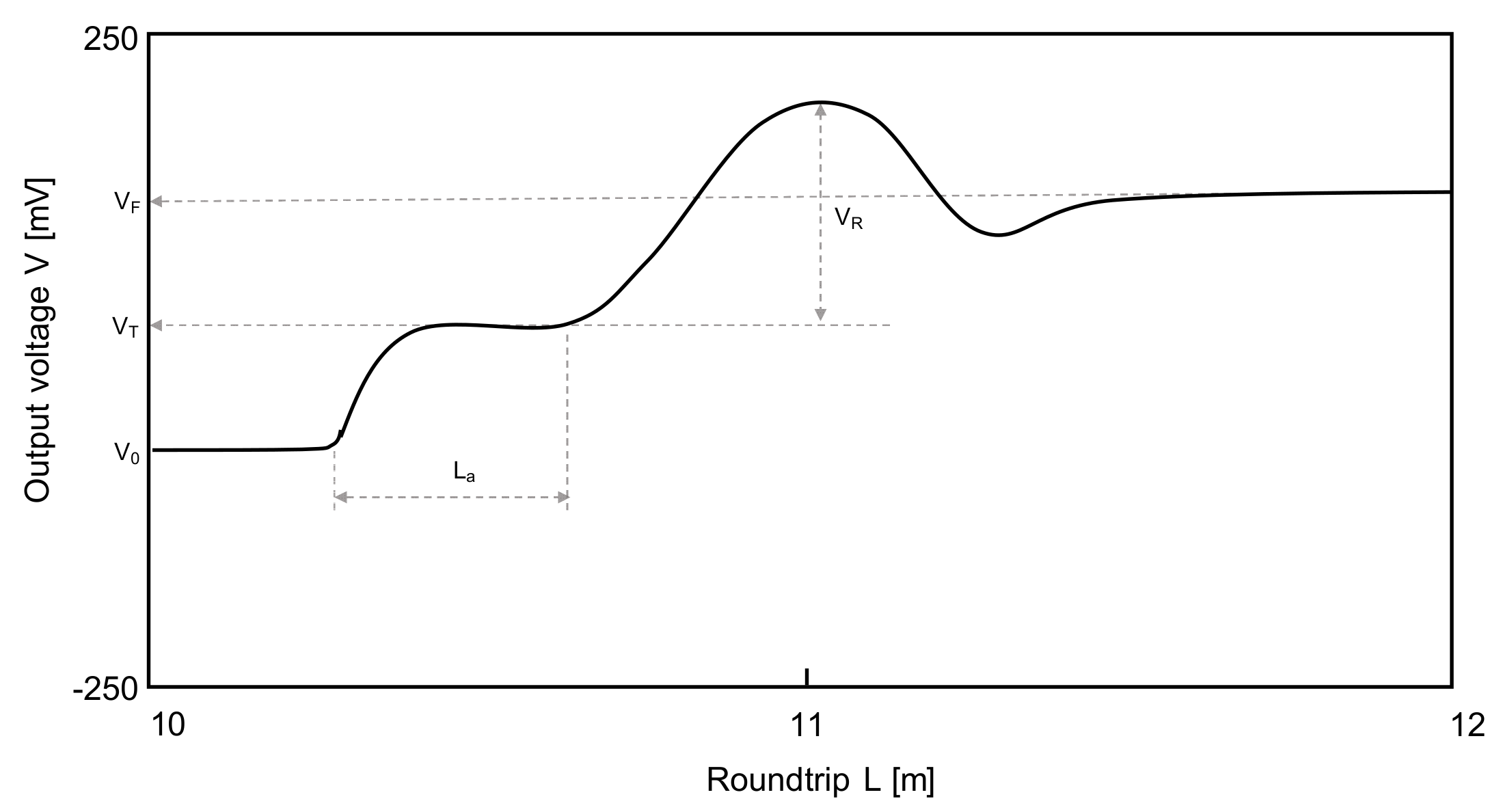
2.2. Hydraulic Conductivity
2.3. Relationship between the Dielectric Constant and Hydraulic Conductivity
3. Laboratory Test
3.1. Specimen
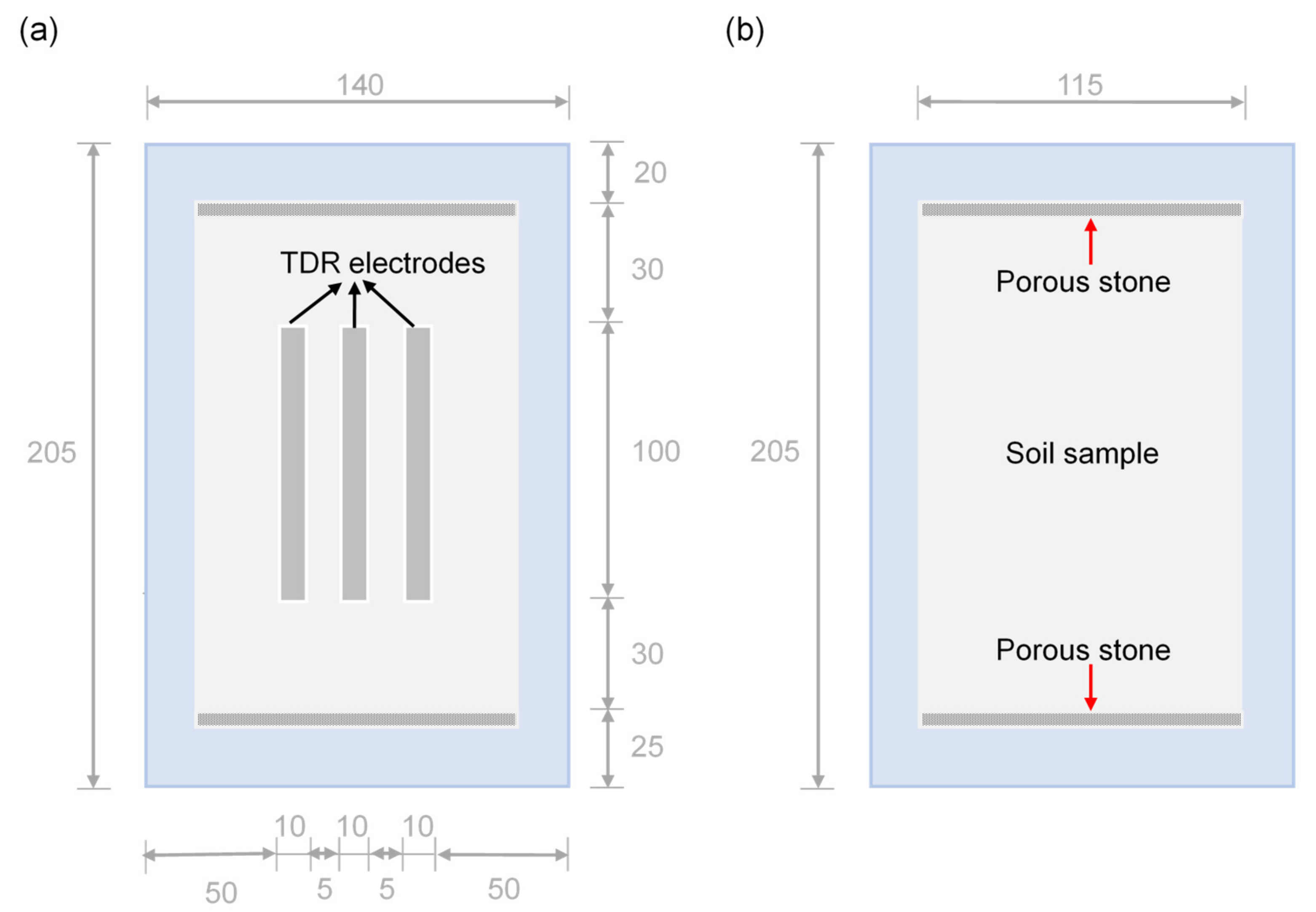
3.2. Cell
3.3. Measurement System
3.4. Performance
4. Results
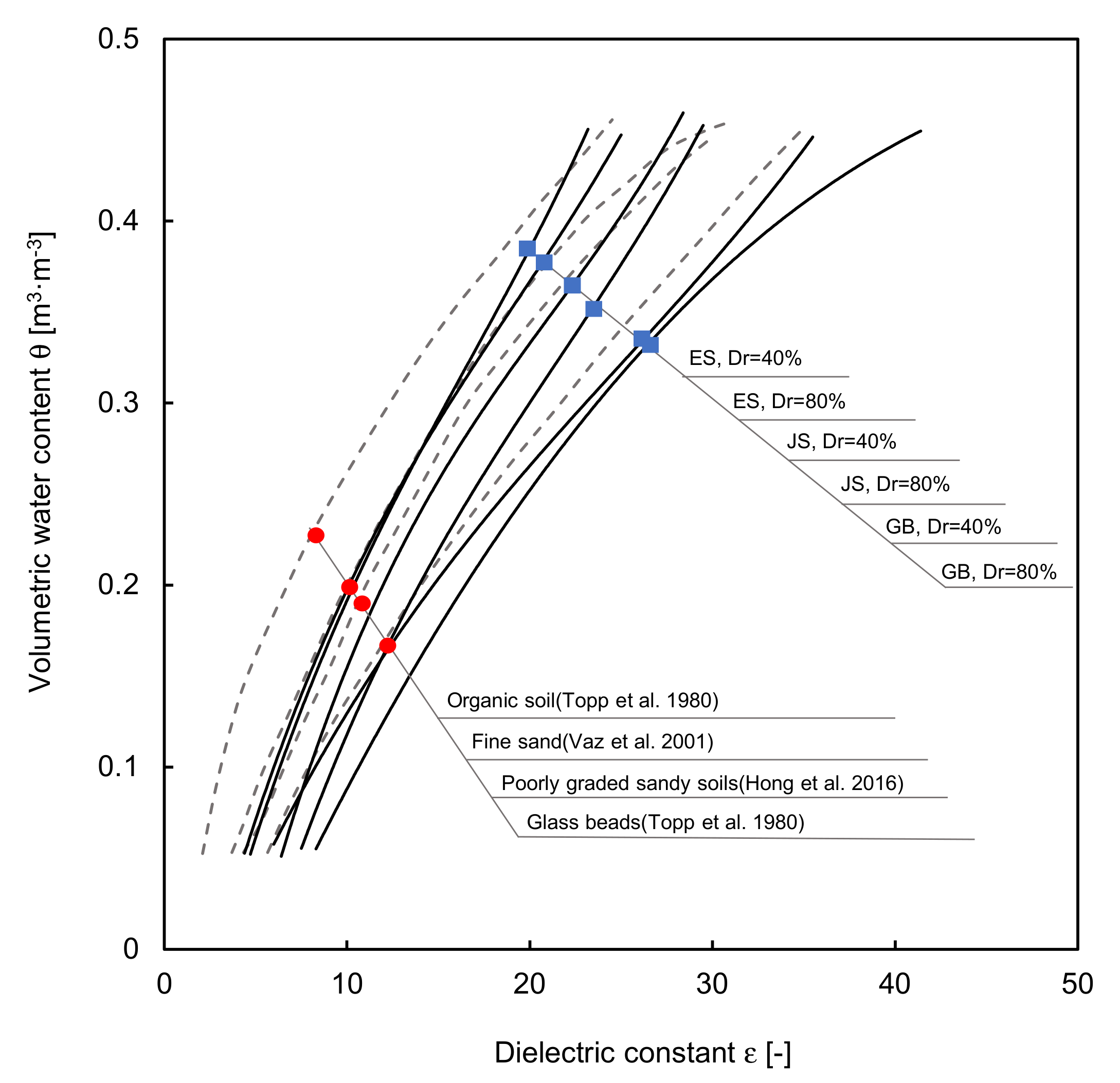
4.1. Verification of the Saturation
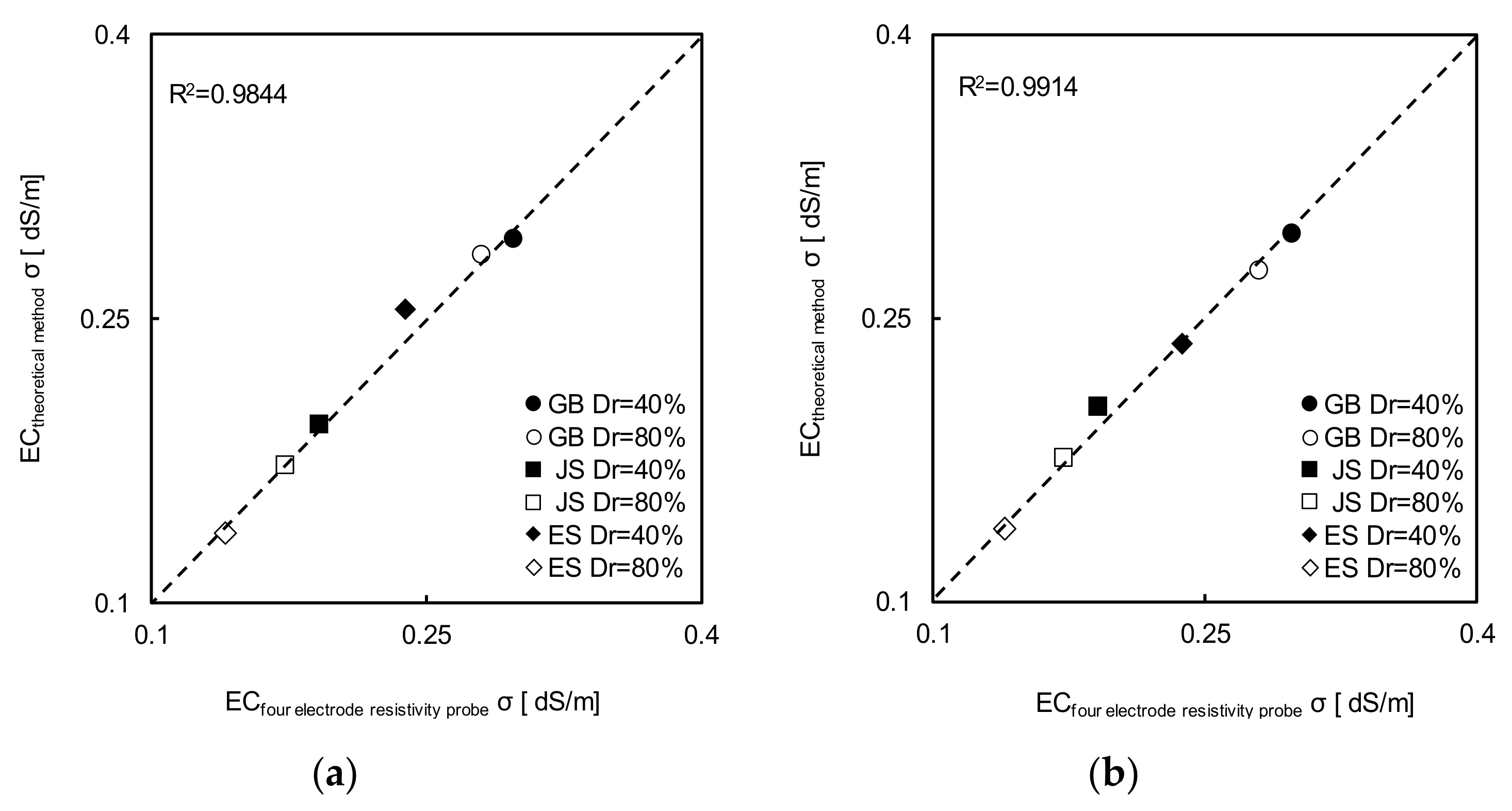
4.2. Electrical Conductivity
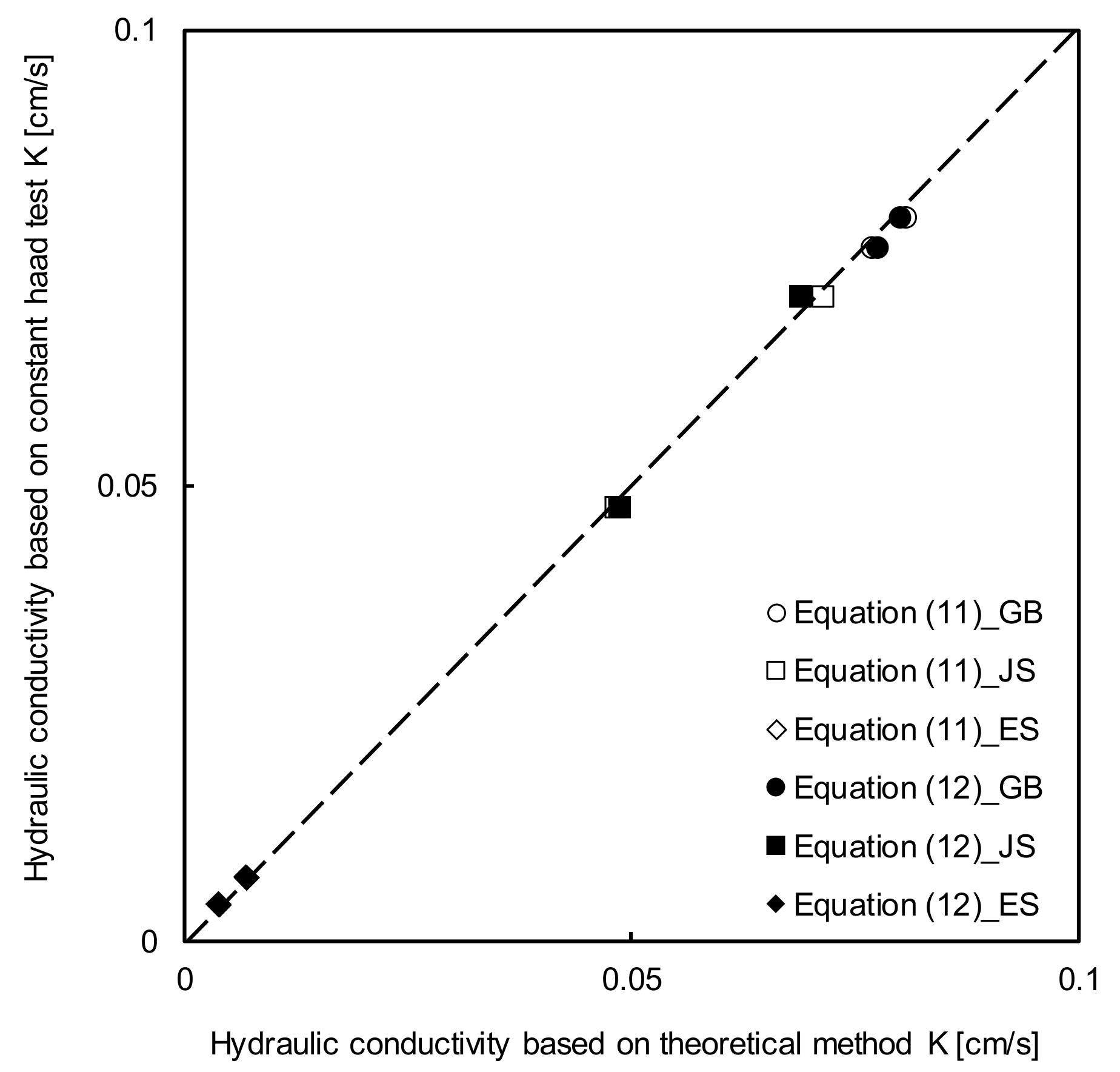
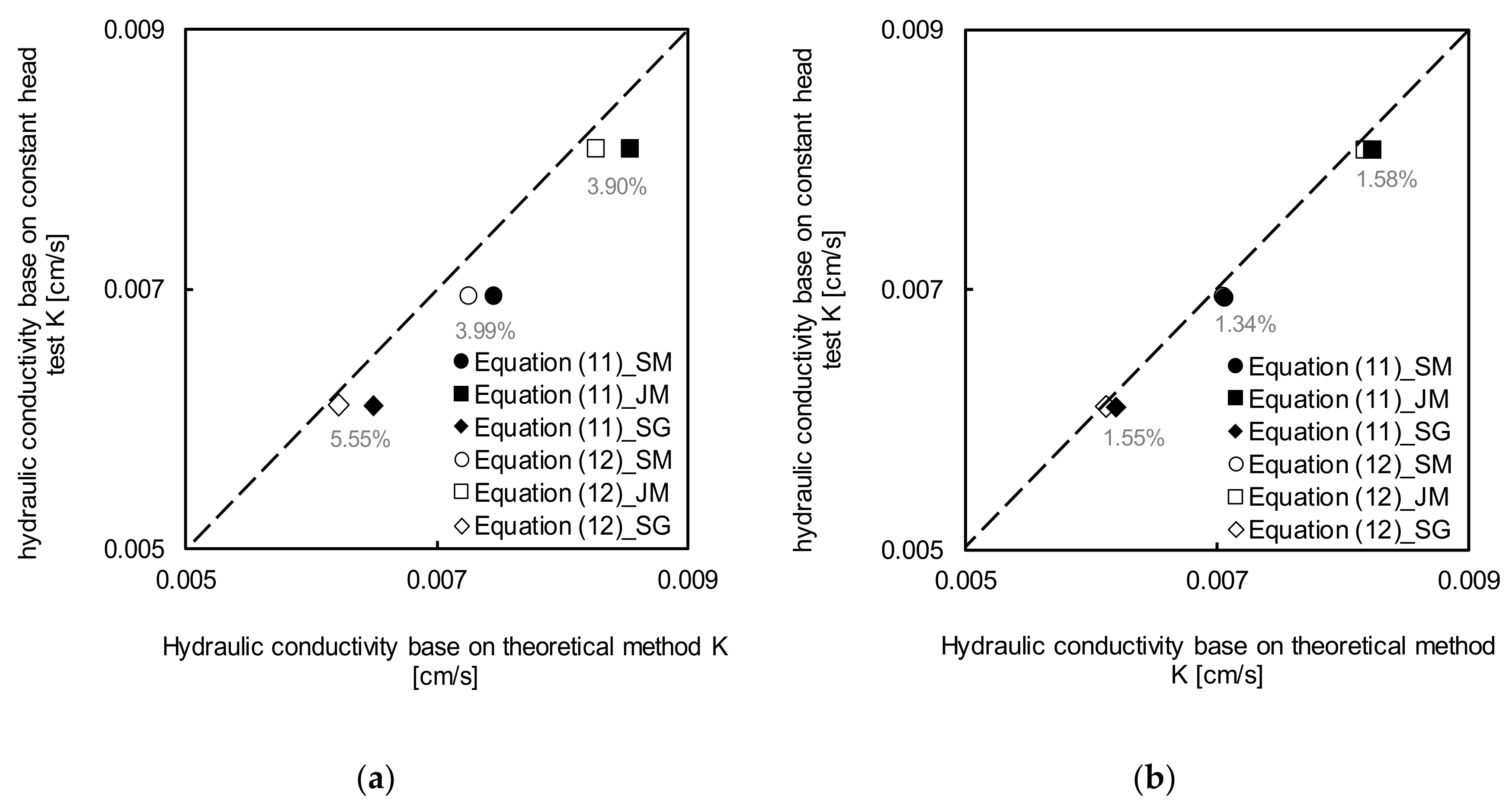
4.3. Hydraulic conductivity
5. Discussion
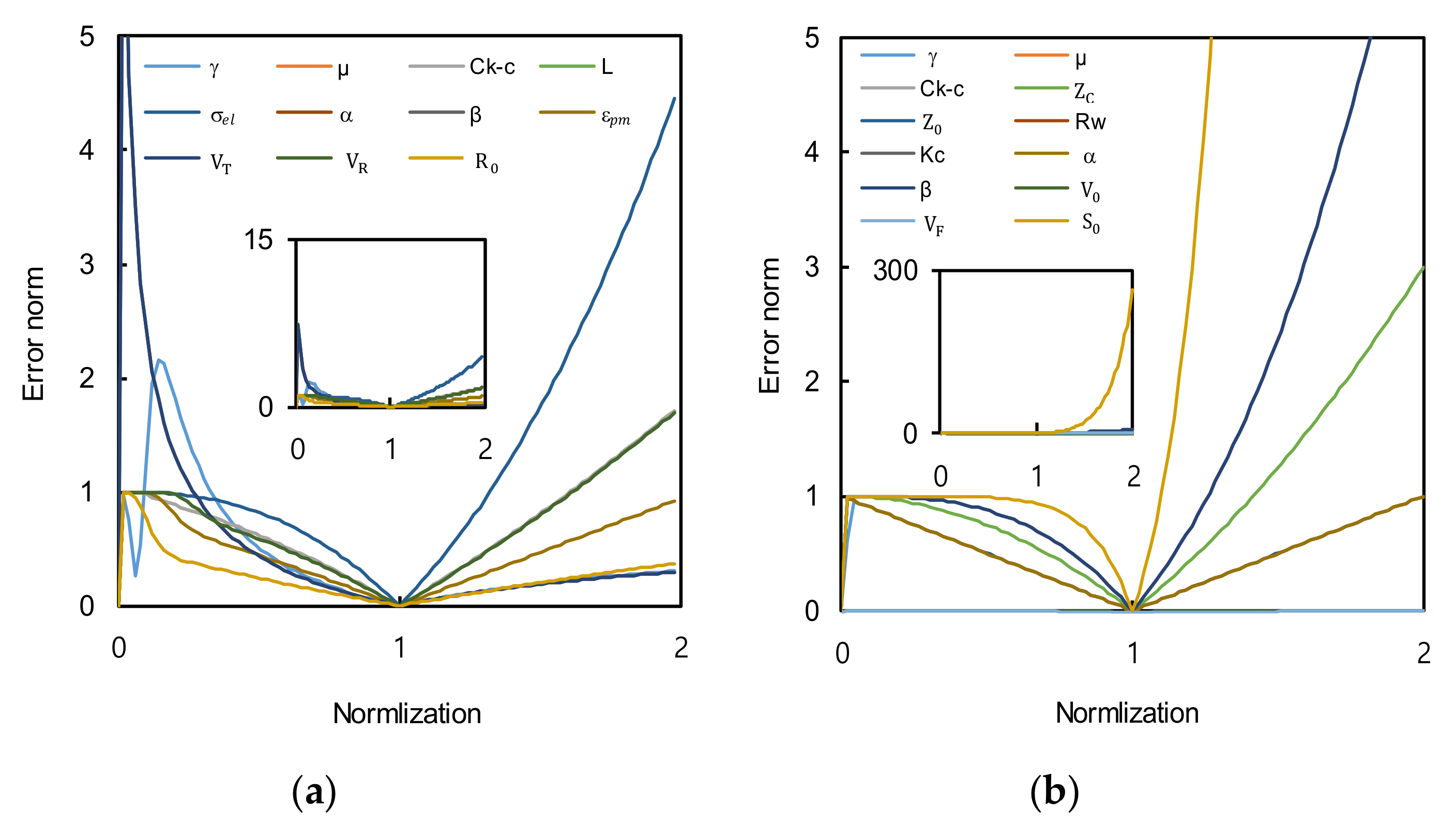
5.1. Sensitivity
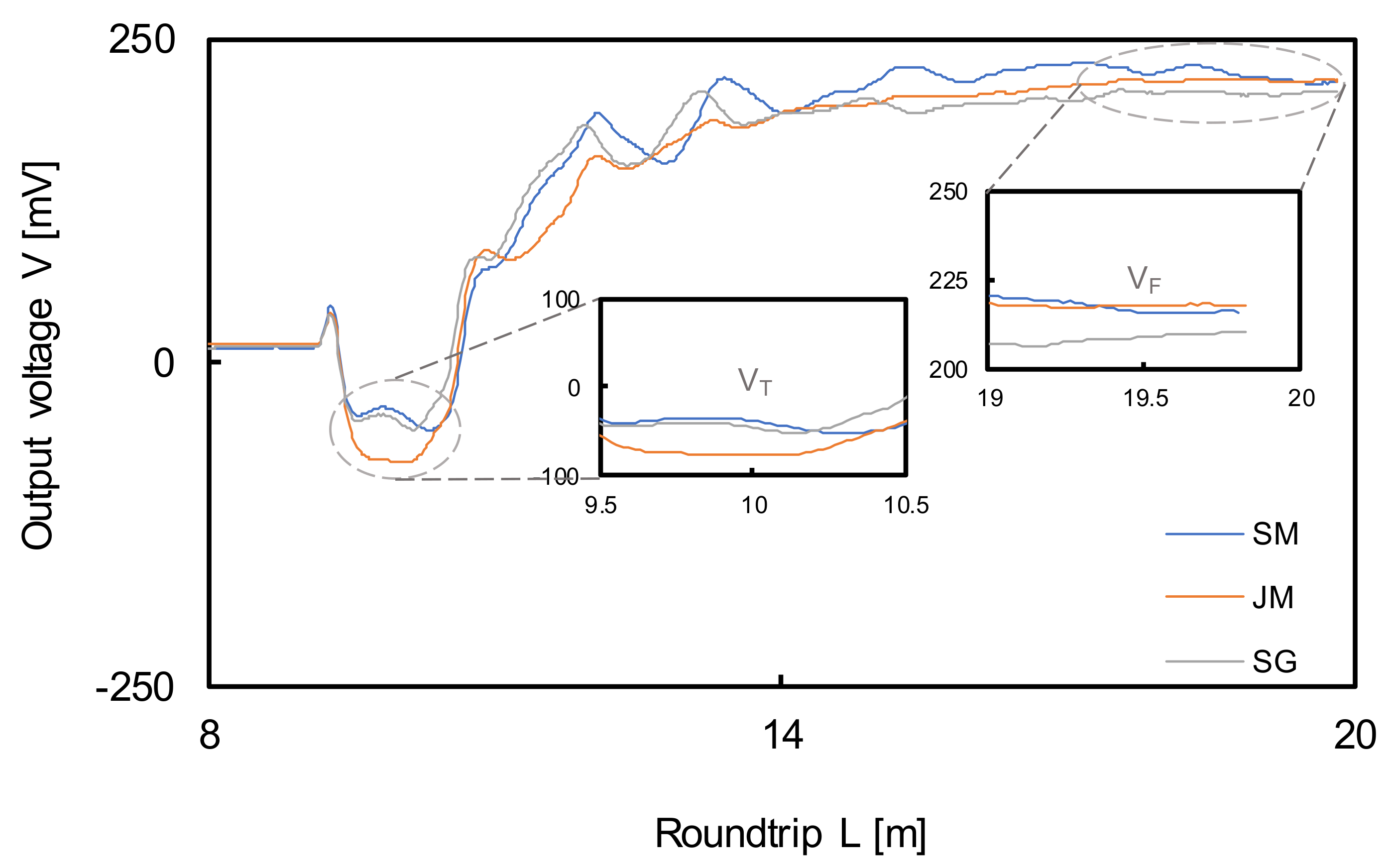
5.2. Field Application
6. Conclusions
- The electrical resistivity of the medium is related to hydraulic conductivity. The electrical conductivity, which is the reciprocal of electrical resistivity, can be estimated by the dielectric constant through the attenuating amplitude of the output voltage.
- Two theories were used to deduce the relationship between the dielectric constant and hydraulic conductivity. The proposed methods were verified by the laboratory test. A reasonable hydraulic conductivity was estimated based on a comparison with a reference value obtained by the constant-head test.
- The proposed equations had many input parameters; the influence of each parameter was investigated through the error-norm technique. Among the various variables, the cementation factor exhibited a high sensitivity; thus, a careful analysis is required for determining the cementation factor.
- The proposed methods were verified through the field test. They can be reliably used to estimate the hydraulic conductivity with high resolution even under field conditions.
- This study is focused on samples with large particle size, and thus, it has an advantage of high reliability when the fine contents are small. However, it is considered that the attenuation of the TDR signal will be different when the soil characteristics are changed in the local area due to the content of fine particles. Further research is needed to reasonably improve the characteristics of the TDR probe, including the diameter of the electrode, penetrated length, and input voltage to increase resolution of the proposed equation in various soil mediums.
Author Contributions
Funding
Conflicts of Interest
References
- Fellner-Feldegg, H. Measurement of dielectrics in the time domain. J. Phys. Chem. 1969, 73, 616–623. [Google Scholar] [CrossRef]
- Hoekstra, P.; Delaney, A. Dielectric properties of soils at UHF and microwave frequencies. J. Geophys. Res. Space Phys. 1974, 79, 1699–1708. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef] [Green Version]
- Drungil, C.E.C.; Abt, K.; Gish, T.J. Soil Moisture Determination in Gravelly Soils with Time Domain Reflectometryd. Trans. ASAE 1989, 32, 177–180. [Google Scholar] [CrossRef]
- Grantz, D.A.; Perry, M.H.; Meinzer, F.C. Using time-domain reflectometry to measure soil water in Hawaiian sugarcane. Agron. J. 1990, 82, 144–146. [Google Scholar] [CrossRef]
- Reeves, T.L.; Elgezawi, S.M. Time domain reflectometry for measuring volumetric water content in processed oil shale waste. Water Resour. Res. 1992, 28, 769–776. [Google Scholar] [CrossRef]
- Caron, J.; Riviere, L.M.; Charpentier, S.; Renault, P.; Michel, J.C. Using TDR to estimate hydraulic conductivity and air entry in growing media and sand. Soil Sci. Soc. Am. J. 2002, 66, 373–383. [Google Scholar] [CrossRef]
- Al-Jabri, S.A.; Lee, J.; Gaur, A.; Horton, R.; Jaynes, D.B. A dripper-TDR method for in situ determination of hydraulic conductivity and chemical transport properties of surface soils. Adv. Water Resour. 2006, 29, 239–249. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Janssen, M.; Lennartz, B. Changes in flow and transport patterns in fen peat following soil degradation. Eur. J. Soil Sci. 2016, 67, 763–772. [Google Scholar] [CrossRef]
- Wyseure, G.C.L.; Mojid, M.A.; Malik, M.A. Measurement of volumetric water content by TDR in saline soils. Eur. J. Soil Sci. 1997, 48, 347–354. [Google Scholar] [CrossRef]
- White, I.; Knight, J.H.; Zegelin, S.J.; Topp, G.C. Comments on ‘Considerations on the use of time-domain reflectometry (TDR) for measuring soil water content’by WR Whalley. Eur. J. Soil Sci. 1994, 45, 503–508. [Google Scholar] [CrossRef]
- Robinson, D.A.; Bell, J.P.; Batchelor, C.H. Influence of iron minerals on the determination of soil water content using dielectric techniques. J. Hydrol. 1994, 161, 169–180. [Google Scholar] [CrossRef]
- Carrier, W.D., III. Goodbye, hazen; hello, kozeny-carman. J. Geotech. Geoenviron. Eng. 2003, 129, 1054–1056. [Google Scholar] [CrossRef]
- Choo, H.; Kim, J.; Lee, W.; Lee, C. Relationship between hydraulic conductivity and formation factor of coarse-grained soils as a function of particle size. J. Appl. Geophys. 2016, 127, 91–101. [Google Scholar] [CrossRef]
- Dalton, F.N.; Herkelrath, W.N.; Rawlins, D.S.; Rhoades, J.D. Time-domain reflectometry: Simultaneous measurement of soil water content and electrical conductivity with a single probe. Science 1984, 224, 989–990. [Google Scholar] [CrossRef]
- Nadler, A.; Dasberg, S.; Lapid, I. Time domain reflectometry measurements of water content and electrical conductivity of layered soil columns. Soil Sci. Soc. Am. J. 1991, 55, 938–943. [Google Scholar] [CrossRef]
- Muñoz-Carpena, R.; Regalado, C.M.; Ritter, A.; Alvarez-Benedi, J.; Socorro, A.R. TDR estimation of electrical conductivity and saline solute concentration in a volcanic soil. Geoderma 2005, 124, 399–413. [Google Scholar] [CrossRef]
- Byun, J.H.; Lee, J.S.; Park, K.; Yoon, H.K. Prediction of crack density in porous-cracked rocks from elastic wave velocities. J. Appl. Geophys. 2015, 115, 110–119. [Google Scholar] [CrossRef]
- Lee, J.S.; Yoon, H.K. Theoretical relationship between elastic wave velocity and electrical resistivity. J. Appl. Geophys. 2015, 116, 51–61. [Google Scholar] [CrossRef]
- Vaz, C.M.; Bassoi, L.H.; Hopmans, J.W. Contribution of water content and bulk density to field soil penetration resistance as measured by a combined cone penetrometer–TDR probe. Soil Tillage Res. 2001, 60, 35–42. [Google Scholar] [CrossRef] [Green Version]
- Hong, W.T.; Jung, Y.S.; Kang, S.; Lee, J.S. Estimation of soil-water characteristic curves in multiple-cycles using membrane and TDR system. Materials 2016, 9, 1019. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Yoon, H.K.; Cho, S.H.; Kim, Y.S.; Lee, J.S. Four electrode resistivity probe for porosity evaluation. Geotech. Test. J. 2011, 34, 668–675. [Google Scholar]
- Kim, J.H.; Yoon, H.K.; Lee, J.S. Void ratio estimation of soft soils using electrical resistivity cone probe. J. Geotech. Geoenviron. Eng. 2011, 137, 86–93. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Winsauer, W.O.; Shearin, H.M., Jr.; Masson, P.H.; Williams, M. Resistivity of brine-saturated sands in relation to pore geometry. AAPG Bull. 1952, 36, 253–277. [Google Scholar]
- Hill, H.J.; Milburn, J.D. Effect of clay and water salinity on electrochemical behavior of reservoir rocks. Trans. AIME 1956, 207, 65–72. [Google Scholar] [CrossRef]
- Wyble, D.O. Effect of applied pressure on the conductivity, porosity and permeability of sandstones. J. Pet. Technol. 1958, 10, 57–59. [Google Scholar] [CrossRef]
- Byun, Y.H.; Hong, W.T.; Yoon, H.K. Characterization of Cementation Factor of Unconsolidated Granular Materials through Time Domain Reflectometry with Variable Saturated Conditions. Materials 2019, 12, 1340. [Google Scholar] [CrossRef] [Green Version]
- Salem, H.S.; Chilingarian, G.V. The cementation factor of Archie’s equation for shaly sandstone reservoirs. J. Pet. Sci. Eng. 1999, 23, 83–93. [Google Scholar] [CrossRef]






| Glass Beads (GB) | Jumunjin Sand (JS) | Extracted Soil from Field (ES) | |
|---|---|---|---|
| Maximum void ratio (emax) | 0.68 | 0.89 | 0.82 |
| Minimum void ratio (emin) | 0.63 | 0.81 | 0.59 |
| Specific gravity | 2.62 | 2.61 | 2.67 |
| Median particle size (D50) | 0.51 (mm) | 0.76 (mm) | 0.95 (mm) |
| Coefficient of uniformity (Cu) | 1.50 | 1.49 | 6.50 |
| Coefficient of curvature (Cc) | 1.09 | 1.01 | 1.16 |
| Theoretically Derived Equation (11) | Theoretically Derived Equation (12) | ||
|---|---|---|---|
| γ (kN/m3) | 9.798 | γ (kN/m3) | 9.798 |
| μ (mPa⋅s) | 1.002 | μ (mPa⋅s) | 1.002 |
| CK-C | 5 | CK-C | 5 |
| S0 (mm) | 2000 | S0 (mm) | 2000 |
| L (m) | 10 | ZC (Ω) | 50 |
| σ (S/m) | 0.002923 | Z0 (Ω) | 50 |
| α | 1 | RW (Ω⋅m) | 0.003356 |
| β | 1.3 | KC | 0.04313 |
| ε | 17.4295 | α | 1 |
| VT (mV) | 210 | β | 1.3 |
| VR (mV) | 15 | V0 (mV) | 248 |
| - | - | VF (mV) | 204 |
| Theoretically Derived Equation (11) | Theoretically Derived Equation (12) | |||||||
|---|---|---|---|---|---|---|---|---|
| Input Value > Reference Value | Input Value < Reference Value | Input Value > Reference Value | Input Value < Reference Value | |||||
High Sensitivity  Low | σel (S/m) | M | VT (mV) | M | S0 (mm) | M | S0 (mm) | M |
| VR (mV) | M | α | C | β | A | β | A | |
| β | A | L (m) | M | KC | M | KC | M | |
| CK-C | A | γ (kN/m3) | M | CK-C | A | CK-C | A | |
| μ (mPa⋅s) | M | σel(S/m) | M | μ (mPa⋅s) | M | μ (mPa⋅s) | M | |
| εpm | M | CK-C | A | ZC (Ω) | C | ZC (Ω) | C | |
| S0 (mm) | M | μ (mPa⋅s) | M | α | C | α | C | |
| VT (mV) | M | VR (mV) | M | RW (Ω⋅m) | M | RW (Ω⋅m) | M | |
| L (m) | M | Β | A | Z0 (Ω) | M | Z0 (Ω) | M | |
| γ (kN/m3) | M | εpm | M | γ (kN/m3) | M | γ (kN/m3) | M | |
| α | C | S0 (mm) | M | V0 (mV) | M | V0 (mV) | M | |
| VF (mV) | M | VF (mV) | M | |||||
| Sikjang Mountain (SM) | Jangnyeong Mountain (JM) | Sutonggol (SG) | |
|---|---|---|---|
| Maximum void ratio (emax) | 0.93 | 0.89 | 0.82 |
| Minimum void ratio (emin) | 0.75 | 0.71 | 0.73 |
| Specific gravity | 2.63 | 2.65 | 2.65 |
| Median particle size (D50) | 8.20 (mm) | 4.20 (mm) | 8.50 (mm) |
| Coefficient of uniformity (Cu) | 6.70 | 9.10 | 6.50 |
| Coefficient of curvature (Cc) | 1.40 | 2.20 | 1.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Yoon, H.-K. Hydraulic Conductivity of Saturated Soil Medium through Time-Domain Reflectometry. Sensors 2020, 20, 7001. https://doi.org/10.3390/s20237001
Lee S, Yoon H-K. Hydraulic Conductivity of Saturated Soil Medium through Time-Domain Reflectometry. Sensors. 2020; 20(23):7001. https://doi.org/10.3390/s20237001
Chicago/Turabian StyleLee, Seungjae, and Hyung-Koo Yoon. 2020. "Hydraulic Conductivity of Saturated Soil Medium through Time-Domain Reflectometry" Sensors 20, no. 23: 7001. https://doi.org/10.3390/s20237001
APA StyleLee, S., & Yoon, H.-K. (2020). Hydraulic Conductivity of Saturated Soil Medium through Time-Domain Reflectometry. Sensors, 20(23), 7001. https://doi.org/10.3390/s20237001





