Dominant Loss Mechanisms of Whispering Gallery Mode RF-MEMS Resonators with Wide Frequency Coverage
Abstract
1. Introduction
2. Design and Fabrication
3. Theoretical Analysis
3.1. Anchor Loss
3.2. Squeezed-Film Damping
3.3. Thermal Elastic Damping
3.4. Phonon-Phonon Interaction Damping
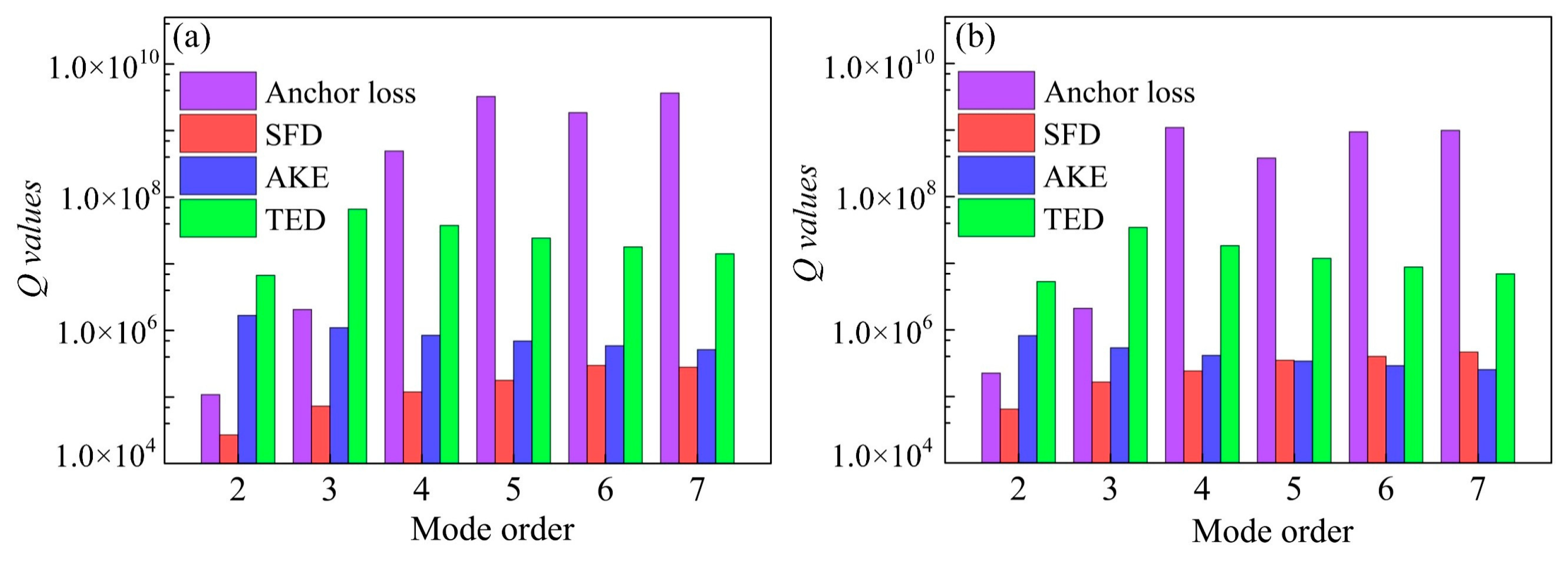
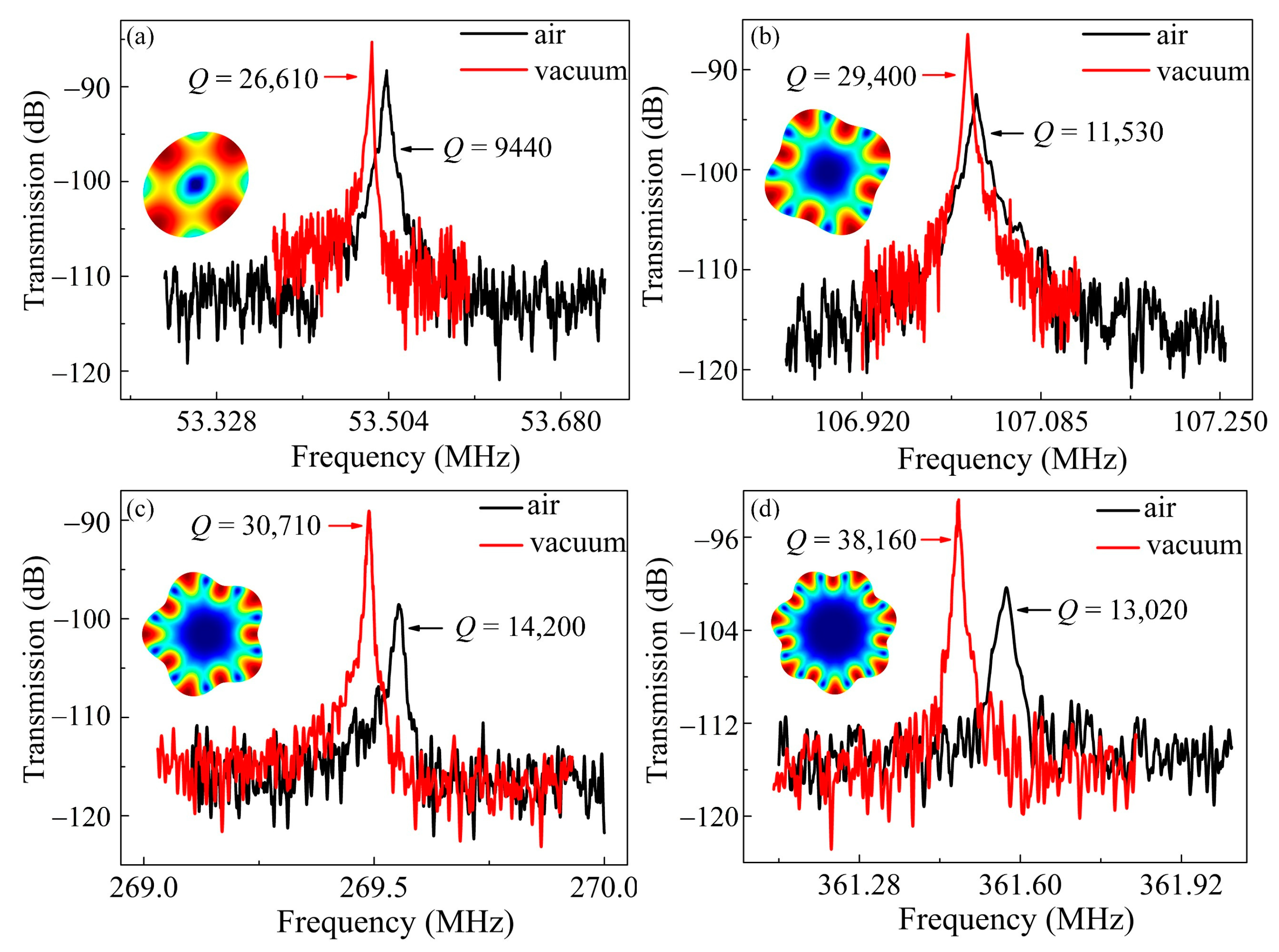
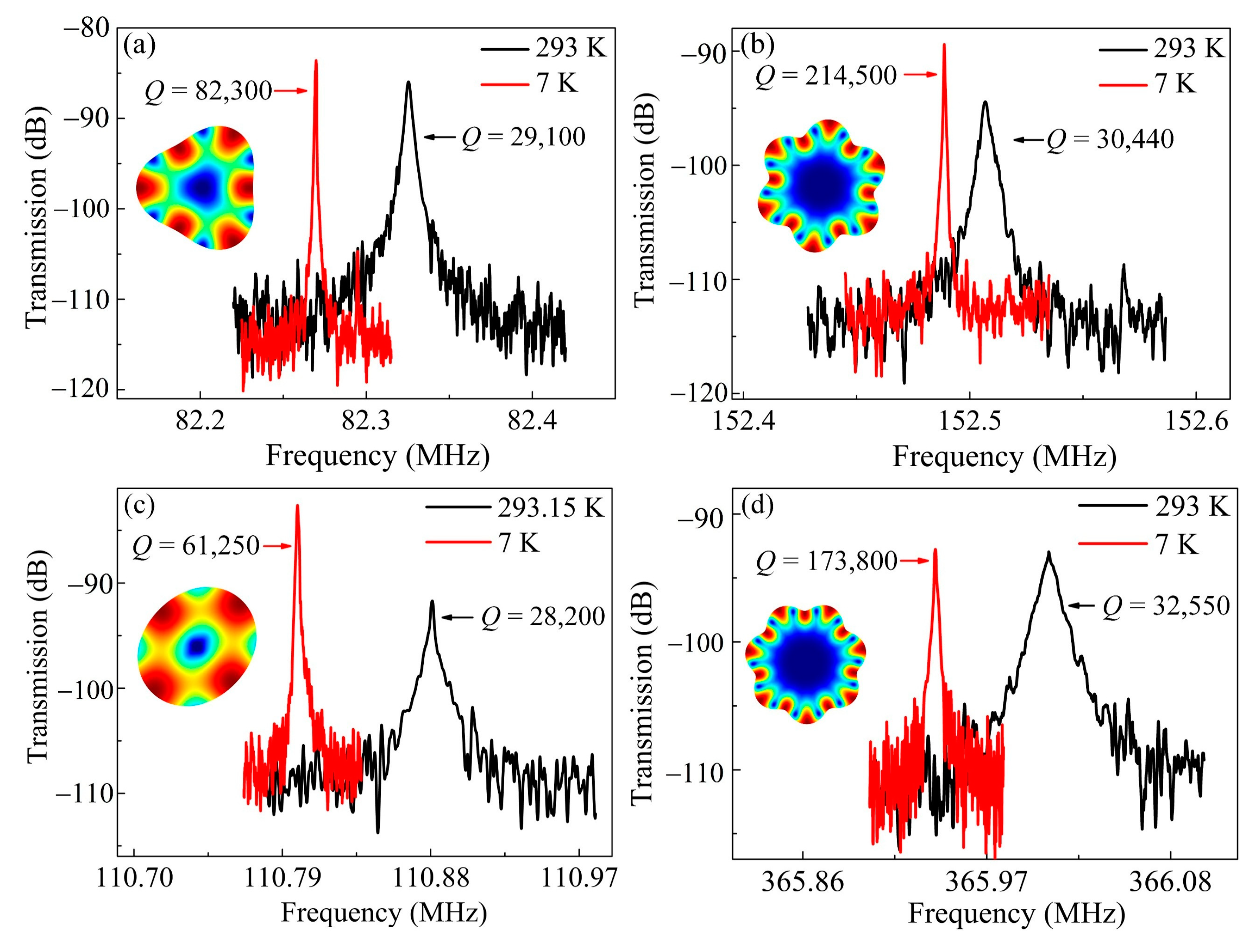
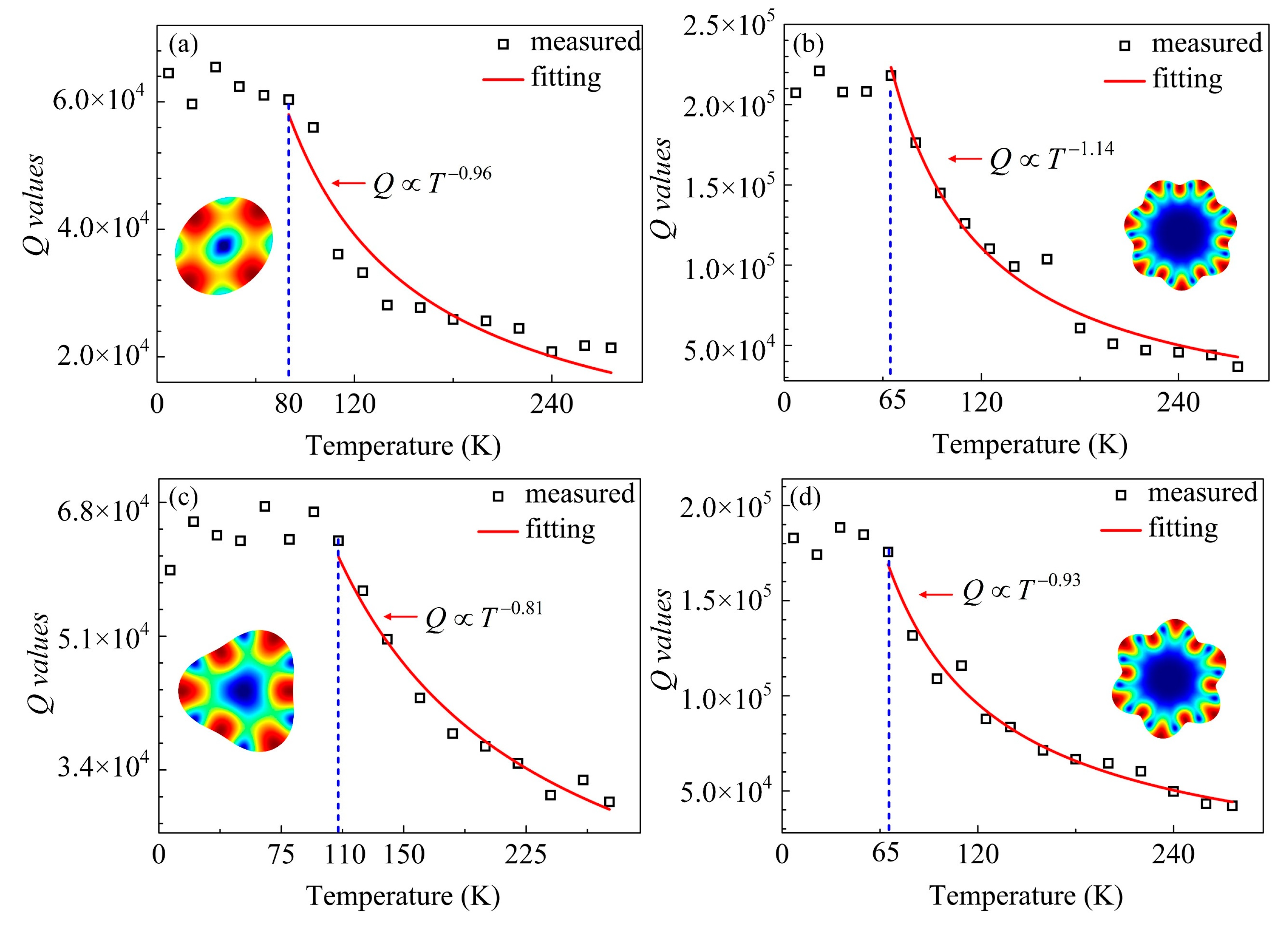
4. Results and Discussions
4.1. Resonator Performance in Air
4.2. Resonator Performance in Vacuum
4.3. Resonator Performance at Cryogenic Temperatures
4.4. Comparison between Theoretical and Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Platz, D.; Schmid, U. Vibrational modes in MEMS resonators. J. Micromech. Microeng. 2019, 29, 123001. [Google Scholar] [CrossRef]
- Uranga, A.; Verd, J.; Barniol, N. CMOS–MEMS resonators: From devices to applications. Microelectron. Eng. 2015, 132, 58–73. [Google Scholar] [CrossRef]
- Wu, G.; Xu, J.; Ng, E.J.; Chen, W. MEMS Resonators for Frequency Reference and Timing Applications. J. Microelectromech. Syst. 2020. [Google Scholar] [CrossRef]
- Nguyen, C.T.-C. MEMS-based RF channel selection for true software-defined cognitive radio and low-power sensor communications. IEEE Commun. Mag. 2013, 51, 110–119. [Google Scholar] [CrossRef]
- Nguyen, C.T.-C. MEMS technology for timing and frequency control. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 251–270. [Google Scholar] [CrossRef]
- Abdolvand, R.; Bahreyni, B.; Lee, J.; Nabki, F. Micromachined resonators: A review. Micromachines 2016, 7, 160. [Google Scholar] [CrossRef]
- Daruwalla, A.; Wen, H.; Liu, C.-S.; Ayazi, F. Low motional impedance distributed lamé mode resonators for high frequency timing applications. Microsyst. Nanoeng. 2020, 6, 1–11. [Google Scholar] [CrossRef]
- Sobreviela, G.; Zou, X.; Zhao, C.; Pandit, M.; Seshia, A.A. An ultra-high-quality factor silicon disk resonator. In Proceedings of the 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 527–530. [Google Scholar] [CrossRef]
- Xereas, G.; Chodavarapu, V.P. Wafer-Level Vacuum-Encapsulated Lamé Mode Resonator with fQ Product of 2.23 × 10 (13) Hz. IEEE Electron Device Lett. 2015, 36, 1079–1081. [Google Scholar] [CrossRef]
- Pourkamali, S.; Ho, G.K.; Ayazi, F. Low-impedance VHF and UHF capacitive silicon bulk acoustic-wave resonators—Part II: Measurement and characterization. IEEE Trans. Electron Devices 2007, 54, 2024–2030. [Google Scholar] [CrossRef]
- Pei, B.; Sun, K.; Yang, H.; Ye, C.; Zhong, P.; Yu, T.; Li, X. Oven-Controlled MEMS Oscillator with Integrated Micro-Evaporation Trimming. Sensors 2020, 20, 2373. [Google Scholar] [CrossRef] [PubMed]
- Kwon, H.-K.; Ortiz, L.C.; Vukasin, G.D.; Chen, Y.; Shin, D.D.; Kenny, T.W. An Oven-Controlled MEMS Oscillator (OCMO) With Sub 10 mw, ±1.5 PPB Stability over Temperature. In Proceedings of the 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 2072–2075. [Google Scholar] [CrossRef]
- Mussi, G.; Carrara, M.; Langfelder, G.; Gattere, G. Polysilicon MEMS Resonator for 28-MHz Oscillators. In Proceedings of the 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum (EFTF/IFC), Orlando, FL, USA, 14–18 April 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Akgul, M.; Ozgurluk, A.; Nguyen, C.T.-C. RF Channel-Select Micromechanical Disk Filters—Part II. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 218–235. [Google Scholar] [CrossRef] [PubMed]
- Ozgurluk, A.; Akgul, M.; Nguyen, C.T.-C. RF Channel-Select Micromechanical Disk Filters—Part I: Design. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 192–217. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ren, Z.; Nguyen, C.-C. 1.156-GHz self-aligned vibrating micromechanical disk resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 1607–1628. [Google Scholar] [CrossRef] [PubMed]
- Tu, C.; Lee, J.E.-Y.; Zhang, X.-S. Dissipation Analysis Methods and Q-Enhancement Strategies in Piezoelectric MEMS Laterally Vibrating Resonators: A Review. Sensors 2020, 20, 4978. [Google Scholar] [CrossRef]
- Rasouli, M.; HajHashemi, M.; Bahreyni, B. Higher-order Lame mode square microresonator with improved quality factor and fQ product. In Proceedings of the 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 498–501. [Google Scholar] [CrossRef]
- Ho, G.K.; Abdolvand, R.; Ayazi, F. High-order composite bulk acoustic resonators. In Proceedings of the 2007 IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Hyogo, Japan, 21–25 January 2007; pp. 791–794. [Google Scholar] [CrossRef]
- Hao, Z.; Pourkamali, S.; Ayazi, F. VHF single-crystal silicon elliptic bulk-mode capacitive disk resonators-part I: Design and modeling. J. Microelectromech. Syst. 2004, 13, 1043–1053. [Google Scholar] [CrossRef]
- Kan, X.; Chen, Z.; Yuan, Q.; Wang, F.; Yang, J.; Yang, F. A Novel Multiple-Frequency RF-MEMS Resonator Based on the Whispering Gallery Modes. IEEE Trans. Electron Devices 2019, 66, 3683–3685. [Google Scholar] [CrossRef]
- Chen, Z.; Kan, X.; Yuan, Q.; Wang, T.; Yang, J.; Yang, F. A Switchable High-Performance RF-MEMS Resonator with Flexible Frequency Generations. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef]
- Rocheleau, T.O.; Naing, T.L.; Ren, Z.; Nguyen, T.C. Acoustic whispering gallery mode resonator with Q > 109,000 at 515 MHz. In Proceedings of the 2012 IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Paris, France, 29 January–2 February 2012; pp. 672–675. [Google Scholar] [CrossRef]
- Tallur, S.; Bhave, S.A. Comparison of fQ scaling in wineglass and radial modes in ring resonators. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 777–780. [Google Scholar] [CrossRef]
- Chandorkar, S.; Agarwal, M.; Melamud, R.; Candler, R.; Goodson, K.; Kenny, T. Limits of quality factor in bulk-mode micromechanical resonators. In Proceedings of the 2008 IEEE 21st international conference on micro electro mechanical systems (MEMS), Wuhan, China, 13–17 January 2008; pp. 74–77. [Google Scholar] [CrossRef]
- Li, W.-C.; Lin, Y.; Kim, B.; Ren, Z.; Nguyen, C.T.-C. Quality factor enhancement in micromechanical resonators at cryogenic temperatures. In Proceedings of the 2009 International Solid-State Sensors, Actuators and Microsystems Conference (TRANSDUCERS 2009), Denver, CO, USA, 21–25 June 2009; pp. 1445–1448. [Google Scholar] [CrossRef]
- Onoe, M. Contour vibrations of isotropic circular plates. J. Acous. Soc. Am. 1956, 28, 1158–1162. [Google Scholar] [CrossRef]
- Yuan, Q.; Luo, W.; Zhao, H.; Peng, B.; Yang, J.; Yang, F. Frequency stability of RF-MEMS disk resonators. IEEE Trans. Electron Devices 2015, 62, 1603–1608. [Google Scholar] [CrossRef]
- Segovia-Fernandez, J.; Cremonesi, M.; Cassella, C.; Frangi, A.; Piazza, G. Anchor losses in AlN contour mode resonators. J. Microelectromech. Syst. 2014, 24, 265–275. [Google Scholar] [CrossRef]
- Binder, D.; Quevy, E.; Koyama, T.; Govindjee, S.; Demmel, J.W.; Howe, R.T. Anchor loss simulation in resonators. In Proceedings of the 2005 IEEE 18th International Conference on Micro Electro Mechanical Systems (MEMS), Miami Beach, Fl, USA, 30 January–3 February 2005; pp. 133–136. [Google Scholar] [CrossRef]
- Bindel, D.S.; Govindjee, S. Elastic PMLs for resonator anchor loss simulation. Int. J. Numer. Methods Eng. 2005, 64, 789–818. [Google Scholar] [CrossRef]
- Akgul, M.; Wu, L.; Ren, Z.; Nguyen, C.T.-C. A negative-capacitance equivalent circuit model for parallel-plate capacitive-gap-transduced micromechanical resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 849–869. [Google Scholar] [CrossRef] [PubMed]
- Bao, M.; Yang, H. Squeeze film air damping in MEMS. Sens. Actuator A Phys. 2007, 136, 3–27. [Google Scholar] [CrossRef]
- Veijola, T.; Kuisma, H.; Lahdenperä, J.; Ryhänen, T. Equivalent-circuit model of the squeezed gas film in a silicon accelerometer. Sens. Actuator A Phys. 1995, 48, 239–248. [Google Scholar] [CrossRef]
- Lifshitz, R.; Roukes, M.L. Thermoelastic damping in micro-and nanomechanical systems. Phys. Rev. B 2000, 61, 5600. [Google Scholar] [CrossRef]
- Antkowiak, B.; Gorman, J.; Varghese, M.; Carter, D.; Duwel, A. Design of a high-Q, low-impedance, GHz-range piezoelectric MEMS resonator. In Proceedings of the 12th International Conference on Solid-State Sensors, Actuators and Microsystems. Digest of Technical Papers, Cat. No. 03TH8664 (TRANSDUCERS 2003), Boston, MA, USA, 8–12 June 2003; pp. 841–846. [Google Scholar] [CrossRef]
- Duwel, A.; Candler, R.N.; Kenny, T.W.; Varghese, M. Engineering MEMS resonators with low thermoelastic damping. J. Microelectromech. Syst. 2006, 15, 1437–1445. [Google Scholar] [CrossRef]
- Tabrizian, R.; Rais-Zadeh, M.; Ayazi, F. Effect of phonon interactions on limiting the fQ product of micromechanical resonators. In Proceedings of the 2009 International Solid-State Sensors, Actuators and Microsystems Conference (TRANSDUCERS 2009), Denver, CO, USA, 21–25 June 2009; pp. 2131–2134. [Google Scholar] [CrossRef]
- Middelmann, T.; Walkov, A.; Bartl, G.; Schödel, R. Thermal expansion coefficient of single-crystal silicon from 7 K to 293 K. J. Phys. Rev. B 2015, 92, 174113. [Google Scholar] [CrossRef]
- Rodriguez, J.; Chandorkar, S.A.; Watson, C.A.; Glaze, G.M.; Ahn, C.; Ng, E.J.; Yang, Y.; Kenny, T.W. Direct Detection of Akhiezer Damping in a Silicon MEMS Resonator. Sci. Rep. 2019, 9, 2244. [Google Scholar] [CrossRef]
- Braginsky, V.B.; Mitrofanov, V.; Panov, V.I. Systems with Small Dissipation; University of Chicago Press: Chicago, IL, USA, 1985. [Google Scholar]
- Kahn, H.; Ballarini, R.; Heuer, A. Thermal expansion of low-pressure chemical vapor deposition polysilicon films. J. Mater. Res. 2002, 17, 1855–1862. [Google Scholar] [CrossRef]
- Iyer, S.S.; Candler, R.N. Mode-and direction-dependent mechanical energy dissipation in single-crystal resonators due to anharmonic phonon-phonon scattering. Phys. Rev. Appl. 2016, 5, 034002. [Google Scholar] [CrossRef]
- Duwel, A.; Lozow, J.; Fisher, C.J.; Phillips, T.; Olsson, R.H.; Weinberg, M. Thermal energy loss mechanisms in micro-to nano-scale devices. In Micro-and Nanotechnology Sensors, Systems, and Applications III; International Society for Optics and Photonics: Orlando, FL, USA, 2011; Volume 8031, p. 80311C. [Google Scholar] [CrossRef]
- McConnell, A.D.; Uma, S.; Goodson, K.E. Thermal conductivity of doped polysilicon layers. J. Microelectromech. Syst. 2001, 10, 360–369. [Google Scholar] [CrossRef]
- Hao, Z.; Ayazi, F. Support loss in the radial bulk-mode vibrations of center-supported micromechanical disk resonators. Sens. Actuator A Phys. 2007, 134, 582–593. [Google Scholar] [CrossRef]
- Yap, L.-Y.; Yap, L.-K.; Ye, W. Air damping in an ultra-high-frequency disk resonator. In Proceedings of the 2003 Nanotechnology Conference and Trade Show-Nanotech 2003, San Francisco, CA, USA, 23–27 February 2003; pp. 316–319. [Google Scholar]
- Lunev, A.; Nikitin, A.; Kaizer, Y.; Lysyannikov, A.; Sokolov, D.; Obvintseva, V. Comparative Analysis of the Dependence of the Bulk Elastic Modulus of the Liquid on Pressure and Gas Factor. J. Phys. Conf. Ser. 2019, 1399, 055083. [Google Scholar] [CrossRef]
- Ng, E.J.; Hong, V.A.; Yang, Y.; Ahn, C.H.; Everhart, C.L.; Kenny, T.W. Temperature dependence of the elastic constants of doped silicon. J. Microelectromech. Syst. 2014, 24, 730–741. [Google Scholar] [CrossRef]
- Liu, X.; Vignola, J.; Simpson, H.; Lemon, B.; Houston, B.; Photiadis, D. A loss mechanism study of a very high Q silicon micromechanical oscillator. J. Appl. Phys. 2005, 97, 023524. [Google Scholar] [CrossRef]
- Van Toan, N.; Ono, T. Progress in performance enhancement methods for capacitive silicon resonators. Jpn. J. Appl. Phys. 2017, 56, 110101. [Google Scholar] [CrossRef]
- Wu, L.; Akgul, M.; Ren, Z.; Lin, Y.; Li, W.-C.; Nguyen, C.T.-C. Hollow stems for higher micromechanical disk resonator quality factor. In Proceedings of the 2011 IEEE International Ultrasonics Symposium, Orlando, FL, USA, 18–21 October 2011; pp. 1964–1967. [Google Scholar] [CrossRef]
- Wang, J.; Butler, J.E.; Feygelson, T.; Nguyen, C.-C. 1.51-GHz nanocrystalline diamond micromechanical disk resonator with material-mismatched isolating support. In Proceedings of the 2004 IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Maastricht, The Netherlands, 25–29 January 2004; pp. 641–644. [Google Scholar] [CrossRef]
- Van Toan, N.; Kubota, T.; Sekhar, H.; Samukawa, S.; Ono, T. Mechanical quality factor enhancement in a silicon micromechanical resonator by low-damage process using neutral beam etching technology. J. Micromech. Microeng. 2014, 24, 085005. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| E | 160 GPa | μ | 65.57 GPa |
| ρ | 2320 kg/m3 | α | 2.6 ppm/K |
| σ | 0.22 | va | 8305 m/s |
| Cv | 1.65 × 106 J/(m3·K) | VD | 5717 m/s |
| κ | 34 W/(m·K) | τph | 1.89 ps |
| λ | 51.52 GPa | γeff | 0.51 |
| Mode Order | 37 μm | 18 μm | ||||
|---|---|---|---|---|---|---|
| Freq. (MHz) | Q | Freq. (MHz) | Q | |||
| Cal. | Meas. | Cal. | Meas. | |||
| 2 | 53.60 | 53.50 | 9440 | 110.17 | 110.11 | 10,080 |
| 3 | 82.11 | 82.70 | 10,400 | 168.77 | 170.46 | 11,550 |
| 4 | 106.71 | 107.02 | 11,530 | 219.35 | 221.70 | 13,060 |
| 5 | 129.74 | 130.58 | 13,890 | 266.70 | 269.55 | 14,540 |
| 6 | 152.03 | 152.51 | 10,200 | 312.51 | 315.95 | 11,640 |
| 7 | 173.90 | 175.11 | 12,450 | 357.50 | 361.57 | 12,800 |
| 37 μm-Radius Resonator | 18 μm-Radius Resonator | |||||||
|---|---|---|---|---|---|---|---|---|
| Cal. | Meas. | Cal. | Meas. | Cal. | Meas. | Cal. | Meas. | |
| 2 | 4.75 | 2.84 | 1.07 | 2.53 | 3.65 | 2.45 | 1.25 | 2.16 |
| 3 | 10.76 | 2.73 | 2.39 | 2.48 | 3.57 | 3.50 | 3.82 | 2.33 |
| 4 | 7.93 | 2.93 | 36.23 | 3.51 | 2.68 | 2.74 | 38.51 | 3.50 |
| 5 | 4.79 | 2.37 | 39.13 | 3.94 | 1.95 | 2.34 | 37.91 | 4.12 |
| 6 | 2.92 | 2.13 | 39.17 | 7.10 | 1.70 | 2.71 | 39.17 | 5.53 |
| 7 | 2.77 | 2.50 | 39.67 | 6.22 | 1.53 | 2.56 | 39.44 | 5.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Jia, Q.; Liu, W.; Yuan, Q.; Zhu, Y.; Yang, J.; Yang, F. Dominant Loss Mechanisms of Whispering Gallery Mode RF-MEMS Resonators with Wide Frequency Coverage. Sensors 2020, 20, 7017. https://doi.org/10.3390/s20247017
Chen Z, Jia Q, Liu W, Yuan Q, Zhu Y, Yang J, Yang F. Dominant Loss Mechanisms of Whispering Gallery Mode RF-MEMS Resonators with Wide Frequency Coverage. Sensors. 2020; 20(24):7017. https://doi.org/10.3390/s20247017
Chicago/Turabian StyleChen, Zeji, Qianqian Jia, Wenli Liu, Quan Yuan, Yinfang Zhu, Jinling Yang, and Fuhua Yang. 2020. "Dominant Loss Mechanisms of Whispering Gallery Mode RF-MEMS Resonators with Wide Frequency Coverage" Sensors 20, no. 24: 7017. https://doi.org/10.3390/s20247017
APA StyleChen, Z., Jia, Q., Liu, W., Yuan, Q., Zhu, Y., Yang, J., & Yang, F. (2020). Dominant Loss Mechanisms of Whispering Gallery Mode RF-MEMS Resonators with Wide Frequency Coverage. Sensors, 20(24), 7017. https://doi.org/10.3390/s20247017





